Cumulative Hazard Ratio Estimation for Treatment Regimes in Sequentially Randomized Clinical Trials

Abstract

The proportional hazards model is widely used in survival analysis to allow adjustment for baseline covariates. The proportional hazard assumption may not be valid for treatment regimes that depend on intermediate responses to prior treatments received, and it is not clear how such a model can be adapted to clinical trials employing more than one randomization. Besides, since treatment is modified post-baseline, the hazards are unlikely to be proportional across treatment regimes. Although Lokhnygina and Helterbrand (Biometrics 63: 422–428, 2007) introduced the Cox regression method for two-stage randomization designs, their method can only be applied to test the equality of two treatment regimes that share the same maintenance therapy. Moreover, their method does not allow auxiliary variables to be included in the model nor does it account for treatment effects that are not constant over time. In this article, we propose a model that assumes proportionality across covariates within each treatment regime but not across treatment regimes. Comparisons among treatment regimes are performed by testing the log ratio of the estimated cumulative hazards. The ratio of the cumulative hazard across treatment regimes is estimated using a weighted Breslow-type statistic. A simulation study was conducted to evaluate the performance of the estimators and proposed tests.

1 Introduction

It is common practice in treatments of chronic diseases for patients to start with an initial therapy based on specific diagnoses. Patients stay on this initial therapy until a predetermined milestone, commonly referred to as response, is achieved, or physicians determine that the treatment is not providing the intended benefit, commonly referred to as non-response. In either case, further treatment could be suggested, which could be a rescue therapy if patients show primary resistance to the initial therapy, or a maintenance therapy if a response is observed. Thus, treatments applied at later stages depend on the responses to the initial therapies, and a comparison across treatments at various stages would be misleading. Instead, dynamic treatment sequences are usually formed based on stage-specific treatments and responses to these treatments during the course of therapy. In order to study the effect of a treatment sequence on the survival outcome, sequentially randomized designs are used in clinical trials. In a sequentially randomized clinical trial, eligible patients are first randomized to receive one of the initial therapies. Patients reaching the second stage will continue to participate in a second randomization to either rescue or maintenance therapies. The procedure continues. This design results in different treatment regimes consisting of an initial therapy, the intermediate response and a second-stage therapy. The analysis and comparisons of such treatment regimes can be done based on classic survival methods, weighted using inverse probabilities of treatment allocations.

The idea of inverse-probability weighting (IPW) to estimate treatment regime effect in two-stage randomization designs was first introduced by Lunceford, Davidian and Tsiatis [2]. Since then the strategy of IPW has been incorporated into many other classical statistical methods to make them applicable to two-stage randomization designs. For example, Guo and Tsiatis [3] extended the Aalen–Nelson estimator to a Weighted Risk Set Estimator (WRSE) using IPW. Hernan, Lanoy, Costagliola and Robins [4] applied IPW in comparing treatment strategies from observational studies using a Cox proportional hazards model under artificial censoring. Lokhnygina and Helterbrand [1] incorporated IPW into the Cox regression method for two-stage randomization designs. Feng and Wahed [5] presented a modified weighted log-rank test for comparing different treatment strategies using IPW. Miyahara and Wahed [6] introduced IPW to Kaplan–Meier estimators with both fixed and time-dependent weights. More recently, Goldberg and Kosorok [7] used IPW methods in Q-learning to estimate treatment effect for censored data from multistage designs. However, except for the work of Hernan et al. [4], all the aforementioned models failed to adjust for baseline covariates.

Proportional hazards models are widely used in analyzing data from clinical trials with time-to-event endpoints. The advantage of the proportional hazards model over nonparametric methods (e.g. a log-rank test) is that auxiliary covariates can be included in the model to explain the variability of the dependent variable further. Even in randomized clinical trials, baseline characteristics are often imbalanced between treatment groups and hence adjustment becomes a consideration. This imbalance is even more problematic for two stages of randomization, since patients proceeding to the second stage are randomized differently based on their intermediate responses. Lokhnygina and Helterbrand [1] proposed to use a Cox regression method to test the equality of two treatment regimes that share the same maintenance therapy in a two-stage randomization setting. However, their method does not allow auxiliary variables to be included in the model nor does it account for treatment effects that are not constant over time, an issue in many medical studies. Therefore, comparisons among treatment regimes in the presence of non-proportional hazards is of importance to health research communities. Wei and Schaubel [8] proposed cumulative treatment effect estimation based on treatment-specific cumulative baseline hazards using a stratified proportional hazards model. Their model assumed proportional hazards with respect to baseline covariates within each treatment group and non-proportional hazards across treatment groups. In this article, we take a similar approach to estimate the cumulative treatment effect for treatment regimes from sequentially randomized clinical trials. Comparisons among treatment regimes are performed by testing the ratio of the estimated cumulative hazards. A simulation study is conducted to evaluate the performance of the estimators and proposed tests. The estimators and proposed tests are also applied to the neuroblastoma data to compare different treatment regimes in a neuroblastoma study with respect to the overall survival.

2 Design Setting and Statistical Model

2.1 Notation

We consider a two-stage randomization design, in which n eligible patients are first randomized to one of the J initial therapies (A₁, … , A_J) and patients achieving a clinical response are then randomized to one of the K second-stage therapies (B₁, … , B_K). By design, non-responders in the first stage are not eligible to receive any treatment in the second stage, similarly to the neuroblastoma study (Sect. 5) that motivated this work. Thus, there are a total of J × K treatment regimes based on this design, namely, A₁B₁, … , A_JB_K. The treatment regime A_jB_k , j = 1, … , J ; k = 1, … , K, is defined as “treat with A_j as initial therapy, then B_k as second-stage therapy if responds to A_j” [2]. This treatment regime consists of an initial treatment (A_j), the intermediate response status, and a second-stage treatment (B_k) in the event the patient responds to the initial treatment. Thus, estimation of the effect of treatment regime A_jB_k will not only include patients who were randomized to receive initial therapy A_j, responded, and then randomized to B_k as second-stage therapy, but also patients who were randomized to A_j and did not respond.

Let X_ji be the indicator for initial therapy A_j such that X_ji = 1 if the ith patient receives initial treatment $A_j({\sum }_{j=1}^J{X}_{\mathit{ji}}=1)$. The response status is denoted by R_i, with R_i = 1 for responders and _Ri = 0 for non-responders. For responders (_Ri = 1), let Z_ki be the indicator for second-stage therapy B_k, i.e., Z_ki = 1 if the ith patient responds and receives second-stage treatment $B_k(R_i{\sum }_{k=1}^K{Z}_{\mathit{ki}}=R_i)$. Let T_i and C_i be the survival and censoring times from the time of first randomization for the ith patient, respectively. We assume that the survival time is independently right censored. Then the observed time and event indicator would be defined as U_i = min(T_i,_Ci) and Δ_i = I (T_i ≤ C_i). If we define V_i as the vector of baseline covariates, the observed data for the ith individual can be described as the set of random vectors {X_ji, R_i, R_iZ_ki, U_i, Δ_i, V_i, j = 1, … , J ; k = 1, … , K}, i = 1, 2, … , n. Note that in this consideration we assume that R_i is always observed, which may not be true for patients who are censored or died prior to response evaluation. Customarily such patients are treated as non-responders and R_i is set to zero for them [2]. Whenever there is no ambiguity, we will drop the subscript i to represent a generic observation from the population.

2.2 Model

Our proposed model assumes proportional hazards within each treatment regime with respect to the baseline covariates V_i. However, the hazard functions for J × K treatment regimes are left unspecified, and could be proportional or non-proportional across regimes. In other words, a stratified proportional hazards model is used to account for the non-proportionality across treatment regimes. More specifically, let us denote the hazard and the cumulative hazard functions for treatment regime A_jB_k as λ_jk (t) and ${\Lambda }_{\mathit{jk}}\left(t\right)={\int }_0^t{\lambda }_{\mathit{jk}}\left(s\right)\mathit{ds}$, respectively. Based on stratified proportional hazards with treatment regimes as strata, the hazard function for treatment regime A_jB_k, j = 1, … , J and k = 1, … , K, could be written as

$${\lambda }_{\mathit{jk}}\left(t\right)={\lambda }_{\mathit{jk}0}\left(t\right)\exp \left\{{\beta }^{T}V\right\},j=1,\dots ,J\text{and}k=1,\dots ,K,$$ (1)

where λ_jk0(t) is the baseline hazard function for treatment regime A_jB_k, and β is a vector of coefficients corresponding to baseline covariates V. Note that in model (1), the parameter vector β is assumed to be constant across regimes, which implies that no interaction between treatment regimes and baseline covariates is assumed. For a general treatment regime, please see Sect. 2.1. Moreover, no functional form is specified for the regime-specific baseline hazard functions. For example, under a two-stage randomization design with J = K = 2, the hazard functions for treatment regimes A₁B₁, A₁B₂, A₂B₁ and A₂B₂ can be written as

$${\lambda }_{11}\left(t\right)={\lambda }_{110}\left(t\right)\exp \left\{{\beta }^{T}V\right\},$$

and similarly, λ₁₂(t) = λ₁₂₀(t) exp{β^T V}, λ₂₁(t) = λ210(t) exp{β^T V}, and λ₂₂(t) = λ₂₂₀(t) exp{β^T V}, respectively. Thus, irrespective of the treatment regimes, the effect of baseline covariate V on the hazard can be quantified by the log hazard ratio parameter β. The forms of the baseline hazard functions λ₁₁₀(t), λ₁₂₀(t), λ₂₁₀(t), and λ₂₂₀(t) are left unspecified, and could be non-proportional. However, we assume proportionality within each regime with respect to the baseline covariates, and the effects of the baseline covariates do not vary across regimes.

3 Inference

Our objective is to draw inference about treatment regimes A_jB_k, j = 1, … , J ; k = 1, … , K. Note that the focus of the inference in model (1) is not the parameter vector β, rather it is to compare the hazards across treatment regimes. Based on the analytical framework of IPW (see for details in [9]) we define the weight function for treatment regime A_jB_k, j = 1, … , J and k = 1, … , K, as

$$W_{\mathit{jki}}=X_{\mathit{ji}}\left\{(1-R_i)+R_i{Z}_{\mathit{ki}}∕{\pi }_{\mathit{jk}}\right\}∕{\pi }_j,$$

where π_j = P(X_ji = 1), and π_jk = P(Z_ki = 1∣X_ji = 1, R_i = 1). Thus, both responders (R_i = 1) to A_j and non-responders (R_i = 0) to A_j are weighted with the inverse of the probability of randomization when evaluating the effect of the treatment regime A_jB_K. The probabilities of being assigned to B_k, k = 1, … , K, could be different for initial treatments A_j, j = 1, … , J. For example, in some two-stage randomization studies, if the patients receive one initial treatment, particular choices in the second stage might be more toxic than others, and hence these patients are randomized with less probability into such choices. Based on the counting process notation described in Fleming and Harrington [10], the event and risk indicators for the ith patient are defined as N_i (t) = Δ_iI (U_i ≤ t), and Y_i (t) = I (U_i ≥ t), respectively. We define the weighted event and risk indicators for treatment regime A_jBk as N_jki = W_jkiΔ_iI (U_i ≤ t) and Y_jki(t) = W_jkiI (U_i ≥ t).

The partial likelihood estimate of β can be obtained by solving the pseudo-score equation [1]:

$$U\left(\beta \right)=\sum _{i=1}^n\sum _{j=1}^J\sum _{k=1}^K{\int }_0^L\left\{V_i-{\overline{V}}_{\mathit{jk}}(t,\beta )\right\}{\mathit{dN}}_{\mathit{jki}}\left(t\right)=0,$$

where

$${\overline{V}}_{\mathit{jk}}(t,\beta )=\frac{\sum _{p=1}^n{V}_p{Y}_{\mathit{jkp}}\left(t\right)\exp \left\{{\beta }^T{V}_p\right\}}{\sum _{p=1}^n{Y}_{\mathit{jkp}}\left(t\right)\exp \left\{{\beta }^T{V}_p\right\}}.$$

Note that in defining U(·), we have utilized the weighted event and risk processes. The estimated vector of coefficients is denoted by $\widehat{\beta }$. Then the Breslow estimator [12] of the cumulative baseline hazard for treatment regime A_jB_k can be obtained as

$${\widehat{\Lambda }}_{\mathit{jk}0}(t,\widehat{\beta })=\sum _{i=1}^n{\int }_0^t\frac{{\mathit{dN}}_{\mathit{jki}}\left(s\right)}{\sum _{p=1}^n{Y}_{\mathit{jkp}}\left(s\right)\exp \left\{{\widehat{\beta }}^T{V}_p\right\}}.$$

A comparison of different treatment regimes can then be carried out in terms of the ratio of the cumulative baseline hazards. The ratio of the cumulative baseline hazards for comparing treatment regimes A_jB_k and A_jB_k is defined as

$${\theta }_{{\mathit{jkj}}^{\prime }{k}^{\prime }}\left(t\right)=\frac{{\Lambda }_{\mathit{jk}0}\left(t\right)}{{\Lambda }_{j^{\prime }{k}^{\prime }0}\left(t\right)}.$$ (2)

This ratio of the cumulative baseline hazards equals the ratio of the cumulative hazards given the same values for covariates, because

$${\theta }_{{\mathit{jkj}}^{\prime }{k}^{\prime }}\left(t\right)=\frac{{\Lambda }_{\mathit{jk}0}\left(t\right)}{{\Lambda }_{j^{\prime }{k}^{\prime }0}\left(t\right)}=\frac{{\Lambda }_{\mathit{jk}0}\left(t\right)\exp \left\{{\beta }^T{V}_i\right\}}{{\Lambda }_{j^{\prime }{k}^{\prime }0}\left(t\right)\exp \left\{{\beta }^T{V}_i\right\}}=\frac{{\Lambda }_{\mathit{jk}}\left(t\right)}{{\Lambda }_{j^{\prime }{k}^{\prime }}\left(t\right)}.$$

The ratio of the cumulative baseline hazards can be estimated by replacing the estimated cumulative baseline hazards in (2). Let us denote the corresponding estimator by ${\widehat{\theta }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }}\left(t\right)$. For unweighted group comparisons, Wei and Schaubel [8] showed that such a ratio converges asymptotically to a Gaussian process. A similar argument outlined in Appendix A can be used to show that ${\widehat{\theta }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }}\left(t\right)$ follows a Gaussian process with mean θjkj’k’(t) and variance function ${\sigma }_{{\mathit{jkj}}^{\prime }{k}^{\prime }}^2\left(t\right)$, where

$$\begin{array}{cc}\hfill {\sigma }_{{\mathit{jkj}}^{\prime }{k}^{\prime }}^2\left(t\right)& =E\left\{{\xi }_{{\mathit{jkj}}^{\prime }{k}^{\prime }i}^2(t,\beta )\right\},\hfill \\ \hfill {\xi }_{{\mathit{jkj}}^{\prime }{k}^{\prime }i}(t,\beta )& =\frac{{\Phi }_{\mathit{jki}}(t,\beta )}{{\Lambda }_{j^{\prime }{k}^{\prime }0}\left(t\right)}-\frac{{\Lambda }_{\mathit{jk}0}\left(t\right){\Phi }_{j^{\prime }{k}^{\prime }i}(t,\beta )}{{\Lambda }_{j^{\prime }{k}^{\prime }0}^2\left(t\right)},\hfill \\ \hfill {\Phi }_{\mathit{jki}}(t,\beta )& =h_{\mathit{jk}}^T(t,\beta ){\Omega }^{-1}\left(\beta \right){\Psi }_i\left(\beta \right)+{\int }_0^t{y}_{\mathit{jk}}^{\left(0\right)}{(s,\beta )}^{-1}{\mathit{dM}}_{\mathit{jki}}(s,\beta ),\hfill \\ \hfill h_{\mathit{jk}}(t,\beta )& =-{\int }_0^t{\overline{v}}_{\mathit{jk}}(s,\beta )d{\Lambda }_{\mathit{jk}0}\left(s\right),\hfill \\ \hfill \Omega \left(\beta \right)& =\sum _{j=1}^J\sum _{k=1}^K{\int }_0^L{\tau }_{\mathit{jk}}(t,\beta )y_{\mathit{jk}}^{\left(0\right)}(t,\beta )d{\Lambda }_{\mathit{jk}0}\left(t\right),\hfill \\ \hfill {\Psi }_i\left(\beta \right)& =\sum _{j=1}^J\sum _{k=1}^K{\int }_0^L\left\{V_i-{\overline{v}}_{\mathit{jk}}(t,\beta )\right\}{\mathit{dM}}_{\mathit{jki}}(t,\beta ),\hfill \\ \hfill {\mathit{dM}}_{\mathit{jki}}(t,\beta )& ={\mathit{dN}}_{\mathit{jki}}\left(t\right)-Y_{\mathit{jki}}\left(t\right)\exp \left\{{\beta }^T{V}_i\right\}d{\Lambda }_{\mathit{jk}0}\left(t\right).\hfill \end{array}$$ (3)

Besides, $y_{\mathit{jk}}^{\left(0\right)}(t,\beta ),{\overline{v}}_{\mathit{jk}}(t,\beta )$ and τ_jk(t,β) are the limiting values of $Y_{\mathit{jk}}^{\left(0\right)}(t,\beta )=\frac{1}{n}{\sum }_{p=1}^n{Y}_{\mathit{jkp}}\left(t\right)\exp \left\{{\beta }^T{V}_p\right\},{\overline{V}}_{\mathit{jk}}(t,\beta )$, and $\frac{{\sum }_{p=1}^n{V}_p{V}_p^T{Y}_{\mathit{jkp}}\left(t\right)\exp \left\{{\beta }^T{V}_p\right\}}{{\sum }_{p=1}^n{Y}_{\mathit{jkp}}\left(t\right)\exp \left\{{\beta }^T{V}_p\right\}}-{\overline{V}}_{\mathit{jk}}(t,\beta ){\overline{V}}_{\mathit{jk}}^T(t,\beta )$, respectively. The variance function can be estimated by ${\widehat{\sigma }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }}^2\left(t\right)=\frac{1}{n}{\sum }_{i=1}^n{\widehat{\xi }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }i}^2(t,\widehat{\beta })$. The detailed steps for computing ${\widehat{\xi }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }i}(t,\widehat{\beta })$ are described in the Appendix B. One might expect that the asymptotic distribution of $\ln \left\{{\widehat{\theta }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }}\right(t\left)\right\}$ would be closer to a Gaussian process than ${\widehat{\theta }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }}\left(t\right)$. Based on the delta method, the variance of $\ln \left\{{\widehat{\theta }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }}\right(t\left)\right\}$ can be estimated by ${\widehat{\sigma }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }}^{\prime }{\left(t\right)}^2=\frac{{\widehat{\sigma }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }}^2\left(t\right)}{{\widehat{\theta }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }}\left(t\right)}$. We will use simulation to investigate the properties of ${\widehat{\theta }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }}\left(t\right)$ and $\ln \left\{{\widehat{\theta }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }}\right(t\left)\right\}$ in a sequentially randomized setting in Sect. 4.

Based on the log ratio estimator of the cumulative baseline hazards, a Wald-type test can be used for comparing different treatment regimes. For example, for comparing treatment regimes A_jB_k and A_j’Bk’ at a specific time point t₀, the null hypothesis can be described as H_jkj’k’ : ln{θ_jkj’k’ (t₀)} = 0, and the test statistic can be written as

$$D_{{\mathit{jkj}}^{\prime }{k}^{\prime }}=\frac{\ln \left\{{\widehat{\theta }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }}\right(t_0\left)\right\}}{{\widehat{\sigma }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }}^{\prime }\left(t_0\right)}.$$

This test statistic is then compared to a standard normal distribution. Because the cumulative hazard can be viewed as an “accumulation” of the hazard over time, the choice of t₀ will depend on the disease-specific survival patterns as well as the treatments. If there are more than two treatment regimes involved, multiple treatment regimes can be compared by performing an overall test of difference among all regimes using the Wald Chi-square test. More specifically, in our case, let θ(t₀) = [θ_jk11(t₀), j = 1, … , J ; k = 1, … , K; jk ≠ 11]^T be the ratios (J K – 1)-dimensional vector of cumulative hazard ratios at t₀, and

$$\Sigma \left(t_0\right)=\left(\begin{array}{cccc}\hfill {\sigma }_{1111}^2\left(t_0\right)\hfill & \hfill {\sigma }_{1111\cdot 1211}\left(t_0\right)\hfill & \hfill \cdots \hfill & \hfill {\sigma }_{1111\cdot \mathit{JK}11}\left(t_0\right)\hfill \\ \hfill {\sigma }_{1111\cdot 1211}\left(t_0\right)\hfill & \hfill {\sigma }_{1211}^2\left(t_0\right)\hfill & \hfill \cdots \hfill & \hfill {\sigma }_{1211\cdot \mathit{JK}11}\left(t_0\right)\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\sigma }_{1111\cdot \mathit{JK}11}\hfill & \hfill {\sigma }_{1211\cdot \mathit{JK}11}\hfill & \hfill \cdots \hfill & \hfill {\sigma }_{\mathit{JK}11}^2\left(t_0\right)\hfill \end{array}\right)$$

be the corresponding variance-covariance matrix. The diagonal elements of ${\sigma }_{\mathit{jk}11}^2\left(t_0\right)$ are the variances of ${\widehat{\theta }}_{\mathit{jk}11}\left(t\right)$, j = 1, …, J; k = 1, … , K. The off-diagonal elements are the covariance between ${\widehat{\theta }}_{\mathit{jk}11}\left(t\right)$ and ${\widehat{\theta }}_{j^{\prime }{k}^{\prime }11}\left(t\right)$, j = 1, … , J ; k = 1, … , K; jk ≠ j’k’. Then for testing H₀ : Λ₁₁(t₀) = ⋯ = Λ_JK(t₀) or equivalently H₀ : ln{θ(t₀)} = 0, the test statistic can be written as

$${\chi }_{\mathit{JK}-1}^2={\left[\ln \left\{\widehat{\theta }\left(t_0\right)\right\}\right]}^T{\widehat{\Sigma }}^{{\prime }^{-1}}\left(t_0\right)\left[\ln \left\{\widehat{\theta }\left(t_0\right)\right\}\right],$$

where

$${\widehat{\Sigma }}^{\prime }\left(t_0\right)={\left(\frac{\partial \ln \left\{\widehat{\theta }\right(t_0\left)\right\}}{\partial \widehat{\theta }\left(t_0\right)}\right)}^T\widehat{\Sigma }\left(t_0\right)\left(\frac{\partial \ln \left\{\widehat{\theta }\right(t_0\left)\right\}}{\partial \widehat{\theta }\left(t_0\right)}\right).$$

This test statistic is then compared to a Chi-square distribution with (J K – 1) degrees of freedom.

4 Simulation Study

For simplicity, a simulation study was carried out under a two-stage randomization design with only two treatment options for each stage (J = K = 2). Under this design, the performance of the ratio estimator, log ratio estimator and proposed tests were assessed under the following scenarios:

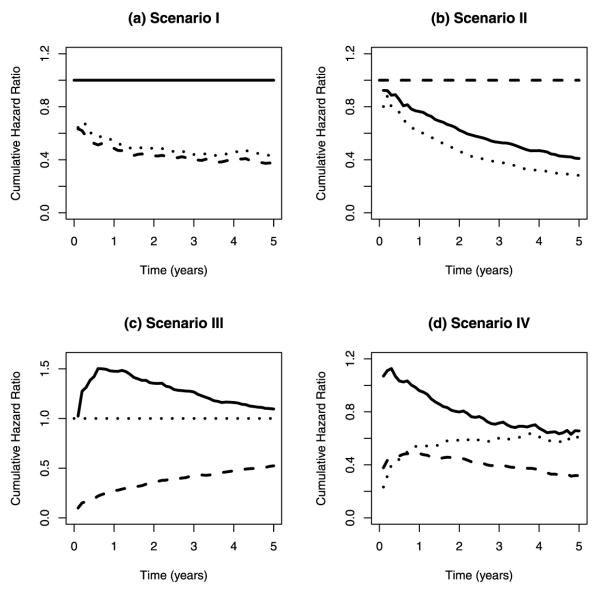
• – Scenario I: The survival distributions for treatment regimes A₁B₁ and A₁B₂ are the same (note that the treatment regimes A₁B₁ and A₁B₂ share the same induction therapy A₁);

• – Scenario II: The survival distributions for treatment regimes A₁B₁ and A₂B₁ are the same (note that the treatment regimes A₁B₁ and A₂B₁ share the same second-stage therapy B₁);

• – Scenario III: The survival distributions for treatment regimes A₁B₁ and A₂B₂ are the same (note that the treatment regimes A₁B₁ and A₂B₂ have different induction and second-stage therapies);

• – Scenario IV: No pattern is specified in the population.

An indicator (X_1i) for initial treatment A₁ was generated following the Bernoulli(0.5) distribution. An indicator for response (R_i) was generated from the Bernoulli distribution with 60 % response rate. An indicator (Z_1i) for second-stage treatment B₁ was drawn from the Bernoulli(0.5) distribution where R_i = 1. Based on the stratified proportional hazards model (1), the death time T_jki for the ith patient in the jkth regime is calculated based on the Weibull distribution using

$$T_{\mathit{jki}}={\left\{-\log \left({\varphi }_i\right)∕\left[{\alpha }_{\mathit{jk}}\exp \left\{{\beta }^T{V}_i\right\}\right]\right\}}^{1∕{\gamma }_{\mathit{jk}}},$$

for j = 1, 2, and k = 0, 1, 2, where ϕ_i was generated from the Uniform(0,1) distribution. V_i = [V_1i, V_2i]^T and both V_1i and V_2i were generated from the Bernoulli(0.5) distribution. The parameter vector β was set to [0.5, 0.5]^T. A variety of values were used for α_jk and γ_jk to assess the properties of the ratio estimator, log ratio estimator and proposed tests under different scenarios (Table 1). Null hypotheses H₁₂₁₁ : ln{θ₁₂₁₁(t)} = 0, H₂₁₁₁ : ln{θ₂₁₁₁(t)} = 0, and H₂₂₁₁ : ln{θ₂₂₁₁(t)} = 0 were true in the population under scenarios I, II and III, respectively. For scenario IV, parameter values were chosen with no pattern. The true cumulative hazard ratios for comparing A₁B₂, A₁B₂, and A₁B₂ to A₁B₂ under different scenarios are plotted in Fig. 1. Censoring time was generated according to the Uniform(τ/2, τ) distribution, where the value of τ was chosen to be 5, resulting in censoring percentage ranging from 10 to 30 %. The sample size was varied from 400 to 1200, and 1000 replications were performed under each scenario. Time t₀ was chosen to be the 75th percentile of the observed time under each scenario. For each sample, the ratios and the log ratios of the cumulative baseline hazards for comparing A₁B₂, A₂B₁, and A₂B₂ to A₁B₁ were calculated, and theWald-type tests were performed based on the log ratio estimates.

Table 1.

Different values for α_jk and γ_jk, j = 1, 2, and k = 0, 1, 2, under different scenarios (for scenario details see Sect. 4)

Scenario	γ 10	γ 11	γ 12	γ 20	γ 21	γ 22	α 10	α 11	α 12	α 20	α 21	α 22	Censoring (%)
I	1.4	1.4	1.4	1.2	1.2	1.2	0.7	0.4	0.4	0.3	0.2	0.25	10
II	1.0	1.5	1.2	1.0	1.5	1.3	0.5	0.2	0.1	0.5	0.2	0.05	23
III	1.2	1.0	1.2	1.2	1.5	1.0	0.1	0.4	0.7	0.1	0.04	0.4	30
IV	1.0	1.5	1.2	1.5	1.0	1.4	0.7	0.4	0.35	0.3	0.2	0.25	10

Fig. 1.

The true cumulative hazard ratios for comparing A₁B₂, A₂B₁, and A₂B₂ to A₁B₁ under different scenarios. Solid line A₁B₂ vs. A₁B₁, dashed line A₂B₁ vs. A₁B₁, dotted line A₂B₂ vs. A₁B₁

Table 2 shows the ratio and log ratio estimates (EST), absolute bias (BIAS), asymptotic standard error (ASE), empirical standard deviation (ESD) and 95 % coverage probability (CP) under each scenario. For example, under scenario I and at a sample size of 800, the estimate of θ₁₂₁₁(t₀) was 1.01 with an absolute bias of 0.01. The asymptotic standard error was 0.119, close to the empirical standard deviation of 0.121. The corresponding coverage probability was 93 % based on the estimate and asymptotic standard error. Similarly, the estimate for the ln{θ₁₂₁₁(t₀)} was 0.00 with an absolute bias of 0.01. The asymptotic standard error (0.118) and empirical standard deviation (0.120) were close. The coverage probability was 94 %, better than that for ${\widehat{\theta }}_{1211}\left(t_0\right)$. In most of the cases, the estimates were approximately unbiased; with the absolute biases differed from 0.00 to 0.02. The asymptotic standard errors were close to the empirical standard deviations, demonstrating that the estimated standard errors were consistent. Most coverage probabilities were close to 95 %, attaining the nominal level. As sample size increased, the estimated standard error decreased and the coverage probability increased. Some of the log ratio estimates were less biased than the corresponding ratio estimates, and the overall coverage probabilities were closer to 95 % based on the log ratio estimates than those based on the ratio estimates.

Table 2.

Simulation results under each scenario (for scenario details see Sect. 4). EST: ratio or log ratio estimate; BIAS: absolute bias; ASE: asymptotic standard error; ESD: empirical standard deviation; and CP: 95 % coverage probability

Scenario	n	θ1211(t0)					ln{θ1211(t0)}
		EST	BIAS	ASE	ESD	CP	EST	BIAS	ASE	ESD	CP
I	400	1.01	0.00	0.166	0.175	0.93	−0.01	0.02	0.165	0.171	0.94
	800	1.01	0.01	0.119	0.121	0.93	0.00	0.01	0.118	0.120	0.94
	1200	1.00	0.01	0.097	0.102	0.93	0.00	0.01	0.097	0.101	0.94
II	400	0.51	0.01	0.084	0.083	0.95	−0.69	0.00	0.167	0.166	0.95
	800	0.51	0.01	0.060	0.061	0.96	−0.69	0.01	0.119	0.121	0.95
	1200	0.51	0.00	0.049	0.051	0.95	−0.69	0.00	0.098	0.100	0.95
III	400	1.14	0.01	0.113	0.105	0.97	0.13	0.00	0.099	0.092	0.97
	800	1.14	0.01	0.082	0.073	0.97	0.13	0.00	0.072	0.064	0.97
	1200	1.14	0.00	0.067	0.058	0.98	0.13	0.00	0.059	0.05	0.98
IV	400	0.79	0.01	0.121	0.126	0.93	−0.24	0.02	0.153	0.157	0.95
	800	0.79	0.01	0.087	0.089	0.92	−0.24	0.02	0.109	0.113	0.93
	1200	0.79	0.01	0.071	0.072	0.94	−0.24	0.02	0.089	0.090	0.94
Scenario	n	θ2111(t0)					ln{θ2111(t0)}
		EST	BIAS	ASE	ESD	CP	EST	BIAS	ASE	ESD	CP
I	400	0.43	0.01	0.075	0.077	0.94	−0.86	0.01	0.174	0.179	0.94
	800	0.43	0.00	0.053	0.052	0.96	−0.86	0.00	0.123	0.122	0.94
	1200	0.43	0.00	0.043	0.044	0.95	−0.86	0.01	0.101	0.103	0.95
II	400	1.02	0.02	0.181	0.197	0.93	0.00	0.00	0.178	0.190	0.94
	800	1.00	0.01	0.128	0.131	0.95	0.00	0.00	0.127	0.129	0.95
	1200	1.01	0.01	0.105	0.108	0.94	0.00	0.00	0.105	0.107	0.95
III	400	0.51	0.02	0.098	0.103	0.94	−0.70	0.01	0.195	0.202	0.94
	800	0.50	0.01	0.070	0.072	0.95	−0.70	0.02	0.140	0.143	0.95
	1200	0.50	0.01	0.057	0.057	0.96	−0.70	0.01	0.115	0.113	0.95
IV	400	0.44	0.01	0.076	0.075	0.95	−0.82	0.02	0.170	0.168	0.95
	800	0.44	0.01	0.053	0.054	0.96	−0.83	0.01	0.121	0.123	0.94
	1200	0.44	0.01	0.044	0.045	0.95	−0.83	0.01	0.099	0.101	0.95
Scenario	n	θ2211(t0)					ln{θ2211(t0)}
		EST	BIAS	ASE	ESD	CP	EST	BIAS	ASE	ESD	CP
I	400	0.49	0.00	0.084	0.088	0.93	−0.72	0.01	0.171	0.182	0.93
	800	0.49	0.00	0.059	0.058	0.95	−0.72	0.01	0.122	0.119	0.96
	1200	0.49	0.00	0.049	0.049	0.93	−0.72	0.01	0.100	0.100	0.95
II	400	0.38	0.00	0.069	0.069	0.94	−0.99	0.01	0.182	0.181	0.94
	800	0.38	0.00	0.049	0.048	0.95	−0.99	0.01	0.130	0.129	0.95
	1200	0.37	0.00	0.040	0.039	0.94	−0.99	0.01	0.106	0.104	0.95
III	400	1.01	0.01	0.175	0.180	0.94	0.00	0.01	0.172	0.177	0.95
	800	1.01	0.00	0.125	0.129	0.94	0.00	0.01	0.124	0.127	0.95
	1200	1.00	0.00	0.102	0.100	0.95	0.00	0.00	0.102	0.099	0.95
IV	400	0.61	0.01	0.101	0.104	0.93	−0.51	0.00	0.165	0.172	0.95
	800	0.60	0.00	0.071	0.071	0.95	−0.51	0.01	0.118	0.117	0.95
	1200	0.60	0.00	0.058	0.058	0.94	−0.51	0.01	0.096	0.097	0.96

Table 3 presents the rejection rates for testing null hypotheses H₁₂₁₁ : ln{θ₁₂₁₁(t)} = 0, H₂₁₁₁ : ln{θ₂₁₁₁(t)} = 0, and H₂₂₁₁ : ln{θ₂₂₁₁(t)} = 0, separately under each scenario. Because the null hypotheses H₁₂₁₁ : ln{θ₁₂₁₁(t)} = 0, H₂₁₁₁ : ln{θ₂₁₁₁(t)} = 0, and H₂₂₁₁ : ln{θ₂₂₁₁(t)} = 0, were true under scenarios I, II and III, respectively, the rejection rates for H₁₂₁₁, H₂₁₁₁, and H₂₂₁₁ were close to the nominal level of 0.05 under scenarios I, II and III, respectively, suggesting that the tests were approximately unbiased. The rejection rates were relatively larger under the smaller sample size of 400. As sample size increased, the rejection rate approached 0.05.

Table 3.

Rejection rates for testing null hypotheses H₁₂₁₁ : ln{θ₁₂₁₁(t)} = 0, H₂₁₁₁ : ln{θ₂₁₁₁(t)} = 0, and H₂₂₁₁ : ln{θ₂₂₁₁(t)} = 0 under different scenarios. Scenarios I, II and III respectively represent null hypotheses H₁₂₁₁, H₂₁₁₁ and H₂₂₁₁, while for scenario IV, all three null hypotheses are false

Scenario	n	H 1211	H 2111	H 2211
I	400	0.059	0.999	0.991
	800	0.053	1.000	1.000
	1200	0.055	1.000	1.000
II	400	0.992	0.064	1.000
	800	1.000	0.048	1.000
	1200	1.000	0.050	1.000
III	400	0.233	0.937	0.050
	800	0.444	1.000	0.050
	1200	0.603	1.000	0.046
IV	400	0.351	0.992	0.864
	800	0.587	1.000	0.994
	1200	0.753	1.000	0.999

5 Analysis of Neuroblastoma Data

From 1991 to 1996, the Children’s Cancer Group conducted a randomized clinical trial to study the effect of a combination of myeloablative chemotherapy, total-body irradiation and transplantation of autologous bone marrow purged of cancer cells (ABMT) to a standard chemotherapy in treating children with high risk neuroblastoma [13]. Since relapse is common after completion of induction therapies among children with high risk neuroblastoma, patients without progressive disease (PD) or histologically confirmed disease (HCD) after induction therapies were then randomly assigned to receive either 13-cis-rectinoic acid (cis-RA) or no further therapy. Therefore, the high risk neuroblastoma clinical trial followed a two-stage randomization design. By the end of the study, a total of 379 children participated in the first randomization, with 190 children assigned to ABMT, and 189 children assigned to chemotherapy. After the completion of the first-stage therapy, 203 children had no PD or HCD, and thus participated in the second randomization. During the second randomization, 102 children were assigned to cis-RA, and 101 patients were assigned to no further therapy. Matthay et al. [13] reported 55 more children who participated in the second randomization, resulting in 130 children assigned to cis-RA and 128 children assigned to no further therapy. These children were not included in our setting because they did not participate in the first randomization. This two-stage randomization design resulted in four treatment regimes: (i) treat with ABMT, followed by cis-RA if no PD or HCD (AC); (ii) treat with ABMT, followed by no further therapy if no PD or HCD (AN); (iii) treat with chemotherapy, followed by cis-RA if no PD or HCD (CC); (iv) treat with chemotherapy, followed by no further therapy if no PD or HCD (CN).

A stratified proportional hazards model based on (1) was applied to the neuroblastoma data, using treatment regimes as strata. The only baseline characteristics found imbalanced among different treatment groups was “Evan’s stage” in Matthay et al. [13], and thus was included in the model as one of the covariates. Additionally, “age” was also included in the model as a continuous covariate. The time to second randomization did not differ significantly across the first stage treatments (p = 0.26). The resulting log ratio estimates of the cumulative baseline hazards and their corresponding 95 % confidence intervals within the time interval of [0, 2000] days are shown in Fig. 2. From the plot of the log ratio estimate of the cumulative baseline hazards comparing treatment regime AN to AC, we observed a notable difference around 450 days. However, the horizontal “zero” line was within the confidence interval most of the time, suggesting that there was no significant difference between treatment regimes AN and AC. In the plot for comparing treatment regime CC to AC the confidence band moved further away from “zero” as time increased. Thus, we would suspect that children following the treatment regime AC had better overall survival compared to those following the regime CC. Besides, the confidence band also became narrower as time increased since there was higher variability with fewer events at the beginning of the study. Similar results were observed from the plot for comparing treatment regime CN to AC. The hazard ratios (95 % confidence interval) for comparing AN, CC, and CN to AC at year 3 were estimated to be 1.10 (0.78, 1.43), 1.13 (0.74, 1.52), and 1.02 (0.67, 1.38), respectively. The hazard ratios (95 % confidence interval) for comparing AN, CC and CN to AC at year 5 were estimated to be 1.22 (0.86, 1.57), 1.38 (0.92, 1.85), and 1.43 (0.95, 1.91), respectively. We also used the Wald Chi-square test to evaluate the overall difference among four treatment regimes at year 5. It resulted in a p-value of 0.17, showing that there was no overall significant difference in the cumulative hazard among four treatment regimes at 5 years. Therefore, we would suspect that children with high risk neuroblastoma would have a similar overall 5-year survival irrespective of the induction therapy they received. After the completion of induction therapies, whether they would be subsequently treated with cis-RA or not, did not significantly improve the overall 5-year survival either.

Fig. 2.

Estimated log ratios of the cumulative baseline hazards and the corresponding 95 % pointwise confidence intervals from the neuroblastoma study. AC: “treat with ABMT, and then followed by cis-RA if no PD or HCD,” AN: “treat with ABMT, and then followed by no further therapy if no PD or HCD,” CC: “treat with chemotherapy, and then followed by cis-RA if no PD or HCD,” CN: “treat with chemotherapy, and then followed by no further therapy if no PD or HCD”

6 Discussion

In this article, we proposed a stratified proportional hazards model to estimate the cumulative treatment effect for treatment regimes from sequentially randomized clinical trials. This approach is similar to that advocated by Wei and Schaubel [8] for a single-stage randomization. Comparisons among treatment regimes were performed by testing the log ratio of the estimated cumulative hazards. Simulation results showed that the ratio estimator was approximately unbiased, and the coverage probabilities were close to the nominal level. However, the log ratio estimator performed better, with smaller absolute biases and better coverage probabilities. The comparative hypothesis testing can also be performed maintaining adequate type I errors from the proposed model under moderate sample size based on the Wald-type tests. In this paper we assumed that the randomization probabilities are known (by design). Estimation of these probabilities from the observed data might result in more efficient estimators.

Wald-type tests were used to assess the survival difference between treatment regimes at a specific time point. Although such point-wise comparisons are of interest in many diseases-specific areas, comparisons of treatment regimes based on overall hazard curves may be of importance alongside the construction of simultaneous confidence bands. This issue is beyond the scope of this manuscript and is being considered as a separate publication.

Appendix A. Outline of the asymptotic normality of ${\widehat{\theta }}_{{\mathit{jkj}}^{\prime }{\mathit{k}}^{\prime }}\left(t\right)$

The following are the equivalent assumptions in sequentially randomized clinical trials to those outlined in Sect. 3 of Wei and Schaubel [8].

1. (X_ji, R_i, R_iZ_ki, U_i, Δ_i, V_i) are i.i.d. random vectors for i = 1, … , n.

2. Elements of V_i have bounded total variation for i 1, … , n

3. The cumulative hazard is finite over a pre-specified interval [0, L] such that P (U_i > L) > 0.

4. (d)

   $$y_{\mathit{jk}}^{\left(1\right)}(t,\beta )=\frac{\partial }{\partial \beta }{y}_{\mathit{jk}}^{\left(0\right)}(t,\beta )\text{and}{y}_{\mathit{jk}}^{\left(2\right)}(t,\beta )=\frac{{\partial }^2}{\partial \beta \partial {\beta }^T}{y}_{\mathit{jk}}^{\left(0\right)}(t,\beta ),$$

   where

   $$y_{\mathit{jk}}^{\left(d\right)}(t,\beta )=\underset{n\to \infty }{\lim }{Y}_{\mathit{jk}}^{\left(d\right)}(t,\beta )\text{for}d=0,1,2,$$

   where

   $$\begin{array}{cc}\hfill Y_{\mathit{jk}}^{\left(d\right)}(t,\beta )& =n^{-1}\sum _{i=1}^n{Y}_{\mathit{jki}}\left(t\right)V_i^{\otimes d}\exp \left\{{\beta }^T{V}_i\right\}\text{for}d=0,1,2,\hfill \\ \hfill \text{where}& V_i^{\otimes 0}=1,V_i^{\otimes 1}=V_i,V_i^{\otimes 2}=V_i{V}_i^T,\hfill \end{array}$$

   with $y_{\mathit{jk}}^{\left(1\right)}(t,\beta )$ and $y_{\mathit{jk}}^{\left(2\right)}(t,\beta )$ bounded away from 0 for t ∈ [0. L] and β in an open set.
5. Positive-definiteness of the matrix

   $$\Omega \left(\beta \right)=\sum _{j=1}^J\sum _{k=1}^K{\int }_0^L{\tau }_{\mathit{jk}}(t,\beta )y_{\mathit{jk}}^{\left(0\right)}(t,\beta )d{\Lambda }_{\mathit{jk}0}(t,\beta ),$$

   where

   $${\tau }_{\mathit{jk}}(t,\beta )=y_{\mathit{jk}}^{\left(2\right)}(t,\beta )∕y_{\mathit{jk}}^{\left(0\right)}(t,\beta )-{\stackrel{‒}{v}}_{\mathit{jk}}{(t,\beta )}^{\otimes 2},$$

Consistency and asymptotic normality of ${\widehat{\theta }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }}\left(t\right)$ Consistency and asymptotic normality of ${\widehat{\theta }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }}\left(t\right)$ can be established in a similar manner as in the proof of Theorems 1 and 2 given in the Web Appendix of Wei and Schaubel [8] as long as the following results hold:

1. $\widehat{\beta }\stackrel{a.s.}{\to }{\beta }_0$.

2. $\sqrt{n}(\widehat{\beta }-{\beta }_0)$ is asymptotically normal

3. ${\widehat{\Lambda }}_{\mathit{jk}}(t,\widehat{\beta })$ is a uniformly consistent estimator of Λ_jk(t, β).

1. Consistency of $\widehat{\beta }$

Recall that β is a solution to the equation

$$U_n\left(\beta \right)=\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^J\sum _{k=1}^K{\int }_0^L\left\{V_i-{\overline{V}}_{\mathit{jk}}(t,\beta )\right\}{\mathit{dN}}_{\mathit{jki}}\left(t\right)=0.$$

First note that the processes Y_jk(t) and N_jk(t) are both cardlag processes and hence they are Donsker. Since the classes {β ∈ B} and {V} are trivially Donsker, the functions Y_jk(t) exp{^βT V}, VY_jk(t) exp{β^T V}, VV^T Y_jk(t) exp{β^T V} are all Donsker for t ∈ [0, L], β ∈ B. The derivative of U_n(β) with respect to β is Ω_n(β), where

$$\begin{array}{cc}\hfill {\Omega }_n\left(\beta \right)=& \sum _{j=1}^J\sum _{k=1}^K{\int }_0^L[\frac{\sum _{p=1}^n{V}_p{V}_p^T{Y}_{\mathit{jkp}}\left(t\right)\exp \left({\beta }^T{V}_p\right)}{\sum _{p=1}^n{Y}_{\mathit{jkp}}\left(t\right)\exp \left({\beta }^T{V}_p\right)}\phantom{]}\hfill \\ \hfill & -\phantom{[}{\left\{\frac{\sum _{p=1}^n{V}_p{Y}_{\mathit{jkp}}\left(t\right)\exp \left({\beta }^T{V}_p\right)}{\sum _{p=1}^n{Y}_{\mathit{jkp}}\left(t\right)\exp \left({\beta }^T{V}_p\right)}\right\}}^{\otimes 2}]\frac{1}{n}\sum _{i=1}^n{\mathit{dN}}_{\mathit{jki}}\left(s\right),\hfill \end{array}$$

where ⊗2 denotes the outer product. All functions in the above expressions are Glivenko–Cantelli and the limiting value $y_{\mathit{jk}}^{\left(0\right)}(t,\beta )$ of $\frac{1}{n}{\sum }_{p=1}^n{Y}_{\mathit{jkp}}\left(t\right)\exp \left({\beta }^T{V}_p\right)$ is bounded away from zero. Therefore,

$$\underset{\beta \in B}{\sup }\mid {\Omega }_n\left(g\right)-\Omega \left(\beta \right)\mid \stackrel{\mathrm{a}.\mathrm{s}.}{\to }0,$$

where Ω(β) is defined in (3). Since Ω(β) is positive semidefinite. U_n(β) is almost surely convex for large n. Therefore, $\widehat{\beta }\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{\beta }_0$.

2. Asymptotic normality of $\sqrt{n}(\widehat{\beta }-{\beta }_0)$

We write Ψ_n(β) as

$${\Psi }_n\left(\beta \right)=\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^J\sum _{k=1}^K{\int }_0^L\left\{V_i-{\overline{v}}_{\mathit{jk}}(t,\beta )\right\}{\mathit{dM}}_{\mathit{jki}}\left(t\right)=0,$$

where

$$M_{\mathit{jki}}(t,\beta )=N_{\mathit{jki}}\left(t\right)-{\int }_0^L{Y}_{\mathit{jki}}\left(t\right)\exp \left({\beta }^T{V}_i\right)d{\Lambda }_{\mathit{jk}0}\left(t\right).$$

Let

$$\Psi \left(\beta \right)=E\left[\sum _{j=1}^J\sum _{k=1}^K{\int }_0^L\left\{V-{\overline{v}}_{\mathit{jk}}(t,\beta )\right\}{\mathit{dM}}_{\mathit{jk}}\left(t\right)\right],$$

where

$${\overline{v}}_{\mathit{jk}}(t,\beta )=\frac{E\left[{\mathit{VY}}_{\mathit{jk}}\right(t\left)\exp \right({\beta }^{T}V\left)\right]}{E\left[Y_{\mathit{jk}}\right(t\left)\exp \right({\beta }^{T}V\left)\right]}.$$

Then the arguments on pages 56 and 57 in Kosorok (2008, Chap. 4, [11]) can be applied to show that $\sqrt{n}(\widehat{\beta }-{\beta }_0)$ weakly converges to a mean zero normal random vector with covariance matrix Ω⁻¹(β₀).

3. Almost sure convergence of ${\widehat{\Lambda }}_{\mathit{jk}}(t,\widehat{\beta })$

Note that

$${\widehat{\Lambda }}_{\mathit{jk}}(t,\widehat{\beta })={\int }_0^t\frac{P_n{\mathit{dN}}_{\mathit{jk}}\left(s\right)}{P_n{Y}_{\mathit{jk}}\left(s\right)\exp \left({\widehat{\beta }}^{T}V\right)},$$

where P_n is the empirical measure, namely, $P_{n}f=\frac{1}{n}{\sum }_{i=1}^{n}f\left(x_i\right)$ for real-valued functions $f:\mathcal{X}\to \mathcal{R}$, $\mathcal{X}$ being the sample space. This is basically the same estimator defined in the first display on page 57 of Kosorok (2008, Chap. 4, [11]). Hence, a straightforward application of the argument therein leads to

$$\underset{t\in [0,L]}{\sup }\mid {\widehat{\Lambda }}_{\mathit{jk}}(t,\widehat{\beta })-{\Lambda }_{\mathit{jk}0}\left(t\right)\mid \stackrel{\mathrm{a}.\mathrm{s}.}{\to }0.$$

With the above results (1–3), it is now straightforward to apply the arguments in the Web Appendix A of Wei and Schaubel [8] to establish that ${\widehat{\theta }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }}\left(t\right)$ is uniformly consistent and asymptotically normal.

Appendix B. Estimation of ${\widehat{\xi }}_{{\mathit{jkj}}^{\prime }{\mathit{k}}^{\prime }i}(\mathit{t},\widehat{\beta })$

The detailed steps for computing ${\widehat{\xi }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }i}(t,\widehat{\beta })$ are as follows:

Step 1: Calculate ${\widehat{\overline{V}}}_{\mathit{jk}}(s,\widehat{\beta })=\frac{{\sum }_{p=1}^n{V}_p{Y}_{\mathit{jkp}}\left(s\right)\exp \left\{{\widehat{\beta }}^T{V}_p\right\}}{{\sum }_{p=1}^n{Y}_{\mathit{jkp}}\left(s\right)\exp \left\{{\widehat{\beta }}^T{V}_p\right\}}$.

Step 2: Calculate

$$\begin{array}{cc}\hfill {\widehat{h}}_{\mathit{jk}}(t,\widehat{\beta })& =-{\int }_0^t{\widehat{\overline{V}}}_{\mathit{jk}}(s,\widehat{\beta })d{\widehat{\Lambda }}_{\mathit{jk}0}(s,\widehat{\beta })\hfill \\ \hfill & =-{\int }_0^t{\widehat{\overline{V}}}_{\mathit{jk}}(s,\widehat{\beta })\sum _{i=1}^n\frac{{\mathit{dN}}_{\mathit{jki}}\left(s\right)}{\sum _{p=1}^n{Y}_{\mathit{jkp}}\left(s\right)\exp \left\{{\widehat{\beta }}^T{V}_p\right\}}\hfill \\ \hfill & =-\sum _{i=1}^n{\int }_0^t\frac{{\widehat{\overline{V}}}_{\mathit{jk}}(s,\widehat{\beta }){\mathit{dN}}_{\mathit{jki}}\left(s\right)}{\sum _{p=1}^n{Y}_{\mathit{jkp}}\left(s\right)\exp \left\{{\widehat{\beta }}^T{V}_p\right\}}.\hfill \end{array}$$

Step 3: Define ${\widehat{\tau }}_{\mathit{jk}}(t,\widehat{\beta })=\frac{{\sum }_{p=1}^n{V}_p{V}_p^T{Y}_{\mathit{jkp}}\left(s\right)\exp \left\{{\widehat{\beta }}^T{V}_p\right\}}{{\sum }_{p=1}^n{Y}_{\mathit{jkp}}\left(s\right)\exp \left\{{\widehat{\beta }}^T{V}_p\right\}}-{\widehat{\overline{V}}}_{\mathit{jk}}(t,\widehat{\beta }){\widehat{\overline{V}}}_{\mathit{jk}}^T(t,\widehat{\beta })$.

Step 4: Calculate

$$\begin{array}{cc}\hfill \widehat{\Omega }\left(\widehat{\beta }\right)=& \frac{1}{n}\sum _{j=1}^J\sum _{k=1}^K{\int }_0^L{\widehat{\tau }}_{\mathit{jk}}(t,\widehat{\beta })\sum _{p=1}^n{Y}_{\mathit{jkp}}\left(t\right)\exp \left\{{\widehat{\beta }}^T{V}_p\right\}d{\widehat{\Lambda }}_{\mathit{jk}0}(t,\widehat{\beta })\hfill \\ \hfill =& \frac{1}{n}\sum _{j=1}^J\sum _{k=1}^K{\int }_0^L{\widehat{\tau }}_{\mathit{jk}}(t,\widehat{\beta })\sum _{p=1}^n{Y}_{\mathit{jkp}}\left(t\right)\exp \left\{{\widehat{\beta }}^T{V}_p\right\}\hfill \\ \hfill & \times \sum _{i=1}^n\frac{{\mathit{dN}}_{\mathit{jki}}\left(t\right)}{\sum _{p=1}^n{Y}_{\mathit{jkp}}\left(t\right)\exp \left\{{\widehat{\beta }}^T{V}_p\right\}}\hfill \\ \hfill =& \frac{1}{n}\sum _{i=1}^n\sum _{j=1}^J\sum _{k=1}^K{\int }_0^L{\widehat{\tau }}_{\mathit{jk}}(t,\widehat{\beta }){\mathit{dN}}_{\mathit{jki}}\left(t\right).\hfill \end{array}$$

Step 5: Calculate

$$\begin{array}{cc}\hfill {\widehat{\Psi }}_i\left(\widehat{\beta }\right)=& \sum _{j=1}^J\sum _{k=1}^K{\int }_0^L\left\{V_i-{\widehat{\overline{V}}}_{\mathit{jk}}(t,\widehat{\beta })\right\}d{\widehat{M}}_{\mathit{jki}}(t,\widehat{\beta })\hfill \\ \hfill =& \sum _{j=1}^J\sum _{k=1}^K{\int }_0^L\left\{V_i-{\widehat{\overline{V}}}_{\mathit{jk}}(t,\widehat{\beta })\right\}\left[{\mathit{dN}}_{\mathit{jki}}\left(t\right)-Y_{\mathit{jki}}\exp \left\{{\widehat{\beta }}^T{V}_i\right\}d{\widehat{\Lambda }}_{\mathit{jk}0}(t,\widehat{\beta })\right]\hfill \\ \hfill =& \sum _{j=1}^J\sum _{k=1}^K{\int }_0^L\left\{V_i-{\widehat{\overline{V}}}_{\mathit{jk}}(t,\widehat{\beta })\right\}{\mathit{dN}}_{\mathit{jki}}\left(t\right)\hfill \\ \hfill & -\sum _{j=1}^J\sum _{k=1}^K{\int }_0^L\left\{V_i-{\widehat{\overline{V}}}_{\mathit{jk}}(t,\widehat{\beta })\right\}{Y}_{\mathit{jki}}\exp \left\{{\widehat{\beta }}^T{V}_i\right\}\hfill \\ \hfill & \times \sum _{i=1}^n\frac{{\mathit{dN}}_{\mathit{jki}}\left(t\right)}{\sum _{p=1}^n{Y}_{\mathit{jkp}}\left(t\right)\exp \left\{{\widehat{\beta }}^T{V}_p\right\}}\hfill \\ \hfill =& \sum _{j=1}^J\sum _{k=1}^K{\int }_0^L\left\{V_i-{\widehat{\overline{V}}}_{\mathit{jk}}(t,\widehat{\beta })\right\}{\mathit{dN}}_{\mathit{jki}}\left(t\right)\hfill \\ \hfill & -\sum _{i=1}^n\sum _{j=1}^J\sum _{k=1}^K{\int }_0^L\frac{\{V_i-{\widehat{\overline{V}}}_{\mathit{jk}}(t,\widehat{\beta }\left)\right\}{Y}_{\mathit{jki}}\exp \left\{{\widehat{\beta }}^T{V}_i\right\}}{\sum _{p=1}^n{Y}_{\mathit{jkp}}\left(t\right)\exp \left\{{\widehat{\beta }}^T{V}_p\right\}}{\mathit{dN}}_{\mathit{jki}}\left(t\right).\hfill \end{array}$$

Step 6: Define

$$\begin{array}{cc}\hfill {\widehat{\Phi }}_{\mathit{jki}}^L(t,\widehat{\beta })=& {\int }_0^t\frac{n}{\sum _{p=1}^n{Y}_{\mathit{jkp}}\left(s\right)\exp \left\{{\widehat{\beta }}^T{V}_p\right\}}d{\widehat{M}}_{\mathit{jki}}(s,\widehat{\beta })\hfill \\ \hfill =& {\int }_0^t\frac{n}{\sum _{p=1}^n{Y}_{\mathit{jkp}}\left(s\right)\exp \left\{{\widehat{\beta }}^T{V}_p\right\}}\hfill \\ \hfill & \times \left[{\mathit{dN}}_{\mathit{jki}}\left(s\right)-Y_{\mathit{jki}}\exp \left\{{\widehat{\beta }}^T{V}_i\right\}d{\widehat{\Lambda }}_{\mathit{jk}0}(s,\widehat{\beta })\right]\hfill \\ \hfill =& {\int }_0^t\frac{{\mathit{ndN}}_{\mathit{jki}}\left(s\right)}{\sum _{p=1}^n{Y}_{\mathit{jkp}}\left(s\right)\exp \left\{{\widehat{\beta }}^T{V}_p\right\}}\hfill \\ \hfill & -{\int }_0^t\frac{{\mathit{nY}}_{\mathit{jki}}\exp \left\{{\widehat{\beta }}^T{V}_i\right\}}{\sum _{p=1}^n{Y}_{\mathit{jkp}}\left(s\right)\exp \left\{{\widehat{\beta }}^T{V}_p\right\}}\sum _{i=1}^n\frac{{\mathit{dN}}_{\mathit{jki}}\left(s\right)}{\sum _{p=1}^n{Y}_{\mathit{jkp}}\left(s\right)\exp \left\{{\widehat{\beta }}^T{V}_p\right\}}\hfill \\ \hfill =& {\int }_0^t\frac{\mathit{nd}{N}_{\mathit{jki}}\left(s\right)}{\sum _{p=1}^n{Y}_{\mathit{jkp}}\left(s\right)\exp \left\{{\widehat{\beta }}^T{V}_p\right\}}\hfill \\ \hfill & -\sum _{i=1}^n{\int }_0^t\frac{{\mathit{nY}}_{\mathit{jki}}\exp \left\{{\widehat{\beta }}^T{V}_i\right\}{\mathit{dN}}_{\mathit{jki}}\left(s\right)}{{\left[\sum _{p=1}^n{Y}_{\mathit{jkp}}\right(s\left)\exp \right\{{\widehat{\beta }}^T{V}_p\left\}\right]}^2}.\hfill \end{array}$$

Step 7: Calculate ${\widehat{\Phi }}_{\mathit{jki}}(t,\widehat{\beta })={\widehat{h}}_{\mathit{jk}}^T(t,\widehat{\beta }){\widehat{\Omega }}^{-1}\left(\widehat{\beta }\right){\widehat{\Psi }}_i\left(\widehat{\beta }\right)+{\widehat{\Phi }}_{\mathit{jki}}^L(t,\widehat{\beta })$.

Step 8: Calculate ${\widehat{\xi }}_{{\mathit{jkj}}^{\prime }{k}^{\prime }i}(t,\widehat{\beta })=\frac{{\widehat{\Phi }}_{\mathit{jki}(t,\widehat{\beta })}}{{\widehat{\Lambda }}_{j^{\prime }{k}^{\prime }0}(t,\widehat{\beta })}-\frac{{\widehat{\Lambda }}_{\mathit{jk}0}(t,\widehat{\beta }){\widehat{\Phi }}_{j^{\prime }{k}^{\prime }i}(t,\widehat{\beta })}{{\widehat{\Lambda }}_{j^{\prime }{k}^{\prime }0}^2(t,\widehat{\beta })}$.