Spatially Weighted Principal Component Analysis for Imaging Classification

Abstract

The aim of this paper is to develop a supervised dimension reduction framework, called Spatially Weighted Principal Component Analysis (SWPCA), for high dimensional imaging classification. Two main challenges in imaging classification are the high dimensionality of the feature space and the complex spatial structure of imaging data. In SWPCA, we introduce two sets of novel weights including global and local spatial weights, which enable a selective treatment of individual features and incorporation of the spatial structure of imaging data and class label information. We develop an e cient two-stage iterative SWPCA algorithm and its penalized version along with the associated weight determination. We use both simulation studies and real data analysis to evaluate the finite-sample performance of our SWPCA. The results show that SWPCA outperforms several competing principal component analysis (PCA) methods, such as supervised PCA (SPCA), and other competing methods, such as sparse discriminant analysis (SDA).

1 Introduction

In various neuroimaging studies, imaging classification is to predict a set of response variables (class labels) Y by using a set of imaging data $\mathit{x}=\{x_d:d\in \mathcal{D}\}\in R^p$ measured on each of N subjects, where $\mathcal{D}$ is a 3-dimensional (3D) volume (or 2D surface) and d is a voxel (or pixel) of $\mathcal{D}$. For instance, Y may include cognitive outcome, disease status, and the early onset of disease, among others, whereas x may include magnetic resonance imaging (MRI) and positron emission tomography (PET), among many others. Moreover, imaging data usually can be represented as data on a graph such that D is a graph with {d₁,..., d_p} as the set of vertexes and an edge set, denoted by ${\mathcal{D}}_E$.

Two major challenges associated with imaging classification include (i) ultra-high dimension, but low sample size and (ii) correlated features with complex spatial structure including spatial smoothness and spatial correlation. For instance, the size of a typical T1 MRI is 256×256×256, and thus MRI contains 256³ = 16,777,216 voxels. In contrast, the number of observations in most neuroimaging studies varies from several dozens to several hundreds. Thus, it is imperative to perform dimension reduction before classification. Moreover, imaging data has an inherent and strong spatial dimension due to the inherent biological structure of objects (Friston, 2007; Lazar, 2008; Ye et al., 2009; Wang et al., 2007; Meyer and Chinrungrueng, 2005). The aim of this paper is to develop a Spatially Weighted Principal Component Analysis (SWPCA) to address the two challenges for high dimensional imaging classification.

Despite of its e cacy and popularity in image applications, principal component analysis (PCA; Jolliffe, 2002) as a general non-supervised dimension reduction technique is known to su er from major limitations. Firstly, each principal component (PC) is a linear combination of the original p features with nonzero loadings, which not only incorporates unnecessary noises but also makes it very di cult to interpret the derived PCs, especially when p >> N. Secondly, PCA treats all the features equally, and thus it may be not well-suited for some problems, in which some regions of interest are more important than others. Thirdly, PCA ignores the inherent spatial smoothness and spatial correlation of imaging data.

Many PCA variants have been proposed to address some of these limitations discussed above (Jolliffe, 2002; Zou et al., 2006; Bair et al., 2006; Skočaj et al., 2007; Shen and Huang, 2008; Leng and Wang, 2009; Pinto da Costa et al., 2011; Allen et al., 2011, etc.). For instance, Bair et al. (2006) proposed a Supervised PCA (SPCA) by conducting standard PCA on marginally selected features. However, SPCA su ers from ignoring the inherent spatial structure of imaging data. Skočaj et al. (2007) proposed a weighted PCA (WPCA) by introducing temporal and spatial weights in order to downweight individual images and individual components of x. However, they only focused on the temporal weights but failed to discuss how to choose the spatial weights which is more interesting in image analysis. Thomaz et al. (2010) introduced a supervised spatially weighted version of PCA (SSWPCA) by using a linear discriminant analysis (LDA) to determine spatial discriminant weights for x in a two-class classification setting and then applying PCA to the sample correlation matrix weighted by those spatial weights. SSWPCA is limited to binary responses and su ers from the “p >> N” problem, which requires further regularization. Recently, Pinto da Costa et al. (2011) proposed another weighted version of PCA based on a weighted rank correlation coe cient using rankings of original data, which is not appropriate for imaging data. Allen et al. (2011) proposed a generalized least squares matrix decomposition framework for two-way regularization PCA, while explicitly accounting for their structural relationship.

The aim of this paper is to develop a supervised dimension reduction method, called Spatially Weighted Principal Component Analysis (SWPCA), for imaging classification. In SWPCA, we introduce two sets of weights including global and local spatial weights, which enables the selection of individual features and the incorporation of both the spatial pattern of imaging data and class label information. We develop an e cient two-stage iterative SWPCA algorithm and its penalized version along with the associated weight determination. We evaluate the finite-sample performance of SWPCA by using two simulation studies and real data analysis, whose results strongly indicate that SWPCA outperforms several competing PCA variants and other competing methods, such as sparse discriminant analysis (SDA; Clemmensen et al., 2011).

The rest of this paper is outlined as follows. In Section 2, we develop the general SWPCA framework and its two-stage algorithm. Section 3 discusses several strategies of determining global and local weights. In Section 4, two simulation studies and real data analysis are conducted to demonstrate the improvement of our SWPCA over other commonly used PCA methods. Concluding remarks and discussions are given in Section 5.

2 Spatially Weighted Principal Component Analysis

2.1 Principal Component Analysis

Principal Component Analysis (PCA) as a basic dimension reduction tool is to project high-dimensional data to a lower dimensional space with a few uncorrelated features, called principal components (PC). Let X = (x₁,..., x_N)^T denote an N × p data matrix of rank q ≤ min(N, p), where N is the number of observations, p is the number of features, and x_i = (x_ij) is a p × 1 vector of features from the i-th object. Denote X̃ = X – 1_Nμ^T as the centered data matrix, where 1_N is an N × 1 vector of ones and μ = (μ₁, · · · ,μ_p)^T is a p × 1 mean vector. Let I_q be a q × q identity matrix. PCA finds a lower-dimensional representation that maximizes the variance of projections. Numerically, PCA can be easily derived by Singular Value Decomposition (SVD) method as follows:

$${\tilde{\mathit{X}}}_{N\times p}={\mathit{U}}_{N\times q}{\mathit{D}}_{q\times q}{\mathit{V}}_{p\times q}^T,$$ (1)

where the columns of A = UD = X̃V are PCs, the columns of V = (v ,..., v_p)^T are principal component directions (principal axes), D is a q × q diagonal matrix with singular values, and the columns of U and V are orthonormal such that U^TU = V^TV = I_q. In image analysis, the data matrix X consists of N images as rows, and each row (i.e., x_i) represents a vectorized image of dimension p, where p is the number of pixels/voxels of the image and generally p >> N. When applying PCA to image data, the mean vector μ is the mean image and the columns of V are called eigenimages.

Alternatively, PCA can be interpreted as approximating the original data in the high-dimensional space by using a low-rank factor model. Specifically, the rank-q factor model can be written as

$${\mathit{x}}_i=\mu +\mathit{V}{\mathit{a}}_i+{∊}_i.$$ (2)

The PCA is then taken to minimize the reconstruction error (RE) defined as the squared distance between the original data and its rank-q approximation as follows:

$${\mathcal{E}}_{pca}=\sum _{i=1}^N{\Vert {\mathit{x}}_i-\mu -\mathit{V}{\mathit{a}}_i\Vert }_2^2=\sum _{i=1}^N\sum _{j=1}^p{({\tilde{x}}_{ij}-{\mathit{v}}_j^T{\mathit{a}}_i)}^2,$$ (3)

where ${\Vert \cdot \Vert }_2$ is the L₂ norm of a vector and x̃_ij = x_ij –μ_j. As seen from (3), ${\mathcal{E}}_{pca}$ can be represented as a summation of individual squared distance for each image at each location (feature), where all the features are treated equally and “independently”. In this sense, standard PCA ignores the underlying spatial pattern of image data, since ${\mathcal{E}}_{pca}$ remains the same no matter where each feature is located. Although the standard PCA loses the spatial information, this is not the case for SWPCA developed below, since we can explicitly incorporate such spatial information by introducing locally spatial weights, which depend on both the edge set ${\mathcal{D}}_E$ and the spatial smoothness of imaging data.

2.2 Spatially Weighted PCA (SWPCA)

In this subsection, we develop a SWPCA to find a lower dimensional representation of imaging data by explicitly accounting for their spatial feature. Since each image x_i consists of p correlated features with clustered spatial structure, PCA may not be well suitable for correlated imaging data. However, SWPCA explicitly incorporates spatial information by introducing two sets of spatial weights to the reconstruction error. Such spatial weights include (i) global weights for the selective treatment of individual features and (ii) local spatial weights for the incorporation of the spatial smoothness and correlation of imaging data.

Let w_j be the global spatial weight for the j-th feature of x_i with ${\sum }_{j=1}^p{w}_j=p$. Let B(j; h) be a neighborhood of the j-th feature at scale h and ω(j, d; h) be the local spatial weight for each neighboring feature d within B(j; h) of feature j such that ${\sum }_{d\in B(j;h)}\omega (j,d;h)=1$. The SWPCA is taken to minimize a weighted reconstruction error (WRE) given by

$${\mathcal{E}}_{swpca}(\mathit{A},\mathit{V};h)=\sum _{i=1}^N\sum _{j=1}^p{w}_j\sum _{d\in B(j;h)}\omega (j,d;h){\{{\tilde{x}}_{id}\left(h\right)-{\mathit{v}}_j^T{\mathit{a}}_i\}}^2,$$ (4)

where A = (a₁ ,..., a_N)^T and V = (v₁,..., v_p) are the N × q and p × q matrices, respectively. Moreover, ${\tilde{x}}_{id}\left(h\right)=x_{id}-{\sum }_{d^{\prime }\in B(d;h)}\omega (d,d^{\prime };h){\stackrel{‒}{x}}_{d^{\prime }}$ is the d-th feature of the centered data ${\tilde{\mathit{x}}}_i\left(h\right)={\mathit{x}}_i-{\widehat{\mu }}_w\left(h\right)$, in which ${\widehat{\mu }}_w\left(h\right)={\left\{{\sum }_{d^{\prime }\in B(d;h)}\omega (d,d^{\prime };h){\stackrel{‒}{x}}_{d^{\prime }}\right\}}_p$ and $\stackrel{‒}{\mathit{x}}={\left\{{\stackrel{‒}{x}}_{d^{\prime }}\right\}}_p=\left({\sum }_{i=1}^N{\mathit{x}}_i\right)∕N$ are the weighted and simple mean images, respectively. The lower-dimensional representation of SWPCA is obtained by minimizing ${\mathcal{E}}_{swpca}(\mathit{A},\mathit{V};h)$ as follows:

$$({\mathit{A}}_h,{\mathit{V}}_h)=\underset{\mathit{A},\mathit{V}}{\arg \min }{\mathcal{E}}_{swpca}(\mathit{A},\mathit{V};h).$$ (5)

Without making any confusion, we omit the script h in most notations.

The global and local weights play a critical role in SWPCA. Specifically, the global weights W_G = {w_j} play a feature selection role and enable a selective treatment of di erent features by upweighting more important features and downweighting noninformative features. Moreover, since imaging data are spatially correlated and contain spatially contiguous regions with sharp edges, the local spatial weights W_L = {ω(j, d; h)} allow us to capture the spatial smoothness of imaging data and accommodate the spatial dependence among imaging features. The scale parameter h can vary in a multiscale manner, while the shape of the neighborhood sets can vary across h and di erent applications. Furthermore, SWPCA provides a supervised dimension reduction solution by incorporating outcome information via the introduced global and spatial weights. In image classification, the global weights can be assigned according to the discriminative ability of each pixel/voxel, i.e., the association between each pixel/voxel in X and the class information in Y ; the local spatial weights can be determined based on the discriminative similarity of neighboring pixel/voxel. More discussions about how class information can be incorporated in SWPCA are given in Section 3.

SWPCA can be regarded as a generalization of PCA, SPCA, and WPCA. For instance, when ω(j, d; h) = 1(j = d), where 1(·) is the indicator function of an event, SWPCA reduces to WPCA with spatial weights. If ω(j, d; h) = 1(j = d) and w_j = 1 for all j and d, (4) reduces to (3) which is the standard PCA problem. If we set ω(j, d; h) = 1(j = d) for all j, d and w_j = 1 only for selected “top” features and 0 for other features, SWPCA reduces to SPCA. More discussions on various choices of these weights and neighborhood scale h are given in Section 3.

We reformat ${\mathcal{E}}_{swpca}(\mathit{A},\mathit{V};h)$ as follows. Let ${\mathit{X}}_h\left\{{\tilde{x}}_{ij}\left(h\right)\right\}=\left\{{\sum }_{d\in B(j,h)}\omega (j,d;h){\tilde{x}}_{id}\right\}$ denote an N × p locally weighted data matrix and ${\mathit{X}}_{\mathit{W},h}={\mathit{X}}_h{\mathit{W}}_p^{1∕2}$, where W_p =diag(w₁, ...,w_p) and ${\mathit{W}}_p^{1∕2}=\mathrm{diag}(\sqrt{w_1},\dots ,\sqrt{w_p})$. Without loss of generality, we assume that all global spatial weights are non-zero for the sake of notation. Even for W_G with zero weights, all results below are valid since only features with non-zero w_j are actually included for computation. We obtain the following lemma, whose proof can be found in the Appendix.

Lemma 1 Minimizing (4) is equivalent to

$$\underset{\mathit{A},\mathit{V}}{\min }\left\{{\Vert {\mathit{X}}_{W,h}-{\mathit{AV}}^T{\mathit{W}}_p^{1∕2}\Vert }_F^2\right\}=\underset{\mathit{A},\mathit{V}}{\min }\left\{Tr\left\{({\mathit{X}}_h-{\mathit{AV}}^T){\mathit{W}}_p{({\mathit{X}}_h-{\mathit{AV}}^T)}^T\right\}\right\},$$ (6)

where ${\Vert \mathit{M}\Vert }_F=\sqrt{Tr\left(\mathit{M}{\mathit{M}}^T\right)}$ is the Frobenius norm.

Equation (6) is invariant to arbitrary rotations of A and V such that AV^T =ÃṼ^T . Such invariant issue is usually solved by imposing orthonormal constraint, i.e., V^TV = I_q. However, such constraint is no longer appropriate for SWPCA, when the global spatial weights are incorporated for individual treatment and selection of features that regulate V . Instead of restricting V , we impose A^TA = I_q, which greatly facilitates the computation of SWPCA.

For ultra-high dimensional data, that is p >> N, PCA su ers from several major limitations. For instance, it is well-known that sample eigenvalues and eigenvectors can be inconsistent as p goes to infinity. Moreover, naive approaches to PC score prediction can be substantially biased towards 0 in the analysis of high-dimensional data. To avoid such limitations, various penalized PCA methods have been developed (Journée et al., 2010; Shen and Huang, 2008; Huang et al., 2008a; Zou et al., 2006; Johnstone and Lu, 2009; Huang et al., 2008b; Witten et al., 2009). Specifically, we consider a regularized SWPCA by including an additional penalty term on V to (6). The minimization problem becomes

$$\underset{\mathit{A},\mathit{V}}{\min }\left\{{\Vert {\mathit{X}}_{W,h}-{\mathit{AV}}^T{\mathit{W}}_p^{1∕2}\Vert }_F^2+\sum _{k=1}^q{\lambda }_k{\Vert {\mathit{v}}_{ck}\Vert }_1\right\},$$ (7)

where v_ck is the k-th column vector of V = (v_c1,..., v_cq) and ${\Vert {\mathit{v}}_{ck}\Vert }_1={\sum }_{j=1}^p\mid v_{jk}\mid$ is the L₁-norm of the p × 1 vector v_ck.

2.3 Two-stage Iterative Algorithms

We develop e cient two-stage iterative SWPCA algorithms to solve the minimization problems (6) and (7). We obtain the following two lemmas pertinent to the algorithm for solving (6).

Lemma 2 Given V , A that minimizes (4) subject to A^T A = I_q is A = PU^T, where P and U are orthogonal matrices obtained from the SVD of X_hW_pV = PDU^T.

Lemma 3 Given A, V that minimizes (4) is $\mathit{V}={\mathit{X}}_h^T\mathit{A}{\left({\mathit{A}}^T\mathit{A}\right)}^{-1}$.

The above lemmas lead to our two-stage iterative SWPCA Algorithm 1 as follows.

Algorithm 1 SWPCA Algorithm

1. Use V derived by standard PCA as an initial value;

2. Given V , conduct SVD on X_hW_pV = PDU^T and then update A = PU^T ;

3. Given A obtained from (b), update $\mathit{V}={\mathit{X}}_h^T\mathit{A}$;

4. Repeat the steps (b) and (c) until convergence;

5. Standardize the final V to obtain Ṽ and Ã.

Our SWPCA algorithm provides a simple and efficient way for the minimization problem (4) with the constraint on A. As a special case of SWPCA, the WPCA with spatial weights can be realized by our SWPCA Algorithm 1, which overcomes the rotational ambiguity problem of the Algorithm in Skočaj et al. (2007). According to our experience, our Algorithm 1 converges much faster compared with that for WPCA. Moreover, keeping V free of scale constraint allows direct extension of our SWPCA algorithm to a sparse version for ultra-high dimensional data. We obtain the following lemma for the sparse case.

Lemma 4 Given fixed A and A^TA = I_q, we have the following results:

1. the minimization problem (7) is equivalent to that of the weighted Lasso given by

   $${\widehat{\mathit{v}}}_{ck}=\underset{{\mathit{v}}_{ck}}{\arg \min }\left\{{\Vert {\mathit{v}}_{ck}-{\mathit{X}}_h^T{\mathit{a}}_{ck}\Vert }^2+{\lambda }_k\sum _{j=1}^p\mid v_{jk}\mid ∕w_j\right\}fork=1,\dots ,q,$$ (8)

   where v_ck is the k-th column vector of V and a_ck is the k-th column of A;
2. the soft thresholding solution of (8) is ${\widehat{\mathit{v}}}_{ck}={\left\{{\widehat{v}}_{jk}\right\}}_{p\times 1}$ with

   $${\widehat{v}}_{jk}=sign\left\{{\left({\mathit{X}}_h^T{\mathit{a}}_{ck}\right)}_j\right\}{\{\mid {\left({\mathit{X}}_h^T{\mathit{a}}_{ck}\right)}_j\mid -{\lambda }_k∕\left(2w_j\right)\}}_{+}forj=1,\dots ,p,$$ (9)

   where sign(·) is the sign function, (·)_j denotes the j-th element of the argument, and {·}₊ is the truncation function that returns the argument if it is nonnegative or 0 otherwise.

Lemma 4 has several important implications. Lemma 4 (i) reformats (7) as a weighted lasso problem of Zou et al. (2006). This result yields an explicit solution ${\widehat{\mathit{v}}}_{ck}$ in Lemma 4 (ii). Moreover, for the features with small spatial weights, the regularized SWPCA automatically increases their penalties and thus their associated ${\widehat{v}}_{jk}$'s have a higher chance to be shrunk to zero. Thus, SWPCA is very useful for eliminating many uninformative features in imaging data. Based on Lemma 4, Algorithm 1 can be extended to the penalized SWPCA algorithm as follows.

Algorithm 2 Penalized SWPCA Algorithm

1. Use V derived by the standard PCA as an initial value;

2. Given V , apply SVD on X_hW_pV = PDU^T and then set A = PU^T ;

3. ’ Given A obtained from (b), update V = {v_jk}_p×q, where v_jk is calculated according to (9);

4. ’ Repeat the steps (b) and (c’) until convergence;

5. Standardize the final V to obtain Ṽ and Ã

The penalized SWPCA algorithm proposed above provides an efficient way to obtain a low-dimensional representation of X even for ultra-high dimensional data. Besides, our penalized SWPCA algorithm can be used to realize the sparse PCA method proposed by Shen and Huang (2008) since SWPCA is considered as a generalization of standard PCA. The sparse PCA algorithm in Shen and Huang (2008) computes PCs in a sequential way, whereas our Algorithm 2 computes all PCs simultaneously at once. Thus, Algorithm 2 may be more appealing and efficient.

One important application of SWPCA is to do prediction. We consider the data matrix with new observations and its locally weighted data matrix, which are denoted by X* and ${\mathit{X}}_h^{\ast }$, respectively. LetÃ* be the low-dimensional projection of X* onto the principal axes Ṽ derived from SWPCA. We obtain the following lemma.

Lemma 5 Given V , the A that minimizes (4) is A = (X_hW_pV)(V^TW_pV)^–1.

Based on Lemma 5,Ã* can be estimated by using $\left({\mathit{X}}_h^{\ast }{\mathit{W}}_p\tilde{\mathit{V}}\right){\left({\tilde{\mathit{V}}}^T{\mathit{W}}_p\tilde{\mathit{V}}\right)}^{-1}$. Withà , class prediction can be efficiently performed using this low-dimensional representation.

3 Spatial Weights for Imaging Classification

In this section, we discuss how to choose various spatial weights and how the class information can be incorporated for imaging classification.

3.1 Global Spatial Weights

The global weights W_G = {w_j} play a feature selection role in SWPCA. For instance, for classification problem, we may use each feature's discriminative importance to assign each component of W_G. Specifically, let θ_j denote a measure of the association between the j-th feature and the class information, i.e., θ_j is a function of the j-th pixel/voxel of image data X and class information Y . Each w_j can be defined as a function of θ_j as

$$w_j=f\left({\theta }_j\right)\text{for}j=1,\dots ,p.$$ (10)

Examples of θ_j include the Pearson correlation and test statistics, among many others. A simple example is to use the Pearson correlation between each feature and class label information. More informative features for classification (or high correlation) are assigned more weights, whereas noninformative features (e.g., correlation less than a given threshold) can be discarded by setting w_j = 0. In this case, θ_j is the Pearson correlation and $w_j=p\mid {\theta }_j\mid ∕{\sum }_j\mid {\theta }_j\mid$. Additionally, the importance scores used in SPCA can also be considered for W_G. Another example is to fit a voxel-wise regression model with imaging data at each location as responses and the class label as covariates. Specifically, we consider an L-class classification problem and define y_il = 1 if i is in class l for i = 1,..., N and l = 1,..., L and 0 otherwise. Consider a voxel-wise linear regression model by fitting x_ij = y^T_iθ_j + ε_ij for i = 1,..., N and j = 1,..., p, where y_i = (1, y_i1,..., y_i,L–1^T and θ_j contains the discriminative information of features at location j. Then, f(θ_j) can be a test statistic and/or its associated p-value for testing H₀ : θ_j = 0 at location j.

3.2 Local Spatial Weights

The local spatial weights W_L = {ω(j, d; h)} play a critical role in incorporating spatial smoothness and correlation of imaging data in SWPCA. This is extremely important for imaging data, since imaging data are spatially dependent and contain contiguous regions with sharp edges in nature. Let B(j, h) be a set of neighboring locations of the j-th feature at scale h. The local weight ω(j, d; h) usually characterizes the “similarity” between feature j and features d ∈ B(j, h) and/or the “similarity” between locations d and j. Specifically, we define ω(j, d; h) at scale h as

$$\omega (j,d;h)=\frac{K_1\{D_1(d,j)∕h\}\cdot K_2\{D_2({\theta }_d,{\theta }_j)∕C_N\}1(d\in B(j,h))}{\sum _{d^{\prime }\in B(j,h)}{K}_1(D_1(d^{\prime },j)∕h\}\cdot K_2\{D_2({\theta }_{d^{\prime }},{\theta }_j)∕C_N\}},$$ (11)

where D₁(d, j) denotes the spatial distance between locations d and j, D₂( θ_d, θ_j) represents the discriminative similarity between θ_d and θ_j, K₁(·) and K₂(·) are two decreasing kernel functions, and h and C_N are bandwidth parameters that may depend on N. The decreasing kernel function K₁(·) gives less weight to the voxel d ∈ B(j, h), whose location is far from the voxel j. The kernel K₂(·) downweights the voxels d with large D₂(θ_d, θ_j), which indicates a large di erence between θ_d and θ_j. By following Polzehl and Spokoiny (2006) and Li et al. (2011), we set K₁(x) = (1 – x)₊ and K₂(x) = exp(–x), which demonstrated excellent performance in many imaging applications. Moreover, the shape and size of B(j, h) can vary across applications and with h.

3.3 Scale Size h

The scale size h plays a critical role in the amount of features incorporated from neighboring voxels in B(j, h) for each j. A simple approach is to fix h according to some prior or empirical information. However, a small h may miss important spatial information, whereas a large h may smooth out some local details and dramatically increase the computational burden. Alternatively, we may consider a sequence of nested neighborhoods corresponding to multiple scales at each location. Specifically, let h = {h₀ < h₁ < ... < h_S} be a sequence of scales with h₀ = 0 and h_S being the maximum scale. The scales can be chosen based on previous studies or empirical experiences. For example, scales can be defined as the radius of spherical neighborhood in a form of {h_s = c^s} with constant c > 1. In our numerical examples, we used c = 1.2 which balanced the computation intensity without losing important spatial information. One may choose an optimal h based on a specific criterion, such as WRE, and then use the PCs extracted based on the optimal h for imaging classification. Alternatively, one may integrate the PCs extracted from all scales h for imaging classification.

For imaging classification, we propose a multi-scale procedure to determine W_G and W_L across multiple scales. Without loss of generality, we consider the cross-sectional studies so that (x_i, y_i) are independent across subjects. Specifically, at a given scale h, we consider a weighted likelihood function given by

$$p(\mathit{X}\mid \mathit{Y},\theta )=\prod _{i=1}^N\prod _{j=1}^p\left\{\prod _{d\in B(j,h)}p{(x_{id}\mid {\mathit{y}}_i,{\theta }_j)}^{\omega (j,d;h)}\right\},$$ (12)

where X and Y , respectively, denote the imaging and class information and p(x_id|y_i, θ_j) is the likelihood function of x_id given y_i. Moreover, as discussed in the voxel-wise linear regression model in Section 3.1, θ_j may contain the discriminative information of features at j. Based on the weighted likelihood function (12), Li et al. (2011) developed a multiscale adaptive regression model (MARM) to spatially and adaptively calculate the estimate of θ_j, denoted by ${\widehat{\theta }}_j\left(h\right)$, as the scale size h ranges from h₀ to h_S. Instead, we borrow the spatial information learned in (12) and the estimated ${\widehat{\theta }}_j\left(h\right)$ to spatially and adaptively construct W_G and W_L across h. We introduce a multi-scale algorithm as follows.

Algorithm 3 Multi-scale Algorithm

Given a series of scales h₀ = 0 < h₁ < ... < h_S, for each feature j,

1. Begin with h₀ = 0 with ω(j, d; h₀) = 1 when d = j and 0 otherwise, calculate the initial association estimate at scale h₀ denoted as ${\widehat{\theta }}_j\left(h_0\right)$ and set s = 1.

2. At scale h_s, update the association estimate ${\widehat{\theta }}_j\left(h_s\right)$ by maximizing (12) based on ω(j, d; h_s–1).

3. Calculate ω(j, d; h_s) in (11) using updated ${\theta }_j={\widehat{\theta }}_j\left(h_s\right)$ and ${\theta }_d={\widehat{\theta }}_d\left(h_s\right)$ and update w_j according to (10) by using ${\theta }_j={\widehat{\theta }}_j\left(h_s\right)$. If s < S, let s=s+1.

4. Repeat steps (b) and (c) until the stopping criterion is met or s = S.

The stopping criterion in Algorithm 3 can be either global or local criteria. For instance, for the global criteria, we may stop the algorithm if WRE cannot be further decreased. For the local criteria at each location j, we may check the improvement of θ_j.

4 Numerical Examples

In this section, we conducted two simulation studies and real data analysis to examine the performance of SWPCA in L-class classification problems, where L is a positive integer. In each simulation study, we compared our SWPCA with PCA, SPCA, and WPCA. For SPCA, we used the importance scores used in Bair et al. (2006) to select “top” important features. For WPCA, we considered two WPCAs by using two different spatial weights which are based on the importance scores of SPCA and W_G of SWPCA, respectively. For PCA, SPCA, and WPCA, imaging data were smoothed using an isotropic Gaussian kernel with different degrees of smoothness including no smoothing, moderate smoothing, and over-smoothing. For the sake of space, we only reported the best results under the moderate degree of smoothness. For SWPCA, we used Algorithm 3 with spherical neighborhoods and {h_s = 1.2^s : s = 1,..., S = 5} to determine optimal scales locally and its associated W_G and W_L. Specifically, we used -log₁₀ of the FDR (False Discovery Rate) corrected p-values for testing the null hypothesis of no group di erences as our global spatial weights W_G. For the local spatial weights, we chose the Euclidean norm for D₁(·), the Mahalanobis norm for D₂(·), and C_N = log(N)χ²_L–1(0.95), where χ²_L–1(b) is the upper 1 – b percentile of the χ² distribution with L – 1 degrees of freedom. For the penalized SWPCA, denoted as PSWPCA, we used the same spatial weights as those of SWPCA and varied λ_k across 0.5, 1.0, 2.0, 5.0, and 10.0. Extracted PCs were then used for class prediction. Since the proposed method is more efficient requiring less components, we chose number of PCs retained based on the amount of total sample variance explained by the standard PCA to assure that at least a certain amount of total variance can be accounted for. Since comparison of different classification methods is not the interest of this paper, we just used three standard classification methods including (i) linear regression (REG), (ii) k-nearest neighbor (k-NN) classification, and (iii) support vector machine (SVM) to evaluate the performance of different PCA methods.

4.1 Simulation Studies

For each simulation study, a total of 100 3D-images were simulated and randomly split into a training set with N = 60 images and a test set of 40 images. We repeated each simulation 100 times, and evaluated the classification performance of different methods by using the average misclassification rate. For simulation studies, the results with K = 2 PCs retained were presented for graphical illustration purpose to display the low-dimensional representation of the simulated data constructed by the PCs extracted by different dimension reduction methods. With 2 PCs, the standard PCA can already account for on average around 60% of the total variance in Simulation I and around 50% in Simulation II.

4.1.1 Simulation Study I

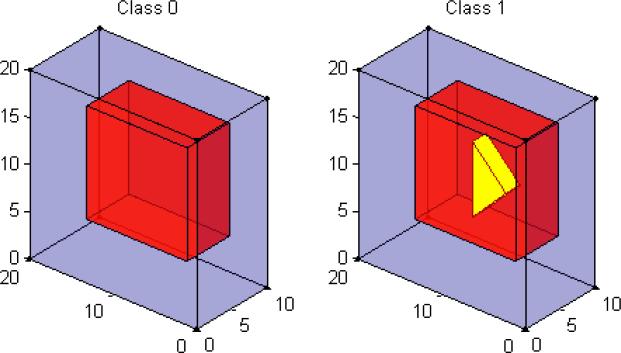
In this study, we simulated 20×20×10 3D-images from a linear regression model: x_ij = θ_j0+ θ_j1y_i+ ε_ij, where ε_ij ~ N(0, 4) for i = 1,..., 100 and j = 1,...,4000. The feature dimension p = 4000 is much larger relative to the training sample size N=60. This is a two-class classification problem with L = 2. The class label y_i is coded as 0 and 1. Thus, μ₀ = {θ_j0 : j = 1,...,4000} is the true mean image of Class 0, whereas μ₁ = {θ_j0 + θ_j1 : j = 1,...,4000} is the true mean image of Class 1. See Figure 1 for a graphical illustration. For μ₀, we divided the 3D image into two different regions of interest (ROIs) with different shapes and then varied θ_j0 as 0 and 1, respectively, across these two ROIs. For μ₁, we divided the 3D image into three different ROIs with different shapes and then varied θ_j0 + θ_j1 as 0, 1, and 2, respectively, across these three ROIs. Figure 1 reveals that the di erence between the two classes only lies in the yellow triangular prism region.

Figure 1.

True mean images for Simulation I. The left panel is the true mean image of Class 0: μ₀, in which purple and red colors represent θ_j0 = 0,1, respectively; the right panel is the true mean image of Class 1: μ₁, in which purple, red, and yellow colors represent θ_j0 + θ_j1 = 0, 1, 2, respectively.

We presented the classification results in Table 1 based on the results obtained from the 100 simulated datasets. We only presented the average misclassification rates and the standard deviations (SD) of misclassification errors. Table 1 reveals that the classification results from the three classification methods show similar pattern across different PCA methods. For SPCA, we varied the number of “top” voxels as 50, 100, 200, 400, and 1000, and the algorithm based on the top 50 voxels outperforms the rest. Overall, SPCAs greatly improve the class prediction over PCA by screening out many uninformative voxels. We denote two WPCAs using the importance scores of SPCA and using W_G of SWPCA as their spatial weights by WPCA-1 and WPCA-2, respectively. The WPCA-1 performs better than PCA, as good as SPCA with relatively large number of top selected voxels, but worse than SPCA with less selected voxels. The WPCA-2 improves the class prediction over WPCA-1 and performs as good as SPCA based on top 50 voxels. Furthermore, SWPCA using Algorithm 1 significantly reduces the misclassification rate to only 2.6% for REG, 3.0% for 5-NN, and 3.3% for SVM with much smaller standard deviations. Finally, PSWPCA based on Algorithm 2 further reduces the misclassification rate.

Table 1.

Average Misclassification Percentage for Simulation I

	PCA	SPCA					WPCA-1	WPCA-2	SWPCA	PSWPCA
	ALL	50	100	200	400	1000	ALL	ALL	ALL	ALL
REG	.302 (.078)	.126 (.052)	.132 (.052)	.142 (.055)	.162 (.057)	.205 (.064)	.199 (.064)	.130 (.056)	.026 (.025)	.025 (.024)
k-NN	.338 (.071)	.135 (.049)	.141 (.049)	.152 (.050)	.182 (.053)	.225 (.071)	.186 (.055)	.156 (.059)	.030 (.029)	.027 (.025)
SVM	.327 (.078)	.140 (.054)	.147 (.055)	.159 (.055)	.183 (.059)	.226 (.072)	.215 (.067)	.152 (.055)	.033 (.029)	.028 (.026)

Standard deviations are in parenthesis. For SPCA, the number of “top” selected voxels used in the algorithm are considered to be 50, 100, 200, 400, and 1000.

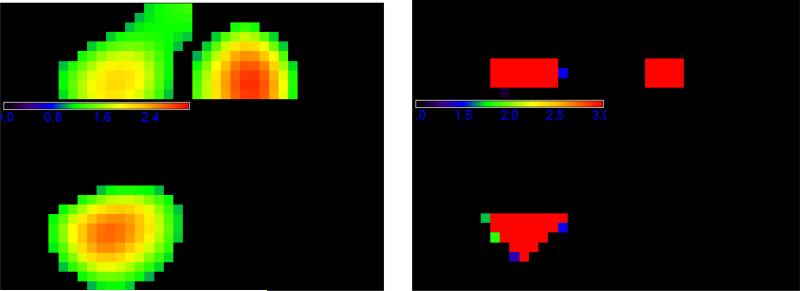
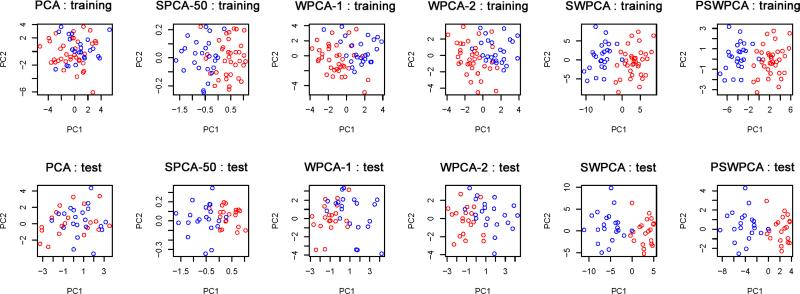
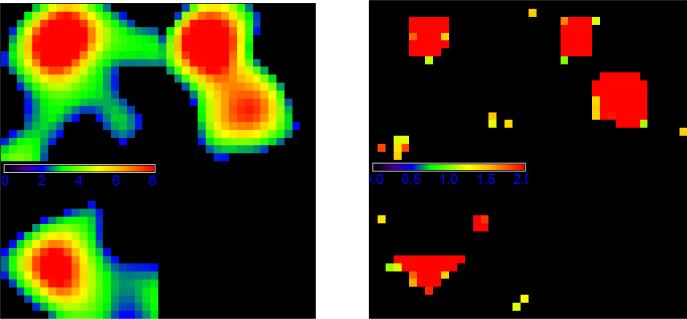
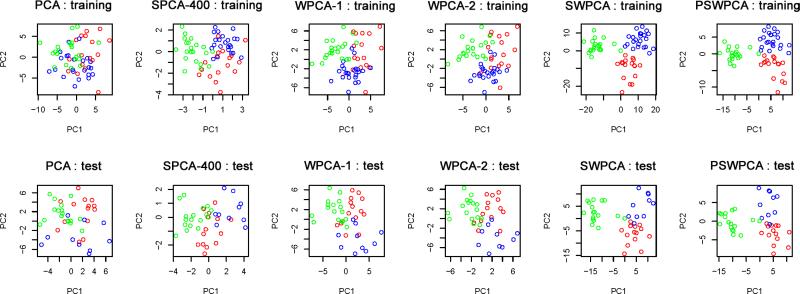
The two different sets of spatial weights used in WPCA-1 and WPCA-2 are illustrated in Figure 2. Figure 2 shows that W_G of SWPCA clearly identifies those “true” voxels which are located in the triangular prism. In contrast, the importance scores of SPCA can only roughly locate the region but not the shape, along with many false positive voxels. Let n_t denote the number of true informative voxels. In Simulation I, n_t = 75 voxels forms the triangular prism. To further evaluate the “feature selection” ability of the weights, we calculate the true positive rate (TP) as the ratio of the true informative voxels to the top ranked n_t voxels. We have TP_SPCA=.63, and TP_SW PCA=.90. These two numbers also explain why WPCA-2 works better than WPCA-1. Moreover, the performance of SPCA is sensitive to the threshold used to determine significant features in SPCA, whereas WPCAs and SWPCAs can include all the voxels by weighing differently without concerning the thresholding issue. To visualize the performance of dimension reduction, we plotted the first two extracted PCs obtained from different PCA methods for one simulated dataset in Figure 3. We observed that the two PCs of SWPCA and PSWPCA can easily separate the two classes, whereas those of other PCA methods cannot.

Figure 2.

Weight illustration for Simulation I: a three-view slice illustration at coordinate (13, 7, 3) of the spatial weights used for WPCA-1 (left panel) and WPCA-2 and SWPCA (right panel). The left panel contains the importance scores of SPCA, while the right panel contains the W_G of SWPCA, i.e., the FDR-corrected -log 10 p-value map.

Figure 3.

Two-dimensional representation for Simulation I. The first two PCs from PCA, SPCA-50 (SPCA based on top 50 voxels), WPCA-1, WPCA-2, SWPCA, and PSWPCA are plotted. The training set (top panels) and test set (bottom panels) are used to extract the PCs. Points with blue and red colors represent true Class 0 and Class 1, respectively.

For additional comparisons, we also applied two non-PCA-type of supervised dimension reduction methods including sparse partial least squares (SPLS; Chung and Keles, 2010) and sparse discriminant analysis (SDA; Clemmensen et al., 2011) to the simulated datasets. See Table 2 for detailed results. For SPLS, since different classifiers can be used, we also applied REG (SPLS-REG), k-NN (SPLS-kNN), and SVM (SPLS-SVM) besides the default one in order to have additional comparisons with various PCA-type of methods presented in Table 1. Table 2 shows that SPLS and SDA yield similar classification performance as SPCA, but they significantly underperform our proposed SWPCA and PSWPCA.

Table 2.

Average Misclassification Percentage for Simulation I (Non-PCA Methods)

SPLS-REG	SPLS-kNN	SPLS-SVM	SPLS	SDA
.130 (.052)	.139 (.056)	.156 (.066)	.128 (.050)	.120 (.050)

Standard deviations are in parenthesis.

4.1.2 Simulation Study II

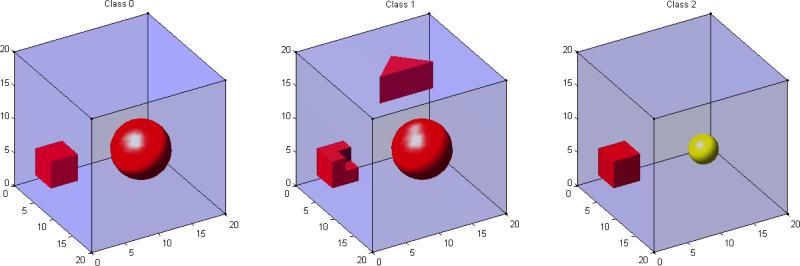
In this simulation study, we simulated 20 × 20 × 20 3D-images from L = 3 classes (coded as 0, 1, 2) according to a linear regression model: x_ij = θ_j0 + θ_j1y_i1 + θ_j2y_i2 + ε_ij, where ε_ij ~ N(0, 9) for i = 1,...,100 and j = 1,...,8000 and y_i1 and y_i2 are dummy variables for Class 1 and Class 2, respectively. Thus, μ₀ = {θ_j0} is the true mean image of Class 0, μ₁ = {θ_j0 + θ_j1} is the true mean image of Class 1, and μ₂ = {θ_j0 + θ_j2} is the true mean image of Class 2. Figure 4 shows the true mean images for each class in 3D. For μ₀, we divided the 3D image into two different ROIs with different shapes and then varied θ_j0 as 0 and 1, respectively, across these two ROIs. For μ₁, we divided the 3D image into two different ROIs with different shapes and then varied θ_j0 + θ_j1 as 0 and 1, respectively, across these two ROIs. For μ₂, we divided the 3D image into three different ROIs with different shapes and then varied θ_j0 + θ_j2 as 0, 1, and 2, respectively, across these three ROIs. Figure 4 reveals that the di erences between the three classes lie in the yellow and red regions.

Figure 4.

True mean images for Simulation II. The left panel is the true mean image of Class 0: μ₀, in which two ROIs with purple and red colors represent θ_j0 = 0 and 1, respectively; the middle panel is the true mean image of Class 1: μ₁, in which two ROIs with purple and red colors represent θ_j0 + θ_j1 = 0 and 1, respectively; the right panel is the true mean image of Class 2: μ₂, in which three ROIs with purple, red, and yellow colors represent θ_j0 + θ_j2 = 0, 1, and 2, respectively.

We presented the classification results in Table 3 based on the results obtained from the 100 simulated datasets. In Table 3, three classification methods, REG, k-NN, and SVM, show similar classification results across different PCA methods. For SPCA, the algorithm based on the 400 or 1,000 top voxels outperforms the rest. Overall, SPCA moderately improves the class prediction over the standard PCA. The WPCA-1 algorithm outperforms PCA and is comparable to SPCAs in cases of 200 or more top voxels. The WPCA-2 algorithm shows better performance than SPCA and WPCA-1. Furthermore, SWPCA and PSWPCA outperform other competing methods and greatly reduce the misclassification rate. The results for the non-PCA methods are given in Table 4. Similarly as Simulation I, SPLS and SDA yield similar but significantly poorer classification performance comparing with the best SWPCA results.

Table 3.

Average Misclassification Percentage for Simulation II

	PCA	SPCA					WPCA-1	WPCA-2	SWPCA	PSWPCA
	ALL	(50)	(100)	(200)	(400)	(1000)	ALL	ALL	ALL	ALL
REG	.461 (.078)	.372 (.126)	.343 (.118)	.302 (.102)	.275 (.084)	.274 (.069)	.305 (.075)	.246 (.069)	.096 (.076)	.092 (.080)
k-NN	.514 (.093)	.381 (.118)	.364 (.112)	.315 (.105)	.295 (.086)	.299 (.075)	.332 (.077)	.268 (.069)	.099 (.079)	.085 (.078)
SVM	.477 (.097)	.372 (.117)	.346 (.112)	.306 (.105)	.278 (.078)	.288 (.067)	.317 (.074)	.258 (.073)	.099 (.076)	.083 (.078)

Standard deviations are in parenthesis. For SPCA, the number of “top” selected voxels used in the algorithm are considered to be 50, 100, 200, 400, and 1000.

Table 4.

Average Misclassification Percentage for Simulation II (Non-PCA Methods)

SPLS-REG	SPLS-kNN	SPLS-SVM	SPLS	SDA
.341 (.119)	.356 (.125)	.337 (.120)	.339 (.112)	.277 (.076)

Standard deviations are in parenthesis.

Figure 5 illustrates two different sets of spatial weights used in WPCA-1 and WPCA-2. It shows that W_G of SWPCA identifies the “true” voxels located in the triangular and cubic shapes. However, the importance scores of SPCA roughly identifies the location of true voxels, but not the shapes. In this simulation study, there are 409 truly informative voxels, and we have TP_SPCA=.59 and TP_SWP CA=.81. In Figure 6, we draw the plots of the first two extracted PCs obtained from all PCA methods for one simulated dataset. From Figure 6, we observe that SWPCA and PSWPCA perform well in separating three classes, but other PCA method do not.

Figure 5.

Weight illustration for Simulation II: a three-view slice illustration at coordinate (7, 6, 16) of the spatial weights used for WPCA-1 (left panel) and WPCA-2 and SWPCA (right panel). The left panel contains the importance scores of SPCA, while the right panel contains the W_G of SWPCA, i.e., the FDR-corrected -log 10 p-value map.

Figure 6.

Two-dimensional representation for Simulation I. The first two PCs for PCA, SPCA-400 (SPCA based on top 400 voxels), WPCA-1, WPCA-2, SWPCA and PSWPCA are plotted. The training set (top panels) and test set (bottom panels) are used to extract the PCs. Points with blue, red, and green colors represent Class 0, Class 1, and Class 2, respectively.

4.2 Real Data Analysis

We applied SWPCA to the Alzheimer's Disease Neuroimaging Initiative (ADNI) data. Alzheimer's Disease (AD) is the most common form of dementia, which progressively causes problems in memory, thinking, behavior, and eventually leads to death. The ADNI study is a large scale multi-site study collecting clinical, imaging, and laboratory data at multiple time points from cognitively normal controls (CN), individuals with amnestic mild cognitive impairment (MCI), and subjects with AD. One of the goals of ADNI is to develop improved methods to track the longitudinal course of AD based on imaging and biomarker data. More information about data acquisition can be found at the ADNI website (www.loni.ucla.edu/ADNI).

“Data used in the preparation of this article were obtained from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database (adni.loni.ucla.edu). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year publicprivate partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer's disease (AD). Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their e ectiveness, as well as lessen the time and cost of clinical trials. The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California, San Francisco. ADNI is the result of e orts of many coinvestigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 subjects but ADNI has been followed by ADNI-GO and ADNI-2. To date these three protocols have recruited over 1500 adults, ages 55 to 90, to participate in the research, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow up duration of each group is specified in the protocols for ADNI-1, ADNI-2 and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2. For up-to-date information, see www.adni-info.org. ”

A subset of the ADNI data including AD patients and CN controls was used here to illustrate the empirical utility of our proposed methods in imaging classification. After removing subjects with missing or low quality imaging data, the data set consists of 390 subjects (218 CN controls and 172 AD patients). Among them, there are 206 males whose mean age is 75.46 years with standard deviation 6.34 years and 184 females whose mean age is 75.50 years with standard deviation 6.40 years. T1-weighted images at the baseline were used for all subjects. The T1-weighted images were preprocessed by standard steps including AC (anterior commissure) and PC (posterior commissure) correction, N2 bias field correction, skull-stripping, intensity inhomogeneity correction, cerebellum removal, segmentation, and registration. After segmentation, the brain were segmented into four different tissues: grey matter (GM), white matter (WM), ventricle (VN), and cerebrospinal fluid (CSF). The imaging pipeline was described in detail in Wang et al. (2011).

We quantified the local volumetric group di erences by generating RAVENS-maps (Davatzikos et al., 2001) for the whole brain and four different types of segmented tissue (GM, WM, VN, and CSF), respectively, using the deformation field obtained during registration. RAVENS methodology is based on a volume-preserving spatial transformation, which ensures that no volumetric information is lost during processing spatial normalization, since this process changes an individual's brain morphology to conform it to the morphology of a template. We obtained the 256 × 256 × 256 RAVENS-maps and then down-sampled them to 128 × 128 × 128 for analysis. A sample RAVENS-map is displayed in the left panel of Figure 7.

Figure 7.

Data and weight illustration for ADNI study. The left panel is a three-view slice illus tration at coordinate (49, 57, 32) of a sample RAVENS-map; the middle panel shows the important scores of SPCA; the right panel illustrates the FDR-corrected – log 10 p-value map used as W_G for WPCA-2, SWPCA and PSWPCA.

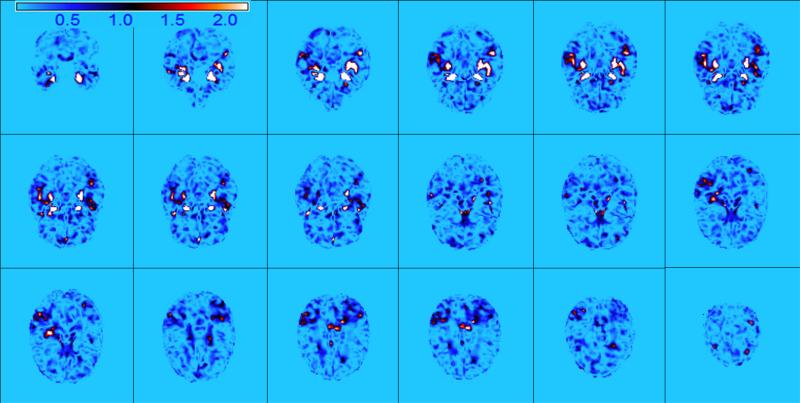
Our goal is to study the empirical performance of SWPCA in classifying subjects from ADNI to AD or CN group based on the whole RAVENS images. We randomly split the imaging data into a training set of 195 images and a test set with the remaining 195 images and repeated this 100 times to calculate the average misclassification rate. For this real data analysis, five PCs were included for classification, which can account for around 90% of the total variance on average in the standard PCA. For PCA, WPCA, and SPCA, the RAVEN images were smoothed by using an isotropic Gaussian kernel with different degrees of smoothness as in the simulation studies. For ultra-high dimensional data like our example, we may pre-filter and assign zero weight to the less “important” voxels instead of assigning non-zero weights to all the voxels in order to improve computational e ciency. For example, for WPCA-2 and SWPCA based on the p-value map, we thresholded all FDR-corrected – log₁₀ p-values at the significance level of 0.01 for W_G. For SPCA, we selected the same number of voxels as the number of non-zero W_G used in SWPCA according to the importance scores. Figure 7 shows some selected views of the importance score image of SPCA and the FDR-corrected – log₁₀ p-value map used in WPCA-2 and SWPCA. Figure 8 presents more slice views of the global spatial weights used in SWPCA and illustrates that some regions of interest in AD studies, such as hippocampus and amygdala, were highly weighted.

Figure 8.

Weight illustration for ADNI study. Selected axial slices show the FDR-corrected -log 10 p-value map used in SWPCA which correctly identifies some important regions reported in the literature for AD, such as hippocampus and amygdala.

In Table 5, we present the classification results that show the similar performance of PCA methods as in the simulation studies. SPCA slightly improves the classification rate over the standard PCA. Both SPCA and WPCA-1 based on the same importance scores show quite similar performance. WPCA-2 performs slightly better than WPCA-1. In addition, SWPCA and PSWPCA outperform all other PCA methods with much lower misclassification rates. Notice that even using simple classification procedures, SWPCA/PSWPCA directly applied to the whole image can already lead to a misclassification percentage around 20% for ADNI data. To illustrate our proposed dimension reduction tool, we applied simple classification procedures. It suggests that the classification performance can be more improved by incorporating more sophisticated procedures.

Table 5.

Average Misclassification Percentage for ADNI Data

	PCA	SPCA	WPCA-1	WPCA-2	SWPCA	PSWPCA
REG	.329 (.029)	.312 (.043)	.307 (.052)	.274 (.029)	.213 (.034)	.198 (.033)
k-NN	.382 (.028)	.343 (.045)	.344 (.052)	.313 (.030)	.254 (.035)	.227 (.041)
SVM	.329 (.029)	.313 (.042)	.310 (.042)	.274 (.030)	.216 (.033)	.215 (.032)

Standard deviations are in parenthesis.

Numerical examples illustrated that SWPCA and its penalized version PSWPCA provided substantial improvement over other commonly used dimension reduction methods in image classification by incorporating spatial and class information via introduced global and local spatial weights. Computationally, SWPCA algorithm provides an efficient implementation, which produces all PCs simultaneously unlike other methods like Shen and Huang (2008) that compute PC one-by-one in a sequential way and converges much faster than the WPCA algorithm by Skočaj et al. (2007) since it does not have arbitrary rotation problem. In practice, the computing time of SWPCA varies depending on the analysis and method used for weight determination.

5 Discussion

This article is to develop a general SWPCA framework to generate low-dimensional representations for high-dimensional imaging classification. By incorporating the global and local spatial weights, SWPCA enables a selective treatment and selection of individual features, accommodates the complex dependence among features of imaging data, and has the ability of utilizing the underlying spatial pattern possessed by imaging data and class label information. SWPCA integrates feature selection, smoothing, and feature extraction in a single framework. In the simulation studies and real data analysis, SWPCA shows substantial improvement over PCA, SPCA, and WPCA.

The contributions of this article are two-fold. Firstly, from an image analysis point of view, our proposal timely responds to a number of growing needs of neuroimaging classification. It may also provide a systematic solution to the integrative analysis of multi-modality imaging data and imaging genetics data (Friston, 2009; Casey et al., 2010). Secondly, from a statistical methodology point of view, our proposal provides a novel and broad framework for the use of covariates with graphic structure to predict clinical outcomes. A large number of models and extensions are potential outcomes within this framework. Although there has been imaging studies utilizing tensor/matrix structure (Li et al., 2005; Park and Savvides, 2007; Li et al., 2010; Zhou et al., 2013), our proposal, to the best of our knowledge, is the first work that integrates the spatial and graphic structure of imaging data into a statistical supervised learning paradigm. Our work can be viewed as a logic extension from the classical classification methods to a functional classification model.

Several important issues need to be addressed in future research. First, we will systematically investigate the theoretical properties of SWPCA and its variations by extending the existing results in the literature (Johnstone, 2001; Baik and Silverstein, 2006; Paul and Johnstone, 2007; Jung and Marron, 2009; Benaych-Georges and Nadakuditi, 2011). Second, we will extend our SWPCA from a classification framework to a regression framework in order to predict more complex univariate and multivariate clinical outcomes. Third, we will develop new global weighting methods based on some joint important feature selection methods and more complex screening methods, such as a robust rank correlation screening in (Li et al., 2012). Many more complexities and new statistical tools will definitely come out these new developments.

A Appendix: Proofs

A.1 Proof of Lemma 1

The WRE ${\mathcal{E}}_{swpca}$ can be rewritten as follows:

$$\begin{array}{cc}\hfill {\mathcal{E}}_{swpon}=& \sum _{i=1}\sum _{j=1}^p{w}_j\sum _{d\in B(j;h)}\omega (j,d;h){({\tilde{x}}_{id}\left(h\right)-{\mathit{v}}_j^T{\mathit{a}}_i)}^2\hfill \\ \hfill =& \sum _{i=1}^N\sum _{j=1}^p{w}_j\left\{\sum _{d\in B(j;h)}\omega (j,d;h){\tilde{x}}_{id}{\left(h\right)}^2-2{\mathit{v}}_j^T{\mathit{a}}_i\sum _{d\in B(j;h)}\omega (j,d;h){\tilde{x}}_{id}\left(h\right)+{\left({\mathit{v}}_j^T{\mathit{a}}_i\right)}^2\right\}\hfill \\ \hfill =& \sum _{i=1}^N\sum _{jj=1}^p{(x_{ij}^w\left(h\right)-\sqrt{w_j}{\mathit{v}}_j^T{\mathit{a}}_i)}^2+C,\text{with}{x}_{ij}^w\left(h\right)=\sqrt{w_j}\sum _{d\in B(j,h)}\omega (j,d;h){\tilde{x}}_{id}\left(h\right),\hfill \\ \hfill =& {\Vert {\mathit{X}}_{W,h}-{\mathit{AV}}^T{\mathit{W}}_p^{1∕2}\Vert }_F^2+C,\hfill \\ \hfill =& {\Vert ({\mathit{X}}_h-{\mathit{AV}}^T){\mathit{W}}_p^{1∕2}\Vert }_F^2+C,\hfill \\ \hfill =& \mathrm{Tr}\left\{({\mathit{X}}_h-{\mathit{AV}}^T){\mathit{W}}_p({\mathit{X}}_h-{\mathit{AV}}^T)\right\}+C,\hfill \end{array}$$

where C is a scalar independent of A and V . Thus, minimizing ${\mathcal{E}}_{swpca}$ is equivalent to minimizing (6) as stated in Lemma 1.

A.2 Proof of Lemma 2

Lemma 2 can be proved by using Theorem 4 of Zou et al. (2006) as follows. We kept their original notations here.

Theorem 4 (Reduced Rank Procrustes Rotation; Zou et al., 2006): Let M_nχp and N_nχk be two matrices. Consider the constrained minimization problem:

$$\widehat{\mathit{A}}=\underset{\mathit{A}}{\arg \min }{\Vert \mathit{M}-{\mathit{NA}}^T\Vert }_F^2,subjectto{\mathit{A}}^T\mathit{A}={\mathit{I}}_k.$$

Suppose the SVD of M^TN is UDV^T , then  = UA^T.

Based on Lemma 1 and the discussion in Section 2.2, we have a similar minimization problem of A given V :

$$\begin{array}{cc}\hfill \widehat{\mathit{A}}=& \underset{\mathit{A}}{\arg \min }{\Vert {\mathit{X}}_{W,h}-{\mathit{AV}}^T{\mathit{W}}_p^{1∕2}\Vert }_F^2,\hfill \\ \hfill =& \underset{\mathit{A}}{\arg \min }{\Vert {\mathit{X}}_{W,h}^T-{\mathit{W}}_p^{1∕2}{VA}^T\Vert }_F^2,\text{subject to}{\mathit{A}}^T\mathit{A}={\mathit{I}}_q.\hfill \end{array}$$ (13)

If we set $\mathit{M}={\mathit{X}}_{W,h}^T$ and $\mathit{N}={\mathit{W}}_p^{1∕2}\mathit{V}$ in Theorem 4, then  that minimizes (13) given V subject to A^TA = I_q is  = PU^T, where P and U are orthogonal matrices from SVD of ${\mathit{M}}^T\mathit{N}={\mathit{X}}_{W,h}{\mathit{W}}_p^{1∕2}\mathit{V}={\mathit{X}}_h{\mathit{W}}_p\mathit{V}={\mathit{PDU}}^T$.

A.3 Proof of Lemma 3

Assuming A is given, we take the derivative of ${\mathcal{E}}_{swpca}$ in (6) with respect to V . By setting it to zero, we obtain the solution

$$\mathit{V}=bf{X}_h^T\mathit{A}{\left({\mathit{A}}^T\mathit{A}\right)}^{-1}.$$

In Algorithm 1, since A derived from Step (b) is subject to A^TA = I_q, V becomes X^T_h A in Step (c).

A.4 Proof of Lemma 4

Since we can write:

$$\begin{array}{cc}\hfill {\Vert {\mathit{X}}_{W,h}-{\mathit{AV}}^T{\mathit{W}}_p^{1∕2}\Vert }_F^2=& Tr\left\{({\mathit{X}}_{W,h}-{\mathit{AV}}^T{\mathit{W}}_p^{1∕2}){({\mathit{X}}_{W,h}-{\mathit{AV}}^T{\mathit{W}}_p^{1∕2})}^T\right\}\hfill \\ \hfill =& Tr\left({\mathit{X}}_{W,h}{\mathit{X}}_{W,h}^T\right)-2Tr\left({\mathit{X}}_{W,h}{\mathit{W}}_p^{1∕2}{\mathit{VA}}^T\right)+Tr\left({\mathit{AV}}^T{\mathit{W}}_p{\mathit{VA}}^T\right)\hfill \\ \hfill =& Tr\left({\mathit{X}}_{W,h}{\mathit{X}}_{W,h}^T\right)-2Tr\left({\mathit{A}}^T{\mathit{X}}_{W,h}{\mathit{W}}_p^{1∕2}\mathit{V}\right)+Tr\left({\mathit{V}}^T{\mathit{W}}_p\mathit{V}\right)\hfill \\ \hfill =& \sum _{k=1}^q\left\{{\mathit{v}}_{ck}^T{\mathit{W}}_p{\mathit{v}}_{ck}-2{\mathit{a}}_{ck}^T{\mathit{X}}_{W,h}{\mathit{W}}_p^{1∕2}{\mathit{v}}_{ck}\right\}+Tr\left({\mathit{X}}_{W,h}{\mathit{X}}_{W,h}{\mathit{X}}_{W,h}^T\right)\hfill \\ \hfill =& \sum _{k=1}^q{\Vert {\mathit{W}}_p^{1∕2}{\mathit{v}}_{ck}-{\mathit{X}}_{W,h}^T{\mathit{a}}_{ck}\Vert }^2+Tr\left({\mathit{X}}_{W,h}{\mathit{X}}_{W,h}^T\right)-\sum _{k=1}^q{\mathit{a}}_{ck}^T{\mathit{X}}_{W,h}{\mathit{X}}_{W,h}^T{\mathit{a}}_{ck},\hfill \end{array}$$

minimizing $\{{\Vert {\mathit{X}}_{W,h}-{\mathit{AV}}^T{\mathit{W}}_p^{1∕2}\Vert }_F^2+{\sum }_{k=1}^q{\lambda }_k{\Vert {\mathit{v}}_{ck}\Vert }_1\}$ is equivalent to the following minimization problem. For each k = 1,..., q, we have

$$\begin{array}{cc}\hfill {\widehat{\mathit{v}}}_{ck}=& \underset{{\mathit{v}}_{ck}}{\arg \min }\left\{{\Vert {\mathit{W}}_p^{1∕2}{\mathit{v}}_{ck}-{\mathit{X}}_{W,h}^T{\mathit{a}}_{ck}\Vert }^2+{\lambda }_k{\Vert {\mathit{v}}_{ck}\Vert }_1\right\}\hfill \\ \hfill =& \underset{{\mathit{v}}_{ck}}{\arg \min }\left\{\sum _{j=1}^p{w}_j{(v_{jk}-{\mathit{x}}_{hj}^T{\mathit{a}}_{ck})}^2+{\lambda }_k\sum _{j=1}^p\mid v_{jk}\mid \right\}\hfill \\ \hfill =& \underset{{\mathit{v}}_{ck}}{\arg \min }\left\{\sum _{j=1}^p{(v_{jk}-{\mathit{x}}_{hj}^T{\mathit{a}}_{ck})}^2+{\lambda }_k\sum _{j=1}^p\mid v_{jk}\mid ∕w_j\right\}\hfill \\ \hfill =& \underset{{\mathit{v}}_{ck}}{\arg \min }\left\{{\Vert {\mathit{v}}_{ck}-{\mathit{X}}_h^T{\mathit{a}}_{ck}\Vert }^2+{\lambda }_k\sum _{j=1}^p\mid v_{jk}\mid ∕w_j\right\},\hfill \end{array}$$

where x_hj is the j-th column of X_h and v_jk is the j-th element of v_ck. This completes the proof of part (i).

Part (ii) can be easily obtained by applying the lemma below to each element of v_ck.

Lemma The minimizer of (β–y)² + λ |β| is $\widehat{\beta }=sign\left(y\right){(\mid y\mid -\lambda ∕2)}_{+}$

The proof of this lemma is straightforward, so we omitted here.

A.5 Proof of Lemma 5

Assuming V is given, we can obtain the solution of A by taking the derivative of (6) with respect to A.