Maximum-Margin Based Representation Learning from Multiple Atlases for Alzheimer’s Disease Classification

Abstract

In order to establish the correspondences between different brains for comparison, spatial normalization based morphometric measurements have been widely used in the analysis of Alzheimer’s disease (AD). In the literature, different subjects are often compared in one atlas space, which may be insufficient in revealing complex brain changes. In this paper, instead of deploying one atlas for feature extraction and classification, we propose a maximum-margin based representation learning (MMRL) method to learn the optimal representation from multiple atlases. Unlike traditional methods that perform the representation learning separately from the classification, we propose to learn the new representation jointly with the classification model, which is more powerful in discriminating AD patients from normal controls (NC). We evaluated the proposed method on the ADNI database, and achieved 90.69% for AD/NC classification and 73.69% for p-MCI/s-MCI classification.

1 Introduction

Accurate AD diagnosis, especially during early stage AD prognosis (i.e., the discrimination between progressive-MCI (p-MCI) and stable-MCI (s-MCI)), is essential to potentially prevent AD conversions via timely therapeutic interventions. The most straightforward ways to AD classification in the literature resort to direct morphometric measurement of spatial brain atrophy based on MRI [1,2]. In such methods, all subjects are spatially normalized into one common space (i.e., a pre-defined atlas) via non-linear registration, in which the same brain region across different subjects can be compared and consequently the anatomical characteristics related to AD can be revealed.

However, due to intrinsic anatomical shape variations, different atlases used in spatial normalization can lead to different morphometric representations for the same subject, which can subsequently cause very different results in the classification. On the other hand, registration of the same subject to different atlases can yield different registration errors, which can also significantly affect classification accuracy. In practice, people tend to empirically select one subject as an atlas if it can achieve the highest classification rate [2,3] (which can also be selected in an automatic manner [4]), or reduce the global registration errors (e.g., using the mean image as the atlas from a set of subjects [5]). Recently, both [6] and [7] proposed to deploy multiple atlases as intermediate references to guide registration, instead of directly registering a subject to the common atlas. Representations generated via different intermediate references are then averaged to reduce the negative impact of registration errors during classification.

Although previous atlas deployment strategies are able to efficiently reduce registration errors, the representation generated from one single atlas or the average representation obtained from multiple atlases is not necessarily the best choice for the classification task. In fact, the high-dimensional representations generated from multiple atlases in their original spaces can form a low-dimensional manifold, in which the optimal representation (i.e., the best one for classification) could lie somewhere within this manifold.

In this paper, we propose a maximum-margin based representation learning (MMRL) method to learn the optimal representation from multiple atlases for AD classification, which can not only reduce the negative impact due to registration errors but also aggregate the complementary information captured from different atlas spaces. First, multiple atlases are selected to serve as unique common spaces based on affinity propagation [8]. Then each studied subject is non-linearly registered to the selected atlases, and multiple representations from different atlas spaces are further generated by an autonomous feature extraction algorithm [9]. Afterwards, we learn the optimal representation from multiple representations (of multiple atlases) in conjunction with the learning of a support vector machine (SVM) [10] based on the maximum-margin criteria. Finally, the learned representation and SVM are used for classification. Unlike traditional methods enforcing a prior in the representation learning (e.g., variance maximization in PCA, or the locality-preserving property in LaplacianScore [11], which is independent from the classification stage), our method learns both the optimal representation and the classifier jointly, in order to make the two different tasks consistently conform to the same classification objective. Experiments on the ADNI database show that our learned representation outperform both the representation generated from one single atlas and the average representation of multiple atlases. Moreover, the joint learning approach is more efficient than the independent learning approaches even when using state-of-the-art dimensionality reduction/feature selection techniques [12,11,13].

2 Method

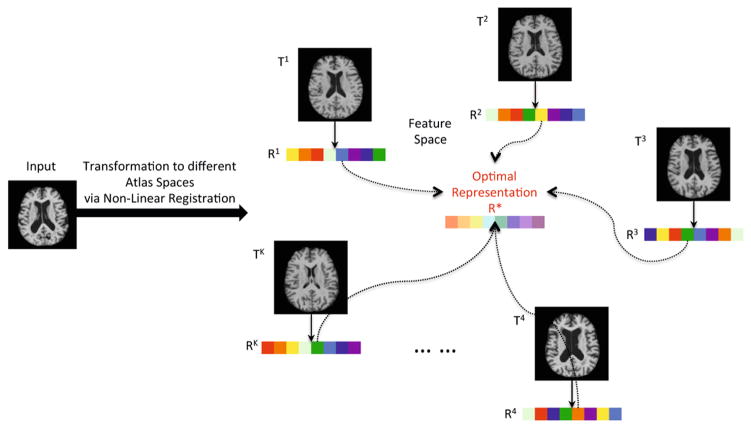
Fig. 1 illustrates the main idea in our proposed method. A subject is first nonlinearly registered to multiple atlases. Volumetric features are then extracted within each atlas space, so that multiple representations are generated from different atlases. Based on the representations obtained, an optimal representation is finally learned to maximize the classification accuracy. We will first present how multiple representative atlases can be selected. Then, the feature extraction method from multiple atlases is described. Finally, a novel maximum-margin based representation learning (MMRL) method is introduced to jointly learn both the optimal representation and the classifier for AD classification.

Fig. 1.

Framework of the proposed method: learning an optimal representation (R^*) from the representations (R¹ ~ R^K) generated in multiple atlas spaces (T¹ ~ T^K)

2.1 Atlas Selection

In order to select the most representative atlases that can capture abundant information of volumetric brain changes related to AD, and also reduce the overall registration errors, affinity propagation (AP) [8] is performed to partition the studied population into K non-overlapping groups (where normalized mutual information of image intensities is used as the similarity measure, and all subjects are linearly aligned in advance). The exemplar image of each group (automatically determined by AP) is then selected as an atlas, and thus a total of K atlases are selected {T₁, T₂, …, T_K}. Different atlases can then be used to capture complementary information for the same subject, by performing feature extraction in each individual atlas space.

2.2 Feature Extraction

We adopt the feature extraction method proposed in [9] to identify the distinctive sets of imaging biomarkers from different atlases and extract the most relevant features in each individual atlas space. First, each subject is non-linearly registered to the K selected atlases. Then, in each atlas space, group analysis using Pearson correlation (for each voxel) is conducted on the training set to yield a response map of the atlas that signifies its voxel-wise discriminative power. Watershed segmentation is then applied to the response map of each atlas to partition the atlas into a large number of non-overlapping local regions. Finally, the M most discriminative regions are identified for each atlas by Pearson correlation using the training subjects. Consequently, for each subject, M features can be extracted by summarizing the gray matter volumes of the M identified regions on each atlas. Since we deployed K atlases for feature extraction, K distinctive representations are generated for one subject, where each representation is comprised of M features.

2.3 Maximum-Margin Based Representation Learning

Given the set of representations of a subject generated from K different atlases X = {x^k ∈ ℝ^M×1, k ∈ [1, K]}, we want to find a new representation x^* ∈ ℝ^M×1, which can yield the best classification result. Suppose that the new representation can be generated by applying a mapping to the set of original representations as:

$$x^{\ast }=f(X)$$ (1)

Our goal is to learn the optimal mapping function f(·) which can yield the best representation x^* for classification. To achieve this goal, we propose a maximum-margin based representation learning method (namely MMRL) to learn f(·) in conjunction with the learning of a SVM classifier, where the jointly learned mapping and classifier are both optimal for the targeted classification task.

Traditional SVM

Given a training set {(x_i, y_i), i ∈ [1, N]}, where x_i ∈ ℝ^M×1 and y_i ∈ {−1, 1} denote the feature vector and label of the i-th subject, respectively, a soft-margin support vector machine (SVM) [10] tries to find a hyperplane that maximizes the margin between two classes of samples and also minimizes the cost of misclassification:

$$\underset{w,b}{argmin}\frac{1}{2}{\Vert w\Vert }_2^2+C\sum _{i=1}^N{[1-y_i(w^{\top }{x}_i+b)]}_{+}$$ (2)

where {w, b} defines the SVM hyperplane, [·]₊ = max(0, ·) denotes the hinge loss function, and C is the balancing factor between the hinge loss and the margin regularization. When the feature vector x̃ of an unknown subject is input, its associated label ỹ can be predicted using the learned hyperplane {w, b} as:

$$\stackrel{\sim }{y}=\text{sign}(w^{\top }\stackrel{\sim }{x}+b)$$ (3)

MMRL

In order to learn the optimal representation x^* (i.e., learning the optimal mapping function f(·)) jointly with the classification model as defined in equation (2), given a training set {(X_i, y_i), i ∈ [1, N]} where $X_i=\{x_i^k,k\in [1,K]\}$ is the set of representations generated from all K atlases, and $x_i^k\in {ℝ}^{M\times 1}$ denotes one representation extracted from the k-th atlas for the i-th subject (using the method described in Section 2.2), we first define the mapping to the new representation as a linear combination of the K existing representations generated from different atlases as:

$$f(X_i\mid {\{A^k\}}_{k=1}^K)=\sum _{k=1}^K{A}^k{x}_i^k$$ (4)

where A^k ∈ ℝ^M×M is a diagonal coefficient matrix to assign different weights to different features of the k-th representation (with all non-diagonal elements equal to zero). Then our goal is to find the optimal mapping $f(·\mid {\{A^k\}}_{k=1}^K)$ and hyperplane {w, b} that maximize the margin between different classes and also reduce the misclassification rate on the training set:

$$\begin{array}{c}\underset{w,b,{\{A^k\}}_{k=1}^K}{argmin}\frac{1}{2}{\Vert w\Vert }_2^2+C\sum _{i=1}^N{[1-y_i(w^{\top }f(X_i\mid {\{A^k\}}_{k=1}^K)+b)]}_{+}\\ \text{s.t.}\forall j,A_j^k>0\text{and}\sum _{k=1}^K{A}_j^k\le 1\end{array}$$ (5)

where $A_j^k$ denotes the j-th diagonal element of the coefficient matrix A^k (i.e., the weight for the j-th feature from the k-th atlas). The inequality constraints in equation (5) confine the estimated weights into the first quadrant of a unit square, so that the generated representation lies within the manifold of original representations and has different importance on different feature locations.

To avoid overfitting, we propose to further partition the features into different groups, where features within the same group will be assigned to the same mapping weights (i.e., $A_{j_1}^k=A_{j_2}^k$ if the j₁-th and j₂-th features are in the same group). Introducing this additional constraint can efficiently reduce the degree of freedom of the proposed model, thus achieving improved generalization with limited training samples. The feature grouping strategy used in our method is implemented by performing affinity propagation [8] on the feature covariance matrix calculated from the training set.

To optimize equation (5), we adopt the coordinate descent method to estimate the parameters. The mapping weights ${\{A^k\}}_{k=1}^K$ and the hyperplane {w, b} are optimized in an iterative manner. In each iteration, one term is optimized while the other is fixed, and thus each optimization step is convex. With the learned mapping $f(·\mid {\{A^k\}}_{k=1}^K)$ and the learned decision boundary {w, b}, given the feature vectors X̃ of an unknown sample extracted from multiple atlases, the associated label ỹ can be predicted as:

$$\stackrel{\sim }{y}=\text{sign}(w^{\top }f(\stackrel{\sim }{X}\mid {\{A^k\}}_{k=1}^K)+b)$$ (6)

in which the optimal representation can be regarded as ${\stackrel{\sim }{x}}^{\ast }=f(\stackrel{\sim }{X}\mid {\{A^k\}}_{k=1}^K)$.

3 Experiments

We demonstrate the advantages of the proposed MMRL method from two aspects: (1) the learned representation from multiple atlases significantly outperforms the representation generated from one single atlas and the average representation of multiple atlases; (2) our joint learning approach is more efficient than several independent representation learning (i.e., dimensionality reduction or feature selection) methods when representations from multiple atlases are utilized. In this section, we will first describe our data and experimental con-figurations; then we will show and discuss the obtained results.

3.1 Data and Experimental Configurations

We evaluated the proposed method on 459 subjects (97 AD, 128 NC, 117 p-MCI, and 117 s-MCI) randomly selected from the ADNI database¹. All subject scans followed the same pre-processing pipeline consisting of bias correction, skull-stripping, and cerebellum-removing. Then the images from all subjects were linearly aligned and segmented into three tissues (i.e., GM, WM, and CSF).

Our experiments were conducted for two different classification tasks, namely AD/NC classification and p-MCI/s-MCI classification. 10-fold cross validation was performed for each task, in which each fold consists of roughly 1/10 of the entire data and roughly the same proportion from each class. In order to reveal the intrinsic characteristics of the MCI patients related to AD, the p-MCI/s-MCI classification was conducted in a transfer learning manner, where in each round 9 folds of the AD/NC data were used for training and 1 fold of the p-MCI/s-MCI data was used for testing (note that the labels of p-MCI and s-MCI were associated with the labels of AD and NC, respectively).

As for the other experimental configurations, linear SVM was used as the benchmark classifier with the default cost term C = 1; the number of selected atlases is K = 10 from affinity propagation, and the number of biomarkers identified on each atlas is M = 20. Optimization of the proposed method was implemented based on CVX².

3.2 Results and Discussion

In Table 1, we compare the classification performance of our learned representation (using MMRL from multiple atlases) with single atlas (SA) representations and the average representation of multiple atlases. For the representations generated from single atlases, we deployed the 10 atlases selected in our method and used each of the 10 atlases to perform feature extraction and classification separately. We report the classification rate of the best atlas (Best_SA) and the average result across the 10 atlases (Mean_SA), respectively. We then report the classification performance (listed as Average in Table 1) obtained by the average representation from multiple representations generated from all 10 atlases. In the table, it is clear that the representation learned by MMRL significantly outperforms both Best_SA and Average according to all evaluation metrics (accuracy, sensitivity, and specificity) for both AD/NC classification and p-MCI/s-MCI classification. Additionally, we show the classification rates obtained by concatenation of multiple representations (Concat) and multiple kernel learning (MKL) [14], which are also lower than the proposed MMRL method.

Table 1.

Comparison of MMRL to the representation generated from single atlas (SA), the average representation from multiple atlases (Average), feature concatenation (Concat), and MKL in AD/NC classification and p-MCI/s-MCI classification, respectively.

Method	AD vs. NC			p-MCI vs. s-MCI
	ACC (%)	SEN (%)	SPEC (%)	ACC (%)	SEN (%)	SPEC (%)
Mean_SA	83.23	82.28	84.06	67.56	70.30	64.71
Best_SA	85.35	82.33	87.69	71.08	72.88	69.02
Average	86.68	85.67	87.63	70.70	73.11	68.18
Concat	84.96	83.33	86.09	66.79	67.73	65.68
MKL [14]	87.55	83.33	90.77	69.42	70.45	68.18
MMRL	90.69	87.56	93.01	73.69	76.44	70.76

Notation: ACC=accuracy, SEN=sensitivity, SPEC=specificity.

Table 2 shows the results comparing MMRL with four popular dimensionality reduction (DR) and feature selection (FS) methods when multiple atlases are used. In the table, PCA and AutoEncoder [12] are DR methods, whereas LaplacianScore [11] and mRMR [13] are the widely used FS techniques. For fair comparison, all techniques reduce the feature dimension to 20 (same as the MMRL learned representation). For AutoEncoder, a widely used configuration with a three-layer architecture [12] was adopted. Our results demonstrate that the proposed joint learning method yields the best classification results (90.69% for AD/NC and 73.69% for p-MCI/s-MCI) in comparison to the others, whose representations are learned prior to the final classification.

Table 2.

Comparison of MMRL to different dimensionality reduction and feature selection methods in AD/NC classification and p-MCI/s-MCI classification, respectively.

Method	AD vs. NC			p-MCI vs. s-MCI
	ACC (%)	SEN (%)	SPEC (%)	ACC (%)	SEN (%)	SPEC (%)
PCA	83.08	81.22	84.55	68.96	72.12	65.68
AutoEncoder [12]	87.60	86.56	88.40	66.42	70.45	62.20
LaplacianScore [11]	87.19	84.56	89.23	67.73	71.36	63.94
mRMR [13]	85.31	83.33	86.79	69.42	69.62	69.17
MMRL	90.69	87.56	93.01	73.69	76.44	70.76

Notation: ACC=accuracy, SEN=sensitivity, SPEC=specificity.

4 Conclusion

In this paper, we introduced a maximum-margin based representation learning (MMRL) method using multiple atlases for AD classification. The proposed method adopts multiple atlases to obtain different representations for the same subject and learns the optimal representation jointly with the classification model based on the maximum-margin criteria. The learned representation can efficiently reduce registration errors and is able to aggregate complementary information captured from different atlas spaces to improve classification, which is more powerful than the representation generated from one single atlas and the average representation of multiple atlases previously used in the literature. In addition, the joint learning approach in MMRL enables both the learned representation and classifier conform to the same classification objective, which is more effective in AD diagnosis than independent representation learning methods. Experiments on the ADNI database demonstrated significant improvements for both AD/NC classification and p-MCI/s-MCI classification.