Gauging the likelihood of stable cavitation from ultrasound contrast agents

Abstract

The mechanical index (MI) was formulated to gauge the likelihood of adverse bioeffects from inertial cavitation. However, the MI formulation did not consider bubble activity from stable cavitation. This type of bubble activity can be readily nucleated from ultrasound contrast agents (UCAs) and has the potential to promote beneficial bioeffects. Here, the presence of stable cavitation is determined numerically by tracking the onset of subharmonic oscillations within a population of bubbles for frequencies up to 7 MHz and peak rarefactional pressures up to 3 MPa. In addition, the acoustic pressure rupture threshold of an UCA population was determined using the Marmottant model. The threshold for subharmonic emissions of optimally sized bubbles was found to be lower than the inertial cavitation threshold for all frequencies studied. The rupture thresholds of optimally sized UCAs were found to be lower than the threshold for subharmonic emissions for either single cycle or steady state acoustic excitations. Because the thresholds of both subharmonic emissions and UCA rupture are linearly dependent on frequency, an index of the form I_CAV = P_r/f (where P_r is the peak rarefactional pressure in MPa and f is the frequency in MHz) was derived to gauge the likelihood of subharmonic emissions due to stable cavitation activity nucleated from UCAs.

1. Introduction

Stable cavitation activity initiated by ultrasound exposure of ultrasound contrast agents (UCAs) has been shown to be beneficial for many types of medical therapy, including drug delivery (Hitchcock et al 2010), thrombolysis (Datta et al 2008), and disruption of the blood brain barrier (Hynynen et al 2001). Stable cavitation is characterized by sustained small amplitude oscillations of the bubble about its equilibrium (Flynn 1964). The bubble’s oscillations radiate pressure to the surrounding fluid, which generates flow around the bubble termed microstreaming (Elder 1959). In contrast, inertial cavitation is typically transient in nature and is characterized by a collapse of the bubble capable of producing shock waves (Holzfuss et al 1998), free radicals (Flynn 1964), fluid jetting (Prosperetti 1984), and erosion of materials (Tomita and Shima 1986). The transient nature of inertial cavitation may limit sustained bioeffects due to destruction of UCAs. The temporal longevity of sustained stable cavitation may promote increased thrombolytic efficacy and drug delivery to distal tissues.

The hallmark of experimental detection of sustained stable cavitation is the presence of a subharmonic (half the driving frequency), which is readily differentiated from harmonics (integer multiples of the fundamental) due to nonlinear propagation (Duck 2002) and cavitation (Neppiras 1980). Strictly speaking, there is no threshold for stable cavitation, as any acoustic pressure greater than zero will initiate bubble oscillations. However, the nonlinear nature of bubble oscillations allows using the subharmonic to detect stable cavitation experimentally (Neppiras 1968, Mestas et al 2003, Vykhodtseva et al 1995, McLaughlan et al 2010). Subharmonic emissions from cavitation are well established theoretically (Eller and Flynn 1969, Prosperetti 1974, Katiyar and Sarkar 2011), and are known to correlate experimentally with several in vivo and in vitro bioeffects, such as ultrasound-enhanced thrombolysis (Prokop et al 2007), disruption of the blood brain barrier (O’Reilly and Hynynen 2010), chemotherapy drug release from micelles (Husseini et al 2005), and enhanced heating in focused ultrasound surgery (Sokka et al 2003). Thus knowledge of the threshold of subharmonic emissions could be used to gauge the potential for clinically beneficial bioeffects.

The mechanical index (MI) was developed to predict the onset of inertial cavitation of free bubbles (i.e. no shell encapsulation of gas) (Apfel and Holland 1991). However, previous reports suggest the MI is a poor indicator of the loss of echogenicity from UCAs (Forsberg et al 2005, Forsberg et al 2006, Miller 2007). At present there is no analogue to the MI for the onset of subharmonic emissions or UCA rupture. Therefore, the aim of this work is to develop an analogous index to predict the occurrence of subharmonics as an indicator of stable cavitation and rupture of UCAs.

Following the work of Datta (2007), the threshold for subharmonic emissions is investigated by numerical calculation of free bubble oscillations as a function of frequency and bubble size. The subharmonic emission threshold is defined here as the peak rarefactional pressure required for the frequency spectrum of the pressure radiated by a bubble to have the first subharmonic (f₀/2) amplitude 20 dB lower than the fundamental amplitude.

This work assumes nuclei for bubble activity originate from UCA rupture. The encapsulating shell of an UCA will rupture when subjected to sufficient tension, thereby releasing the encapsulated gas (Forbes et al 2008, Yeh and Su 2008, Chen et al 2003, Porter et al 2006, Sboros et al 2003, Guan and Matula 2004). The released gas either dissolves rapidly or coalesces due to secondary Bjerknes forces (Ammi 2006, Postema et al 2002). The rupture threshold is defined here as the peak rarefaction pressure required for the shell of an UCA to expand beyond its linear elastic limit (Marmottant 2005). The rupture threshold will be numerically calculated for the shell properties of several commercially available UCAs: Definity^® (Bristol-Meyers Squibb Medical Imagin, N. Billerica, MA), Optison^® (Mallinckrodt, Inc. Hazelwood, MO), and Sonozoid™ (Nycomed Amersham, Oslo, Norway), as a function of frequency and size. In addition, the inertial cavitation threshold will be calculated as a function of frequency following Holland and Apfel (1989). The resultant subharmonic and UCA rupture thresholds will be compared to the inertial cavitation threshold to define the ultrasound parameter space over which subharmonic emissions can be used as a reliable indicator of stable bubble activity in the absence of inertial cavitation.

2. Methods

2.1. Free bubble dynamics

The radial oscillations of free bubbles were calculated by numerical integration of the Gilmore Equation using a fourth-order Runge–Kutta algorithm in MATLAB^® (The Mathworks, Natick, MA). The Gilmore equation is valid to high Mach numbers (Prosperetti and Lezzi 1986, Vokurka 1986) and accounts for damping due to acoustic radiation and viscosity. Thermal damping is neglected (Church 1989). Note, however, damping due to acoustic radiation and viscosity dominates over thermal damping for bubbles larger than resonant size (Leighton 1994), and that the optimal size bubble for subharmonic emissions are well-known to be larger than resonant size (Eller and Flynn 1969, Prosperetti 1974). The details of the Gilmore equation are discussed in further detail by Gilmore (1952), Cramer (1980), and Church (1989). Briefly, the Gilmore equation has the form

$$(1-\frac{Ṙ}{C})RṘ+\frac{3}{2}(1-\frac{Ṙ}{3C}){Ṙ}^2=(1+\frac{Ṙ}{C})H+\frac{R}{C}(1-\frac{Ṙ}{C})\frac{\mathrm{d}H}{\mathrm{d}R},$$ (1)

where R is the time dependent bubble radius, the diacritical dot denotes the derivative with respect to time, C is the sound speed in the fluid at the bubble wall, and H is the liquid enthalpy. The enthalpy was calculated with a Tait equation of state following Lastmax and Wentzell (1981). Once (1) was solved for the time-dependent bubble size and bubble wall velocity, the pressure radiated by the bubble was calculated following Akulichev (1971).

Stable cavitation was analyzed at steady state behavior to mimic the conditions of sustained bubble activity. The transition to steady state was determined by the time constant associated with damping of the bubble (Leighton 1994), and was typically less than ten acoustic cycles. The acoustic excitation was a single ultrasound pulse of 110-cycle duration. The final 100 acoustic cycles of the radiated pressure (all steady state oscillations) were used for analysis by sampling. The resultant waveform was sampled at 300 MHz, Hann windowed, and the frequency content was calculated using the fast Fourier transform (FFT) algorithm in MATLAB.

2.2. Encapsulated bubble dynamics

The Marmottant model (Marmottant et al 2005) was used to investigate the rupture threshold of UCAs. This model was chosen because it clearly defines a rupture radius, R_RUPT, whereby UCA radii larger than R_RUPT will rupture the shell, and the encapsulated gas will be liberated. The model is described in further detail by Marmottant et al (2005) and Katiyar and Sarkar (2011). Briefly, the Marmottant model has the form

$${\rho }_0(R\ddot{R}+\frac{3}{2}{Ṙ}^2)=(1-\frac{3\kappa Ṙ}{C_0})(P_0+\frac{2\sigma (R_0)}{R_0}){\left(\frac{R_0}{R}\right)}^{3\kappa }-\frac{2\sigma (R)}{R}-\frac{4Ṙ}{R}(\mu +\frac{{\kappa }_S}{R})-P_0+P_{ac}\text{sin}(\omega t),$$ (2)

where R is the time-dependent UCA radius, R₀ is the initial UCA radius, the diacritical dot denotes the derivative with respect to time, ρ₀ is the fluid density, κ is the polytropic exponent, C₀ is the fluid sound speed, P₀ is the ambient pressure, μ is the fluid viscosity, P_ac is the acoustic pressure amplitude, ω is the angular frequency, and κ_S is the surface dilatational viscosity from the shell. The surface tension σ is piecewise dependent on the size of the UCA:

$$\sigma (R)\{\begin{array}{cc}0\hfill & R\le R_{\text{BUCK}}\hfill \\ \chi [{\left(\frac{R}{R_{\text{BUCK}}}\right)}^2-1]\hfill & R_{\text{BUCK}}\le R\le R_{\text{RUPT}},\hfill \\ {\sigma }_0\hfill & R\ge R_{\text{RUPT}}\hfill \end{array}$$ (3)

where χ is the elastic compression modulus, σ₀ is the surface tension of the host fluid, R_BUCK is the buckling radius and is set equal to R₀, and the rupture radius, R_RUPT, is defined as

$$R_{\text{RUPT}}=R_{\text{BUCK}}{(1+{\sigma }_0/\chi )}^{1/2}.$$ (4)

The UCA rupture threshold, P_RUPT, is calculated for both single cycle and steady state acoustic excitations. As with the free bubble, the transition to steady state is taken as the time constant associated with damping of the UCA (Marmottant et al 2005).

2.3. Shell and fluid constants

The values of constants used in (1)–(4) are shown in tables 1 and 2. Calculations were performed for host fluids of water at 22 °C and blood at 37 °C. UCA dynamics were calculated using the shell properties of Definity (Santin et al 2010), Optison (Santin et al 2010), and Sonozoid (Katiyar and Sarkar 2011). The gas content of both free and encapsulated bubbles was assumed to be octafluoropropane, the gas core of Definity (Shankar et al 1999). In addition to ambient atmospheric pressure (~100 kPa), physiological conditions were investigated by repeating the calculations in blood at 95 mmHg (13 kPa) and 130 mmHg (17 kPa) ambient pressures elevated relative to atmospheric pressure. These ambient pressures are representative of the mean arterial pressures for optimal (i.e. healthy individual) and hypertensive conditions (Wallace and Levy 1980), respectively. Physiologic pressures are time dependent, but on a time scale at least five orders of magnitude slower than the bubble dynamics considered here.

Table 1.

Fluid constants used in (1) and (2).

Constant	Water	Blood	Reference
C0 (m s−1)	1480	1540	Cramer 1980/Yang and Church 2005
m	7.00	7.00	Church 1989
ρ0 (kg m−3)	998	1060	Apfel and Holland 1991
σ0 (N m−1)	0.0725	0.0560	Apfel and Holland 1991
κ	1.09	1.09	Shankar et al 1999
μ (kg (m s)−1)	1.00 × 10−3	5.00 × 10−3	Apfel and Holland 1991
Pv (kPa)	2.66	6.12	Lauterborn 1976/Grollman 1928
P0 (kPa)	100.00	100.00	–

Table 2.

Shell constants used in (2).

UCA	κS (kg s−1)	χ (N m−1)	Reference
Definity	2.40 × 10−9	0.380	Santin et al 2010
Sonazoid	1.20 × 10−8	0.530	Katiyar and Sarkar 2011
Optison	7.65 × 10−9	0.930	Santin et al 2010

2.4. Frequency range of calculations

Calculations were performed between 0.1–7 MHz. The lowest frequencies are applicable for penetration across the skull for thrombolysis (Ammi et al 2008, McDannold et al 2006). The upper range was limited to 7 MHz because the resonant size of free bubbles in blood becomes a complex number at higher frequencies (see, for instance, equation (4.86) in Leighton (1994)).

3. Results

3.1. Steady state radius–time curve

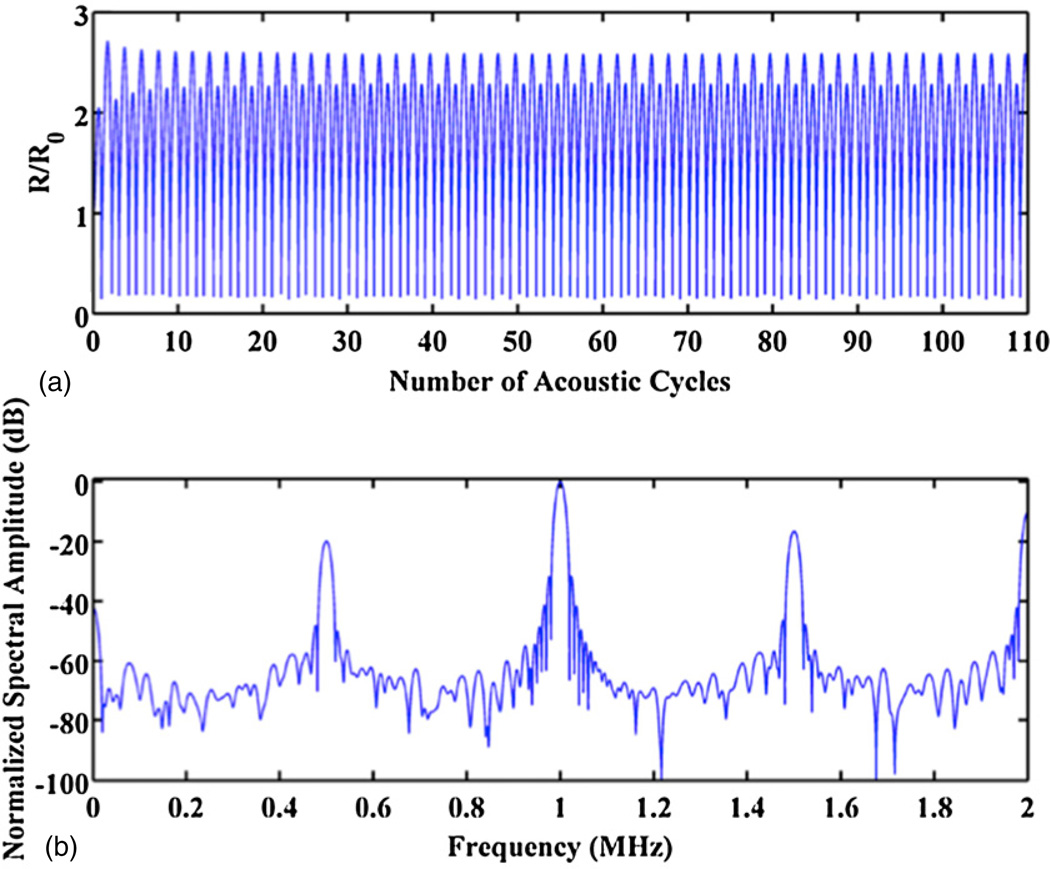
A representative radius–time curve of a free bubble (R₀ ~ 3.0 µm, f = 1 MHz) at the subharmonic threshold is seen in panel (a) of figure 1. The damping time constant is approximately 5 acoustic cycles. The final 100 acoustic cycles are steady state oscillations. The corresponding FFT of the radiated pressure is shown in panel (b). The subharmonic component is approximately 20 dB less than the fundamental, and, therefore, the subharmonic threshold as previously defined has been reached.

Figure 1.

(a) Representative calculated radius–time curve using the Gilmore equation. The driving frequency is 1 MHz, R₀=3.0 µm, and the peak rarefactional pressure is 0.26 MPa. The host fluid is blood at atmospheric pressure. (b) FFT of the bubble’s radiated pressure waveform, normalized to the amplitude of the fundamental component. The subharmonic component at 500 kHz is ~20 dB lower than the fundamental, and thus the subharmonic threshold has been reached.

3.2. Optimal bubble size for subharmonic emissions

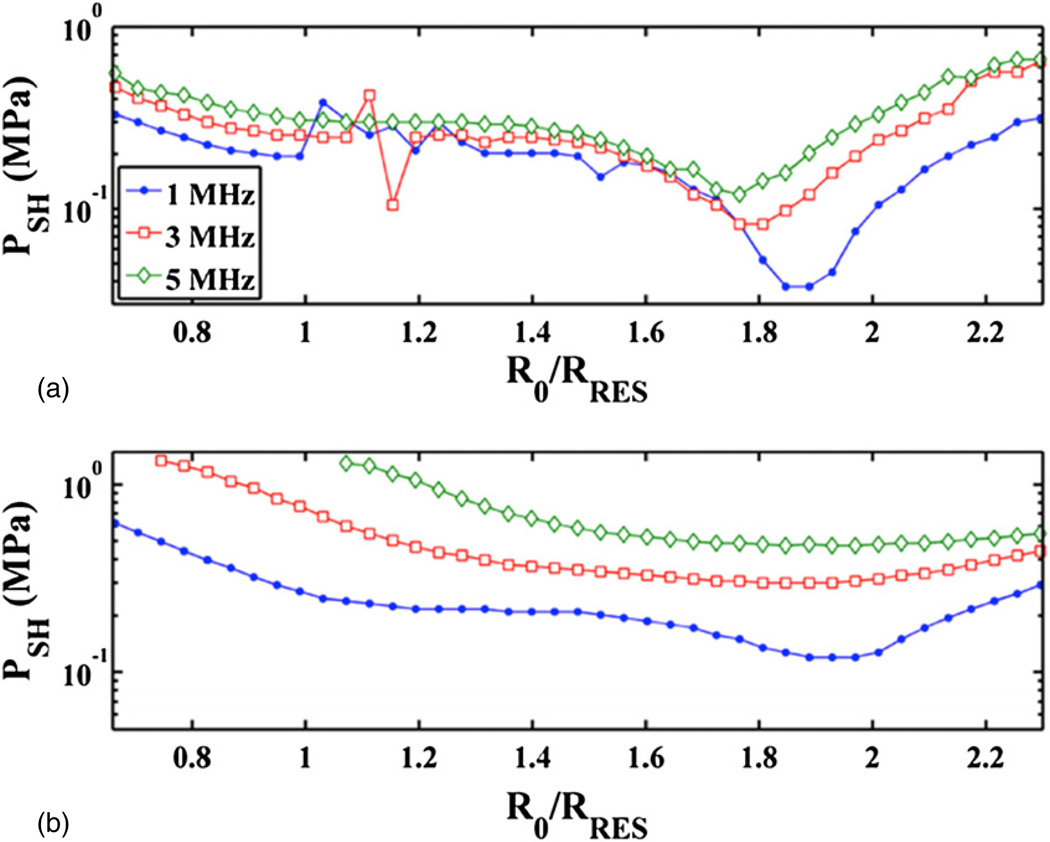
The subharmonic threshold is shown as a function of initial bubble size at select frequencies in figure 2. Both host fluids, blood and water, were at atmospheric pressure. The trends of the curves indicate that the subharmonic threshold is minimum for a bubble resonant at the subharmonic. Water (panel (a)) has a local minimum at the resonant size. Blood (panel (b)) has a local minimum at the resonant size below 2 MHz. Above 2 MHz there is only a global minimum. The subharmonic threshold of optimally sized bubbles (i.e. the bubble size which corresponds to the minimum stable cavitation threshold) represents the lower bound of driving pressures required to initiate subharmonic emissions. Any increase in the driving pressure would extend the range of bubble sizes capable of producing subharmonic emissions.

Figure 2.

The threshold for subharmonic emissions, P_SH, as a function of initial bubble size, R₀, normalized to the resonant size, R_RES, at 1, 3, and 5 MHz. The host fluid is water (a) and blood at atmospheric pressure (b). The legend is shown in the top panel only.

3.3. Subharmonic threshold as a function of frequency

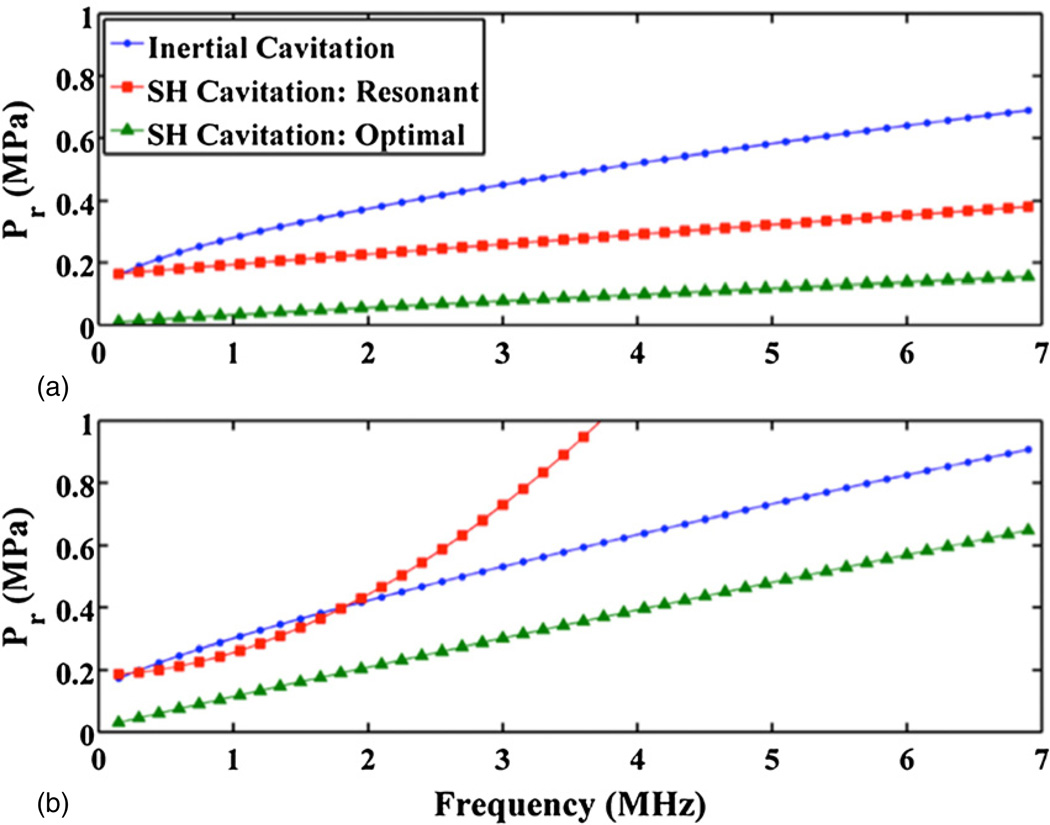
The frequency dependence of the subharmonic threshold was determined for both bubbles of optimal and resonant size. The threshold of optimally sized bubbles is the paramount objective of these calculations. Physical processes, such as microstreaming, are most pronounced for resonant sized bubbles (Leighton 1994). The subharmonic and inertial cavitation thresholds for water and blood (atmospheric pressure) are shown in panels (a) and (b), respectively, of figure 3. The inertial cavitation thresholds have been calculated following Holland and Apfel (1989). The trends of the stable and inertial cavitation thresholds in blood at 95 mmHg and 130 mmHg ambient pressure were similar to those in panel (b) of figure 3. Following Apfel and Holland (1991), the frequency dependence of the inertial and subharmonic thresholds were fit to a two-parameter model of the form

$$\frac{P_r^{a_1}}{f}=a_2,$$ (5)

where P_r is the peak rarefactional pressure in MPa, f is the frequency in MHz, and a₁ and a₂ are fitting parameters. This model indicates there is a trade-off between the peak rarefactional pressure and driving frequency for the generation of subharmonic emissions from stable cavitation. The fitting parameters a₁ and a₂ for each host fluid and ambient pressure are shown in table 3.

Figure 3.

Calculated thresholds reported in peak rarefaction pressure (P_r) for inertial cavitation and subharmonic emissions from resonant and optimal size bubbles. The host fluids are water (a) and blood (b) at atmospheric pressure.

Table 3.

Coefficients of two-parameter fit, equation (5), for the frequency dependence of the inertial cavitation threshold of optimally sized bubbles (P_ICOPT) following Apfel and Holland (1991), subharmonic threshold of optimally sized bubbles (P_SHOPT), and subharmonic threshold for resonant sized bubbles (P_SHRES). The goodness-of-fit parameters coefficient of determination r² and standard error σ_X̄ are also shown.

Threshold type	Fluid	Deviations from ambient pressure (mmHg)	a1	a2	r2	σX̄ (MPa)
PICOPT	Water	0	2.10	6.00 × 10−2	0.997	1.10 × 10−2
PICOPT	Blood	0	1.67	1.30 × 10−1	0.996	1.80 × 10−2
PICOPT	Blood	95	1.85	2.10 × 10−1	0.994	2.70 × 10−2
PICOPT	Blood	130	1.93	2.30 × 10−1	0.993	2.90 × 10−2
PSHOPT	Water	0	1.21	1.50 × 10−2	0.995	4.00 × 10−3
PSHOPT	Blood	0	1.10	8.80 × 10−2	0.999	5.00 × 10−3
PSHOPT	Blood	95	1.12	8.80 × 10−2	0.998	6.00 × 10−3
PSHOPT	Blood	130	1.13	8.70 × 10−2	0.999	6.00 × 10−3
PSHRES	Water	0	2.65	1.00 × 10−2	0.944	1.90 × 10−2
PSHRES	Blood	0	0.650	2.80 × 10−1	0.990	8.00 × 10−2
PSHRES	Blood	95	0.670	2.80 × 10−1	0.988	8.20 × 10−2
PSHRES	Blood	130	0.680	2.80 × 10−1	0.988	8.40 × 10−2

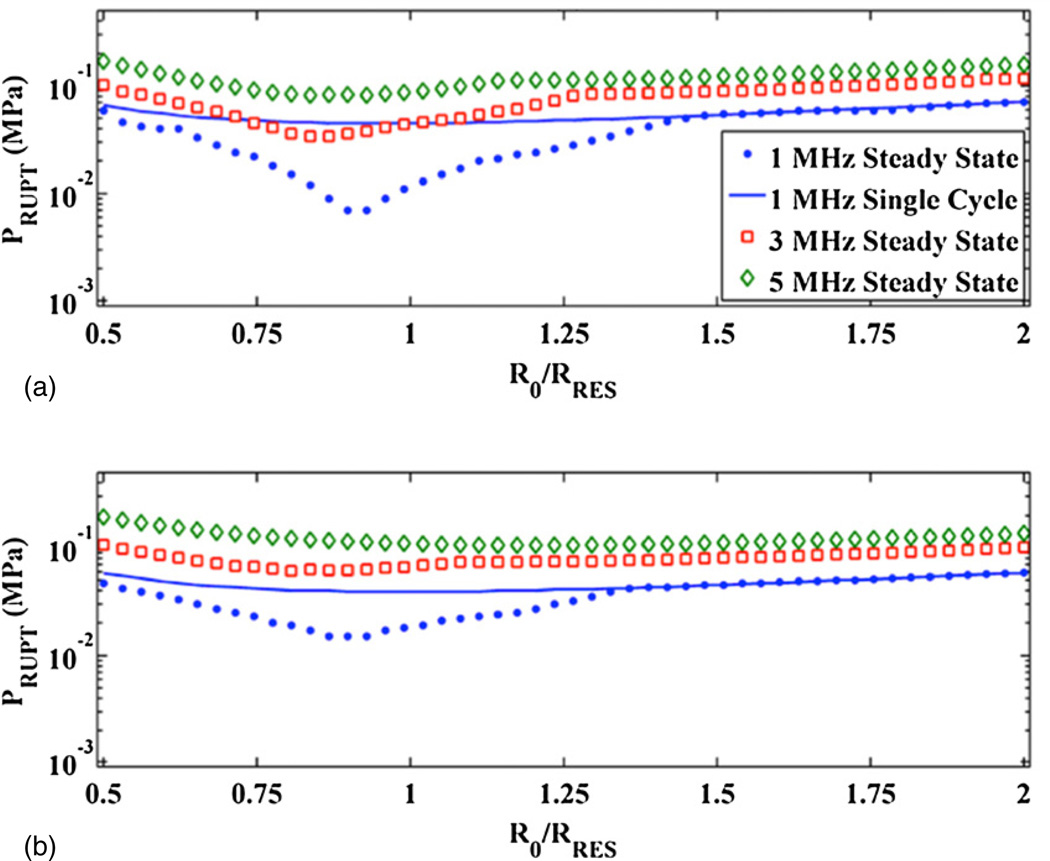
3.4. UCA rupture threshold

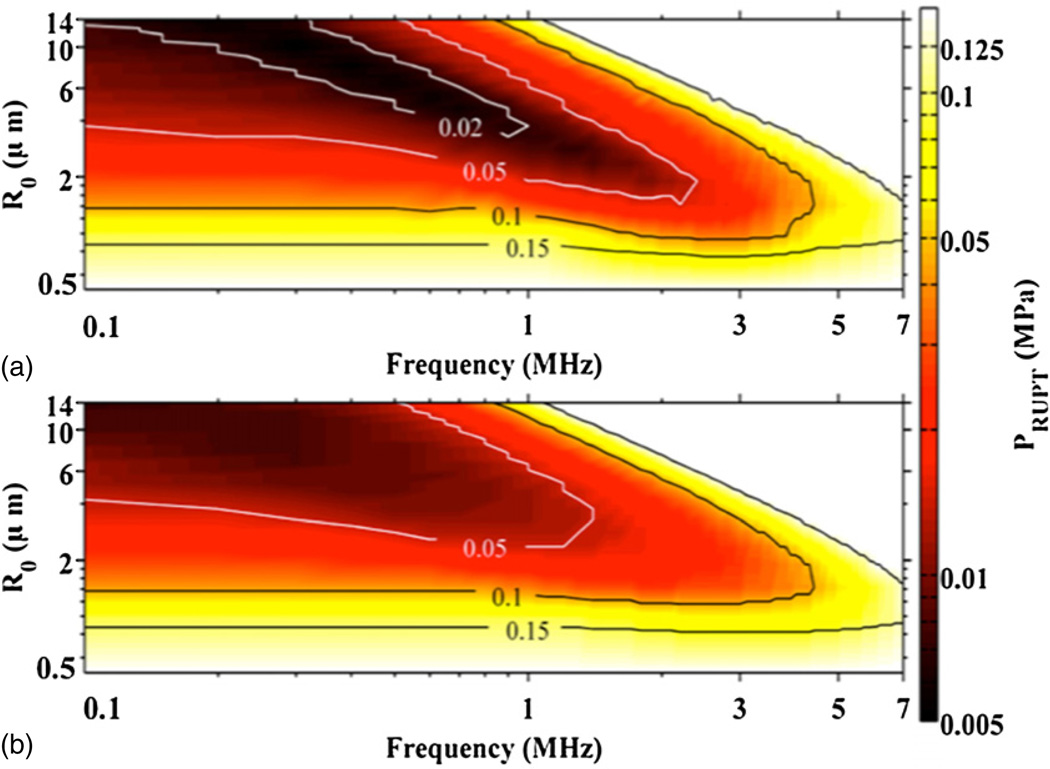
The frequency and size dependence of the UCA rupture threshold are shown in figure 4. Steady state acoustic excitations are shown in panel (a), and single cycle acoustic excitations are shown in panel (b). The host fluid is blood at atmospheric pressure for both panels, and the shell properties correspond to Definity. The qualitative trends in figure 4 are similar for all tested host fluids and ambient pressures. The minimum rupture threshold occurs near the UCA resonant size, as shown in figure 5. Figure 5 also demonstrates the steady state and single cycle rupture thresholds coincide except near the UCA resonant size. Hence, the frequency dependence of the rupture threshold of an optimal size UCA was calculated as the minimum threshold for UCA rupture. The frequency dependence of both the steady state and single cycle rupture thresholds were calculated. Each set of calculations were fitted using (5). The fitting parameters a₁ and a₂ are shown in table 4 for the shell parameters of Definity for all tested host fluids, ambient pressures, and acoustic excitation schemes. In addition, the fitting parameters are shown for UCAs with the shell parameters of both Optison and Sonazoid in blood at atmospheric pressure for steady state and single cycle acoustic excitations.

Figure 4.

UCA rupture threshold, PRUPT, as a function of UCA size and frequency for steady state acoustic excitation (a) and single cycle acoustic excitations (b). Contour lines are shown for the peak rarefaction pressure at 0.02, 0.05, 0.1, and 0.15 MPa. The host fluid is blood at atmospheric pressure, and the shell properties of the UCA correspond to Definity.

Figure 5.

UCA rupture threshold, PRUPT, near the linear resonant size at 1 MHz, 3 MHz and 5 MHz in water (a) and blood (b) at atmospheric pressure. The shell properties of the UCA correspond to Definity. All plots are for steady state acoustic excitations, except for the solid line, which corresponds to single cycle acoustic excitation at 1 MHz.

Table 4.

Coefficients for determining the rupture threshold of a resonant sized UCA via (5). ‘1 cycle’ and ‘Steady State’ refers to single cycle and steady state acoustic excitations, respectively. The goodness-of-fit parameters coefficient of determination r² and standard error σ_X̄ are also shown.

UCA	Fluid	Deviations from ambient pressure (mmHg)	Acoustic excitation	a1	a2	r2	σX̄ (MPa)
Definity	Water	0	1 cycle	1.56	6.98 × 10−3	0.993	3.10 × 10−3
Definity	Water	0	Steady state	0.708	3.60 × 10−2	0.994	3.40 × 10−3
Definity	Blood	0	1 cycle	1.46	8.02 × 10−3	0.993	3.00 × 10−3
Definity	Blood	0	Steady state	1.03	2.00 × 10−2	0.992	4.00 × 10−3
Definity	Blood	95	1 cycle	1.49	7.55 × 10−3	0.991	3.00 × 10−3
Definity	Blood	95	Steady state	0.994	2.17 × 10−2	0.992	4.00 × 10−3
Definity	Blood	130	1 cycle	1.50	7.44 × 10−3	0.991	3.40 × 10−3
Definity	Blood	130	Steady state	0.991	2.19 × 10−2	0.992	3.90 × 10−3
Optison	Blood	0	1 cycle	1.33	5.95 × 10−3	0.997	1.40 × 10−3
Optison	Blood	0	Steady state	1.17	9.03 × 10−3	0.994	2.10 × 10−3
Sonazoid	Blood	0	1 cycle	1.16	1.66 × 10−2	0.993	3.60 × 10−3
Sonazoid	Blood	0	Steady state	1.03	2.16 × 10−2	0.997	2.30 × 10−3

3.5. Development of an index to predict subharmonic emissions and UCA rupture

For all ambient pressures in blood, the coefficients for a₁ and a₂ listed in table 3 can be approximated by a₁ ~ 1, and a₂ ~ 0.09 for the subharmonic threshold of optimally sized bubbles. A similar generalization can be made about the steady state rupture threshold of UCAs in blood: for all UCA considered (Definity, Sonazoid, and Optison), the fitted coefficients for (5) (from table 4) are a₁ ~ 1, and a₂ ~ 0.02. Because both of these thresholds have the same frequency dependence, an index I_CAV is proposed here of the form

$$I_{\mathrm{C}\mathrm{A}\mathrm{V}}=\frac{P_r}{f},$$ (6)

where P_r is the peak rarefaction pressure amplitude in MPa and f is in MHz. The likelihood of UCA rupture increases for I_CAV > 0.02, and the likelihood of subharmonic emissions from stable cavitation increases for I_CAV > 0.09.

The MI is used to describe inertial cavitation and is therefore concerned with the potential bioeffects associated with the mechanical energy of bubble collapse. I_CAV, in contrast, describes bubble oscillations where the pressure at the interface of the bubble prevents an inertial collapse (Flynn 1964), and the mechanical energy during the expansion is as relevant as the contraction. Thus, the bubble dynamics considered here are concerned with the cavitation process as a whole (i.e. not just the collapse), and (6) can be viewed as a ‘cavitation index’.

4. Discussion

4.1. Limitations of models and methods

4.1.1. Acoustic excitation

A single ultrasound pulse of 110 cycles was used as the main source of acoustic excitation to ensure steady state bubble oscillations. The assumption of a long pulse duration is most relevant to therapeutic applications using continuous wave and pulsed ultrasound exposure of contrast agents, such as ultrasound-enhanced thrombolysis (Datta et al 2008, Prokop et al 2007). However, the pulse duration for imaging modalities varies between a few acoustic cycles for B-mode imaging and up to tens of cycles for pulse Doppler mode (Duck et al 1987). In the calculations presented here, the transition to steady state oscillations for optimally sized free bubbles eliciting subharmonic emissions was less than ten acoustic cycles for frequencies greater than 500 kHz, and less than one acoustic cycle for frequencies greater than 1.2 MHz. Similarly, the number of cycles required for optimally sized UCAs to reach steady state oscillation ranges from 1 to 8 acoustic cycles below 1 MHz and only 1 acoustic cycle above 1 MHz. Thus the bubble behavior predicted by this computational model is also applicable for the pulse durations of clinical B-Mode and Doppler ultrasound insonation of echo contrast agents. Note that for broadband excitation typical of B-Mode imaging pulses, linear bubble oscillations may also be initiated at the subharmonic of the center frequency due to an appreciable subharmonic frequency content within the primary wave. Thus for broadband pulses, the cavitation index overestimates the threshold for subharmonic emissions because of the potential for such emissions due to scattering of the primary wave.

4.1.2. Definition of subharmonic threshold

The choice of −20 dB for the ratio of the subharmonic to fundamental spectral amplitude as the definition of the threshold was arbitrary. However, if a ratio of −45 or −5 dB were assumed instead, the subharmonic threshold changed only approximately by 20% (30–150 kPa) and was frequency dependent. However, the subharmonic threshold exceeded the inertial cavitation threshold for subharmonic to fundamental spectral amplitude ratios greater than −10 dB. There was little difference in the subharmonic threshold when this ratio was between −20 and −40 dB (7% difference and less than 55 kPa absolute difference). Such small variations in the pressure threshold are typically within the accuracy of most experimental measurements. Thus the choice of−20 dB is sufficiently robust. Recently bioeffects studies have included the measurement of subharmonic emissions as an indication of stable cavitation (Prokop et al 2007, O’Reilly and Hynynen 2012, Husseini et al 2005). A −20 dB subharmonic to fundamental spectral amplitude ratio was chosen to enable comparison of the calculated threshold of subharmonic emissions with the threshold of bioeffects.

4.1.3. Other sources of subharmonic frequencies

Volumetric oscillations were presumed as the only source of subharmonic emissions. Surface wave oscillations are also capable of subharmonic emissions (Faraday 1831). However, the radiated pressure is not appreciable far from the bubble (Leighton 1994), and therefore assumed to be negligible compared to volumetric oscillations. UCAs are also known to produce subharmonic emissions, which are exploited for contrast imaging (Frinking et al 2000) and for non-invasive estimation of dynamic fluid pressure (Adam et al 2005, Andersen and Jensen 2010, Dave et al 2011). However, the amplitude of the subharmonic is strongly dependent on the driving frequency, and is only appreciable when the driving frequency is between the resonant frequency and twice the resonance frequency (Katiyar and Sarkar 2011). Furthermore, the calculated subharmonic thresholds for Definity, Optison, and Sonazoid were found to be larger than the rupture threshold.

4.2. Comparison of calculations with previous results

4.2.1. Measured subharmonic thresholds in water

The two-parameter fit, (5), seems robust in comparison to values in the literature of the threshold for stable cavitation. The numerical calculations agree within 27% (12 kPa for absolute difference) with the results of Mestas et al (2003) at 473 kHz. Neppiras (1968) measured the subharmonic threshold emissions in air-saturated tap water to be 18 and 77 kPa at 18 and 28 kHz, respectively. The fit of the calculations are an order of magnitude lower, 1.2 and 1.7 kPa at 18 and 28 kHz, respectively. However, the measured values are within 70 kPa of the 95% confidence interval of the fit. The fit may not be valid for Neppiras’s measurements because such low frequencies were not considered in the calculation. In addition, the optimal size for subharmonic emissions at such low frequencies would exceed 300 µm diameter. The subharmonic threshold would increase if such large bubbles were not present in Neppiras’s measurements.

4.2.2. Measured UCA rupture

The calculated UCA rupture thresholds of Optison and Sonozoid were compared against the measurements of Chen et al (2003). The acoustic excitations in these calculations were modified to match the transducer properties of Chen et al. The agreement between the predictions of the Marmottant equation and the measurements were quite good (within 2%) for pulse durations longer than 2 acoustic cycles. The variation between the measured and predicted rupture thresholds was greater at two acoustic cycles, although was still within 15%. In addition, the rupture threshold of Definity over the frequency range 1–7 MHz and pulse duration (1–10 cycles) was compared to the measurements of Yeh and Su (2008). There was a large relative difference between the calculations and measurements (greater than 100%), but the absolute difference was relatively small (less than 65 kPa).

4.2.3. Theoretical predictions

The calculated optimal bubble size for subharmonic emissions were determined to be resonant at the subharmonic frequency, which has been well establish previously (Eller and Flynn 1969, Prosperetti 1974). Eller and Flynn (1969) developed an analytic model to predict the pressure threshold for subharmonic emissions, P_SH, at the optimal size to be of the form

$$P_{\mathrm{S}\mathrm{H}}=\frac{6P_0}{\pi }\delta ,$$ (7)

where δ is the dimensionless damping constant. Viscous and radiation damping terms were substituted into (7) following Eller (1970). Thermal damping was neglected because it was not included in the Gilmore equation. The deviation between (7) and the numerical calculations was less than 5% (10 kPa absolute difference) in water, although was as much as 20% (up to 100 kPa) in blood. The deviation between the two increases with frequency. This suggests the inclusion of viscosity and surface tension during volumetric oscillations (not accounted for by Eller and Flynn) becomes important as the frequency increases.

The dependence of the subharmonic threshold on bubble size in figure 2 was also observed by Katiyar and Sarkar (2011). Note that these authors fixed the bubble size and varied the frequency in their calculations, and found a range of frequencies and bubble sizes for which subharmonic emissions were not possible. The irregularities in the curve near R₀/R_RES ~ 1.0–1.2 in water at 1 and 3 MHz in figure 2 correspond to this same range of frequencies. Interestingly, the threshold for the second subharmonic (f/3) was found in the present calculations to be lower than the first subharmonic in this region.

4.3. Applicable range of the cavitation index

4.3.1. Deration of acoustic pressure

To define the cavitation index for an ultrasound system, the peak rarefactional pressure must be appropriately derated to allow for in vivo attenuation effects (AIUM 2004, WFUMB 1998, Duck and Bacon 1988). The derated pressure should be reported in MPa, and divided by the center frequency in MHz.

4.3.2. Frequency range

Some care must be taken regarding the validity of the cavitation index to predict UCA rupture lower than 1 MHz. Most commercially available UCAs are engineered to be resonant sized at frequencies between 2 and 10 MHz (Klibanov 2002), and the sizes are less than 10 µm(Bouakaz and de Jong 2007). For anUCAwith the shell properties of Definity, the resonant frequency for a 10 µm sized bubble is approximately 800 kHz. Thus, for frequencies lower than 800 kHz, the assumptions of the cavitation index break down because sufficiently sized nucleation sites are not present. Inherent in the development of the cavitation index is the assumption that the presence of optimally sized bubbles exist to nucleate bubble activity and subharmonic emissions. However, resonant sized bubbles effectively do not exist in blood beyond 7 MHz, as discussed in section 2.4. Because the optimal size for subharmonic emissions is resonant at the subharmonic, the cavitation index is only applicable for frequencies between 800 kHz and 14 MHz.

4.3.4. Use of subharmonic emissions to indicate stable cavitation

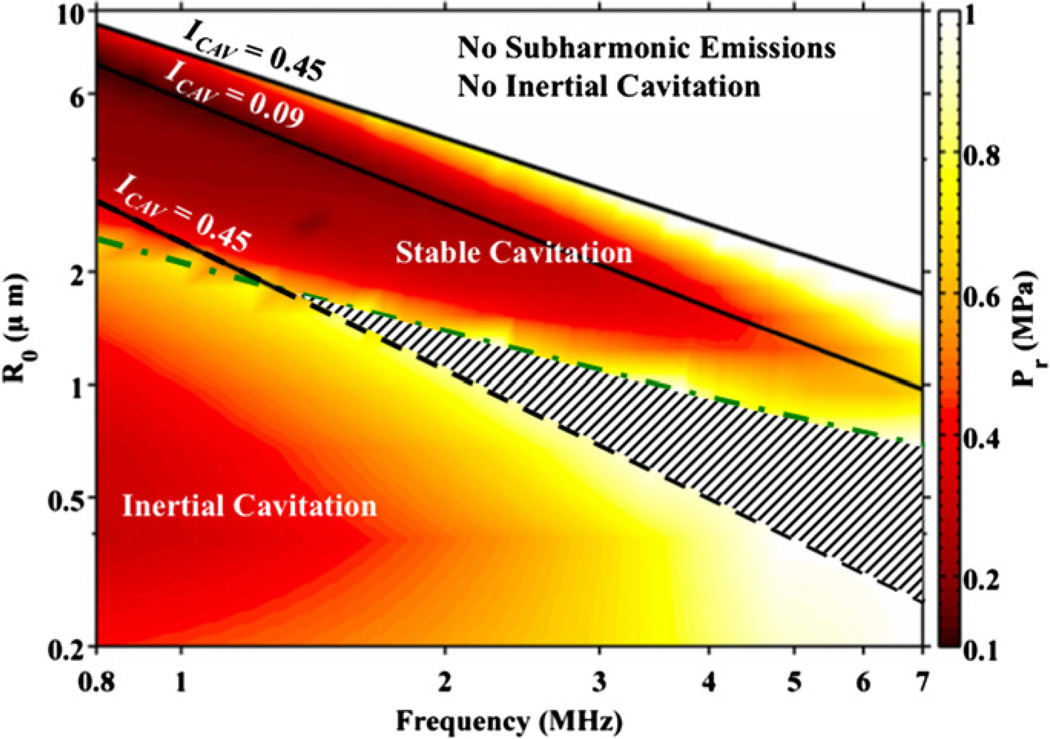
Subharmonic emissions are used to indicate the presence of stable cavitation. To explore the relationship between subharmonic emissions and certain bubble activity, the threshold for subharmonic emissions due to stable cavitation and the threshold for inertial cavitation are shown in figure 6. The host fluid is assumed to be blood at atmospheric pressure with all nuclei sizes present. For bubble sizes below the green dashed line, the color scale indicates the threshold for inertial cavitation. These smaller bubbles have a lower threshold for inertial cavitation than for subharmonic emissions due to stable cavitation. For bubble sizes above the green dashed and dotted line, the color scale indicates the threshold for subharmonic emissions. These larger bubbles will produce subharmonic emissions before they will collapse inertially. The I_CAV = 0.09 line in figure 6 corresponds to the minimum conditions necessary for subharmonic emissions from optimally sized bubbles. The range of bubble sizes capable of subharmonic emissions when I_CAV = 0.45 are also shown. Finally, the region above the optimal conditions for subharmonic emissions indicates where neither subharmonic emissions due to stable cavitation nor inertial cavitation are likely at acoustic rarefactional pressure amplitudes less than or equal to 1 MPa.

Figure 6.

The threshold for subharmonic emissions (bubble sizes above the dashed and dotted line) and inertial cavitation (bubble sizes below the dashed and dotted line) as a function of bubble size and frequency. The solid lines demark the point at which the cavitation index (I_CAV) is 0.45 and 0.09 (I_CAV = 0.09 indicates the optimal bubble size for subharmonic emissions). The striped region indicates subharmonic emissions are due to inertial cavitation. The region labeled ‘No subharmonic emissions, No inertial cavitation,’ indicate neither subharmonic emissions nor inertial cavitation are likely for peak rarefactional pressures less than 1 MPa.

Interestingly, the region within the I_CAV = 0.45 lines (indicating a high likelihood of subharmonic emissions) and region for inertial cavitation do not overlap for frequencies less than 1.3 MHz. Above 1.3 MHz, there is an overlapping region where inertial cavitation occurs before the cavitation index reaches 0.45 (shown as the striped region in figure 6). Here, subharmonic emissions occur due to inertial cavitation, which typically elicits a broadband frequency response. An I_CAV value of 0.45 was chosen as the limit for which the cavitation index scales with the potential for subharmonic emissions from stable cavitation. Above this value, other types of bubble activity are more likely at all frequencies.

4.5. Comparison of cavitation index and MI

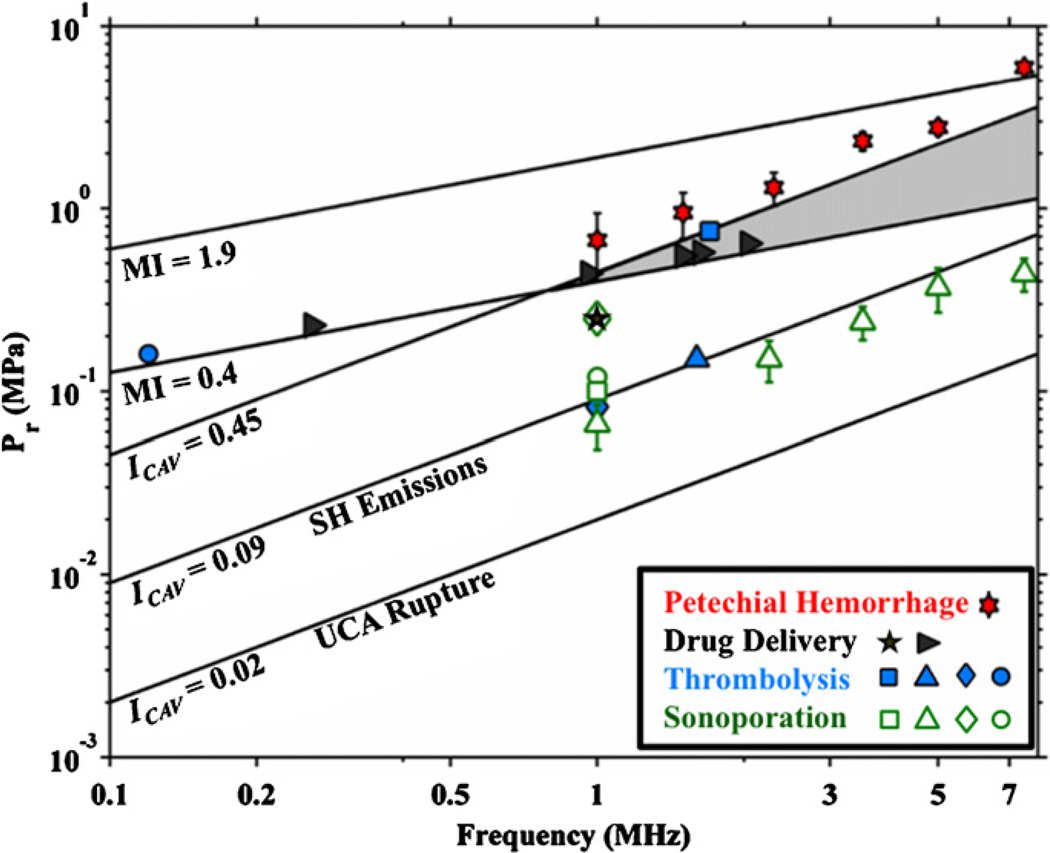
A comparison should be made between the cavitation index and the MI, because the latter is the standard indicator for adverse, nonthermal bioeffects (i.e. inertial cavitation) (AIUM 2004). The peak rarefactional pressure is plotted as a function of frequency for an MI of 0.4 and 1.9 in figure 7. The range of cavitation index values for which subharmonic emissions from stable cavitation occur (I_CAV 0.09 to 0.45), and the peak rarefactional pressure for which rupture of UCAs (I_CAV = 0.02) occur are also shown in figure 7. An MI of 0.4 is the lowest output for which inertial cavitation is expected from diagnostic ultrasound when optimally sized gas bodies are present (Apfel and Holland 1991, Holland et al 2000, Nelson et al 2010), and an MI of 1.9 is the diagnostic ultrasound maximum exposure limit allowed by the United States Food and Drug Administration (AIUM 2004). It is interesting to note that the liberation of gas bodies from UCA rupture occurs well below an MI of 0.4.

Figure 7.

The peak rarefactional pressures (P_r) required as a function of frequency for the MI to be 0.4 and 1.9. The lines labeled I_CAV = 0.09 and I_CAV = 0.45 demarcate the parameter space over which subharmonic emissions from stable cavitation are likely. The shaded region indicates overlay between the MI and cavitation index. The line demarking ‘UCA Rupture’ indicates the P_r required for the cavitation index to be 0.02 as a function of frequency. Bioeffects from sonoporation ( (Greenleaf et al 1998), (Juffermans et al 2009), (Rahim et al 2006), (Miller and Dou 2004)), thrombolysis ( (Datta et al 2008), (Prokop et al 2007), (Porter et al 2001), (Petit et al 2012)), drug delivery ( (Hitchcock et al 2010), (McDannold et al 2008)), and petechial hemorrhage ( (Miller et al 2008)) are also shown.

There is a range of pressures for frequencies greater than 1 MHz where both inertial cavitation and subharmonic emissions due to stable cavitation are expected. This region is shaded in gray in figure 7. Subharmonic emissions from stable cavitation are likely to occur when 0.09 ≤ I_CAV ≤ 0.45. Above 1 MHz, however, the likelihood of inertial cavitation increases before the cavitation index reaches 0.45. As there will be an ample supply of cavitation nuclei from ruptured UCAs, it is likely inertial cavitation will occur before the threshold for subharmonic emissions from stable cavitation is reached in this shaded region.

4.6. Comparison with selected bioeffects

The cavitation index was developed to gauge the likelihood of subharmonic emissions from stable cavitation, to help predict potential bioeffects associated with stable cavitation. The ability of the cavitation index to predict such bioeffects ultimately will rely on experimental verification. Data for select bioeffects in the presence of UCAs are also shown in figure 7: in vitro thrombolysis, in vitro sonoporation, ex vivo and in vivo drug delivery, and in vivo petechial hemorrhage. Interestingly, thrombolysis, drug delivery, and sonoporation (‘beneficial’ bioeffects) appear in most cases to be within the range of acoustic pressures suggested by the cavitation index. In particular, the lowest acoustic pressures for subharmonic emissions correlate well with most cases of sonoporation and thromobolysis. Cases where these beneficial bioeffects did not correlate with the cavitation index are below 800 kHz. As previously discussed, the cavitation index is not valid for frequencies less than 800 kHz. Consequently, larger acoustic pressures are needed to rupture the (non-optimally sized) UCAs and initiate the stable cavitation process. Note that the threshold of petechial hemorrhage in vivo is approximately predicted by a cavitation index of 0.49 (Miller et al 2008). Note that at I_CAV = 0.49, any subharmonic emissions present are more likely from inertial cavitation than from stable cavitation.

5. Conclusions

The threshold of subharmonic emissions was investigated in the context of nucleation from UCAs. A cavitation index was developed from the resultant calculations to predict the thresholds for subharmonic emissions and UCA rupture. The set of calculations used to develop the cavitation index were found to agree with previously published results (both theoretical and experimental), which validate the models used.

Implementation of the cavitation index depends on the application: UCA rupture is predicted for I_CAV > 0.02. This threshold is most appropriate for predicting the destruction threshold of UCA for contrast enhanced imaging applications. Subharmonic emissions are predicted for I_CAV ≥ 0.09, and are associated with potential beneficial bioeffects. It should be noted that the subharmonic threshold is larger than the acoustic pressure required to rupture UCAs. Therefore, once the criteria for subharmonic emissions are met (I_CAV ≥ 0.09), ample nuclei will exist for stable cavitation from previously ruptured UCAs. The rupture threshold predicted by the cavitation index is appropriate for most imaging modalities where optimally sized UCAs are abundant. However, the reliability of the cavitation index is not accurate for frequencies lower than 800 kHz. Similarly, optimally sized bubbles for subharmonic emissions are absent for frequencies greater than 14 MHz. Thus, the cavitation index does not reliably predict the threshold for subharmonic emissions due to stable cavitation above 14 MHz.

It should be noted that the threshold for subharmonic emissions (I_CAV = 0.09) and UCA rupture (I_CAV = 0.02) are lower than the threshold of inertial cavitation predicted by the MI (MI = 0.4). The MI has been a ‘catchall’ predictor of bioeffects due to inertial cavitation, but is often applied beyond its range of applicability. The prompt, free bubble nuclei Apfel and Holland predicted are far different from gas encapsulated UCAs. The cavitation index introduced here may be more appropriate for determining the threshold of UCA rupture, and the threshold of subharmonic emissions due to the presence of stable cavitation.