In vivo photothermal optical coherence tomography for non-invasive imaging of endogenous absorption agents

Abstract

In vivo photothermal optical coherence tomography (OCT) is demonstrated for cross-sectional imaging of endogenous absorption agents. In order to compromise the sensitivity, imaging speed, and sample motion immunity, a new photothermal detection scheme and phase processing method are developed. Phase-resolved swept-source OCT and fiber-pigtailed laser diode (providing excitation at 406 nm) are combined to construct a high-sensitivity photothermal OCT system. OCT probe and excitation beam coaxially illuminate and are focused on tissues. The photothermal excitation and detection procedure is designed to obtain high efficiency of photothermal effect measurement. The principle and method of depth-resolved cross-sectional imaging of absorption agents with photothermal OCT has been derived. The phase-resolved thermal expansion detection algorithm without motion artifact enables in vivo detection of photothermal effect. Phantom imaging with a blood phantom and in vivo human skin imaging are conducted. A phantom with guinea-pig blood as absorber has been scanned by the photothermal OCT system to prove the concept of cross-sectional absorption agent imaging. An in vivo human skin measurement is also performed with endogenous absorption agents.

1. Introduction

Micro-scale non-invasive cross-sectional imaging of endogenous agents in vivo may attain further level of investigation and diagnosis of diseases. Optical coherence tomography (OCT) enables non-invasive in vivo biopsy of biological samples [1] by imaging the micro-scale inner structure of tissue. In addition to obtaining structural information from the backscattering intensity, the measurement of optical absorption has been attempted; i.e., spectroscopic [2,3], pump-probe [4], and photothermal OCT [5–9]. Spectroscopic OCT classifies tissue according to the spectrum attenuation, which is the combination of absorption and scattering [2]. To extract the absorption of a target, an appropriate wavelength range should be adopted for the absorption peak of the target; e.g., visible light for chromophores such as hemoglobin [3]. Pump-probe OCT uses the transient absorption to contrast absorption materials according to change in absorption of a probe beam due to absorption of a modulated pump beam. Photothermal OCT contrasts absorbers through measurement of the optical path length (OPL) change due to the photothermal effect and has been applied to the in vivo measurement of oxygen saturation [10].

Photothermal OCT has advantages over other OCT methods in that there is no restriction on the selection of the wavelength of the probe; i.e., the probe beam of OCT and the excitation beam for the photothermal effect are totally decoupled. Hence, there is no need to alter the core part of OCT while photothermal OCT can be adapted for different absorbers by changing the excitation wavelength. This allows the use of excitation light that maximizes the photothermal effect and a probe of near-infrared light to optimize imaging penetration. However, in vivo cross-sectional imaging with endogenous agents has not been demonstrated.

Exogenous agents, such as metal nanoparticles [6–9,11–16], carbon nanotubes [17], and biocompatible nanoparticles [18], can be designed to fulfill the requirements of applications, and the absorption coefficients of exogenous agents are usually larger than those of endogenous absorption agents. In addition, in vivo imaging employing photothermal OCT is severely affected by the bulk motion of samples. Namely, the OPL change due to the photothermal effect is measured by the phase-resolved processing of OCT and is disturbed by the bulk tissue motion. To obtain a cross-sectional depth-resolving absorption contrast, the accumulation of OPL change due to the photothermal effect should be resolved [5, 9, 19, 20]. These hurdles make the in vivo photothermal OCT imaging of endogenous agents challenging.

In this study, we demonstrate photothermal OCT for in vivo absorption contrast imaging. A theoretical model relating the photothermal effect and the measurement of the local OPL change by phase-resolved OCT is investigated. A new phase processing scheme that achieves depth-resolved absorption-agent imaging and eliminates bulk-motion artifacts is developed. Spatio-temporal modulation and demodulation of thermal excitation are used to extract and enhance photothermal signals. The signal with a tissue phantom is evaluated. The performance of the depth-resolving absorption-agent imaging is evaluated with a phantom incorporated guinea-pig blood. In vivo human skin imaging of endogenous absorption agents is then demonstrated.

2. Principle of photothermal OCT imaging

Photothermal OCT locates the distribution of absorption materials within tissue by measuring local OPL change induced by light absorption. To measure a tiny local OPL change, a phase-sensitive nanoscale OPL change measurement method that uses complex OCT signals, such like Doppler OCT processing, is used.

By describing the temperature distribution upon laser excitation, the measurement of local OPL change by phase-resolved OCT, and the relationship between the phase measurement of OCT and the temperature distribution, the concept of the localization of absorbers is developed.

2.1. Model of temperature change due to laser excitation

The three-dimensional temperature distribution due to the absorption of light is modeled by the heat conduction equation. By assume some specific conditions, the solutions in analytical forms are obtained. In the presented method (Section 3), we cannot assume that absorption coefficient is homogeneous [6,21], heat transfer due to laser excitation is steady periodic condition [7,22], or excitation laser beam size is significantly large [19]. Hence, here we describe from the basic heat conduction solution.

When the material is infinite and thermal properties are homogeneous, the temperature distribution can be expressed with a Green’s function as [23]

$$\mathrm{\Delta }T(\mathbf{r},t)=\underset{-\infty }{\overset{\infty }{\iiint }}\underset{0}{\overset{t}{\int }}\frac{\text{exp}\left[-\frac{{\left|\mathbf{r}-{\mathbf{r}}^{\prime }\right|}^2}{4\kappa (t-t^{\prime })}\right]}{{\left[4\pi \kappa (t-t^{\prime })\right]}^{3/2}}\frac{\dot{q}({\mathbf{r}}^{\prime },t^{\prime })}{\rho c_V}d{t}^{\prime } d{x}^{\prime } d{y}^{\prime } d{z}^{\prime },$$ (1)

where ΔT(r, t) is the distribution of the temperature change from the initial constant temperature: T(r, t) = T₀ + ΔT(r, t), q̇ is the volumetric heat generation rate, and spatial coordinate r = (x, y, z). κ, ρ, and c_V are the thermal diffusivity, density, and specific heat capacity, respectively.

Endogenous absorbers of a tissue become the heat sources by illuminating an excitation laser. Consider that an excitation laser profile on a sample surface is a spatial Gaussian distribution and the distribution of the excitation laser intensity at the sub-surface obeys the Lambert–Beer’s law, the rate of heat generation q̇ can be then described as [24]

$$\dot{q}(\mathbf{r},t)=Y_{\text{H}}\frac{2P(t)}{\pi w_{\text{E}}^2}{e}^{-2\frac{{\left(x-x_{\text{E}}\right)}^2+{\left(y-y_{\text{E}}\right)}^2}{w_{\text{E}}^2}}{\mu }_{\alpha }(\mathbf{r})e^{-{\int }_0^z\mu (x,y,l)dl},$$ (2)

where μ_α(r) and μ(r) are the three-dimensional distributions of the absorption and attenuation coefficients in the tissue, respectively. Y_H is the heat yield by a unit optical energy, z₀ is the depth location of the sample surface, (x_E, y_E) is the illumination point of the excitation laser, w_E is the radius of the excitation beam and P(t) is the temporal profile of the excitation laser power.

By substituting Eq. (2) into Eq. (1), the distribution of the temperature change is described as

$$\begin{array}{ll}\mathrm{\Delta }T(\mathbf{r},t)=\hfill & \frac{Y_{\text{H}}}{\rho c_V}\frac{2}{\pi w_{\text{E}}^2}\underset{-\infty }{\overset{\infty }{\iiint }}\underset{0}{\overset{t}{\int }}P(t^{\prime })\frac{\text{exp}\left[-\frac{{\left|\mathbf{r}-{\mathbf{r}}^{\prime }\right|}^2}{4\kappa (t-t^{\prime })}\right]}{{\left[4\pi \kappa (t-t^{\prime })\right]}^{3/2}}{e}^{-2\frac{{\left(x^{\prime }-x_{\text{E}}\right)}^2+{\left(y^{\prime }-y_{\text{E}}\right)}^2}{w_{\text{E}}^2}}\hfill \\ \hfill & \times {\mu }_{\alpha }({\mathbf{r}}^{\prime })e^{-{\int }_{z_0}^{z^{\prime }}\mu (x^{\prime },y^{\prime },l)dl}d{t}^{\prime } d{x}^{\prime } d{y}^{\prime } d{z}^{\prime }.\hfill \end{array}$$ (3)

When a point absorber in the tissue is assumed, μ_α(r) = μ_αδ(|r − r_a|). Then Eq. (3) is rewritten as

$$\mathrm{\Delta }{T}_{\delta }(\mathbf{r},t)=\frac{Y_{\text{H}}}{\rho c_V}\frac{2}{\pi w_{\text{E}}^2}{e}^{-2\frac{{\left(x_a-x_{\text{E}}\right)}^2+{\left(y_a-y_{\text{E}}\right)}^2}{w_{\text{E}}^2}}{\mu }_{\alpha }{e}^{-{\int }_{z_0}^{z_a}\mu (x_a,y_a,l)dl}\underset{0}{\overset{t}{\int }}P(t^{\prime })\frac{\text{exp}\left[-\frac{{\left|\mathbf{r}-{\mathbf{r}}_a\right|}^2}{4\kappa (t-t^{\prime })}\right]}{{\left[4\pi \kappa (t-t^{\prime })\right]}^{3/2}}d{t}^{\prime },$$ (4)

where r_a = (x_a, y_a, z_a) is the location of the point absorber. Equations (3) and (4) suggest that peaks of temperature change are located at the absorbers in the region illuminated by the excitation laser; i.e., (x_E, y_E). The temporal integration term of Eq. (4) represents the temporal change of the temperature and thermal diffusion from the point absorber.

2.2. Absorption contrast obtained by phase-resolved photothermal OCT

In photothermal OCT, the temperature change is obtained from a phase-resolved OCT measurement. In detail, the temperature change induces a tissue displacement and a refractive index change. Then, they are measured as OPL change by using phase-resolved OCT. This subsection describes the principle of phase-resolved OCT and then formulates the relationship between the distribution of the temperature change and the displacement of tissue.

2.2.1. Local optical path length change measurement by OCT

The complex OCT signal detected by Fourier-domain OCT, Γ, is expressed as

$$\mathrm{\Gamma }(x,y,z,t)=\eta \left|E_{\text{ref}}\right|\left|E_{\text{s}}(x,y,z,t)\right|e^{i\varphi (x,y,z,t)},$$ (5)

where E_s(x, y, z, t) is the electric field of probe beam backscattered from the point (x, y, z) at time t, E_ref is the electric field of the reference beam, ϕ is the phase difference between the backscattered and reference light, and η is the factor of the conversion from the light energy to signal.

A temporal phase shift Δ_tϕ(z, t; Δt) = ϕ(z, t + Δt) − ϕ(z, t) is proportional to a temporal OPL change as [19, 25]

$$\begin{array}{ll}\frac{{\mathrm{\Delta }}_t\varphi (z,t;\mathrm{\Delta }t)}{2k_{\text{c}}}=\hfill & \left[{\int }_{z_0(t+\mathrm{\Delta }t)}^{z(t+\mathrm{\Delta }t)}{n}_s(l,t+\mathrm{\Delta }t)dl+n_o{z}_0(t+\mathrm{\Delta }t)\right]\hfill \\ \hfill & -\left[{\int }_{z_0(t)}^{z(t)}{n}_s(l,t)dl+n_o{z}_0(t)\right],\hfill \end{array}$$ (6)

where z₀(t) is the axial position of the surface of the tissue at time t, Δt is the time separation for temporal phase shift calculation, n_s and n_o are the refractive indexes of the tissue and the surrounding media, respectively, and k_c is the central optical wavenumber of the light source in vacuum. Δ_t indicate the temporal variation in the quantity to its right. In this and the following equations, the transversal positions are omitted for simplicity, without losing generality.

To resolve the accumulated OPL change along depth, axial differentiation should be applied to resolve a local OPL change at a local tissue [5,19,20,26]. The axial differentiation of Eq. (6) with axial separation Δz becomes as

$$\frac{{\mathrm{\Delta }}_z{\mathrm{\Delta }}_t\varphi (z,t;\mathrm{\Delta }z,\mathrm{\Delta }t)}{2k_{\text{c}}}={\int }_{z_a(t+\mathrm{\Delta }t)}^{z_b(t+\mathrm{\Delta }t)}{n}_s(l,t+\mathrm{\Delta }t)dl-{\int }_{z_a(t)}^{z_b(t)}{n}_s(l,t)dl,$$ (7)

where z_a and z_b are above and bottom surface positions of a local tissue region where Δz = z_b(0) − z_a(0) and $z=\frac{z_a(0)+z_b(0)}{2}$. Because of axial phase differentiation, the surface movement effect [25] has been removed.

By assuming that the axial separation Δz is significantly larger than the temporal thickness change due to thermal expansion of the local region, then, z_b(t) − z_a(t) ≈ Δz. Then, Eq. (7) is expanded as

$$\frac{{\mathrm{\Delta }}_z{\mathrm{\Delta }}_t\varphi (z,t;\mathrm{\Delta }z,\mathrm{\Delta }t)}{2k_{\text{c}}\mathrm{\Delta }z}=\overline{n_s}(z,t)\frac{{\mathrm{\Delta }}_{t}w(z_b,t;\mathrm{\Delta }t)-{\mathrm{\Delta }}_{t}w(z_a,t;\mathrm{\Delta }t)}{\mathrm{\Delta }z}+\overline{n_s}(z,t+\mathrm{\Delta }t)-\overline{n_s}(z,t),$$ (8)

where w is the distribution of the axial displacement of the tissue, $\overline{n_s}(z,t)=\frac{1}{\mathrm{\Delta }z}{\int }_{z_a}^{z_b}\overline{n_s}(l,t)dl$ is the mean refractive index of the the local region.

2.2.2. Thermal effects and local optical path length change

Photothermal effect alter the OPL due to thermal expansion and refractive index change [19]. The relationship between the temperature distribution resulting from laser excitation and tissue displacement depends on the mechanical properties of a tissue. By assuming the tissue to be a linear elastic body, the strain–stress relationship (with thermal stress generated by the temperature distribution) can be expressed using Duhamel–Neumann relations [27] as ε_ij = ∑_k,l S_ijklσ_kl + δ_ijα_iΔT, where S_ijkl, ε_ij, and σ_kl are entries of the compliance, strain, and stress tensors, respectively. ΔT is the temperature change, α is a linear expansion coefficient, and δ_ij is the Kronecker delta. The subscripts i, j, k, l are integers and denote the orthogonal directions of Cartesian coordinates (1, 2, 3 are corresponding to x-, y-, and z-directions). In the case of an isotropic material,

$${\epsilon }_{ij}=\frac{1+\nu }{E}{\sigma }_{ij}+{\delta }_{ij}\left(-\frac{\nu }{E}{\sigma }_{kk}+\alpha \mathrm{\Delta }T\right),$$ (9)

where E and ν are Young’s modulus and Poisson’s ratio, respectively.

According to the definition of the axial strain ${\epsilon }_z=\frac{\partial w}{\partial z}$, where ε_z is an alias of ε₃₃, the first term of the left part of Eq. (8) can be approximate measurement of the change of axial strain as

$$\frac{{\mathrm{\Delta }}_{t}w(z_b,t;\mathrm{\Delta }t)-{\mathrm{\Delta }}_{t}w(z_a,t;\mathrm{\Delta }t)}{\mathrm{\Delta }z}\cong {\mathrm{\Delta }}_t{\epsilon }_z(z,t).$$ (10)

The thermal expansion also causes the lateral thermal strain as shown in Eq. (9). This will cause lateral displacement of tissue and decorrelation phase noise could be occurred [28, 29]. However, it will cause only nanometer scale displacement; the effect of such small lateral displacement can be ignored.

According to Eq. (9), the axial strain ε_z = [σ_z − ν(σ_x + σ_y)]/E + αΔT, where σ_x = σ₁₁ and σ_y = σ₂₂. The first term of the left part of Eq. (8) can be replaced with axial strain change [Eq. (10)] and the refractive index change is considered due to temperature change as

$$\frac{{\mathrm{\Delta }}_z{\mathrm{\Delta }}_t\varphi (z,t;\mathrm{\Delta }z,\mathrm{\Delta }t)}{2k_{\text{c}}\mathrm{\Delta }z}=\left[\alpha n_s(z,t)+\frac{d{n}_s}{dT}\right]{\mathrm{\Delta }}_t\mathrm{\Delta }T(z,t;\mathrm{\Delta }t)+n_s(z,t)\frac{{\mathrm{\Delta }}_t{\sigma }_z-\nu ({\mathrm{\Delta }}_t{\sigma }_x+{\mathrm{\Delta }}_t{\sigma }_y)}{E},$$ (11)

where $\frac{d{n}_s}{dT}$ is the thermal coefficient of the refractive index, Δ_tσ_x,y,z are the changes in stresses during the time lag of Δt at time t.

Because the temperature distribution represents the distribution of absorbing tissue [Eq. (3)], Eq. (11) represents the absorber’s distribution when stresses after Δt are close to the initial condition (Δσ_x = Δσ_y = Δσ_z = 0). Note that the tissue properties except optical properties are assumed to be homogeneous for simplicity. The real biological tissues are perhaps mechanically inhomogeneous and not infinite. Then, stress changes Δ_tσ_x,y,z are not zeros. Real axial strain should be obtained by solving the constitutive equation. As discussed before, $\frac{d{n}_s}{dT}$ will be negative value by assuming the main content of tissues is water [6]. Moreover, $\frac{d{n}_s}{dT}$ is also depending on the density of the material [24]. Hence, the state of the thermal expansion also affect the refractive index change because the expansion alter the density. When the refractive index change is dominant comparing to thermal expansion, Eq. (11) will have negative peak at the location of absorber.

3. Methods

3.1. Phase-sensitive swept-source photothermal OCT system

Phase-sensitive swept-source OCT is developed to measure photothermal OPL change. A schematic diagram of the experimental setup is shown in Fig. 1. The light source is an MEMS-based wavelength-wept laser (AXSUN Technologies Inc., Billerica, Massachusetts) with a center wavelength of 1310 nm, scanning rate of 47 kHz and scanning range of 100 nm. Photocurrent from the balanced photoreceiver (Model 1817-FC, New Focus, Newport corporation, Irvine, California) is filtered by an RF low-pass filter (LP62CH3-0S, R&K Co., Ltd., Shizuoka, Japan, 62-MHz cut-off frequency) and sampled by a high-speed digitizer (ATS9350, Alazar Technologies Inc., Pointe-Claire, Quebec, Canada). The k-clock output from the swept laser source is used for the external sampling clock of the digitizer to linearly sample spectral interference signals in terms of the optical wavenumber. A fiber Bragg grating (FBG, reflection at 1266 ± 0.2 nm) is used to generate a trigger that is used to recognize the start of wavelength sweeping. The trigger is detected by the photodetector (PDA10CF, Thorlabs Inc.) and the electric trigger signal is sent to the digitizer. The incident power of the probe on the sample is 29 mW. Sensitivity of 110 dB was achieved.

Fig. 1.

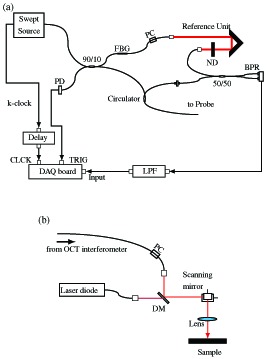
Schematic diagram of the photothermal OCT system. (a) The schema of the OCT engine and (b) the configuration of probe. Light from the source split and coupled by 90/10 fiber coupler where 90% portion directed to probe arm. FBG: fiber-Bragg grating, BPR: balanced photoreceiver, ND: neutral density filter, PD: photodetector, PC: polarization controller, DM: shortpass dichroic mirror, and LPF: lowpass filter.

In the probe arm [Fig. 1(b)], a fiber-pigtailed laser diode with a wavelength of 406 nm (LP406-SF20, Thorlabs Inc., Newton, New Jersey) is used as a photothermal excitation laser. The injection current and temperature of the laser diode are controlled through the laser diode mount with thermo-electric coolers (TCLDM9, Thorlabs Inc.) and laser diode controllers (LDC220C and TED200C, Thorlabs Inc.). The excitation laser is coaxially combined with the OCT probe using a short pass dichroic mirror (DMSP805R, Thorlabs Inc.). The galvanometric scanner and excitation laser modulation are controlled and synchronized using a function generator board (PCI-6713, National Instruments, Austin, Texas).

To minimize sampling jitter, the arrival timing of photocurrent from the balanced receiver, triggers generated by the FBG, and k-clock output to the digitizer are synchronized by adjusting optical fiber lengths and introducing an electronic delay (DB64, Stanford Research Systems, Sunnyvale, California) in the k-clock line. High phase stability close to noise-limited sensitivity ( $1/\sqrt{\text{SNR}}$) [30] was achieved.

To maximize the signal-to-noise ratio of photothermal imaging, the probe and excitation beams are precisely aligned to illuminate the tissue coaxially. Off-axis displacement results in ineffective photothermal imaging as suggested by Eq. (3). The beams focus into the tissue with e⁻² spot diameters of approximately 18 μm (probe) and 12 μm (excitation).

The maximum permissible exposure (MPE) in a period of 10 s for skin is 10,000 W m⁻² for the probe beam (MPE_P) from IEC 60825-1 [31]. The current injected to the laser modulates the laser intensity and the peak power is approximately 5 mW. For the excitation beam, the continuous illumination with averaging power of 5 mW is the most restricted condition. Here we use the peak power of 5 mW as the average power for safety. The MPE of this condition is 2,000 W m⁻² for the excitation beam (MPE_E). The accessible emissions in the case of skin are calculated as 3,014 W m⁻² and 519 W m⁻² for the probe and excitation beams, respectively. The wavelengths of the probe and the excitation beams are shown as additive in Table 2 of Ref. [31], hence, the exposure of the current configuration is below the safety limit as $\frac{3,014\text{W} {\text{m}}^{-2}}{{\text{MPE}}_{\text{P}}}+\frac{519\text{W} {\text{m}}^{-2}}{{\text{MPE}}_{\text{E}}}=0.561<1$.

The correspondence between the sign of phase shift and the direction of the axial movement of a sample has been confirmed by using manually translated scattering sample before the experiments.

3.2. Excitation and detection protocol

The axial distribution of the temporal alteration of temperature change is obtained from Eq. (11). A large temporal temperature change using high-intensity excitation and/or long time lag providing sufficient time for heating tissue is preferred for high-sensitivity measurement. However, the excitation laser intensity is limited by the safe exposure limit. Additionally, the temporal increase in temperature gradually reduces as the temperature change ΔT increases because the temperature distribution is going to be approaching the steady state temperature distribution (See Section 4.1). Moreover, a long time lag between OCT measurements Δt can collapse the phase-sensitive measurement of OCT. In the phase-sensitive method, OCT signals should be measured at the same location in tissues to preserve their correlation between different time points [28,29,32]. A time lag that is too long will generate huge displacement owing to sample motion and reduce the correlation. The following protocol is designed to address these issues.

The excitation, scanning, and detection timing is schematically shown in Fig. 2. For better sensitivity and a weaker effect of sample motion, it is necessary to measure just after turning on or turning off the excitation and to measure again after a time interval that is as short as possible. Hence, the excitation laser is sequentially switched on and off as moving to the next measurement location on the sample. Excitation and cooling times that are sufficient to warm and cool a region having a size similar to or larger than that of the OCT probe beam are required to detect photothermal signals efficiently. Suitable times may be comparable to the time constant, $t_{\text{s}}=\frac{w_{\text{P}}^2}{4\kappa }$ [33]. The radius of the current OCT probe beam is w_P = 9 μm and the thermal diffusivity of water is κ_water = 0.143 × 10⁻⁶ m²/s, resulting in t_s = 142 μs. Several tens of sets of OPL change measurements are acquired at each location (M-scan). Hence, the duration of the acquisition at a single location is approximately 1 ms. The modulation frequency of the excitation laser is approximately 200 Hz to 300 Hz. The probe beam is translated by the galvanometric scanning mirror during around 400 μs temporal margin. This margin is required to stabilize the galvanometric scanning mirror. Afterward, the next excitation state is realized and the M-scan acquisition begins.

Fig. 2.

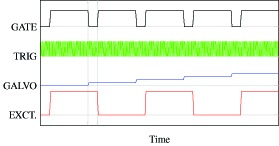
Timing of the excitation and detection. GATE: the gate signal turns on and off acquisition, TRIG: A-scan trigger, GALVO: the waveform that controls the fast scanning galvanometer mirror, EXCT.: the waveform to modulate the photothermal excitation diode laser.

3.3. Signal processing

To extract the photothermal signal, two-dimensional (2D) phase differences for approximating mixed second-order partial derivatives (axial and temporal) are calculated for M-scan data. The flow of the processing is described in Fig. 3. The Hermitian product between axial profiles with a lag of Δn lines is calculated as

$$H_t\left(x_l,z_m,t_n\right)\equiv \sum _{j=-s}^s{\mathrm{\Gamma }}^{*}(x_l,z_{m+j},t_n)\mathrm{\Gamma }(x_l,z_{m+j},t_n+\mathrm{\Delta }n\delta t),$$ (12)

where δt is temporal interval between consecutive lines. Here, axial averaging with a kernel size of 3 (s = 1) is applied to enhance the phase sensitivity. The Hermitian product with axial pixel separation of Δm is then obtained as

$$H_{t,z}(x_l,z_m,t_n)\equiv H_t^{*}(x_l,z_{m-\mathrm{\Delta }m/2},t_n)H_t(x_l,z_{m+\mathrm{\Delta }m/2},t_n).$$ (13)

The phase of Eq. (13) is a local OPL change [Fig. 3(c)]. The Hermitian product is averaged over time within the M-scan as

$$H_{t,z}^{\prime }(x_l,z_m)\equiv \sum _{n=0}^{N-\mathrm{\Delta }n-1}M(x_l,z_m,t_n)H_{t,z}(x_l,z_m,t_n),$$ (14)

where N is the total number of axial scans at the same location and M is a mask defined as

$$M=\{\begin{array}{ll}1\hfill & \sqrt{\left|H_t,z\right|}>\theta \hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}.$$

The mask M with a threshold level θ discards low–SNR data.

Fig. 3.

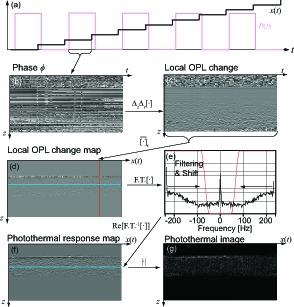
The flow of the photothermal OCT processing. (a) A schematic diagram of scanning and excitation waveforms. (b) A raw 2D phase map of one M-scan. The signal processing described in Section 3.3 is applied ((c)–(g)) to obtain photothermal image.

The phase of the product represents the 2D phase difference [Fig. 3(d)] as

$${\mathrm{\Delta }}_z{\mathrm{\Delta }}_t\varphi \left(x_l,z_m;\mathrm{\Delta }m\delta z,\mathrm{\Delta }n\delta t\right)\equiv \text{arg}\left[H_{t,z}^{\prime }(x_l,z_m)\right],$$ (15)

where δz is axial interval between consecutive pixels. This 2D phase difference Δ_zΔ_tϕ is associated with the temperature change and represents the distribution of the absorption agent as expressed in Section 2.2.2.

Because the excitation of the laser is modulated (Section 3.2), the photothermal signal Δ²ϕ_t,z is also modulated along the spatio-temporal direction. When the excitation laser is turned on, temperature change increases and tissue around light absorbers expands. In contrast, the temperature change is going to be flat due to thermal diffusion and expanded tissues constrict when the excitation laser is turned off. The photothermal signal that is synchronized with excitation modulation is extracted by spatio-temporal frequency filtering and de-modulated. The 2D phase difference is Fourier transformed along the spatio-temporal direction, x(t), as

$${\mathrm{\Delta }}_z{\mathrm{\Delta }}_t\varphi (x_l,z_m)\stackrel{ℱ}{\to }{\mathrm{\Delta }}_z{\mathrm{\Delta }}_t\mathrm{\Phi }({\nu }_L,z_m).$$

The Fourier spectrum Δ_zΔ_t Φ is multiplied with a Tukey window w(ν_L) centered at the modulation frequency (i.e., the Nyquist frequency) which is a high pass filter to pass through frequency components over 20 % of the Nyquist frequency [Fig. 3(e)] and then demodulated as

$${\mathrm{\Delta }}_z{\mathrm{\Delta }}_t\tilde{\mathrm{\Phi }}\left({\nu }_L,z_m\right)\equiv \{\begin{array}{ll}w\left({\nu }_L-f_m\right){\mathrm{\Delta }}_z{\mathrm{\Delta }}_t\mathrm{\Phi }({\nu }_L-f_m,z_m)\hfill & 0<{\nu }_L\hfill \\ w\left({\nu }_L+f_m\right){\mathrm{\Delta }}_z{\mathrm{\Delta }}_t\mathrm{\Phi }\left({\nu }_L+f_m,z_m\right)\hfill & {\nu }_L\leqq 0\hfill \end{array},$$ (16)

where f_m is the modulation frequency of the excitation. The demodulated spectrum is then inversely Fourier transformed as

$${\mathrm{\Delta }}_z{\mathrm{\Delta }}_t\tilde{\mathrm{\Phi }}\left({\nu }_L,z_m\right)\stackrel{{ℱ}^{-1}}{\to }{\mathrm{\Delta }}_z{\mathrm{\Delta }}_t\tilde{\varphi }(x_l,z_m).$$

The real part of the filtered and demodulated phase difference normalized by temporal and axial intervals represents the distribution of photothermal response [Fig. 3(f)] as

$$I_{\text{ph}}(x_l,z_m)\equiv \frac{\text{Re}\left[{\mathrm{\Delta }}_z{\mathrm{\Delta }}_t\tilde{\varphi }(x_l,z_m)\right]}{\mathrm{\Delta }m\delta z\mathrm{\Delta }n\delta t}.$$ (17)

The sign of I_ph represents the response is in-phase or out-of-phase to the excitation modulation. As discussed in Section 2.2.2, they are according to whether thermal expansion or refractive index change is dominant. Then, the photothermal OCT image, i.e. the magnitude of [Eq. (17)] reveals the distribution of absorbers [Fig. 3(g)].

Because modulated and non-modulated terms are separated in the spatio-temporal frequency domain [Eq. (16)], only the half of the detection bandwidth can be used for each term. It means that this method requires two times dense spatial sampling comparing to full band detection. This condition can be expressed as Δx/R < π/8 [34], where Δx is the spatial sampling step and $R=2\sqrt{\kappa \tau }$ is the thermal diffusion length and τ is the duration time of heating. In the current setup, τ equals to half the period of the modulation, 1 to 2 ms, then the lateral separation between successive M-scans should be less than 9.4 μm.

3.3.1. Artifact removal

The real phase of the OCT signal consists of not only photothermal OPL change but also the Doppler phase shift due to bulk motion of the sample and blood flow, and the texture of the tissue. However, these factors are canceled out in the above processing as explained as follows. The phase of the OCT signal can thus be generally expressed as

$$\varphi ={\varphi }^{(\text{ph})}(x,z,t)+{\varphi }^{(\text{b})}(x,t)+{\varphi }^{(\text{tx})}(x,z)+{\varphi }^{(\text{bf})}(x,z,t),$$ (18)

where ϕ^(ph), ϕ^(b), ϕ^(tx), and ϕ^(bf) are phase components of the photothermal effect, bulk phase shift, structural texture, and blood flow, respectively. By applying temporal and axial derivatives such as those described in Eq. (15), the structural texture and the phase shift due to bulk sample motion are removed as

$$\frac{{\partial }^2\varphi (z,t)}{\partial z\partial t}=\frac{{\partial }^2{\varphi }^{(\text{ph})}(z,t)}{\partial z\partial t}+\frac{{\partial }^2{\varphi }^{(\text{bf})}(z,t)}{\partial z\partial t}.$$ (19)

The blood flow term is modulated by blood pulsation with frequency usually less than 2 Hz. Hence, if the excitation frequency is higher than 2 Hz [in this paper, approximately 200 Hz to 300 Hz (Section 3.2)], this term can also be excluded. After temporal averaging $\overline{{\varphi }_{t,z}}(x,z)=\frac{\overline{{\partial }^2\varphi [x,z,t]}}{\partial z\partial t}$, spatio-temporal filtering is applied to extract the component at the excitation modulation frequency, f_m, and the low-frequency component such as pulsation is filtered out. Only the photothermal effect, then, remains as

$${\overline{{\varphi }_{t,z}}\left[x(t),z\right]|}_{f=f_{\text{m}}}={\overline{{\varphi }_{t,z}^{(\text{ph})}}\left[x(t),z\right]|}_{f=f_{\text{m}}}.$$ (20)

All phase components except that of the photothermal effect are removed as shown above. However, decorrelation due to displacement increases the phase noise [28, 29, 32]. This term manifests as artifacts in photothermal imaging. To mitigate the term, temporal averaging divided by the standard deviation of the 2D difference is replaced by the expression in Eq. (15) as

$${\mathrm{\Delta }}_z{\mathrm{\Delta }}_t{\varphi }^{\prime }(x_l,z_m)=\frac{\text{arg}\left[H_{t,z}^{\prime }(x_l,z_m)\right]}{\sqrt{\mathit{Var}\left[\text{arg}\left[H_{t,z}(x_l,z_m,t_n)\right]M\left(x_l,z_m,t_n\right)\right]}}.$$ (21)

Spatio-temporal filtering and demodulation are then applied.

4. Results

4.1. Photothermal signal verification with porcine liver

A porcine liver has been scanned by the photothermal OCT. One hundred axial lines were detected at a single location and 256 transversal positions (1 mm) were measured. The corresponding excitation modulation frequency was 235 Hz. The 2D phase difference was calculated with a time lag of 213 μs and an axial separation of 34.8 μm (refractive index of 1.38). The total acquisition time was approximately 0.68 seconds.

Figure 4 shows the photothermal signals of a porcine liver. Temporal and axial distributions of local OPL change in consecutive M-scans when heating stage [Fig. 4(a)] and cooling stage [Fig. 4(b)] are shown. The profile of the local OPL change at a certain depth (arrow in Fig. 4) presents the temporal slope of local OPL change [Fig. 4(c)]. Within one period of modulation of excitation, we assume the the laser power P(t) is constant at the former half period and turned off at the later half.

$$P(t)=\{\begin{array}{ll}P\hfill & (t\le \tau )\hfill \\ 0\hfill & (t>\tau )\hfill \end{array}$$ (22)

Temporal profile of photothermal signals in a M-scan [Eq. (11)] are related to the temporal derivative of Eq. (4). By introduce Eq. (22),

$$\frac{\partial \mathrm{\Delta }T(\mathbf{r},t)}{\partial t}\propto \{\begin{array}{ll}\frac{P}{{\left(4\pi \kappa t\right)}^{3/2}}\text{exp}\left(-\frac{{\left|\mathbf{r}\right|}^2}{4\kappa t}\right)\hfill & (t\le \tau )\hfill \\ \frac{P}{{\left(4\pi \kappa \right)}^{3/2}}\left[\frac{1}{t^{3/2}}\text{exp}\left(-\frac{{\left|\mathbf{r}\right|}^2}{4\kappa t}\right)-\frac{1}{{(t-\tau )}^{3/2}}\text{exp}\left(-\frac{{\left|\mathbf{r}\right|}^2}{4\kappa (t-\tau )}\right)\right]\hfill & (t>\tau )\hfill \end{array}$$ (23)

Eq. (23) is fitted to the experimental data. As shown in Fig. 4(c), they are in good agreement.

Fig. 4.

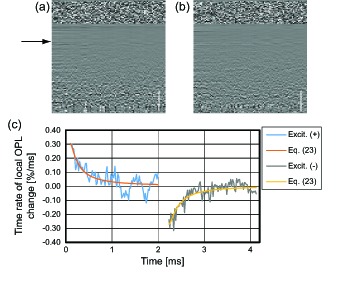
Photothermal signals in M-mode scan. Phase derivatives of two consecutive M-scans (a) when the excitation laser is on and (b) after the laser is turned off. (c) Temporal profile of photothermal signal. Scale bars are 500 μm in tissue. Each profile obtained at a certain depth of the porcine liver (black arrow).

Figure 5 shows cross-sectional OCT and photothermal images with/without excitation laser illumination. For quantitative comparison, the normalization process [Eq. (21)] was skipped. With photothermal excitation, the photothermal signal appeared inside of the liver tissue. At the surface of the tissue, strong negative signal is obtained. The reason may be the shrinkage of the superficial layer by dehydration due to photothermal excitation because the photothermal signals before frequency filtering are close to zero at locations when the excitation laser off (data is not shown). The positive and negative values are appeared inside of the tissue. This might be present the magnitude of the thermal expansion and refractive index change are comparable. For absorption contrast, the magnitude of photothermal signal is obtained and mapped. The signal-to-noise ratio is measured as the ratio of averaged photothermal signal magnitude with excitation to that of without excitation. The averaged signals are calculated within the white boxes shown in Fig. 5. The SNR of ∼ 7.2 was obtained. For a comparison, Fourier transform method is applied for phase derivative Δ_zΔ_tϕ. Because the probe beam is scanned along lateral direction during the modulation, not peak magnitude detection but bandpass filtering around the modulation frequency and inverse Fourier transform were applied. They are shown in Fig. 5 Each image show the case of without and with excitation. With this Fourier transform method, SNR is measured as ∼ 4.8. The proposed method might have the advantage in sensitivity over the previous phase modulation detection technique at least 1.5 times.

Fig. 5.

The images are compared. 213 us separation, 34.9 um separation, 235 Hz modulation. For quantitative comparison, normalization [Eq. (21)] was not applied. Scale bars are 500 μm in tissue.

4.2. Phantom imaging

A phantom was imaged to validate the depth-resolving performance of the developed photothermal OCT in locating absorbers. A scattering phantom was made by fixing 1 % soybean oil lipid emulsion (Intralipos®20%, Otsuka Pharmaceutical Factory Inc., Japan) with 10 % porcine gelatin (G2500, Sigma-Aldrich Corp., St. Louis, MO) and injecting guinea-pig blood. The size of a red blood cell of a guinea pig is close to that of a human. The diameter of the red blood cell was ∼ 7 μm and the mean corpuscular volume was ∼ 80 μm³ [35], whereas the values for a human are ∼ 8 μm and ∼ 90 μm³, respectively. The blood was diluted with Alsever’s solution to 50 % for preservation.

The phantom with guinea-pig preserved blood was scanned by photothermal OCT. The excitation modulation period was 4.26 ms, corresponding to a frequency of 235 Hz. The 2D phase difference was calculated with a time lag of 213 μs and an axial separation of 34.8 μm (refractive index of 1.38). One hundred axial lines were detected at a single location and 256 transversal positions were measured. The total acquisition time was approximately 0.68 seconds.

The beam scanning was aimed at the location of injected guinea-pig blood. Photothermal signals generated within the phantom with the excitation laser [Fig. 6(d)] were not present without excitation [Fig. 6(c)]. This contrast was not obtained in conventional structural OCT intensity images [Figs. 6(a) and 6(b)]. These signals probably represent the location of injected blood. The presented photothermal OCT thus provides depth-resolved contrast of absorption materials.

Fig. 6.

OCT (a, b) and photothermal OCT (c, d) images of a phantom made of gelatin and soybean oil emulsion with guinea-pig blood. The left (a, c) and right (b, d) columns show images without and with excitation, respectively. Scale bars are 500 μm in tissue.

4.3. In vivo human skin imaging

To demonstrate the feasibility of the developed photothermal OCT, in vivo imaging of human skin was conducted. The imaging was performed in two regions; i.e., around a mole of the outer forearm and in a non-mole region. Fifty axial lines were detected at a single location and 256 × 128 transversal positions (0.5 × 0.5 mm²) were measured. A settling time of 425 μs (20 axial lines) was set after the transition of the galvanometric scanning mirror. The excitation modulation period was then 2.98 ms; i.e., the modulation frequency was 335.7 Hz. In addition, the excitation laser was turned on and off along the slow scanning direction (1.3 Hz) to obtain the photothermal OCT image with and without excitation modulation sequentially. The phase difference was calculated with a time lag of 213 μs (10 axial lines) and axial separation of 34.8 μm (refractive index of 1.38). The acquisition time of one B-scan was around 0.38 seconds. The total volumetric acquisition time was 49 seconds.

Two volumes were scanned on human skin. The images are shown in Fig. 7 [7(a)–7(h): around a mole, 7(i)–7(p): normal skin]. To create en-face images of photothermal OCT, the magnitudes of photothermal signals were integrated along the depth. For reference, the phase-resolved Doppler OCT algorithm [36] with bulk motion correction [37] was applied for MB-scans without excitation to contrast the blood flow distribution. The photothermal OCT images of the mole with excitation modulation clearly show strong signals close to the skin surface [Figs. 7(c) and 7(d), orange arrows]. There is a clear difference in the comparison with the photothermal image obtained without excitation [Figs. 7(e) and 7(f), orange arrows]. The strong signal might correspond to melanin in the mole. In addition to the skin’s melanin, a strong photothermal signal of hair is seen in photothermal OCT images obtained with excitation (green arrows).

Fig. 7.

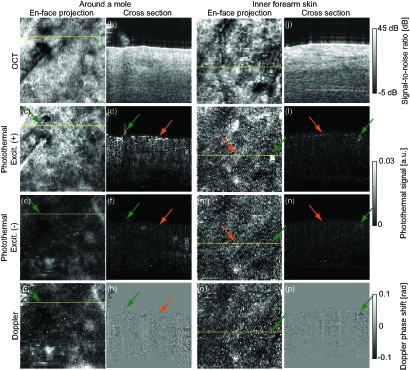
Volumes of OCT (first row) and photothermal OCT (second and third rows) images of human skin. Images in the the fourth row are images of Doppler blood flow for comparison. Two volumes around a mole (a–h) and of normal skin (i–p) are obtained. En-face projections (left) indicate the locations of the cross-sectional images (left).

Although the intensity is weak, there is structure in the photothermal image obtained without excitation [Fig. 7(e)]. It is clear that the signature in the en-face projection image well matches blood flow imaging using a Doppler phase shift [Fig. 7(g)]. Decorrelation phase shift noise due to blood flow might generate these artifacts.

In the case of normal inner forearm skin, a layered signal, definitely weaker than signal of the mole, is seen in the superficial skin with excitation [Figs. 7(k)–7(n), orange arrows]. This supports the idea that the photothermal signal of melanocyte at the epidermis is detected. A strong photothermal signal and blood flow signal are observed in the slightly deep tissue [Figs. 7(l) and 7(p), green arrows], which is not clear in the photothermal image obtained without excitation [Fig. 7(n), green arrow]. The appearance of this signal in the cross section and en-face image is in good agreement with the structure of capillaries in skin [38] and skin angiographies obtained in other studies [39, 40]. The signal might therefore correspond to a capillary of the skin.

5. Discussions

To increase the speed of photothermal OCT imaging, increasing the excitation modulation frequency required. However, a higher modulation frequency reduces the photothermal signals [6] since the maximum modulation frequency which retains the photothermal signal is limited by the size of the probe beam [33]. Optical coherence microscopy with other detection scheme is required to use high modulation frequency without loss of photothermal signal strengths [41]. We have been applied half period of modulation for each M-scan to achieve high imaging speed and low modulation frequency. In this configuration, Fourier transform method can not applied directly. The photothermal signals are estimated at each M-scan and modulation is applied with transversal beam scanning. Frequency filtering in spatio-temporal frequency domain. This algorithm is not only adapted for the presented detection protocol, but efficient to detect non-sinusoidal modulation as shown in Section 4.1.

For depth-resolved photothermal OCT imaging, the accumulation of OPL change due to the photothermal effect is resolved by differentiating phase information along axial direction after temporal differentiation. The temporal differentiation removes the texture noise (Section 3.3.1) and prevents the phase signal from the decorrelation noise due to axial separation. The direct phase differentiation between two depths [5, 19] should be affected by the decorrelation noise due to large separation between two depths compared to the axial resolution [42, 43]. On the other hand, the differentiation between adjacent pixels [9] makes OPL change very small because the magnitude of OPL change is proportional to a measured tissue thickness, i.e., the separation of two measurement depths. The other approach is calculating the slope of OPL change [20]. This is derived from the temperature change inside of a homogeneous absorption tissue. It assumes that the cumulative OPL change is monotonically increase or decrease. However, this assumption is controversial in inhomogeneous tissue. The photothermal effect on OPL consists of the thermal expansion and the refractive index change, and these effects probably cancel to each other [6, 12]. Although the magnitude of the coefficient of thermal expansion is roughly 2 times of that of the refractive index change [6, 12], real volume expansion and axial displacement are depends on mechanical confinement [26]. For example, if a stiff layer exists at the tissue surface, internal tissue cannot expand axially but its lateral expansion reduces the density of the tissue and then refractive index. In this case, the refractive index change play a main role of the OPL change. Hence, in biological tissues, it is hard to conclude that the thermal expansion is the dominant effect in the OPL change.

The contrast of blood in vivo requires further investigation. The photothermal signal of blood was probably generated by not only thermal expansion and refractive index change but also complex movement of blood cells due to the convection. The current theoretical model does not consider fluid such as blood. Thermal dynamics of fluid in a tube should thus be taken into account. Modeling of the photothermal effect with blood is required to optimize and understand the photothermal OCT measurement of blood. However, as shown in the phantom measurement, an advantage of photothermal OCT is that the technique can detect static blood due to such as hemorrhage. This may be difficult to obtain by employing Doppler or other motion contrast methods that are used to contrast blood flow [44].

The mismatch of the wavelengths between the excitation and probe beams cause a chromatic aberration issues. If longitudinal focal shift occurs, it will alter the laser fluence rate. However, in our configuration, the longitudinal focal shift was around 150 μm according to ray-tracing (OpticStudio, ZEMAX, LLC, Redmond, Washington). It was only around half the Rayleigh range of 280 μm. On the other hand, the transversal focal shift induces the offset between heated location and the OCT probe beam. This is affect to the temporal temperature change profile at the location of OCT probe beam. Hence, if the characteristic length is long enough to cover the offset plus beam spot size of the probe beam, there is no significant signal loss. However, too large offset results in the image mismatch between OCT and photothermal OCT images. It is expected around 5 μm in maximum when 0.5 mm transversal scan is applied in the current setup. Since the spot sizes of the excitation and probe beams are 12 μm and 18 μm, the effect of transversal focal shift would be negligible.

The limitation of the imaging depth is the combination of the limited penetration depth of OCT imaging and the limited fluence depth of the excitation laser. In this study, a single-mode fiber-pigtailed diode laser was selected because it provides a small illumination beam spot, high response of temporal output modulation, and stable operation at low cost. Some studies have expected the penetration depth of a blue (∼ 400 nm) wavelength to be less than 1 mm. A red (∼ 630 nm) wavelength is an alternative that provides deep penetration of tissue; additionally, consumer products of the laser diode are available for this wavelength. However, the imaging depth of photothermal OCT does not rely only the light penetration depth but fluence depth, i.e., light intensity times absorption coefficient [Eq. (2)]. Because absorption coefficients of endogenous agents, such as hemoglobin and melanin, at blue wavelength range are stronger than other visible lights, there is a certain depth where the blue wavelength exhibits higher fluence rate comparing to other visible lights and it might be deeper than the light penetration depth.

The photothermal fluence rate f_PhTh is defined as

$$f_{\text{PhTh}}(z)\equiv {\mu }_a^{(\text{agent})}{I}_0\text{exp}\left[-\left({\mu }_s^{(\text{skin})}+{\mu }_a^{(\text{skin})}\right)z\right],$$ (24)

where ${\mu }_{\text{a}}^{(\text{agent})}$ is the absorption coefficient of an absorption agent, ${\mu }_{\text{s}}^{(\text{skin})}$ and ${\mu }_{\text{a}}^{(\text{skin})}$ are scattering and absorption coefficients of skin, respectively, and z is the depth from the surface.

Figure 8 plots the photothermal fluence rate profiles of hemoglobin in skin for blue (405 nm) and red (630 nm) wavelengths. The plot indicates the strength of the photothermal signal against the depth of blood within skin. The absorption and scattering coefficients of hemoglobin ( ${\mu }_{\alpha }^{(\text{hemoglobin})}(405 \text{nm})=1,400 {\text{cm}}^{-1}$, ${\mu }_{\alpha }^{(\text{hemoglobin})}(630 \text{nm})=26 {\text{cm}}^{-1}$) [45] and the human skin ( ${\mu }_s^{(\text{skin})}(405 \text{nm})=70 {\text{cm}}^{-1}$, ${\mu }_s^{(\text{skin})}(630 \text{nm})=20 {\text{cm}}^{-1}$, ${\mu }_{\alpha }^{(\text{skin})}(405 \text{nm})=3.8 {\text{cm}}^{-1}$, ${\mu }_{\alpha }^{(\text{skin})}(630 \text{nm})=0.75 {\text{cm}}^{-1}$) [46] are used in this numerical simulation. The transition point is located around 1 mm depth. It means that photothermal signal with blue excitation laser will be higher than that of red wavelength till depth of around 1 mm. Because the absorption coefficients of absorbers and attenuation of tissues are variable, the optimum excitation wavelength varies on each target. To determine the imaging depth of photothermal OCT, the SNR-dependent noise of phase-resolved OCT and the conversion factor from the laser fluence to photothermal signal magnitude should be accounted.

Fig. 8.

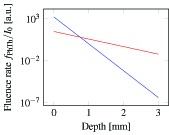
Simulated axial fluence profile of the photothermal effect of hemoglobin in skin for 400 nm (blue line) and 630 nm (red line) wavelengths.

6. Conclusion

We presented a new photothermal OCT detection scheme for the imaging of endogenous absorption agents. A photothermal excitation protocol was designed and a phase processing method developed to sense thermal expansion in in vivo photothermal imaging. A phantom experiment demonstrated that the method has the ability to locate absorbers in a cross section. Non-invasive in vivo imaging of the human skin demonstrated the possibility of photothermal OCT applications.