Fibre-coupled multiphoton microscope with adaptive motion compensation

Abstract

To address the challenge of sample motion during in vivo imaging, we present a fibre-coupled multiphoton microscope with active axial motion compensation. The position of the sample surface is measured using optical coherence tomography and fed back to a piezo actuator that adjusts the axial location of the objective to compensate for sample motion. We characterise the system’s performance and demonstrate that it can compensate for axial sample velocities up to 700 µm/s. Finally we illustrate the impact of motion compensation when imaging multiphoton excited autofluorescence in ex vivo mouse skin.

1. Introduction

Since the first demonstration of multiphoton microscopy [1], non-linear laser-scanning optical microscopy techniques have become well established for studying the structure and function of biological systems, including in vivo. However, in vivo studies must address the challenge presented by sample motion that is inherent in living systems and can degrade image resolution and contrast. Following the first demonstration of in vivo multiphoton fluorescence imaging of human skin [2], a number of compact and flexible systems have been developed to translate this to a clinical setting [3,4] but the challenges associated with imaging parts of the body that are hard to keep still, e.g. the neck and chest, have not yet been fully addressed. To this end we present, to the best of our knowledge, the first fibre-coupled multiphoton microscope with integrated adaptive motion-compensation that we believe will find utility as a handheld device for clinical imaging.

A variety of strategies have been proposed to suppress motion-induced image degradation in high resolution optical microscopy. Mechanical techniques that physically immobilise tissue can significantly reduce motion amplitude [5,6] but this approach potentially disrupts normal physiological processes and can distort local anatomy. A less invasive approach uses the image data to monitor 3D changes in the sample position. These methods rely on the acquisition of multiple images and so are better suited to compensating for slow tissue drift [7] or periodic motion [8]. Gated imaging techniques use conventional medical sensors (electrocardiogram [9] or plethysmograph [10]) to monitor motion inducing processes (heartbeat and breathing respectively) and trigger image acquisition during the stationary points of the cycle. The advantages of these methods must be weighed against their lack of flexibility as they can only compensate for motion deriving from the physiological processes being monitored. Finally, optical displacement sensors that operate in parallel with the imaging system have been used to give high speed, high accuracy measurements of the position of the sample surface. Typically, position data is fed back to an actuator to shift the position of the objective to keep the same plane in the sample in focus. This approach has been demonstrated previously using a non-imaging spectral domain optical coherence tomography (SDOCT) sensor placed adjacent to a confocal reflectance imaging system [11]. This system could compensate motion with an amplitude of up to 60 μm at average speeds of up to 72 μm.s⁻¹ and maintained the focus to within 5 μm. In subsequent work by the same group, a similar approach was used to demonstrate axial motion compensation in a hand-held SDOCT imaging system that achieved an RMS surface error of 2.93 μm when the probe was hand-held [12]. An alternative system used an off-axis optical focus sensor with a multiphoton imaging system [13] in order to reduce motion in the spina lamina I neurons of anaesthetized male Wistar rats to less than the axial resolution of the imaging system. The accuracy and precision of this system was, however, influenced by local tissue structure, as optical scattering from multiple depths within the sample broaden the size of the spot used for surface tracking.

Here we present a motion compensation system that uses a non-imaging SDOCT approach [11] to monitor the position of the sample surface in a multiphoton scanning system that is being developed to enable clinical imaging of surface regions on the human body affected by patient motion. Our approach has the advantage of being an on-axis technique that measures the sample surface position at the centre of the microscope field of view and is therefore less susceptible to any non-rigid motion of the tissue surface.

2. Experimental setup

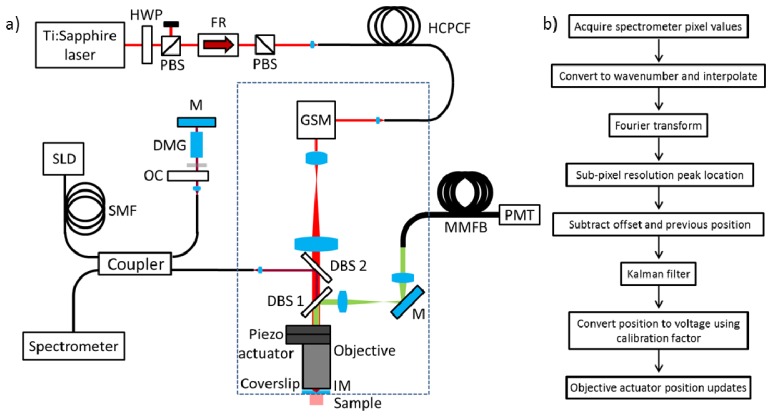
Figure 1(a) shows a schematic diagram of the multiphoton microscope with active motion compensation system. In this device optical fibres allow heavy and/or bulky pieces of equipment to be physically separated from a small imaging head that can be handheld. The whole system is controlled using two data acquisition boards (National Instruments PCIe 6363 and USB 6002) and a C++ custom control code running on a desktop PC (Hewlett Packard Z620). Fluorescence images are built up from photon events detected by the photon multiplier tube (PMT) that are processed by a time-correlated single photon counting (TCSPC) card (Becker & Hickl SPC-830).

Fig. 1.

(a) A schematic of the experimental setup (components inside the dashed rectangle are found in the imaging head) DBS1: 705 nm Dichroic beamsplitter; DBS2: 905 nm Dichroic beamsplitter; DMG: Dispersion matching glass; FR: Faraday rotator; GSM: Galvanometric scanning mirrors; HWP: Half waveplate; HCPCF: Hollow core photonic crystal fibre; IM: Immersion media (water); M: Mirror; MMFB: Multimode fibre bundle; OC: Optical chopper: PBS: Polarising beamsplitter; PMT: Photon multiplier tube; SMF: Single mode fibre; SLD: Superluminescent diode; (b) Flowchart for axial motion compensation.

2.1 Fibre-coupled multiphoton microscope

A custom single-mode air-core photonic band-gap optical fiber is used to deliver 90 fs pulses with a centre wavelength of 761 nm from a mode-locked Ti:Sapphire laser (Spectra Physics Mai Tai HP) to the body of the imaging head that includes the microscope objective and scanner. This weighs 2 kg and has overall dimensions of 35x15x5 cm. The fiber is based on a standard 7-cell core design: it has a core diameter of 7.4 µm and a cladding pitch of 2.3 µm. The zero-GVD wavelength is at 762 nm where the dispersion slope is ~20 ps.nm⁻².km⁻¹. For the pulse lengths and energies used here, the fiber nonlinearity can be neglected. A pair of X-Y galvanometric scanning mirrors (Camtech 6210H) and scan and tube lenses (Thorlabs LSM02-BB and AC508-100) act to scan the beam angle at the overfilled back aperture of a water immersion microscope objective lens (Olympus UPLSAPO60XW). The fluorescence generated by the scanned focal spot is epi-collected by the objective lens and separated from the excitation light using a dichroic beam splitter (Semrock FF705-Di01, DBS1 in Fig. 1(a)). A pair of lenses (Thorlabs AC254-100 and AC254-40) are used to relay the fluorescence onto the end face of a 2.86 mm diameter active area fibre bundle that guides the light to a hybrid PMT (Becker & Hickl HPM-100-40). Multiphoton images are acquired with a line scan time of 3.9 ms, allowing a 256-by-256 pixel image to be acquired in 1 s. The point spread function of this imaging system was determined by recording fluorescence images of single sub-resolution fluorescent beads (Life Technologies FluoSpheres F-8781, 24 nm diameter) mounted on a microscope slide. The FWHM of the lateral and axial point spread functions were measured in water as 0.34 µm and 2.18 µm respectively.

2.2 Motion compensation system

The output from a superluminescent diode (Superlum 930-B-I-10-PM) operating at 930 ± 35 nm is split by a 50/50 polarisation maintaining fibre coupler into two arms of a low coherence interferometer. As shown in Fig. 1, the sample arm is incorporated in the imaging head where a dichroic beam splitter (Chroma zt1064spr-dc, DBS2 in Fig. 1(a)) is used to direct light through the objective lens and onto the sample. The back-scattered light is coupled back down the illumination fibre where it is recombined with light from the reference arm that is retro-reflected by a dielectric mirror. The length of the reference arm is adjusted by translating the mirror until the optical path length between the two arms is 100 µm. A 70 mm piece of BK7 glass in the reference arm is used to approximately match the dispersion in the sample arm introduced by the objective lens. After recombination in the fiber coupler, the resulting optical interference pattern is recorded by a spectrometer (Ocean Optics USB2000+ ). Following the principles of SDOCT [14], the optical path difference between each arm of the interferometer – and hence the relative position of the sample – is encoded in the frequency of the spectrally resolved interference fringes, which can be extracted using the algorithm shown in Fig. 1(b). The spectral axis of the spectrometer data is converted to units of wavenumber and then interpolated to provide equally spaced values. The wavenumber data is then transformed into the spatial domain using a discrete Fourier transform (DFT) and the sample position is located to sub pixel accuracy by quadratic interpolation about the peak. A predefined offset and the previous sample position are subtracted from the current value and passed to a predictive Kalman filter. The output from this filter is then multiplied by a measured distance-to-voltage calibration factor and sent to the piezo actuator (PI P-725 PIFOC) that controls the position of the microscope objective. The motion compensation code updates at 343 Hz and the whole system operates with a measured latency of 15 ms, which is mitigated by the use of the Kalman filter that uses knowledge of this latency and previous position measurements to produce optimized estimates of the current sample position [15]. The piezo actuator provides 250 µm of travel and uses an onboard position sensor to respond to voltage programming commands in closed loop. The closed loop bandwidth of the actuator was measured to be 19 Hz. The spectrometer has a minimum acquisition time of 1 ms. This places a practical limit on the maximum measurable sample velocity due to the loss of fringe contrast resulting from the range of optical path lengths recorded in one acquisition time. An optical chopper placed in the interferometer reference arm is used to decrease the effective acquisition time of the spectrometer by a factor of five, increasing the maximum measurable velocity – corresponding to complete wash-out of the interference fringes on the sensor – to 1.16 mm.s⁻¹.

2.3 Ex vivo mouse skin specimens

Ex vivo mouse skin was obtained from a male, 90 day old c57BL/6 mouse. The mouse was given a terminal dose of anaesthetic (Pentobarbitone) and the sacrifice was confirmed by cervical dislocation. Once excised, hair removal cream was used to ensure good optical access to the skin surface. Finally the sample was washed with Hanks Balanced Salt Solution, and kept hydrated under transport using a wet gauze.

3. Results

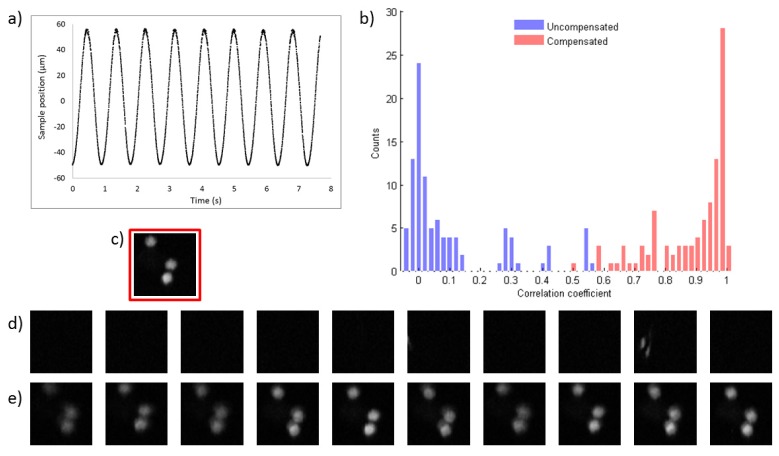
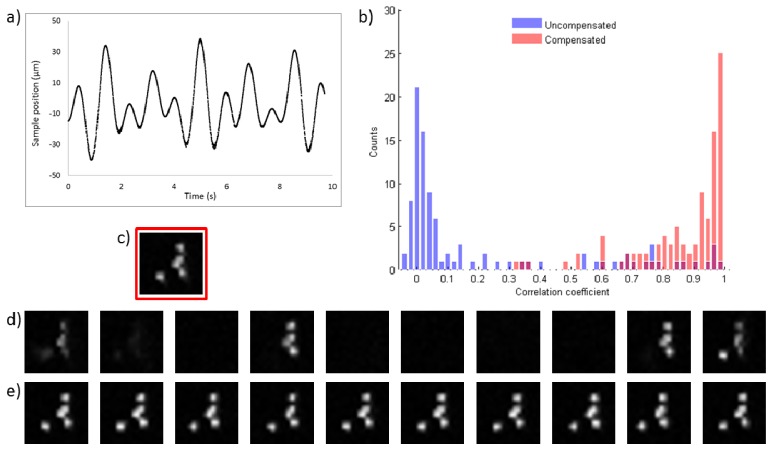
We characterised the performance of the SDOCT motion compensation system by acquiring multiphoton fluorescence images of a sample mounted on a second piezo actuator (PI P-721 PIFOC) to provide a well-controlled motion. The adaptive nature of our motion compensation system means that irregular and aperiodic motion can be accommodated. In Figs. 2 and 3 the performance of the motion compensation system is illustrated using a sample of blue fluorescent beads (Life Technologies FluoSpheres F-8814, 1 µm diameter) mounted on a glass slide. In Fig. 2 the bead sample is oscillating at a single frequency (1.1 Hz) with a peak-to-peak displacement of 100 µm. The frequency of 1.1 Hz was chosen to be typical of the pulse rate in humans. In Fig. 3 the bead sample is moving with a multi-harmonic motion profile given by the sum of three sinusoids with frequencies of 0.83, 1.26 and 1.6 Hz and with peak-to-peak displacements of 13.8, 27.6 and 46 μm respectively.

Fig. 2.

Data in this figure is derived from 64 × 64 pixel multiphoton images of 1 µm blue fluorescent beads acquired for 250 ms. a) The measured motion profile (1.1 Hz, 50 µm amplitude). b) Histograms showing the 2D correlation coefficient values obtained by correlating 100 consecutive images acquired from an uncompensated (blue) and compensated (red) bead sample with a static in focus reference image shown in c). The mean values of the correlation coefficients were measured as 0.1 (uncompensated) and 0.88 (compensated) respectively. The mean value of the correlation coefficient for a static sample was measured to be 0.99. Ten consecutive images acquired from uncompensated and compensated samples are shown in d) and e) respectively.

Fig. 3.

Data in this figure is derived from 64 × 64 pixel multiphoton images of 1 µm blue fluorescent beads acquired for 250 ms. a) The measured multiharmonic motion profile. b) Histograms showing the 2D correlation coefficient values obtained by correlating 100 consecutive images acquired from an uncompensated (blue) and compensated (red) bead sample with a static in focus reference image shown in c). The mean values of the correlation coefficients were measured as 0.19 (uncompensated) and 0.82 (compensated) respectively. The mean value of the correlation coefficient for a static sample was measured to be 0.97. Ten consecutive images acquired from uncompensated and compensated samples are shown in d) and e) respectively.

To quantify the ability of the motion compensation system to enable the acquisition of accurate images, we used the 2D correlation coefficient $C_n$, defined in Eq. (1) for two images $I_{\text{static}}$ and $I_n$ with mean pixel values ${\overline{I}}_{\text{static}}$ and ${\overline{I}}_n$, to measure the similarity of each image in a sequence to a reference image acquired in the absence of motion ( $I_{\text{static}}$) with the sample in the focal plane.

$$C_n=\frac{{\displaystyle \sum _{\text{pixels}}^{}(I_{\text{static}}-{\overline{I}}_{\text{static}})\times (I_n-{\overline{I}}_n)}}{\sqrt{{\displaystyle \sum _{\text{pixels}}^{}{(I_{\text{static}}-{\overline{I}}_{\text{static}})}^2\times {\displaystyle \sum _{\text{pixels}}^{}{(I_n-{\overline{I}}_n)}^2}}}}$$

The results shown in Figs. 2 and 3 demonstrate the effectiveness of the motion compensation system in reducing the impact of sample motion on image quality. The narrow axial extent of the bead sample means it provides a stringent test of the system’s ability to keep the same sample plane in focus. The motion compensation system increases the mean value of the correlation coefficient from 0.1 to 0.88 for the simple sinusoidal motion and from 0.19 to 0.82 for the multi-harmonic case.

Note that the multi-harmonic profile will produce occasional turning points in vicinity of the focal plane. When this occurs we would expect to see peaks in the 2D correlation coefficient for uncompensated image data as the sample is approximately in focus and quasi-static. This leads to a higher mean value of the correlation coefficient for the uncompensated multi-harmonic motion.

A characterization of the response of the SDOCT motion compensation system to sinusoidal sample motion is presented in Fig. 4 , obtained using a scattering sample (Scotch tape on white card). For each amplitude of sample oscillation, data was acquired for increasing oscillation frequencies up to the point that the tracking algorithm could no longer lock on to the peak from the sample surface. The performance of the motion compensation system was analyzed by calculating the root mean square (RMS) of the difference (tracking error) between the sample and objective positions as measured by the calibrated on-board capacitive positions sensors on each actuator. The RMS tracking error was found to be less than the experimental FWHM of the axial point spread function of the multiphoton imaging system for all sample amplitudes studied, with tracking maintained up to maximum sample velocities of 800 – 900 µm.s⁻¹, except for the case of the maximum oscillation amplitude of 7 µm for which this was true only up to a maximum sample velocity of approximately 700 µm.s⁻¹. We note that for frequencies higher than ~10Hz, the closed-loop bandwidth of the piezo actuator starts to limit the performance rather than the ability of the SDOCT to track the sample position.

Fig. 4.

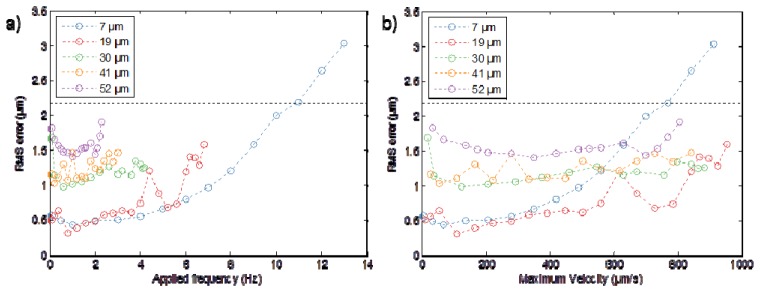
Characterization of the root mean square (RMS) tracking error for the SDOCT motion compensation system obtained using a sample consisting of a piece of Scotch tape on white cardboard. The RMS tracking error was calculated by comparing the sinusoidal motion of the sample, measured using the calibrated capacitive position sensor in the actuator moving the sample, with the actual motion of the microscope objective, measured using the calibrated capacitive position sensor in the actuator controlling the position of the objective. (a) RMS tracking error plotted as a function of sinusoidal oscillation frequency of the sample for a given oscillation amplitude. Each curve was measured for increasing sample oscillation frequency until the point that the SDOCT peak tracking software was no longer able to follow the position of the sample surface. b) The same data as shown in a) but with the RMS tracking error now plotted as a function of the maximum sample velocity. The horizontal black line indicates the extent of the axial point spread function for our imaging system (2.18 µm).

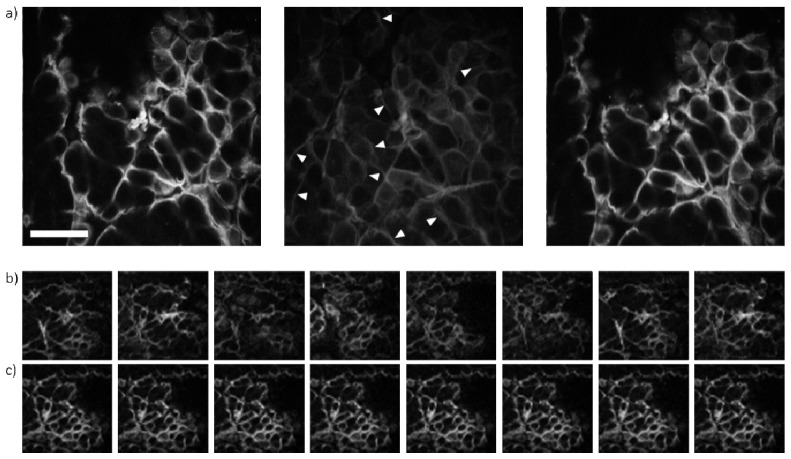
The impact of motion compensation on multiphoton autofluorescence images of freshly excised mouse skin is presented in Fig. 5 . For this study, the mouse tissue was mounted on the actuator, which was driven with single sinusoid of 15 µm amplitude and a frequency of 1.1 Hz. All images were acquired using 18 mW of power in the focal plane. In Fig. 5a) 30 s acquisitions were used to integrate 30 frames into a single 256 × 256 pixel image. As a result of the uncompensated motion, features from planes above and below the desired plane are visible in the uncompensated image (white arrow heads in Fig. 5a)). These features are absent when motion compensation is used. The single frame 64 × 64 pixel images (acquisition time 250 ms) in Fig. 5b) sample the motion profile of the tissue and clearly show the features present in different layers of the tissue. In Fig. 5c) where compensation is used, the same features are consistently present in the images, illustrating the ability of the system to keep the position of the focal plane to a fixed plane in the tissue.

Fig. 5.

a) Multiphoton autofluorescence images of the upper layers of an ex vivo sample of mouse skin that was held static (left), uncompensated (centre), and compensated (right). The white arrowheads in the uncompensated image show features from neighbouring axial sections of the tissue that are not present in the image acquired from the static specimen. The scale bar is 50 µm. (b, c) Consecutive multiphoton autofluorescence images acquired from an uncompensated (b) and compensated (c) tissue sample. The same motion profile (single sinusoid with an amplitude of 15 µm and a frequency of 1.1 Hz) was used for all images acquired in the presence of motion in this figure.

4. Discussion

Our motion compensation system follows the approach described in references [11, 12] but with several differences. First, the microscope objective in our system is relatively massive compared to the graded-index lenses used in the fibre-based systems described in [11,12]. Second, our system makes the SDOCT distance measurements directly through the imaging objective, as opposed to a measurement via a fibre that is adjacent to the imaging lens. In our system, the spectrometer exposure time of 0.2 ms limits the maximum theoretical sample velocity that can be measured to 1.16 mm.s⁻¹ (at which velocity the SDOCT fringes are completely washed out). The data presented in Fig. 4 shows that we can measure and compensate sample velocities up to ~700-900 µm.s⁻¹ for sinusoidal sample motion profiles with amplitudes up to 52 µm (the maximum range of the piezo actuator used to move the sample). For higher sample motion frequencies, the maximum closed-loop frequency response of the piezo positioner controlling the objective imposes an upper limit on the sample oscillation frequency that can be compensated in our system. In comparison, the maximum sample velocity compensated by the system presented in reference [11] was 113 µm.s⁻¹ for a sample frequency of 0.3 Hz and amplitude of 60 µm. In reference [12], motion compensation realised while the probe was hand-held was demonstrated with an RMS tracking error of 2.93 μm.

In reference [13] the off-axis optical focus sensor approach is not an interferometric technique and so is not limited by the need to resolve interference fringes. This enables higher sample velocities to be followed more easily and axial tracking of sinusoidal sample amplitudes up to 100 µm and frequencies up to 2 Hz with tracking error kept below the 3-5 µm axial resolution was demonstrated, corresponding to maximum sample velocities up to 1.25 mm.s⁻¹. However, scattering of the off-axis tracking beam from multiple depths within the specimen leads to a broadening of the detected spot that is dependent on local tissue structure and reduces the accuracy of the position measurement. This is not the case for the on-axis SDOCT surface tracking presented here, which locks on to the first detected peak corresponding to the sample surface.

5. Conclusion

An all fibre-coupled multiphoton microscope with onboard active axial motion compensation designed for in vivo handheld clinical application to skin is presented. The performance of the motion compensation system was analysed and demonstrated to function well for physically relevant time and distance scales. An increase in the mean value of the 2D correlation coefficient of images acquired from fluorescent bead samples undergoing purely sinusoidal motion increased from 0.1 to 0.88 while for multi-harmonic motion the 2D correlation coefficient increased from 0.19 to 0.82. Further, enhanced fidelity of ex vivo mouse skin images in the presence of 30 µm peak-to-peak motion at 1.1 Hz is demonstrated. Further work will be undertaken to make the imaging head more ergonomic for clinical imaging applications by reducing the weight and size of the system.