Accurate real-time depth control for CP-SSOCT distal sensor based handheld microsurgery tools

Abstract

This paper presents a novel intuitive targeting and tracking scheme that utilizes a common-path swept source optical coherence tomography (CP-SSOCT) distal sensor integrated handheld microsurgical tool. To achieve micron-order precision control, a reliable and accurate OCT distal sensing method is required; simultaneously, a prediction algorithm is necessary to compensate for the system delay associated with the computational, mechanical and electronic latencies. Due to the multi-layered structure of retina, it is necessary to develop effective surface detection methods rather than simple peak detection. To achieve this, a shifted cross-correlation method is applied for surface detection in order to increase robustness and accuracy in distal sensing. A predictor based on Kalman filter was implemented for more precise motion compensation. The performance was first evaluated using an established dry phantom consisting of stacked cellophane tape. This was followed by evaluation in an ex-vivo bovine retina model to assess system accuracy and precision. The results demonstrate highly accurate depth targeting with less than 5 μm RMSE depth locking.

1. Introduction

Accurate and precise tool tip manipulation is imperative when performing microsurgery. A well-known barrier to precision in microsurgery is, physiological hand tremor, occurring predominating in the 6-12 Hz frequency domain with several hundred-micron-order amplitude [1, 2]. Retinal microsurgery is performed by passing microsurgical tools through trocars that provide access through the eye wall (sclera). The trocar not only provides safe access into the eye but it also guides and stabilizes the surgical tools and acts as a remote center of motion (RCM). As a result, the lateral motion of the surgical tool is relatively well stabilized. In the case of axial motion, it is the surgeon that currently provides all of the guidance and control. The freehand tool movements are guided predominantly by visual information acquired from the surgeon’s view in the operating microscope. Such tool tip visualization is limited in the axial direction by the ability to resolve small changes in position as well as by obstruction of the retinal surface by the tool shaft and tip. A variety of robot-assisted systems have been developed to actively overcome such a limitation and to achieve the surgical objectives while minimizing surgical risks [3–9]. Early in the evolution of this technology, it was the main point to develop a robot-assisted system with high accuracy and user-friendly operating manipulation [3–7]. Recently, diverse active tool-tips and sensors have been applied to the system to enhance its functionality [8,9].

In parallel, Riviere, et al. has been developing a handheld microsurgical system that has differentiated itself from traditional robotic arm based systems [10–15]. The handheld system operates independently without the assistance of external equipment such as a robotic arm by using its own embedded sensors and actuators. The advantages and disadvantages of the two assistance systems are numerous and are still being elucidated. However, advantages of the handheld systems include but are not limited to: lower cost, potential disposability, greater portability, ease of packaging, lower production costs, ease of use, adaptability, ease of customization and elimination of the large, costly cumbersome, robotic-assist systems that must now otherwise be clumsily implemented in the human clinical setting. A fundamental challenge of any handheld microsurgical tool is cancellation of hand tremor. A variety of motion sensors including accelerometer, magnetometer, position-sensitive detectors with infrared LED, etc. and small size of actuators such as piezo-electric motors and voice coils have been introduced. Moreover, a frequency analysis based tremor model has been previously built in accordance with the roughly sinusoidal nature of tremor [10].

Optical coherence tomography (OCT) has recently emerged as an effective imaging modality to support microsurgery due to its micron-order resolution and subsurface imaging capability [17–23]. Microscope mounted OCT systems now play a significant roles in intraoperative visualization for forward viewing during actual surgical procedures. Our research group has established a potential role for a real-time OCT intraoperative guidance system with fast computational speed using a graphic processing unit (GPU) that is forward viewing and incorporated into the actual handheld tools [24–35]. Unlike typical OCT imaging, this application uses OCT as a distal sensor and its potential effectiveness for ocular microsurgery has been demonstrated [29–35]. The motion compensation that is based on the feedback from the OCT distal sensor effectively suppresses undesired axial motion; as a result, the frequency region related to hand tremor is significantly decreased [34]. This result was applied to microsurgical tool development and improved performance has been demonstrated [35]. We have strategically chosen to incorporate common-path OCT (CP-OCT) into handheld microsurgery tools that are comparatively simple in design, relatively affordable and have the potential to be used as disposable surgical products.

An important difference between intraoperative OCT imaging and OCT distal-sensing is that in application, OCT distal sensing information is used to measure the physical distance of the sensor from the retinal surface. Moreover, in order to utilize OCT as an effective distal sensor, additional signal processing is required to identify and track the surface of a complex target tissue in a complex environment. While surface detection can be simplified to simple peak detection for tissues having a single layer or a dominant reflective surface; the retina has a complex multi-layered anatomy with multiple optically reflecting interfaces that serve as its optical signature. As in a complex surgical environment there is no guarantee that the strongest reflected signal always comes from the retinal surface or surface pathology, the characteristic reflective signal of the retina serves as an advantage that is utilized in the present signal processing algorithms. If this were not anticipated in advance, erroneous reflective data could result in consequential false distance information. Furthermore, real-time operation increases the complexity of the analysis by introducing motion, reduced time for making decisions, and a reduced amount of information available to make real time decisions. Evaluation of multi-layered structures requires edge detection analysis rather than peak detection to correctly find the surface [29]. Edge detection further enhances the surface detection method as the A-scan signal from retina has multi-peak complexity. Therefore, we developed and incorporated a robust distance sensing method utilizing a shifted cross-correlation algorithm. It uses all of the signature information available in the A-scan to determine distance, rather than just the first peak; thus, the system produces robust distance data regardless of whether erroneous data is encountered.

In addition to achieve accurate and stable distal sensing, the handheld system must be designed to efficiently and effectively utilize the distance information to rapidly control the mechanical actuator for accurate and precise manipulation. It is important to appreciate that the time required for the OCT signal to be implemented into tool action requires heavy computational processing including averaging, Fourier transformation, surface detection, and that there is a communication delay that results in time gap between sampling and compensating motion. Therefore, we utilized a GPU to reduce the processing time in the design of this system. Additionally, a predictor was developed to achieve more effective compensation. The predictor based on Kalman filter is used for the system latency compensation. A performance evaluation of this system is presented using a dry phantom consisting of 20 layers of cellophane tape. This is followed by an evaluation in a biologically relevant model, the ex-vivo bovine retina.

2. Theory

2.1 Spatially shifted cross-correlation

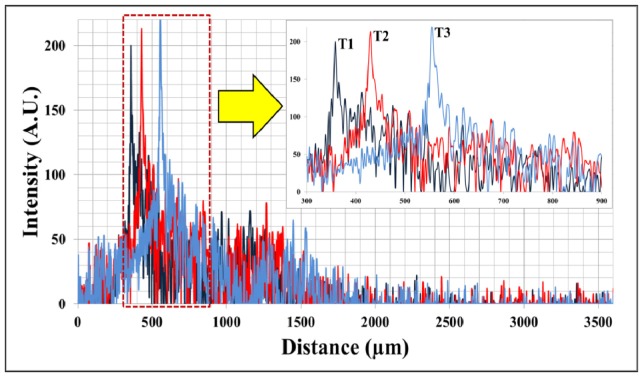
As shown in Fig. 1 , the series of A-scan data at T1, T2 and T3 show spatially shifted but mutually correlated waveforms. Because the A-scan data reflects the optical characteristics of the sample below the CP-OCT fiber sensor, it is natural that there is correlation between the spatially and temporally adjacent A-scan data. Thus, we can use this correlation to measure the distance variation. This method can be more effective than an edge detection algorithm to measure the distance variation when the A-scan data has a low signal-to-noise ratio and does not contain a dominant peak. Here is a brief overview of the spatially shifted cross-correlation scheme.

$$X_i*Y_{i+n}=\frac{{{\displaystyle \sum }}_i\left(X_i-m_X\right)\left(Y_{i+n}-m_Y\right)}{\sqrt{{{\displaystyle \sum }}_i{\left(X_i-m_X\right)}^2{{\displaystyle \sum }}_i{\left(Y_{i+n}-m_Y\right)}^2}}={\rho }_{-n}$$ (1)

where m_X and m_Y are the means of the sampled discrete A-scan data, X_i and Y_i and the subscript i and n are the index of A-scan data and shifted value respectively. The calculation of the cross-correlation between A-scan data generally requires a long computation time. Moreover, we need to compare the first A-scan data with every shifted version of the next A-scan data. This is a prohibitively time consuming operation and is not practical for a real-time system; thus, we need to calculate the equation more efficiently [36]. The numerator of the Eq. (1) can be modified as

$${\rho }_n^{num}={\displaystyle \sum }_i{X}_i^1{Y}_{n-i}^2$$ (2)

where $X_i^1=X_i-m_X$, $Y_i^1=Y_i-m_Y$, and $Y_i^2=Y_{-i}^1$. Considering the numerator is the convolution of the anterior A-scan data X¹ with the reversed shifting posterior A-scan data Y², this equation can efficiently be calculated based on the discrete correlation theorem with the fast Fourier transform F:

$${\rho }_n^{num}={ℱ}^{-1}\left(ℱ\left(X^1\right)·ℱ\left(Y^2\right)\right)={ℱ}^{-1}\left(ℱ\left(X^1\right)·{ℱ}^{*}\left(Y^1\right)\right)$$ (3)

where we used the convolution theorem: time reversal of the signal in time domain is equivalent to the complex conjugate in the Fourier transform. Additionally, the denominator of Eq. (1) is constant regardless of the shifting variable n. By searching n that achieves maximum ρ, we can rapidly find the maximum matching point and distance variation between the two sequential A-scan data with two FFT (forward and inverse) instead of N-times direct cross-correlation computations.

Fig. 1.

Three consecutive A-scan data of 20-stacked layers of adherent cellophane tape near the DC line (multi-layered phantom sample); the upper right inserted graph is a partial magnified graph of area in dotted red square in lower entire graph.

2.2 Kalman filter

A faster system response is essential in decreasing involuntary hand tremor and to rapidly respond to target motion. The faster system response improves the accuracy of motion compensation over all frequency ranges [34]. However, there is an inevitable time delay between the distal measurement and subsequent compensation due to the processing time, and also the communication delay between heterogeneous devices such as the workstation and the motor driver. Such a time delay can produce outdated and incorrect tool compensation signal especially in the case of a rapid target or hand movements. To avoid the potential risk of outdated compensation, a predictor is required. Here, we utilized a Kalman filter to adjust for the overall system latency. In this work, the Kalman filter was used as an algorithm that provides an efficient recursive solution to minimize the mean of the squared error [37]. Kalman filters have historically been extensively utilized in a broad area of tracking and assisted navigation systems [38–40]. The Kalman filter serves as an appropriate predictor in our case because it supports estimations of past, present, and future states even when the precise modeling of in our case tremor, is unknown. A portion of the unknown in this system e.g. results from potential encounters with a transiently obstructed imaging axis in the eye (such as blood); this would briefly present erroneous signal to the OCT distal sensor.

The Kalman filter consists of a set of mathematical equations. The equations can be divided into two main categories: 1) Prediction step and 2) Update step.

• •
  Prediction step is

  $$\begin{array}{c}{\hat{\mathit{x}}}_{t|t-1}={\mathit{F}}_t{\hat{\mathit{x}}}_{t-1|t-1}+{\mathit{B}}_t{\mathit{u}}_t\\ {\mathit{P}}_{t|t-1}={\mathit{F}}_t{\mathit{P}}_{t-1|t-1}{\mathit{F}}_t^T+{\mathit{Q}}_t\end{array}$$
• •
  Update step is

  $$\begin{array}{c}{\hat{\mathit{x}}}_{t|t}={\hat{\mathit{x}}}_{t|t-1}+{\mathit{K}}_t\left({\mathit{y}}_t-{\mathit{H}}_t{\hat{\mathit{x}}}_{t|t-1}\right)\\ {\mathit{K}}_t={\mathit{P}}_{t|t-1}{\mathit{H}}_t^T{\left({\mathit{H}}_t{\mathit{P}}_{t|t-1}{\mathit{H}}_t^T+{\mathit{R}}_t\right)}^{-1}\\ {\mathit{P}}_{t|t}=\left(\mathit{I}-{\mathit{K}}_t{\mathit{H}}_t\right){\mathit{P}}_{t|t-1}\end{array}$$

where $\hat{x}$ is an estimated state, y is a measurement variable, and u is an control variable. The matrices F, B, P, Q, H, R, and K describe process equation, control variable mapping, error covariance, process noise covariance, measurement variable mapping, measurement noise covariance, and Kalman gain, respectively. If the tool tip is assumed to move along a straight line in axial direction, 1D motion equation can be applied for the modelling of Kalman filter. Additionally, we assume that the acceleration is a random variable having Gaussian distribution with zero mean and variance σ² when the tool tip gets to the target position. Then, we can derive the matrices.

$$\begin{array}{c}{\mathit{x}}_t=\left[\begin{array}{c}{x}_t\\ v_t\end{array}\right]=\left[\begin{array}{cc}1& \Delta t\\ 0& 1\end{array}\right]\left[\begin{array}{c}{x}_{t-1}\\ v_{t-1}\end{array}\right]+a_t\left[\begin{array}{c}\Delta t^2/2\\ \Delta t\end{array}\right]={\mathit{F}}_t{\mathit{x}}_{t-1}+{\mathit{w}}_t\\ {\mathit{y}}_t=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]{\mathit{x}}_t+\left[\begin{array}{c}{r}_t\\ 0\end{array}\right]={\mathit{H}}_t{x}_t+{\mathit{b}}_t\end{array}$$

where x, v, a, b are the position, velocity, acceleration of the tool tip, and observation noise. The process and measurement noise covariance are defined respectively as

$$\begin{array}{c}{Q}_t=var\left({\mathit{w}}_t\right)=E\left[{\mathit{w}}_t{\mathit{w}}_t^T\right]={\sigma }^2\left[\begin{array}{cc}\Delta t^4/4& \Delta t^3/2\\ \Delta t^3/2& \Delta t^2\end{array}\right]\\ R_t=var\left({\mathit{b}}_t\right)=E\left[{\mathit{b}}_t{\mathit{b}}_t^T\right]=\left[\begin{array}{cc}{r}_t^2& 0\\ 0& 0\end{array}\right]\to \left[\begin{array}{cc}{r}_t^2& 0\\ 0& c_1\end{array}\right]\end{array}$$

where c₁ is small constant and the reason to change the form of R_t is to prevent zero value determinant during Kalman gain calculation. When it comes to error covariance, we set

$$P_0=\left[\begin{array}{cc}{c}_2& 0\\ 0& c_2\end{array}\right]$$

where c₂ is suitably large constant because we do not know the starting position. Because our system actively compensates the deviation distance from the target position, we can set the control variable and its mapping matrix as

$${\mathit{B}}_t{\mathit{u}}_t=\left[\begin{array}{cc}-1& 1\\ 0& 0\end{array}\right]\left[\begin{array}{c}y\\ y_{tgt}\end{array}\right]$$

where y is the measured position and y_tgt is the target position.

3. Materials and methods

3.1 System

The handheld CP-OCT distal sensor system consists of three main modules: SS-OCT, a workstation, and a piezoelectric linear motor driven handheld tool as shown in Fig. 2(a) . Figure 2(b) shows the CAD design of the handheld tool. The OCT system consists of a swept source OEM engine (AXSUN, central wavelength λ₀: 1060nm, sweeping rate: 100kHz, scan range: 3.7mm in air), a photo-detector and a digitizer with a sampling rate of up to 500MSPS with 12-bit resolution, a Camera Link DAQ Board, and a Camera Link frame grabber (PCIe-1433, National Instruments). The workstation (Precision T7500, Dell) with general-purpose computing on graphics processing units (GPGPU, GeForce GTX590, Nvidia) processes the sampled spectral data and control the linear motor. The parallel processing (CUDA, Nvidia) of the GPGPU can reduce the processing time considerably in FFT, background noise subtraction and averaging, which is mainly responsible for the processing delay [24, 25]. The handheld tool uses a piezoelectric linear motor (LEGS-LL1011A, PiezoMotor) which has a maximum speed of 15 mm/s, maximum stroke of 80 mm, stall force of 6.5 N, and a resolution of less than 1 nm. The communication protocol between the motor driver and the workstation is RS232 and the protocol is implemented virtually on top of USB protocol. For this reason, it is important to configure the USB settings suitable for the short and frequent message transmission to minimize the communication delay, which is another factor of the system delay. Specifically, buffer size and timeout for transmission are the parameters that need to be adjusted. The buffer size was fitted for the most frequent message size and the timeout was set at the minimum value. The housing of the handheld tool as shown in Fig. 2(b) was made by a 3D printing machine. The dimensions of the handheld tool are 3.6 cm diameter and 9 cm length. The optical fiber for distal sensing is attached to the end of the needle and the needle-to-tube connector (RN Coupler-p/n, Hamilton) is mounted into the handheld tool to give a greater load to the linear motor similar to realistic application.

Fig. 2.

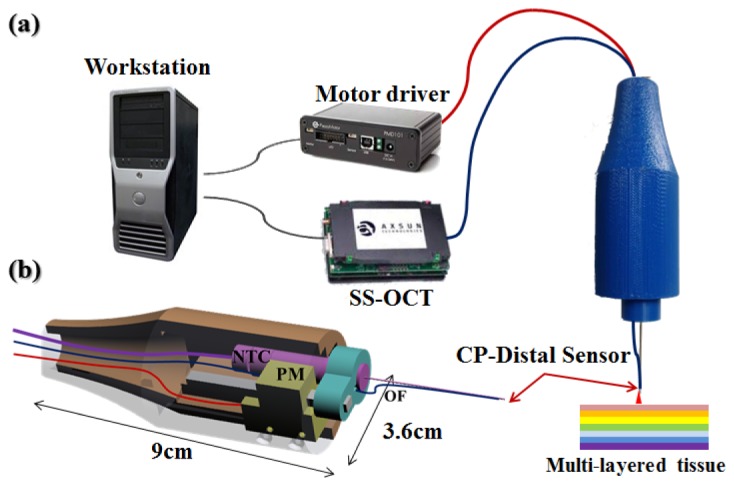
a) Active depth targeting and locking microsurgery system, b) CAD cross-sectional image of handheld tool (NTC: needle-to-tube connector, PM: piezo-motor, OF: optical fiber).

3.2 The control algorithm

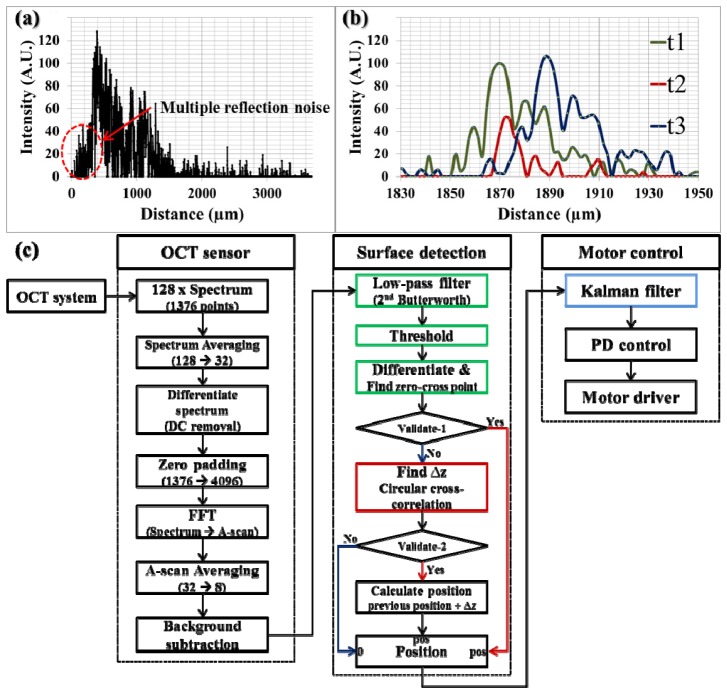
The sampled spectral data is sequentially processed in the following three steps as shown in Fig. 3(c) . The first step is to transform the spectral data to A-scan data similar to that in typical OCT imaging. Specifically, 128 spectra each consisting of 1376 data points are transmitted from the frame grabber in every 1.28 ms. The system response or sampling rate should be determined based on the computational performance. Comparing to the previous work in our group [34], the system response can be improved from 500 Hz to 780 Hz with the help of parallel processing with GPU. The total computational and communication delay is 650 µs on average and we reserved the other half of time ( = 630 µs) for variable system performance. Four sequential spectra are averaged to increase the signal-to-noise ratio (SNR) followed by a discrete differentiation to remove the DC component in frequency domain. Then, zero padding is applied to increase the data points of the averaged spectra from 1376 to 4096 before fast Fourier transform (FFT). After the transformation, additional averaging and background subtraction are conducted on the A-scan data. As a result, we have 8 A-scan data and each A-scan data has 2048 data points that covers a 3686.4 µm axial distance in the air (1.8 µm between each data point). Note that it is important to remove the background noise in A-scan data for the subsequent A-scan matching process using shifted cross-correlation in order to find the distance variations since this process is susceptible to the stationary background noise. The final processed A-scan data are used for the next step, the surface detection.

Fig. 3.

a) A-scan data of ex-vivo open bovine retina, b) three consecutive A-scan data of stacked layers of adherent cellophane tape, c) data processing flowchart consisting of 1) OCT data process, 2) Surface detection, and 3) Motor control.

As shown in Fig. 3(a), peak detection is not suitable for the surface detection in a sample with a complex multi-layered structure. Alternatively, an edge detection scheme can be used. For the edge detection, first, 2nd order Butterworth low-pass filtering is applied to extract the envelope shape of the A-scan data because the A-scan data contains multiple local maxima and minima that hinder the edge detection. Then, a thresholding is applied to discriminate the signal from the noise. The noise level without sample ( = background noise) determines the minimum thresholding value. Whereas, the maximum value is set to be adaptive to the maximum intensity of the current signal because the noise level, as indicated by the area with red dotted circle in Fig. 3(a) between the sample and the zero delay line, increases as the fiber sensor tip approaches the sample. This is because multiple reflections in close proximity induce stronger interference; as a result, the noise level also increases. Next, the first zero-cross point is identified to find the surface after a discrete differentiation.

Two processes validate the calculated position: checking the value itself (if the position is zero, the detection is failed) and comparing it with the previous position. According to the failure of position detection, there are two possible cases. If the intensity of A-scan data is smaller than the threshold value, the surface detection is considered to be failed even though the A-scan data still has sufficient features to find the surface as shown in Fig. 3(b). In another case, we see that the distance variation between the two consecutive positions has an abnormally large value as compared to the presumed maximum value. This is mainly because the predominant reflective layer within a sample makes the adaptive thresholding too high so that it erases the surface peak as well as the background noise. To make up for the limitations of simple edge detection, we used a spatially shifted cross-correlation as described in the previous section. As shown in Fig. 3(b), the A-scan data at t2 has similar features as the A-scan data at t1 and t3 in spite of its low intensity. In this case, spatially shifted cross-correlation can find the matching point and distance variation as a result. The result is validated based on the normalized cross-correlation value, which reflects how the two A-scan data look similar. In the real implementation, we set 60% as a threshold.

Finally, the calculated position data is transmitted to the third step, motor control module. Instead of using the position data directly to control the motor, a Kalman filter is applied as a predictor for more accurate motion compensation. The predictor is needed to make up for the time delay between the distal measurement and the actuator movement due to the processing and communication delay, which is 650 µs on average in the implemented system. The previous prediction value is alternatively used as an input data when position detection is failed in the previous step as long as the number of consecutive failure is smaller than the predetermined value. This predicted position is then used to calculate the actual compensating length through modified proportional-derivative (PD) control. Typical proportional-integral-derivative (PID) control is not appropriate because the distance between sample surface and tool tip is continuously varying. At the same time, the compensating length should be calculated in accordance with the separate length between target and tool tip and current speed of the tool. The parameters of PD control are modified adaptively based on the current trend of the process [41]. Finally, the compensating value is transmitted to the motor driver.

4. Experimental results and discussion

4.1 Phantom experiment

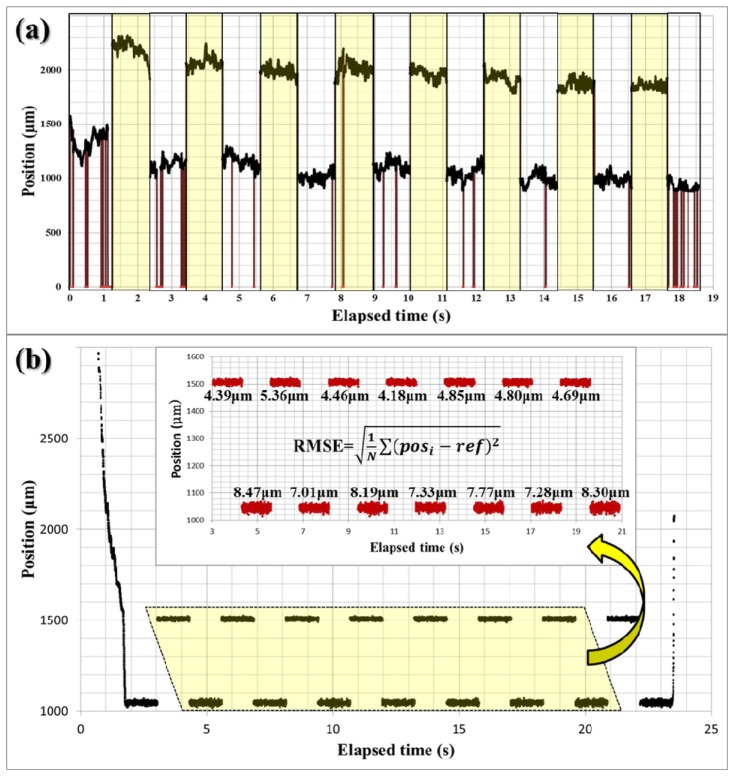
Two different experiments were conducted to evaluate the performance of the proposed distal sensing algorithm with the dry phantom in each case consisting of 20-stacked layers of adhesive cellophane tape. The phantom was set on the table at a 10-degree tilt angle to better represent the non-perpendicular orientation of instruments in application. First, we tested the effectiveness of the edge detection with the shifted cross-correlation method by comparing it with the edge detection only. The experiment was conducted with a random delay for a blind test and the shifted cross-correlation method was repeatedly turned on and off in every 1.28s. The offset value ( = 921.6μm) was intentionally added to the data from the test using the edge detection with shifted cross-correlation (yellow region) to easily distinguish these two different cases as shown in Fig. 4(a) . The dark red vertical lines in Fig. 4(a) indicates detection failure and the number of vertical lines or the failure rate in the yellow region is much lower than in the other region (white region). In fact, only a single case of failure at around 8.1 second was observed over the 20-second observation when the shifted cross-correlation method was used. The failure rate without the shifted cross-correlation method was 28 incidents/s and 0.3 incidents/s with the shifted cross-correlation method. These results clearly indicate that the addition of the shifted cross-correlation methodology can greatly improve the stability of the OCT distal sensor.

Fig. 4.

Dry phantom experiment: a) evaluation test for the surface detection algorithm with the auxiliary shifted cross-correlation in non-depth-locking freehand, b) evaluation test for the depth-locking with the predictor based on Kalman filter: the upper inserted graph is a magnified graph of area in dotted yellow trapezoid in the entire graph.

In the second experiment, we evaluate the effectiveness of the predictor based on a Kalman filter. During the experiment, the predictor method was also repeatedly turned on and off in each 1.28s inclement. The offset value ( = 460.8μm) was added to the data with a predictor to easily differentiate the result from the data without the predictor. In fourteen consecutive trials were conducted in total to maintain a fixed position and the results are shown in Fig. 4(b). The upper graph in Fig. 4(b) is a magnified view of the area in the dotted yellow trapezoid. The magnified view includes the RMSE for each trial. The average RMSE without the predictor is 7.76 µm and the average RMSE with the predictor is 4.68 µm. This result shows that the predictor operated effectively to make up for the processing time delay by deducing a more probable position when the linear motor actually operated.

4.2 Bovine retina experiment

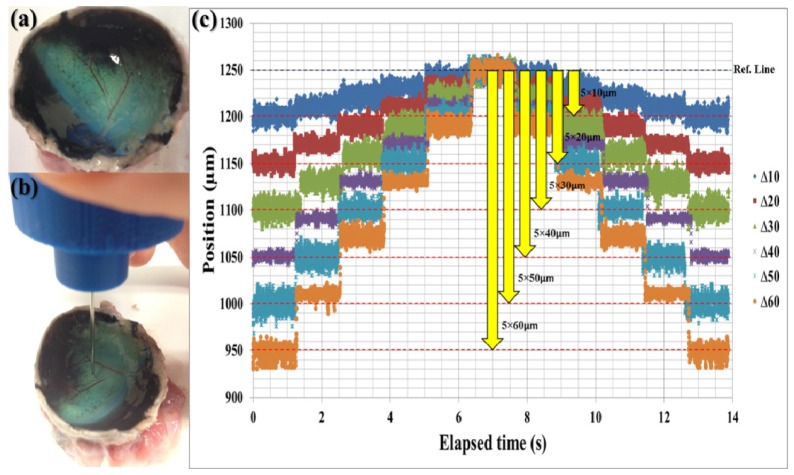
To evaluate the performance of the overall compensation system, we used an ex-vivo bovine retina model. Figure 5(a) shows the ex-vivo bovine retina after removing cornea, lens, and vitreous humor. The experiment was conducted on the same day as death thereby preserving the multi-layered structure of bovine retina, which gradually degrades beginning after the first few hours of the post mortem. We designed the experiment to evaluate the performance of the system in terms of dynamic depth targeting and precise depth locking by repeatedly holding and changing the position in a prescribed manner. Specifically, the user carried the tool tip to the surface of retina as shown in Fig. 5(b) and the experiment starts when the tool tip reached the predetermined offset distance. The offset distances were predetermined to be six different jumping distances from 10µm to 60µm in order to maintain the same reference line. Moreover, the system was programed to hold its current position for 1.28s ( = 1000 data points) to evaluate its depth-locking performance.

Fig. 5.

Bovine retina experiment: a) bovine retina after removing cornea, lens, and vitreous humor, b) snapshot of the experiment, c) depth targeting and locking experiment result with six different jumping distance from 10 µm to 60 µm.

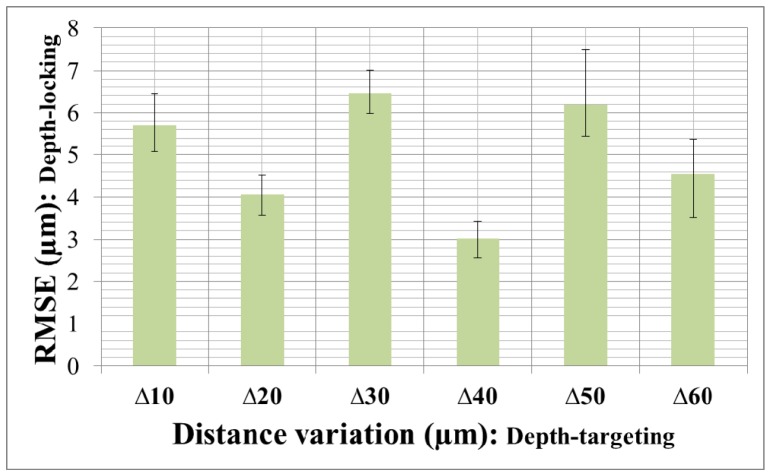
As shown in Fig. 5(c), the system consistently adjusted the needle position in accordance with the predetermined jumping distance. In total, there were 60 depth-targeting and 66 depth-locking trials. Table 1 shows the specific RMSE values of each depth-locking trial in Fig. 5(c). Figure 6 shows the average RMSE and standard deviation error bar with different jumping distance. The total average, maximum, and minimum of RMSE were 4.996 µm, 8.129 µm and 2.104 µm respectively. The average depth locking RMSE, 4.996 µm, is smaller than 1/5 thickness of inner nuclear layer (INL), 27 ± 8 µm (Mean ± Standard deviation), which is thinnest layer in human retina [42, 43]. Even worst RMSE, 8.129 µm, is about 1/3 of INL thickness. These figures demonstrate the potential for this microsurgery system to be used for targeting and delivering a therapeutic agent into specific layer of the human retina.

Table 1. Optical Constants of Thin Films of Materials [µm].

	∆10	∆20	∆30	∆40	∆50	∆60
1	5.264	4.562	6.750	2.944	8.129	5.939
2	5.080	3.774	6.222	3.108	7.404	3.950
3	6.473	4.297	7.161	3.038	5.447	5.488
4	4.683	3.416	5.494	3.376	5.630	3.141
5	5.233	5.017	6.114	3.891	5.061	4.823
6	6.286	4.007	5.838	3.170	5.761	4.981
7	6.367	4.078	6.427	2.600	5.513	4.344
8	6.830	3.938	6.377	2.887	5.642	3.937
9	5.148	4.187	6.685	3.181	5.275	5.118
10	5.259	3.200	7.342	2.104	6.826	2.941
11	6.063	4.255	6.603	2.982	7.277	5.388

Fig. 6.

Averages of RMSE with standard deviation error bar of the bovine retina experiment. The x-axis labels mean jumping distance and the y-axis indicates the means and standard deviations of the measurement specified in Table 1.

5. Conclusion

In conclusion, we have demonstrated a novel motion compensation control methods that allows accurate depth targeting and precise depth locking with micron-order RMSE. We have evaluated the technology in a dry phantom and in biological specimens possessing a multi-layered tissue structure. Future work will focus on implementing the potential for precise tool tip actions that this technology enables. The retina is an ideal model in which to assess the ability to e.g. use a derivative technology such as a high precision micro-injector system to accurately place potentially therapeutic agents in previously inaccessible retinal layers and micro-forceps system to precisely peel the epithelial layer of retina.