Optimized interstitial PDT prostate treatment planning with the Cimmino feasibility algorithm

Abstract

The primary aim of this study was to determine whether optimized photodynamic therapy (PDT) treatment planning (seeking optimized positions, lengths, and strengths of the light sources to satisfy a given dose prescription) can improve dose coverage to the prostate and the sparing of critical organs relative to what can be achieved by the standard PDT plan. The Cimmino algorithm and search procedures based on that algorithm were tested for this purpose. A phase I motexafin lutetium (MLu)-mediated photodynamic therapy protocol is ongoing at the University of Pennsylvania. PDT for the prostate is performed with cylindrical diffusing fibers of various lengths inserted perpendicular to a base plate to obtain longitudinal coverage by a matrix of parallel catheters. The standard plan for the protocol uses sources of equal strength with equal spaced (1-cm) loading. Uniform optical properties were assumed. Our algorithms produce plans that cover the prostate and spare the urethra and rectum with less discrepancy from the dose prescription than the standard plan. The Cimmino feasibility algorithm is fast enough that changes to the treatment plan may be made in the operating room before and during PDT to optimize light delivery.

I. INTRODUCTION

Photodynamic therapy (PDT) is a treatment modality employing light of an appropriate wavelength in the presence of oxygen to activate a photosensitizing drug which then causes localized cell death or tissue necrosis. PDT has been used with a surface illumination technique to treat many superficial tumors including skin, lung, esophagus, and bladder.¹ This technique is inadequate for large bulky tumors in solid organs because of limited light penetration into tissue. A more efficient illumination scheme for such tumors is interstitial light delivery whereby optical fibers are placed directly into the bulky tumors or organs.

The prostate gland is an organ that appears to be a good target for interstitial PDT. Tumors of the prostate are often confined to the prostate itself so that brachytherapy techniques used for the placement of radioactive seed implants can be adapted for the placement of interstitial optical fibers.² Several preclinical studies have evaluated the feasibility of delivering PDT to the prostate via this interstitial approach.^3–7 The development of an interstitial light delivery technique required improved understanding of light dosimetry, critical in planning the configuration of multiple fibers within the organ or tumor. Based on the results of a preclinical study in canines,⁸ we have initiated a protocol for motexafin lutetium (MLu)-mediated PDT of the prostate in patients at the University of Pennsylvania.⁹ MLu is a second generation synthetic photoactive drug that has a Q-band absorption peak at 732 nm.^10,11

At present, measurements at more than a few sample points within the patient during the clinical procedure are difficult to make. The state of the art is to obtain measurements before the actual clinical procedure, and to assume that during the procedure all these distributions are uniform throughout the prostate and static in time. We have previously shown that the human prostate has an inhomogeneous light-opacity distribution in vivo, which calls into question some of these assumptions.^12,13

A number of optimization algorithms used in brachytherapy are of interest for prostate photodynamic therapy. The most common ones are simulated annealing algorithms^14–16 and genetic algorithms.^17–19 Gradient algorithms also have been applied.²⁰ In general, gradient algorithms give reproducible solutions but may be trapped in local minima far from the global minimum.²¹ Simulated annealing and genetic algorithms avoid getting trapped in local minima, but are relatively slow because they are stochastic algorithms.

To the best of our knowledge, optimization algorithms for photodynamic therapy have not yet been validated and reported in the literature. In this study, we describe and evaluate a systematic search procedure, based on the Cimmino feasibility algorithm,^22,23 that optimizes the locations, lengths, and strengths of light sources for photodynamic treatment. The Cimmino feasibility algorithm is an iterative linear algorithm which was first applied to radiotherapy inverse problems by Censor et al.^23–25 The algorithm is safer than most common optimization algorithms outlined earlier since it always converges and, if the prescribed dose constraints are not all satisfied, it reverts to the least-squares solution.²⁶

II. MATERIALS AND METHODS

A. Diffusion theory and determination of optical properties

The transport scattering $({\mu }_s^{\prime })$ and absorption (μ_a) coefficients characterize the scattering and absorption properties of tissue. With the diffusion approximation, the light fluence rate ϕ at a distance r from a point source can be expressed as²⁷

$$\varphi =\frac{S·{\mu }_{\text{eff}}^2}{4\pi r·{\mu }_a}·e^{-{\mu }_{\text{eff}}r}=\frac{S·3{\mu }_s^{\prime }}{4\pi r}·e^{-{\mu }_{\text{eff}}r},$$ (1)

where S is the power of the point source [mW]; ϕ(r) is the the fluence rate [mW/cm²]; the quantity ${\mu }_{\text{eff}}=\sqrt{3·{\mu }_a·{\mu }_s^{\prime }}$²⁷ is the effective attenuation coefficient in tissues, applicable over a wider range of μ_a and ${\mu }_s^{\prime }$ than the traditional definition ${\mu }_{\text{eff}}=\sqrt{3·{\mu }_a·({\mu }_s^{\prime }+{\mu }_a)}$.²⁸ The PDT dose is defined as the product of light fluence and photosensitizer concentration. For simplicity, we use the light fluence (fluence rate × exposure time, ϕ·t) for the PDT dose throughout the paper, assuming uniform drug concentration.

For a cylindrical diffusing fiber (CDF) of length l, the light fluence rate at a point can be calculated with Eq. (1) by the discretized superposition:

$$\varphi =\sum _{i=1}^N\frac{s·\mathrm{\Delta }x·{\mu }_{\text{eff}}^2·e^{-{\mu }_{\text{eff}}{r}_i}}{4\pi {\mu }_a{r}_i}=\frac{3sl{\mu }_s^{\prime }}{4\pi }·\left(\frac{1}{N-1}\sum _{i=1}^N\frac{e^{-{\mu }_{\text{eff}}·r_i}}{r_i}\right),$$ (2)

where s is the light energy released per unit time per unit length [mW/cm], also called the unit-length source strength. The differential Δx = l/(N − 1) is the length of the elemental (discretized) source segment. The odd integer N is the number of points used in the summation over the source [parentheses in Eq. (2)], with one point always placed in the middle of the CDF. The distance between the ith point of the linear light source and the observing point is $r_i=\sqrt{x_i^2+h^2}$, where x_i = (i − 1 − (N − 1)/2)Δx is the cylindrical coordinate along the fiber from the center of the linear source and h is the distance perpendicular to the fiber axis. The numerical value of the summation should be independent of N (or Δx) if N is large enough. We found that accurate results of the summation can be obtained if Δx ≤ 0.1 cm. In all our calculations N = 201 was used.

In theory, measurements of ϕ at two different distances r from a point source of known power S are sufficient to determine both μ_a and ${\mu }_s^{\prime }$. The two free parameters (μ_a and ${\mu }_s^{\prime }$) are inherently separable because for a CDF of given length the magnitude of the fluence rate near the light source (h = 0) is determined by ${\mu }_s^{\prime }$ only and the slope of the spatial decay of the light fluence rate is determined by μ_eff only. Measurements at multiple sites allow evaluating the variation of these optical characteristics within the prostate volume. Since Eq. (1) is a nonlinear equation of two free parameters μ_a and ${\mu }_s^{\prime }$, we used a differential evolution algorithm developed by Storn et al.²⁹ This algorithm is simple and robust, and converges faster and with more certainty than both the adaptive simulated annealing and the annealed Nelder and Mead approach.²⁹ We modified the algorithm to require that all parameters (μ_a and ${\mu }_s^{\prime }$) were positive.³⁰ The effect of this variation of optical properties on the kernels for a point light source was examined. A summary of the average optical properties in each patient before and after PDT is listed in Table I.

Table I.

In vivo optical properties measured at 732 nm in human prostate. The values in parentheses are the standard deviation (s.d.) of the average values measured from different locations of the same prostate. No s.d. is listed if only one data point is available.

	Before PDT			After PDT
Patient number	μa (cm−1)	${\mu }_s^{\prime }(\mathrm{c}{\mathrm{m}}^{-1})$	δ (cm)	μa (cm−1)	${\mu }_s^{\prime }(\mathrm{c}{\mathrm{m}}^{-1})$	δ (cm)
2	0.09	29.8	0.34	0.09	43.7	0.29
3	0.15	22.0	0.31	0.07	33.4	0.37
4	0.43 (0.28)	7.69 (4.76)	0.41 (0.14)	0.51	1.67	0.63
5	0.21	11.8	0.37	0.13	7.18	0.60
6	0.27 (0.27)	10.5 (11.2)	0.50 (0.05)	0.19 (0.20)	18.9 (18.4)	0.45 (0.06)
7	⋯	⋯	⋯	0.30 (0.08)	23.7 (13.9)	0.24 (0.11)
9	0.53 (0.36)	6.61 (4.51)	0.41 (0.09)	0.64 (0.25)	7.00 (5.59)	0.33 (0.10)
10	0.63 (0.32)	4.62 (2.87)	0.42 (0.10)	0.19 (0.05)	9.27 (4.47)	0.54 (0.31)
11	0.67 (0.17)	6.39 (3.18)	0.32 (0.10)	0.83 (0.45)	5.45 (3.89)	0.38 (0.16)
12	0.71 (0.43)	8.99 (6.51)	0.32 (0.12)	0.30 (0.06)	20.2 (4.8)	0.28 (0.08)
13	0.27 (0.14)	18.5 (11.6)	0.30 (0.07)	0.26 (0.09)	17.0 (8.8)	0.31 (0.07)
14	0.72 (0.11)	3.37 (1.37)	0.39 (0.11)	⋯	⋯	⋯
15	⋯	⋯	⋯	⋯	⋯	⋯

B. Patient selection, surgical, and PDT procedure

A Phase I clinical trial of motexafin lutetium (MLu)-mediated PDT in patients with locally recurrent prostate carcinoma was initiated at the University of Pennsylvania. The protocol was approved by the Institutional Review board of the University of Pennsylvania, the Clinical Trials Scientific Review and Monitoring Committee (CTSRMC) of the University of Pennsylvania Cancer Center, and the Cancer Therapy Evaluation Program (CTEP) of the National Cancer Institute. A total of 15 patients were treated, of which 14 patients have undergone measurement of optical properties (one patient yielded no results due to heavy bleeding). Each patient who signed the informed consent document underwent an evaluation, which included an MRI of the prostate, bone scan, laboratory studies including PSA (prostatic specific antigen), and a urological evaluation. Approximately two weeks prior to the scheduled treatment a transrectal ultrasound was performed for treatment planning. An urologist drew the target volume (the prostate) on each slice of the ultrasound images. These images were spaced 0.5 cm apart and were scanned with the same ultrasound unit used for treatment.

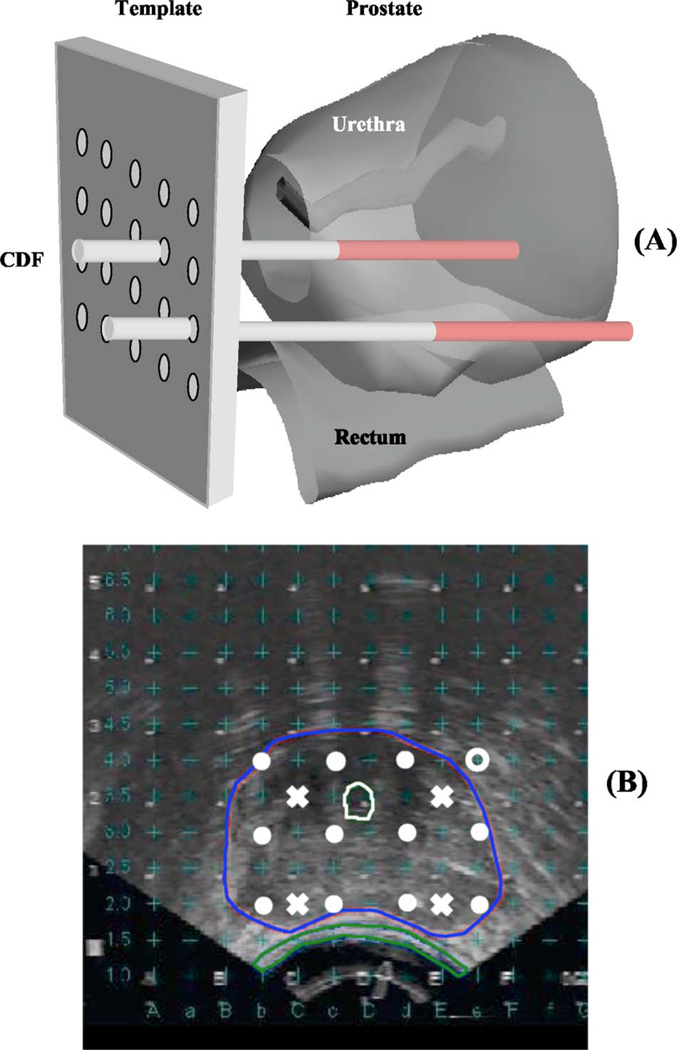
A built-in template with a 0.5-cm grid projected the locations of possible light sources relative to the prostate. A treatment plan was then prepared to determine the locations and lengths of the light sources. Cylindrical diffusing fibers (CDF) with active lengths 1–5 cm were used as light sources. The CDF sources were parallel, spaced 1 cm apart and the light power per unit length was less than or equal to 150 mW/cm for each CDF. The length of the CDF at a particular position within the prostate was selected to cover the full length of the prostate [see Fig. 1(a)]. For practical reasons, clinical application often required that the prostate be divided into four quadrants. Four isotropic detectors were used, each placed in the center of one quadrant. A fifth isotropic detector was placed in an urethral catheter to monitor the light fluence in the urethra [Fig. 1(b)].

Fig. 1.

(a) Experimental setup for measuring the in vivo optical properties of human prostate. The prostate template was drilled with a 0.5-cm equal spaced grid. Cylindrical diffusing fibers (CDF) were inserted into the catheters to illuminate the entire prostate gland. (b) Transrectal ultrasound image. Isotropic detectors (“×”) were placed in one of the catheters, which is located at a distance between 0.5 and 1.1 cm from the light source (“ ●”). The detector reading at each location is peaked to ensure that it is at the middle of the CDF.

The patients were anesthetized in the operating room with general anesthesia to minimize patient movement during the procedure. Transrectal ultrasound-guided biopsies for MLu measurements were obtained prior to light delivery. The ultrasound unit was used to guide needle placement in the operating room. A template was attached to the ultrasound unit and was matched to the same 0.5-cm grid used for treatment planning. Four detector catheters (one for each quadrant) were inserted into the prostate. These detectors were kept in place during the entire procedure of PDT treatment. Four additional preplanned treatment catheters for light sources were then inserted 0.5 or 0.7 cm away from the detector catheters [Fig. 1(b)]. These source catheters were used for both light delivery and measurement of optical properties. A 15-W diode laser (model 730, Diomed, Ltd., Cambridge, United Kingdom) was used as the 732-nm light source.

C. Searching with the Cimmino feasibility algorithm

The “forward” problem of PDT is to find the dose distribution when the source locations, lengths, and strengths are all known. The “inverse” problem of PDT is the concern of this paper.

The “simple” inverse problem of PDT is to find individual source strengths that collectively deliver a prescribed minimum dose to the (target) prostate without exceeding specified maximum dose values for the target and nontarget regions (urethra, rectum, and unspecified background), when given all the source locations and source lengths. The Cimmino feasibility algorithm^22–26 is used in this paper as the method of choice to determine directly a “best” solution for the simple inverse problem.

The “general” inverse problem is to find not only the source strengths but the source locations and lengths as well, to best satisfy the dose prescription. This problem requires a search over different source positions and source lengths. At each step of the search new source positions and lengths are examined and the Cimmino algorithm is applied to solve the simple inverse problem. If the Cimmino-derived source strengths give a better dose distribution (relative to the dose prescription) than any found for previous source positions and lengths, these source strengths are stored as the new standard along with the new source lengths and positions, and the search is continued. When no significant improvement (with respect to the user chosen dose prescription) is found, the search is ended.

The discretized simple inverse problem can be written

$$b_i^{\text{min}}\le \sum _j{A}_{ij}{x}_j\le b_i^{\text{max}}(i=1,\dots ,I;j=1,\dots ,J)$$ (3a)

or in matrix form as

$${\mathbf{b}}^{\text{min}}\le \mathbf{A}\mathbf{x}\le {\mathbf{b}}^{\text{max}}$$ (3b)

where I is the number of voxels (or constraint points); b^max and b^min are the dose bounds on the voxels; J is the number of light sources; a component of matrix A denoted A_ij gives the dose absorbed at voxel i per unit strength of light source j. A positive lower bound prescribes a minimum dose for a prostate (target) voxel; it is zero for nonprostate voxels. An upper bound on dose is provided for every voxel. The goal is to find the vector x of source strengths that satisfies the inequality constraints of expression (3b).

The matrix A is a precalculated two-dimensional table (or kernel) for sources of all allowed lengths. The source lengths are discretized in 0.5-cm steps, corresponding to the length of the smallest possible segment of a light source (the light seed). The dose at a point due to a particular light source is found by specifying the perpendicular distance of the point to the source axis and the longitudinal distance of the point to the source midpoint, and then reading the proper component A_ij. The dose at any point is then found by summing the dose contributions of all the sources. The opacities for light absorption and scatter (assumed to be constant in this paper) are built into the kernel.

The operation of the Cimmino feasibility algorithm can be visualized in terms of a J-dimensional space whose coordinate axes correspond to the strengths of the light sources. Any point x in the positive “2^J-tant” (where x_j ≥ 0 for all j) corresponds to a particular set of non-negative source strengths, and thus to a dose distribution given by Ax. (A 2^J-tant is called a quadrant in 2D, and an octant in 3D.) The upper and lower inequalities of a voxel i form a hyperslab region in the positive 2^J-tant that contains allowable dose to the voxel. A point in the positive 2^J-tant that lies within the hyperslab of every voxel (that is, satisfies all inequalities), is called a feasible solution.

The Cimmino algorithm can start from an arbitrary point in the positive 2^J-tant, but the work reported here always started from the origin (x = 0).²³ In each iteration, only those constraints are used that are violated by the current estimate x of the unknown optimal result x^opt. Rays are directed from x perpendicularly toward each violated hyperplane, and a resultant vector, computed as a linear combination of the rays, shifts x to a new position in the 2^J-tant. The new estimate x of x^opt will always be closer to the specified dose prescription [expression (3)] than the previous estimate.³¹

If there are few constraint points and many sources there is a better chance that every inequality can be satisfied, that is, that a feasible solution for expression (3) exists. If there are more than one feasible solution [that is, several feasible x^opt exist], the Cimmino algorithm will choose the first feasible solution it finds, determined primarily by the starting point and a relaxation parameter.²³

For the PDT problem of interest there are significantly more constraints (voxels) than light sources, so that most often there are no feasible solutions. For this case it has been shown³¹ that the Cimmino algorithm will always converge to a unique least-squares (compromise) solution.

The least-squares solution can be shifted somewhat by introducing importance weights for the volumes (i.e., for the prostate, urethra, rectum, and background). Each volume is given a non-negative importance weight by the user. (For example, the user chooses weight 100 for the prostate, 50 for both the urethra and rectum, and 10 for the background.) The sum of the importance weights is normalized to unity. (Since the sum of the chosen weights in the example is 210, the normalized organ weights are 0.48, 0.24, 0.24, and 0.04, respectively). The importance weight of each constraint point is set equal to the normalized importance weight of its volume divided by the number of constraint points in that volume. (So if there are 1000 constraint points in the prostate, the weight of each is 0.000 48, and similarly for the voxels in other organs.) Thus the importance weights of all the voxels again sum to unity. (The default is to give equal importance to each organ, thus a normalized weight of 0.25 in the example). These weights are applied within the algorithm.^23,26 Importance weighting of the volumes in the domain of calculation allows relatively more of the error of the compromise solution to fall on the less important volumes. It also allows additional constraint points to augment those of the discretization grid, e.g., extra constraint points to better define the peripheral dose of the prostate. As additional constraint points are added to the prostate, the importance weight of each prostate constraint point decreases in such a way that the normalized importance weight of the entire prostate remains constant.

The Cimmino feasibility algorithm was chosen because it is linear, conceptually simple, relatively fast, easy to constrain to positive source strengths (the positive 2^J-tant), allows importance weighting of the volumes, and converges to a unique least-squares compromise solution when not every constraint can be satisfied.³¹ It is well-behaved, and will not create unpleasant surprises. It is ideal for both the simple inverse problem of PDT and as an “optimizing” tool for the general inverse problem. No attempt was made to code other algorithms for the PDT inverse problem.

When dose distributions derived from different sets of constraints (dose bounds) or search strategies are compared, there is the difficulty that the compromise solution may involve both underdosing to the prostate and overdosing to some of the volumes. To simplify comparison, it may be useful to renormalize the dose after the Cimmino calculation is completed. Since the PDT dose from a set of sources is a linear combination of the contributions of the individual sources, the Cimmino-derived source strengths can be increased proportionately until the minimum PDT dose received by every voxel within the prostate equals or exceeds the prescribed lower bound for the prostate PDT dose. With the minimum PDT dose to the prostate equal to the minimum prescribed PDT dose, the only comparison needed is for the overdoses. The underdosing to the prostate has been translated to an overdosing of the other volumes and the prostate itself. This process is called “renormalization.”

At present a medical physicist chooses the number of CDFs, the particular template holes (or “slots”) for source insertion, the length of the CDF for each slot, the position of the CDF within each slot (retraction), and a single duration of illumination for the entire set of sources. This is a tedious and time-consuming process that requires contours from ultrasonic tomographic images, visualization of three-dimensional volumes (prostate, urethra, and rectum) and their intersections with linear light sources, estimation of the mean opacity of the prostate, and visualization of the scattered light distribution within the prostate, for different choices of source parameters.

The template currently being used for source insertion is a plate with a square array of 13 × 13 = 169 holes (slots for linear light sources) spaced 0.5 cm apart [Fig. 1(b)]. For the particular patient data being used as a benchmark, only 51 slots are situated to allow the light source either to penetrate the prostate or approach within a 0.1-cm margin. In present clinical practice, sources are separated by 1 cm, that is, every other template slot. Thus for the benchmark patient, only 12 of the 169 template slots are used for sources.

The light source is a tube of illumination, 0.1 cm in diameter and at most 5 cm in length from template base to maximum penetration. Creating the illumination within the tube are “light seeds” of 0.5 cm length (thus 0.5 cm between the centers of adjacent light seeds). The algorithms of this study enforce two clinical requirements: (1) the seeds within a light source are contiguous (i.e., no gaps occur between light seeds), and (2) each light source has at least two seeds. Although violation of these restrictions might yield mathematically improved light distributions, the clinical use of short discontinuous light sources requires greater precision and increased time for in vivo placement, thus an increased risk to the patient.

There are three mathematical problems. (1) Given CDFs with every quantity specified, namely, the number of CDFs, the template slots, the source lengths, and the retractions of the CDF into the slot, find the source strengths (emitted power multiplied by duration of illumination [J]) to satisfy the prescribed PDT dose constraints. (2) Given the number and locations of the source slots, find the optimal source parameters (source lengths and retractions) and source strengths. (3) Given only the number of CDFs and the allowed set of template slots, find the particular source slots, source parameters, and source strengths that are optimal. These three problems must be solved for two cases: individual source strengths (sources may have different strengths), and uniform source strength (all sources have the same strength). The case of uniform source strength with all source slots and parameters specified is the present practice in the clinic and is our baseline for improvement. These different problems are listed in Table II.

Table II.

Summaries of optimization problems solved in this paper.

Problems	No. of CDFs	Slots	Lengths	Retractions	Strengths
1	Given	Given	Given	Given	Find
2	Given	Given	Find	Find	Find
3	Given	Find	Find	Find	Find

The first problem, with all quantities specified, requires only a Cimmino feasibility solution for the source strengths. The second and third problems require search procedures over allowed slots, source lengths, and retractions (as appropriate). These problems are “combinatorial,” so that exhaustive searches are not possible in very short time. Nonexhaustive searches risk encountering local minima, so that finding the solution for the “absolute-minimum” discrepancy cannot be guaranteed or even recognized. Thus the key to the second and third problems is a good search strategy.

The weighted discrepancy (or objective function) determined after each run of the Cimmino algorithm is the weighted sum of the overdose or underdose at each constraint point with respect to the prescribed PDT dose bounds,

$$\text{Wgtd discrep}=\sum _{i=1}{w}_i[\text{dim}(d_i^{\text{min}},d_i)+\text{dim}(d_i,d_i^{\text{max}})]$$ (4a)

where

$$\text{dim}(x,y)=\{\begin{array}{cc}\hfill x-y,\hfill & \hfill x>y\hfill \\ \hfill 0,\hfill & \hfill x\le y.\hfill \end{array}$$ (4b)

The first term in brackets on the right-hand side of Eq. (4a) gives the underdose and the second term gives the overdose at constraint point i. The underdose is the amount that the minimum PDT dose constraint $d_i^{\text{min}}$ exceeds the calculated PDT dose d_i. The overdose is the amount the calculated PDT dose exceeds the maximum PDT dose constraint $d_i^{\text{max}}$. A constraint point that satisfies both the upper and lower PDT dose constraints contributes no discrepancy. The sum can be over all constraint points (total weighted discrepancy) or over just constraint points of a specific organ (weighted discrepancy of the organ). The factor w_i is the importance weight of the constraint point, which has been normalized by the number of voxels of each organ.

The total weighted discrepancy between the calculated PDT dose and the prescribed PDT dose bounds is sensitive to the number and positioning of the constraint points. Our constraint points are determined by identical fixed grids in each slice of a rectangular prism that circumscribes the prostate plus a 0.1-cm margin. This grid will encompass the entire urethra and part of the rectum. The number of grid points is 13 × 13 × number of slices distributed within the walls of the encompassing prism. Additional constraint points can be inserted in each slice around the contours of a named volume. In this paper, these additional constraint points are added only for the prostate. Since calculation time to obtain the solution (source strengths and, when appropriate, slot positions and source parameters) increases with the number of constraint points, we have limited that number to a few thousand.

To check the solution obtained with the chosen constraint points, a dose volume histogram (DVH) is calculated for a much finer 3D grid after the optimal solution is obtained for any of the three mathematical problems described earlier. The DVH uses a rectangular prism that encompasses every named volume (prostate, urethra, and rectum) plus a 0.1-cm margin, and sample points numbering 101 × 101 × number of slices. The time needed to calculate the DVH is only a second or so because no feasibility or search procedures are involved.

For the second mathematical problem, the template slots are given and the search is for source lengths and positions within the template slots. The source lengths are initialized to maximum length and then geometrically pruned so that no source extends out of the prostate. Then the computer tries to eliminate an end seed of a source (at the proximal or distal source end relative to the template). This attempt is done for each source in turn. If a solution of lower discrepancy is found, it is taken as the new optimum solution. If no seed can be eliminated from any source to give a lower total weighted discrepancy, the computer tries to add an end seed to a source. Iteration (elimination and addition of end seeds) continues if lower discrepancy solutions are found. Failure to improve the solution after an iteration ends the search.

For the third mathematical problem, sources of maximum length are embedded initially in every template slot. All CDFs that never approach within a margin (usually 0.1 cm) of the prostate are immediately eliminated. The remaining sources are geometrically pruned from maximum length so as not to extend out of the prostate. The Cimmino solution at this iteration gives the least possible discrepancy. However, usually the number of sources still exceeds what is clinically feasible. The computer then eliminates the source of least (calculated) strength and repeats the Cimmino calculation and source elimination until the maximum allowed number of sources is present. Since this elimination process is quick but not perfect, each source in turn is then allowed to shift to any of four neighboring template positions when that slot is vacant. (After a shift, the source length will conform to the prostate geometry at the new position.) If a better Cimmino solution results from the shift, it is kept, otherwise the shifted source is replaced to its previous position, and the search continues. When no further improvement can be obtained from shifting sources, the final template slots are stored and the program reverts to the search described in the previous paragraph for the source lengths and retractions in the given slots.

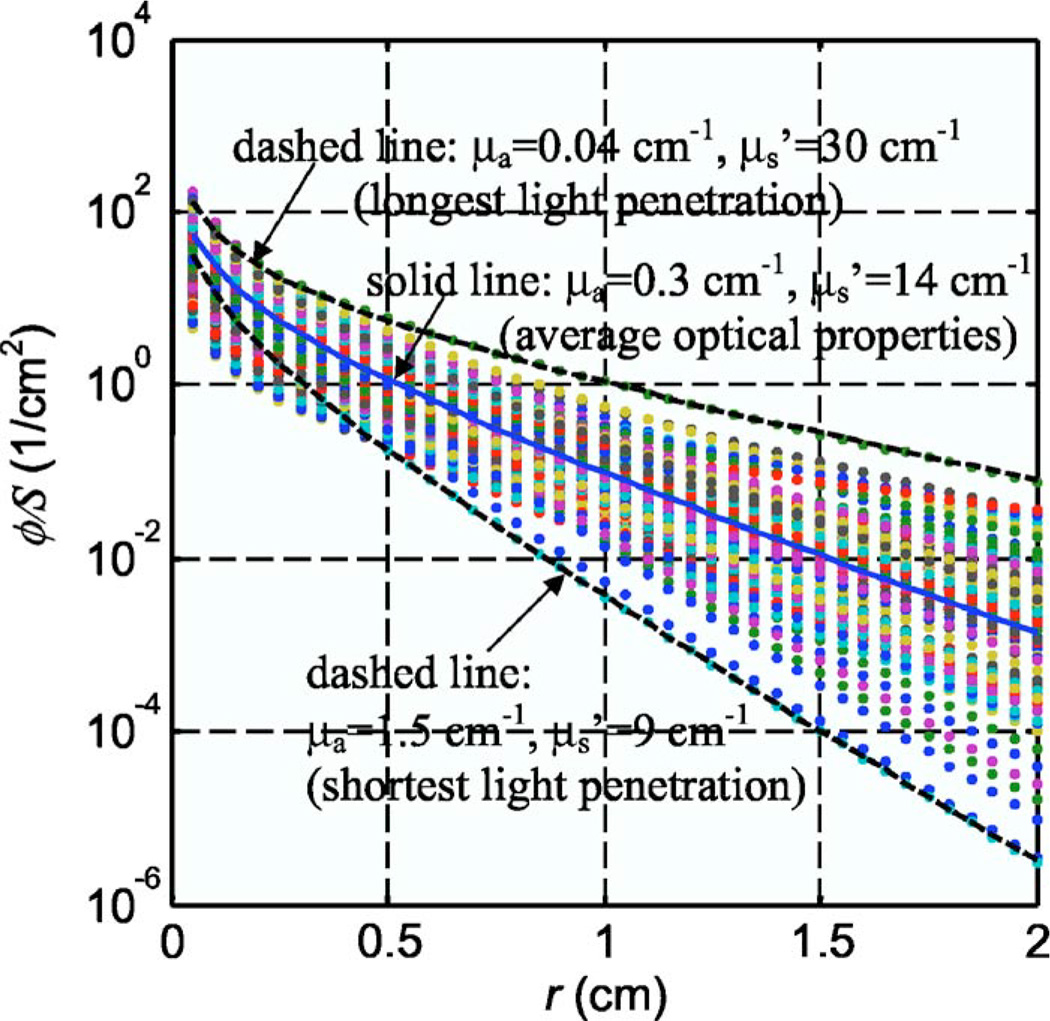
To check the effect of different optical properties on Cimmino feasibility results, two different sets of uniform optical opacities were chosen: (a) the average opacities measured for all prostate patients, μ_a = 0.3 cm⁻¹ and ${\mu }_s^{\prime }=14\mathrm{c}{\mathrm{m}}^{-1}$ and (b) the opacity values measured for the patient with the greatest penetration depth (see Fig. 2), μ_a = 0.04 cm⁻¹ and ${\mu }_s^{\prime }=30\mathrm{c}{\mathrm{m}}^{-1}$.

Fig. 2.

Light fluence rate per source strength, ϕ/S, for a point source for the optical properties determined from human prostate. The solid line corresponds to ϕ/S for the average optical properties: μ_a = 0.3 cm⁻¹, ${\mu }_s^{\prime }=14\mathrm{c}{\mathrm{m}}^{-1}$. The dashed lines correspond to ϕ/S for the longest and shortest light penetrations: μ_a = 0.04 cm⁻¹, ${\mu }_s^{\prime }=30\mathrm{c}{\mathrm{m}}^{-1}$ and μ_a = 1.5 cm⁻¹, ${\mu }_s^{\prime }=9\mathrm{c}{\mathrm{m}}^{-1}$, respectively.

We studied three problems. (1) Cimmino 1 optimizes source strengths only (problem 1 of Table II); (2) Cimmino 2 optimizes source strengths, template locations, lengths, and retractions (problem 3 of Table II); Cimmino 3 is the same as Cimmino 2 with a lower constraint for rectum; (3) Cimmino 4 optimizes source lengths and strengths for all possible (51) CDFs that intersect the prostate (problem 2 of Table II).

Summaries of source strengths and weighted discrepancies of the Cimmino calculations are shown in Tables III and IV, respectively. The optimization parameters used in the paper for all Cimmino calculations are listed in Table V. Table III shows the resulting source strengths for the CDFs obtained from Cimmino-based search algorithms. For each Cimmino method, there is a tenfold ratio in source strength for the two different optical properties. This shows the critical importance of optical properties in determining the PDT dose coverage of the prostate.

Table III.

Source strengths obtained using various Cimmino-based search algorithms with renormalization. Cimmino 1: optimize source strengths only; Cimmino 2: optimize source lengths, strengths, and template slot locations; Cimmino 3: the same as Cimmino 2 with a different constraint for rectum; and Cimmino 4: optimize source lengths, and strengths for 51 CDFs filling the entire prostate. This is shown for the average and the most transparent prostate optical properties: Opt 1: μ_a = 0.3 cm⁻¹, ${\mu }_s^{\prime }=14\mathrm{c}{\mathrm{m}}^{-1}$; Opt 2: μ_a = 0.04 cm⁻¹, ${\mu }_s^{\prime }=30\mathrm{c}{\mathrm{m}}^{-1}$, respectively. The calculation time is for a Dell PC with 2.8 GHz Pentium IV processor and 1 Gbyte RAM. The source strengths for the standard plan are 410.83 and 24.86, for Opt 1 and Opt 2, respectively. These source strengths (in units of J/cm) give prescribed light fluence of 100 J /cm² to cover the prostate.

	Cimmino 1		Cimmino 2		Cimmino 3		Cimmino 4
Source No.	Opt 1	Opt 2	Opt 1	Opt 2	Opt 1	Opt 2	Opt 1	Opt 2
1	286.22	19.26	267.66	33.36	296.82	33.36	22.76	3.78
2	232.24	19.20	271.56	18.38	292.12	18.38	22.50	3.54
3	264.92	16.04	222.82	14.56	312.78	14.56	18.58	3.46
4	242.40	17.00	213.14	23.52	240.62	23.52	21.92	4.04
5	350.54	21.92	349.38	13.18	344.94	13.18	42.84	6.52
6	293.08	20.38	358.48	29.32	244.36	29.32	21.92	3.36
7	595.94	30.18	219.50	11.30	239.14	11.30	22.80	2.96
8	429.26	26.50	293.76	13.08	159.44	13.08	29.32	3.54
9	306.20	21.82	219.16	27.70	171.24	27.70	30.22	3.76
10	289.82	18.20	351.70	25.58	229.26	25.58	30.96	3.90
11	290.28	17.74	258.80	19.80	241.88	19.80	37.26	5.20
12	391.96	25.96	209.24	19.94	183.74	19.94	21.54	3.24
⋯							⋯	⋯
Calculation time (s)	1	1	272	223	309	224	17	18

Table IV.

Summary of the calculation results with renormalization of source strengths. “Wgtd discrep” means weighted discrepancy and “back” means background. The optimization grid gives the constraint points (a few thousand) used for the Cimmino feasibility algorithm while the DVH grid is finer and gives many sample points (a few tens of thousands) to calculate the DVH after the source parameters and source strengths have been obtained.

	Opt 1 (μa = 0.3 cm−1, ${\mu }_s^{\prime }=14\mathrm{c}{\mathrm{m}}^{-1}$ Wgtd discrep for organs (DVH grid)				Opt 2 (μa = 0.04 cm−1, ${\mu }_s^{\prime }=30\mathrm{c}{\mathrm{m}}^{-1}$ Wgtd discrep for organs (DVH grid)
Algorithms	Prostate	Urethra	Rectum	Back	Prostate	Urethra	Rectum	Back
Standard	220	138	29.1	20.4	32.5	30.1	1.70	1.41
Cimmino 1	168	89.9	7.77	8.28	18.2	13.1	0.131	0.439
Cimmino 2	102	45.0	0.001 20	4.65	9.46	0.824	0.00	0.291
Cimmino 3	84.5	36.0	0.47	5.47	9.46	0.824	0.00	0.291
Cimmino 4	5.35	5.53	0.005 30	0.159	6.71	6.08	0.008 20	0.0003
	Total wgtd discrep				Total wgtd discrep
	Optim grid		DVH grid		Optim grid		DVH grid
Standard	392		408		59.8		65.7
Cimmino 1	240		274		28.3		31.9
Cimmino 2	101		152		8.53		10.6
Cimmino 3	93.2		126		8.53		10.6
Cimmino 4	5.88		11.0		9.12		12.8

Table V.

Optimization parameters used for various Cimmino-based search algorithms in the paper. The lower dose constraints, d^min, are kept at 100 for prostate and 0 for all other critical structures (rectum, urethra, and background). The normalized importance weights, w_i, are kept at 100 for all calculations unless explicitly stated otherwise. Opt 1: μ_a = 0.3 cm⁻¹, ${\mu }_s^{\prime }=14\mathrm{c}{\mathrm{m}}^{-1}$; Opt 2: μ_a = 0.04 cm⁻¹, ${\mu }_s^{\prime }=30\mathrm{c}{\mathrm{m}}^{-1}$. The numbers in parentheses are for Opt 1 without normalization (dashed lines in Fig. 6).

Figures	Cimmino names	Problems	The upper dose constraints, dmax
			Opt 1				Opt 2
			Prostate	Urethra	Rectum	Back	Prostate	Urethra	Rectum	Back
4–7	Cimmino 1	1	300 (500)	300	300	300	300	300	300	300
4–8	Cimmino 2	3	300 (500)	300	300	300	300	300	300	300
4–7	Cimmino 3	3	300 (500)	300	200	300	300	300	200	300
4–7	Cimmino 4	2 or 3	300	200	300	300	200	200	200	300
8(a)		3	Vary	300	300	300
8(b)		3	Vary	300	300	300

In Table IV, we compared the total weighted discrepancy of the constraint points that were used to find the source strengths with that of the DVH sample points. The total weighted discrepancy of the DVH sample points was larger than that of the constraint points, probably because it included more points, and was thus more representative of reality. The total weighted discrepancy generally decreases for better DVH, except for Cimmino 4 when the optical properties had the largest optical penetration depth. This latter case corresponded to a different upper PDT dose bound for prostate, rectum, and urethra (200%). All other calculations, except for Cimmino 3, use an upper bound of 300% (see Table V).

III. RESULTS AND DISCUSSION

Optical properties measured in 13 patients have been summarized in Table I. The heterogeneity of optical properties in human prostates was somewhat smaller than that observed in canine prostates at 732 nm.⁷ Overall μ_a varied between 0.07 and 1.62 cm⁻¹ (mean 0.3 ± 0.2 cm⁻¹) and ${\mu }_s^{\prime }$ varied between 1.1 and 44 cm⁻¹ (mean 14 ± 11 cm⁻¹). The effective attenuation coefficient μ_eff varied between 0.91 and 6.7 cm⁻¹, corresponding to an optical penetration depth (δ = 1/μ_eff) of 0.2–1.1 cm. The mean values of μ_eff and δ were 2.9 ± 0.8 cm⁻¹ and 0.4 ± 0.1 cm, respectively. This penetration depth was substantially larger than that of 0.1–0.25 cm reported for 630 nm⁶ but was smaller than the 0.5–3 cm observed in normal canine prostate at 732 nm.⁷ The most probable explanation is that canine prostate has a different glandular/structure content than that of the human prostate. While the mean reduced scattering coefficient in canine was 3.6 ± 4.8 cm⁻¹,⁷ it was 15 ± 11 cm⁻¹ in human at the same wavelength (732 nm).¹² The increased reduced scattering coefficient resulted in an increased effective attenuation coefficient, or a reduction of optical penetration depth, assuming the absorption coefficient remains the same.

Figure 2 shows the light fluence rate per power, ϕ/S, as a function of distances from a point source for all the optical properties measured in patients (119 data points, symbols). The average optical properties (μ_a = 0.3 cm⁻¹, ${\mu }_s^{\prime }=14\mathrm{c}{\mathrm{m}}^{-1}$) produced an optical kernel approximately in the middle of the range of kernel variations (solid line in Fig. 2). As a result, they were used for most analyses in the current study. Since the corresponding optical penetration depth (δ = 0.28 cm) was shorter than the spacing between the catheters (0.5 cm), we also examined the extreme case where the optical penetration depth was greatest. This corresponded to μ_a = 0.04 cm⁻¹, ${\mu }_s^{\prime }=30\mathrm{c}{\mathrm{m}}^{-1}$ (δ = 0.5 cm, upper dashed line in Fig. 2). We did not show results for the optical properties (μ_a = 1.5 cm⁻¹, ${\mu }_s^{\prime }=9\mathrm{c}{\mathrm{m}}^{-1}$) with the shortest optical penetration depth (δ = 0.16 cm) since it behaved similarly to that of the average optical properties, which had an optical penetration depth shorter than the spacing of the template (0.5 cm).

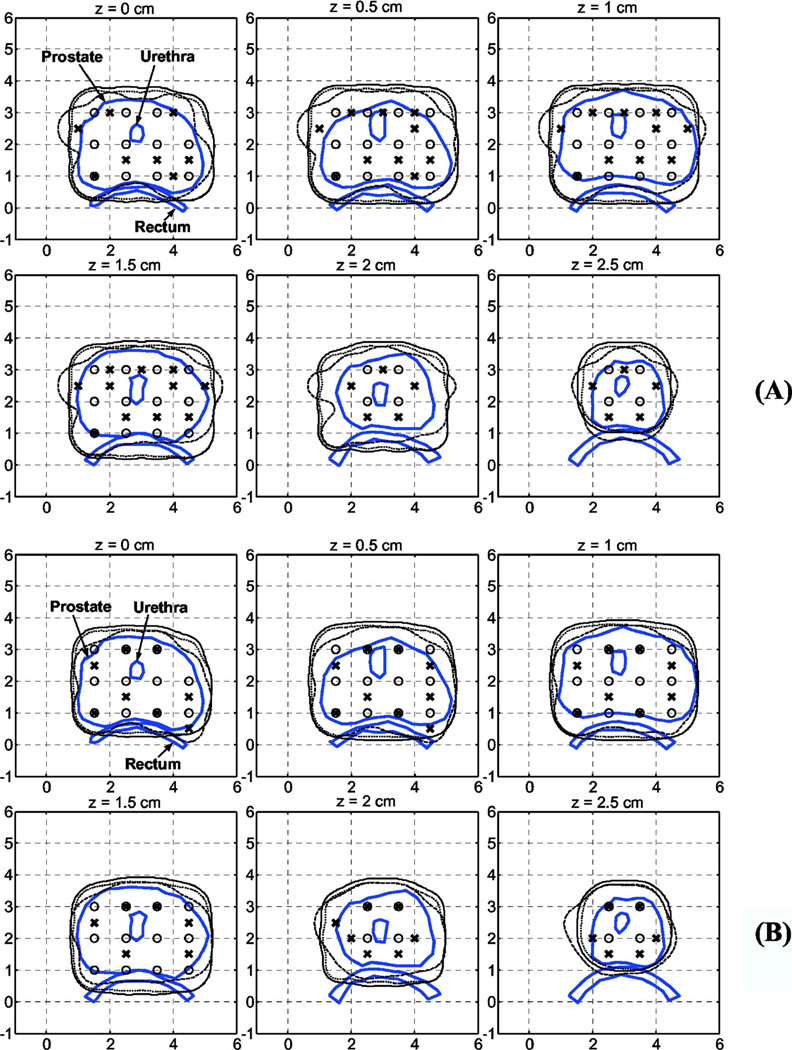
Figure 3 compares computer runs of optimized 100% isodose distributions of Cimmino 1 and Cimmino 3 with the standard plan. We used our standard plan, based on geometrical coverage, 1-cm spaced loading, and uniform source strength as our default plan to judge the improvement made by the Cimmino feasibility algorithm and the search strategies. There was no substantial difference in the isodose distributions of equal-source-strength and individual-source-strength (Cimmino 1 of Fig. 3). This was true for both the average and most penetrating optical properties found in the human prostate [Figs. 3(a) and 3(b)]. However, substantial sparing of rectum was obtained when the source positions were also optimized (Cimmino 3). This is not surprising since for shorter light penetration depths, the light coverage is determined more by the light source location than the source strength, provided all other conditions are the same. The Cimmino feasibility algorithm is fast enough for this problem to obtain clinical near real-time optimization (less than 300 s, see Table III).

Fig. 3.

Comparison of 100% isodose lines for the manual standard plan (solid line) vs Cimmino 1 (dotted line) and Cimmino 3 (dashed line) for two optical properties: (a) μ_a = 0.3 cm⁻¹, ${\mu }_s^{\prime }=14\mathrm{c}{\mathrm{m}}^{-1}$, and (b) μ_a = 0.04, ${\mu }_s^{\prime }=30\mathrm{c}{\mathrm{m}}^{-1}$. (○) The source positions in the standard plan or Cimmino 1. (×) The source positions in Cimmino 3. The source strengths are summarized in Table III.

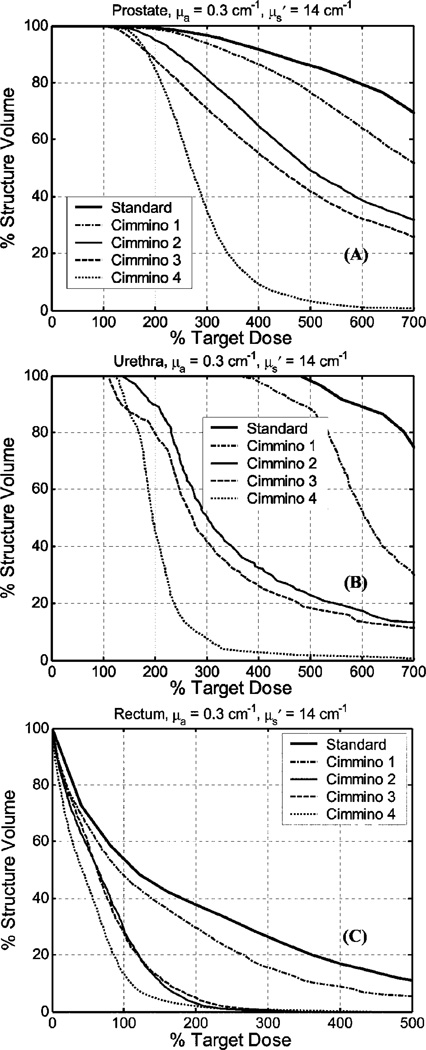
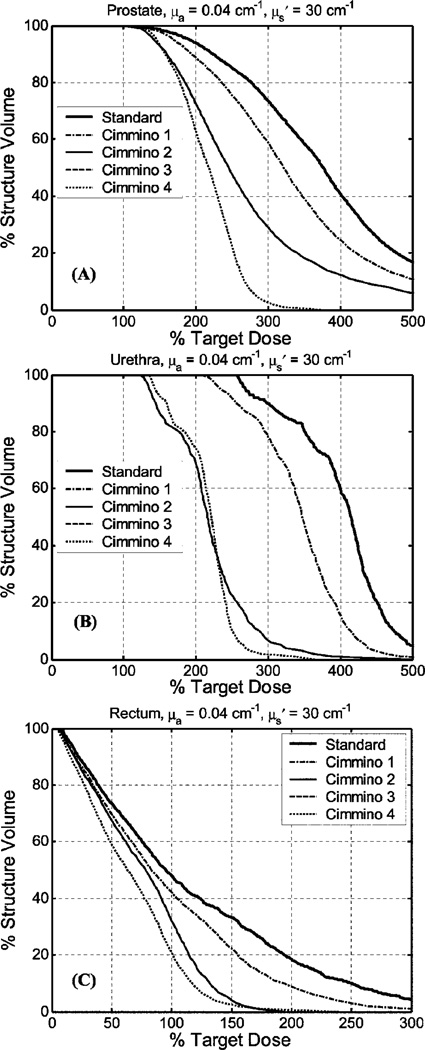
The DVHs for prostate, urethra, and rectum are shown in Fig. 4 for average optical properties (μ_a = 0.3 cm⁻¹, ${\mu }_s^{\prime }=14\mathrm{c}{\mathrm{m}}^{-1}$) and in Fig. 5 for the largest optical penetration (μ_a = 0.04 cm⁻¹, ${\mu }_s^{\prime }=30\mathrm{c}{\mathrm{m}}^{-1}$). All plans performed so far used source strength renormalization to guarantee prescribed PDT dose coverage over the entire prostate.

Fig. 4.

DVH comparison of the manual standard plan vs the Cimmino-based search results for optical properties μ_a = 0.3 cm⁻¹, ${\mu }_s^{\prime }=14\mathrm{c}{\mathrm{m}}^{-1}$ for (a) prostate, (b) urethra, and (c) rectum. The standard plan uses uniform 1-cm source loading with uniform-strength. The optimized results are: Cimmino 1 uses the same fixed source positions and source parameters as the standard plan but Cimmino optimized weights for each source; Cimmino 2 finds optimized source lengths, loading, and template locations for 12 linear sources with upper constraints of 300% for rectum and urethra; Cimmino 3 is the same as Cimmino 2 but with upper constraints of 200% for rectum and urethra; Cimmino 4 uses Cimmino optimized source lengths, loading and template for all 51 possible CDF sources through the prostate. See Table IV for the upper dose bounds used for each Cimmino-search algorithm.

Fig. 5.

Comparison of DVH of manual standard plan vs Cimmino-based search results for optical properties μ_a = 0.04 cm⁻¹, ${\mu }_s^{\prime }=30\mathrm{c}{\mathrm{m}}^{-1}$ for (a) prostate, (b) urethra, and (c) rectum. The definition of the standard and Cimmino 1–4 are the same as in Fig. 4. Cimmino 2 and 3 produced identical DVH, i.e., the solid and dashed lines overlapped.

When the DVHs were compared, the dosimetry improved going from the standard plan to Cimmino 1, Cimmino 2, Cimmino 3, and Cimmino 4 in that order for the average optical properties, see Fig. 4. Since the optical penetration was less than 0.5 cm, the standard plan used 1-cm spaced loading to uniformly cover the entire prostate with 12 CDFs. Cimmino 1, which optimizes the source strength only, did not provide significant improvement over the standard plan, as discussed before. When one started to optimize the source locations (e.g., for Cimmino 2 and 3), one observed a substantial improvement over the standard plan, not only for the coverage of the target (prostate) but also for the PDT dose reduction of the urethra and rectum. This is expected since the optical range of each source is so short that the geometrical locations of the source determine where the doses are delivered. Cimmino 3, which used 200% upper constraint for rectum, gave better results than Cimmino 2, which used 300% upper constraint for rectum. For comparison, we also examined the case of all possible (51) linear sources through the prostate (Cimmino 4). Not surprisingly, we got the best DVH with this option, although it is clinically impractical to use so many sources. The DVH for this option represents the best possible mathematical solution.

Similar comparison was also made for the longest optical penetration depth, as shown in Fig. 5. DVH results were similar to the case of the average optical properties except that we did not see any difference between Cimmino 2 and 3, probably because the PDT dose was already optimized even with a higher upper PDT dose bound for the rectum. Comparing Figs. 4 and 5, we concluded that the rectum sparing was improved when the optical penetration of the prostate is less than 0.3 cm. Less significant improvement was observed when the optical penetration was longer. The result showed that for low opacities (greater light penetration) the rectal sparing of the 12-source plan was not much worse than that of the 51-source plan (Fig. 5). For the average optical parameters, however, improved rectum sparing can be achieved with more CDFs (Fig. 4).

Solution of the first mathematical problem allows comparison of individual source strengths versus a single uniform strength for all user-chosen sources. Solution of the second problem allows a similar comparison but with source lengths, retractions, and strengths chosen by prostate geometry and minimum PDT dose discrepancy. A solution of the third problem allows the treatment planner to find automatically the best (or almost-best) light sources and source strengths from just the specified PDT dose constraints to the prostate and organs, and the choice for the number of sources. Such a solution would be virtually impossible to find by human visualization and estimation. Automatic source selection and weighting becomes even more important if it is necessary to limit PDT dose to the urethra and rectum without compromising treatment effectiveness to the prostate.

The selection of the number of light sources is as much a clinical as a mathematical problem. To find mathematically the best number of linear light sources to insert, one can rerun repeatedly any procedure used to solve problem 3 with different numbers of sources. However changing the number of CDFs differs from rearranging source positions and solving for source strengths; it involves a tradeoff between (a) fewer sources—less homogeneous dose coverage, higher source strengths, but fewer surgical complications, and (b) more sources—better dose coverage, lower source strengths, but more surgical complications). Thus choosing the number of sources requires clinician input based on medical experience and judgment.

Each search procedure allows the number of CDFs to be decreased by one. A new optimization calculation is then performed and the resulting PDT dose distribution compared with the previous. The decrease in the number of CDFs can be continued iteratively. If the number of sources can be decreased without significantly increasing discrepancy between the prescribed and optimized PDT dose distribution, fewer sources need be used, thereby reducing the complication of the procedure and discomfort of the patient.

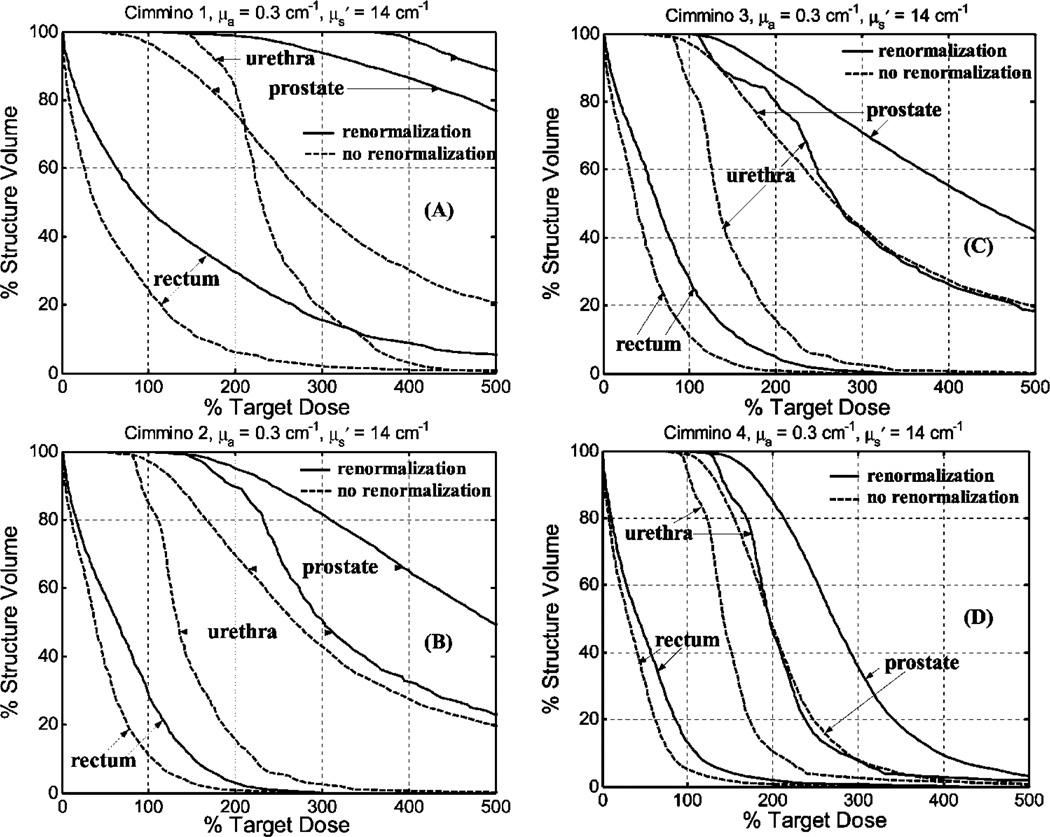
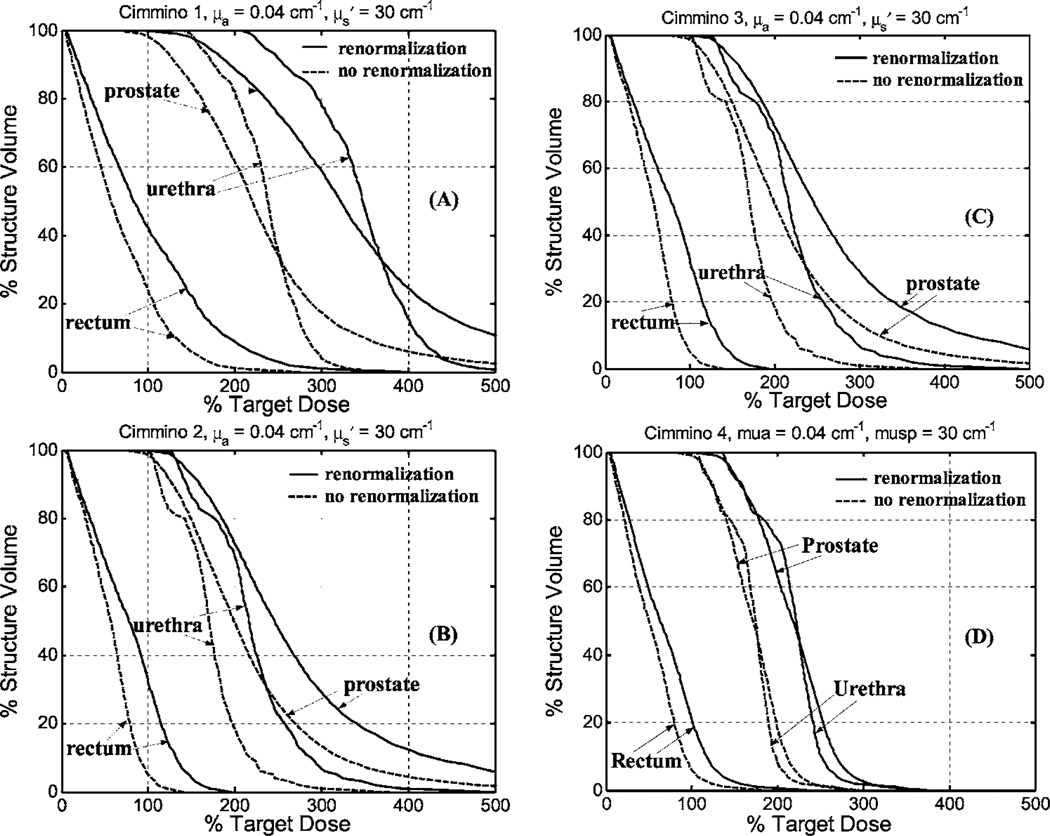
We also compared DVH between Cimmino feasibility algorithms with and without renormalization. Figure 6 is for average optical properties and Fig. 7 is for optical properties of greatest penetration. For average optical properties and 12 CDFs, only 96% of the volume of the prostate was covered to prescribed PDT dose without renormalization of the source strengths. The upper dose bounds were set to 300% with, and 500% without, renormalization. (A higher upper bound was used without renormalization because coverage of the prostate volume to prescribed dose fell to 93% with the lower dose bound.) For the optical properties of larger penetration, the volume coverage was 97% with 12 CDFs. When more light sources were used (e.g., 51 CDFs for Cimmino 4), the prostate was adequately covered for the range of optical properties without renormalization. This may provide an indication as to when one can be sure sufficient source locations are obtained. For the Cimmino-based search algorithms 1–3, the ratios of the total source strengths with and without renormalization were 1.9–2.5 for the average optical properties, which implies that treatment time can be reduced by factors of 1.9–2.5 if renormalization is not applied. For the optical properties with the largest penetration, the ratios were approximately 1.5 among the Cimmino-based search algorithms 1–3.

Fig. 6.

Comparison of DVH for Cimmino-based search algorithm with (solid lines) and without (dashed lines) renormalization of source strengths for prostate coverage for optical properties μ_a = 0.3 cm⁻¹, ${\mu }_s^{\prime }=14\mathrm{c}{\mathrm{m}}^{-1}$. The results are: (a) Cimmino 1; (b) Cimmino 2; (c) Cimmino 3; (d) Cimmino 4.

Fig. 7.

Comparison of DVH for Cimmino-based search algorithm with (solid lines) and without (dashed lines) renormalization of source strengths for prostate coverage for optical properties μ_a = 0.04 cm⁻¹, ${\mu }_s^{\prime }=30\mathrm{c}{\mathrm{m}}^{-1}$. The results are: (a) Cimmino 1; (b) Cimmino 2; (c) Cimmino 3; (d) Cimmino 4.

We also studied how importance weighting of the named volumes (prostate, urethra, rectum, or background) would affect the Cimmino results. The prostate (target) importance weight was allowed to vary between 100 and 500 relative to an importance weight of 100 for the other volumes. (Before any calculation, importance weights are normalized so that their sum over all volumes is unity.) For both the average optical properties and the optical properties of greatest penetration, the different values of importance weight had negligible effect on the DVH of any of the named volumes. For this reason, the importance weight of every named volume was chosen to be the same.

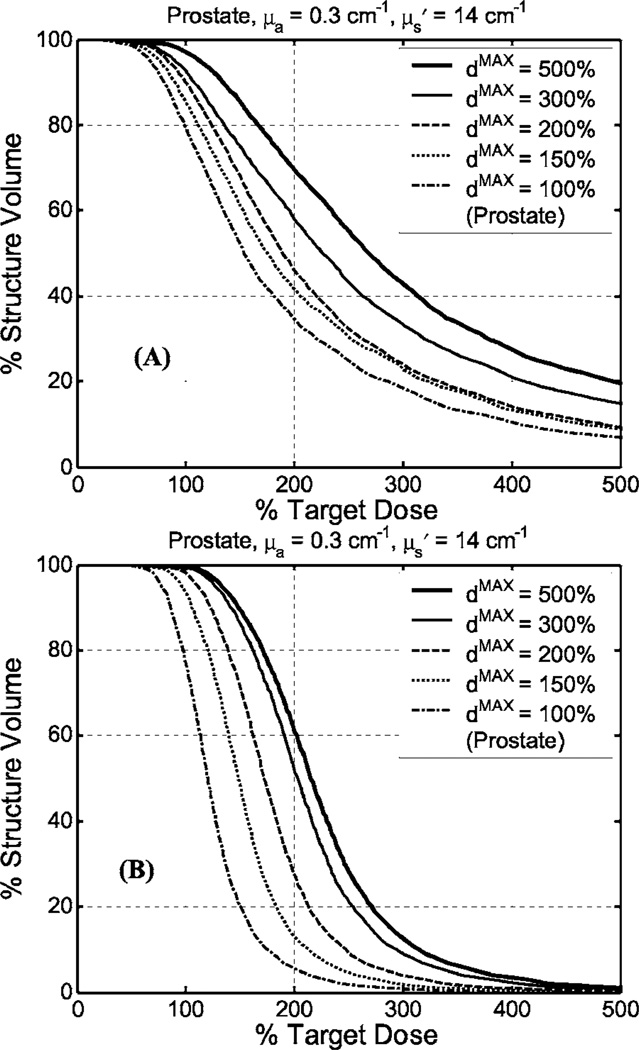
To examine the effect of upper dose bounds on the Cimmino results, we repeated the Cimmino feasibility algorithm using 12 or 51 CDFs, respectively, for the average optical properties without renormalization, as shown in Figs. 8(a) and 8(b). The best upper dose bound was 500% for 12 CDF and 200% for 51 CDF. Under this condition, 97% volume of prostate was covered by the 100% dose line without renormalization. This conclusion was also valid for the greatest optical penetration depth (data not shown), where the percentage volume of 100% dose coverage was higher than that for the average optical properties. The effect of upper dose bounds on the critical organs (urethra and rectum) was generally negligible (for upper bounds changing from 150% to 500%, data not shown). As a result, we kept upper bounds for the critical organs at 300% for all our optimization algorithms (see Table IV).

Fig. 8.

Comparison of DVH for Cimmino-based search algorithm (problem option 3) with various upper dose bounds (d^max) for prostate for (a) 12 CDFs and (b) 51 CDFs for the average optical properties. No renormalization is used.

The present paper assumes uniform (homogeneous) optical properties. An open question is whether optimized solutions for inhomogeneous media will further improve over the present uniform-medium calculations. Another open question is the number of control/constraint/sample points required to guarantee the optimized outcome. Further studies are also needed to determine the minimum number of CDFs needed to achieve complete coverage.

IV. CONCLUSIONS

The question addressed is whether any significant advantage may derive from methods that allow different strengths for the CDFs and/or choose the geometry (locations, lengths) of the light sources. Our comparison shows: (1) It is important to measure the optical properties of a patient because it determines the light fluence distribution. This effect is more predominant than optimizing the source position, length, and strength. (2) For the range of optical properties in the human prostate, when CDF positions and strengths are both found by a search based on the Cimmino feasibility algorithm, there is significant improvement over the current standard method of equal-source-strength optimization. (3) Computer optimization saves the user time in setup and reduces human stress. The Cimmino feasibility algorithm is fast enough to be the core of search algorithms to obtain clinical real-time optimization.