Between-Network Connectivity occurs in brain regions lacking layer IV input

Abstract

To better understand the cortical circuitry underlying connectivity between large-scale neural networks, we develop a novel, data-driven approach to identify potential integration subregions. Between-Network Connectivity (BNC) associated with any anatomical region is the amount of connectivity between that point and all large-scale networks, as measured using simple and multiple correlations. It is straightforward to calculate and applicable to functional networks identified using Independent Components Analysis. We calculated BNC for all fMRI voxels within the brain and compared the results to known regional cytoarchitectural patterns. Based on previous observations of the relationship between macroscopic connectivity and microscopic cytoarchitecture, we predicted that areas with high BNC will be located in paralimbic subregions with an undifferentiated laminar structure. Results suggest that the anterior insula and dorsal posterior cingulate cortices play prominent roles in information integration. Cytoarchitecturely, these areas show agranular or dysgranular cytologies with absent or disrupted cortical layer IV. Since layer IV is the primary recipient of feed-forward thalamocortical connections, and due to the exclusive nature of driving connections to this layer, we suggest that the absence of cortical layer IV might allow for information to be exchanged across networks, and is an organizational characteristic of brain-subregions serving as inter-network communication hubs.

1. Introduction

As we observe the world around us, our brains constantly process external input and create predictions about future events. These predictions are generated by constantly changing patterns of intrinsic activity within the brain, combining internal states, past experiences, and future predictions (Engel et al., 2001). Our integrated conscious experience likely emerges from the interaction of these patterns (Tononi, 2004). While the areas where this integration occurs is a topic of active investigation (Bullmore and Sporns, 2012), the mechanisms by which it occurs are currently unknown.

In neuroimaging, integration frequently refers to an area’s total connectivity throughout the entire brain (Buckner et al., 2009; Cole et al., 2010). However, integration in this sense does not distinguish connectivity within a sensory or processing system from connectivity between systems. Alternatively, integration may refer to areas where connectivity converges across sensory or higher-level systems. In this sense of the term, multimodal integration areas refer to association and paralimbic areas where sensory information from visual, somatosensory and auditory systems converges (Sepulcre et al., 2012; Yeo et al., 2011).

Integration may also refer to areas that are both highly connected throughout the brain and whose connections are bridges between segregated processing networks. In this sense, integration areas refer to connector hubs (Guimera and Amaral, 2005; Valencia et al., 2009; Zamora-López et al., 2010) or the rich club hubs of the brain’s structural core (Hagmann et al., 2008; van den Heuvel and Sporns, 2011).

Recent studies link the macroscale connectivity of rich-club and connector hubs to their microscale cytoarchitecture (Hilgetag and Grant, 2010; Scholtens et al., 2014). Based on the white matter tracings in cats and macaque, these areas have reduced cytoarchitectural differentiation into cortical layers (Beul et al., 2014; Zamora-López et al., 2011). However, this hypothesized relationship between macroscale connectivity and microscale cytoarchitecture has yet to be tested in functional networks, or in the human brain.

Examining the relationship between macroscale connectivity and microscale cytoarchitecture requires the identification of specific integration areas of the cortex. Many potential integration areas are in paralimbic regions of the cortex, including the insula and cingulate gyrus (Buckner et al., 2009; Hagmann et al., 2008; He et al., 2009; Rubinov and Sporns, 2011; Sepulcre et al., 2012; van den Heuvel et al., 2012; Zamora-López et al., 2010). Each paralimbic region includes gradients of agranular, dysgranular, and granular cortical lamination patterns (Mesulam, 1998; Morecraft et al., 2004; Morel et al., 2013; Vogt et al., 2005). Agranular cortex lacks cortical layer IV, the primary recipient of thalamic projections. Dysgranular cortex features a minimal and inconsistently present layer IV; granular cortex has fully developed layer IV. This variety of cytoarchitectural differentiation, within candidate integration areas, presents an opportunity to test the relationship between macroscale connectivity and microscale cytoarchitecture.

We hypothesize that, within paralimbic regions, agranular or dysgranular subregions are strongly connected to many large-scale networks, while adjacent granular subregions lack this trait. We test this hypothesis in the human brain by developing a novel Independent Component Analysis-based measure of the amount of integration potentially associated with a specific voxel, Between-Network Connectivity (BNC). Using BNC, we observe that areas whose connectivity bridges many large-scale networks occur in discrete regions of the cortex. Furthermore, we show that within paralimbic areas, BNC is associated with agranular or dysgranular subregions.

2. Materials and Methods

2.1 Subjects and experimental procedure

Twenty-seven healthy subjects (12 men, 15 women, mean age = 32 ± 3 years) were recruited from the general community. Exclusion criteria included axis I disorders, neurologic illness, or major medical illness. Subjects provided written informed consent as approved by the Colorado Multiple Institutional Review Board.

2.2 fMRI data acquisition and preprocessing

Resting state images were acquired on a 3 T whole-body MR scanner (General Electric, Milwaukee, WI, USA) using a standard quadrature head coil. A high-resolution 3D T1-weighted anatomical scan was collected. Functional scans were acquired with the following parameters: TR 2000 ms, TE 32 ms, FOV 240 mm², matrix size 64 × 64, voxel size 3.75 × 3.75 mm², slice thickness 3 mm, gap 0.5 mm, interleaved, flip angle 70°. Resting fMRI scan duration was 10 min, with subjects instructed to rest with eyes closed. Data were preprocessed using SPM8 (Wellcome Dept. of Imaging Neuroscience, London, UK) in Matlab 2009b. All subjects had less than 2 mm of movement. The first four images were excluded for saturation effects. Images were realigned to the first volume, normalized to the Montreal Neurological Institute (MNI) space, and smoothed using a 8 mm FWHM Gaussian kernel.

Voxel time series were processed to remove sources of noise and minimize the influence of movement. All voxel time series were detrended and band-pass filtered between 0.01 and 0.1 Hz. Signals for white matter, cerebral spinal fluid, and global grey matter, along with six head realignment parameters were regressed out. Since these precautions have been shown to minimize, but not remove the influence of movement on fMRI time series, additional precautions were used as recommended by Power et al. (Power et al., 2012). fMRI volumes with excessive movement were identified through calculating framewise displacement (FD) and removing volumes with FD > 0.5 along with preceding and following volumes.

2.3 Independent Component Analysis of fMRI data

Spatial independent component analysis (ICA) was carried out using GIFT v1.3i (Calhoun et al., 2001)(http://icatb.sourceforge.net). Thirty-four components were estimated based on minimum description length (MDL) criteria and extracted using the infomax algorithm (Bell and Sejnowski, 1995; Li et al., 2007). Voxel time series were temporally concatenated across subjects and then variance-normalized in ICA preprocessing. Two data reductions steps were used, with 70 and 34 PCA components included after each. Resulting component spatial maps were reconstructed with GICA3 and scaled to z-scores (Erhardt et al., 2011). All spatial maps and time courses were visually inspected to identify noise components. Seven components were identified as artifacts based on spatial distributions that were primarily in CSF or white matter, or high-frequency oscillations, and were excluded from further analysis. The remaining 27 components and all associated grey-matter voxels were used to calculate inter-network connectivity for each voxel.

2.4 Measuring Inter-Network Connectivity

Following large-scale network identification with ICA, we define a function that measures the amount of “integration” that occurs between these networks at a particular voxel. This function will be referred to as Between-Network Connectivity (BNC). We begin by more carefully defining what is meant by “integration” in this context and what BNC will measure:

1. Definition. Between-Network Connectivity is the influence of linear dependencies among large-scale networks on the linear prediction of a voxel’s activity.

The function will have the following desirable attributes:

1. The range of BNC is between zero and one.

2. BNC = 0 if a voxel is only connected to a single independent network.

3. BNC = 1 if a voxel is strongly connected to all correlated networks.

In the context of fMRI, the pattern of a voxel’s activity is its time series. Using ICA, large-scale networks are ICA components. Following back-reconstruction in GIFT, each ICA component for each subject has an associated time series (Erhardt et al., 2011). Linear prediction is a regression equation, with the voxel’s time series as the response variable and ICA components’ time series as predictor variables. Let x_v represent the centered and scaled time course for voxel v as a linear combination of back-reconstructed ICA time courses:

$${\mathit{x}}_v=\sum _{i\in K}^{|K|}{\beta }_{vi}{\mathit{a}}_i+\mathit{e}$$ (2)

where K is the set of non-noise ICA components, |K| is its cardinality (the number ICA components in the set). Each a_i is the back-reconstructed time course for component i, β_vi are standardized regression weights, and e the error term. Let the population coefficient of determination from (2) be denoted as R²_v. Similarly, let r²_vi denote the population squared simple correlation between the time series from voxel v and ICA component i.

From definition (1) of BNC, it is clear that if there is no linear dependence (i.e., no correlations) among ICA components, then BNC must be equal to zero in all cases. For equation (2), this occurs if and only if the population coefficient of determination is equal to the sum of population squared simple correlations between voxel v and component i (Cohen et al., 2003):

$$R_v^2=\sum _{i\in K}^{|K|}{r}_{vi}^2$$ (3)

Or equivalently, subtracting R²_v from both sides results in an equation that describes an absence of BNC:

$$0=\sum _{i\in K}^{|K|}{r}_{vi}^2-R_v^2$$ (4)

Since all terms in equation (4) are bounded and since there are a finite number of terms, the right hand side of (4) is bounded even in cases where the equality does not hold. By finding the upper and lower bounds of this equation (see supplementary materials), the right hand side of (4) can be scaled to the desired maximum of 1. We define the normalized BNC associated with voxel v as:

$$BN{C}_v=\frac{1}{|K|-1}(\sum _{i\in K}^{|K|}{r}_{vi}^2-R_v^2)$$ (5)

Intuitively, equation (5) describes the difference between the total connectivity to all large-scale networks, as summed squared correlations, and the amount of variance explained by the networks, in the form of R²_v. This excess variance is shared among the networks and voxel v, consistent with the concept of between-network connectivity.

Equation (5) meets the desirable attributes listed above: 1. While (5) may take on negative values in individual samples, these cases are artifactual, located in white matter and cerebral spinal fluid (see supplementary materials), and will only rarely occur in the population. Alternatively, the normalization factor (|K| - 1) ensures equation (5) is less than or equal to 1. The range of (5) is therefore [0,1]. 2. The case where voxel v is connected to a single independent network is a special case of equation (3), and substitution of these values into (5) demonstrates that BNC is 0 in this case. 3. Lastly, the case were voxel v is strongly connected to all correlated networks was considered in finding the bounds of the ride hand side of equation (4). In this case, the difference between the summed squared correlations and R²_v approaches (|K| −1) and equation (5) approaches 1.

Several important features of equation (5) deserve further consideration. The normalization factor (|K| −1) ensures the upper limit is independent of the number of components, while individual values of BNC may change based on the number of components chosen for ICA. This suggests the method we have used to determine the normalization factor is less than ideal and can be improved upon by future studies. However, since the number of components is consistent for all voxels within any study, equation (5) can be used to compare voxels and subjects within a study.

Other functions of BNC are possible using definition (1), including a similar equation using summed squared β coefficients (see supplementary materials). While this definition is possible, it is also problematic due to the relatively large number of terms in the regression equation and consequent inaccuracy in estimating β coefficients. Multicollinearity, a strong correlation among regressor variables, has a more damaging effect on the estimation accuracy of regression coefficients relative to correlation coefficients and the coefficient of determination (Cohen et al., 2003). These observations motivated their use in equation (5).

So far, we have discussed BNC from a population point of view. In practice, we will have to estimate the number of independent components K as well as their time courses. To estimate the former, we use information-theoretic criteria such as Minimum Descriptive Length (Li et al., 2007). The estimation of the latter is accomplished by back-reconstruction during ICA (Erhardt et al., 2011). Based on these estimates, we then compute the empirical correlation coefficients for r²_vi and the multiple coefficient of determination from (2) using stand linear regression software. The estimates are then entered into equation (5) to obtain an estimate of BNC for each voxel.

2.5 Data analysis

To identify common large-scale networks, group mean ICA spatial maps were correlated with published ICA templates (Shirer et al., 2012). Thresholded spatial maps for each ICA component were created by overlaying the top 70% of all voxels onto the single-subject structural MRI image in SPM8 (http://www.fil.ion.ucl.ac.uk/spm/).

BNC was calculated as above using GIFT ICA output and voxel time series. Values were averaged across subjects and the results projected onto the PALS-B12 group cortical surface rendering using Caret5 (Van Essen, 2005; Van Essen et al., 2001). Additionally, to determine the significance of individual voxels, BNC values were converted into z-scores and then entered into a one-sample t-test for group-level analysis in SPM8. Whole-brain spatial maps of BNC were thresholded at p < 0.01, FDR corrected (Benjamini and Hochberg, 1995), and projected onto the PALS-B12 group cortical surface rendering using Caret5 (Van Essen, 2005; Van Essen et al., 2001).

The pattern of higher-level connectivity for select locations within the brain were displayed as weighted and unweighted bipartite graphs using Statistical Parametric Networks (Ginestet and Simmons, 2011). In this display, anatomical locations are displayed as red circles within silhouettes of a brain from three viewpoints (“glass brains”). Each line represents a correlation between a node representing anatomical point within the brain and a node representing an ICA network. Since the ICA networks are de-localized entities, they are displayed as purple circles above the brain. Correlations between the response and predictor variables in equation (2) were converted to z-scores, tested against a Bonferroni-corrected threshold of 0.001 and projected onto glass brain silhouettes of saggital, coronal and axial sections.

The relationship between BNC and cytology was tested using commonly observed cytoarchitectural gradients, based on gradual laminar differentiation between adjacent regions (Flynn, 1999; Vogt, 2009). This technique was necessary since current anatomical atlases used in fMRI either are not based on cytology, or currently do not include paralimbic regions. Cingulate subregions were identified using the method detailed by Vogt (Vogt, 2009). Six point locations within paralimbic regions were chosen based on their proximity to macroscopic landmarks such as the marginal ramus, parietal-occipital sulcus, cingulate sulci, and gyri of the insula. Cingulate subregions and associated cytology were determined using a template of the cingulate with these landmarks (Vogt, 2009). Locations were displayed on the T1 template provided in SPM with traced sulci. BNC was tested by constructing a gradient vector running from agranular subregions (insula & anterior cingulate cortex) or dysgranular subregion (posterior cingulate cortex), to the neighboring granular subregion. BNC was calculated along this line and correlated with distance from the agranular/dysgranular end for each subject. Results were transformed into Fischer-transformed into z-scores, scaled to standard error, and z-tested with a direction determined by the cytological gradient.

3. Results

3.1 Identifying large-scale networks within the brain

We first identified large-scale networks within the brain using resting-state fMRI in 27 subjects. fMRI was chosen for its ability to measure connectivity throughout the entire brain with good spatial resolution. Independent Components Analysis (ICA) was chosen for spatial separation of large-scale networks, because it is data-driven and does not rely on the selection of seed-regions or a predetermined grey matter atlas. Twenty-seven non-artifactual components were identified with spatial distributions corresponding to known large-scale networks (Greicius et al., 2003; Shirer et al., 2012). These included sensorimotor, visual, auditory, executive function, and salience processing networks (Supplementary Figure 1). The Default Mode Network, a network associated with introspection and prominent when subjects are not engaged in a task (Greicius et al., 2003), was divided into ventral, anterior and posterior components (vDMN, aDMN, and pDMN respectively).

3.2 Measuring Between-Network Connectivity at each point in the brain

After large-scale networks were identified, we devised a measure that identifies areas within the brain where the network’s patterns of activity converge. Voxel-specific Between-Network Connectivity (BNC) quantifies how widespread a voxel’s connections are distributed among the large-scale networks. BNC is the amount of redundant information in a multiple regression analysis of a single voxel and the large-scale networks. It is the sum of squared correlations between a voxel and every large-scale network, minus the explained variance of the regression model (see section 2.4 for a detailed explanation).

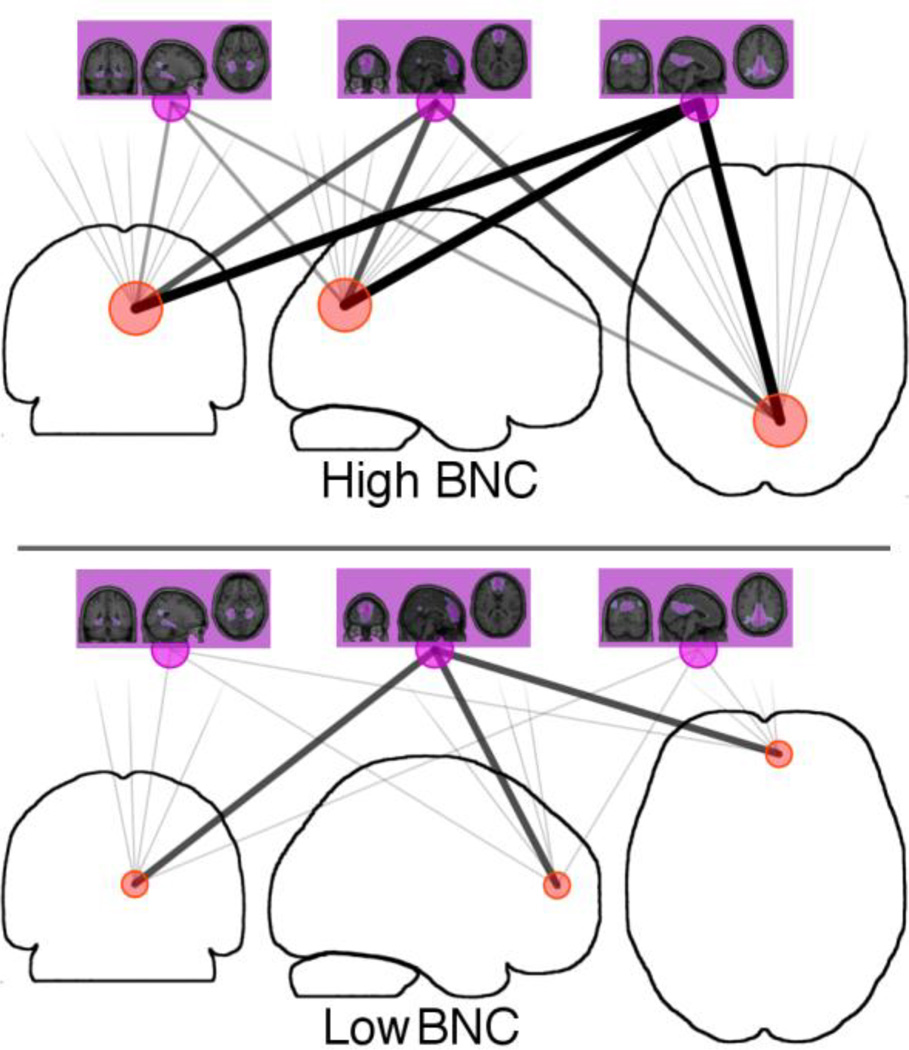
Descriptively, a voxel with high BNC will have many connections of varying strengths, to many large-scale networks (Figure 1). This indicates a point within the brain where the signals of many networks converge, potentially allowing for them to mix together. In contrast, a voxel with low BNC will have only weak connections to the large-scale networks, or will only be associated with a single network. This indicates a point within the brain that is only processing information related to a single network, or at most a small number of networks.

Figure 1.

Measuring voxel-specific Between-Network Connectivity (BNC) using ICA. Each voxel within the brain (red circles) is correlated with (grey lines) each a large-scale network (purple circles and associated spatial maps from Figure 1). Top: Voxels with strong connections to many higher-level networks can mediate information exchange between these networks. These voxels will have high BNC. Bottom: Voxels with a strong connection to a single larger network and weak connections to other networks will have a low BNC.

3.3 Mapping between-network connectivity throughout the brain

Mean BNC values for each voxel ranged from 0 to 0.047. The lower bound of the BNC measure is expected to be 0, corresponding to a voxel that is connected to a single independent network. The upper bound of BNC is 1, corresponding to a voxel that is strongly connected to all correlated networks. Individual subject values ranged from −0.01 to +0.13. Negative values in individual subjects were rare, scattered throughout white matter and cerebral spinal fluid, and inconsistently located across subjects (Supplementary Figures 2–8).

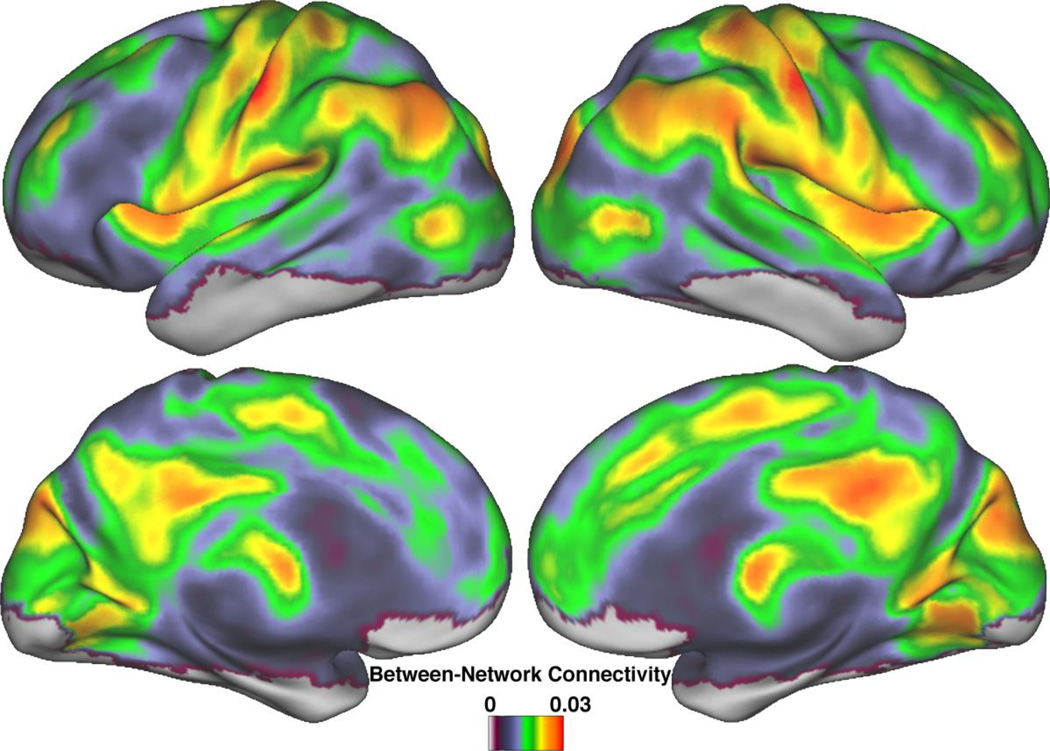
A whole-brain map of BNC averaged across subjects revealed local peaks around discrete cortical regions (Figure 2). Most areas of high BNC were bilateral, including the post-central gyrus, parietal operculum, inferior parietal region, dorsal posterior cingulate cortex, and anterior insula. Lateralized areas of high BNC were all on the right side and included the temporoparietal junction, posterior bank of the post-central sulcus, and the cuneus. The only subcortical region with high BNC was the anterior thalamus.

Figure 2.

Between-Network Connectivity throughout the brain. Local peaks of high BNC are found throughout the cortex. Association areas such as the insula and parietal lobes are especially prominent, as are areas of the DMN, such as the dorsal posterior cingulate and left inferior parietal cortices. Shown are BNC values for each voxel averaged across subjects, prior to statistical testing.

Paralimbic areas with high BNC were located bilaterally in areas with agranular or dysgranular cytology. The agranular insula showed bilateral clusters of high BNC. Similarly, within the posterior cingulate cortex, bilateral clusters of high BNC were located anteriorly and superiorly in dysgranular regions of the cortex. In contrast, no granular paralimbic subregion showed high BNC.

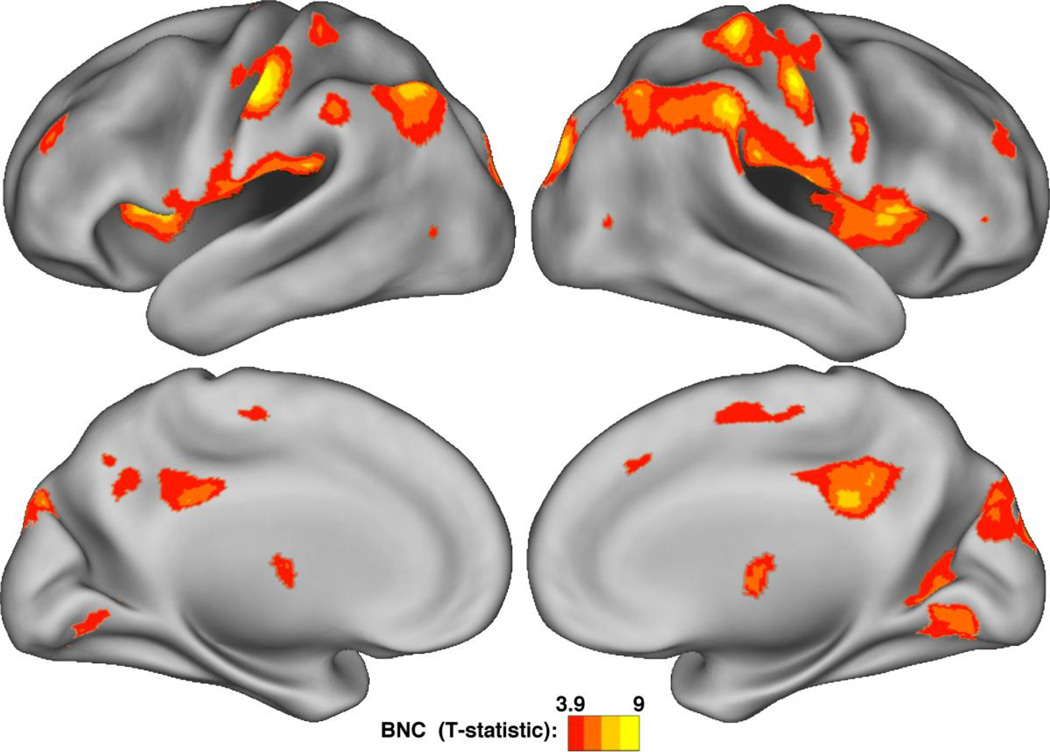
To identify clusters of statistically significant inter-network connectivity throughout the entire brain, we constructed a whole-brain map of BNC for each subject and entered the results into a t-test, thresholded at p < 0.01 (FDR corrected, (Benjamini and Hochberg, 1995). The results demonstrated a close between T-values and mean BNC values for all voxels (r=0.95, Supplementary Figure 9). Voxels with significant BNC clustered in discrete regions of the cortex (Figure 3), in a pattern similar to the local peaks of mean BNC values (Figure 2).

Figure 3.

Clusters of significant Between-Network Connectivity. Statistically significant clusters of high BNC are centered around local peaks of high BNC (Figure 2), including the insula, inferior parietal lobes, and the dorsal posterior cingulate. All voxels p < 0.01 by a one-sample t-test, FDR corrected.

3.4 Between-Network Connectivity within paralimbic regions

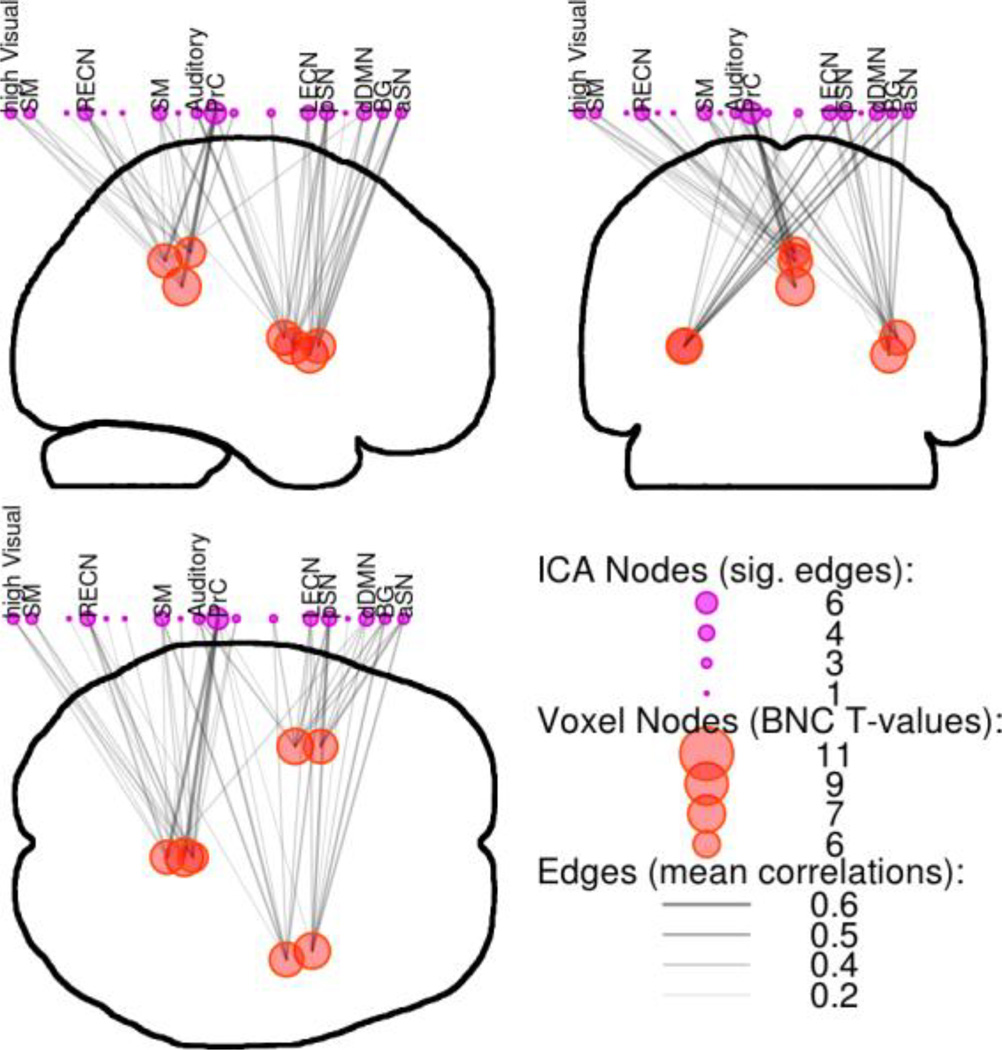
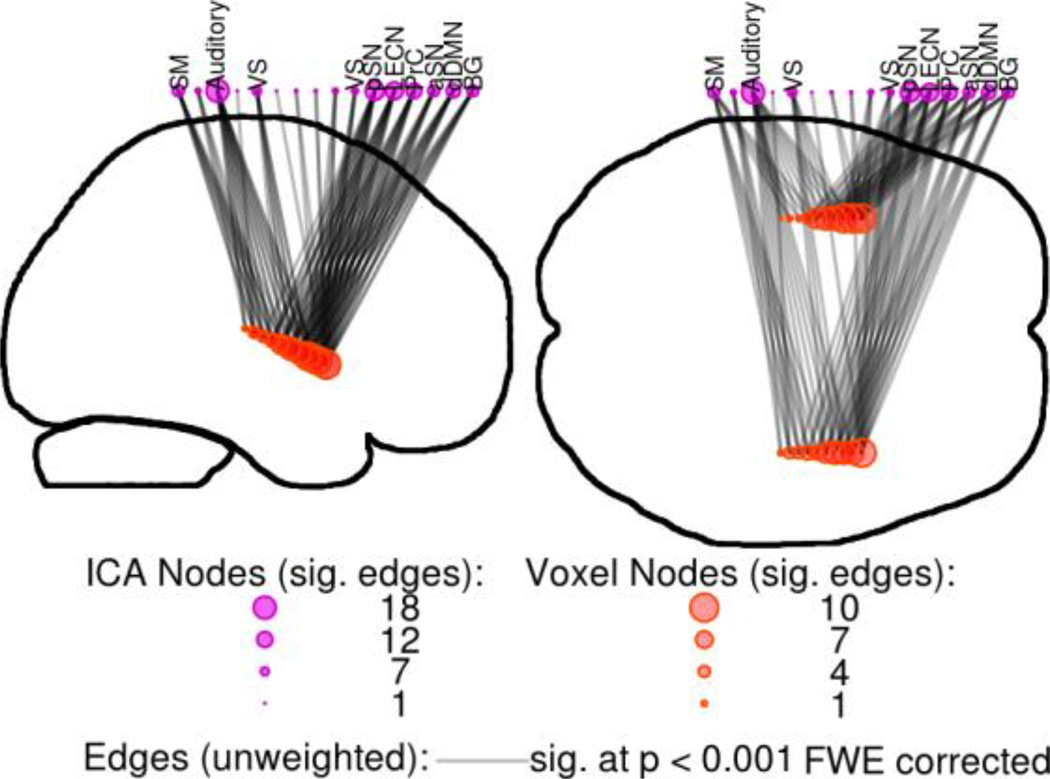
BNC identified three clusters of high inter-network connectivity within the paralimbic regions (Figure 4). The first was within the dorsal posterior cingulate cortex (PCC) and located along the midline and just above the splenium of the corpus collosum. Two other clusters of high BNC were located in the anterior insula, approximately located in the short gyri. As expected, each peak location within the clusters connected to many large-scale networks that spanned a wide variety of processing modalities. Even at the robust statistical threshold of p < 0.001 Bonferroni-corrected, the total connectivity of these few points spanned most of the networks identified with ICA (Figure 4). No clusters of high BNC were located within the anterior cingulate gyrus.

Figure 4.

Between-Network Connectivity within paralimbic regions. Voxels with high BNC had many strong connections to many networks. Shown are the top voxels (red circles) from clusters of BNC within paralimbic regions, along with their significant connections (edges: grey lines, sig. at p < 0.001 Bonferroni-corrected) to large-scale networks (purple circles). SM=Sensorimotor, RECN & LECN=Right & Left Executive Control Networks, PrC=Precuneus network, aSN & pSN=anterior & posterior Salience Networks, dDMN=dorsal Default Mode Network, BG=Basal Ganglia network.

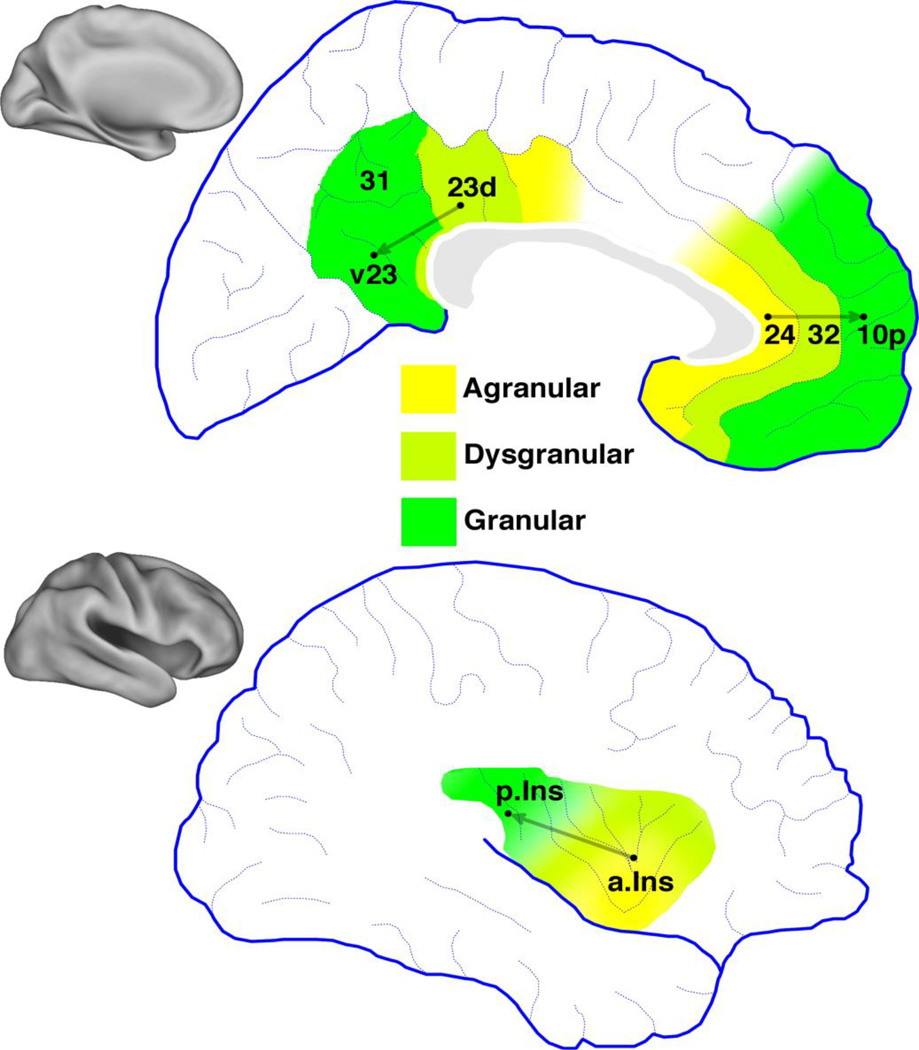
We hypothesized that Between-Network Connectivity within paralimbic regions would be associated with agranular or dysgranular cytoarchitecture. To test this, we measured voxel BNC values within paralimbic regions and compared the results to known regional differences in cytology. Six locations were selected based on recognizable anatomical landmarks (Figure 5, labeled black dots). Within the dorsal posterior cingulate gyrus, we selected one point location from dysgranular subregion 23d, and a point from granular ventral subregion v23 (Vogt, 2009). Within the pregenual anterior cingulate gyrus, we selected a point from agranular subregion 24 and a point from granular subregion 10p (Ongür et al., 2003). Within the insula, we selected a point in the agranular anterior insula, located in the short gyri, and a point in the posterior granular insula, located near the end of the long gyri (Flynn, 1999). For each of these paralimbic regions, a conceptual line can be drawn that begins in the agranular or dysgranular subregion and ends in a granular subregion (Figure 5). Based on hypothesis, we predicted that distance along this line would negatively correlate with BNC for each voxel. To test this hypothesis, BNC along each line was extracted for each subject and entered into a one-way t-test with a threshold of p < 0.05 (Table 1).

Figure 5.

Cytology of paralimbic regions. Each has subregions with granular, agranular, or dysgranular cytologies depending the presence, absence, or inconsistent presence of cortical layer IV. Labels are based on the numbers assigned to Brodmann’s Areas (Ongür et al., 2003; Vogt, 2009). Posterior cingulate cortex includes dorsal and ventral subregions of Brodmann’s area 23, dysgranular region 23d and ventral region v23. The pregenual anterior cingulate cortex includes agranular region 24, dysgranular region 32, and granular region 10p. The insula is divided into an agranular anteroventral subregion, a posterodorsal granular, and a dysgranular transition zone between these two poles (Flynn, 1999). Grey vectors represent cytoarchitectural gradients running between subregions.

Table 1.

Paralimbic cytology compared to BNC along cytoarchitectural gradients. Regions included the posterior cingulate cortex (PCC, Vogt, 2009), pregenual anterior cingulate (pACC, Ongür et al., 2003; Vogt, 2009), and insula (Kurth et al., 2010; Ongür et al., 2003). For each region, a vector was drawn running from agranular to dysgranular to granular subregions. BNC was correlated with distance from the agranular/dysgranular end. We predicted that BNC would negatively correlate along this line. Statistics reported as Z-scores ± standard error, n.s. = non-significant.

		MNI coordinates:
Area:	Region:	x:	y:	z:	Cytology:	Statistic:	P-value:
L. PCC	23d	−6	−34	40	dysgranular
	v23	−6	−52	25	granular	Z = −2.62 (±0.2)	p = 0.004
R. PCC	23d	6	−34	40	dysgranular
	v23	6	−52	25	granular	Z = −2.48 (±0.2)	p = 0.006
L. pACC	24	−6	38	10	agranular
	10p	−6	56	10	granular	Z = 0.03 (±0.2)	n.s.
R. pACC	24	6	38	10	agranular
	10p	6	56	20	granular	Z = 0.82 (±0.2)	n.s.
L. Insula	Iai	−39	11	−2	agranular
	Ig2	−39	−16	10	granular	Z = −2.17 (±0.2)	p = 0.015
R. Insula	Iai	39	11	−2	agranular
	Ig2	39	−16	10	granular	Z = −2.92 (±0.2)	p = 0.002

The results supported the hypothesis for most areas tested. BNC significantly decreased along the cytoarchitectual gradient bilaterally in the PCC (z-score ± standard error, left: Z = −2.62 ± 0.2, p < 0.005, right: Z = −2.48 ± 0.2, p < 0.01) and insula (z-score ± standard error, left: Z = −2.17 ± 0.2, p < 0.05, right: Z = −2.92 ± 0.2, p < 0.005). Within the pregenual anterior cingulate cortex, however, results were not significant.

Visual inspection of higher-level connectivity along these gradients supported these results (Figure 6). Locations nearer to the agranular anterior insula were associated with many robust connections to many large-scale networks including the dDMN, anterior Salience network (aSN), and left Executive Control Network (LECN). Locations nearer to the granular posterior insula were associated with only a few networks, primarily the Sensorimotor (SM) and Auditory networks. The total number of significant connections was greatest near the anterior insula, and decreased steadily in the posterior direction, and was minimal within the posterior insula. Similar results were obtained for cytoarchitectural gradients with the PCC. The dysgranular dorsal PCC showed the greatest amount of connectivity to large-scale networks, while the granular ventral PCC was associated with a few networks. In both paralimbic regions, high BNC was associated with subregions featuring agranular or dysgranular cytoarchitecture.

Figure 6.

Points along a cytoarchitectural gradient within the insula and their correlations to large-scale networks. Anterior voxels (red circles) had many connections (edges, grey lines) to a wide variety of networks (purple circles). In contrast, posterior voxels were only connected to a few networks. All edges p < 0.001 Bonferroni-corrected. See Figure 4 caption for abbreviations.

4. Discussion

This study revealed a relationship between the cytology of paralimbic regions and their ability to connect across, and potentially integrate information between large-scale networks. As hypothesized, agranular or dysgranular paralimbic subregions, with absent or reduced layer IV, were identified as integration areas. We also have introduced a new data-driven approach for measuring inter-network connectivity, BNC, which takes advantage of the full spatial resolution provided by fMRI. This method identifies integration areas within the brain that have high inter-network connectivity, and associated with cytoarchitectural gradients and subregions.

4.1 Between-Network Connectivity and multimodal connectivity

Whole-brain BNC (Figure 2) both agrees with and complements previous reports of connectivity within the brain. Many areas of high BNC were previously associated with high total connectivity or identified as multimodal integration areas. These include the PCC, temporoparietal junction, inferior parietal lobe, anterior insula, and thalamus (Buckner et al., 2009; Cole et al., 2010; Sepulcre et al., 2012). Parts of the postcentral gyrus and the medial cuneus demonstrated a high BNC but were not previously identified as multimodal integration areas (Sepulcre et al., 2012). Based on this observation, these subregions may combine unimodal sensory processing with processing in other systems.

Areas previously identified as connector hubs also showed BNC (He et al., 2009; Valencia et al., 2009). However, the reverse is not always true. The thalamus and temporoparietal junction have been identified as connector hubs in some (Valencia et al., 2009) but not all studies (He et al., 2009), possibly due to differing anatomical resolution. Lastly, most rich-club hubs such as the PCC, paracentral lobule, and parietal lobes, were associated with high BNC (Hagmann et al., 2008; van den Heuvel and Sporns, 2011). However, other regions such as the insula, cuneus and fusiform gyri, are instead part of the “extended rich-club” identified using a high-resolution network (van den Heuvel and Sporns, 2011).

4.2 Microscale cytoarchitecture and macroscale network architecture

Neural connectivity between distinct cortical layers has been used to distinguish feedforward from feedback projections within the primate visual system, and consequently identify a processing hierarchy based on cytoarchitectural connectivity (Felleman and Van Essen, 1991). Paralimbic and multimodal processing regions were fit into this hierarchical model with difficulty. Based on the regions they are connected to paralimbic regions were placed near the top of this hierarchy. However, the observed laminar pattern of afferent and efferent connectivity, which defined positions of other areas within this hierarchy, would have placed paralimbic regions at a lower level. Subsequent investigations in primate prefrontal cortices and the cat visual suggested that cytoarchitectural differences and the distance between pairs of regions predicted their connectivity, rather than their relative position in a processing hierarchy (Barbas and Rempel-Clower, 1997; Beul et al., 2014; Hilgetag and Grant, 2010).

Mesulam (Mesulam, 1998) proposed a more general hierarchy based on converging lines of distributed, parallel processing systems. Although not based on cytological criteria, the organization of neurons into layers was most prominent in specialized sensory regions at the periphery of the hierarchy and progressively decreased, as processing lines converged, into paralimbic regions at the core. Further investigations into cytology and connectivity within the cat brain confirmed many features of this model, demonstrating that rich-club hubs have low cytological differentiation with dysgranular or agranular cytologies, such as in paralimbic regions (Beul et al., 2014; Zamora-López et al., 2011). However, why these zones of converging macroscale connectivity feature relatively undifferentiated microscale cytoarchitecture is unknown.

4.3 Inter-network connectivity is related to cortical circuitry

Inter-network connectivity within paralimbic subregions was associated with agranular or dysgranular subregions. This cytological classification is based on the granular appearance of neurons in cortical layer IV. Granular subregions have a fully developed layer IV. Agranular subregions lack layer IV, and dysgranular subregions are intermediate between these states. This layer is notable for several reasons, including its importance for thalamocortical input to the cortex.

Thalamic input to the cortex may be especially important for generating and stabilizing the large-scale networks (Doria et al., 2010; Edelman and Gally, 2013; Sporns, 2011). During development, large-scale networks emerge at the same time as thalamocortical projections (Doria et al., 2010). Thalamic stimulation projecting to layer IV results in patterns of cortical activity that is indistinguishable from spontaneously arising cortical activity (MacLean et al., 2005). This thalamic input is capable of activating the same underlying cortical circuitry that generates intrinsic activity, including the large-scale networks.

Afferent thalamic connections to layer IV have several distinguishing features. They are the main source of primary sensory input to the cortex (Wang et al., 2013). They act to synchronize and stabilize the dynamics of widespread cortical regions (Chawla et al., 2001). Input to cortical layer IV functions as driving input, strongly affecting cortical activity (Lee and Sherman, 2008). In contrast, modulatory input to superficial and deeper cortical layers shows a weak but prolonged effect (Sherman and Guillery, 1998). Lastly, thalamocortical input to layer IV forms part of feed-forward reentry circuits between the cortex and thalamus (Shipp, 2005). In these reentry circuits, a single pattern of input activity dominates in a winner-take-all manner (Douglas and Martin, 2004).

The synchronizing, driving input with exclusive dynamics, characteristic of afferent connections to cortical layer IV, generates and stabilizes large-scale networks (Chawla et al., 2001; Sherman and Guillery, 2011; Wang et al., 2013). However, this same circuitry may create barriers to integrating and exchanging information between these networks. The driving nature of layer IV input creates strong competition between patterns of activity. Simultaneously, winner-take-all dynamics prevent multiple patterns of intrinsic activity from accessing the same circuitry. This reasoning offers a plausible interpretation of the present observation that this driving circuitry is absent or modified within the regions of the cortex specialized for high inter-network connectivity, such as integration areas. In essence, by relaxing the winner-take-all competition between patterns of intrinsic activity created by this driving input, integration areas may be better able to mix together and evaluate the incoming signals associated with large-scale networks. This absence may allow other forms of afferent input to take precedence, possibly including modulatory input.

4.4 Conculsions

In summary, this study describes a novel, data-driven method, BNC, which uses ICA to identify areas within the brain where activity from many large-scale networks converge. This study extends prior work on the location of potential multimodal integration areas, such as rich-club hubs, which evaluate information from multiple processing systems. Additionally, this work supports an observed relationship between rich-club hubs and cytological differentiation, by demonstrating that paralimbic subregions with high BNC feature agranular or dysgranular cytology. These subregions lack cortical layer IV, with its strongly competitive and exclusive characteristics. An absence of the driving thalamocortical input to this layer may facilitate the mixing of incoming signals from throughout the brain. These findings advance our understanding of the functional organization of the brain by demonstrating that the ability to potentially integrate information on large scales is reflected in microscopic circuitry.

Highlights.

• Integration areas mediate information exchange between large-scale networks

• This paper describes a novel data-driven method to identify integration areas

• Paralimbic integration areas are associated with agranular cytoarchitecture