A noninvasive method for coronary artery diseases diagnosis using a clinically-interpretable fuzzy rule-based system

Abstract

Background:

Coronary heart diseases/coronary artery diseases (CHDs/CAD), the most common form of cardiovascular disease (CVD), are a major cause for death and disability in developing/developed countries. CAD risk factors could be detected by physicians to prevent the CAD occurrence in the near future. Invasive coronary angiography, a current diagnosis method, is costly and associated with morbidity and mortality in CAD patients. The aim of this study was to design a computer-based noninvasive CAD diagnosis system with clinically interpretable rules.

Materials and Methods:

In this study, the Cleveland CAD dataset from the University of California UCI (Irvine) was used. The interval-scale variables were discretized, with cut points taken from the literature. A fuzzy rule-based system was then formulated based on a neuro-fuzzy classifier (NFC) whose learning procedure was speeded up by the scaled conjugate gradient algorithm. Two feature selection (FS) methods, multiple logistic regression (MLR) and sequential FS, were used to reduce the required attributes. The performance of the NFC (without/with FS) was then assessed in a hold-out validation framework. Further cross-validation was performed on the best classifier.

Results:

In this dataset, 16 complete attributes along with the binary CHD diagnosis (gold standard) for 272 subjects (68% male) were analyzed. MLR + NFC showed the best performance. Its overall sensitivity, specificity, accuracy, type I error (α) and statistical power were 79%, 89%, 84%, 0.1 and 79%, respectively. The selected features were “age and ST/heart rate slope categories,” “exercise-induced angina status,” fluoroscopy, and thallium-201 stress scintigraphy results.

Conclusion:

The proposed method showed “substantial agreement” with the gold standard. This algorithm is thus, a promising tool for screening CAD patients.

INTRODUCTION

Coronary heart disease also known as coronary artery disease (CAD) is a chronic disease in which the coronary arteries, responsible for transporting oxygenated blood to heart muscles, get narrowed and are not able to convey enough fresh blood to this blood-pumping organ.[1,2] Narrowing of blood vessels is usually due to arteriosclerosis, a common arterial disease in which increased areas of degeneration and cholesterol (CHOL) deposit plaques form on the inner surfaces of the arteries blocking blood flow.[3,4] In case of reduced blood supply, the heart does not receive enough oxygen and nutrition to operate properly resulting in angina pectoris and heart attack. The symptomatic or asymptomatic reduction in coronary artery flow, may occur with exercise or at rest, and may end up with a myocardial infarction, depending on the severity of obstruction and the speed of its development.[5,6] CAD, the most common form of cardiovascular disease (CVD), has the prevalence of 6.9% in men and 6% in women.[7]

Despite the background of increasing health care expenses, CAD has a significant influence on global economics as a principal cause of disability and loss of efficiency.[8] CAD is a major cause of death and disability in developed countries. Although CAD mortality rates have dropped over the past four decades, CAD remains responsible for about one-third of all deaths in people over age 35.[6,7,9]

According to the World Health Organization, more than 60% of the global burden of the CAD occurs in developing countries.[10] CAD is the leading cause of death worldwide: 3.8 million men and 3.4 million women each year.[11] Overall, the prevalence of CAD in Iran (≥20 years old) was reported within 1.1-36.0% in different studies.[12] The age-adjusted (≥30 years old) prevalence of CAD was reported as 21.8% (22.3% in women and 18.8% in men) in Tehran, Iran.[13] The prevalence of CAD among people aged 35-79 years was reported to be 19.4% (21.9% in women and 16.0% in men) in an urban population in Isfahan, Iran.[14] Over the past decade, new scientific evidence strongly supporting the role of preventive interventions in the maintenance of health has focused much needed attention and efforts on cardiovascular prevention.[15] Thus, the prevention of CAD is a major goal and has been focused on many international health programs.

Coronary heart disease risk assessment could be detected by the physicians to predict the CAD occurrence in the near future to control its progress in patients.[16] One of the methods of CAD risk assessment is the investigation of its risk factors.[4,17] Hypertension, high levels of low-density lipoprotein cholesterol (LDL-C), low levels of high-density lipoprotein cholesterol (HDL-C), high total cholesterol, high triglycerides, diabetes mellitus, smoking, obesity, aging, gender, physical inactivity, age, socioeconomic and psychological stress, family history of CAD, and various genetic factors[8,18,19,20] are some of the CAD risk factors reported in the literature. A variety of meta-analysis studies have been performed on other CAD risk factors. For example, it was shown that depression,[21] job strain,[22] anxiety,[23] a diet poor in fruit and vegetable[24] and frequent fried-food consumption[25] significantly increase the risk of CAD.

Medical diagnosis is a difficult and complex task, and computer-aided diagnosis systems are technologies designed to decrease observational oversight.[26] A computer-aided diagnosis would be desirable for performing the classification and decision procedures since the computers can store large amount of data without distortion over long periods of time while performing complex logical and mathematical operations at very high speed.[27,28] Computer-based medical diagnosis systems have been promoted for their potential to improve the quality of health care, including their application to support and improve clinical decisions.[29,30]

Computer-aided medical diagnosis is usually performed via classification, also known as “supervised learning.” In machine learning, “classification” is the problem of identifying to which category (class) a new observation belongs, based on a training set containing observations (features) whose category membership is known (gold standard).[31] A large number of classifiers have been proposed in the literature. Most of them use a black-box modeling approach without paying attention to the underlying mechanisms.[32] Examples of these classifiers are linear and quadratic discriminant analysis, support vector machines, k-nearest neighbors, Naïve Bayesian classifier. Accordingly, these classifiers cannot be clinically interpreted which is not desirable in clinical applications.[33] Rule-based classification systems such as the decision tree and its variants, on the other hand, can provide interpretable classification rules.[34,35]

The medical knowledge and the resulting diagnosis are pervaded by uncertainty. Fuzzy set theory on the other hand was conceived with the formalization of the vague knowledge.[36,37] It is very difficult to define sharp borders between various symptoms and diseases. Thus, the framework of the fuzzy system is very useful to deal with the absence of sharp boundaries of the sets of symptoms, diagnosis, and phenomena of diseases.[38,39] Also, fuzzy logic is a useful tool for building expert systems for decisionmaking in the field of medical diagnosis.[40] Accordingly, fuzzy rule-based classification systems are now quite popular in the field of medical diagnosis.[41,42,43] These systems create clinically interpretable rules that take into account the overlap between different diagnosis classes. Therefore, these systems are proved to have better performance in comparison with that of crisp rule-based systems (such as decision tree).[44,45]

In this paper, a fuzzy rule-based system was designed to diagnose CAD based on a limited set of features recorded noninvasively in a case-control study. The rest of the paper is organized as follow: Information about the study population, recorded features, and the data mining methodology is given in the next section. Then, the results of the classification and the extracted rules are reported in the “results” section and finally, the discussion about the clinical validity of the proposed system and the comparison with other classifiers will be provided in the “discussion” section.

MATERIALS AND METHODS

Experimental methods

In this work, the CAD dataset from the University of California (UCI, Irvine), which is available online (https://archive.ics.uci.edu/ml/datasets/Heart+Disease), taken from the Cleveland Clinic Foundation datasets, is used for training and testing the proposed system.[46,47,48,49] This dataset has been considered as a benchmark for various computer-aided CAD diagnosis systems.[50] This database consisted of 303 records with 76 attributes (features).

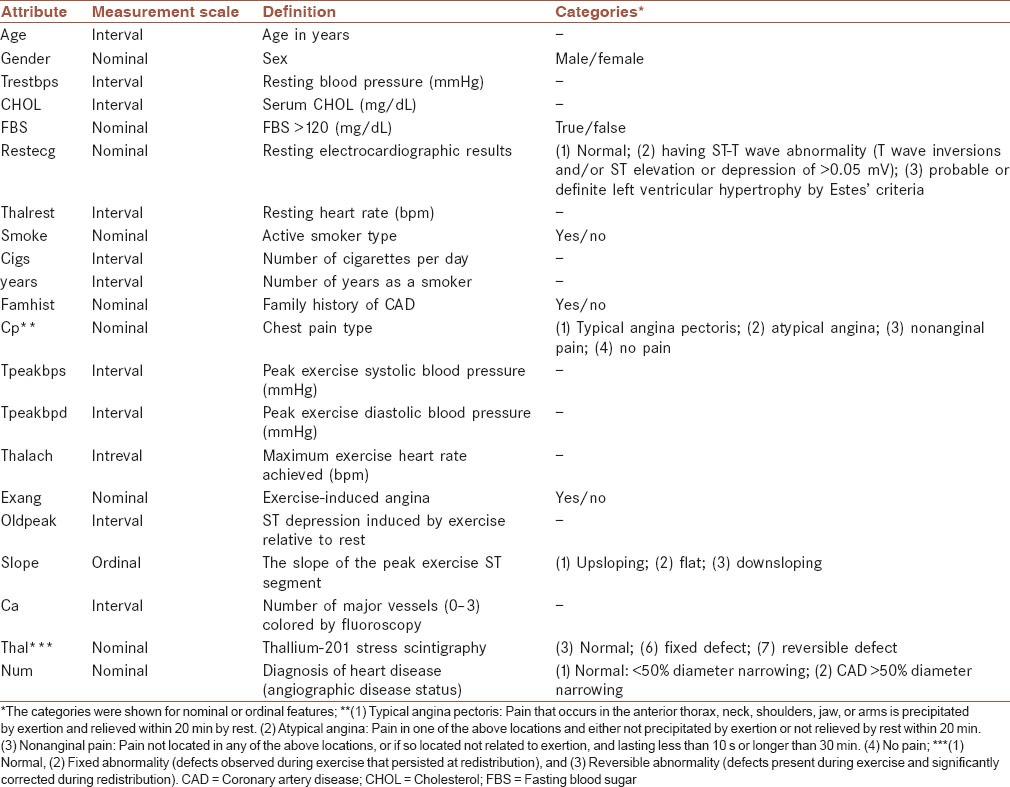
The experimental protocol can be found elsewhere in details.[47,51] However, it is briefly mentioned as follows. A number of 303 consecutive patients referred for coronary angiography at the Cleveland Clinic between May 1981 and September 1984 participated in the experiment. No patient had a history or electrocardiographic evidence of prior myocardial infarction or known valvular or cardiomyopathic diseases. The following attributes were collected: Age, gender, resting blood pressure (trestbps), CHOL, fasting blood sugar (FBS), resting electrocardiographic results (restecg), active smoker type, number of cigarettes per day, number of years as a smoker, family history of CAD (famhist), chest pain type (cp). In addition, patients underwent 3 noninvasive tests as part of a research protocol. The results of these tests (exercise electrocardiogram, thallium scintigraphy and cardiac fluoroscopy) were not interpreted until after the invasive gold standard test (coronary angiograms) had been read. The CAD status was considered when narrowing of at least one of the coronary arteries was more than 50%, shown by angiography.[52] The definition of attributes, their measurement scales and categories in the raw dataset were listed in Table 1.

Table 1.

The attributes of the raw Cleveland CAD dataset

Preprocessing

In our study, discretization was used on the attribute intervals. In machine learning, discretization refers to the process of converting or partitioning continuous attributes to discretized variables. Discretization is typically used as a preprocessing step for machine learning algorithms because it can significantly impact the performance of classification algorithms used for data analysis.[53,54] Discretization is a technique to find cut points to partition the range into a small number of intervals by maintaining good class consistency.[55,56,57] We used a set of cut points taken from the literature, indicating the diagnosis properties of individual attributes as below to create ordinal-scale variables:

1. “age:” “Young adult” (18-35 years old), “middle-aged adults” (36-55 years old), and “older adults” (older than 55 years old);[58]

2. “CHOL:” “Desirable” (<200 mg/dL), “borderline high” (200-239 mg/dL) and “high” (≥240 mg/dL);[17]

3. “Trestbps:” “Low” (90-100 mmHg), “normal” (100-120 mmHg), “prehypertension” (120-139 mmHg), “stage 1 hypertension” (140-159 mmHg) and “stage 2 hypertension” (≥60 mmHg);[59]

4. “Cigs:” Five categories 0, 1-9, 10-19, 20-39, and ≥40;[60]

5. “Thalrest:” The following categories were extracted (“excel’t,” “good,” “above av,” “average,” “below av” and “poor”) based on resting heart rate (HR) chart considering gender, age and resting HR;[61]

6. “Oldpeak” and “thalach:” The ST depression was divided by the maximum exercise HR (ST/HR slope), also known as HR adjustment of exercise-induced ST segment depression.[62,63] Then, the cut points of 0.01 and 0.02 μV/beat/min were used to derive three ordinal classes: “low,” “medium” and “high.”

Fuzzy rule-based system

Rule generation includes both rule extraction and refinement. One of the methods for extracting rules from the input-out data is neuro-fuzzy rule generation.[64,65] It combines the powerful description of fuzzy classification techniques with the learning capabilities of Neural Networks. In the neuro-fuzzy classification methods, the feature space is partitioned into multiple fuzzy subspaces that are controlled by fuzzy if-then rules. For determining an optimum fuzzy region, the parameters of the fuzzy rules should be optimized.[66] The classifier consists of the following layers: Fuzzy membership, fuzzification, defuzzification, normalization and output.[67] The K-means clustering method was used to obtain the initial parameters and to formulate the fuzzy if-then rules.[65]

A fuzzy classification rule Ri, which describes the relation between the input feature space and the classes, can be defined as follows:

Ri: If x_p1 is Ф_il and … and x_pj is Ф_ij and R and x_pn is Ф_in then class is out_k.

where xpj is the j^th feature of the p^th sample, outk is the k^th class label, and Ф_ij is the fuzzy set of the j^th feature in the i^th rule.[67,68] In the neuro-fuzzy method used in this study, scaled conjugate gradient (SCG) algorithm was used to speed up the learning procedure in which the parameters of the Takagi–Sugeno–Kang fuzzy inference system (FIS) were tuned in the training set by shortening the training time per iteration. This method was referred to as neuro-fuzzy classifier (NFC) in this manuscript. In this FIS, “and,” “or,” “implication” from the antecedent to the consequent and “aggregation” of the consequents across the rules operators were product, probabilistic or “probor” (algebraic sum), minimum and maximum. Weighted defuzzification was also used. Note that Probor (x, y) = x + y−x × y.

Feature selection

In many classification problems, a lot of candidate attributes are used for problem representation. Many of these are usually irrelevant or redundant.[69] Thus, feature selection (FS) is used to detect relevant features usually leading to an increase in classifier accuracy.[70] In this work, two supervised FS methodologies were used: (1) A statistical FS method, multiple logistic regression (MLR),[71] and (2) a deterministic FS approach, sequential FS (SFS).[72] MLR, known as feature vector machine in machine learning, can be used to select statistically significant features.[73] In our study, the intercept point was not used in the MLR. In SFS, the classifier starts with an empty set and added features until the accuracy was no longer improved by adding more features.

Validation

The performance of the classifier was assessed using the “hold-out” method, an approach to out-of-sample evaluation, in which the dataset was randomly split into two equal-size mutually exclusive sets (training and test sets). The classifier was trained on the training set and tested on the test set.[74] The performance measures of the classification are listed in Table 2. The following performance measures were used: Sensitivity (Se), Specificity (Sp), Accuracy (Acc), and Precision (Pr) along with other indices reported in Table 2. Additionally, the McNemar's (Gillick) statistical test was used[75] to compare the performance of the NFC with different configurations (e.g., with or without FS) on the test set. Classification was performed using Matlab, Statistics Toolbox Release 2011a (The MathWorks, Inc., Natick, Massachusetts, USA) and the NFC toolbox.[67,76] All statistical analyses and calculations were performed using the SPSS statistical package, version 18.0 (SPSS Inc., Chicago, IL, USA).

Table 2.

The reported performance measures

RESULTS

The number of subjects analyzed was 272 (68% male) out of total 303 in the Cleveland CAD dataset. The excluding criterion was the existence of missing value in any attribute. The characteristics of the raw dataset in the CAD and normal groups are shown in Table 3.

Table 3.

The attributes of the raw Cleveland dataset for normal and CAD groups, along with their categories (percentage) for nominal/ordinal variables and (minimum-maximum) mean ± SD for interval variables

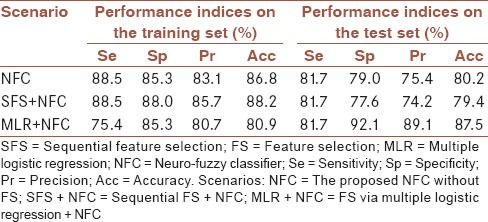
The performance of the NFC without FS, and with SFS/MLR on the preprocessed (discretized) Cleveland CAD dataset is shown in Table 4, in the hold-out validation framework. The feature set selected using SFS was (“thal,” “ST/HR slope,” “cp,” “ca,” “CHOL,” “trestbps,” “restecg,” “sex,” and “famhist”) from which the training accuracy increased from 72.1% to 88.2% during SFS procedure. Adding more features did not increase the accuracy. MLR, on the other hand, proposed the following five features (“age,” “exang,” “ca,” “thal,” and “ST/HR slope”). These features were statistically significant (P < 0.05) when running MLR in “Enter” mode excluding the intercept point in the model. Overall, MLR + NFC outperformed other classifiers in the training and test sets. It also required less input attributes for the decision-making procedure in comparison with those of other tested methods. McNemar's test indicated that the performances of the SFS + NFC and MLR + NFC were higher in the training and test sets, respectively (P < 0.05). Since no tuning was performed in the test set and also because of required input attributes, MLR + NFC was chosen as the best classifier and used for further analysis.

Table 4.

The performance of the proposed NFC without FS, with SFS/MLR in the hold-out validation framework on the training and test sets

The improvement of the classification error for MLR + NFC on the training set is shown in Figure 1. It depicted the fast reduction of root mean square error via SCG in the tuning procedure. The algorithm stopped at the iteration no. 100 since no significant improvement was made during the learning procedure.

Figure 1.

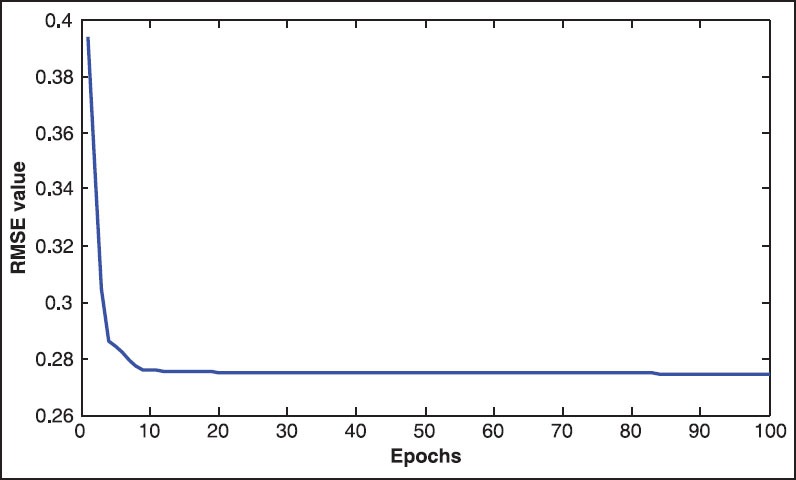
The improvement of the classification error for multiple logistic regression + neuro-fuzzy classifier on the training set versus epochs analyzed

The MLR + NFC method that had been tuned on the training set was tested this time on the whole dataset for overall accuracy assessment. The resulting confusion matrix was shown in Table 5. The overall accuracy of the proposed classifier was 84.2%. Meanwhile, Cohen's kappa coefficient, a statistical measure of inter-rater agreement, was 67.75% (P < 0.05) showing “substantial agreement”[77] between the classifier's outcome and that of coronary angiography.

Table 5.

The overall confusion matrix of the MLR + NFC method*

The proposed fuzzy rule-based system (MLR + NFC) was shown in Figure 2. The system has two fuzzy rules. Each rule was related to an outcome diagnosis class. A diagnosis example was taken from the test set in the fuzzy rules to clarify the decision-making procedure. For a typical subject whose CAD was confirmed with angiography, the discretized attributes were as the following: Older adult age category, Angina was not induced by exercise, two major vessels colored by fluoroscopy, thallium-201 stress scintigraphy test showed reversible defect and ST/HR slope was high. These attributes were used as the input of the fuzzy system. The range of the output is within (0.9, 2.1) with the cut-off value of 1.5 = (0.9 + 2.1)/2. If the output of the fuzzy system is higher or equal than 1.5, the subject has CAD. The output of the fuzzy system (based on the noninvasive tests) is 1.81, in agreement with that result of the gold standard (angiography). The first and second rules in Figure 2 have been extracted for normal and CAD subjects, respectively.

Figure 2.

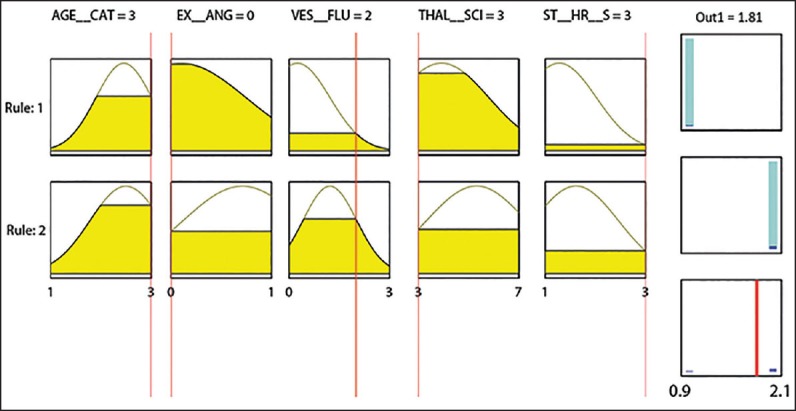
The extracted fuzzy rules from the training set. AGE__CAT: Age category, EX__ANG: Exercise-induced angina, VES_FLU: The number of vessels colored by fluoroscopy, THAL_SCI: Thallium-201 stress scintigraphy category, and ST__HR__S: Heart rate adjustment of exercise-induced ST segment depression category. Fuzzy rules 1 and 2 were related to normal and coronary artery diseases (CAD) classes, respectively. The overall output of the fuzzy system (1.81 in this example), is higher or equal to 1.5 indicating that the subject had CAD that was in agreement with what obtained from the gold standard (angiography). For the description of the input feature categories, refer to the section “preprocessing"

DISCUSSION

Primary prevention, aiming at preventing heart and blood vessel disease in individuals who have not had a heart attack or symptoms of CAD and have no known clinical evidence of CAD, is highly recommended in comparison with secondary prevention for individuals with known CAD. This requires changing the lifestyle by quitting smoking, bringing down high blood pressure, controlling diabetes, maintaining a healthy body weight, doing regular exercises, following a heart-healthy diet to lower CHOL, LDL, and triglycerides, and to raise HDL, reducing stress and Limiting alcohol consumption.[8,78]

It has been suggested to integrate the prediction, prevention and intervention programs of CAD for more effective primary/secondary prevention.[17,79] Invasive coronary angiography is the gold standard for establishing the presence, location, and severity of CAD.[80,81] However, this technique is invasive, costly[81] and associated with a small but definite risk of morbidity (1.5%) and mortality (0.15%).[82,83] Therefore, a convenient, noninvasive alternative method for coronary angiography can provide significant clinical and economic benefits for the public health care system.[84] A number of noninvasive CAD diagnosis methods have been proposed in the literature. Among which, fluoroscopy and stress thallium scintigraphy, are the two most popular. Unfortunately, the diagnostic accuracy of these methods in comparison with that of the gold standard, coronary angiography, ranges between 35% and 75%.[85,86] Thus, the purpose of our work was to design a computer-aided noninvasive CAD diagnosis system using data mining methods to improve the diagnosis accuracy by combining the results of the noninvasive clinical tests and other attributes recorded from the subjects [Table 1].

A number of computer-aided CAD diagnosis systems have been proposed in the literature[47,50,87,88,89,90,91,92,93] whose performance was tested on the Cleveland CAD dataset [Table 6]. Most of them use the black-box mathematical methodology that is not acceptable in medicine where the clinical interpretation of the decision-making procedure is critical. Our proposed fuzzy rule-based system, on the other hand, provided interpretable linguistic terms [Figure 2], which could be regarded as a fuzzy version of the decision tree classifier.[94] For example, the comparison of rule 1 (normal) and rule 2 (CAD) in Figure 2 shows that the higher the ST/HR slope, and age, the higher the risk of CAD. Also, angina induced by exercise increases the risk of having CAD. Also, the last two categories of thallium-201 stress scintigraphy test (fixed and reversible defects) have higher CAD risk. The above rules are clinically acceptable. However, number of major vessels colored by fluoroscopy had a medium effect on the CAD diagnosis that could be due to the small sample size of the study population. It might be related to the fact that the sensitivity of fluoroscopy could be as low as 35% in some cases,[86] and the system learned it from the training set. Meanwhile, the proposed system (MLR + NFC) only requires five input attributes for the diagnosis that is less than what has been proposed in the literature. Smaller number of required attributes facilitates the diagnosis procedure.

Table 6.

Comparison of the proposed system outcome with similar research

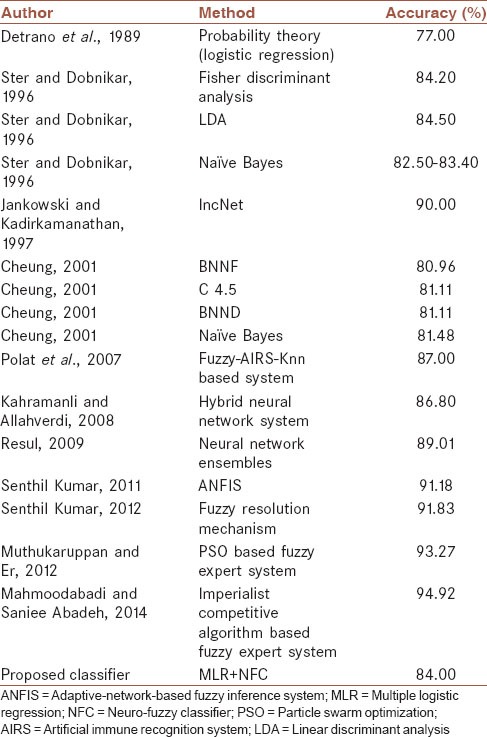
The overall accuracy of the proposed FIS (MLR + NFC) was 84% [Table 5]. Since the number of normal subjects in the dataset was higher than CAD [Table 3], the F₁-socre was also calculated (=82%) since it is an unbiased accuracy measure in unbalanced datasets. The type I error (α) and the power of the proposed diagnosis test were 0.1 and 76%. Reducing α down to 0.05 and increasing power to 80%, improves the clinical reliability of the proposed system that is the focus of our future activity. The following strategies could be taken in this regard:

1. The selected mixed-type features in MLR could be weighted based on the clinical importance and (or) tuned using particle swarm optimization[95] embedded with Generalized Minkowski Metrics.[96] Tuning the feature weights, might improve the performance of the designed classifier;

2. Although the sample size of the Cleveland dataset is not low, some important features such as body mass index (BMI) are missing.

We are thus going to design an automated CAD risk assessment program, based on the findings of this study, in collaboration with Isfahan Healthy Heart Program[97] whose dataset is quite rich.

In addition to the hold-out validation method, we also used a 10-fold cross-validation in which the original sample was randomly partitioned into 10 equal-size subsamples. Of the 10 subsamples, a single subsample was retained as the validation data for testing the model, and the remaining 9 subsamples were used as training data. The cross-validation process was then repeated 10 times (the folds), with each of the 10 subsamples used exactly once as the validation data. The results from the folds were averaged to estimate a single estimation.[98] The overall cross-validation accuracy of the proposed classifier was 83%. Guarding against testing hypotheses suggested by the data (type III errors[99]) was done by cross-validation. Comparison with other diagnosis methods designed on the Cleveland CAD dataset, our proposed method ranked in the top first quartile [Table 6].

Although the BMI was not used in our model, it is well-known that BMI is positively correlated with CHOL.[100,101,102] In our dataset, age was positively correlated with hypertension, CHOL, and FBS. This might explain that age in the final model could capture information about CHOL, hypertension, FBS, and BMI as well. The number of cigarettes per day and number of years as a smoker were positively correlated with thallium-201 stress scintigraphy categories. Thus, this attribute could capture the smoking information. Gender was associated with the exercise-induced angina status. Thus, information about the gender could be captured by exercise-induced angina. This is, in fact, the property of MLR that takes into account the interaction between attributes and reports the compact attribute set. Accordingly, most of the input risk factors could be taken into accounts directly/indirectly. Among the features selected, the following ones have been selected in another manuscript:[103] “ST/HR slope,” “cp,” “age,” “trestbps.”

CONCLUSION

We proposed an interpretable fuzzy rule-based system that could noninvasively predict the CAD based on “age,” “exercise-induced angina status”, number of major vessels colored by fluoroscopy, thallium-201 stress scintigraphy result and ST/HR slope. The proposed computer-aided system was promising in CAD diagnosis and could be implemented as a web-based diagnostic decision support system. However, its performance could be improved by introducing weights to the input attributes taking into account the clinical relevance/priority of the features.

AUTHOR'S CONTRIBUTION

HRM contributed in the conception and design of the work, drafting and revising the draft, approval of the final version of the manuscript, and agreed for all aspects of the work. SG contributed in the conception of the work, revising the draft, approval of the final version of the manuscript, and agreed for all aspects of the work.