Motor control hierarchy in joint action that involves bimanual force production

Abstract

The concept of hierarchical motor control has been viewed as a means of progressively decreasing the number of variables manipulated by each higher control level. We tested the hypothesis that turning an individual bimanual force-production task into a joint (two-participant) force-production task would lead to positive correlation between forces produced by the two hands of the individual participant (symmetric strategy) to enable negative correlation between forces produced by two participants (complementary strategy). The present study consisted of individual and joint tasks that involved both unimanual and bimanual conditions. In the joint task, 10 pairs of participants produced periodic isometric forces, such that the sum of forces that they produced matched a target force cycling between 5% and 10% of maximum voluntary contraction at 1 Hz. In the individual task, individuals attempted to match the same target force. In the joint bimanual condition, the two hands of each participant adopted a symmetric strategy of force, whereas the two participants adopted a complementary strategy of force, highlighting that the bimanual action behaved as a low level of a hierarchy, whereas the joint action behaved as an upper level. The complementary force production was greater interpersonally than intrapersonally. However, whereas the coherence was highest at 1 Hz in all conditions, the frequency synchrony was stronger intrapersonally than interpersonally. Moreover, whereas the bimanual action exhibited a smaller error and variability of force than the unimanual action, the joint action exhibited a less-variable interval and force than the individual action.

there is an intimate relation between the hierarchical structure of human motor control (Bernstein 1967; Gelfand and Tsetlin 1966) and motor redundancy (Latash 2012; Turvey 1990). The concept of hierarchical motor control has been viewed as a means of progressively decreasing the number of variables manipulated by each higher-control level of a hierarchy, alleviating the problem of motor redundancy. For example, Gorniak et al. (2007b) suggested how the central nervous system can organize force-stabilizing synergies simultaneously at two levels of a motor control hierarchy in a bimanual action that involves two-finger movements within a hand: the upper level distributes the action between the hands, and the lower level distributes each hand's action between the involved fingers. They examined force-stabilizing synergies that required negative covariation of finger or hand forces in a task of constant force production by two hands. The result showed that negative covariation of the two finger forces within a hand during the bimanual task was weaker than that in a unimanual task [also see Gorniak et al. (2007a) and Kang et al. (2004)].

Coordination that may occur intentionally between individuals with a common goal in a motor task has recently been studied using the term “joint action” [defined by Ganesh et al. (2014); Masumoto and Inui (2014b); Newman-Norlund et al. (2008); Sebanz et al. (2006); and Skewes et al. (2015)]. For example, Bosga and Meulenbroek (2007) asked pairs of participants to perform a virtual lifting task using constant uni- or bimanual isometric force, although they did not examine the hierarchical relation between bimanual and joint actions. The forces produced by the two participants were negatively correlated when visual feedback of their forces was available, indicating the use of complementary forces to control a virtual bar. Masumoto and Inui (2013b) asked 10 pairs of participants to produce periodic unimanual isometric forces, such that the sum of forces that they produced matched a target force that cycled between 5% and 10% of maximum voluntary contraction (MVC) with an interval of 1,000 ms. When the total force was visible, the correlation between the forces produced by the two participants was highly negative, and the coherence between the force-time series produced by the two participants was highest at the target interval. These findings indicate that the two participants simultaneously adopted both complementary and temporal synchronous strategies.

There are data on the control of force production in intrapersonal unimanual (Masumoto and Inui 2010) and bimanual actions (Diedrichsen et al. 2003; Masumoto and Inui 2012, 2013a; Ranganathan and Newell 2008) and in an interpersonal (joint) unimanual action (Bosga and Meulenbroek 2007; Masumoto and Inui 2013b, 2014b). However, to study the hierarchical organization of the motor control system in intra- and interpersonal actions, it is necessary to obtain data on force control in a joint bimanual action. It is predicted that the finger forces of the two hands are combined into a single collective unit (i.e., a decrease in the number of variables) to enable complementary force production between participants. Thus we hypothesized that turning a bimanual force-production task into a joint force-production action would lead to positive correlation between forces produced by the two hands and negative correlation between forces produced by two participants. In the present study, we examined how the central nervous system controls force production and timing simultaneously at three levels of a motor control hierarchy in a joint action that involves bimanual force production: a top level that controls the total force produced by the two participants, a middle level that distributes the force between the two participants, and a bottom level that distributes the force generated by the two hands of each participant.

MATERIALS AND METHODS

Participants

Participants were 20 healthy men without any apparent neurological disorders (mean age = 23.8 yr; SD of age = 2.4 yr). Handedness was tested using the Edinburgh Handedness Inventory (Oldfield 1971). All 20 participants were right-hand dominant, and the mean laterality quotient score was +96.01 (SD = 7.34). All participants gave informed consent, and the Ethical Committee of Naruto University of Education approved the procedures. The work conformed to the principles of the Declaration of Helsinki.

Procedure

The present study consisted of an individual task, performed by one participant, and a joint task, performed by two participants paired randomly. Both tasks consisted of unimanual and bimanual conditions, giving a total of four conditions in this study: the individual-unimanual, individual-bimanual, joint-uinmanual, and joint-bimanual conditions (Table 1). The individual task was conducted using one-half of the setup shown in Fig. 1A. In the individual-unimanual condition, the participants were seated facing the load cell with their palms resting on a support surface, 6 cm above the table (see Fig. 1A). In this posture, the participants made periodic isometric pressing movements with the right or left index finger at the metacarpophalangeal joint with a target peak force of 10% MVC, a target valley force of 5% MVC, and a target peak-to-peak interval (PPI) or valley-to-valley interval (VVI) of 1,000 ms (Fig. 1B). The target force and the force output of the load cell were displayed on a monitor so that the participant could see the difference between the actual force and target force. In the individual-bimanual condition, the participant was required to produce force using both index fingers, and the sum of the two finger forces was required to match the target force, which was for both hands, and the sum of the forces produced by the two fingers was displayed on the monitor.

Table 1.

A matrix to show 4 experimental conditions

Individual-unimanual	Joint-unimanual
Individual-bimanual	Joint-bimanual

Fig. 1.

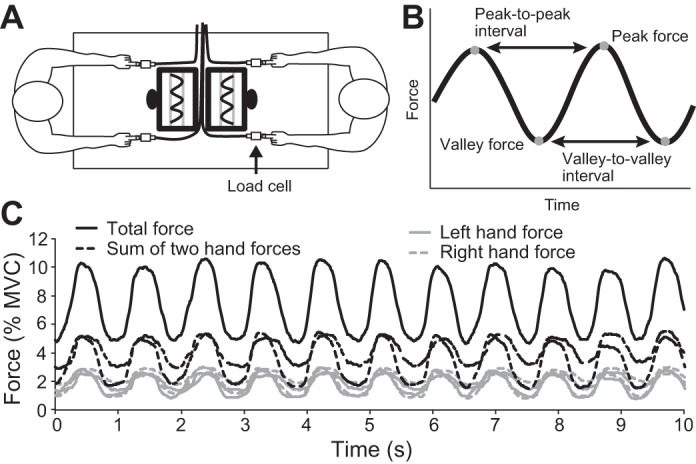
Experimental setup, dependent variables, and example data showing the forces produced by the 2 hands of each of 2 participants in the joint-bimanual condition and the total force. A: the individual task was performed by 1 participant using ½ of the setup shown in the drawing, and the joint task was conducted by 2 participants using the setup shown in the drawing. B: definition and measurement of dependent variables. C: the black line represents the total force, i.e., the sum of the forces produced by both hands of both participants. The 2 black, dashed lines represent the sums of the forces produced by each participant. The 2 gray, solid lines represent the left-hand force produced by each participant, and the 2 gray, dashed lines represent right-hand force produced by each participant. MVC, maximum voluntary contraction.

In the joint-bimanual condition, two participants were seated on chairs at opposite ends of a table facing the load cell and monitor (Fig. 1A). They produced the target force, such that the sum of the forces produced by both index fingers of the two participants was the target peak force of 10% MVC or the target valley force of 5% MVC with the target interval. The force generated was thus summed across participants, rather than two hands. In the joint-unimanual condition, each participant was required to produce force using his right index finger, and the sum of the forces produced by the right index fingers of the two participants was required to match the target. In the joint task, the target force for the pair and the sum of the forces produced by the two participants were displayed on the monitor. The participants were instructed to synchronize the timing of production of forces with the partner's timing. The participants could not see the other's action because of the two monitors between them, and they were instructed not to verbally communicate with each other.

At the start of the experimental session, each participant performed a maximal isometric contraction three times, and the force generated at the finger tip of each index finger was recorded as MVC. The participant was instructed to place the distal pad of the index finger in contact with the load cell and then to apply as much pressure as possible to the load cell and maintain that force output for 3 s without lifting the hand or forearm. His wrist was fixed to the rest on which the load cell was mounted by Velcro straps (Magic Tape; Kuraray, Tokyo, Japan). The MVC (mean = 43.3; SD = 10.9 N) was determined as the average of three trials. The target force is the sum of 10% or 5% MVCs produced by the left and right finger in the bimanual condition and the sum of 10% or 5% MVCs produced by the two participants in the joint task.

The order of the conditions performed by the participants was varied randomly. The participants practiced each condition separately, with the corresponding test trial following immediately after the practice trials. They pressed their fingers against the load cell for 60 cycles in five practice trials for each condition. During practice trials, the pressing rate was prescribed by means of an audible metronome (Model SQ100-88; Seiko Holdings, Tokyo, Japan) at a 500-ms interval. Although the target interval (PPI and VVI) was 1,000 ms, the participants were instructed to synchronize peak and valley forces on the load cell with the metronome at a 500-ms interval. The visual information provided to the participant was the same in the practice trials and the test trials, but the participant was instructed to produce the force without the metronome pulse in the test trials.

Apparatus and Measurements

The output of the load cell (Model LUB-5KB; Kyowa Electronic Instruments, Tokyo, Japan; rated 5 kg), pressed by participants, was amplified (Model MCC-8A; Kyowa Electronic Instruments), converted from analog to digital (PowerLab/8sp; ADInstruments, Dunedin, New Zealand), and recorded on a personal computer (Vostro 200; Dell, Round Rock, TX). The force output was also displayed on a 20-inch computer monitor (1440 × 900 pixel resolution), located ∼60 cm in front of the participant. Data were sampled at a frequency of 1,000 Hz by a 16-bit analog-to-digital converter with a low-pass filter at 100 Hz. Figure 1C shows data collected from two participants in the bimanual condition of the joint task. Peak force, valley force, PPI, and VVI were measured using software (Emile Soft, Tokushima, Japan) for analysis of force and interval.

Data Analysis

The test trials were analyzed. The initial and final five cycles of the force-time series were removed to avoid the effects of the initial stabilization period and any premature cessation of force production, and the values were calculated from the middle 50 cycles in each trial. Complementary strategy, frequency synchrony, phase synchrony, accuracy of force production and interval, and variability of force and interval were calculated as dependent variables, as described below.

To quantify the complementary strategy of force production in the individual-bimanual condition (Table 2), correlation coefficients were calculated between the peak forces produced by the two hands and between the valley forces produced by the two hands. To quantify the complementary strategy of force production in the joint-bimanual condition, correlation coefficients were calculated for each participant between the peak forces produced by the two hands and the valley forces produced by the two hands (the intrapersonal joint-bimanual condition). Correlation coefficients were also calculated for each pair of participants between the total peak forces produced by the two participants and between the total valley forces produced by the two participants (the interpersonal joint-bimanual condition). In the joint-unimanual condition, correlation coefficients were calculated for each pair of participants between the peak forces produced by the two participants and between the valley forces produced by the two participants.

Table 2.

A matrix to show analysis levels (intra- vs. interpersonal) for the analyses of correlation, cross-spectral coherence, and relative phase angle

Intrapersonal individual-bimanual	Interpersonal joint-unimanual
Intrapersonal joint-bimanual	Interpersonal joint-bimanual

The cross-spectral coherence was calculated to quantify the frequency synchrony between the forces produced by the two hands in the individual-bimanual condition. The coherence evaluated the correlation of the two force-time series at different frequencies. In the intrapersonal joint-bimanual condition, the coherence was calculated to evaluate the frequency synchrony between the forces produced by the two hands. In the interpersonal joint-bimanual condition, the coherence was calculated to evaluate the frequency synchrony between the sum of the forces produced by the two hands of each participant. In the joint-unimanual condition, the coherence was calculated to evaluate the frequency synchrony between forces produced by the two participants. The coherence was calculated over all force-time series (100 samples/s), with a window length of 200 points (frequency resolution of 0.5 Hz) using the mscohere command in GNU Octave Forge, version 3.6.1 (freeware; John W. Eaton). Thus the peak coherence over all frequencies was used as an estimate of the frequency synchrony between forces produced by the two hands or participants.

The distribution of relative phase angles between the force-time series produced by the two hands or participants was used to quantify the phase synchrony between their force outputs. The continuous relative phase was first computed using the Hilbert transform (Rosenblum and Kurths 1998), which was calculated by using the Hilbert command in GNU Octave Forge. The distribution of relative phase angles examined the concentration of relative phase angles between forces produced by two hands or participants across nine 20° regions of relative phase (0–20°, 21–40°, 41–60°, 61–80°, 81–100°, 101–120°, 121–140°, 141–160°, 161–180°). The phase synchrony was indicated by a high concentration of relative phase angles near 0°, whereas an even distribution indicated no phase synchrony.

Absolute error (AE) was calculated to assess the accuracy of force and interval. AE was calculated by averaging the size of the error (i.e., the difference between the produced and the target forces or intervals), regardless of sign, over the 50 cycles. SD of peak force, valley force, PPI, and VVI was calculated to evaluate the variability of force and interval.

Statistical Analysis

In the unimanual condition, the difference for AE and SD of force and interval between the left and right hands was analyzed using a 2 × 2 ANOVA of hand (left hand, right hand) × force (peak force, valley force) or interval (PPI, VVI). Because there was no significant difference for the AE and SD of force and interval between the left and right hands, the forces and intervals produced by the left or right hands were treated as a single level under factor condition: AE of force [hand, F(1, 76) = 0.22; force, F(1, 76) = 1.69], SD of force [hand, F(1, 76) = 0.02; force, F(1, 76) = 3.87], AE of interval [hand, F(1, 76) = 2.36; force, F(1, 76) = 1.55], and SD of interval [hand, F(1, 76) = 1.98; force, F(1, 76) = 0.55].

Analysis of complementary strategy.

Correlation coefficients were standardized using a Fisher z-transformation for averaging across pairs and then analyzed using a 4 × 2 ANOVA of condition (individual-bimanual, intrapersonal joint-bimanual, joint-unimanual, interpersonal joint-bimanual) × force. Masumoto and Inui (2010, 2012) found that the valley force was markedly more variable than the peak force in an isometric force-production task. The present study also showed the same result in the SD of force in the individual task (see Fig. 7A). The present study thus analyzed peak and valley forces separately.

Fig. 7.

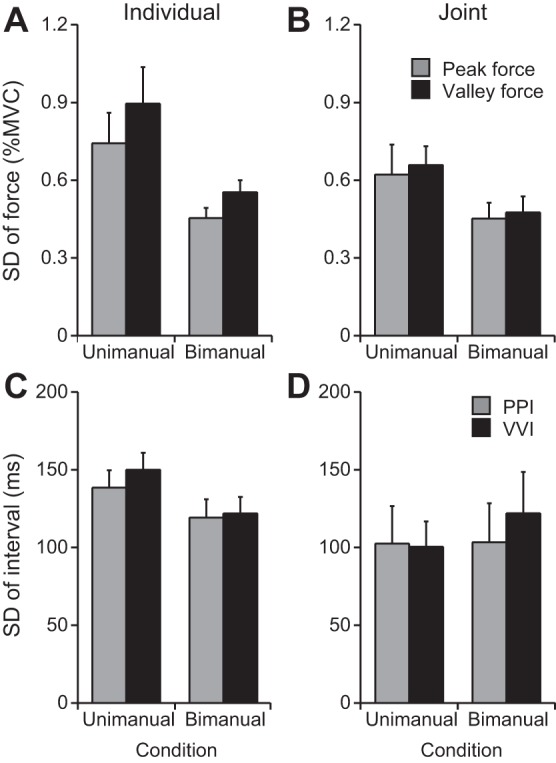
SD of force and interval. Error bars show the between-participants SE. A: SD of peak and valley forces in the individual-unimanual and individual-bimanual conditions. B: SD of peak and valley forces in the joint-unimanual and joint-bimanual conditions. C: SD of PPI and VVI in the individual-unimanual and individual-bimanual conditions. D: SD of PPI and VVI in the joint-unimanual and joint-bimanual conditions.

Analysis of coherence.

Cross-spectral coherence was analyzed using a one-way ANOVA to examine the main effects between forces produced by two hands or participants.

Analysis of distribution of relative phase angles.

Analysis of the distribution of relative phase angles: a 4 (condition) × 9 (phase region: 0–20°, 21–40°, 41–60°, 61–80°, 81–100°, 101–120°, 121–140°, 141–160°, 161–180°) ANOVA was performed to examine the main effects on phase region. When an interaction of condition and phase was found, separate analyses on phase region were performed.

Analysis of accuracy and variability in force and interval.

AE of force and interval and SD of force and interval were analyzed using a 2 × 2 × 2 ANOVA of task (individual, joint) × condition (unimanual, bimanual) × force or interval. When a significant main effect of condition was found, post hoc multiple comparisons were performed using Tukey's honestly significant difference test to detect differences between conditions. Statistical significance was defined at P < 0.05.

RESULTS

The novel findings of the present study are that in the joint-bimanual condition, the correlation between forces produced by the two hands of each participant was strongly positive, whereas that between forces produced by the two participants was negative. The coherence between force-time series produced by two hands or two participants was highest at 1 Hz in all conditions. The complementary force production was greater interpersonally than intrapersonally, but the synchronization of performance to each other's timing was higher intrapersonally than interpersonally.

Complementary Strategy

Figure 2 shows the forces produced by two hands or two participants in each of four conditions (also see Tables 3 and 4). The correlation between the forces produced by the two hands (Fig. 2A) or the two participants (Fig. 2, C and D) was negative in the individual-bimanual, joint-unimanual, and interpersonal joint-bimanual conditions, whereas the correlation between the forces produced by the two hands (Fig. 2B) was positive in the intrapersonal joint-bimanual condition.

Fig. 2.

Distribution of forces produced by 10 participants or pairs. A: distribution of forces produced by both hands in the individual-bimanual condition. B: distribution of forces produced by both hands in the intrapersonal joint-bimanual condition. C: distribution of forces produced by 1 hand of 2 participants in the joint-unimanual condition. D: distribution of the sum of force produced by both hands of 2 participants in the interpersonal joint-bimanual condition. A: dashed lines represent the target force (left finger force + right finger force = 5% or 10% of MVC). C and D: dashed lines represent the target force (the force produced by participant A + the force produced by participant B = 5% or 10% of MVC). The data points represent the force produced by both hands (A and B) and the force produced by the pair of participants (C and D). The gray points represent peak forces, and the black points represent valley forces.

Table 3.

Correlation coefficients calculated for each participant between the peak forces produced by the 2 hands and between the valley forces produced by the 2 hands under the individual-bimanual and intrapersonal joint-bimanual conditions

Pair	1		2		3		4		5		6		7		8		9		10
Participant	A	B	A	B	A	B	A	B	A	B	A	B	A	B	A	B	A	B	A	B
Individual-bimanual
Peak force	0.19	−0.18	−0.20	−0.12	0.06	−0.12	−0.37	−0.53	0.01	−0.65	0.19	−0.39	−0.84	0.22	0.55	−0.19	0.03	0.16	−0.13	0.02
Valley force	0.08	−0.17	−0.21	0.08	−0.03	−0.04	−0.59	−0.11	−0.04	−0.61	0.12	0.03	−0.03	−0.15	0.58	−0.16	−0.20	0.40	−0.12	0.08
Joint-bimanual
Peak force	0.47	0.43	0.51	0.73	0.76	0.55	−0.41	0.77	0.11	0.28	0.67	0.48	0.67	0.75	0.36	0.98	0.51	0.78	0.15	0.50
Valley force	0.33	0.52	0.79	0.79	0.51	0.72	−0.25	0.75	0.53	0.32	0.79	0.72	0.60	0.90	0.34	0.96	0.37	0.82	0.38	0.47

Table 4.

Correlation coefficients calculated for each pair of participants between the total peak forces produced by the 2 participants (A and B) and between the total valley forces produced by the 2 participants under the joint-unimanual and interpersonal joint-bimanual conditions

Pair	1	2	3	4	5	6	7	8	9	10
Joint-unimanual
Peak force	−0.53	−0.43	−0.39	−0.43	0.02	−0.28	−0.17	−0.45	−0.35	−0.56
Valley force	−0.38	−0.31	−0.38	−0.34	−0.31	−0.48	−0.16	−0.23	−0.12	−0.63
Joint-bimanual
Peak force	−0.57	−0.33	−0.51	−0.81	−0.40	−0.37	−0.36	−0.64	−0.47	−0.41
Valley force	−0.52	−0.23	−0.26	−0.44	−0.24	−0.53	−0.52	−0.63	−0.40	−0.02

Table 3 shows correlation coefficients calculated for each participant between the peak forces produced by the two hands and the valley forces produced by the two hands under the individual-bimanual and intrapersonal joint-bimanual conditions. Whereas more than one-half coefficients (24/40) were negative under the individual-bimanual condition, the majority of the coefficients (38/40) was positive under the intrapersonal joint-bimanual condition. Table 4 shows correlation coefficients calculated for each pair of participants between the total peak forces produced by the two participants and between the total valley forces produced by the two participants under the joint-unimanual and interpersonal joint-bimanual conditions. All coefficients except one (39/40) were negative in both conditions.

Figure 3 shows the mean correlation coefficients in each of the four conditions. The correlation differed across conditions [F(3, 112) = 64.01, P < 0.0001] but did not differ across force. The correlation between hands was more positive in the intrapersonal joint-bimanual condition than in the other three conditions. The correlation between participants in the joint-unimanual (P < 0.05) and interpersonal joint-bimanual (P < 0.005) conditions was more negative than the correlation between hands in the individual-bimanual condition. In the joint task, the two participants in a pair thus adopted a complementary strategy, whereby one person compensated for force errors of the other person. The most important result is that the correlation between the forces produced by two hands was strongly positive in the intrapersonal joint-bimanual condition (Figs. 2B and 3A). Two hands adopted a symmetric strategy of force production, whereas two participants adopted a complementary one.

Fig. 3.

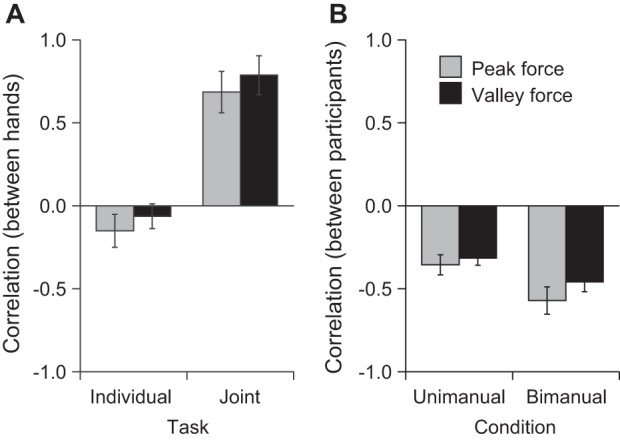
Mean correlation coefficient between the forces produced by the left and right hands or by the 2 participants in a pair. Error bars show the between-participants SE. A: mean correlation between forces produced by 2 hands in the individual-bimanual and intrapersonal joint-bimanual conditions. B: mean correlation between forces produced by 2 participants in the joint-unimanual and interpersonal joint-bimanual conditions.

Temporal Synchronous Strategy

Analysis of frequency.

Figure 4 shows the mean cross-spectral coherence between force-time series produced by two hands (Fig. 4, A and B) or participants (Fig. 4, C and D). The coherence was highest at 1 Hz in all conditions, indicating that each hand or participant synchronized the time-force series with the other hand or participant at the target interval. An analysis of the peak coherence [F(3, 56) = 10.78, P < 0.0001] indicated that the peak coherence of the force produced by two hands (Fig. 4, A and B) was higher than that of the force produced by two participants [Fig. 4, C (P < 0.0001) and D (P < 0.05)]. Thus although the complementary force production was greater interpersonally than intrapersonally, the synchronization of their performance to each other's timing was higher intrapersonally than interpersonally.

Fig. 4.

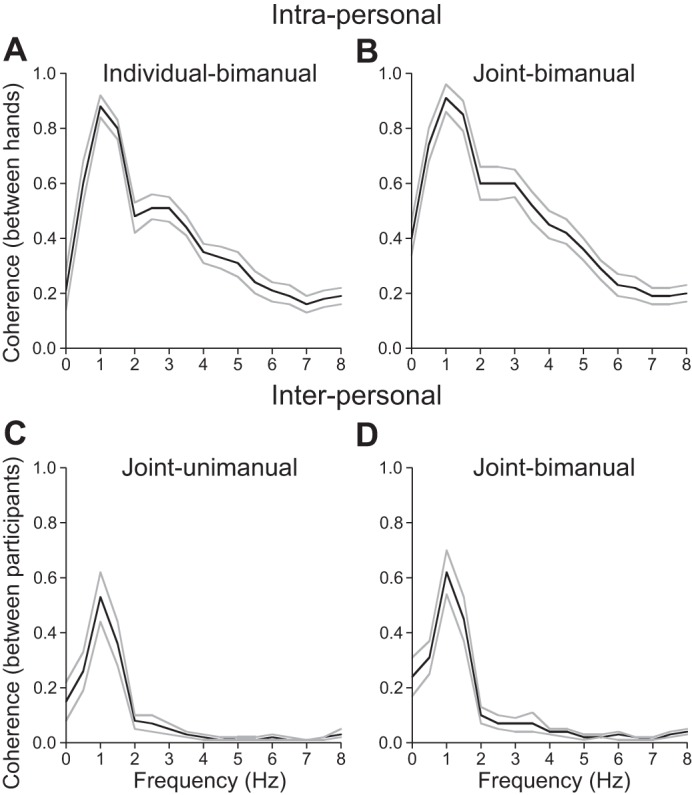
Cross-spectral coherence between force-time series produced by 2 hands or participants. A: the coherence between force-time series produced by the left and right hands in the individual-bimanual condition. B: the coherence between force-time series produced by the left and right hands in the intrapersonal joint-bimanual condition. C: the coherence between force-time series produced by 1 hand of each participant in the joint-unimanual condition. D: the coherence between the sums of force-time series produced by both hands of each participant in the interpersonal joint-bimanual condition. Black lines represent the between-hands (A and B) or between-participants (C and D) mean, and 2 gray lines represent the SE.

Analysis of phase.

To examine the phase synchrony between force-time series produced by two hands or participants, Fig. 5 shows the distribution of relative phase angles for four conditions. An analysis of the relative phase angles showed a main effect on phase region [F(8, 504) = 190.88, P < 0.0001], and an interaction of condition and phase region was significant [F(24, 504) = 11.09, P < 0.0001]. Separate analyses on phase region showed that whereas the percentage of occurrence for the 0–20° phase region [F(3, 56) = 12.19, P < 0.0001] was markedly higher in the individual-bimanual and intrapersonal joint-bimanual conditions than in the joint-unimanual (P < 0.0001) and interpersonal joint-bimanual conditions (P < 0.005), the percentage for the 21–40° phase region [F(3, 56) = 4.99, P < 0.005] was lower in the intrapersonal joint-bimanual condition than in the joint-unimanual (P < 0.05) and interpersonal joint-bimanual conditions (P < 0.01). Whereas the percentage for the 41–60° phase region [F(3, 56) = 8.65, P < 0.0001] was lower in the individual-bimanual and intrapersonal joint-bimanual conditions than in the joint-unimanual (P < 0.005) and interpersonal joint-bimanual conditions (P < 0.05), the percentage for the 61–80° phase region [F(3, 56) = 6.25, P < 0.005] was lower in the individual-bimanual (P < 0.005) and intrapersonal joint-bimanual conditions (P < 0.05) than in the joint-unimanual condition. The percentage for the 81–100° phase regions [F(3, 56) = 2.93, P < 0.05] was lower in the individual-bimanual condition than in the joint-unimanual condition (P < 0.05). Whereas the relative phase occurrence increased mainly in the 0–20° phase region under all four conditions, similar to the frequency synchrony, the phase synchrony was higher intrapersonally than interpersonally.

Fig. 5.

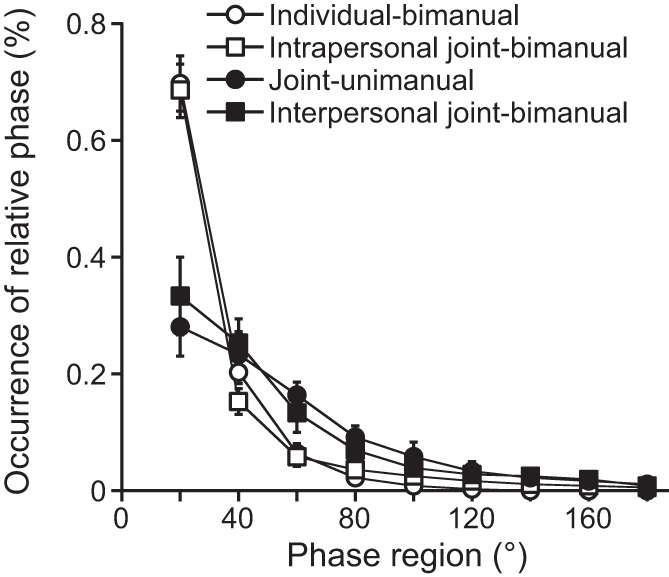
Distribution of relative phase angles as a function of the 9, 20° regions of relative phase (i.e., 0–20°, 21–40°, 41–60°, . . ., 161–180°) for 4 conditions. Error bars show the between-participants SE.

Accuracy of Force Production and Movement Interval

Figure 6A shows AE of force production in the individual task, and Fig. 6B shows AE of force production in the joint task. AE of force production differed across tasks [F(1, 152) = 8.02, P < 0.01] and conditions [F(1, 152) = 6.79, P < 0.05] but did not differ across forces. There was no interaction of task and condition. Post hoc tests indicated that AE of force was smaller in the bimanual condition than in the unimanual condition and smaller in the joint task than in the individual task. Figure 6 shows AE of interval in the individual task, and Fig. 6D shows AE of interval in the joint task. AE of interval did not differ across conditions, tasks, or forces.

Fig. 6.

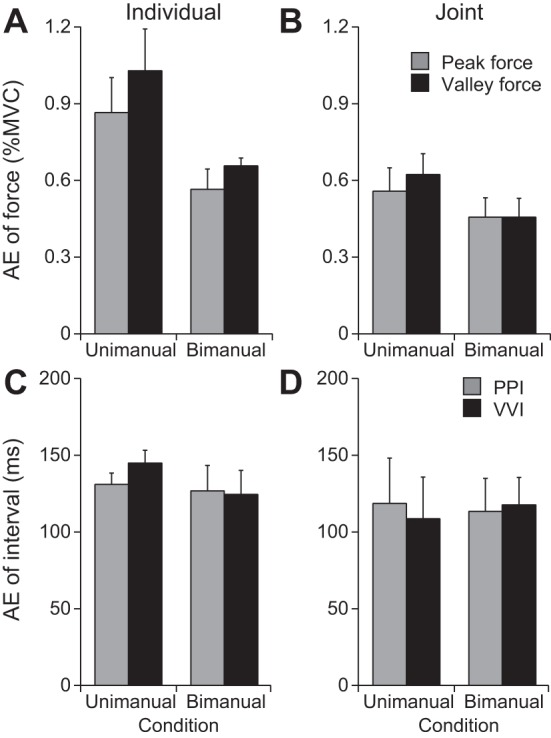
Absolute error (AE) of force and interval. Error bars show the between-participants SE. A: AE of peak and valley forces in the individual-unimanual and individual-bimanual conditions. B: AE of peak and valley forces in the joint-unimanual and joint-bimanual conditions. C: AE of peak-to-peak interval (PPI) and valley-to-valley interval (VVI) in the individual-unimanual and individual-bimanual conditions. D: AE of PPI and VVI in the joint-unimanual and joint-bimanual conditions.

Variability of Force and Movement Interval

Figure 7A shows SD of force in the individual task, and Fig. 7B shows SD of force in the joint task. SD of force differed across tasks [F(1, 152) = 4.10, P < 0.05] and conditions [F(1, 152) = 20.70, P < 0.0001] but did not differ across forces. There was no interaction of task and condition. Post hoc tests indicated that SD of force was smaller in the bimanual condition than in the unimanual condition and smaller in the joint task than in the individual task.

Figure 7C shows SD of interval in the individual task, and Fig. 7D shows SD of interval in the joint task. SD of interval did not differ across conditions in either force but did differ across tasks [F(1, 152) = 4.33, P < 0.05]. There was no interaction of condition and task. The post hoc test indicated that SD of interval was smaller in the joint task than in the individual task.

DISCUSSION

Relations Between Motor Redundancy and Hierarchical Motor Control

In the present study, the negative correlation between forces was stronger in the joint-unimanual and interpersonal joint-bimanual conditions than in the individual-bimanual condition, indicating that the complementary force production was stronger interpersonally than intrapersonally. In the joint task, the target force was shared redundantly between two participants, and thus each participant in the pair adopted a complementary strategy of force so that one person compensated for force errors of the other. However, in the intrapersonal joint-bimanual condition (Figs. 2B and 3A), the correlation between forces produced by two hands was strongly positive. This new finding indicates that because a symmetric strategy of the bimanual force production decreased the number of control variables, two participants were able to adopt a complementary strategy with the total forces produced by the two hands. From a hierarchical view of motor control in the joint-bimanual condition, the bottom level of the hierarchy is the force produced by the hand, and the middle level is the control of the joint action (see Fig. 8).

Fig. 8.

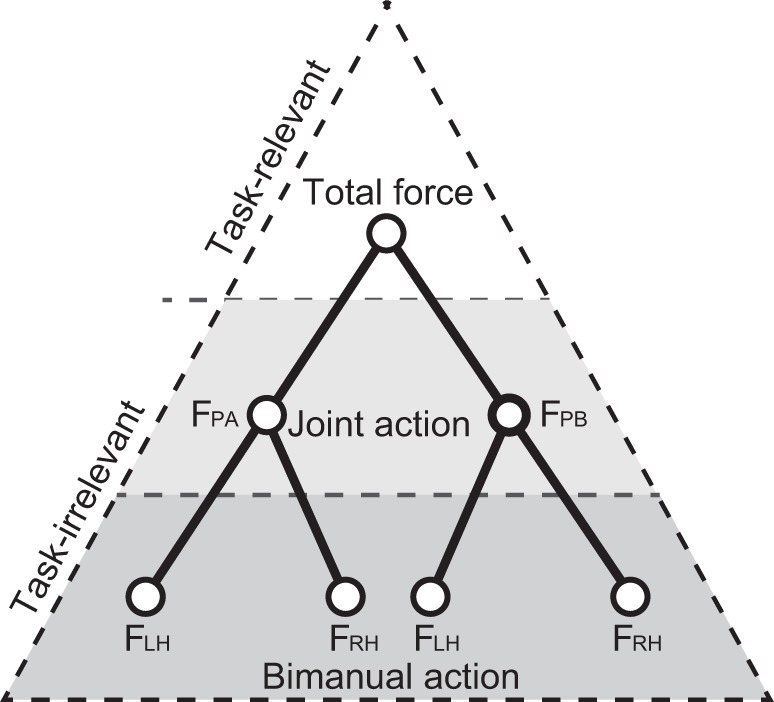
A simplified scheme of the proposed motor control hierarchy in the joint-bimanual condition. F_PA, the force produced by participant A; F_PB, the force produced by participant B; F_RH, the force produced by the right hand; F_LH, the force produced by the left hand; Task-relevant, task-relevant dimension (i.e., task error); Task-irrelevant, task-irrelevant dimension (i.e., redundancy).

A symmetric strategy reflects a tendency to coordinate the fingers of the two hands into a single collective unit. This feature has been observed in several previous studies on bimanual coordination (Kelso et al. 1979; Masumoto and Inui 2012; Ranganathan and Newell 2008), and the high stability of this strategy may be a main reason why it is selected. Gorniak et al. (2007b) showed that negative covariation of finger forces within a hand during the bimanual task was weaker than in a unimanual task. In the present study, we found a strong positive correlation of bimanual force production in the intrapersonal joint-bimanual condition. Therefore, the present study highlights that a motor control hierarchy within an individual can be extended to intra- and interpersonal actions.

In addition, according to the task requirement, the time-force series generated by one hand or participant was synchronized with that generated by another hand or participant at the target interval in all conditions. However, such frequency or phase synchrony was not observed without visual feedback but only when the image of the total or partner force was present (Masumoto and Inui 2013b). Because the present study gave participants the total force displayed on a monitor under all conditions, it corroborated the result of the previous study. Such synchronization also indicates a symmetric strategy of the timing of force production between two hands or participants, which can be viewed as a decrease in the number of variables manipulated by a higher controller. After the controller decreases the number of degree of freedom of movement timing between two hands or participants, it appears to release the degree of freedom of force production between two hands or participants.

Based on the relation between a motor control hierarchy and the task-relevant or task-irrelevant dimension, we suggest that the scheme depicted in Fig. 8 can account for the present findings. To interpret the negative correlation between forces produced by two hands or participants as a solution to the problem of redundancy in motor control, we need to interpret the data in terms of the uncontrolled manifold hypothesis (Latash et al. 2002; Scholz and Schöner 1999). The hypothesis suggests that the nervous system should minimize the variance in the sum of the two forces (the task-relevant dimension), but the difference between the forces (the task-irrelevant dimension) would be allowed to accumulate. The input into the highest level comes from the task requirement (e.g., target total force), and the output from the lowest level acts on the muscles that control the fingers. In the individual-bimanual condition, coordination of forces between hands is task relevant, whereas that between fingers within the hand is task irrelevant. In the joint-bimanual condition, however, variability of total force at the top level may be viewed as the task-relevant dimension, and variability of forces produced by participants (middle level) and hands (bottom level) may be viewed as the task-irrelevant dimensions. To enable complementary force production between the two participants at the middle level of the hierarchy, the bimanual symmetric force production is required to decrease the degree-of-freedom number (i.e., the number of variables) in the bottom level. The relation between lower and upper levels of a motor control hierarchy is required to decrease the degree-of-freedom number in the lower level.

Complementary Force Production is Stronger, and Synchronization is Weaker Interpersonally than Intrapersonally

In the present study, the complementary force production is stronger interpersonally than intrapersonally. Reed et al. (2006) have also found an interpersonal complementary relationship in a joint target-acquisition task [also see Skewes et al. (2015)]. They asked pairs of participants to move a mark on a disk into a target as quickly as possible and hold it there. Whereas one participant contributed more to acceleration and the other to deceleration, the participants performed faster interpersonally than individually. In bimanual coordination, Masumoto and Inui (2012) showed that the forces produced by both hands were combined over all force levels without vision, whereas the strategy for the bimanual force control changed from force-error compensation to symmetric force production, with an increase in force with vision [also see Hu et al. (2011) and Ranganathan and Newell (2008)]. In addition, interhemispheric information processing across the corpus callosum increases with force level in a bimanual coordination task (Diedrichsen et al. 2003). Thus a symmetric strategy of force production is often observed in bimanual coordination, rather than force-error compensation, and the redundancy decreases in many cases. By contrast, communicating information between two participants in a pair during the joint task does not depend on neuroanatomical linkages between the control centers but visuomotor linkages between the participants. The visuomotor linkages appear to promote stronger complementary force production than the interhemispheric information-processing system.

Synchronization of their performance to each other's timing was stronger intrapersonally than interpersonally. The bimanual control of timing depends on interhemispheric or subcortical information processing. Previous studies on bimanual timing control have shown that bimanual coordination of continuous drawing of a circle depends on interhemispheric information processing across the corpus callosum (Spencer et al. 2003), whereas bimanual discrete tapping is controlled by the cerebellum (Kennerley et al. 2002). Thus the periodic bimanual action in the bimanaual condition in the present study presumably depends on interhemispheric information processing across the corpus callosum. By contrast, in the interpersonal control of timing, the two participants in a pair were loosely coupled via visuomotor linkages. The interhemispheric information-processing system appears to promote stronger synchronization of performance than visuomotor linkages.

In the present study, we further observed higher levels of coherence for frequencies above 2 Hz intrapersonally (Fig. 4, A and B) but not interpersonally. Whereas physiological tremor is present at higher frequencies, between 5 and 12 Hz in force recording (Elble and Randall 1976), processes related to slow sensorimotor actions are located in the 0- and 4-Hz band of the force power spectrum (Slifkin et al. 2000). Thus because the coherence in the present study was related to visuomotor action, the participant presumably synchronized the timing of production of forces with the partner's timing in the fine control of bimanual force production except attempting to match the target interval.

Control of Force and Timing

The AE and SD of force were smaller in the bimanual action than in the unimanual action and smaller in the joint action than the individual action. These results indicate that force was controlled more accurately in the bimanual action than the unimanual action, consistent with our previous study (Masumoto and Inui 2012). These results also indicate that force was controlled more accurately in joint action, which was performed with visuomotor linkages between participants, than in the individual action, which involved neuroanatomical linkages between the control centers, corroborating the result of Masumoto and Inui (2013b).

In addition, the SD of the interval was smaller in the joint action than in the individual action, consistent with the result of Masumoto and Inui (2013b) and suggesting that the effect was due to visuomotor linkages between participants. Vesper et al. (2011) have also found that the temporal variability of participants' actions was smaller interpersonally than individually in a two-choice reaction time task. They asked pairs of participants to press a key in synchrony in the task, indicating that the less variable the actions were, the better the interpersonal coordination was. They point out that reducing one's variability may be a coordination strategy to make oneself more predictable in joint actions. Moreover, in a joint discrete force production (Masumoto and Inui 2014a), whereas participants with low-force variability always produced a stronger force than those with high-force variability, the former produced force more complementarily than the latter. Based on such an interpersonal coordination strategy that the variability of human actions is smaller interpersonally than individually, joint actions exhibit larger performance gains than individual actions.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: J.M. and N.I. conception and design of research; J.M. performed experiments; J.M. analyzed data; J.M. and N.I. interpreted results of experiments; J.M. prepared figures; J.M. and N.I. drafted manuscript; J.M. and N.I. edited and revised manuscript; J.M. and N.I. approved final version of manuscript.