Abstract
In macromolecular design, conformational energies are sensitive to small changes in atom coordinates, so modeling the small, continuous motions of atoms around low-energy wells confers a substantial advantage in structural accuracy; however, modeling these motions comes at the cost of a very large number of energy function calls, which form the bottleneck in the design calculation. In this work, we remove this bottleneck by consolidating all conformational energy evaluations into the precomputation of a local polynomial expansion of the energy about the “ideal” conformation for each low-energy, “rotameric” state of each residue pair. This expansion is called Energy as Polynomials in Internal Coordinates (EPIC), where the internal coordinates can be sidechain dihedrals, backrub angles, and/or any other continuous degrees of freedom of a macromolecule, and any energy function can be used without adding any asymptotic complexity to the design. We demonstrate that EPIC efficiently represents the energy surface for both molecular-mechanics and quantum-mechanical energy functions, and apply it specifically to protein design to model both sidechain and backbone degrees of freedom.
2 Introduction
Computational design algorithms are an effective approach to engineer proteins and discover new drugs for many biomedically relevant challenges, such as drug resistance prediction,1 peptide-inhibitor design,2 and enzyme design.3 Protein design algorithms search through large sequence and conformational spaces for sequences that will fold to a desired structure and perform a specific function. One of the key challenges in protein design is modeling and searching the many continuous conformational degrees of freedom inherent in proteins and other molecules. Protein design algorithms must estimate optimal values for all these degrees of freedom in order to optimize the sequence of the protein, or to optimize the chemical structure of the ligand if used for drug design. Molecular dynamics simulations can be used for this purpose if the protein sequence and ligand are known, because they can move all of the molecule’s degrees of freedom,4 but these simulations are computationally expensive and must be run separately for each sequence or ligand chemical structure. Hence, this direct simulation approach is unsuitable for searching large combinatorial design spaces. For example, many protein design problems require searching over trillions of sequences—far too many for individual molecular dynamics runs.
To address the combinatorially large sequence spaces inherent to protein design, dedicated protein design algorithms efficiently choose an amino-acid type and conformation for each residue in a protein that, together, minimize some energy function.5 Since the sidechain conformations of each amino-acid type are generally found in clusters, known as rotamers,6 the protein design problem has often been treated as a discrete optimization problem. In this case, the output is a set of rotamer assignments (a rotamer, including amino-acid type, is assigned to each residue). The objective function is an energy function, which maps conformations to their energies. However, because proteins are continuously flexible and have backbone as well as sidechain flexibility, some of the protein’s internal coordinates will likely have functionally significant variations from the rotamer’s “ideal” value (at the center of the cluster). Clashing ideal rotamers can often be converted to favorable conformations by relatively small adjustments in the sidechain conformations.7,8 Small adjustments in the backbone conformation away from the wild-type backbone can also be functionally significant.9–11 As a result, modeling of continuous flexibility has been shown to dramatically improve the accuracy of structural modeling in designs,8,11 even using a limited set of degrees of freedom, and has led to designs that perform well experimentally.1–3,5,7,12 Furthermore, attempts to mimic this effect by discrete sampling at a finer resolution have been shown to either poorly approximate the continuous solutions, or to be computationally prohibitive.8 Modeling additional continuous degrees of freedom, with the goal of modeling all conformational variations that significantly impact protein function, is expected to increase the accuracy of designs further.
Modeling of continuous flexibility in protein design can still exploit our knowledge of rotamers, because rotamers provide an excellent prior estimate of where “energy wells” in the conformational space of the protein are likely to be. Residues’ sidechains will usually be found in the region of conformational space fairly close (e.g., within 10–20° for sidechain dihedrals) to an ideal rotamer, even with a relatively small rotamer library.13 As a result, if by using a “minimization-aware” search process one can find the nearest ideal rotameric conformation to the true Global Minimum-Energy Conformation (GMEC) of a protein, the GMEC itself can generally be found by local minimization initialized to that ideal rotameric conformation. Thus, protein design can fully account for continuous sidechain flexibility while still functioning as a “minimization-aware” search7 over discrete rotamer space. This same paradigm can be extended to continuous backbone flexibility if ideal conformations that include backbone motions—”residue conformations” or RCs11—are included in the search.
Such “minimization-aware” search can take multiple forms. For example, the iMinDEE algorithm8 produces a gap-free, provably accurate list of rotamer assignments in order of lower bound on minimized energy. iMinDEE performs energy minimization on each of these rotamer assignments in that gap-free order until the lower bound exceeds the best minimized energy Eb enumerated so far. At this point, any subsequently enumerated assignments would be guaranteed to have higher minimized energies than Eb, so Eb is provably the global minimum energy. iMinDEE enumerates rotamer assignments efficiently using the A* search algorithm.14,15 Monte Carlo search over rotamer space can also incorporate minimization,16,17 but without any provable guarantees. A Monte Carlo search will be minimization-aware if continuous minimization is performed for sequences and conformations during (rather than after) the search and the minimized energy is used in the calculation of acceptance probabilities for new rotamer assignments, as in16 and the final phase of.17 Nevertheless, a method without provable guarantees will likely require more conformations and sequences to be minimized to obtain the same gain in accuracy as iMinDEE, because unlike in iMinDEE, the conformations being minimized are not guaranteed to be the most promising ones. Furthermore, there is no finite number n for a given protein design problem such that enumerating n conformations by Monte Carlo is guaranteed to yield the GMEC.
Any minimization-aware method, however, will require a large number of subroutine calls to local minimization. Continuous energy minimization is computationally expensive, even with molecular mechanics-type energy functions that prioritize speed over accuracy. This causes the minimization of the energy function to be the bottleneck in protein design with continuous flexibility.
This bottleneck becomes more severe when more sophisticated energy functions are introduced. Computational protein design is typically performed with energy functions that prioritize speed over accuracy. For example, they typically use simplified implicit solvation models, such as EEF1.18 Vizcarra et al. 19 have investigated the use of the Poisson-Boltzmann model, a much more accurate implicit solvation model, in protein design. They found it to be amenable to representation as a sum of residue-pair interactions—the form required for most protein design algorithms— but orders of magnitude more expensive than EEF1. Other methods to improve energy function accuracy are likely to face the same problem. For example, quantitatively accurate descriptions of most molecular interactions require computation of the electronic structure using quantum chemistry, but methods to do this are very computationally intensive.20 Methods to reduce the number of calls to an energy function needed in protein design could allow more accurate energy functions to be used, and thus yield more accurate results.
In protein design with only discrete flexibility, precomputation methods are typically used to reduce the number of energy function calls needed—that is, the number of conformations for which the energy must be evaluated. Before the design is started, the interaction energy of each pair of ideal, rigid rotamers at different residue positions is precomputed and stored in an energy matrix. Then, an ideal rotamer is chosen for each residue based on the energies in this matrix, and no further calls to the energy function are needed during the actual design calculation. The number of energy function calls required is thus quadratic in the number of residues in the system (that is, it scales as the number of pairs of residues). A precomputed energy matrix is, however, of limited use if we want to model continuous flexibility. No benefit in design is gained by performing post-hoc minimization on the best conformation found using ideal rotamers.8 This is true even if a high degree of flexibility is used for minimization, e.g., if molecular dynamics techniques are used, because the designed sequence is already determined before minimization is performed. In contrast, a minimization-aware search performs local continuous minimization for all rotamer assignments that might be optimal, in order to find the true GMEC.7
Thus, an analogous energy matrix precomputation method for continuous flexibility would be very useful. It would ensure a polynomial number of energy function calls for minimization-aware protein design, in contrast to the exponential number of calls that may arise in minimization of all possibly optimal rotamer assignments (since the number of such assignments may be exponential with respect to the number of residues modeled). The search for rotamer assignments itself is unlikely to admit a polynomial-time algorithm, because it is NP-hard even to approximate.21,22 But a method to precompute pairwise energies for continuously flexible design would change the overall time cost from
(a large rotamer search cost) times (the energy function cost)
to
(a large rotamer search cost) plus (the energy function cost).
The rotamer search cost will necessarily be exponential in the worst case, if one wants to obtain the GMEC or an approximation to the GMEC within a fixed error threshold. But the energy function cost will be merely quadratic in the number of residues, indicating that the pairwise energy precomputation shifts the bottleneck away from the energy function calls. This brings the same improvement to minimization-aware design that energy matrix precomputation brought to non-continuously-flexible design.
We now present a pairwise energy precomputation method that admits continuous flexibility: EPIC (Energy as Polynomials in Internal Coordinates). EPIC computes a representation of the pairwise energy for each rotamer pair, not just at the rotamers’ ideal values of the internal coordinates, but for values within specified ranges around the ideal ones (Fig. 1). This computation is performed before the rotamer search computation is begun. This allows the rotamer search to substitute the new quickly evaluable representation for the original energy function. EPIC is implemented in the OSPREY7,23,24 open-source protein design package, which has yielded many designs that performed well experimentally—in vitro 1–3,25–28 and in vivo 1,2,25,26 as well as in non-human primates.25 EPIC provides a significant speedup when used with OSPREY’s default AMBER29,30- and EEF118-based energy function, but is also shown to be suitable for representing quantum-mechanical energies.
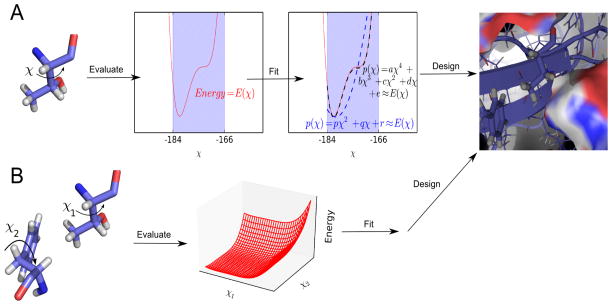
Figure 1.
(A) The energy of each residue is represented by EPIC as a polynomial in the internal coordinates, such as sidechain dihedrals χ. Low-degree, inexpensive polynomials (blue) are tried first, and the degree is increased as needed to achieve a good fit (black) to the actual energy function (red). These polynomials are then used for design in place of the full energy function. (B) Interactions between pairs of residues are represented in terms of both residues’ internal coordinates.
This paper makes the following contributions:
A compact, closed-form representation of energy as a function of continuous internal coordinates of a protein system.
A modified least-squares method to compute this representation.
A modified implementation of the iMinDEE 8 and DEEPer11 protein design algorithms, integrated into the OSPREY1,3,7,23,24 open-source protein design package, that makes use of this representation to achieve substantial speedups. It is available online24 as free software.
Computational experiments showing that compact and accurate EPIC representations are possible both for the standard energy function in OSPREY and for energies obtained by quantum chemistry at the SCF and MP2 levels of theory.
Computational experiments showing that EPIC greatly speeds up minimization-aware protein design calculations, thus allowing designs to include not only more flexible residues, but also more conformational flexibility at those residues.
3 Methods
3.1 Preliminaries
EPIC, like most previous protein design algorithms, is designed for pairwise energy functions. Pairwise energy functions are sums of intra+shell and pairwise terms. Intra+shell terms are functions of the amino-acid type and conformation of one residue, and pairwise terms are functions of the amino-acid types and conformations of two residues. Each pairwise term represents the interaction between a pair of flexible residues, while each intra+shell term represents the internal energy of a residue plus its interactions with non-flexible “shell” residues (those that are frozen in a single, fixed conformation throughout the entire calculation). EPIC could be easily modified to include some higher-order terms for defined combinations of more than two residues: these terms can also be represented as polynomials in their residues’ degrees of freedom.
To find the GMEC, we must find an amino-acid type and conformation for each flexible residue such that the sum of intra+shell terms for all flexible residues, plus the sum of pairwise terms for all pairs of flexible residues, is minimized. This problem is referred to as conformational search. Conformational search can also comprise sequence search, by searching for the best conformation across many sequences’ conformational spaces. Many algorithms are available for this problem, including iMinDEE8 and DEEPer,11 which solve it with provable accuracy. EPIC can be used in any conformational search algorithm that models continuous flexibility, because it provides polynomials that can be directly substituted for intra+shell and pairwise terms of the energy function.
The essence of EPIC is to exploit the fact that for each pairwise or intra+shell energy, the energy in the vicinity of the minimum can be described well by a relatively low-degree polynomial (usually quadratic total degree, sometimes higher; see Fig. 5B). This description is computed using a modified least-squares method. We will refer to the states to which a residue may be assigned as residue conformations (RCs; cf. DEEPer11). In the absence of backbone flexibility, each RC will correspond to a sidechain rotamer. Within a residue conformation, the residue’s continuous energy variations can be described by a set of internal coordinates, which are subject to box constraints (i.e., bounds on each internal coordinate).
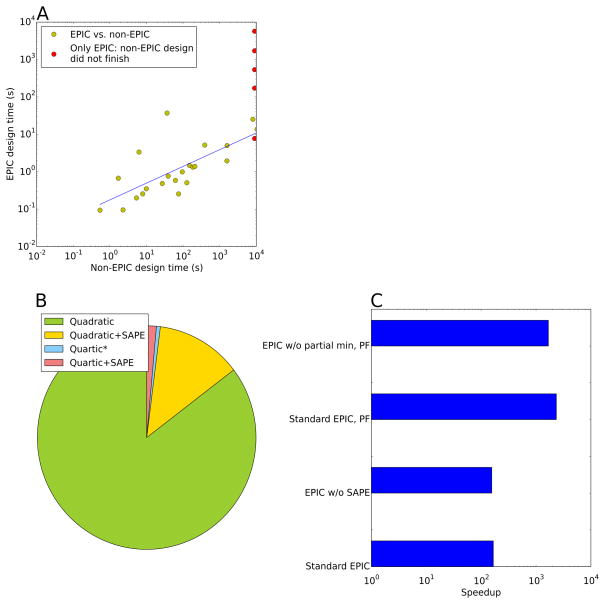
Figure 5.
(A) A* times with and without EPIC. Five designs that did not finish without EPIC are shown on the right in red. (B) Proportions of each type of fit (see Section 3.6) required in EPIC calculations. The “quartic*” category includes both full quartic fits and quadratic fits with quartic terms added for D10 or for D100. Fits were all made as high-degree as needed to obtain a residual below 0.0001, as described in Section 3.6. Some fits have substantially lower residuals, especially quadratic fits without SAPE, since no lower fit degrees were allowed. (C) Speedups due to different EPIC methods compared to A* based on pairwise lower-bound energies; standard EPIC includes both SAPE and minimization of partial conformations. PF denotes partition function calculations; the others are GMEC calculations.
Herein, the word “polynomial” will be used in two very different senses in the description of EPIC below. First, EPIC is a polynomial representation of the energy, namely, a polynomial function with respect to the internal coordinates that is explicitly constructed by the EPIC algorithm. Second, a measure m of the computational complexity of an algorithm can be described as “polynomial”5,31 if, for input size n, m grows no faster than nd for a fixed exponent d. In this case, one can construct a polynomial with respect to the size of the input that will be an upper bound on the computational cost, no matter how large the input is (n). For this purpose, we will consider either the time or the number of energy function calls as m—these two measures of computational complexity are related to each other by a constant factor in current protein design algorithms with continuous flexibility, since energy function calls generally dominate the cost of these algorithms. For example, precomputation of an EPIC representation must be performed only once for every pair of RCs at different residues, and thus the number of polynomial fits (and thus the total time for precomputation of EPIC fits) does not grow faster than the square of the number of residues being modeled. On the other hand, protein design itself has been shown to be NP-hard,21,22 which means no polynomial-time algorithm is likely to exist for it. In other words, for every polynomial p(nr) in the number nr of residues, there are protein design problems of nr residues that are not expected to be solvable in time p(nr). A problem only solvable by exponential-time algorithms—those that take time scaling as bn, where b is a constant and n is the size of the input—would typically be considered NP-hard.
Energy function calls are typically the bottleneck in protein design algorithms that model continuous flexibility. EPIC, however, ensures that the number of energy function calls in a protein design calculation is linear in the number of RC pairs, and thus polynomial in the size of the input (Fig. 2).
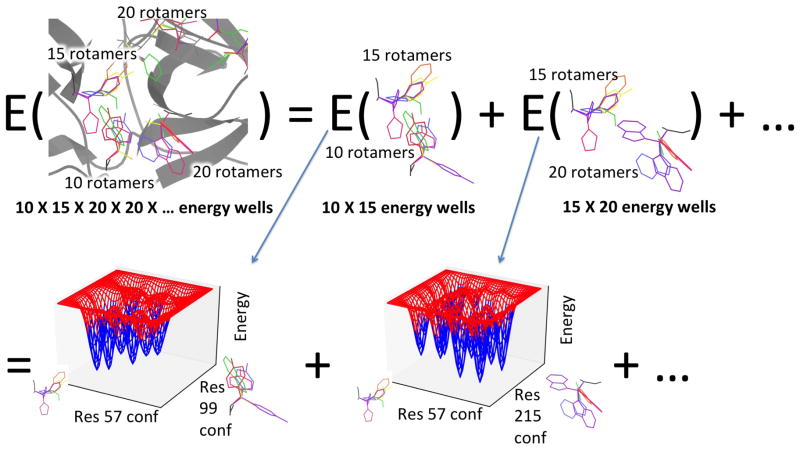
Figure 2.
The number of energy wells in a protein system scales exponentially with the number of flexible residues, leading to an exponential number of energy function calls, but EPIC can replace most of these calls with quick evaluations of low-degree polynomials. (Top) A protein may have an energy well for every combination of rotamers (rainbow) at different residues. The global minimum-energy conformation (GMEC) of a protein may be in any of these wells. We model the energy as a sum of pairwise energy terms. Each pairwise term will have wells for pairs of rotamers, but there are far fewer wells of this kind—a number quadratic in the number of residues. We can easily afford the energy function calls needed to characterize each pairwise well. (Bottom) By precomputing a polynomial representation (blue) of the energy within each well of each pairwise term (red), we enable computation of any pairwise term in any pairwise well, and thus of the full protein energy in any energy well of the protein, solely by a quick evaluation of polynomials.
3.2 Basic least-squares method
Consider two interacting residues i and j. Let us start with the “well-behaved” case where there exists a low-degree polynomial representation of a pairwise energy throughout the allowed ranges of both residues’ internal coordinates (of the form in Eq. 1).
We employ the notation introduced in the DEEPer algorithm.11 Suppose we have RCs ir and js with pairwise energy E(ir, js, x), where x is the vector of internal coordinates (for example, dihedrals) affecting residues i and j when they have the amino-acid types corresponding to ir and js. Let , where the minimum is taken with respect to the internal coordinates over their allowed ranges for the current RCs. This definition of E⊝ is consistent with iMinDEE8 and DEEPer.11 x0(ir, js) is the set of internal coordinates that minimizes the pairwise energy.
We seek a multivariate polynomial pir,js(x) such that
| (1) |
is a good approximation to E(ir, js, x). This multivariate polynomial is approximately a finite, low-degree Taylor expansion about the minimum. However, we use least-squares fits because we have found that they perform much better than Taylor expansions that are based on numerical derivatives. The fits are performed using a training set with ten times as many samples as there are parameters (polynomial coefficients) in the fit; the sampling procedure is described in Section 3.7. The fits are cross-validated with an independent set of samples (Section 3.6). The constraint p(0) = 0 is applied, so the real energy and the polynomial will agree exactly at the minimum-energy point. This constraint is easily implemented by not including a constant term in the polynomial, and reflects the need for the highest accuracy to be attained for the lowest-energy, and thus most biophysically reasonable, conformations. As a result of this constraint, all values of the polynomial on its domain will be nonnegative. Fitting begins with a multivariate quadratic fit and then moves up to higher degrees as needed (see Section 3.6). Since polynomials are linear with respect to their coefficients, the fitting is a linear least-squares problem.
This method can be generalized without modification to intra+shell energies as well as to any continuous degrees of freedom, such as newly modeled backbone perturbations11 or rigid-body motions of ligands. In every case, the number of variables for the polynomial will be the number of continuous degrees of freedom that define the conformation of the residue or residue pair of interest. For example, in a pairwise energy computation for a rotamer of lysine and a rotamer of valine with only sidechain flexibility, the polynomial will be in five variables (the four dihedrals of lysine and one dihedral of valine). The polynomial coefficients are real numbers.
Let r be an RC assignment, represented as a tuple of RCs with one RC for each residue. Let ir be the rotamer in r at residue i. To approximate the minimized energy of an enumerated conformation r, instead of minimizing the full energy
| (2) |
with respect to the system’s continuous degrees of freedom x, we simply minimize the polynomial approximation
| (3) |
with respect to x. These least-squares approximations achieve high accuracy for the low-energy wells of rotamers and local backbone motions, i.e., the portions of conformational space where both the continuous degrees of freedom and the energy are relatively close to the local minimum of the pairwise energy. Higher energies may also be found close in conformational space to the local minimum, but these energies indicate strained conformations unlikely to be seen in nature. Thus, for a “well-behaved” energy term whose energy is unstrained throughout the bounds on continuous degrees of freedom that define our current RCs, EPIC simply performs a least-squares fit of the energy, to represent it as a multivariate polynomial with respect to the continuous degrees of freedom.
Many RCs do however contain both regions with feasible energies and regions with higher energies that represent biophysically inaccessible conformations such as steric clashes. These RCs present difficulties for the basic least-squares fit, but the following algorithmic modification avoids this problem.
3.3 Modified least-squares method
To handle RCs with high-energy regions, we note that we do not necessarily need the polynomial to be a good approximation for the energy throughout the entire region allowed by the box constraints. We merely require that Eq. (2) be a good approximation for Eq. (3) when used with biophysically feasible, minimized values of x. In particular, we can expect that the optimal, minimized structure has no clashes or other particularly large local strains. We have the advantage that while interaction energies in proteins can rise steeply towards infinity in the case of steric clashes, there is no physical phenomenon that will cause interaction energies to decrease steeply towards negative infinity. So energies are relatively well-behaved in low-energy regions. We can thus effectively partition the conformational space into relatively smooth, low-energy regions that we approximate accurately, and high-energy regions that we can rule out.
Let us denote the energy relative to the minimum as E′(ir, js, x − x0(ir, js)) = E(ir, js,, x) − E⊝(ir, js) in the pairwise case, or E′(ir, x − x0(ir)) = E(ir, x) − E⊝(ir) in the intra+shell case. Our requirements for a “good approximation” of the energy can be defined rigorously in terms of two upper bounds b1 and b2 that we place on E′. For each intra+shell or pairwise energy term, we estimate an upper bound b1 on E′ that we expect to hold for all minimized conformations that we want to output (the GMEC, or the lowest-energy c conformations if we are computing a c-conformation ensemble). The algorithm will be able to check if b1 is valid or not, so we can try again with a higher b1 if needed. Additionally, we need a second, possibly looser upper bound b2 on E′ that we are confident will be valid for all minimized conformations that we compute during our search, whether they turn out to be the GMEC or not. The value of b2 must be the same for all intra+shell and pairwise terms (b1 can be term-specific, though in practice a single value for b1 is convenient).
If EPIC is being used with the iMinDEE algorithm for conformational search,8 we can provably obtain the GMEC without considering any conformations whose energies E′ exceed the pruning interval, 8 an upper bound computed by iMinDEE for the difference between the lowest conformational energy lower bound (based on pairwise minimum energies) and the GMEC. Thus, when running iMinDEE, we can set b2 equal to the iMinDEE pruning interval. When b2 is set equal to the pruning interval, we know it is a valid upper bound on E′ for all minimized conformations computed during the search, and thus our GMEC calculation is provable. We can also do this when running DEEPer,11 which is essentially a backbone-flexible version of iMinDEE. For other algorithms we may want to set b2 based on knowledge of the system being designed—setting b2 = 2b1 is likely to be an acceptable heuristic.
Our polynomial only needs to be a good fit to E′ for values of the internal coordinates where E′ ≤ b1. For E′ > b1, we will require that the polynomial lie above b1. This will ensure that when we enumerate conformations in order of minimized energy computed using polynomials, as long as the thresholds b1 are chosen correctly, we will obtain non-clashing conformations before conformations with clashes, and these non-clashing conformations’ energies will be accurately represented by the polynomial fits. Furthermore, we will require that for b1 < E′ < b2, the polynomial should be a lower bound on E′ (Fig. 3). This will ensure that regardless of what thresholds b1 were used, we never overestimate a conformational energy that is below the threshold b2, and thus never exclude it from the enumerated list of conformations. The requirement to be a lower bound is easy to satisfy, because clashing van der Waals interactions are very steep and thus will tend to rise much more quickly than the polynomial fits. Thus, when we perform polynomial fits using thresholds, we know we will be getting a gap-free list of conformations in order of energy. If the thresholds b1 were chosen to be too low, some higher-energy conformations with underestimated energy might be included as well, but these will be limited to minimized conformations containing energy terms with E′ > b1. This condition can be checked easily. If desired, the run can be redone with increased b1 thresholds to eliminate this error. Thus, the choice of b1 affects the ultimate speed of the algorithm but not its correctness.
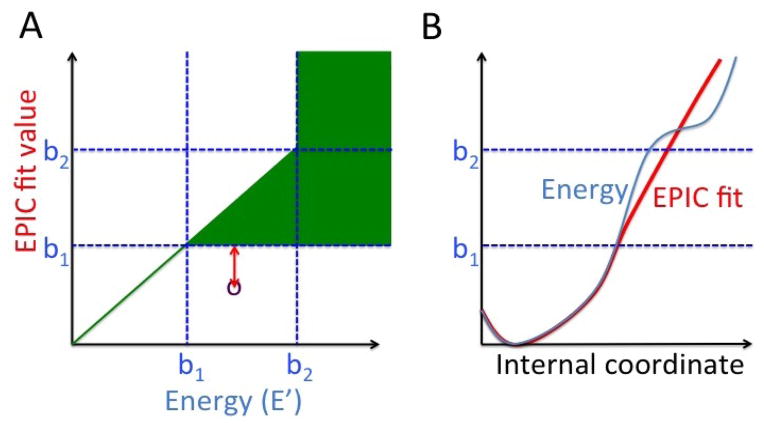
Figure 3.
(A) For each energy value E′, there is a range of “ideal” values for the EPIC fit (green). For the energies below cutoff b1, which may be found in favorable conformations, this range is just the energy (the range has zero width). For higher energies, the range is defined using the cutoffs b1 and b2. For fitting purposes, EPIC fit values are penalized by the amount they lie outside the ideal range (the purple point represents a sample conformation for a given EPIC fit incurring the penalty indicated in red). (B) Example of curves satisfying these conditions. The EPIC fit matches the energy closely up to the cutoff b1, after which it deviates from the energy, but stays in the target region shown in A, by staying below the energy. Once the energy is over b2, the EPIC fit can be either above or below the true energy without leaving the target region.
For our experiments in this work (Section 4), we have set b1 to 10 kcal/mol. This threshold was found to be sufficient for all experiments described in this work, and most other EPIC designs that we have tried. Physically, any pair of residues whose interaction energy is 10 kcal/mol worse than the optimal interaction for its current RC pair is likely in a highly strained conformation such as a steric clash. Thus a design requiring b1 greater than 10 kcal/mol is likely to be biologically infeasible. For example, the protein is likely to unfold or undergo a large and unexpected structural change rather than suffer this local strain.
Let us use z to denote a vector in the domain of our polynomial fit p. p is considered a good representation of the energy if, for some small ε > 0, the following conditions are satisfied:
For z such that E′(ir, js, z) ≤ b1, |pir,js(z) − E′(ir, js, z)| < ε.
For z such that b1 < E′(ir, js, z) < b2, b1 − ε < pir,js(z) < E′(ir, js, z) + ε.
For z such that b2 ≤ E′(ir, js, z), b1 − ε < pir,js(z).
These conditions are illustrated in Fig. 3. They can be achieved using a modified least-squares fit, using special “one-sided” penalties to enforce the inequalities in conditions 2 and 3, along with usual (two-sided) least-squares penalties to enforce condition 1. The objective function is the sum of terms from each sample in the training set. For a sample z such that E′(ir, js, z) ≤ b1, the objective function term is (pir,js(z) − E′(ir, js, z))2 (as is typical for least squares). A term of this form is also used if the lower-bounding condition is violated, i.e., if E′ < b2 but p > E′. Otherwise, the objective function term for z is (pir,js(z) − b1)2 for pir,js(z) < b1, and 0 for pir,js(z) ≥ b1.
If the modified least-squares method is applied to a set of samples that mostly have E′ > b1, then overfitting to the few points with E′ < b1 may occur no matter how many samples there are. As an extreme case, if all samples have E′ > b2, then almost any polynomial with very large values throughout its domain will give a 0 value for the objective function, but this may still provide a very poor description of the energy landscape. To avoid this situation, when a test set of n samples is being drawn and n/2 samples with E′ > b1 have been drawn already, then if more samples come up with E′ > b1, they are redrawn to ensure that a sufficient number of samples with E′ ≤ b1 is available (Section 3.7). Minimization-aware dead-end elimination pruning8 (both singles and pairs pruning) is performed before computation of the polynomial fits, since the pruned rotamers and pairs won’t be needed during enumeration. This pruning usually eliminates the clashing rotamers and pairs, leaving rotamers and pairs that are well suited for simple polynomial representations.
This objective function can be optimized efficiently because it is convex with respect to the polynomial coefficients (see Section 3.4). But we found general-purpose convex minimizers to be rather time-consuming for the higher-order fits. To address this, the algorithm described in Section 3.4 was developed. It exploits specific properties of the objective function to obtain a more efficient and reliable fit than a general-purpose convex minimizer would be likely to obtain.
3.4 A fast algorithm for modified least-squares fitting
The following algorithm performs a modified least-squares fit, providing a useful polynomial for energy terms that include both low-energy regions, where an accurate polynomial representation of the energy surface is required, and high-energy regions that we must exclude from our search.
Let us represent our polynomial fit p(z) as p · y(z), where p is the polynomial’s vector of coefficients, y(z) is the corresponding vector of monomials built from the degree-of-freedom values z, and · is the standard inner product. For example, if z consists of the two dihedrals z1 and z2 and we are performing a quadratic fit, then y(z) will have the elements 1, z1, z2, , and z1z2. For each sample s in our training set of samples (see Section 3.7), let zs be the vector of degree-of-freedom values, and let ys = y(zs) be the corresponding vector of monomials. Let be the energy for the sample, where the minimum-energy point is defined to have zero energy. Then, a modified least squares fit consists of minimizing the objective function f to obtain best-fit polynomial coefficients pb:
| (4) |
where { } denotes the set of samples whose energies are less than or equal to b1. If we define P1 to be the set of sample points such that either
| (5) |
or
| (6) |
and we define P2 to be the set of sample points such that
| (7) |
then our objective function f becomes
| (8) |
Thus, if we know P1 and P2, minimizing the objective function is a basic least squares problem and can be solved analytically. Like basic least squares, this algorithm operates on a single “training” set of samples and provably minimizes the objective function (i.e., the error) for that training set.
We can show the objective function is convex with respect to p by noting that the contribution from each sample s is a function of the single linear combination u = p · ys of the elements of p. This contribution depends on , but it is always convex (and piecewise quadratic). If , the contribution is just the parabola . If , it’s the “truncated” or “flat-bottomed” parabola given by (b1 − u)2 for u ≤ b1, 0 for , and for . Otherwise (if ), the contribution is the “one-sided” parabola given by (b1 − u)2 for u < b1 and 0 otherwise. Hence, the objective function is a sum of convex functions, making it convex itself. Thus, minimizing the objective function to find p is tractable, with any local minimum being the global minimum. As a result, we know that if for any sets of samples P1 and P2 we have coefficients p that minimize Eq. (8) and satisfy the conditions Eq. (5–7), then the coefficients p are globally optimal.
The algorithm finds P1 and P2 iteratively. As an initial guess, P1 can be initialized to s such that , and P2 to be empty. (This corresponds to assuming that the one-sided restraints can all be satisfied perfectly.) This is followed by performing the basic least-squares computation of minimizing Eq. (8), which returns coefficients p, and recalculating P1 and P2 from p using the conditions Eq. (5–7). This procedure is then repeated using the new P1 and P2 until a self-consistent solution is found. Generally, only a small minority of the samples will be moved in and out of the least-squares problem at each iteration, so the least-squares matrix can be updated quickly at each step—this is useful because forming this matrix is the bottleneck. Typically, only a few iterations are needed.
This algorithm is actually a special case of Newton’s method, because its estimate for the objective-function minimum at each iteration is the minimum of the local quadratic Taylor expansion of the objective function. This minimum can be found analytically because the local expansion is convex.
In our implementation of this algorithm, by far the bulk of its time cost is spent in forming the matrix for the first basic least-squares fit (with initial P1 and P2). The subsequent fits are much faster because they are only sparse updates. Thus, the modified least-squares fitting is only negligibly more expensive than the first basic least-squares fitting.
3.5 Sparse atom-pair energies (SAPE)
SAPE is a method to reduce the degrees of polynomials needed by EPIC by including some non-polynomial terms in the representation of the energy.
The need for higher-order polynomial fits is driven by large values of higher derivatives. These values are contributed primarily by a small number of van der Waals (vdW) terms between pairs of atoms that are very near each other. It is possible to obtain substantial time and memory savings by evaluating these terms explicitly and fitting the rest of the energy function to a polynomial. To select atom pairs whose vdW terms are to be evaluated explicitly, a cutoff distance (3 or 4 Å; see Section 3.6) is chosen. Then, an atom pair’s vdW terms are evaluated explicitly if and only if the atoms can be found within that distance of each other within the bounds on internal coordinates for the given residue conformations. These terms are not polynomials in the degrees of freedom because they are inverse powers of distances between atoms, and the atom coordinates themselves are in general not polynomial functions of the degrees of freedom. For example, the expressions for atom coordinates in a sidechain in terms of the sidechain dihedral angles will include sines and cosines of those angles.
Once we decide to evaluate vdW terms for a given pair of atoms, it costs negligible extra time and memory to also calculate the electrostatic interaction between these atoms (since we already have the distance between the atoms).
3.6 Attaining the required accuracy
We will now describe the methods used to choose polynomial degrees for EPIC fits and ensure that fits of sufficient accuracy are obtained.
Fit accuracy is checked and controlled using cross-validation. For cross-validation purposes, a mean-square error is computed, with absolute error used below E′ =1 kcal/mol and relative error above. This can be seen as a weighting of the error terms: the weight is 1 for E′ ≤ 1 and 1/min(E′, b1) for E′ ≥ 1 (this levels off at b1 to avoid excessive underweighting of the one-sided constraints). These weights, which are continuous with respect to E′, are also used during the least-squares fitting.
Cross-validation is used to select the degree of the polynomial that is fit. Low-degree polynomials save time and memory both during the A*/enumeration step and during the precomputation step, but may not provide a sufficiently good representation. Hence, we proceed through a sequence of increasingly expensive fits (Fig. 1A), and each time a fit is completed, it is cross-validated with an independently drawn set of samples. Like the training set, this cross-validation sample set has ten times as many samples as fit parameters. If the mean-square error is below a specified threshold, the fit is stored, and if it is above, we proceed to the next method. The default threshold value is set to 10−4. However, limited investigation suggests larger thresholds still tend to keep the errors in conformations’ minimized energies small compared to thermal energy, and thus are likely acceptable as well. It is also useful to avoid doing fits with very large number of parameters, as these have enormous time and memory costs both in the enumeration and precomputation steps. Thus, OSPREY is currently set to refuse to do fits with over 2000 parameters—this way, computations that would have prohibitive time costs may still be satisfactorily completed with a slightly higher error threshold than usual.
Some of the fits use lower-degree terms for all degrees of freedom and higher-order terms for selected degrees of freedom. These selected degrees of freedom are eigenvectors vk of the Hessian from a modified least-squares quadratic fit (step 1 in the list of steps below). Letting λk be the eigenvalue corresponding to vk, we define
| (9) |
for q > 0. Let us define fn to be a polynomial fit of total degree d (e.g., f2 is a quadratic fit); fd(Dq) to be a fit to a polynomial of total degree d in all degrees of freedom plus terms of total degree d + 1 and d + 2 in the degrees of freedom in Dq; and s(n, c) to be a polynomial fit of total degree d plus SAPE with a cutoff of c Å. Fits were tried in the following order: f2, s(2, 3), f2(D10), f2(D100), f4, s(4, 4), f4(D10), f4(D100), f6, and s(6, 4).
The Stone-Weierstrass theorem32 guarantees that a sufficiently high-degree polynomial can approximate any function on any closed and bounded portion of Cartesian space to any desired accuracy. In other words, it guarantees that any energy function can be represented by EPIC to arbitrary accuracy if we allow sufficiently high-degree polynomials. The basis of Bernstein polynomials can be used to construct such approximations with guaranteed convergence to any function.33 However, for the purpose of energy representation for protein design, modified least squares is likely to provide good approximations using much lower-degree polynomials than we would obtain using the Bernstein basis, because we do not need close approximations of the high energy in clashing regions. In these regions, we only need a reasonable lower bound that is much higher than the rotameric wells. This strategy keeps the polynomial degrees low enough to be practical.
3.7 Sampling to train and validate least-squares fits
Training and validation sets for EPIC fits consist of sample conformations of the residue(s) involved, specified as vectors of internal coordinates, drawn from throughout the allowed region of conformational space.
By default, samples for both training and validation sets were sampled uniformly (i.e., each degree of freedom was sampled uniformly and independently from the interval corresponding to the current rotamer or RC). Ten samples were always used in each of these training and validation sets for each parameter in a fit. However, if most of the samples corresponded to energies above the threshold b1 (see Section 3.3), then overfitting could result, because for such samples there are infinitely many polynomial values that yield zero error. To avoid this, we need sufficient samples from the set B of conformations with energies below b1; B is the set of conformations where the polynomial needs to be quantitatively accurate. We ensure sufficient samples from B by rejecting samples outside B whenever we desire n samples in total and we already have n/2 samples outside B, and thus drawing the rest of our samples uniformly from B by rejection sampling. If 10,000 samples are rejected consecutively, indicating that B is too small for efficient rejection sampling, then the Metropolis algorithm34 is used to sample from B.
We have confidence in the parameters obtained by fitting to the training samples for three reasons. First, a useful measure of the accuracy of a polynomial approximation to the energy surface is that there is a low probability that any region of the energy surface deviates significantly from the polynomial approximation (except for high-energy regions approximated by similarly high values of the polynomial). Since our cross-validation of each polynomial fit uses a large number of independent samples—ten times the number of parameters—we are left with a very low chance that our cross-validation samples will miss any such regions. Thus an insufficiently accurate polynomial surface will be detected upon cross-validation and remedied by an increase in polynomial degree. Second, errors in the minimized energies obtained using polynomial approximations are consistently low, as shown in our computational experiments (Table 1). Third, we expect the energy function to be relatively smooth in the vicinity of a minimum, since the gradient must be zero at the minimum, and thus we expect a polynomial of relatively low order (e.g., the Taylor series of the energy) to yield a good approximation in the vicinity of a minimum.
Table 1.
GMEC calculation test cases. EPIC with SAPE solved each of these cases; in most cases, A* without EPIC was slower or did not finish within the time limit (†). Minimization (“Min.”) speedup (ratio of single-conformation minimization time without EPIC vs. time with EPIC) is reported for EPIC with and without SAPE. Similarly, A* speedup denotes the ratio of total A* time without EPIC vs. time with EPIC. Fit times (times to calculate the EPIC polynomials) and total calculation times (Tot. time) are reported for EPIC calculations with SAPE, in minutes, calculated without parallelization of fitting. “GMEC energy error” is the absolute difference between GMEC energies calculated with and without EPIC, and is reported in kcal/mol. “Fit DNF” means the time limit was exceeded during polynomial fit precomputation, and “Bad fit” means that fits for EPIC without SAPE, even at the maximum allowed polynomial degree, did not accurately represent the energy. This problem is rescued by SAPE for these cases. When neither A* without EPIC nor EPIC without SAPE was successful, the A* speedup without SAPE cannot be calculated and is listed as “n/a.” EPIC was performed with minimization of partial conformations in all cases.
| Protein name | PDB code | Mutable residue count | Min. speedup with SAPE | Min. speedup no SAPE | A* speedup with SAPE | A* speedup no SAPE | Fit time (min) | Tot. time (min) | GMEC energy error |
|---|---|---|---|---|---|---|---|---|---|
| Scorpion toxin | 1aho | 7 | 26.58 | 13.60 | 26.88 | 48.84 | 42 | 49 | 0.01 |
| Scorpion toxin | 1aho | 9 | 23.59 | 14.53 | 105.70 | 143.52 | 435 | 456 | 0.03 |
| Scorpion toxin | 1aho | 12 | 29.66 | Fit DNF | >142.9† | n/a | 566 | 1119 | 0.04 |
| Scorpion toxin | 1aho | 14 | 26.49 | Fit DNF | >4.30† | n/a | 8079 | 19446 | 0.05 |
| Cytochrome c553 | 1c75 | 6 | 41.03 | 24.48 | 102.23 | 73.78 | 57 | 63 | 0.01 |
| Atx1 metal- lochaperone | 1cc8 | 7 | 36.49 | Bad fit | 75.97 | Bad fit | 332 | 630 | 0.05 |
| Bucandin | 1f94 | 7 | 15.89 | 5.03 | 250.13 | 179.70 | 243 | 427 | 0.03 |
| Nonspecific lipid-transfer protein | 1fk5 | 6 | 35.25 | 144.14 | 24.17 | 24.87 | 4 | 6 | 0.01 |
| Transcription factor IIF | 1i27 | 7 | 27.66 | Fit DNF | 320.41 | Fit DNF | 2205 | 3793 | 0.03 |
| Ferredoxin | 1iqz | 9 | 59.36 | 132.22 | 96.37 | 127.82 | 36 | 41 | 0.02 |
| Trp repressor | 1jhg | 7 | 41.16 | Bad fit | 139.39 | Bad fit | 162 | 367 | 0.04 |
| Fructose-6-phosphate aldolase | 1l6w | 6 | 194.30 | 178.60 | 152.26 | 77.73 | 197 | 264 | 0.03 |
| Cephalosporin C deacetylase | 1l7a | 8 | 157.71 | Fit DNF | >3170† | n/a | 3341 | 4784 | 0.04 |
| PA-I lectin | 1l7l | 6 | 58.21 | 141.90 | 30.77 | 32.60 | 41 | 55 | 0.01 |
| Phosphoserine phosphatase | 1l7m | 7 | 69.84 | 340.73 | 810.68 | 998.47 | 246 | 624 | 0.03 |
| alpha-D- glucuronidase | 1l8n | 5 | 355.82 | 443.00 | 0.99 | 0.93 | 691 | 1410 | 0.01 |
| Granulysin | 1l9l | 7 | 50.66 | 34.25 | 2.54 | 13.60 | 94 | 119 | 0.01 |
| gamma-glutamyl hydrolase | 1l9x | 5 | 111.57 | 468.00 | 1.86 | 1.87 | 103 | 264 | 0.00 |
| Ferritin | 1lb3 | 5 | 103.05 | 33.31 | 51.68 | 49.33 | 148 | 174 | 0.01 |
| Cytochrome c | 1m1q | 8 | 80.79 | 61.94 | 320.23 | 486.77 | 39 | 97 | 0.05 |
| Hypothetical protein YciI | 1mwq | 8 | 60.05 | 48.30 | 56.10 | 16.41 | 60 | 133 | 0.00 |
| Ponsin | 2o9s | 14 | 68.32 | Bad fit | >45.81† | n/a | 218 | 1732 | 0.41 |
| Scytovirin | 2qsk | 10 | 64.94 | 35.45 | 296.06 | 329.99 | 95 | 188 | 0.12 |
| Dihydrofolate reductase | 2rh2 | 14 | 54.92 | 30.28 | 771.86 | 521.44 | 9 | 37 | 0.01 |
| Putative monooxygenase | 2ril | 8 | 159.98 | 580.00 | 28.36 | 66.72 | 7 | 11 | 0.01 |
| dpy-30-like protein | 3g36 | 4 | 36.44 | 17.96 | 5.77 | 10.00 | 23 | 30 | 0.05 |
| HIV gp120 | 3u7y | 16 | 141.17 | Bad fit | >14.33† | n/a | 1773 | 7762 | 0.06 |
A* without EPIC did not finish within the time limit, so we report a lower bound on the speedup: the ratio of the time limit (17 days) to the A* time with EPIC and SAPE.
3.8 Application in proteins design algorithms
Once the polynomials are computed, they can be used in protein design algorithms wherever the energy function would ordinarily be called. The GMEC will simply be the set of rotamers for which the minimized value of Eq. (3) with respect to x has the lowest possible value.
The simplest method to provably find the GMEC using EPIC is to use a protein design algorithm that enumerates conformations in order of a lower bound, and then instead of minimizing the full energy (Eq. 2), merely minimizing the polynomial-based energy (Eq. 3) to compute the energy for each enumerated conformation (Fig. 2). For example, iMinDEE/A*8 can be used for this enumeration process, and we use this algorithm in our computational experiments (Section 3.10).
EPIC can also be applied in free energy calculations using the K* algorithm,7,12 which approximates binding constants as ratios of partition functions computed from low-energy conformations enumerated by A*. During these calculations, one can simply use the polynomials instead of the energy function to compute the partition function, given the enumerated RC assignments. This method gives a constant-time speedup, determined by the ratio of time to evaluate the energy function versus the EPIC energy.
An additional speedup is possible for branch-and-bound protein design algorithms (e.g., A*14,15) that use a tree structure for conformational search. These algorithms build nodes that each represent a subset of conformational space and are scored using a lower bound on the conformational energies in that space. In each node’s conformational space, some residues are restricted to a single RC; these RCs are referred to as assigned to their respective residues. At each level of the tree, an RC is assigned to one more residue. One can use the EPIC polynomials to improve the lower-bound energy for each of these nodes. At each node, we need to compute a lower bound L for the conformational energy qr, which is defined in Eq. (3): that is, we compute L such that
| (10) |
for all RC assignments r and all degree-of-freedom values x that are part of the node’s conformational space. If r is known (i.e., if RCs are fully assigned at all residue positions), then a tight lower bound can be computed trivially by local minimization with respect to x. Otherwise, we let qr(x) = E⊝(r) + Ep(r, x), where Ep consists only of EPIC polynomials:
| (11) |
| (12) |
Now, if we compute lower bounds L⊝ and Lp such that L⊝ ≤ E⊝(r) and Lp ≤ Ep for all r, x in our conformational space, then L = L⊝ + Lp will satisfy Eq. (10), giving us a valid lower bound. Computation of L⊝ has been described previously, because lower bounds of this form are computed in iMinDEE8 and DEEPer.11 To compute Lp, we use the fact that EPIC polynomials are always nonnegative; thus, for any r and x and any subset S of the residues we are modeling,
| (13) |
If we let S be the set of residues with fully assigned RCs, then there is only one possible RC ir for each residue i ∈ S, and so we can find the minimum of Eq. (13),
| (14) |
exactly by local minimization with respect to x. Eq. (14) is a lower bound on Ep(r, x), and thus we set Lp equal to it, giving us a score for our node. We note that Lp is strictly nonnegative, because Eq. (13) and thus Eq. (14) are always nonnegative.
Because this continuous minimization with respect to x is more expensive and has to be performed separately at each node, it is evaluated in a lazy31 fashion in our A* implementation. Nodes are assigned the traditional, discrete lower bound L⊝ when they are generated; this bound is fast to compute. The A* priority queue contains nodes both with and without the polynomial contribution Lp included. When a new node is popped from the queue, we check if Lp is present or not. If it is, we expand the node, and if it is not, we compute Lp and insert the node back in the priority queue. This ensures that nodes come off the priority queue in order of their complete lower bound L⊝ + Lp, as is necessary for A* to function correctly. However, it also ensures that we do not waste time computing Lp for nodes whose L⊝ is high enough to preclude expansion. This method gives a combinatorial speedup, since a high polynomial contribution for a partial conformation can effectively prune an entire branch of the A* tree. In practice, though, the large constant speedup from EPIC minimization of fully assigned conformations tends to be more significant (Section 4.1, Table 2).
Table 2.
Partition function calculation results. EPIC was performed with SAPE in all cases. As in Table 1, EPIC solved all cases, and cases for which A* without EPIC did not finish are denoted by †.
| Protein name | PDB code | Mutable residue count | A* speedup due to EPICa | A* speedup due to partialb |
|---|---|---|---|---|
| Histidine triad protein | 2cs7 | 14 | >48.48† | 1.52 |
| Ponsin | 2o9s | 14 | >1131† | 0.96 |
| Transcriptional regulator AhrC | 2p5k | 11 | >256.0† | 1.34 |
| Scytovirin | 2qsk | 10 | 5698.04 | 1.01 |
| Hemolysin | 2r2z | 12 | >217.7† | 1.24 |
| Dihydrofolate reductase | 2rh2 | 14 | >50.45† | 2.16 |
| Putative monooxygenase | 2ril | 8 | 1121.34 | 1.01 |
| alpha-crystallin | 2wj5 | 15 | >29.06† | 0.80 |
| Cytochrome c555 | 2zxy | 14 | >8.87† | 3.32 |
| High-potential iron-sulfur protein | 3a38 | 13 | >1916† | 1.40 |
| ClpS protease adaptor | 3dnj | 12 | >50.25† | 0.93 |
| Putative monooxygenase | 3fgv | 10 | >9639† | 1.57 |
| Protein G | 3fil | 14 | >1475† | 1.31 |
| Viral capsid | 3g21 | 15 | >7.84† | 1.21 |
| dpy-30-like protein | 3g36 | 4 | 211.87 | 0.91 |
| Hfq protein | 3hfo | 10 | >194.8† | 1.45 |
| Cold shock protein | 3i2z | 14 | >872.8† | 1.24 |
| Trypsin | 3pwc | 10 | >624.2† | 1.04 |
| Trypsin | 3pwc | 11 | >131.8† | 2.07 |
A* without EPIC did not finish within the time limit, so we report a lower bound on the speedup: the ratio of the time limit (17 days) to the A* time with EPIC.
Ratio of total A* time without EPIC vs. total A* time with EPIC and minimization of partial conformations.
Ratio of total A* time with EPIC but no minimization of partial conformations vs. total A* time with EPIC and minimization of partial conformations.
3.9 Complexity of energy evaluations
The speedup due to EPIC can be explained in terms of the asymptotic costs of EPIC polynomial evaluations compared to direct energy function calls. The cost of evaluating an EPIC polynomial scales as the number of terms in the polynomial. This cost is itself a polynomial (usually quadratic) in the number of internal coordinates of the residue pair (or single residue, in the intra+shell case) of interest. By contrast, the cost of evaluating a molecular mechanics-based energy function is generally quadratic in the number of atoms involved, since distances between all pairs of atoms need to be considered. EPIC achieves a marked speedup because most residues have far more atoms than significantly flexible internal coordinates. For example, most protein residues have two or fewer sidechain dihedrals, but over ten atoms. The remaining internal coordinates—bond length, angles, etc.—are relatively inflexible. Polynomial evaluations are also performed entirely by addition and multiplication, which are much faster than the more complicated elementary operations (trigonometric functions, square roots, etc.) needed to evaluate molecular mechanics energy terms.
When quantum-mechanical energy functions are introduced, all the electrons must be accounted for explicitly, and even fairly approximate quantum-chemical methods have time costs that are higher-order polynomials with respect to the number of electrons. For example, any method that accounts for repulsions between all atomic orbitals (e.g., Hartree-Fock and all post-Hartree-Fock methods) must calculate repulsion integrals for all quadruples of atomic orbitals, and there are at least as many atomic orbitals as electrons. And there are far more electrons than there are atoms, and far more atoms than internal coordinates, giving EPIC an extreme performance advantage. Yet EPIC can represent the same energy surface to a high degree of accuracy, once the EPIC polynomials have been precomputed.
Whether EPIC is used or not, these types of pairwise energy evaluations must be performed for every pair of residues in a design system. In general, this means the number of pairwise energy evaluations needed is quadratic with respect to the number of residues in the system. This number can be reduced if a cutoff is applied to remove interactions between distant residues. However, this speedup applies equally for EPIC and non-EPIC calculations.
3.10 Computational Experiments
Protein design calculations were performed in OSPREY1,3,7,23,24 with and without EPIC to investigate (a) what previously intractable systems become newly tractable with EPIC, (b) what speedups EPIC brings to conformational enumeration for previously tractable systems, and (c) what types of polynomial representations are needed for these purposes. EPIC runs were performed with SAPE and with conformational minimization for partially assigned conformations during A* search, and for comparison, runs with either one of these features omitted were also performed.
Times were compared for the A* search, including conformation enumeration and minimization, because this is the portion of the design that is not guaranteed to complete in polynomial time and thus is the bottleneck. As part of the EPIC runs, GMEC energies were also computed using the regular energy function to compare to the EPIC results, and the ratio of minimization times with and without EPIC was computed. For runs with multiple conformations very close in energy to each other (within the error range of EPIC, typically <0.1 kcal/mol), the time ratios were averaged.
All minimizations were performed using a cyclic coordinate descent minimizer, which is now included in OSPREY. Default OSPREY energy function settings were used where applicable: AMBER with EEF1 solvation and a distance-dependent dielectric constant of 6. Rotamers were determined using the Penultimate rotamer library.13
Test systems were chosen to evaluate both partition function and GMEC calculations, and to include all three types of continuous degrees of freedom used in OSPREY: sidechain dihedrals, backbone perturbation (shear and backrub) parameters,11 and rigid-body rotations and translations of strands. Some of the tests are intended to be within the scope of previous methods, allowing a quantitative comparison of running times, while others are intended to show EPIC can compute previously intractable GMECs and partition functions with provable accuracy.
For GMEC calculations (Table 1), the first set of systems used was taken from Gainza, Roberts, and Donald,8 and featured only sidechain dihedral flexibility. The structures for these correspond to PDB codes 2o9s, 2qsk, 2rh2, 2ril, and 3g36. The second set of systems was taken from Hallen, Keedy, and Donald,11 and included both sidechain and backbone flexibility. The structures’ PDB codes were 1aho, 1c75, 1cc8, 1f94, 1fk5, 1i27, 1iqz, 1jhg, 1l6w, 1l7a, 1l7l, 1l7m, 1l8n, 1l9l, 1l9x, 1lb3, 1m1q, and 1mwq. Three variants of the 1aho system with more residues were tried as well. Finally, a GMEC calculation was performed for the complex of the HIV surface protein gp120 with the broadly neutralizing antibody NIH45-46 (PDB code 3u7y35).
To investigate the application of EPIC to partition function calculations (Table 2), we first chose systems with only sidechain dihedral flexibility from Gainza, Roberts, and Donald8 and calculated a partition function for the unliganded protein, with wild-type amino acids at all residue positions, to within 97% guaranteed accuracy. Partition function calculations such as these are the key operation in K*7,12 calculations. The structures for these correspond to PDB codes 2cs7, 2o9s, 2p5k, 2qsk, 2r2z, 2rh2, 2ril, 2wj5, 2zxy, 3a38, 3dnj, 3fgv, 3fil, 3g21, 3g36, 3hfo, and 3i2z. Furthermore, a K* run is presented for trypsin with a small-molecule inhibitor (PDB code 3pwc); the run is tractable with EPIC but fails to finish without it. Unlike the calculations for the other, monomeric structures, the K* run for trypsin involves calculation of three partition functions: one for the protein, one for the ligand, and one for the complex.
Each design was allowed 17 days of total runtime, after which those that had not finished were deemed to have exceeded the time limit and were terminated. A* times with EPIC ranged from 0.7 seconds to 4 days, and the speedups due to EPIC are shown in Tables 1 and 2.
In these experiments, fitting was performed without parallelization. However, the computation of the EPIC polynomial for each pair of RCs is an independent operation, so each can be done in parallel, meaning that parallelization to p processors will give a p-fold speedup as long as p does not approach the number of RC pairs. OSPREY currently supports computation of each residue pair in parallel, so the speedup holds as long as p does not approach the number of residue pairs. In practice however, for large systems, pruning and A* take longer than the polynomial fitting, so this parallelization may not be necessary. Additionally, once the EPIC fits have been computed for a system, there may be a large number of computations that can be performed using it—calculation of partition functions for many sequences, computation of GMECs for various subsets of the sequence space, etc. These extensive reuses of the fits may be especially desirable when designing a library of sequences for experimental testing—if one performs various optimizations with different assumptions and tests top sequences from each optimization, the results will be more robust to errors in the assumptions.
To investigate the ability of EPIC to represent quantum-mechanical energy functions, EPIC calculations were also performed on the aspartame dipeptide (extracted from PDB code 1a8j36) with the energies for EPIC samples evaluated using NWChem37 instead of using OSPREY’s usual energy function. Calculations were performed at the SCF level of theory with STO-3G and with 6-31G** basis sets, and also at the MP2 level of theory with a STO-3G basis set.20 For each rotamer of each residue, dihedrals were sampled within the allowed range for the rotamer and the total energy of the dipeptide was fit to a polynomial.
3.11 Applications of EPIC to other algorithms
For this study, EPIC was implemented in the context of the OSPREY protein design package OSPREY1,3,7,23,24 to run along with the algorithms (iMinDEE, DEEPer, and K*) and pairwise energy functions already implemented in OSPREY. However, EPIC would enable some other capabilities in different implementations.
First, EPIC can be applied in the context of other protein design algorithms. For example, one can apply it an iterative algorithm like FASTER38 or Monte Carlo34 that tries to find a suitably low-energy conformation by accepting or rejecting rotamer changes based on the energies of conformations with these changes. Whenever the energy is needed for a rotamer assignment, the EPIC energy for the protein can be locally minimized starting at the ideal internal coordinate values for that rotamer assignment. In this case, the matrix of EPIC polynomials substitutes directly for the matrix of pairwise rotamer energies commonly used to calculate conformational energies for these algorithms in the absence of continuous flexibility. EPIC could even be used for molecular dynamics, since most residue pairs in a molecular dynamics trajectory4 will spend most of their time in fairly relaxed conformations—the region of conformational space modeled by EPIC. In all these cases, EPIC energy evaluations would be markedly faster than regular energy function calls, particularly for expensive energy functions. Thus, EPIC would provide a substantial speedup for any algorithm whose bottleneck is energy function calls.
For docking algorithms39 that require sidechain optimization or local backbone optimization, EPIC can be used both for conformation scoring and for conformational optimization using any of the above algorithms.
3.12 EPIC can accommodate higher-than-pairwise energies
EPIC was implemented in this work to handle pairwise energy functions (in the sense of a sum of 1-body and 2-body energies with no terms dependent on three or more residues’ degrees of freedom), because these are currently typical for protein design and include the AMBER, CHARMM, and EEF1 energy functions we use in OSPREY. However, the true energy of proteins is not exactly pairwise decomposable, and EPIC could easily accommodate higher-order terms. EPIC simply requires that each energy term correspond to a set D of degrees of freedom, constrained to a region in which they are relatively well-behaved (e.g., dihedrals at each residue constrained to a single rotamer); we can sample D subject to the constraints and then fit the energies as a polynomial function with domain D. Thus, for any set R of more than two interacting residues, for each RC assignment to those residues, we can fit an EPIC polynomial, and thus describe the energy terms for R.
In practice, the number of sets of residues that can interact significantly is quite limited, because residues typically must be physically near each other to have significant higher-than-pairwise interactions. For example, if we have a Ramachandran-based potential, its terms each depend on the ψ and ϕ backbone dihedrals of a certain residue r, and thus depend on the conformations of the three residues r − 1, r, and r + 1. Likewise, the conformation of a residue i can induce polarization effects in a nearby residue j that will affect the interactions of j with another residue k, and this effect can be quantified using quantum chemistry, but i and j have to be physically very close to each other (≪1 nm) for this effect to be significant (and j and k have to be fairly close too—probably subnanometer as well, since the potential of an induced dipole falls off faster than 1/d2 with distance d). Hence, EPIC can be used to model any realistic energy function, by accounting for all sets of residues with significant energetic interactions.
4 Results
Computational experiments were performed to measure what kinds of polynomial fits are necessary to accurately model different proteins with different degrees of freedom and energy functions, and what speedups EPIC brings to DEE/A* and K* calculations. The results demonstrate that EPIC brings a substantial speedup to design calculations when proteins are modeled as in previous OSPREY designs.1,3,8,11,23 They also show that EPIC efficiently represents energies calculated by quantum chemistry, and is a potentially decisive tool for using both realistic, continuous flexibility and quantum-mechanical energy functions in protein design.
4.1 Application to protein designs
First, computational experiments were performed to compare GMEC search with and without EPIC, as described in Section 3.10. Key portions of the design calculation were timed with and without EPIC to determine the speedup for these portions (Table 1). On average, minimization of fully enumerated conformations was 79-fold faster using EPIC than with traditional energy function calls. Overall A* speedups due to EPIC averaged 167-fold (Fig. 5A). The overall A* speedup is likely greater than the minimization speedup because of the way OSPREY’s standard energy function is implemented. Each time the energy function is run on a new sequence, setup time (e.g., initialization of the energy function) is required to identify electrostatic, van der Waals, and solvation terms that will be necessary for that sequence. This setup time is eliminated by EPIC, and is not counted as part of the minimization time here, but it may be performed an exponential number of times without EPIC, since minimizations may be required for an exponential number of sequences. Runs that did not finish without EPIC are not included in these averages. 85% of the fits in these experiments were quadratic, with no SAPE needed (Figure 5B). GMECs from EPIC runs showed good agreement between energies from minimization of EPIC energies and energies from the actual energy function. The average energy difference was 0.04 kcal/mol, which is less than one-tenth of thermal energy at room temperature (0.592 kcal/mol, calculated as the universal gas constant times a room temperature of 298° K) and thus functionally insignificant.
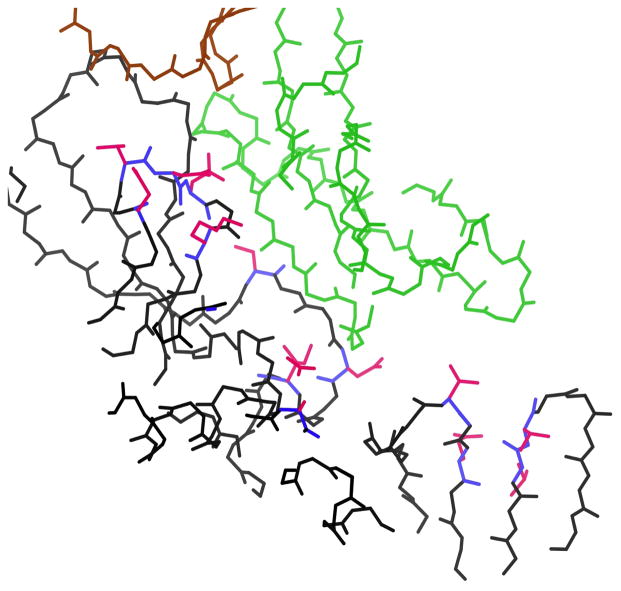
Five of the 27 systems finished only with EPIC, demonstrating that EPIC allows design of larger and more diverse systems than were previously designable. For example, a redesign of the complex of HIV surface protein gp120 with the antibody NIH45-46 did not finish when run without EPIC, but finished with EPIC using about a day of A* time (Fig. 4). This redesign allowed the mutation of 16 residues all over the gp120 surface in the interface—five in the D-loop of gp120,40 which is central to the interaction with NIH45-46, and the other 11 scattered through other parts of the interface in various types of secondary structure. Redesigns of the gp120 surface to achieve specific binding to particular antibodies has been instrumental in the development of probes to isolate these antibodies from sera.28 Redesign of the antibody surface of a gp120-antibody complex has also been effective in optimizing antibody affinity,25 which is useful for passive immunization and immunogen design. Interestingly, the redesign of the NIH45-46 complex yielded 12 top conformations within 0.06 kcal/mol of each other—two from the top sequence and ten from a double mutant. This high density of favorable conformations suggests the complex is entropically favored, a result consistent with the observed high affinity of NIH45-46 for gp120, attained through extensive affinity maturation of the antibody.
Figure 4.
Mutatable residues in the redesign of the surface of the HIV surface protein gp120 in complex with the broadly neutralizing antibody NIH45-46 (PDB code 3u7y35). This design finished only when EPIC was used. Mutatable residues, blue backbone and pink sidechains; gp120, black backbone; NIH45-46 heavy chain, green backbone; NIH45-46 light chain, brown backbone.
Two variations of EPIC were also tried for these systems. It was found that minimization of partial conformations during A* (Section 3.8) provides a speedup (2.3-fold on average), though it is not nearly as great as the speedup from faster minimization of fully assigned conformations (Fig. 5). Furthermore, EPIC without SAPE was often effective; however, under some circumstances it was unable to provide accurate fits (as usual, trying only the polynomial degrees described in Section 3.6). In systems where EPIC without SAPE was effective, it averaged insignificantly (1.1-fold) slower than EPIC with SAPE for A*. However, there were four systems that required SAPE to give accurate results (out of 27; Table 1), including the HIV gp120 complex with antibody NIH45-46 (Fig. 4). There were also four systems that exceeded the time limit during fitting. These limitations on EPIC without SAPE do not indicate a fundamental theoretical barrier, because in principle the Stone-Weierstrass theorem guarantees an accurate fit if the polynomial degree is sufficiently increased (see Section 3.6). However, they do indicate that EPIC without SAPE may sometimes require polynomial degrees that are prohibitively time-consuming for typical protein designs, and/or a higher numerical precision than the double precision efficiently supported in Java and thus used in OSPREY.
Experiments were also performed to compare partition function calculations with and without EPIC (Table 2). To obtain a provably good approximation to the partition function,7,12 many more conformations must be enumerated and minimized than for GMEC calculations. As a result, marked speedups were achieved by EPIC (Fig. 5C). Out of the 19 systems for which EPIC finished, only three finished without EPIC (average speedup 2000-fold). The speedup in EPIC designs from minimization of partial conformations was only modest (1.4-fold).
With an A* speedup of 2–3 orders of magnitude, designs that would previously take years can be performed with EPIC in days. This will allow many designs that would otherwise be considered intractable to be completed using EPIC.
4.2 Quantum-mechanical energies
In addition to classical mechanics-based energy functions, we also used EPIC to fit conformational energies of the aspartame dipeptide calculated using quantum-mechanical models of electronic structure. EPIC fits for aspartame showed that quantum-mechanical energies and AMBER and EEF1 energies can be represented by polynomials of very similar degree, i.e., energy surfaces from quantum chemistry are just as polynomial-like as energy surfaces from molecular mechanics. SAPE was not found to significantly increase the accuracy of the fits, and thus were not included, though it is likely that reparameterized van der Waals and/or electrostatic terms (or other specially fit functions of the atom-pair distance) would be able to improve fit quality. This discrepancy indicates that the atom-pair energies used in SAPE are a poor approximation to the interactions between the same atom pairs predicted by quantum mechanics, and thus that energies returned by quantum-mechanical and molecular-mechanics methods are substantively different.
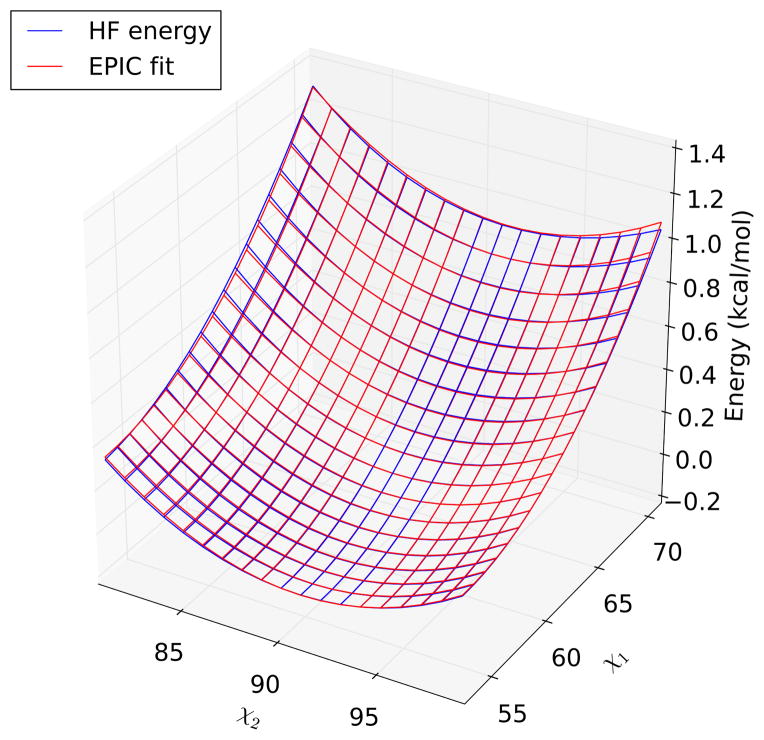
For Phe 2 of aspartame, the same types of polynomial fits were needed for Hartree-Fock with a STO-3G basis set, Hartree-Fock with a 6-31G** basis set, and the usual AMBER/EEF1 energy function (Fig. 6). These were quadratic fits for three rotamers and a quadratic fit plus quartic fits on D10 for the fourth. MP2 with a STO-3G basis set also required quadratic fits for the first three rotamers, and required a quadratic fit plus quartic fits on D100 for the fourth.
Figure 6.
Intra-residue energy calculated for Phe 2 of aspartame using Hartree-Fock theory with a STO-3G basis set, and quadratic EPIC fit, as a function of the two sidechain dihedrals. The fit is very close to the energy surface, though a slight discrepancy is visible in the upper right-hand corner (χ1 ≈ 70°, χ2 ≈ 100°).
For Asp 1, AMBER/EEF1 required quadratic terms plus quartic terms on D10 for three rotamers and on D100 for two. Both Hartree-Fock and MP2 with a STO-3G basis set required slightly simpler fits: only quadratic for one rotamer, quadratic plus quartic terms on D10 for three, and quadratic plus quartic terms on D100 for one.
These results show that quantum and polarization-type effects can be represented effectively by polynomial fits, and the polynomial degrees needed are essentially the same as for AMBER/EEF1.
5 Conclusions
EPIC eliminates the current bottleneck in minimization-aware protein design by performing energy function calls only in a precomputation step. It thus opens several avenues for more accurate and efficient design calculations. More residues can now be mutated, and more ligands can be tested. Additional continuous conformational degrees of freedom (e.g., in the backbone) can be modeled, and minimization can be performed over a greater range for each degree of freedom when appropriate. In this sense, EPIC helps protein design algorithms emulate the extensive continuous flexibility of molecular dynamics algorithms, while searching an exponentially large sequence space that would be intractable for molecular dynamics-based design. Furthermore, more accurate but (previously) slower energy functions can be incorporated without any asymptotic increase in computation time.
The polynomial representation of energy provided by EPIC could also allow dedicated algorithms for polynomials to be used in energy calculations. For example, since exact derivatives of polynomials are trivial to compute, EPIC is very amenable to rapid calculation of energy derivatives with respect to internal coordinates, which are used in many minimization algorithms.41,42 Note that the gradient of the EPIC polynomials may not approximate the gradient of the energy (i.e., forces) to the same degree of accuracy as the polynomials approximate the energy, because the polynomials are fit to the energies rather than the forces. Thus, differentiation of the fit polynomial may amplify noise. However, when we are numerically minimizing the polynomial approximation to the energy, we require derivatives of the polynomials themselves.
EPIC fits are tractable, accurate approximations that provide a new understanding of the energy landscape of proteins in the vicinity of ideal rotamers, and more generally in the vicinity of energy minima. This is useful because the high dimensionality of conformational space makes direct visualization difficult.
By enabling better modeling both of conformational space and of conformational energies, EPIC moves us closer to the goal of algorithms that can produce reliable predictions for our biomedically and biologically important protein and drug design problems. EPIC is thus offered to the protein design community both as an immediate speedup in designs and as an enabling technology for future improvements.
Software Availability
Our implementation of EPIC, as part of the OSPREY1,3,7,23,24 open-source protein design software package, is available for free download at http://www.cs.duke.edu/donaldlab/osprey.php.
Acknowledgments
We would like to thank all members of the Donald lab for helpful comments, and the PhRMA foundation (MAH) and NIH (grant R01-GM-78031 to BRD) for funding.
References
- 1.Frey KM, Georgiev I, Donald BR, Anderson AC. Proc Natl Acad Sci U S A. 2010;107:13707–13712. doi: 10.1073/pnas.1002162107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Roberts KE, Cushing PR, Boisguerin P, Madden DR, Donald BR. PLoS Comput Biol. 2012;8:e1002477. doi: 10.1371/journal.pcbi.1002477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chen CY, Georgiev I, Anderson AC, Donald BR. Proc Natl Acad Sci U S A. 2009;106:3764–3769. doi: 10.1073/pnas.0900266106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Rapaport DC. The Art of Molecular Dynamics Simulation. 2. Cambridge University Press; Cambridge, England: 2004. [Google Scholar]
- 5.Donald BR. Algorithms in Structural Molecular Biology. MIT Press; Cambridge, MA: 2011. [Google Scholar]
- 6.Janin J, Wodak S, Levitt M, Maigret B. J Mol Biol. 1978;125:357–386. doi: 10.1016/0022-2836(78)90408-4. [DOI] [PubMed] [Google Scholar]
- 7.Georgiev I, Lilien RH, Donald BR. J Comput Chem. 2008;29:1527–1542. doi: 10.1002/jcc.20909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gainza P, Roberts K, Donald BR. PLoS Comput Biol. 2012;8:e1002335. doi: 10.1371/journal.pcbi.1002335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Georgiev I, Donald BR. Bioinformatics. 2007;23:i185–i194. doi: 10.1093/bioinformatics/btm197. [DOI] [PubMed] [Google Scholar]
- 10.Georgiev I, Keedy D, Richardson JS, Richardson DC, Donald BR. Bioinformatics. 2008;24:i196–i204. doi: 10.1093/bioinformatics/btn169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hallen MA, Keedy DA, Donald BR. Proteins: Struct, Funct, Bioinf. 2013;81:18–39. doi: 10.1002/prot.24150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lilien RH, Stevens BW, Anderson AC, Donald BR. J Comput Biol. 2005;12:740–761. doi: 10.1089/cmb.2005.12.740. [DOI] [PubMed] [Google Scholar]
- 13.Lovell SC, Word MJ, Richardson JS, Richardson DC. Proteins: Struct, Funct, Genet. 2000;40:389–408. [PubMed] [Google Scholar]
- 14.Hart PE, Nilsson NJ, Raphael B. IEEE Transactions on Systems Science and Cybernetics. 1968;4:100–107. [Google Scholar]
- 15.Leach AR, Lemon AP. Proteins: Struct, Funct, Bioinf. 1998;33:227–239. doi: 10.1002/(sici)1097-0134(19981101)33:2<227::aid-prot7>3.0.co;2-f. [DOI] [PubMed] [Google Scholar]
- 16.Li Z, Scheraga HA. Proc Natl Acad Sci U S A. 1987;84:6611–6615. doi: 10.1073/pnas.84.19.6611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wang C, Schueler-Furman O, Baker D. Protein Sci. 2005;14:1328–1339. doi: 10.1110/ps.041222905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lazaridis T, Karplus M. Proteins: Struct, Funct, Bioinf. 1999;35:133–152. doi: 10.1002/(sici)1097-0134(19990501)35:2<133::aid-prot1>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
- 19.Vizcarra CL, Zhang N, Marshall SA, Wingreen NS, Zeng C, Mayo SL. J Comput Chem. 2008;29:1153–1162. doi: 10.1002/jcc.20878. [DOI] [PubMed] [Google Scholar]
- 20.Cook DB. Handbook of Computational Quantum Chemistry. Dover Publications, Inc; Mineola, NY: 2005. [Google Scholar]
- 21.Pierce NA, Winfree E. Protein Eng. 2002;15:779–782. doi: 10.1093/protein/15.10.779. [DOI] [PubMed] [Google Scholar]
- 22.Chazelle B, Kingsford C, Singh M. INFORMS Journal on Computing, Computational Biology Special Issue. 2004;16:380–392. [Google Scholar]
- 23.Gainza P, Roberts KE, Georgiev I, Lilien RH, Keedy DA, Chen CY, Reza F, Anderson AC, Richardson DC, Richardson JS, Donald BR. Methods Enzymol. 2013;523:87–107. doi: 10.1016/B978-0-12-394292-0.00005-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Georgiev I, Roberts KE, Gainza P, Hallen MA, Donald BR. OSPREY (Open Source Protein Redesign for You) User Manual. 2009:94. Available online: www.cs.duke.edu/donaldlab/software.php. Updated, 2012.
- 25.Rudicell RS, et al. J Virol. 2014;88:12669–12682. doi: 10.1128/JVI.02213-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gorczynski MJ, et al. Chemistry and Biology. 2007;14:1186–1197. doi: 10.1016/j.chembiol.2007.09.006. [DOI] [PubMed] [Google Scholar]
- 27.Stevens BW, Lilien RH, Georgiev I, Donald BR, Anderson AC. Biochemistry. 2006;45:15495–15504. doi: 10.1021/bi061788m. [DOI] [PubMed] [Google Scholar]
- 28.Georgiev I, Acharya P, Schmidt S, Li Y, Wycuff D, Ofek G, Doria-Rose N, Luongo T, Yang Y, Zhou T, Donald BR, Mascola J, Kwong P. Retrovirology. 2012;9:P50. [Google Scholar]
- 29.Weiner PK, Kollman PA. J Comput Chem. 1981;2:287–303. [Google Scholar]
- 30.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. J Am Chem Soc. 1995;117:5179–5197. [Google Scholar]
- 31.Cormen TH, Leiserson CE, Rivest RL, Stein C. Introduction to Algorithms. 3. MIT Press; Cambridge, MA: 2009. [Google Scholar]
- 32.Stone MH. Mathematics Magazine. 1948;21:167–184. [Google Scholar]
- 33.Bernstein SN. Communications de la Societé Mathématique de Kharkoff. 1912;13:1–2. [Google Scholar]
- 34.Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E. J Chem Phys. 1953;21:1087–1092. [Google Scholar]
- 35.Diskin R, Scheid JF, Marcovecchio PM, West J, Anthony P, Klein F, Gao H, Gnanapragasam PNP, Abadir A, Seaman MS, Nussenzweig MC, Bjorkman PJ. Science. 2011;334:1289–1293. doi: 10.1126/science.1213782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Edmunson AB, Manion CV. Clinical Pharmacology and Therapeutics. 1998;63:580–593. doi: 10.1016/S0009-9236(98)90109-6. [DOI] [PubMed] [Google Scholar]
- 37.Valiev M, Bylaska EJ, Govind N, Kowalski K, Straatsma TP, van Dam HJJ, Wang D, Nieplocha J, Apra E, Windus TL, de Jong WA. Comput Phys Commun. 2010;181:1477–1489. [Google Scholar]
- 38.Desmet J, Spriet J, Lasters I. Proteins: Struct, Funct, Bioinf. 2002;48:31–43. doi: 10.1002/prot.10131. [DOI] [PubMed] [Google Scholar]
- 39.Cerqueira NMFSA, Bras NF, Fernandes PA, Ramos MJ. Proteins: Struct, Funct, Bioinf. 2009;74:192–206. doi: 10.1002/prot.22146. [DOI] [PubMed] [Google Scholar]
- 40.Kwong PD, Wyatt R, Robinson J, Sweet RW, Sodroski J, Hendrickson WA. Nature. 1998;393:648–659. doi: 10.1038/31405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Hestenes MR, Stiefel E. Journal of Research of the National Bureau of Standards. 1952;49:409–436. [Google Scholar]
- 42.Nocedal J, Wright SJ. Numerical Optimization. 2. Springer-Verlag; Berlin: 2006. [Google Scholar]