Conformation of a Clathrin Triskelion in Solution

Abstract

A principal component in the protein coats of certain post-golgi and endocytic vesicles is clathrin, which appears as a three-legged heteropolymer (known as a triskelion) that assembles into polyhedral cages principally made up of pentagonal and hexagonal faces. In vitro, this assembly depends upon the pH, with cages forming more readily at low pH and less readily at high pH. We have developed procedures, on the basis of static and dynamic light scattering, to determine the radius of gyration, R_g, and hydrodynamic radius, R_H, of isolated triskelia, under conditions where cage assembly occurs. Calculations based on rigid molecular bead models of a triskelion show that the measured values can be accounted for by bending the legs and a puckering at the vertex. We also show that the values of R_g and R_H measured for clathrin triskelia in solution are qualitatively consistent with the conformation of a triskelion in a “D₆ barrel” cage assembly measured by cryoelectron microscopy.

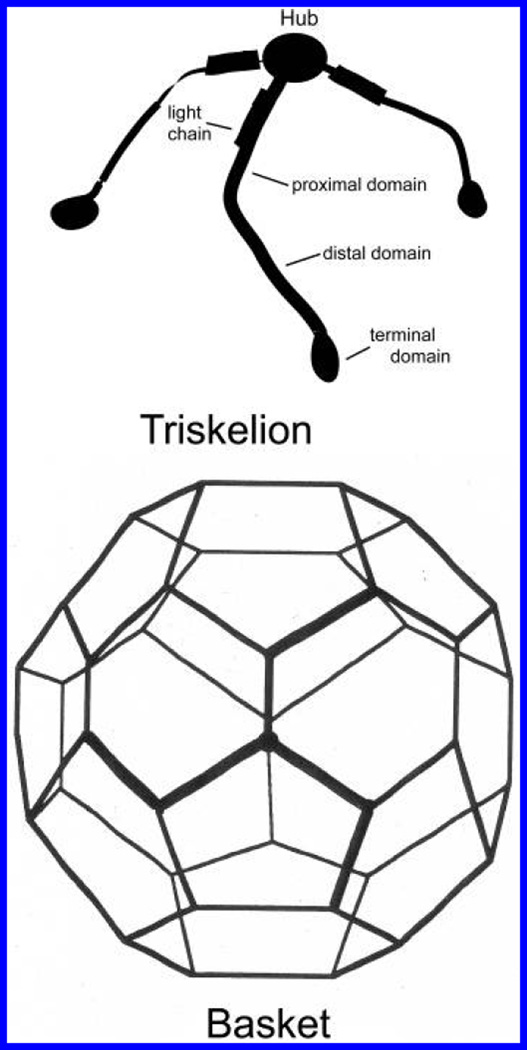
A major component of the protein coats of certain endocytic vesicles is clathrin, a heteropolymer composed of a 192 kDa heavy chain and a variable, ca. 23–27 kDa, associated light chain (1). Three clathrin molecules join at a common hub to form a three-legged “triskelion”, which is the basic building block of the coats. Each leg is approximately 3.0 nm thick and 52.0 nm in length and ends in a globular “terminal domain” of radius 5.0 nm. By convention, a leg is divided into a proximal segment adjoining the central hub, a linker region, and a distal segment that connects with the terminal domain. A clathrin heavy chain runs the entire length of the leg, with a light chain attached near the common hub (see Figure 1). In vitro, the triskelia assemble into polyhedral cages (or “baskets”) composed of pentagonal and hexagonal faces (2), mimicking the structures seen on the outside of endocytic vesicles. One can dissociate baskets or uncoat vesicles by changing the properties of the solution in which they are suspended (e.g., by changing pH and ionic strength) (3) or by adding an uncoating ATPase (4).

Figure 1.

Cartoons of an isolated clathrin triskelion and a polyhedral clathrin basket. The struts of the latter are formed from intertwined legs of four adjoining triskelia (two distal and two proximal segments).

Triskelia assemble at low pH to form baskets (3) or at higher pH, when clathrin assembly proteins (e.g., AP-2, AP-180, etc.) are added (5). It is not currently known why these conditions favor assembly. Possible mechanisms supporting assembly at low pH include conformational changes in the tertiary structure of the triskelia, which might relieve steric hindrances to basket assembly, and enhanced interactions between the intertwined triskelia that form the basket struts. The role of APs as assembly proteins may be to increase mechanical linkages between the triskelia (5–7).

In this paper, we report light-scattering measurements on clathrin in solution, including conditions where assembly occurs. From static light scattering (SLS),¹ we determine the radius of gyration (R_g), and from dynamic light scattering (DLS), we determine the hydrodynamic radius (R_H) of triskelia that have not polymerized into baskets. Although one does not obtain atomic and molecular coordinates as one might from a diffraction experiment or cryoelectron microscopy (cryoEM) tomography, light scattering provides weighted averages that are sensitive to different aspects of the spatial distribution of triskelion mass. In addition, the light-scattering techniques are noninvasive and thus allow one to assess the native state of clathrin in solution.

We compared the measured values of R_g and R_H with corresponding quantities calculated for a simplified model of a clathrin triskelion. The model was designed, in particular, to show dependences on triskelial pucker and leg bending. Where possible, we used leg segment dimensions based on X-ray and EM structural data. Using our model, we inferred that both R_g and R_H are intimately linked to the geometric attributes of the triskelia and that, taken together, they provide a sensitive measure of the solution conformations of these complex objects. Analysis of the measurements indicates that, over a large range of pH, individual triskelia are puckered in solution.

Recently, 3D structures of “D₆ barrel” clathrin cages have been used to infer a molecular model of a single clathrin triskelion (8). The D₆ barrel is a polyhedral assembly of 36 clathrin triskelia and associated AP2 assembly complexes. Calculations of R_g and R_H based on this model agree fairly well with our light-scattering measurements on free clathrin triskelia but indicate that a triskelion assumes a slightly more compact structure when incorporated into the cages.

MATERIALS AND METHODS

Clathrin Sample Preparation

Clathrin was purified from coated vesicles of bovine brain as previously described by Morgan et al. (6). The protein was stored in “dissociation buffer”, 0.5 M tris(hydroxymethyl)aminomethane (Tris)-HCl at pH 7.0 and 3 mM dithiothreitol (DTT), at a protein concentration of 3–4 mg/mL at 4 °C, and used within 2 weeks of purification. For light scattering, buffers were filtered 3 times through 0.22 µm cellulose acetate filters (Corning) prior to use. The buffer was exchanged by overnight dialysis through a 10 000 Da molecular-weight cutoff membrane (Pierce) into 10 mM Tris-HCl at pH 8.0 and 3 mM DTT. The protein was diluted to 0.34 mg/mL and clarified by centrifugation at 400000g for 15 min in an Optima Max Ultracentrifuge (Beckman), using an MLA130 rotor. After centrifugation, the entire supernatant was taken. The protein concentration was found to remain constant to within 0.01 mg/mL.

Soluble triskelia were prepared (3) for light scattering at different pH by adding 100 µL of 1 M 2-(N-morpholino)-ethanesulfonic acid (MES) buffer to 0.9 mL of precentrifuged protein solution; thus, the final concentration of MES buffer was 0.1 M. Samples were then incubated 1 h on ice and centrifuged at 400000g for 15 min to remove any assembled baskets. The top 80% of the supernatant was carefully taken. The preparation was confirmed, by DLS, to consist of monodisperse clathrin triskelia. The clathrin concentration in these samples was determined by absorbance measurements at a wavelength of 280 nm, using an absorption coefficient, ε₂₈₀, of 6.94 × 10³ M⁻¹ cm⁻¹ (1.07 g⁻¹ cm⁻¹), as estimated from the amino acid sequence.

Light Scattering: Experimental Setup

We used a Brookhaven light-scattering instrument (Brookhaven Instruments Corp., Holtsville, NY) for both SLS and DLS measurements. An argon-ion laser (Lexel) beam, emitting at a wavelength of 514.5 nm, was directed onto the sample. Dependent upon the sample concentration, the incident intensity was adjusted to give a detectible scattered intensity of 100 000 counts/s at a 90° scattering angle and fixed detection pinhole (400 µm or 1 mm in diameter). The scattered light was collected by a photomultiplier tube (EMI-PMT model 9863) and processed by a BI-9000 AT data-acquisition board (Brookhaven Instruments Corp.). For DLS, the board calculates and generates the intensity–intensity time-correlation functions.

A 1 mL volume of sample, loaded in a 1 in. diameter cylindrical light-scattering cuvette, was placed in a decalin index-matching bath attached to a precision goniometer (Brookhaven Instruments). The temperature of the bath was measured before and after each measurement, using a digital thermometer (±0.1 °C).

SLS

Scattered light intensity was measured every 2°, from a scattering angle of θ = 50° to 150°. The background scattering intensity from the cuvette and solvent was less than 1% of the detected signal in all experiments. In the Guinier regime (qR_g ≪ 1), the angular dependence of the scattered intensity, I(q), is well-approximated by a Gaussian profile with a width related to the R_g

$$I(q)~\text{exp}(-\frac{1}{3}{q}^2{R_{\mathrm{g}}}^2)$$ (1)

where the scalar quantity q is the magnitude of the Bragg scattering wave vector (9), viz.

$$q=\frac{4\pi n}{\lambda }\text{sin}(\theta /2)$$ (2)

with λ, θ, and n being the wavelength, the scattering angle, and the refractive index of the solution, respectively. The logarithm of the intensity profile was plotted against q² and fit to a straight line, using the method of least squares. The slope of the line is 1/3R_g² (10). For any given sample, the measurements were repeated 4 times, and the fit yielded values for R_g reproducible within ±3% (0.8 nm).

DLS

DLS was performed at scattering angles of 90° and 150°. Photon counts collected over prescribed intervals were autocorrelated over a time range, 1 ≤ τ ≤ 10⁴ µs, to provide the autocorrelation function of the scattered light, c(τ) = 〈I(t)-I(t + τ)〉/〈I〉.² Data were collected in the homodyne mode, from which we determined the field correlation function, g(τ), by the following formula

$$c(\tau )=A[1+B{|g(\tau )|}^2]$$ (3)

where A and B are constants (9). Using the cumulant method, we fit the logarithm of the measured field correlation function up to the second cumulant by the equation (11)

$$\mathrm{l}\mathrm{n}|g(\tau )|=-D{q}^2\tau +\frac{1}{2}\mu q^4{\tau }^2$$ (4)

where q is given by eq 2, D is the average translational diffusion coefficient, and μ is related to the width of the distribution of the diffusion coefficient. Both D and μ are the fitting parameters. We then determine the mean R_H from the Stokes–Einstein relation

$$D=k_{\mathrm{B}}T/6\pi \eta R_{\mathrm{H}}$$ (5)

where k_B is Boltzmann’s constant, T is the temperature, and η is the solvent viscosity. For a given sample, two correlation functions were collected at θ = 90° and two at θ = 150° and fitted with the expression in eq 4, yielding values for R_H reproducible within ±1% (0.2 nm). Here, the buffer viscosity (for 0.1 M MES) was taken to be 1.05 times that of water, in accordance with measurements made with an Ostwald viscometer at 20 °C (data not shown).

Hydrodynamic Modeling

Transport properties of clathrin triskelia were calculated using HYDRO (12) and ZENO (13). To employ these programs, triskelia of differing shapes were approximated by groups of connected spheres.

Calculations primarily were performed with HYDRO (12, 14), which uses a hydrodynamic interaction tensor and Stokes’ solution for flow around a sphere to determine the frictional force on a rigid bead model by an iterative matrix inversion of the hydrodynamic equations (14). The resultant frictional force on the structure is then related to the R_H. A recent experimental study of the hydrodynamic properties of nanoscopic rings showed extremely good quantitative agreement between measurements and parameters computed by this method (15).

ZENO uses a Monte Carlo, numerical path integral technique to estimate the translational diffusivity by making an analogy between isotropic angular averaged hydrodynamics and electrostatics (13, 16). Similar to HYDRO, it also uses an iterative algorithm. It allows for more complex models than HYDRO, with the latter being limited to 2000 beads. When we compared these programs, ZENO gave results for R_H within 1% of those determined by HYDRO, for all models tested.

RESULTS

Light Scattering

Native clathrin assembles into closed, basket-like structures at a low pH and low salt concentration (3). The baskets can be removed by centrifugation, while unassembled clathrin remains in the supernatant. Above pH 6.5, basket formation occurs relatively slowly and is only weakly dependent upon pH, whereas at pH 6.0, most of the clathrin is quickly incorporated into closed polyhedra. After the baskets were centrifuged from these samples, DLS measurements made on the supernatants show highly monodisperse scatterers having an average value R_H = 16.9 nm for the apparent R_H. The reduced second moment, μ/D², had an average value of 0.06 ± 0.03 and did not vary significantly with pH.

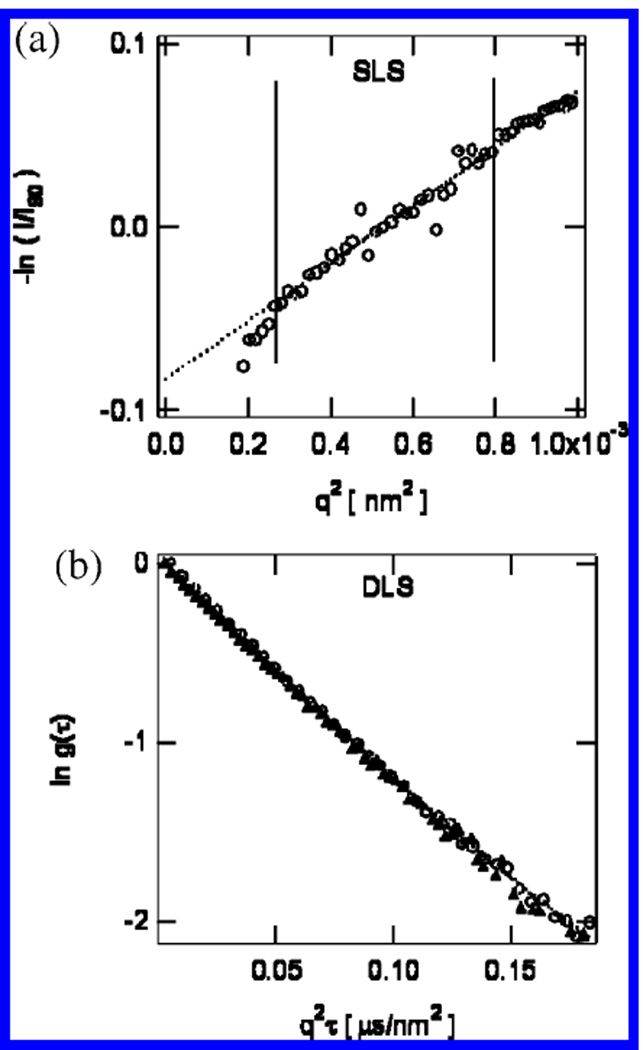
Results from light scattering are shown in Figures 2 and 3. Figure 2a shows typical SLS data for clathrin in solution, where the vertical lines indicate the q range over which the data were fit to a linear function to determine the value of R_g (see eq 1). In Figure 2b, typical DLS data are shown as well as the result of the quadratic fit (see eq 4) used to determine the value of R_H (see eqs 4 and 5). Figure 3 shows results derived from light-scattering measurements as described above.

Figure 2.

(a) Typical SLS data, for clathrin in solution at pH 6.25. The open circles indicate SLS data. The dotted line indicates a linear fit to the data from q² = 0.25 to 0.80 × 10³ nm⁻² (θ = 60–120°). (b) Typical DLS data, for clathrin in solution at pH 6.0, taken at angles of 90° and 150°. Circles indicate DLS data taken at an angle of 150°. Triangles indicate light scattering data taken at an angle of 90°. The dotted lines indicate quadratic fits to the data.

Figure 3.

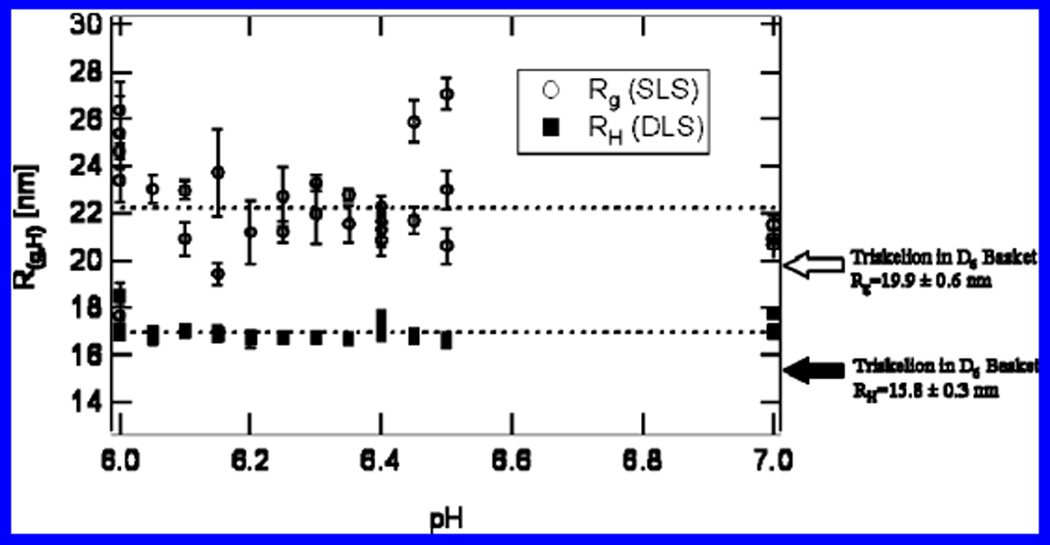
R_g and R_H of free clathrin triskelia measured by SLS and DLS. The abscissa indicates the pH of the buffered solution. Both measurements appear to be independent of pH. The arrows point to the values calculated by ZENO (13, 16) for the triskelial structure noted for clathrin in an assembled basket (8). Each data point was taken on a different sample. Error bars represent standard deviations of four measurements on the same sample.

We measured a R_H and R_g for free clathrin in solutions of different pH and found that, within experimental error, they are almost independent of pH. As previously mentioned, clathrin baskets were removed by centrifugation prior to light scattering. Even so, at low pH, clathrin continues to assemble, albeit at slower rates because of the reduced clathrin concentrations resulting from the elimination of polymerized material (the protein concentration after centrifugation at pH 6.0 was 0.11 ± 0.03 mg/mL). Thus, we acquired data as soon as possible after the centrifugation step. Measurements took on the order to 2–10 min to complete. If one ignores the data taken at pH 6.0, which were the most difficult points to repeat because of continuing assembly into baskets, one finds an average value of R_g = 22.2 ± 1.8 nm and R_H = 16.9 ± 0.3 nm, with no obvious systematic pH dependence. Light-scattering measurements of triskelia immersed in 0.5 M Tris buffer at pH 7.0 yield similar values (data not shown).

The bold arrows in Figure 3 indicate the values of R_H and R_g calculated by applying ZENO (13, 16) to the triskelial structure found in a D₆ basket assembled in the presence of AP2 assembly complexes (8) mentioned in the Introduction. Interestingly, the R_H and R_g derived from the solution measurements are close to but somewhat greater than values calculated for the configuration of the clathrin triskelion in the basket (see Table 1).

Table 1.

Experimental Values and Theoretical Calculations of R_H and R_g of Clathrin Triskelion^a

	RH (nm)	Rg (nm)
light-scattering measurement	16.9 ± 0.3	22.2 ± 1.8
HYDRO calculation using	14.8	19.3
a 21 Å resolution structure with the hydration layer	15.3
ZENO calculation using	15.4 ± 0.3	19.9 ± 0.6
a 12.5 Å resolution structure with the hydration layer	15.8 ± 0.3

^aThe R_H and R_g of clathrin from light scattering is displayed in the first row. Other rows show theoretical predictions based on clathrin structures taken from cryoEM measurements of D₆ clathrin basket assemblies.

The calculations of R_H and R_g for the shape of a triskelion within a basket were initially performed with HYDRO. A modified 2.1 nm resolution structure for a clathrin triskelion in a D₆ basket was generously provided by T. Kirchhausen³ (1). This structure was used to generate a rigid bead model for a clathrin triskelion, which HYDRO could then use to calculate an approximate R_H and R_g. The 192 coordinates of this structure located the centers of contiguous 3.0 nm beads, with these centers being, on average, 0.76 ± 0.10 nm apart. The bead diameter was chosen to equal the average leg thickness of 3.0 nm, determined from the partial crystal structure for the clathrin proximal leg⁴ (17). This model was then completed by the addition of 5.0 nm beads to the ends of the legs to account for unresolved terminal domains, in accordance with another partial crystal structure⁵ (18). The R_g was calculated with this model, but a 0.3 nm hydration layer was added for the calculation of the R_H (see e′ in Figure 7). The results of HYDRO calculations on this structure are shown in the second and third rows of Table 1.

Figure 7.

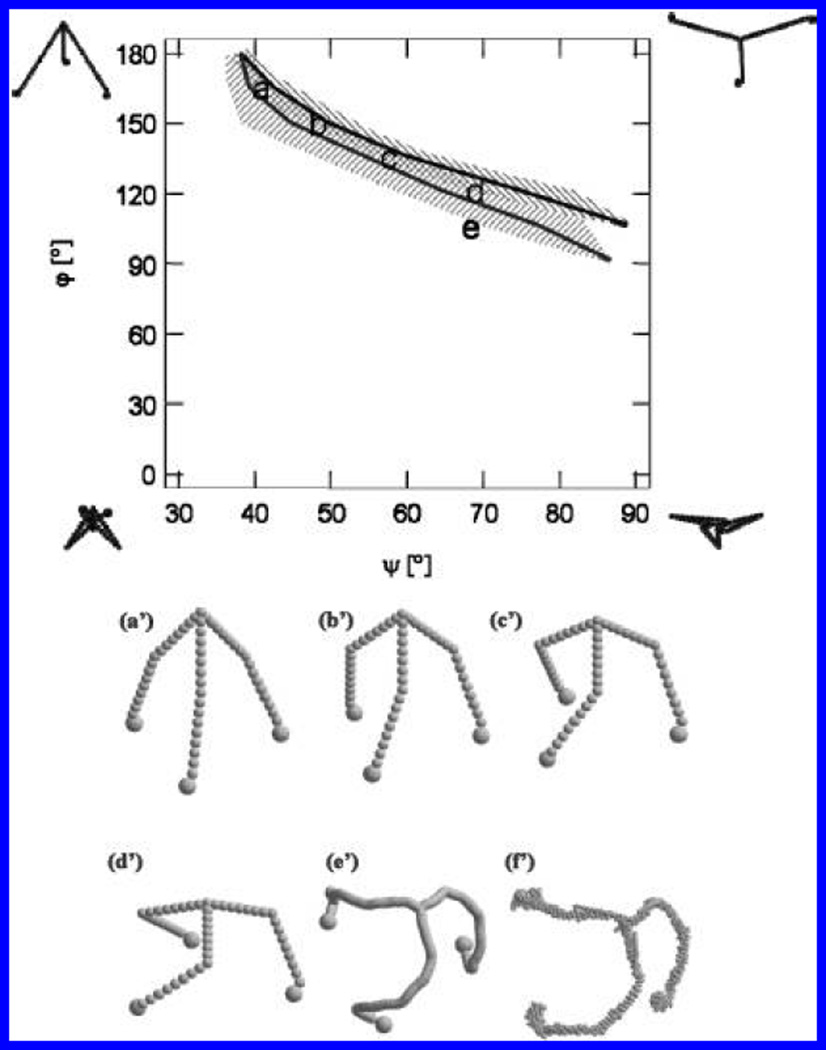
Values of (φ, ψ) for which calculations based on the segmented bead model match the values for both R_g (lower line) and R_H (upper line) determined from light-scattering measurements. The upper and lower bands indicate those values of (φ, ψ) lying within 1 standard deviation of the lines appearing in parts a and b of Figure 5, respectively. The region of overlapping bands indicates the range of angles that are compatible with the experimental data. Letters (a–d) indicate models in accordance with experimental data; (e) indicates the corresponding (φ, ψ) for a triskelion in a D₆ basket (see the text). Extreme triskelion shapes corresponding to the (φ, ψ) at the four corners of the graph are also shown. (a′–d′) indicate the models specified by the corresponding (φ, ψ), and (e′ and f′) show models of a clathrin triskelion derived from 2.1 and 1.25 nm resolution cryoEM tomography of D₆ barrels, respectively.

Recently, a higher resolution structure for clathrin in a D₆ basket became available. In this structure, presented in the form of C_α coordinates of each amino acid in the protein, the terminal domains and part of the light-chain peptides are now resolved, at 1.25 nm resolution (8). Following the method of Tirado Garcia et al. (19), amino acids were approximated by spheres of radius 0.36 nm. This radius was then increased by 0.3 nm to simulate a hydration layer for calculation of R_H. In this case, the amino acids were each approximated by a sphere of radius 0.66 nm. The resulting model contained 5100 spheres, which necessarily overlapped to represent the overall dimensions of the triskelion (see f′ in Figure 7). HYDRO is limited to 2000 spheres and thus could not be used to calculate R_H in this case. Instead, ZENO (13) was used to perform the hydrodynamic calculations. Results are shown in rows four and five of Table 1. Because of the complexity of this model, convergence is slow and uncertainties (which are shown next to each calculated value) need to be noted.

Modeling

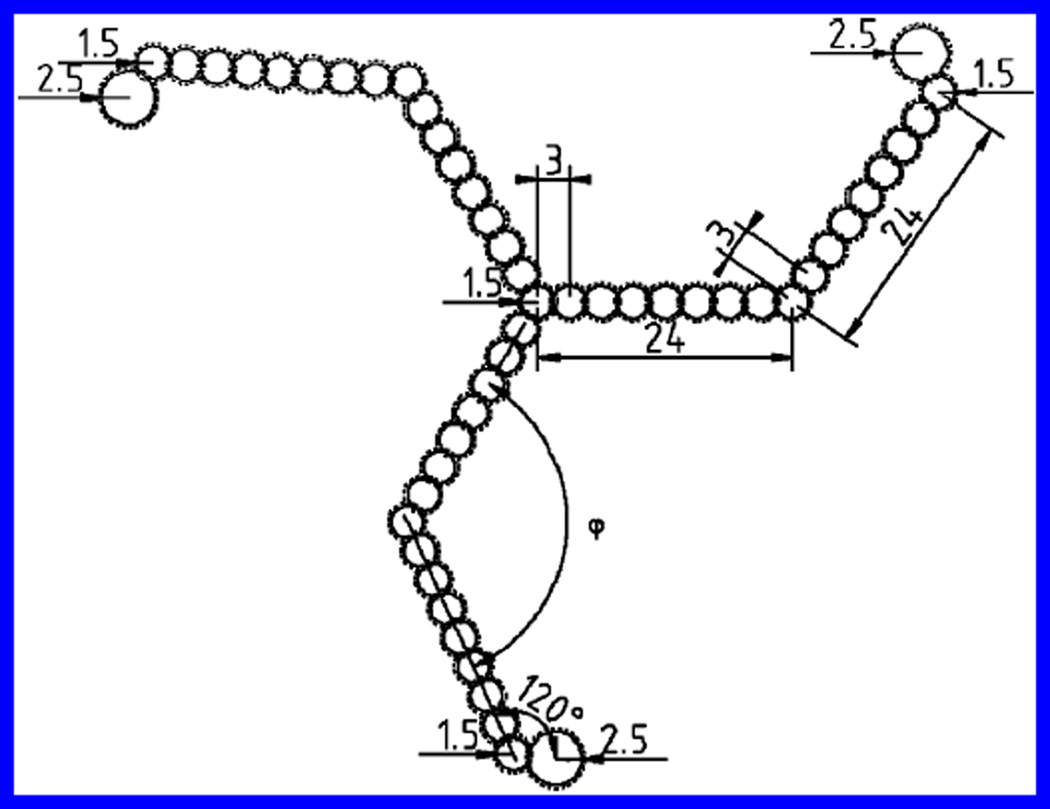
To estimate the sensitivity of R_g and R_H to changes in clathrin pucker and leg bending, we used a simpler model of a clathrin triskelion (see Figure 4). While our model differs from the protein structures described above, it still captures essential features and uses the most recent estimates of the dimensions of the clathrin heavy chain and terminal domain. Each leg was given a length of 52 nm, in correspondence with measurements made from transmission electron microscopy (TEM) images of clathrin (20–22). To model the solution structures for a comparison with DLS data, here, also, a bead diameter of 3.0 nm, derived from the partial crystal structure for the clathrin proximal leg⁶ (17), was augmented by an additional 0.6 nm to approximate the effect of a layer of bound water needed when calculating R_H. Thus, 16 beads (total diameter of 3.6 nm) were used, with centers spaced 3.0 nm apart. In contrast, the calculations of R_g were performed for structures modeled with 16 beads of 3.0 nm in diameter, because the layer of bound water is indistinguishable in SLS measurements. One sphere of the same diameter was also placed at the hub where the legs join. A larger bead of diameter 5.0 nm was added at the end of each leg to account for the terminal domain, in accordance with the aforementioned partial crystal structure⁷ (18). Again, when calculating R_H, an additional 0.6 nm was added to this bead to account for bound water.

Figure 4.

Diagram of a simple model of a clathrin triskelion showing dimensions used in our model. Arrows pointing toward a circle indicate the radius of the circle. Lengths are in nanometers, and angles are in degrees. The dotted lines indicate the added hydration layer.

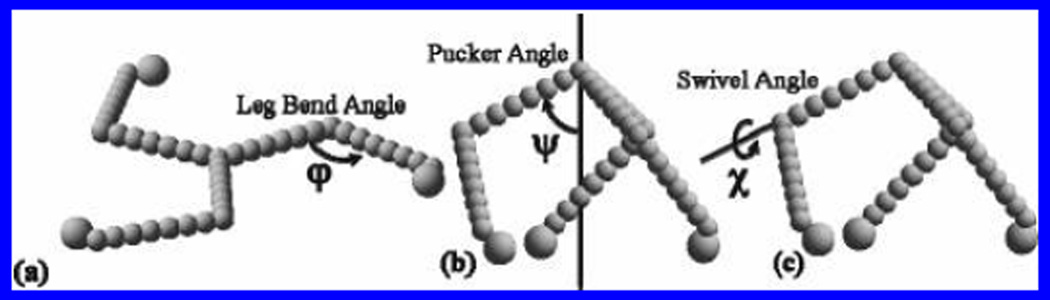
Each leg included a bend halfway down its length and an out-of-plane pucker measured with respect to a perpendicular line passing through the vertex. A third angle χ, the “swivel angle”, was varied along the axis of the central leg segment parametrically with ψ, the “pucker angle”. In this way, we changed the model structure from planar (Figure 5a), similar to that seen in transmission electron micrographs of individual triskelia, to puckered (parts b and c of Figure 5), similar to the cryoEM structure (see e′ and f′ in Figure 7). We assumed 3-fold symmetry about the perpendicular. Changing the angles φ, ψ, and χ, we were able to obtain a quantitative estimate of the sensitivity of R_g and R_H to the conformation of the triskelion. We found that the R_g is much more sensitively dependent upon the conformation than is the R_H. Both quantities, however, vary considerably for the cases studied and together provide a distinctive measure of any change in solution conformation. In parts a and b of Figure 6, we show R_H and R_g calculated for different values of bend angle, φ, and pucker angle, ψ, and compare them with values measured from the experiment (represented by the shaded planes). Note that at ψ = 90° there is no pucker (i.e., the molecule is completely planar), whereas when φ = 180°, the legs are completely straight (see Figure 5).

Figure 5.

Examples of simple bead models of a clathrin triskelion. (a) Leg-bend angle, φ, and (b) pucker angle, ψ, were varied from 30° to 180° and 30° to 90°, respectively. (c) Swivel angle, χ, was varied parametrically with the pucker angle according to the equation χ = 3(ψ − 30)/2, where χ is measured from the vertical axis shown in b.

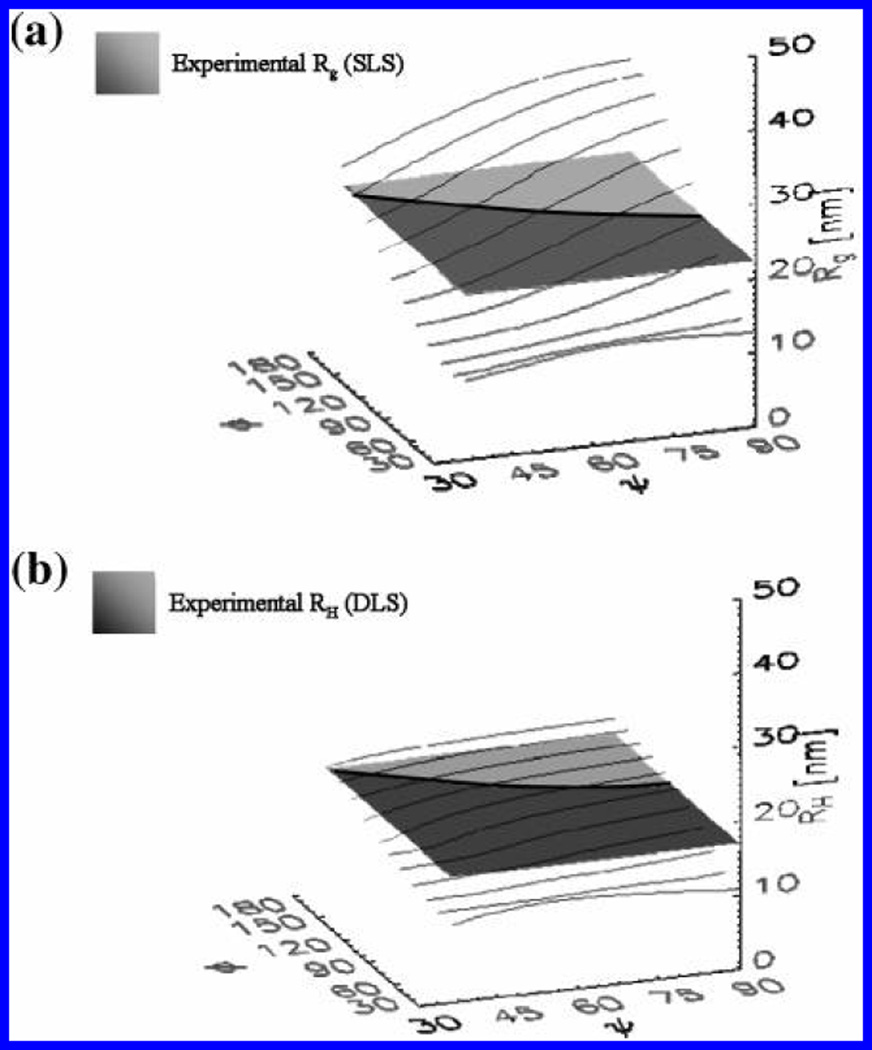
Figure 6.

Variation of R_g and R_H with triskelial conformation. (a) Values of R_g calculated for our model are shown in the thin black curves. The shaded surface is a flat plane drawn parallel to the plane defined by the φ,ψ axes (related to the leg-bend and pucker angles in our model). It shows the average, experimentally measured, value R_g = 22.2 nm. Hence, the dark line indicates the locus of (φ, ψ) values commensurate with the measured R_g. (b) Values of R_H calculated for our model are shown in the thin black curves. Similar to what is shown in a, the shaded surface is a flat plane drawn at the average experimentally measured value R_H = 16.9 nm and the dark line indicates the intersection of the plane with calculated values.

There is considerable degeneracy, in that several pairs of (φ, ψ) are consistent with the measured values. To show this, we combined the information from Figure 6 to produce Figure 7. The upper and lower shaded regions in Figure 7 indicate (φ, ψ) pairs yielding values of R_H and R_g, respectively, lying within 1 standard deviation of the measured values. One can see that there is a very narrow band of model conformations (indicated by the overlap region) that are consistent with both the R_g and R_H measured by light scattering of free clathrintriskelia in solution. Some compatible structures are shown in a′–d′ of Figure 7. We also indicate the conformations that correspond to the (φ, ψ) values at the corners of the graph. The letter “e” locates the (φ, ψ) pair that was found to be most similar to structures shown in e′ and f′ of Figure 7.

SUMMARY AND DISCUSSION

Previous TEM investigations indicated a characteristic, pinwheel-like shape for isolated clathrin triskelia absorbed to mica surfaces, with the triskelia having a preferred orientation that depends upon the buffer in which they are suspended (3, 20). On the basis of these studies, quantitative analysis of images of differing handedness (20) led to the inference that free triskelia are puckered, with their hubs raised above the plane defined, e.g., by the ends of each of the legs. In those studies, to ensure that they did not associate, the triskelia were suspended in buffers of pH 8.0 when affixed to the mica substrates. We have expanded this work by using DLS and SLS to investigate the conformations of individual clathrin triskelia when free in solution and also extending the investigation to a lower range of pH (pH 6.0–6.5). The experimental shape descriptors are the R_g and R_H. Using light scattering, possible structural perturbations of the triskelia because of interactions with EM grids are eliminated.

This study yields three main conclusions. First, we confirm that clathrin legs are bent and puckered in solution. To obtain this result, we used HYDRO to calculate R_g and R_H for particular test structures and systematically varied parameters to see which conformations are consistent with the measured data. Yoshimura et al. (23), in a more limited study, investigated triskelia in slightly alkaline solutions but modeled them by two dissimilar planar objects when fitting either R_g or R_H. Using this approach, Yoshimura et al. concluded that the solution structures of triskelia in low ionic strength TRIS and TEA buffers (pH 8.0) are not discernibly different, even though triskelia in such samples demonstrate a different handedness when placed onto mica surfaces. In our study, we use identical nonplanar models when calculating R_g and R_H to determine the solution conformations of the triskelia.

Second, there seems to be a difference between the solution and basket-associated conformations. CryoEM of small D₆ barrels yields coordinates of a puckered triskelion (24). Quantitative predictions of R_g and R_H calculated for these shapes differ from values measured for triskelia in solution. However, the structures are relatively close, indicating that the insertion of a triskelion into such an assembly does not require that it undergo a major conformational change. In this regard, we note that baskets of differing sizes are found even when they are reconstituted in vitro from purified clathrin alone (2, 3, 25) and that slight differences in the leg conformation are observed when one compares triskelia localized to different positions in baskets reconstituted in the presence of AP2 (24). Moreover, the baskets are limited in size (few exceeding ca. 120 nm in diameter), suggesting that, beyond a certain point, a conformation-linked unfavorable energy term may start to overwhelm favorable interaction energy gained because of the association of the clathrin legs (7, 26). The fact that these might be mechanical in nature is suggested by the fact that large reconstituted clathrin structures are observed only when the triskelia lack distal segments, in which case leg bending is suppressed and large, essentially flat, structures are observed (27).

Finally, significant conformational changes in clathrin triskelions are not observed across the pH range known to make the difference between clathrin cage assembly and disassembly. We have observed that, within experimental error, R_g and R_H do not change as the pH is lowered from 7.0, where basket formation is inhibited, through the “assembly transition” (pH 6.5 → 6.3), to a value (pH 6.0) where essentially all triskelia are rapidly incorporated into baskets. One might have expected conformational changes to occur as conditions were varied from those that disfavor basket assembly to those that elicit polymerization. However, as previously mentioned, basket formation is effected by attractive interactions between clathrin legs that are resisted by leg bends and other triskelion shape changes. Thus, our failure to find a significant conformational change is important, because it suggests that lowering the pH may affect the mechanical properties of the triskelia (e.g., the rigidity) or enhance interleg interactions that favor basket formation [e.g., by changing the ionization state of histidine groups (28)].

The light-scattering methods employed in this study may not be sufficiently sensitive to demonstrate very small (subnanometer) changes in the solution structure of the triskelia. Perhaps other methods could provide information about triskelia in solution. However, several that immediately come to mind are not yet developed to the point where they can be usefully employed to study molecules of such size. NMR spectroscopy, for example, currently is limited to proteins whose molecular weight does not exceed ca. 40–50 kDa, whereas triskelia have a molecular weight that is an order of magnitude greater (>600 000 kDa). Similarly, CryoEM is problematic because of the irregular shapes of the triskelia and the slenderness of their legs. Analytical ultracentrifugation in effect provides the same information as does DLS (the Svedberg coefficient, S, can be directly related to R_H) but, by itself, does not yield enough information to discriminate between various model conformations. Measurements of R_g (which is more sensitive to the triskelial shape than R_H) are needed if one wishes to narrow the range of possible structures and thereby eliminate uncertainty about the triskelial shape. Using DLS, we are able to determine R_H on the same sample as that used for R_g.

In summary, this paper utilizes DLS and SLS techniques, in a consistent way, to study the solution structures of clathrin triskelia. We conclude that a triskelion has an intrinsic pucker, that the solution structure differs from that of a triskelion in a D₆ basket, and that significant conformational changes do not occur as the pH is lowered below the assembly transition.