Abstract
While measurement evaluation has been embraced as an important step in psychological research, evaluating measurement structures with longitudinal data is fraught with limitations. This paper defines and tests a measurement model of derivatives (MMOD), which is designed to assess the measurement structure of latent constructs both for analyses of between-person differences and for the analysis of change. Simulation results indicate that MMOD outperforms existing models for multivariate analysis and provides equivalent fit to data generation models. Additional simulations show MMOD capable of detecting differences in between-person and within-person factor structures. Model features, applications and future directions are discussed.
Keywords: Measurement, Factor Analysis, Dynamical Systems, Longitudinal Data, Structural Equation Modeling
Multivariate measurement is a central feature of modern behavioral science. The necessity of multivariate techniques for measurement is due largely to the complexity of the traits we study and the difficulties of studying these complex traits through the lens of observed and reported behavior. If measurement can be defined as “the assignment of numerals to objects or events according to rules (Stevens, 1946),” then measurement models provide rules by which multivariate item-level responses are projected onto latent dimensions representing psychological traits.
Measurement models, whether they are based on factor analysis, item response modeling or another paradigm, provide a paradigm for translating item-level responses into measurements useful in subsequent analyses. One possible weakness of this set of approaches is their reliance on cross-sectional data. This is a significant limitation, as longitudinal data can answer a variety of questions that cannot be solved with cross-sectional data, specifically those pertaining to intraindividual changes and interindividual differences in change (Baltes & Nesselroade, 1979). Analyses of multivariate longitudinal data often begin with some type of measurement model, but the evaluation of measurement models often fails to take advantage of longitudinal information included in the data. Instead, the measurement structure at a particular occasion is evaluated (often the first occasion), then that established factor structure or set of trait scores is used for a subsequent longitudinal analysis.
A number of potential problems can occur when cross-sectional results are extended to longitudinal analyses. The equality of the interindividual and intraindividual structures is an assumption, and one that should be tested. Molenaar’s (2004; 2009) work on ergodicity directly analyses the distinction between between-person and within-person structures, finding that very specific conditions for them to be equivalent. Similar issues present themselves in state-trait distinctions. Analysis of a single timepoint further assumes that measurement structures are invariant over all timepoints, which should instead be tested using existing techniques for assessing measurement invariance (Meredith, 1964a, 1964b, 1993) or differential item functioning (Drasgow, 1982; Millsap & Everson, 1993).
Perhaps most importantly, the use of cross-sectional data for measurement evaluation ignores how the observed variables change over time. Bereiter (1963, p. 15) argued that “[a] necessary and sufficient proof of the statement that two tests ‘measure the same thing’ is that they yield scores which vary together over changing conditions.” If observed variables indicate a particular latent construct that changes over time, changes in the set of observed variables should show the same type of measurement structure found in a cross-sectional analysis. Put more simply, if changes in observed variables are caused by a common latent construct, then those observed variables should have similar dynamics, where dynamics refer to the pattern and structure of change. Assessing only between-person differences in initial level is not a sufficient test of a measurement structure for constructs believed to show some degree of development, lability or change.
The goal of this work is to define and test a novel method for multivariate longitudinal measurement that directly models the structure of change, termed the measurement model of derivatives (MMOD). This model will rest on the use of longitudinal item-level data to test whether changes in observed variables can be accurately represented by the factor structure that represents cross-sectional differences. If a latent construct really does cause observed change in manifest variables, then all of the manifest variables that indicate that construct should change in the same way that the construct changes, and this should be observable both in the item-level longitudinal trends and item covariances across measurement occasions. The presented tests and use of this model show that that a small number (3–5) of repeated measurements of a set of test items can be used to assess the utility of a particular factor structure in the measurement of change. The ensuing sections will show the need for this method, describe existing models for longitudinal measurement, present the proposed model, report on a set of simulation studies that compare the proposed model to existing alternatives, and provide an empirical example to demonstrate the use and interpretation of this model.
Demonstration of the Problem
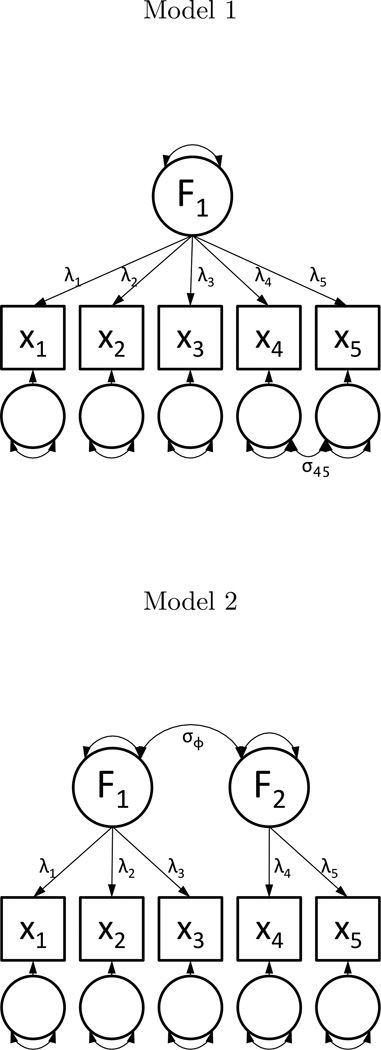
The importance of this issue can best be expressed through application. Figure 1 contains two different measurement models that may be fit to five variables measured at a single occasion. In the first model, all items load on a shared common factor, with items x4 and x5 maintaining a residual covariance (σ4,5). This model reflects a common cause for all items manifested in a unidimensional construct, save a presumably small residual association due to shared content or another issue not relevant to the substantive interpretation of the common factor. The second model contains two oblique factors with simple structure, where the first factor predicts items x1 through x3 while the last factor predicts items x4 and x5, and the factors share a covariance (σϕ). This model is substantively different than the first, as it represents the observed data has being caused by two related but distinct latent constructs. Despite the difference in the number of factors and factor loading pattern, these two models are equivalent when fit to a single occasion of data. Both contain a total of 16 free parameters: five residual variances, five item means, five factor loadings and a single covariance. Both models fit equally well to any five-variable covariance matrix and would yield identical fit statistics. The parameters from either of the models can be transformed into the parameters of the other, as shown in Table 1.
Figure 1.
Comparison of Two Factor Models
Note. Path diagrams for two equivalent factor models with varying substantive interpretations. Factor and residual variance terms may be assumed to unity without loss of generality.
Table 1.
Equivalence of One- and Two-Factor Models
| One-Factor Model | Two Factor Model | |
|---|---|---|
| λ1–3 | = | λ1–3 |
| λ4 | = | λ4 * σϕ |
| λ5 | = | λ5 * σϕ |
| σ4,5 | = | λ4 * λ5 * (1 − (σϕ)2) |
Note. Transformation of model parameters from a one-factor model with a single residual covariance between items 5 and 6 and a two-factor model with a factor covariance. λx=factor loading for variable(s) x; σ4,5=residual covariance between items 5 and 6 in one-factor model; σϕ=factor covariance from two-factor model.
The above example of two models with equivalent fit but discrepant interpretations is but the cleanest example of a larger class of problems involving single occasion measurement where two or more models may have wildly different substantive interpretations but equivalent or near equivalent fit to the data. These types of problems are common across a wide range of disciplines across psychology. Affect research depends on whether positive and negative affect are treated as a single dimension, two factors or a larger number of dimensions (Leue & Beauducel, 2011). Studies of behavioral genetics depend on the specificity or generality of the latent psychiatric and substance use constructs being investigated (Kendler, Prescott, Myers, & Neale, 2003). Several anxiety and mood constructs rely on a state-trait distinction, which require repeated measurements to differentiate time-invariant states from labile traits (Spielberger, Gorsuch, & Lushene, 1969; see also the lability-modulation model for mood, Cattell, Cattell, & Rhymer, 1947; Wessman & Ricks, 1966). In cognitive and developmental psychology, the differentiation-dedifferentiation hypothesis deals specifically with the idea that the dimensionality of intelligence varies across the lifespan, and thus doesn’t have an invariant number of factors (Garrett, 1946). Similar examples likely exist in other domains where the distinction between one or more measurement structures is substantively important but difficult to detect.
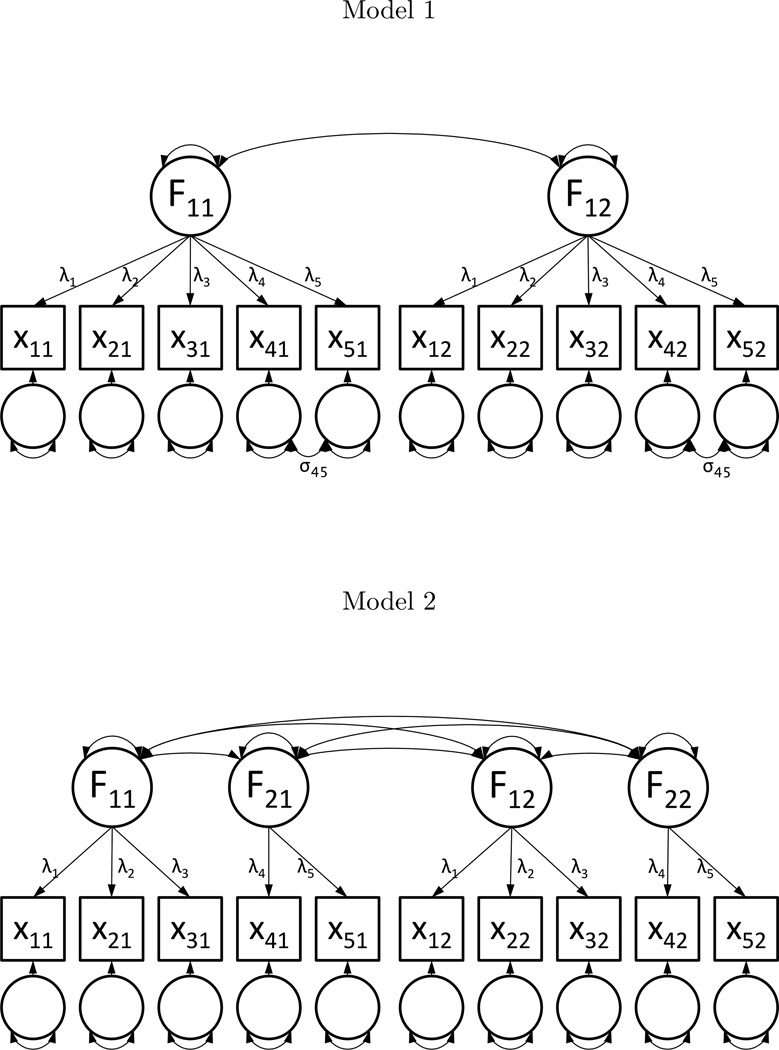
In addition to some degree of uncertainty regarding dimensionality, the above examples all share the ability to extend to longitudinal data. It is in that extension that those examples may differentiate from one another. While the two models in Figure 1 are equivalent in a single timepoint, they make very different hypotheses about subsequent change. Adding a second occasion to Figure 1 extends those two models to the models shown in Figure 2, and in doing so shows the differences between these two models. The equality of these models no longer holds when the second occasion is added, as the second model contains additional five additional free parameters to describe the change in the additional latent factors. If the first model is correct, the individual manifest variables should change in a way that is proportional to the common factor and be explained by a single factor covariance and two residual covariances, whereas the second model hypothesizes a more complex longitudinal trend with six factor covariances, yielding a three degree of freedom difference between the models absent any factorial invariance constraints. Adding invariance constraints raise the degree of freedom difference between the models to four (weak factorial invariance; Meredith, 1993), five (strong) or six (strict).1. While the substantive interpretations of these two models does not change with the additional data, the ability to differentiate between these two models comes when the data includes information about item-level change.
Figure 2.
Comparison of Two Factor Models
Note. Path diagrams for extensions of Figure 1 models to two occasions.
The information on item-level change provided by longitudinal data is one way to test hypotheses about measurement structure that are otherwise difficult to answer with a single occasion of measurement. When the models being compared are as simple and well-defined as the example in Figure 1, this type of testing can be done using a pair of confirmatory models. However, many applications will have additional variables, more occasions of measurement and less clearly defined models. Those cases require a more general method for the incorporation of item-level change into measurement evaluation.
Extant Multivariate Longitudinal Approaches
While a large set of models have been developed for the analysis of longitudinal data, the majority of them deal exclusively with the analysis of longitudinal trends and not with measurement. Approaches like autoregression, mixed-effect models and latent growth curves all evaluate the change processes on existing manifest variables, whether they be univariate measurements or output of some previously estimated measurement model. Similarly, approaches like latent differential equations (LDE; Boker, Neale, & Rausch, 2004; Boker, 2007) and the curve-of-factors (CUFFS; McArdle, 1988) models do incorporate latent trait measurement but require that the structure of the latent variables under investigation be known. These methods depend on separate measurement evaluation prior to use to determine that latent structure, and the focus of these models is not to evaluate the measurement structure using repeated measures data, but rather the longitudinal trajectory of latent factors already established as reliable measures. These models can tell you how some variable Y changes over time, but cannot tell you whether Y is a reliable or valid measure of the construct of interest. As such, these approaches aren’t appropriate tools for establishing the structure of item-level change.
Several analytic approaches developed for longitudinal analysis are relevant to the discussion of measurement evaluation in longitudinal contexts, each with its own set strengths and limitations. These approaches include longitudinal extensions to item response models, McArdle’s (1988) factor-of-curves model, and Cattell’s differential-R technique factor analysis (1974), each of which are now discussed in turn.
Longitudinal Item-Response Models
Item response modeling encompasses a range of models for the assessment of continuous latent traits from observed categorical data (see Baker, 2001; Embretson & Reise, 2000; Hambleton, Swaminathan, & Rogers, 1991 for overviews), several of which have been developed for the application to repeated measures data. Fischer (1989) derived a version of his linear logistic model with relaxed assumptions (LLRA; Fischer, 1973) for use with longitudinal data, in which treatment and trend effects are added for repeated measurements. While this model does allow for repeated administration of the same items, traits are still assumed invariant over time, which makes this model unable to test the invariance of latent traits.
Embretson (1991) presents a version of the multidimensional Rasch (1960) model for learning that allows for individual differences in change. Embretson’s model relies on a simplex structure for multidimensional traits to define traits at each occasion as change, but requires a unique set of items at every observation so that local independence of items can be assumed. The Rasch model may also be specified as a mixed-effect or multilevel model that includes time as one level of the analysis, though these methods require either the same restrictions on item repetition as Embretson’s model (Tan, Ambergen, Does, & Imbos, 1999) or dispersion parameters to address some of the distributional problems caused by repeated administration of the same items (Johnson & Raudenbush, 2006). Other approaches simply assume local independence and fit traditional binary and polytomous item response models to multiple occasions of data (Andrade & Tavares, 2005; Meade, Lautenschlager, & Hecht, 2005; Millsap, 2009).
Differential R-Technique
Cattell’s differential R or dR-technique factor analysis provides for the inclusion of multiple occasions into a measurement model in a straightforward and meaningful way (Nesselroade & Cable, 1974). At its most basic level, dR-technique factor analysis is simply a factor analysis of difference scores calculated from two occasions of measurement. An alternative approach, called a “factor of difference scores,” extends dR-technique models by simultaneously analyzing an initial level and a difference score (McArdle & Nesselroade, 1994). This approach is perhaps the most promising for the analysis of manifest variable dynamics, because“if metric invariance does not fit both the starting point factors and difference factors, then the factorial interpretation of the changes can be interpreted from these difference loadings (McArdle, 1994).”
These models are perhaps the most promising of those listed here. Stating two occasions of measurement as a difference score and an initial or mean level provides no misfit to the longitudinal trend of the data, essentially providing a projection of the data into an alternate space for analysis. However, a factor of difference scores is not scalable to other numbers of observations, being restricted to only two measurement occasions. For a model like the factor of difference scores to be used, there must be an inherent and meaningful way to incorporate three or more timepoints.
Factor of Curves (FOCUS)
The Factor-of-Curves (FOCUS) model provides a unique approach to the use of dynamic information in measurement (McArdle, 1988), and is an extension of differential R-technique to multiple occasions. In this model, longitudinal multivariate data can be conceptualized as a set of univariate time-series, each modeled as a latent growth curve. Latent growth curve models (Duncan, Duncan, Strycker, Li, & Alpert, 1999; Laird & Ware, 1982; McArdle & Epstein, 1987; Raykov, 1993) describe repeated measurements as a set of individually varying intercept and slope parameters. In a FOCUS model, these intercepts and slopes of person i measured at time j and on item k are then predicted by common factors, as shown in Equations 1–3. Equation 1 describes the growth curves for each item, where each longitudinally measured item yijk is decomposed into its own level (Lik) and slope (Sik). The level factors for all items are fitted with a common factor Ai in Equation 2, and the slope factors are fit with a common factor Bi in Equation 3.
| (1) |
| (2) |
| (3) |
While the FOCUS model quite literally gets at the structure of change processes, this model has a few features that present problems for the analysis of the structure of dynamics. This model requires correct specification of the shape of the underlying growth curves, and thus depends on precise knowledge of the shape and structure of the dynamic processes. Whatever misfit incurred in the fitting of the FOCUS model may be due to misspecification of the measurement model, the growth curve model, or some interaction between the two. Whatever problems occur when selecting and fitting the growth curve portion of model model will undoubtedly affect the measurement model, and the misfit from these growth curves may bias the structure and invariance of the retained factor solution. Latent growth curve models have poor power to detect individual differences in slopes with fewer than five observations absent low residual variances and large sample sizes (Hertzog, Lindenberger, Ghisletta, & Oertzen, 2006; Hertzog, Oertzen, Ghisletta, & Lindenberger, 2008). When applied to the FOCUS model, factors representing growth are likely to incur additional misfit and poorer reliability, which could again be misinterpreted as a problem with the measurement structure rather than the longitudinal trend. Additionally, growth factors tend to be positively correlated under typical applications of latent growth curve models. This association is not problematic in most settings, but stronger correlations between growth factors will negatively affect power to detect differences in factor structure between them2.
Measurement Model of Derivatives
The limitations of the models reviewed thus far outline some of the requirements for assessing measurement structures in longitudinal data. Such a model should allow for repeated assessments of the same manifest variables, to avoid the applicability problems of the longitudinal item response models and related factor analytic approaches. The model should be scalable to any number of timepoints and not be restricted to two-occasion cases. Finally, a proposed model should not incur misfit in the measurement of change the way the FOCUS model can, as to avoid confusion between misfit in the measurement model and misfit in the longitudinal or process model.
One alternative is to define new variables that represent change and directly analyze those variables. The derivatives of the observed data provide a great opportunity to describe change in a way that avoids the limitations of existing models. Derivatives may be defined as a transformation of the data rather than a model, and thus do not contribute misfit to the change variables. Derivatives are inherently scalable, such that we can define as many orders of derivative as we have timepoints in any particular longitudinal dataset. Most importantly, derivatives have inherent meaning, such that the kth derivative of a variable describes how much that variable changes in unitsk per unit change in timek. This allows us to define units for these derivatives, and additionally think of the second derivative of any particular variable or test item similarly to how we would think of a quadratic term in other longitudinal models.
The following section will define a measurement model of derivatives (MMOD) to address the limitations of the reviewed extant models. This model included two parts: a data transformation which restated longitudinal data as a set of derivatives or change variables, and a multidimensional factor model where factor structures are fit to each order of derivatives. Both of these steps are now discussed in turn.
Derivative Transformation Methods
While the estimation and numerical approximation of derivatives encompasses a large number of methods, we’ll restrict this discussion to two methods for approximating derivatives from discrete data developed for psychological applications: (generalized) local linear approximation (GLLA; Boker, Deboeck, Edler, & Keel, 2010) and generalized orthogonal linear derivatives (GOLD; Deboeck, 2010). Both of these methods define the kth derivative of a variable as the weighted sum of repeated measurements of that variable, with the weights depending on the (centered) set of observation times t and the order of derivative k.
For example, three occasions of measurement on some variable y may be transformed into the zeroth (yt), first (ẏt) and second derivatives (ÿt) of y. The zeroth derivative represents position or level, and is given by the equality in Equation 4. The first derivative represents velocity or rate of change with respect to time, and can be approximated at time t as the change from time t − 1 to time t + 1 per unit time as given in Equation 5. Finally, the second derivative represents acceleration or rate of change with respect to quadratic time, and can be approximated using the difference in the first derivative estimated from times t − 1 and t and the first derivative estimated from times t and t + 1, as shown in Equation 63.
| (4) |
| (5) |
| (6) |
Equations 4–6 define the zeroth, first and second derivatives as a linear combination of the observed variables, and thus these derivatives can be expressed as a simple weighted sum. The zeroth derivative sets these weights at 0, 1, and 0 times the first, middle and last occasion, with the zeros omitted from Equation 4. The first derivative defines the weights as , 0, and (Equation 5), while the second derivative is , 1 and times the three occasions, respectively (Equation ??). These weights can be concatenated into a weight matrix W, where each column corresponds to a desired order of derivative and each row to a timepoint for a particular variable, as shown in Equation 7. The first column contains the weights for the zeroth derivative (0, 1, 0), and the second and third columns contain the weights for the first and second derivatives, respectively. When put into this matrix, these weights may then be used to transform the dataset in a single multiplication rather than individual calculations for each order of derivative. If a dataset Y has repeated measurements in each column, multiplying it by a weight matrix W would yield a dataset of derivative-transformed data D, as shown in Equation 8.
| (7) |
| (8) |
Deboeck (2010) pointed out that the non-orthogonality of the GLLA weight matrices can bias covariances between estimated derivatives. GOLD derivatives orthogonalize W, preventing this bias. While the orthogonality of this derivative method should aid the proposed model, this benefit is an empirical question to be answered in the ensuing analyses. The GOLD derivatives version of the 3 occasion W matrix is given in Equation 9.
| (9) |
The orthogonality of GOLD derivatives provide not just a methodological benefit for the ensuing model, but also aide in interpretation. The cross-products of any pair of columns in W sum to zero, just like planned contrasts in ANOVA and regression. The new derivative variables that are created restate repeated measures data in terms of development or change rather than occasion or timepoint. These derivative variables are not abstractions, but planned contrasts defined in terms of particular types of change relevant to answer questions about longitudinal measurement. In Equation 9, the first column represents between-person differences in mean level, while the second and third columns represent different types of within-person change. The various item-level derivatives can be though of in similar terms as growth or change factors in a growth curve model, with zeroth derivatives representing intercepts, first derivatives slopes and second derivatives quadratic slopes. The only difference between these derivatives and other change scores is that whatever measurement error is present in the data is not removed via error terms but instead retained and distributed among the new derivative variables to must be handled elsewhere in the analysis. These derivative variables are not a model for change, but a restatement of longitudinal data that allows for subsequent modeling of the measurement structure of item-level change.
It should be noted that not all uses of derivative transformation proceed as described here. First, derivatives can be estimated as latent variables rather than explicitly calculated. These latent differential equations model (LDE; Boker et al., 2004; Boker, 2007) invert the weight matrix W to create a loading matrix L and specifies regressions of observed longitudinal data on latent derivatives, such that the observed data is the product of the derivatives and the loading matrix. This method has benefits over transformation methods when missing or ordinal values are present in observed data, but is otherwise equivalent and conceptually identical to the manifest transformations described thus far.
Second, many applications of dynamical systems analysis retain fewer orders of derivatives than occasions of measurement or skip occasions to smooth the data (Boker & Nesselroade, 2002), both of which assume a particular measurement model where a smaller number of derivatives are sufficient to describe all of the occasions of longitudinal data. This assumption may be appropriate in some contexts, and does allow for the inclusion of residual variance terms to “remove” errors from the data. However, the fitting of such a measurement model conflicts with fitting a concurrent measurement model, as the results of that model would depend on how many orders of derivative are retained. Retaining as many orders of derivatives as occasions of measurement should obviate this concern, though that is an empirical question and a focus of the ensuing simulation studies.
Defining the Measurement Model of Derivatives (MMOD)
The availability of derivative estimation methods allows for the implementation of a measurement model of derivatives (MMOD). The model can be presented in two steps. In the first step, observed rows4 of data yi with columns representing longitudinal variables is transformed into a set of item-level derivatives using a transformation matrix W (Equation 10) or loading matrix L (Equation 11). These derivatives can then be analyzed using a common factor model, an example of which is given in Equation 12. Equations 11 and 12 may be collapsed into Equation 13, showing that the model may be applied directly to the raw data yi. Thus, the measurement model of derivatives is an application of the common factor model to assess the measurement structure of change defined by an orthogonal local linear derivative approximation.
| (10) |
| (11) |
| (12) |
| (13) |
There are several important features of the above model. First, derivative transformation is full-dimensional, meaning that there should be as many orders of estimated item-level derivatives as there are occasions of measurement. This ensures that derivative transformation remains a transformation rather than a model or projection, and that no misfit is incurred in this step. The model is as scalable as the derivative transformation method, meaning any number of timepoints may be used. When two occasions of measurement are used, this model reduces to a version of differential-R technique factor analysis, with the zeroth derivative representing means, sums or overall levels and the first derivative estimated in the same way as a change score. Finally, the use of GOLD derivatives provides orthogonal transformation of the longitudinal item-level data for the factor analysis of variables representing change.
One of this model’s primary benefits is its handling of time information. All of the derivatives in a given row of data may be considered to be estimated at the same time, or cover the same time interval. Derivative transformation thus restates longitudinal data as multidimensional data, and each of these new derivative dimensions represents a different type of change. Invariance tests that would compare the invariance of factor structures across timepoints in longitudinal models instead compare factor structures across varying types of change. In doing so, we can test whether the factor structure of zeroth derivatives, which represent between-person differences in levels or means, compare to the factor structure of higher derivatives, which represent varying patterns of change.
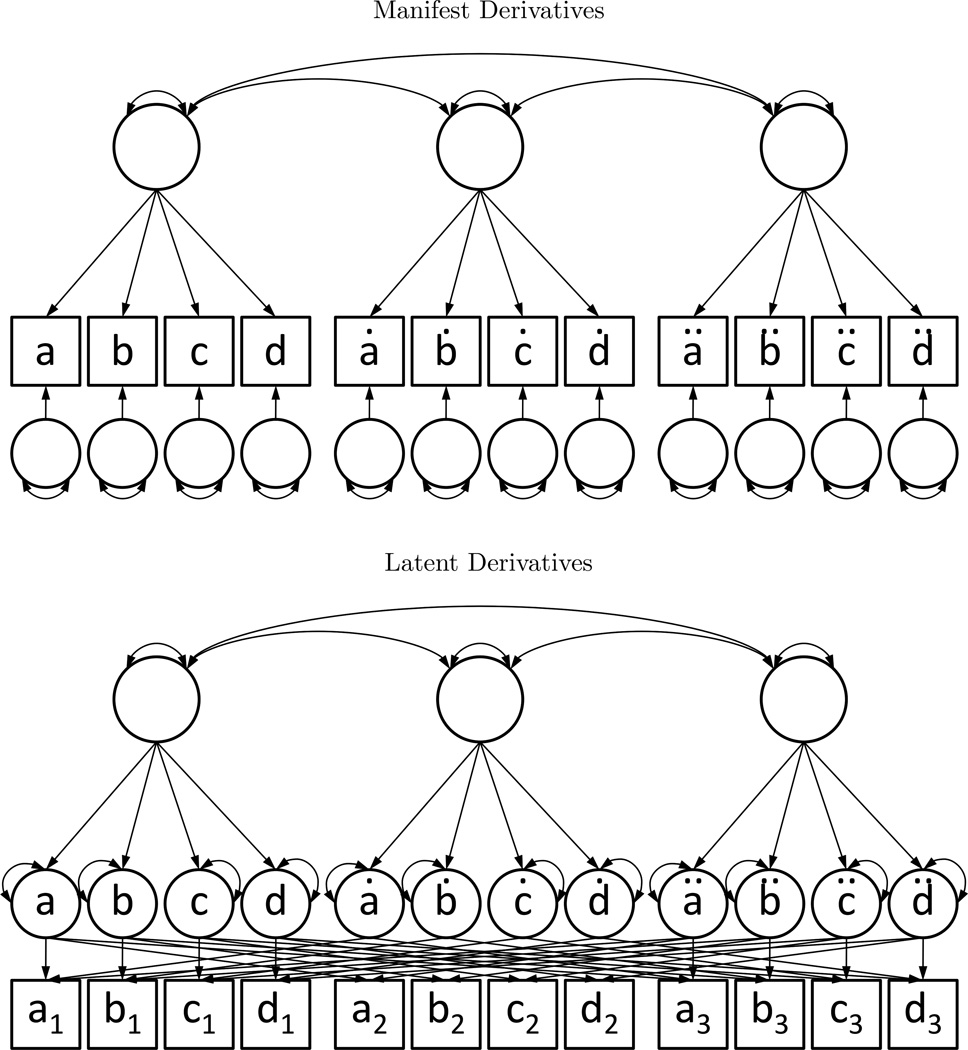
The application of the model depends on the method of derivative transformation. For continuous, complete data, derivative transformation may be carried out as a data processing step. Fitting the model to derivative-transformed data affords the use of exploratory factor analyses as well as a number of other descriptive statistics. Alternatively, derivative transformation may be done in latent space using the L matrix from Equation 11. In this version of the model, a set of latent variables representing the derivatives of the manifest variables are created. The loading matrix L defines the set of fixed factor loadings between the latent derivatives and manifest variables. Finally, the latent derivatives are given residual variance terms while the manifest variables are not, reflecting the fact that this is a transformation of the observed data rather than a model. Latent derivative transformation thus requires no data processing than would normally be required for existing multivariate longitudinal models, and allows for the analysis of datasets with missing values. These two presentations of the model are shown in Figure 3.
Figure 3.
Two Presentations of the Measurement Model of Derivatives
Note. Path diagrams for two versions of the measurement model of derivatives. The manifest derivatives version uses the data transformation shown in Equation 12, while the latent derivative version uses the model specification found in Equation 13.
While the proposed measurement model of derivatives has a number of theoretical benefits over existing longitudinal approaches, these benefits must be empirically tested to establish their validity and usefulness. The following sections present a pair of simulations studies designed to test various features of the model. In the first simulation, the importance of full-dimensional, orthogonal derivative transformation is evaluated by comparison to alternative derivative and change-score estimation methods. The second simulation tests the ability of the proposed model to detect violations of factorial invariance undetectable with a single timepoint, specifically violations of ergodic assumptions.
Simulation 1
The first simulation is designed to compare the measurement model of derivatives to existing models for longitudinal data in the case where measurement in invariant over time. This is a critical step in the evaluation of the proposed model, as the measurement model of derivatives would be of limited utility if the proposed transformation led to poor overall model fit. Data were first generated assuming an invariant factor structure and the structural parameters described in the Data Generation section. Then, the proposed model, the data generation model and a number of comparison models were fit to the data. The comparison models vary with respect to their definitions of change variables and whether or not these change variables are defined through transformation (full-dimensional) or estimation (reduced-dimensionality). Finally, these models are compared both in terms of absolute (χ2, CFI, RMSEA) and relative fit.
Data Generation
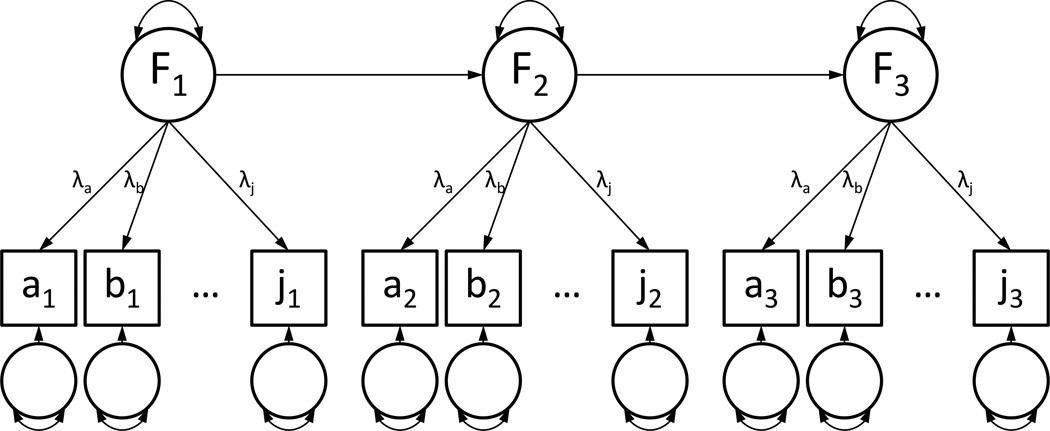
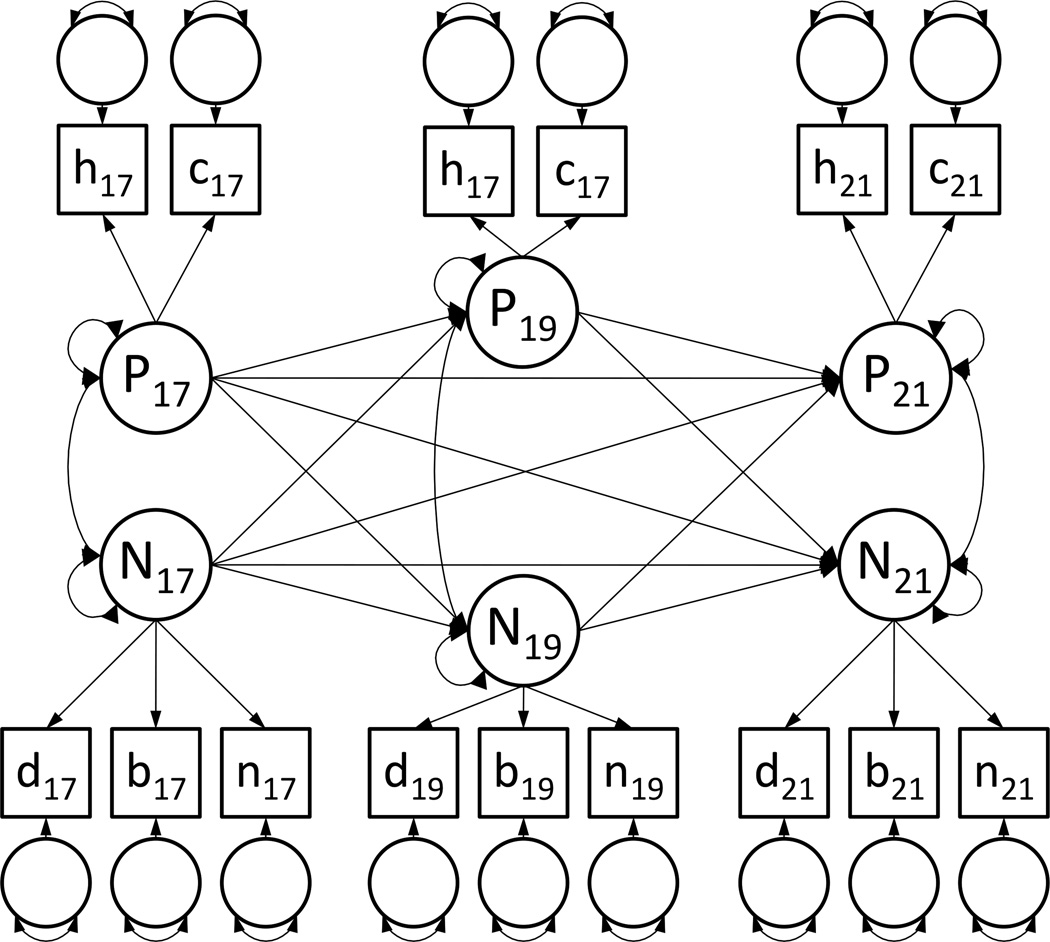
This simulation used a factor-at-timepoint model for data generation, as this type of structure is assumed for many longitudinal analyses. A three-occasion version of the data generation model is presented in Figure 4. Several variations of this data generation model were used, varying in the number of timepoints, factors per timepoint, number of items per timepoint, factor loadings and sample size. A table of these simulation parameters and their possible values is presented in Table 2.
Figure 4.
Data Generation Model for Simulation 1
Note. Factor-at-timepoint model used for data generation and model fitting in Simulation 1. Presented version includes a single factor at each of three timepoints and ten items.
Table 2.
Data Generation Parameters for Simulation 1
| Parameter | Levels | Values |
|---|---|---|
| Timepoints | 3 | 3, 4, 5 |
| Items per Timepoint | 2 | 10, 20 |
| Factors per Timepoint | 3 | 1, 2, 3 |
| Loadings (Standardized) | 3 | .4, .6, .8 |
| Factor Autocorrelation | 2 | .4, .8 |
| Sample Size | 3 | 250, 500, 1000 |
The set of simulation parameters were used to create 324 simulation conditions in the factorial design shown in Table 2, with each condition replicated 100 times. All models had invariant simple structure, such that items loaded on one and only one factor, and items loaded on the same factor at every occasion5. Conditions with multiple factors per timepoint were simulated with factor intercorrelations of 0.5. Manifest variables were assumed to have zero means and unit variances, so residual variance terms were defined as 1−λ2, where λ2 is that item’s factor loading. Data generation took place in R (R Development Core Team, 2012) using the mvtnorm library (Genz et al., 2012), and all datasets were output as files for analysis as described in the next section.
Comparison
A total of seven models were fit to each simulated dataset, six of them drawn from a 3 × 2 factorial design. The measurement model of derivatives using GOLD derivatives as detailed earlier was compared to two alternative models: a generalized local linear approximation version of the model (hereafter referred to as the GLLA model) and the Factor-of-Curves (FOCUS) model. These three models are very similar, as all can be described as transforming manifest data into a set of derivative or growth factors for a second-order factor analysis. They differ primarily in their loading matrices and my extension, level of orthogonality, as shown in Table 3. The orthogonality of these three loading matrices is shown through the sums of squares and cross-products (SSCP) of each of the loading matrices. GOLD is fully orthogonal, as demonstrated by diagonal SSCP matrix. GLLA is partially orthogonal, such that comparisons between even-order and odd-order derivatives are orthogonal while even-even and odd-odd comparisons are oblique. Finally, FOCUS is fully oblique, as all growth factors have non-zero cross-products with all other growth factors. These three models created three levels of orthogonality, and represents the first factor of the 3 × 2 design.
Table 3.
Loading Matrices for GOLD, GLLA & FOCUS Derivative Methods
| Method | GOLD | GLLA | FOCUS | |||
|---|---|---|---|---|---|---|
| Loading Matrix(L′) | ||||||
| SSCP (L′L) |
Note. Loading or L matrices for measurement model of derivatives, GLLA and FOCUS models. SSCP refers to the sums of squares and cross-products of each of the presented L matrices.
The second factor in the factorial design was the number of extracted derivative or growth factors. The version of MMOD described here demands t derivative factors per item, where t is the number of timepoints. However, traditional applications of the FOCUS model use fewer than t growth factors. To test the importance of the dimensionality of the transformation, two versions of each model will be created. One version maintains full dimensionality, where t derivative/growth factors are extracted and no manifest residual variance terms are included. Another version shows reduced dimensionality by extracting t − 1 derivative growth/factors and including a manifest residual variance term for each item, constrained to equality across all timepoints. The full and reduced dimensionality versions of each model are identified with subscripts F and R.
The final model fit to all datasets was the data generation model, shown in Figure 4. This model provides a reference for the previous models. In total, seven models are fit to each simulated data set: full and reduced dimensionality versions of MMOD, GLLA and FOCUS (denoted MMODF, MMODR, GLLAF, GLLAR, FOCUSF, FOCUSR) and the reference model. Item-level derivatives and change factors were estimated in latent space rather than using the manifest variable transformation method, ensuring that identically formatted data was used in all simulation conditions. All models were fit with Mplus (Muthén & Muthén, 1998–2007) and model syntax and results were created and read using user-defined functions in R. A subset of the models fit in this simulation were refit using OpenMx (Version 0.5; Boker et al., 2011) as an additional and recommended check on both the model and the software used to estimate it (Wilkinson & Statistical Inference, 1999), finding no difference in results.
Results
Mean fit statistics for all seven models across all simulation conditions are presented in Table 4. The three reduced dimensionality models show only marginal differences and reasonable fit overall by CFI and RMSEA (CFI∈[0.89, 0.91], RMSEA∈[0.030, 0.034]). The three full-dimensionality models show marked differences from one another, as both the full-dimensional GLLA and FOCUS versions of the model (GLLAF and FOCUSF, respectively) show large deficits in fit relative to their reduced-dimensionality versions and provide unacceptable fit both by CFI (GLLAF =0.07, FOCUSF =0.00) and RMSEA (GLLAF =0.163, FOCUSF =0.253). Unlike the other models, MMODF actually provides improved fit over MMODR by all metrics (CFI=0.97, RMSEA=0.011).
Table 4.
Mean Model Fit for Simulation 1
| Model | Converge | χ2 | χ2/df | CFI | RMSEA | ||||
|---|---|---|---|---|---|---|---|---|---|
| FOCUSR | 75.2% | 3360.94 | (2656.23) | 2.00 | (1.66) | 0.89 | (0.08) | 0.034 | (0.024) |
| GLLAR | 97.0% | 3200.51 | (2788.80) | 1.80 | (1.29) | 0.90 | (0.07) | 0.031 | (0.021) |
| MMODR | 96.8% | 3080.26 | (2567.69) | 1.74 | (1.21) | 0.91 | (0.07) | 0.030 | (0.020) |
| FOCUSF | 43.6% | 51825.47 | (45190.00) | 38.70 | (26.25) | 0.00 | (0.00) | 0.253 | (0.048) |
| GLLAF | 74.7% | 32527.02 | (34153.45) | 16.78 | (12.01) | 0.07 | (0.20) | 0.163 | (0.038) |
| MMODF | 91.1% | 2107.87 | (1704.59) | 1.06 | (0.06) | 0.97 | (0.05) | 0.011 | (0.008) |
| Reference | 99.1% | 2111.38 | (1703.24) | 1.06 | (0.06) | 0.97 | (0.05) | 0.011 | (0.008) |
Note. Mean fit statistics, their standard deviations and convergence rates for each of the seven comparison models aggregating across all simulation parameters. Means taken across all converged models with free (unconstrained) factor loadings across timepoints, derivative factors or growth factors. Reported means are taken as grand mean of cell means to prevent models with poor convergence from oversampling simpler (and thus, better fitting) simulation conditions. Models differ in their number of sample sizes and timepoints (and thus, degrees of freedom), the chi2/df column shows the ratio of the chi2 of each model to its degrees of freedom, and thus partially adjusts for this heterogeneity. Proportional and conceptually identical results are found for each combination of degrees of freedom and sample size.
Perhaps more importantly, the full-dimensional MMOD model provides near-equivalent fit to the data-generation or reference model. There is a slight improvement in fit of the MMOD over the data generation model by χ2 (Δχ2=3.51) that is reduced when the comparison is restricted to datasets on which both models converge (Δχ2=1.65 in jointly converged cases). The only notable difference between the MMOD and reference models is the difference in convergence rates, with MMOD converging in only 91.1% of the simulated datasets. The logistic regression analysis presented in Table 5 reveals that MMOD convergence is improved most greatly with stronger factor loadings , stronger relationships between factors (R2=.141) and simpler factor structures , with small but significant effects of increased sample size and fewer occasions.
Table 5.
Predicting MMOD Convergence from Simulation Parameters
| Raw Coefficient | Odds Ratio | ||||||
|---|---|---|---|---|---|---|---|
| Parameter | Estimate | S.E. | Estimate | Lower CI | Upper CI | ||
| Intercept | 4.14 | (2.57) | 63.08 | 50.98 | 78.05 | ||
| Occasions4 | −0.68 | (0.07) | .001 | 0.50 | 0.44 | 0.58 | |
| Occasions5 | −0.90 | (0.07) | 0.41 | 0.36 | 0.47 | ||
| Items20 | 1.82 | (0.06) | .056 | 6.20 | 5.51 | 6.97 | |
| Factors2 | −1.89 | (0.09) | .120 | 0.15 | 0.13 | 0.18 | |
| Factors3 | −3.43 | (0.09) | 0.03 | 0.03 | 0.04 | ||
| Loadings.6 | 2.88 | (0.07) | .267 | 17.75 | 15.46 | 20.38 | |
| Loadings.8 | 5.49 | (0.16) | 242.61 | 177.30 | 331.99 | ||
| Auto.8 | −3.02 | (0.07) | .141 | 0.05 | 0.04 | 0.06 | |
| n500 | 1.18 | (0.06) | .057 | 3.25 | 2.88 | 3.68 | |
| n1000 | 2.23 | (0.07) | 9.31 | 8.04 | 10.78 | ||
Note. Logistic regression of convergence (1=converged, 0=failure) on six simulation parameters. Simulation parameters treated as factors or dummy-coded variables, with 3 occasions, 10 items, 1 factor, loadings of 0.4, autoregression of 0.4 and a sample size of 250 treated as the baseline condition. R2 indicates variance accounted for by each simulation parameter. Auto=Factor Autocorrelation, Load=Factor Loadings, n=Sample Size. , calculated as when each predictor was removed from the model. for full model. C-index (area under ROC curve) = 0.94.
Summary
The primary findings of the first simulation are the near equivalence between MMOD and the data generation model and the importance of full-dimensional, orthogonal derivative estimation. The full-dimensional version of the proposed measurement model of derivatives showed equal fit to the data generation model in CFI and RMSEA and a small improvement in fit by χ2 or −2 log likelihood. This small improvement could be attributable to a number of factors, including sampling variation, and interactions between derivative transformation and the numerical precision of the statistical software. As this difference amounts to less than 0.1% of the mean χ2 statistic and is unobservable in the other model fit statistics, it seems reasonable to conclude that the measurement model of derivatives and the data generation model fit equally well. The only noticeable downside to the full-dimensional MMOD is a decreased convergence rate (91.9%).
Alternative versions of the model that depend on either reduced-dimensionality or oblique derivative transformation all showed significant deficits relative to the data generation model, indicating that the information retained in full-dimensional MMOD transformation is important and should be retained. Unlike the orthogonal MMOD, non-orthogonal FOCUS and GLLA models show worse fit in full-dimensional versions of the model, most likely due to the inherent covariances between orders of derivative created using these methods. These covariances are artifacts of non-orthogonal transformation, and the addition of additional parameters to handle these artifacts creates a problem of simultaneously modeling longitudinal structures and measurement structures that this model was designed to avoid. These fit problems preclude the set of reduced-dimensionality and non-orthogonal models from further analyses.
While the results of this simulation show that MMOD doesn’t find differences in factor structures between orders of derivatives when none exist, the first simulation did not provide any conditions where differences between timepoints or orders of derivatives could be found. The next portion of the study deals with the ability of MMOD to detect differences in factor structures between initial levels and change patterns.
Simulation 2
The second simulation pertains to the ability of MMOD to detect measurement problems, specifically those undetectable in a single timepoint analysis. Differences in structure between individual levels (between-person) and within-person changes represent one type of violation of ergodicity assumptions. When these assumptions are violated, between-person analyses can reveal factor structures that bear no resemblance to any of the within-person structures present in the data (Molenaar, 1997, 1999). The following simulation will rely on data simultaneously generated under two different factor structures: one factor structure for between-person differences in overall level, and a second factor structure that governs within person change around those levels. As MMOD contains derivative orders both for between-person differences in overall level (zeroth derivatives) and for within-person change (first and higher derivatives), then the zeroth and higher-order derivatives should identify and select the appropriate between-person and within-person data generation models, respectively.
Data Generation
Data generation proceeded in much the same manner as in the first simulation. The number of timepoints, items per timepoint and sample size were varied in the same manner and with the same values as before. The magnitude of the factor loadings were also varied, though the possible values for this simulation parameter was restricted to 0.6 and 0.8 as the 0.4 condition showed a relatively high rate of non-convergence in the first simulation.
The primary difference between the first and second simulations was the difference in factor structures. The first simulation had a single factor structure that jointly described between-person differences and within-person changes. The second simulation maintained two distinct factor structures: one that describes how people differ from one another but does not describe change, and a second that describes how people vary around their own mean. The between-person factors varied across people but not across time, while the within-person factors varied across people and time. This structure is described in Equations 14, where observed data y for person i at time t depends on an individually varying mean across all timepoints (µi), some number of latent factors varying across individuals and timepoints (Wit), with factor loadings (Λw) and an error term (εit). In addition to the within-person factor structure represented by Wit, individual means µi depend on factors that vary between persons but not across time (Bi) and a between-person error term (γi), as shown in Equation 15. These two factor structures are combined in Equation 16.
| (14) |
| (15) |
| (16) |
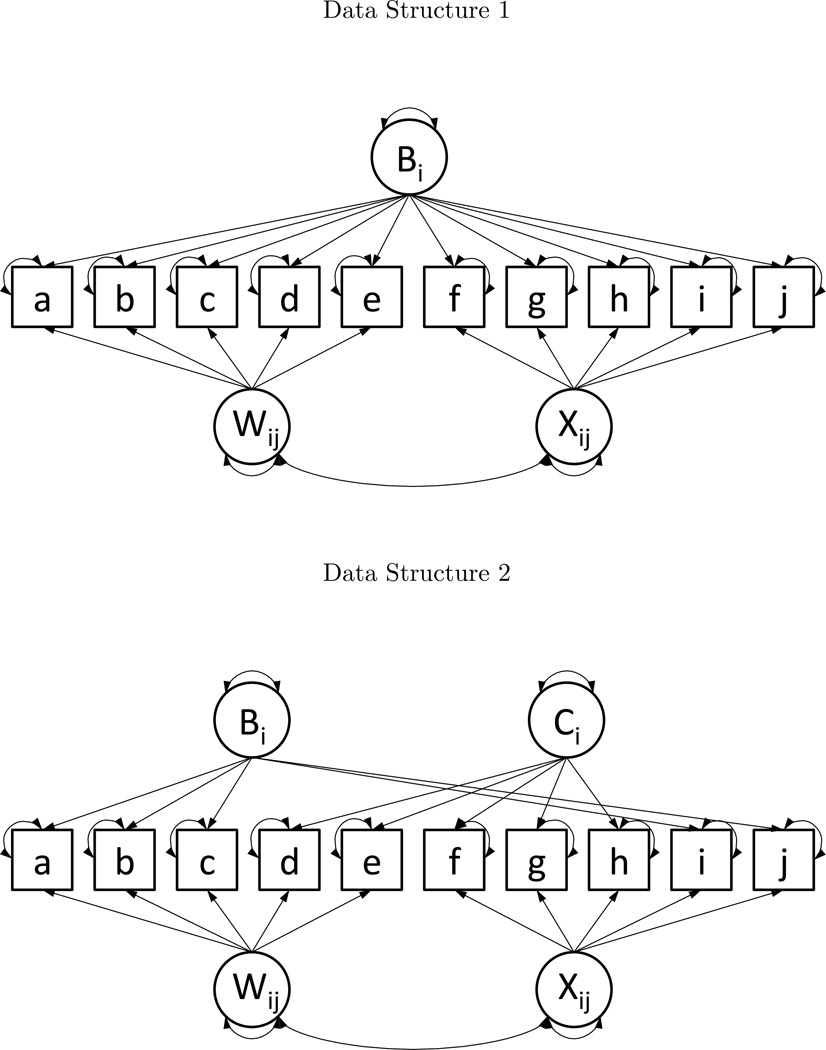
The specific form of these factor structures is presented in Figure 5. The first structure features a single between-person factor that loads on all timepoints (Bi) and two within-person factors (Wij, Xij). The second structure includes two between-person factors covering the middle and endpoint items (Bi, Ci) and two within-person factors covering the first and last halves of the items (Wij, Xij).
Figure 5.
Data Generation Models for Simulation 2
Note. Path diagrams for two data generation models for Simulation 2. Factors subscripted with only i indicate factors that vary between individuals but are fixed longitudinally, and appear above the items they load on. Factors subscripted ij vary both between and within individuals, and appear below the items they load on.
The presence of different between-person (Λb) and within-person factor structures (Λw) presents an additional opportunities to affect the simulation. In addition to the simulation parameters previously used in the first simulation, the ratio of variances between the between-person and within-person factors was also varied, including simulated values of 0.5, 1 and 2.
Comparison
Five different factor structures were used in models fit to the simulated data. The first is a one-factor model, identical to the between-person factor in Figure 5’s Data Structure 1. Two different two-factor models were also included: the first represented to the between-person factor structure in Data Structure 2, and the second represented by the within-person structure in both data structures. These two structures will be referred to as “2b” and “2w”, respectively. In addition, three- and four-factor models were created, with the ten or twenty items split evenly across the three or four factors and representing simple structure. Each of these five structures was fit to the zeroth and non-zeroth (hereafter, higher-order) derivatives in a 5×5 factorial design.
Results
Fit statistics for the set of higher derivatives are presented together in Table 7, while the fit for the zeroth derivatives are presented separately in Table 8. Each of these tables presents the mean fit for a particular factor structure (1, 2b, 2w, 3 or 4 factors), aggregating across all factor structures for the other set of derivatives. For instance, the fit statistics reported for the one-factor higher-order derivative models are the mean of all models with one factor per non-zero order of derivatives.
Table 7.
Mean Model Fit for Higher-Order Derivatives
| Occasions | One Between-Person Factor | Two Between-Person Factors | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Structure | χ2 | DF | CFI | RMSEA | χ2 | DF | CFI | RMSEA | |||||||
| 3 | 1 | 834.38 | (516.22) | 390 | 0.969 | (0.027) | 0.039 | (0.019) | 1120.17 | (700.03) | 390 | 0.948 | (0.030) | 0.052 | (0.021) |
| 2w | 609.84 | (370.60) | 377 | 0.983 | (0.022) | 0.025 | (0.020) | 899.97 | (504.79) | 377 | 0.962 | (0.024) | 0.044 | (0.018) | |
| 2b | 828.61 | (515.37) | 377 | 0.968 | (0.027) | 0.040 | (0.020) | 1126.32 | (701.24) | 377 | 0.947 | (0.031) | 0.053 | (0.021) | |
| 3 | 738.87 | (456.65) | 360 | 0.974 | (0.025) | 0.036 | (0.019) | 1040.89 | (622.15) | 360 | 0.953 | (0.028) | 0.051 | (0.020) | |
| 4 | 593.81 | (386.54) | 339 | 0.982 | (0.023) | 0.026 | (0.022) | 910.02 | (514.88) | 339 | 0.961 | (0.024) | 0.048 | (0.019) | |
| 4 | 1 | 1411.26 | (692.50) | 719 | 0.965 | (0.024) | 0.038 | (0.016) | 1716.87 | (917.83) | 719 | 0.950 | (0.027) | 0.046 | (0.017) |
| 2w | 957.01 | (387.21) | 695 | 0.986 | (0.017) | 0.021 | (0.015) | 1271.69 | (526.88) | 695 | 0.971 | (0.018) | 0.035 | (0.013) | |
| 2b | 1410.52 | (696.75) | 695 | 0.966 | (0.024) | 0.038 | (0.016) | 1731.86 | (919.14) | 695 | 0.950 | (0.028) | 0.047 | (0.018) | |
| 3 | 1215.43 | (555.57) | 662 | 0.974 | (0.021) | 0.034 | (0.015) | 1552.23 | (753.18) | 662 | 0.958 | (0.023) | 0.044 | (0.016) | |
| 4 | 911.28 | (409.34) | 620 | 0.986 | (0.017) | 0.022 | (0.016) | 1268.32 | (541.45) | 620 | 0.970 | (0.018) | 0.038 | (0.014) | |
| 5 | 1 | 2160.77 | (931.00) | 1147 | 0.961 | (0.023) | 0.037 | (0.014) | 2486.64 | (1186.62) | 1147 | 0.949 | (0.027) | 0.042 | (0.015) |
| 2w | 1394.76 | (385.03) | 1109 | 0.988 | (0.014) | 0.018 | (0.012) | 1741.29 | (538.61) | 1109 | 0.975 | (0.015) | 0.030 | (0.011) | |
| 2b | 2156.14 | (927.35) | 1109 | 0.962 | (0.023) | 0.037 | (0.014) | 2517.84 | (1188.01) | 1109 | 0.948 | (0.027) | 0.044 | (0.016) | |
| 3 | 1824.97 | (667.58) | 1055 | 0.972 | (0.019) | 0.032 | (0.012) | 2203.16 | (898.10) | 1055 | 0.959 | (0.021) | 0.040 | (0.014) | |
| 4 | 1306.41 | (413.89) | 985 | 0.988 | (0.014) | 0.019 | (0.013) | 1709.60 | (557.80) | 985 | 0.975 | (0.015) | 0.032 | (0.011) | |
Note. Mean and standard deviations of fit indices for models with ten items and specified number of occasions and higher-order derivative factor loading pattern. Degrees of freedom presented for when a one factor structure is fit to the zeroth-order derivatives.
Table 8.
Mean Model Fit for Zeroth Derivatives
| Occasions | One Between-Person Factor | Two Between-Person Factors | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Structure | χ2 | DF | CFI | RMSEA | χ2 | DF | CFI | RMSEA | |||||||
| 3 | 1 | 940.00 | (589.43) | 369 | 0.960 | (0.030) | 0.045 | (0.021) | 1241.83 | (762.50) | 369 | 0.938 | (0.033) | 0.057 | (0.021) |
| 2w | 510.63 | (187.31) | 360 | 0.991 | (0.009) | 0.019 | (0.015) | 947.88 | (527.10) | 360 | 0.961 | (0.020) | 0.047 | (0.019) | |
| 2b | 933.77 | (581.43) | 360 | 0.960 | (0.030) | 0.045 | (0.021) | 1190.49 | (728.47) | 360 | 0.941 | (0.032) | 0.056 | (0.021) | |
| 3 | 736.80 | (376.76) | 350 | 0.974 | (0.019) | 0.037 | (0.017) | 901.94 | (488.13) | 350 | 0.962 | (0.022) | 0.046 | (0.017) | |
| 4 | 496.34 | (189.06) | 339 | 0.991 | (0.010) | 0.020 | (0.015) | 824.94 | (429.46) | 339 | 0.968 | (0.017) | 0.043 | (0.017) | |
| 4 | 1 | 1418.45 | (735.86) | 662 | 0.964 | (0.027) | 0.038 | (0.017) | 1749.68 | (927.86) | 662 | 0.948 | (0.029) | 0.047 | (0.017) |
| 2w | 967.18 | (368.84) | 649 | 0.986 | (0.013) | 0.022 | (0.015) | 1449.02 | (700.35) | 649 | 0.964 | (0.020) | 0.040 | (0.015) | |
| 2b | 1405.28 | (726.80) | 649 | 0.964 | (0.026) | 0.038 | (0.017) | 1687.33 | (888.56) | 649 | 0.950 | (0.029) | 0.046 | (0.017) | |
| 3 | 1205.46 | (541.36) | 635 | 0.974 | (0.019) | 0.033 | (0.015) | 1378.86 | (650.12) | 635 | 0.965 | (0.021) | 0.039 | (0.015) | |
| 4 | 949.48 | (372.71) | 620 | 0.986 | (0.013) | 0.022 | (0.015) | 1309.83 | (603.94) | 620 | 0.969 | (0.018) | 0.037 | (0.015) | |
| 5 | 1 | 2024.75 | (928.01) | 1039 | 0.965 | (0.026) | 0.035 | (0.015) | 2387.20 | (1136.21) | 1039 | 0.952 | (0.028) | 0.042 | (0.015) |
| 2w | 1563.24 | (602.96) | 1022 | 0.983 | (0.016) | 0.023 | (0.015) | 2091.43 | (928.00) | 1022 | 0.964 | (0.021) | 0.037 | (0.014) | |
| 2b | 2006.64 | (922.80) | 1022 | 0.965 | (0.025) | 0.035 | (0.015) | 2322.78 | (1094.53) | 1022 | 0.954 | (0.028) | 0.041 | (0.015) | |
| 3 | 1797.56 | (753.38) | 1004 | 0.973 | (0.020) | 0.030 | (0.014) | 1994.56 | (865.33) | 1004 | 0.966 | (0.023) | 0.035 | (0.014) | |
| 4 | 1539.61 | (606.24) | 985 | 0.983 | (0.016) | 0.023 | (0.015) | 1937.40 | (834.24) | 985 | 0.968 | (0.020) | 0.034 | (0.014) | |
Note. Mean and standard deviations of fit indices for models with ten items and specified number of occasions and zeroth derivative factor loading pattern. Degrees of freedom presented for when a one factor structure is fit to the higher order derivatives.
The results for the higher-order derivatives in Table 7 conform to the original hypothesis. Regardless of the simulated between-person structure, the higher-order derivatives retain the two-factor (within) structure by all fit measures, at worst providing equivalent fit by CFI to the more complex four-factor solution when only a single between-person factor is present in the data.
However, the results for the zeroth derivatives do not support the original hypotheses, as the retained factor solutions for the two between-person structures do not reflect the data generation model. When a single factor governed between-person differences, the two-factor (within) factor structure was retained. When the two-factor (between) structure was used to generate between-person data, a four-factor structure was retained.
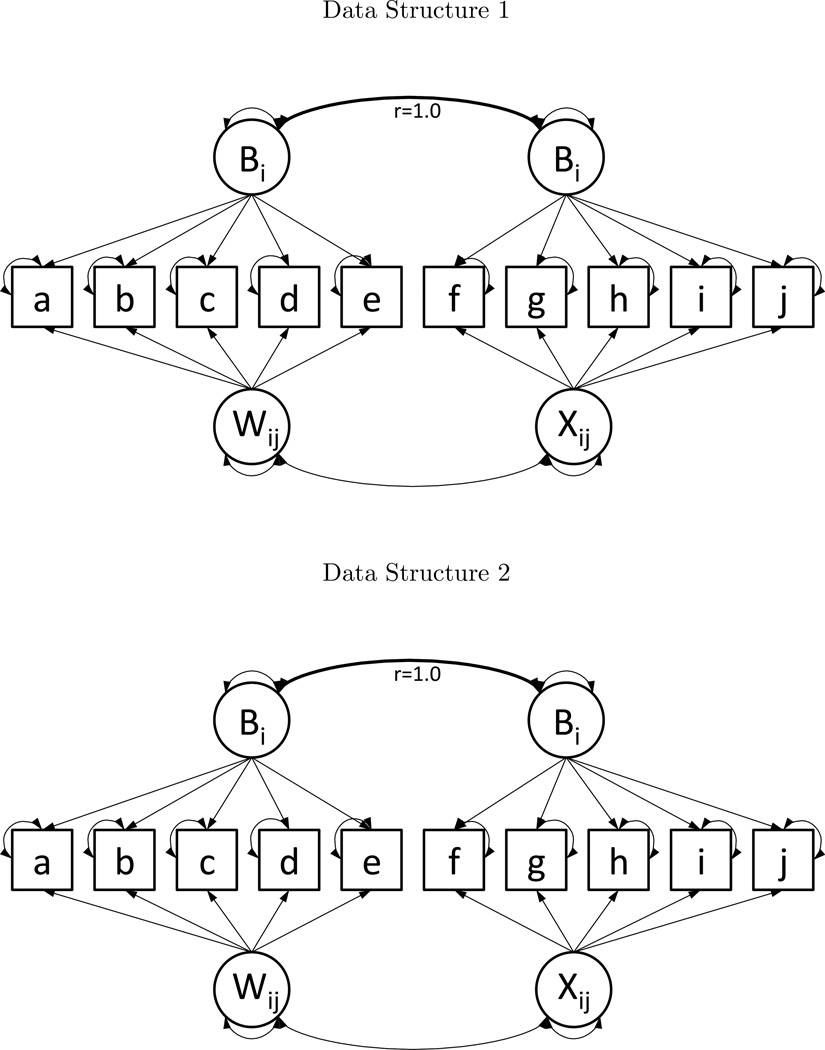
While this failure to support the original hypothesis requires revision of the interpretation of the zeroth derivative factors, the specific models that were retained can provide some insight. Figure 6 presents and alternative pair of path diagrams that are equivalent to the models presented in Figure 5. The models retained for the zeroth derivatives are in fact equivalent to a mixture of the between-person and within-person factor structure when described as shown in Figure 6.
Figure 6.
Alternate Specification of Simulation 2 Data Generation Models
Note. Path diagrams showing alternate forms of data generation models Simulation 2. Factors subscripted with only i indicate factors that vary between individuals but are fixed longitudinally, and appear above the items they load on. Factors subscripted ij vary both between and within individuals, and appear below the items they load on.
The assertion that the zeroth derivatives represent a mixture of the between-person and within-person factor structures is testable given the existing design in this simulation. The ratio of between-person to within-person factor variances was a parameter in this simulation. If zeroth derivatives represent a mixture of two different factor structures with identical loading patterns and discrepant factor correlations, then the factor correlations should vary as a function of the ratio of factor variances. That is, the factor correlations bolded in the top of each diagram in Figure 6 should increase when there is more variance between individuals than within, and decrease when there is more variance within individuals than between. Regressing the affected factor correlations on the set of simulation parameters can aide in the interpretation of zeroth derivatives.
This regression is presented in Table 9. The largest predictor of these factor correlations was the ratio of between-person to within-person variance, explaining nearly all of the variance explainable by the simulation parameters (and thus, nearly all variation attributable to cell means). It appears that higher order derivatives represent within-person factor structures in this simulation, while zeroth derivatives represent a mixture of between- and within-person factor structures.
Table 9.
Predicting Zeroth-Order Factor Correlations from Simulation Parameters
| Structure 1 | Structure 2 | |||||
|---|---|---|---|---|---|---|
| Parameter | Estimate | S.E. | R2 | Estimate | S.E. | R2 |
| Intercept | 0.836 | (0.002) | 0.835 | (0.004) | ||
| vEqual | 0.194 | (0.002) | .827 | 0.194 | (0.003) | .684 |
| vB>W | 0.432 | (0.002) | 0.487 | (0.003) | ||
| Occasions4 | 0.024 | (0.002) | .008 | 0.021 | (0.003) | .006 |
| Occasions5 | 0.043 | (0.002) | 0.046 | (0.003) | ||
| Load.8 | 0.003 | (0.002) | .000 | −0.015 | (0.003) | .001 |
| n500 | 0.003 | (0.002) | .000 | −0.026 | (0.003) | .003 |
| n1000 | 0.003 | (0.002) | −0.032 | (0.003) | ||
| Main Effects | .835 | .694 | ||||
| All Interactions | .835 | .707 | ||||
Note. Regression of Fisher-transformed factor correlations amongst theorized between-person factors on simulation parameters.
Example
The final phase of this analysis is an empirical demonstration using data from the National Longitudinal Survey of Youth. The NLSY 1997 sample (NLSY97) is a longitudinally-measured sample of adolescents and young adults born between 1980 and 1984 and assessed from 1997 onward on a range of psychological, health and demographic variables. This empirical example evaluates a five-item depression scale used from the year 2000 onward, with each of the five items assessed with a 4-point Likert scale. All five items ask respondents to report how often they felt “like a nervous person”, “calm and peaceful”, “down or blue”, “like a happy person” and “depressed” in the last month, hereafter referred to as “Nervous”, “Calm”, “Down”, “Happy” and “Depressed”. Data from the cohort born in 1983 includes 1,397 individuals assessed longitudinally in 2000, 2002 and 2004 (ages 17, 19 and 21). In the ensuing analyses, exploratory and confirmatory models will be fit to a data polychoric correlation matrix estimated from this sample. Further details about the access and preparation of the data and coding examples are available in the Appendix.
The first part of this example will show a conventional analysis of single occasions of measurement. Exploratory analyses of any single occasion of measurement show strong support for a unidimensional depression factor. The observed polychoric correlation matrix at age 17 shows a single eigenvalue greater than 1 (λ1=3.011), while the second eigenvalue falls well below 1.0 and any parallel analysis criterion (λ2=0.685), with comparable results for the other occasions. Subsequent factor models of each occasion of measurement show strong standardized factor loadings, with consistent positive loadings on the items “Nervous” (Age 17 loading=0.590), “Down” (0.812), and “Depressed” (0.732), and consistent negative loadings on the items “Calm” (−0.656) and “Happy” (−0.746). Despite the evidence for a single latent construct, fit of this model was relatively acceptable for single occasions (Age 17: CFI=0.907, TLI=0.814, RMSEA=0.190, SRMR=0.066), but poor for all three occasions assessed longitudinally (CFI=0.785, TLI=0.738, RMSEA=0.139, SRMR=0.076).
Residual diagnostics from the initial exploratory factor analysis show one clue to the poor fit. The items “Calm” and “Happy” show a consistent residual correlation between 0.10 and 0.15 at every wave of the study. Incorporating this residual correlation into subsequent confirmatory factor models between these two items improved the fit for both single occasion (, p<.001) and longitudinal versions of the model (, p<.001). While the absolute fit indices noticeably improve for the single occasion model (CFI=0.967, TLI=0.914, RMSEA=0.126, SRMR=0.044), and longitudinal models still show poor fit, with low values CFI and TLI and an increase in SRMR over the simpler model (CFI=0.836, TLI=0.795, RMSEA=0.123, SRMR=0.081).
While the structure of this dataset could be assessed by fitting a variety of competing confirmatory models, adding more residual covariances to improve fit or turning to modification indices, such a process would likely result in a model that included paths with little theoretical value or replicability. The measurement model of derivatives instead can directly evaluate whether the proposed structure (single factor, with or without a residual covariance) can explain the longitudinal associations between the five items on the depression scale. As the data is in the format of a covariance matrix, that matrix may be transformed as described in Equations 10–13 and the Manifest Derivatives path diagram in Figure 3, and each order of derivative analyzed in the same way a single occasion of data would be. The five item-level zeroth derivatives showed the same pattern of results as the single occasion analysis: a strong single eigenvalue greater than one (λ1,2=[3.350, 0.638]), poor fit without the residual correlation between “Calm” and “Happy” (CFI=0.884, TLI=0.769, RMSEA=0.249, SRMR=0.070), and improved fit with the residual correlation (, p<.001, CFI=0.963, TLI=0.906, RMSEA=0.159, SRMR=0.044). The higher derivatives showed similar effects, with improved fit when the residual correlation between “Calm” and “Happy” was included for both the first derivatives (CFI=0.975, TLI=0.937, RMSEA=0.092, SRMR=0.044) and second derivatives (CFI=0.953, TLI=0.884, RMSEA=0.108, SRMR=0.045). Removing the residual correlation lead to a significant loss in fit ( =127.22, first derivatives; =176.11, second derivatives) and poorer overall fit for both the first derivatives (CFI=0.907, TLI=0.815, RMSEA=0.157, SRMR=0.069) and second derivatives (CFI=0.828, TLI=0.656, RMSEA=0.185, SRMR=0.089).
The interpretation of the residual correlation for the derivative-transformed data is different than in other contexts. For a single timepoint, a residual correlations can be due to measurement artifacts or other issues not thought of as related to the construct. With derivative-transformed data generally and the higher derivatives specifically, the persistence of this residual correlation indicates that additional factors are needed. The residual correlation between the first and second derivatives of “Happy” and “Calm” means that those items change in a different way than the rest of the scale, and the changes in these two variables are correlated. As shown in Figure 1, this model with a single residual correlation can be restated as a two-factor model, with the three negative items loading on one factor and the two positive items loading on a second. This model fits exactly as well as the models with residual correlation listed in the preceding paragraphs, and their factor loadings and factor correlations are presented in Table 10. Single occasion analyses show that these two factors correlate −0.777. Looking at the derivative transformed data reveals that while the between person differences in these two factors (zeroth derivatives) correlate −0.804, linear and curvilinear changes in these variables correlate −0.720 and −0.623, respectively. While individuals who report negative emotions don’t report positive ones (and visa versa), the way that these two sets of items change from age 17 to 21 is more complex than can be explained by a single factor.
Table 10.
Factor Loadings for Two-Factor Models
| MMOD | |||||
|---|---|---|---|---|---|
| Factor | Item | Age 17 | Zeroth | First | Second |
| Negative | Nervous | 0.581 | 0.647 | 0.472 | 0.481 |
| Down | 0.856 | 0.894 | 0.836 | 0.709 | |
| Depressed | 0.757 | 0.795 | 0.734 | 0.729 | |
| Positive | Calm | 0.717 | 0.834 | 0.581 | 0.591 |
| Happy | 0.863 | 0.887 | 0.849 | 0.820 | |
| Factor Correlation | −0.777 | −0.804 | −0.720 | −0.623 | |
Note. Standardized factor loadings and factor correlation for confirmatory factor models fit to single occasion (age 17), and single order of derivative (zeroth, first, second). Items “Nervous”, “Down” and “Depressed” load on a common factor for negative items, while “Calm” and “Happy” load on a common factor for positively-worded items. All latent variables identified with unit variance. Item residual variances estimated but omitted from table, as standardized values can be calculated as 1-loading2.
Analyzing the set of derivatives together provides two benefits. First, the fit of the two factor model can be assessed with the entirety of the data (CFI=0.942, TLI=0.919, RMSEA=0.063, SRMR=0.037), showing that two factors do a reasonably good job of explaining the dynamics in the data. Furthermore, we can test for factorial invariance in the derivative-transformed space, and find that there is a significant loss of fit when factor loadings are constrained across order of derivatives (, p<.001) with small changes in fit indices (CFI=0.936, TLI=0.917, RMSEA=0.064, SRMR=0.042). Constraining the loadings across the first and second derivative factors had a much smaller effect (, p=.077), indicating that most of the variation in factor structures is due to differences between the structure of individual differences and the structure of within-person change.
Applying the retained two-factor solution to the untransformed data allows for more informed analysis of the longitudinal trend, as shown in Tables 11 and 12. The first comparisons in Table 11 shows that the two-factor model (Model 2b) provides improved fit over the one factor model (Model 1) by the likelihood ratio test (, p<.001) and superior fit to both both one factor models (Models 1 and 2a) by CFI, TLI, RMSEA and SRMR. This two-factor model is shown in Figure 7, and contains no invariance constraints, covariances between the two factors at each occasion, and regressions between factors at different occasions. Models 3–5 make restrictions on the longitudinal regressions between these factors, showing that the cross-factor regressions may be constrained to equality (Model 3c vs Model 2c: , p=.605), such that all regressions of a positive factor on a negative factor can be held equal to regressions of a negative factor on a positive factor at the same ages. Subsequent comparisons show that the autoregressive structures of the negative factors can be constrained to be equal to the autoregressions among the positive factors (Model 4 vs. Model 3c: , p=.923), but the regressions of the positive factor on the negative and negative on the positive could not be removed entirely (Model 5 vs Model 4: , p<.001).
Table 11.
Comparing Longitudinal Models of NLSY97 Depression
| Model | χ2 (df) | χ2 (df) | p | CFI | TLI | RMSEA | SRMR | |
|---|---|---|---|---|---|---|---|---|
| 1a | One Factor Model | 2423.64 (87) | 0.783 | 0.738 | 0.139 | 0.076 | ||
| 2a | + Residual Correlation | 1846.16 (84) | 577.48 (3) | < .001 | 0.836 | 0.795 | 0.123 | 0.081 |
| 2b | Two Factor Model | 1427.11 (75) | 996.53 (12) | < .001 | 0.874 | 0.824 | 0.114 | 0.063 |
| 3a | Pos→Neg=0 | 1438.20 (78) | 11.08 (3) | .011 | 0.874 | 0.830 | 0.112 | 0.064 |
| 3b | Neg→Pos=0 | 1433.29 (78) | 6.18 (3) | .103 | 0.874 | 0.831 | 0.112 | 0.063 |
| 3c | Neg→Pos=Pos→Neg | 1428.96 (78) | 1.85 (3) | .605 | 0.875 | 0.831 | 0.111 | 0.064 |
| 4 | Neg→Neg=Pos→Pos | 1429.44 (81) | 0.46 (3) | .923 | 0.875 | 0.838 | 0.109 | 0.064 |
| 5 | No Neg↔Pos Regressions | 1452.10 (84) | 22.66 (3) | < .001 | 0.873 | 0.841 | 0.108 | 0.064 |
Note. Model fit statistics for longitudinal models of depression for the 1983 cohort of the NLSY97 sample. All models to best fitting (bottom) model in preceding section. Neg→Neg indicates set of 3 possible autoregression (age 17 predicting ages 19 and 21, and age 19 predicting age 21), while Neg→Pos indicates set of three possible cross-loadings (negative factor at age 17 predicts positive factor at ages 19 and 21, and negative factor at age 19 predicts positive factor at age 21).
Table 12.
Parameters for NLSY97 Longitudinal Model
| Loadings | Age 17 | Age 19 | Age 21 | |||
| Nervous | 0.618 | (0.026) | 0.618 | (0.029) | 0.578 | (0.027) |
| Down | 0.824 | (0.024) | 0.842 | (0.031) | 0.822 | (0.028) |
| Depressed | 0.756 | (0.024) | 0.760 | (0.029) | 0.830 | (0.028) |
| Calm | 0.722 | (0.025) | 0.737 | (0.030) | 0.788 | (0.028) |
| Happy | 0.844 | (0.024) | 0.859 | (0.034) | 0.869 | (0.030) |
| Covariances | Age 17 | Age 19 | Age 21 | |||
| Pos ↔ Neg | −0.808 | (0.019) | −0.472 | (0.022) | −0.456 | (0.018) |
| Regressions | Age 17 → 19 | Age 17 → 21 | Age 19 → 21 | |||
| Autoregressions | 0.746 | (0.053) | 0.463 | (0.089) | 0.236 | (0.070) |
| Cross-Factor | 0.135 | (0.045) | 0.226 | (0.088) | −0.222 | (0.068) |
Note. Standardized parameter estimates and their standard errors for a three-occasion longitudinal model of depression using NLSY97 data.
Figure 7.
NLSY97 Two-Factor Model for Depression at Ages 17, 19 and 21
Note. Longitudinal common factor model for five-item NLSY97 depression scale. Positive and negative factors correlate at each age, and all factors at ages 19 and 21 are regressed on all previously measured factors. Factors at age 19 were offset not to indicate difference in parameters, but only to make the set of factor regressions more legible.
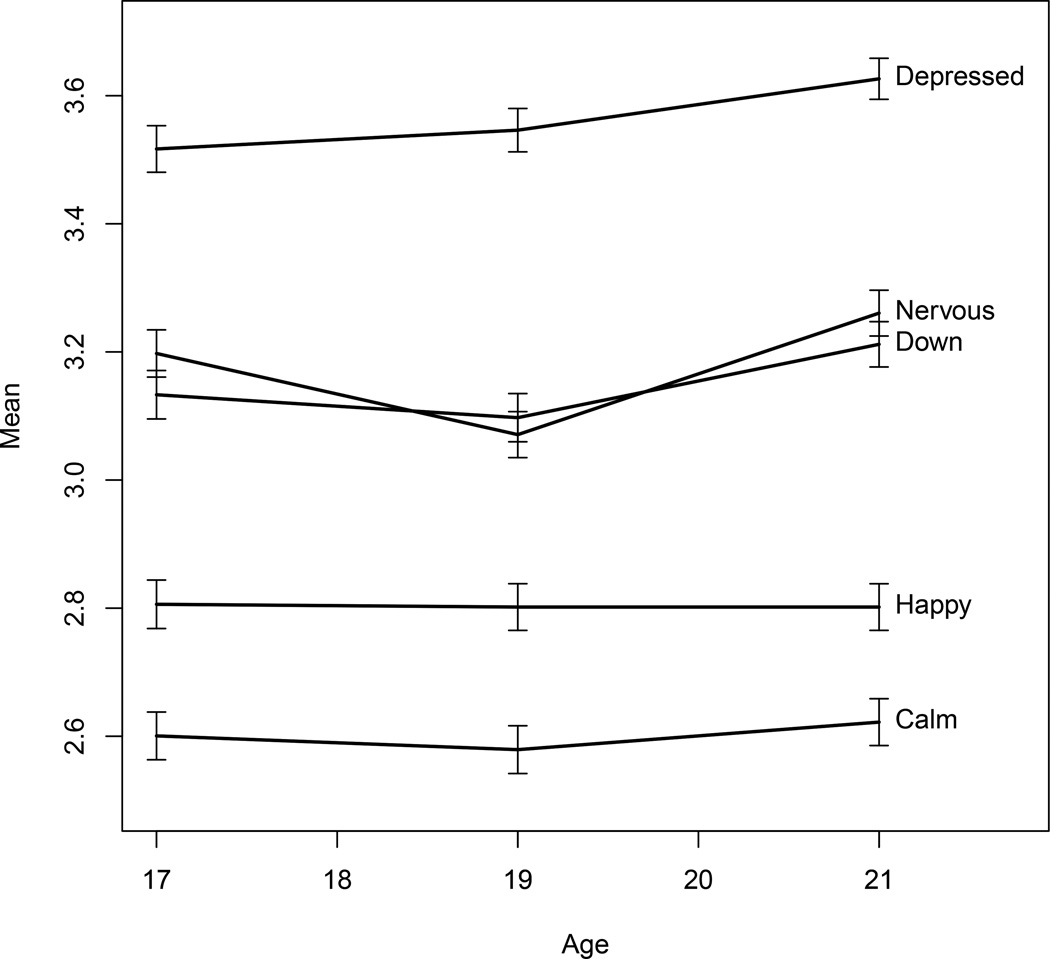
The model parameters for Model 4 in Table 12 show relative stability in both factors from age 17 to 19, indicated not only by the strong autocorrelation between these ages (β=0.746), but also the consistency of factor loadings across these two ages. However, changes to both the factor structure and the dynamics of each factor appear at age 21, including significant increases in the factor loadings of the “Depressed” and “Calm” items on their respective factors, and a negative factor regression parameter (βPos19→Neg21 = βNeg19→Pos21 = −0.222) despite all other regressions and autoregressions being positive. The two-factor structure is further validated by viewing the means of all five items at each age in Figure 8. The items “Calm” and “Happy” show no increase or decrease with age, as indicated graphically and via paired t-tests comparing ages 17 and 21 (tCalm=0.96, p=.340; tHappy=−.020, p=.844, all df=1396), while “Nervous”, “Down” and “Depressed” show significant changes across those ages (tNervous=−3.01, p=.003; tDown=−3.54, p<.001; tDepressed=−5.29, p<.001). Despite the similarity of the dynamics of the two factors, derivative-transformed factor models, longitudinal analysis of raw data and a plot of item means across age show that the two positive items have different dynamics than the other three items.
Figure 8.
Mean Trends for Depression Items
Note. Longitudinal means for each of the five items in the NLSY97 depression scale. Items “Calm” and “Happy” were found to load on the positive factor, while items “Nervous”, “Down” and “Depressed” loaded on the negative factor. All items were scored on a 4-point Likert scale, and the two positive items were reverse-scored so that increases in item means indicated increased depression.
Discussion
The preceding sections defined, tested and critiqued a measurement model of derivatives (MMOD). This model included two parts: a data transformation which restated longitudinal data as a set of derivatives or change variables, and a multidimensional factor model where factor structures are fit to each order of derivatives. This technique utilizes local linear approximation to transform observed item-level data into item-level derivatives, which represent the relationship of each variable such that the kth derivative can be interpreted as the rate of change with respect to timek. These derivatives were also designed as an orthogonal set of contrasts, allowing the subsequent factor model to be treated as a multidimensional model.
The presented simulations provide a series of tests for the proposed model. In the first simulation, MMOD outperformed all comparison models, specifically versions of MMOD and FOCUS that included non-orthogonal transformations and modeled fewer derivatives or change variables than timepoints. In addition, the model performed equivalently to the data generation model, indicating that MMOD does not bias invariant structures existing in the data.
The second simulation was used to investigate the capacity for MMOD to detect the type of non-ergodic structures that would be undetectable with a single occasion analysis. The results of this simulation showed that the higher-order derivative factors indicated the factor structure of within-person change, while the zeroth derivative factors represent a mixture of between-person and within-person structures. The presence of this mixture is evidenced by the selection of the simplest factor structure that encapsulates the two structures, and the results of a regression indicating that the factor correlation structures vary as a function of the ratio of between-person to within-person factor variance.
The specific meaning of the zeroth derivatives merits further discussion based on the results of the second simulation. It should first be noted that the use of the term mixture does not merely connote a combination, but rather a mixture distribution. Assuming that the factor structures are invariant over the between-person and within-person structures (which is demonstrated in Figure 6), these two factors may be summed to create a single factor whose distribution is the sum of the between-person and within-person distributions. As both of these factors were drawn from independent normal distributions, this distribution should be normal as well, with the factor correlations reflecting the different factor correlations in the two underlying structures as well as their relative variances.
The regression results from Table 9 support this interpretation of zeroth derivatives as this combination of the two sources of variance in this simulation. The presence of this mixture can be understood by considering the zeroth derivative as the within-person mean. When a single occasion is factor analyzed, there is no way to differentiate the between-person and within-person effects, and the single occasion can be interpreted as a mean of that sole observation. As additional occasions are added, this mean becomes an increasingly reliable measure of between-person differences, and the effects of the within-person structures decrease. Were dozens of timepoints used, the zeroth derivative would likely become a more “pure” measure of between-person factor structure. However, using only three, four or five observations still allows for significant within-person effects in the same way that the mean of three to five observations may include a great deal of variability.
It should be further noted that this result is due in part to the lack of variance in factor loadings in this simulation. In the second simulation, the one-factor model describing between-person structures is a special case of the two-factor model for within-person variation. This nesting of the one- and two-factor structures only exists when the one-factor loading structure is proportional to the two-factor loading structure. This is unlikely to be the case in real-world settings, as demonstrated in the empirical example. Introducing variability in factor loadings in a future simulation would address this concern. Determining the correct conditions and associated statistical power to separate between-person and within-person effects is an important direction for future research.
Selecting Timepoints for Analysis
Determining the ideal number of occasions for the use of MMOD is an important question for future study. While the model can theoretically handle any number of timepoints, a measurement model to dozens or hundreds of occasions of multivariate longitudinal data could be difficult to write, estimate and interpret. Furthermore, the model showed decreased convergence rates as additional timepoints were included. While convergence failures are certainly a concern, they can be explained by a feature of derivative estimation. Figure 9 presents derivative-transformed model-implied data from a five occasion version of Simulation 1. The plot represents the correlation between any pair of item-level derivatives, which drop precipitously as the order of derivative increases.
Figure 9.
Intercorrelation Between Increasing Derivative Orders
Note. Expected inter-derivative correlations for the zeroth through fourth item-level derivatives. Expected data generated from Simulation 1 condition with five timepoints, one common factor with an autoregression of 0.8, and factor loadings of 0.4, 0.6 and 0.8 constant across all items. Neither the sample size nor the number of items affect the expected correlation between like-orders of item-level derivatives.
The small correlations between the higher order item-level derivatives can explain some of the convergence failures seen in the simulations. Higher orders of derivatives increasingly represent unique factors and measurement error in this simulation, as there is little meaningful variance in third and fourth derivatives when data follow the autoregressive structure used in this simulation. Attempting to fit factor models to these orders of derivatives yields weak factor loadings very dependent on sample fluctuations in unique variance terms. However, the lack of signal in the third and fourth derivatives will not be the case in all datasets. Some samples may show little variance in even the first and second derivatives, while others may show meaningful and modelable individual differences over many types and scales of change.
Determining the correct number of timepoints to model is an empirical and sample-specific question, and the answer to that question depends in part on the number of derivatives over which meaningful variance. Summary statistics and plots of derivative-transformed data could be used to inform the correct dimensionality for their particular research question such that orders of derivatives with little meaningful variance can be omitted or modeled differently. Additionally, the effects of within-person variation on the zeroth derivative described in the previous section are likely to decrease with additional observations. Applications of this model to developmentally relevant constructs must also consider the correct interpretation of “time”, as age or other measures may be better suited to describe repeated measurements. Balancing these opposing needs is an important topic for future study, and answers to questions of dimensionality are likely to be sample and research question specific.
Selecting the number and spacing of timepoints will have impact on how the higher derivatives should be interpreted, and this decision should be made using a combination of sample statistics, knowledge of the design and the specific research questions to be asked. Researchers should consider diurnal, weekly and seasonal effects when relevant, as well as other time-varying covariates that may impact measurement structures. For example, bi-weekly affect measurement may reveal different structures for zeroth and higher derivatives. This effect may reveal general differences in between-person and within-person structures, or may indicate different structures for the work-week and weekend depending on the sampling interval. When multiple timescales are available, models such as MMOD should be applied to varying numbers of and intervals between timepoints to greater determine the size, scope, and meaning of effects.
Computation Complexity
Among the potential weaknesses of this approach is the added computational demand. Many of the non-convergences in the presented simulations were not driven by the optimizer directly, but were instead errors reached when the model exceeded software memory limits. Latent transformation of derivatives requires that in addition to the items*timepoints observed variables, the set of latent variables includes not only the common factors, but the set of items*timepoints derivative factors as well, leading to a number of very large matrices being used in the model estimation. While manual transformation wasn’t used in the first simulation to prevent rounding error from affecting comparisons to the reference model, carrying out the derivative transformation prior to analysis can greatly reduce these issues. Future directions for this approach should include further study of the structure of this model, one goal of which should be to speed up or simply covariance matrix inversion (full data matrix S in RAM notation, latent variable matrix Ψ in LISREL notation).
Ordinal data makes the fitting of this model more complex. Using even a few timepoints of item level data greatly increases the scale of the optimization and dimension of the multivariate integration underlying maximum likelihood estimations of categorical data. Applications of MMOD to categorical data with many items or timepoints will see the same problems facing any other categorical data SEM. As such, immediate use of this model is likely to utilize approaches like weighted least squares and Bayesian methods. Future directions for this work should include alternative ways of specifying this model, including but not limited to bi-factor and/or state-space models that project factors onto multiple timepoints of item-level data with highly constrained factor patterns and residual structures.
Summary
The results of the simulations and data analysis indicate that the measurement model of derivatives can identify the latent structure or structures in longitudinal data, utilizing information about item-level change that is not used in other measurement models. The use of an orthogonal derivative method transforms data into a multidimensional space where many of the problems associated with longitudinal data are mitigated, allowing researchers to more directly analyze the structure of change. If we are to continue asking questions about change, development and dynamics, we must maintain and expand longitudinal methodology to answer those questions. Evaluating the ability of the latent trait models to adequately describe change is one step in that direction. The proposed method is one way of achieving this goal, but more important than the use of this model is the understanding that the dynamics and changes found in latent variables must come from manifest dynamics and changes.
Table 6.
Data Generation Parameters for Simulation 2
| Parameter | Levels | Values |
|---|---|---|
| Structure | 2 | 1/2, 2/2 |
| Timepoints | 3 | 3, 4, 5 |
| Items per Timepoint | 2 | 10, 20 |
| Loadings | 2 | .6, .8 |
| Ratio of B/W Variances | 3 | .5, 1.0, 2.0 |
| n | 3 | 250, 500, 1000 |
Acknowledgments
The author wishes to thank John Nesselroade and Steve Boker for their comments and review of this work. Parts of this work were completed as a doctoral disstertation at the University of Virginia. The author was supported by grants T32 AG20500 (University of Virginia) and R25 DA026119 (Virginia Commonwealth University) during the writing of this article.
Appendix
Additional Materials for Empirical Example
Data for this empirical example is available from the National Longitudinal Survey of Youth, and can be downloaded from the United States Bureau of Labor Statistics website (http://www.bls.gov/nls/nlsy97.htm). The five-item depression scale measured in the year 2000 consists of the variables “nervous00”, “calm00”, “down00”, “happy00” and “depressed00”; the three-occasion longitudinal data for this example came from the 2000, 2002 and 2004 samples, with the other variables appended with the year of data collection. A total of 1,397 individuals who were born in 1983 completed all variables at each of these three waves, and thus were included in this analysis.
While full-information maximum likelihood could have been used to fit these models to raw data, the restriction to complete case analysis and a sample moment matrix was done for several reasons. The primary reason was to make an easily replicable empirical example, and the use of a sample moment matrix rather than raw data means that the complete dataset used for analysis can be included in this paper. This data matrix is printed in Table A1. Furthermore, using only complete cases allowed for estimation of the data’s polychoric correlation matrix without incurring any bias from missing data, and that correlation matrix could be accurately described by a single sample size of 1,397 for the estimation of model fit statistics.
Table A1.
NLSY97 Depression Data
| n00 | c00 | b00 | h00 | d00 | n02 | c02 | b02 | h02 | d02 | n04 | c04 | b04 | h04 | d04 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| nervous00 | 1.000 | −0.470 | 0.490 | −0.355 | 0.476 | 0.470 | −0.345 | 0.343 | −0.269 | 0.296 | 0.454 | −0.252 | 0.231 | −0.166 | 0.265 |
| calm00 | −0.470 | 1.000 | −0.482 | 0.609 | −0.357 | −0.272 | 0.422 | −0.303 | 0.388 | −0.199 | −0.275 | 0.345 | −0.246 | 0.315 | −0.234 |
| down00 | 0.490 | −0.482 | 1.000 | −0.610 | 0.630 | 0.276 | −0.315 | 0.446 | −0.307 | 0.317 | 0.271 | −0.310 | 0.368 | −0.259 | 0.290 |
| happy00 | −0.355 | 0.609 | −0.610 | 1.000 | −0.495 | −0.240 | 0.368 | −0.341 | 0.458 | −0.274 | −0.214 | 0.361 | −0.265 | 0.399 | −0.295 |
| depressed00 | 0.476 | −0.357 | 0.630 | −0.495 | 1.000 | 0.286 | −0.291 | 0.398 | −0.267 | 0.456 | 0.261 | −0.224 | 0.289 | −0.241 | 0.416 |
| nervous02 | 0.470 | −0.272 | 0.276 | −0.240 | 0.286 | 1.000 | −0.474 | 0.490 | −0.389 | 0.483 | 0.498 | −0.285 | 0.242 | −0.252 | 0.250 |
| calm02 | −0.345 | 0.422 | −0.315 | 0.368 | −0.291 | −0.474 | 1.000 | −0.438 | 0.634 | −0.367 | −0.320 | 0.440 | −0.290 | 0.345 | −0.283 |
| down02 | 0.343 | −0.303 | 0.446 | −0.341 | 0.398 | 0.490 | −0.438 | 1.000 | −0.560 | 0.653 | 0.346 | −0.338 | 0.394 | −0.337 | 0.401 |
| happy02 | −0.269 | 0.388 | −0.307 | 0.458 | −0.267 | −0.389 | 0.634 | −0.560 | 1.000 | −0.437 | −0.274 | 0.371 | −0.335 | 0.446 | −0.348 |
| depressed02 | 0.296 | −0.199 | 0.317 | −0.274 | 0.456 | 0.483 | −0.367 | 0.653 | −0.437 | 1.000 | 0.266 | −0.238 | 0.295 | −0.227 | 0.451 |
| nervous04 | 0.454 | −0.275 | 0.271 | −0.214 | 0.261 | 0.498 | −0.320 | 0.346 | −0.274 | 0.266 | 1.000 | −0.446 | 0.445 | −0.382 | 0.454 |
| calm04 | −0.252 | 0.345 | −0.310 | 0.361 | −0.224 | −0.285 | 0.440 | −0.338 | 0.371 | −0.238 | −0.446 | 1.000 | −0.492 | 0.685 | −0.472 |
| down04 | 0.231 | −0.246 | 0.368 | −0.265 | 0.289 | 0.242 | −0.290 | 0.394 | −0.335 | 0.295 | 0.445 | −0.492 | 1.000 | −0.557 | 0.702 |
| happy04 | −0.166 | 0.315 | −0.259 | 0.399 | −0.241 | −0.252 | 0.345 | −0.337 | 0.446 | −0.227 | −0.382 | 0.685 | −0.557 | 1.000 | −0.538 |
| depressed04 | 0.265 | −0.234 | 0.290 | −0.295 | 0.416 | 0.250 | −0.283 | 0.401 | −0.348 | 0.451 | 0.454 | −0.472 | 0.702 | −0.538 | 1.000 |
Note. Polychoric correlations between five observed depression items in the years 2000, 2002, 2004 (ages 17, 19 and 21).
This data is used as the input data for the following example code. Data preparation was done using R 2.15.3 (R Development Core Team, 2012). Exploratory factor models were fit using the psych library (Revelle, 2013), while confirmatory models were fit using OpenMx (Boker et al., 2011).
Transforming Observed Data into Derivative Data
The use of MMOD presented in this paper were fit to the transformed data matrix. Moment matrices may be transformed into the covariances between derivatives just as raw data can be reshaped into derivative-transformed data. Raw data is transformed using by post-multiplying a data matrix Y by a weight matrix W to yield a derivative-transformed data D, as shown in Equation 17. If we assume that Y is centered, then Y′Y is the sums of squares and cross-products of Y, and is the covariance matrix of Y, Cov(Y). By equivalent logic, is the covariance matrix of D, Cov(D). We can take the transformation of raw data shown in Equation 17 and premultiply both sides of the equation by their own transpose and divide by n, as shown in Equations 18 through 20. Once the terms are rearranged in Equation 21 and 22, we can see that covariance matrices can be transformed as easily as raw data, in this case by pre- and post-multiplying the observed covariance matrix by the same weight matrix used for raw data.
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
The weight matrix can be created as described in Equation 9; a function to create this matrix is available both in Deboeck’s (2010) paper and via his web resources for this paper6, though the referenced equation demonstrates the three-occasion case for this example. It should be noted that Deboeck’s Contrasts function creates an L matrix as described in Equation 11, so the resulting matrix should be both inverted and transposed to create the weight matrix. This matrix may be expanded for the five-variable scale by taking the kronecker product of this matrix and a 5 × 5 identity matrix. The code below demonstrates data import and formatting for both raw and covariance matrix data, assuming both datasets are contained in at or text files.
# load required libraries
require(OpenMx)
# load raw and covariance data
rawData <− read. table(”nlsyRaw. txt”)
covData <− read. table(”nlsyCov. txt”)
# make weight matrix with Deboeck ’s functions
source(”GOLD.R”)
weight <− t (solve (Contrasts (1:3, 2)))
# make weight matrix without Deboeck ’s functions
weight <− matrix(
c(1/3, 1/3, 1/3,
−1, 0, 1 ,
1/2, −1, 1/2),
nrow=3, ncol=3)
# expand weight matrix for full data
fullWeight <− kronecker (weight, diag (5))
# transform the data
rawDeriv <− rawData %*% fullWeight
covDeriv <− t(fullWeight) %*% covData %*% fullWeight
dimnames(covDeriv) <− dimnames(covData)
Fitting MMOD to Transformed Data
Once the data is transformed, model fitting proceeds like any other factor model. The transformation did not affect the variable names, so the column and variable name “nervous00” refers to the age 17 value of “nervous” in the untransformed data, but the zeroth derivative of “nervous” in the transformed data. The code below first creates a vector of variable names, which keeps us from typing the same fifteen variable names over and over. Next, an object called mmod1 is created, which will contain the MxModel object and store our model. Data is added with the mxData function, and type="RAM" is added so that we can specify this model with paths. The manifest and latent variables are declared, then a series of mxPath statements specify what parameters are in the model. The first mxPath statement creates five factor loadings from the latent variable “F0” to the five item-level zeroth derivatives. Subsequent statements add the rest of the factor loadings, fix the factor variances to identify the model, add factor correlations, and add residual variance terms. Finally, the model is run using the mxRun command, and its results viewed using the summary function.
# one factor MMOD model, transformed data obsVar <− colnames(covData) mmod1 <− mxModel(”One Factor MMOD”, mxData(covDeriv, type=”cov”, numObs=1397), type=”RAM”, manifestVars=obsVar, latentVars=c(”F0”, ”F1”, ”F2”), # factor loadings mxPath(from=”F0”, to=c(”nervous00”, ”down00”, ”depressed00”, ”calm00”, ”happy00”), free=TRUE), mxPath(from=”F1”, to=c(”nervous02”, ”down02”, ”depressed02”, ”calm02”, ”happy02”), free=TRUE), mxPath(from=”F2”, to=c(”nervous04”, ”down04”, ”depressed04”, ”calm04”, ”happy04”), free=TRUE), # factor variances mxPath(from=c(”F0”, ”F1”, ”F2”), arrows=2, values=1, free=FALSE), # factor correlations mxPath(from=c(”F0”, ”F1”, ”F2”), arrows=2, connect=”unique. bivariate”, free=TRUE), # residual variances mxPath(from=obsVar, arrows=2, values=1) ) mmodRes1 <− mxRun(mmod1) summary(mmodRes1)
Fitting MMOD to Untransformed Data
When the measurement model of derivatives is fit to untransformed data, the derivative transformation must be done in latent space. To do this with a path model, one must create a set of new latent variables corresponding to the derivatives. These latent derivatives predict the observed variables with fixed loadings set to the values of our weight matrix. This can be done with the following mxPath statement:
longWeight <− as. vector(t(solve(weight))) mxPath(from=c(”nerv0”, ”nerv1”, ”nerv2”), to=c(”nervous00”, ”nervous02”, ”nervous04”), connect=”all. pairs”, free=FALSE, values=longWeight)
First, we need to turn our weight matrix into a set of loadings. As described in Equations 10 and 11, these loadings can be found in the L matrix, which is the inverse of our weight matrix. The object longWeight inverts the weight matrix, then turns it into a vector of loadings, such that the first three elements of the vector correspond to the zeroth derivative, the next three to the first derivative, and the final three to the second derivative. The ensuing mxPath statement lists the three latent derivatives in the from argument, and the three observed items in the to argument. The connect argument is used to state how the set of from variables relates to the set of to variables; in this case, we want all possible combinations ("all.pairs"). This will create nine paths: from nerv0 to nervous00 (latent zeroth derivative to first occasion), then from nerv0 to nervous02 (latent zeroth derivative to second occasion) and so on until from nerv2 to nervous04 (latent second derivative to third occasion). These latent derivatives (nerv0, nerv1, and nerv2) then stand in for the manifest variables in the rest of the model.
The full model is presented in the final section of code. In addition to a vector of variable names, we also create a vector of latent derivatives for easy reference elsewhere in the model. Data are loaded, options set and variables declared just as with the first model, but the set of latent variables includes not only the three common latent variables, but also the vector of 15 latent derivatives. The first five mxPath statements transform each of the five items. The subsequent mxPath statements have the exact same function as they did in the first model, but the latent derivatives replace the observed variables. The model is then run and viewed using mxRun() and summary().
# one factor MMOD model, untransformed data
obsVar <− colnames(covData)
latDeriv <− c(”nerv0”, ”down0”, ”dep0”, ”calm0”, ”happy0”,
”nerv1”, ”down1”, ”dep1”, ”calm1”, ”happy1”,
”nerv2”, ”down2”, ”dep2”, ”calm2”, ”happy2”)
longWeight <− as. vector(t(solve(weight)))
mmod2 <− mxModel(”One Factor MMOD 2”,
mxData(covData, type=”cov”, numObs=1397),
type=”RAM”,
manifestVars=colnames(covData),
latentVars=c(”F0”, ”F1”, ”F2”, latDeriv),
# transformation
mxPath(from=c(”nerv0”, ”nerv1”, ”nerv2”),
to=c(”nervous00”, ”nervous02”, ”nervous04”),
connect=”all. pairs”,
free=FALSE, values=longWeight),
mxPath(from=c(”down0”, ”down1”, ”down2”),
to=c(”down00”, ”down02”, ”down04”),
connect=”all. pairs”,
free=FALSE, values=longWeight),
mxPath(from=c(”dep0”, ”dep1”, ”dep2”),
to=c(”depressed00”, ”depressed02”, ”depressed04”),
connect=”all. pairs”,
free=FALSE, values=longWeight),
mxPath(from=c(”calm0”, ”calm1”, ”calm2”),
to=c(”calm00”, ”calm02”, ”calm04”),
connect=”all. pairs”,
free=FALSE, values=longWeight),
mxPath(from=c(”happy0”, ”happy1”, ”happy2”),
to=c(”happy00”, ”happy02”, ”happy04”),
connect=”all. pairs”,
free=FALSE, values=longWeight),
# factor loadings
mxPath(from=”F0”,
to=c(”nerv0”, ”down0”, ”dep0”, ”calm0”, ”happy0”),
values=0.5, free=TRUE),
mxPath(from=”F1”,
to=c(”nerv1”, ”down1”, ”dep1”, ”calm1”, ”happy1”),
values =0.5, free=TRUE),
mxPath(from=”F2”,
to=c(”nerv2”, ”down2”, ”dep2”, ”calm2”, ”happy2”),
values =0.5, free=TRUE),
# factor variances
mxPath(from=c(”F0”, ”F1”, ”F2”),
arrows=2, values=1, free=FALSE),
# factor correlations
mxPath(from=c(”F0”, ”F1”, ”F2”),
arrows=2, connect=”unique. bivariate”, free=TRUE),
# residual variances(only for latent derivatives !)
mxPath(from=latDeriv, arrows=2, values=1)
)
mmodRes2 <− mxRun(mmod2)
summary(mmodRes2)
While not presented, there are many additional ways to specify this model in OpenMx. When raw data is used, item means should also be specified. Categorical raw data would further demand both that thresholds be specified and identification criteria be met for each ordinal variable. Beyond path modeling, models may be presented using whatever matrices the user pleases. This is especially convenient for the measurement model of derivatives, as whatever user-defined algebra is used to create an expected covariance could simply be pre- and post-multiplied by an explicit weight matrix, making transitions between transformed and untransformed analysis as simple as adding or removing a single fixed matrix from the model.
The above model could easily be specified in a variety of other software packages. The added complexity of the measurement model of derivatives makes only two added demands beyond conventional longitudinal models. First, the package must support the added latent variables for derivative transformation. While most if not all packages should allow this, the added variables may slow down optimization for some models. Second, ordinal data versions of the measurement model of derivatives must allow for observed variables to have a residual variance of zero, as all observed variables are fully explained by the set of latent derivatives. Some software packages have default values for the mean and residual variance of manifest ordinal variables of zero and one, respectively. These defaults must be removed for the use of this technique on raw ordinal data.
Footnotes
Both models estimate 10 factor loadings, 10 residual variances and 10 intercepts, assuming constrained factor means and variances for identification and no factorial invariance constraints. The models only differ in the number of covariances, with the first model containing three (one latent covariance and two residual covariances) and the second model containing six (all latent variable covariances), for a three degree of freedom difference. If weak factorial invariance is assumed, each model estimates only five factor loadings, but frees all factor variances at the second occasion, moving the degree of freedom difference between the models to four (three covariances and one additional variance parameter in the second model). With strong factorial invariance, factor means may be estimated at the second occasion (one in the first model, two in the second model), making it a five degree of freedom difference. Finally, strict factorial invariance would constrain all residual variances and covariances, saving five residual variance parameters in the second model but six total parameters (five variances and the residual covariance) in the first, yielding a six degree of freedom difference.
Both Meredith & Tisak (1990) and Hancock & Choi (2006) discuss orthogonal growth curves and show their equivalence to (more typical) oblique growth curves. These methods are especially useful for testing the significance of particular growth factors in isolation of the other factors.
Both the first and second derivatives are divided by the total time elapsed (two, in this example) to define the units of change as “per unit of time”. In the case of the first derivative, not only does this adjustment scale the rate of change to the correct unit of time, but makes this derivative equivalent to the mean of the changes from t − 1 to t and from t to t + 1 . In either case, multiplying the entire set of weights by a constant will only affect the scale of each variable, not its correlations with other variables.
row vectors from a full rank data matrix Y.
When multiple factors were estimated at any particular timepoint, the number of items for that timepoint were evenly split amongst the factors. In conditions with two factors per timepoint, the first factor loaded on only the first five (10 items per timepiont) or first ten (20 items per timepoint) items, with the second factor loading only on the second five or ten items. In conditions with three factors per timepoint, the items were split such that three, three and four (10 item conditions) or six and seven items (20 item conditions) were assigned to each factor.
References
- Andrade DF, Tavares HR. Item response theory for longitudinal data: population parameter estimation. Journal of Multivariate Analysis. 2005;95(1):1–22. [Google Scholar]
- Baker F. The basics of item response theory. University of Maryland, College Park, MD: ERIC Clearinghouse on Assessment and Evaluation; 2001. [Google Scholar]
- Baltes PB, Nesselroade JR. History and rationale of longitudinal research. In: Nesselroade JR, Baltes PB, editors. Longitudinal research in the study of behavior and development. New York: Academic Press, Inc.; 1979. pp. 1–39. [Google Scholar]
- Bereiter C. Some persisting dilemmas in the measurement of change. In: Harris CW, editor. Problems in measuring change. Madison, WI: University of Wisconsin Press; 1963. [Google Scholar]
- Boker SM. Specifying latent differential equations models. In: Boker SM, Wenger MJ, editors. Data analytic techniques for dynamical systems in the social and behavioral sciences. Mahwah, NJ: Lawrence Erlbaum Associates; 2007. pp. 131–159. [Google Scholar]
- Boker SM, Deboeck PR, Edler C, Keel PK. Generalized local linear approximation of derivatives from time series. In: Chow EFFHSM, editor. Statistical methods for modeling human dynamics: An interdisciplinary dialogue. New York: Taylor & Francis; 2010. pp. 161–178. [Google Scholar]
- Boker SM, Neale MC, Maes H, Wilde M, Spiegel M, Brick T, et al. Openmx: An open source extended structural equation modeling framework. Psychometrika. 2011;76(2):306–317. doi: 10.1007/s11336-010-9200-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boker SM, Neale MC, Rausch J. Latent differential equation modelign with multivariate multi-occasion indicators. In: van Montfort K, Oud H, Satorra A, editors. Recent development on structural equation models: Theory and applications. Dordrecht, the Netherlands: Kluwer Academic Publishers; 2004. pp. 151–174. [Google Scholar]
- Boker SM, Nesselroade JR. A method for modeling the intrinsic dynamics of intraindividual variability: Recovering the parameters of simulated oscillators in multi-wave data. Multivariate Behavioral Research. 2002;37:127–160. doi: 10.1207/S15327906MBR3701_06. [DOI] [PubMed] [Google Scholar]
- Cattell RB, Cattell AKS, Rhymer RM. P-technique demonstrated in determining psychophysical source traits in a normal individual. Psychometrika. 1947;12:267–288. doi: 10.1007/BF02288941. [DOI] [PubMed] [Google Scholar]
- Deboeck PR. Estimating dynamical systems: Derivative estimation hints from sir Ronald a. fisher. Multivariate Behavioral Research. 2010;45:725–745. doi: 10.1080/00273171.2010.498294. [DOI] [PubMed] [Google Scholar]
- Drasgow F. Biased test items and differential validity. Psychological Bulliten. 1982;92:526–531. [Google Scholar]
- Duncan TE, Duncan SC, Strycker LA, Li F, Alpert A. An introduction to latent variable growth curve modeling: Concepts, issues, and applications. Mahwah, N. J.: Lawrence Erlbaum Associates, Publishers; 1999. [Google Scholar]
- Embretson SE. A multidimensional latent trait model for measuring learning and change. Psychometrika. 1991;56:495–516. [Google Scholar]
- Embretson SE, Reise SP. Item response theory for psychologists. Mahwah, NJ: Lawrence Erlbaum; 2000. [Google Scholar]
- Fischer GH. Linear logistic test model as an instrument in educational research. Acta Psychologica. 1973;37:359–374. [Google Scholar]
- Fischer GH. An irt-based model for dichotomous longitudinal data. Psychometrika. 1989;54(4):599–624. [Google Scholar]
- Garrett HE. A developmental theory of intelligence. The American Psychologist. 1946;1:372–378. doi: 10.1037/h0056380. [DOI] [PubMed] [Google Scholar]
- Genz A, Bretz F, Miwa T, Mi X, Leisch F, Scheipl F, et al. mvtnorm: Multivariate normal and t distributions [Computer software manual] 2012 Available from http://CRAN.R-project.org/package=mvtnorm (R package version 0.9-9992) [Google Scholar]
- Hambleton RK, Swaminathan H, Rogers HJ. Fundamentals of item response theory. Newbury Park, CA: Sage; 1991. [Google Scholar]
- Hancock GR, Choi J. A vernacular for linear latent growth models. Structural Equation Modeling: A Multidisciplinary Journal. 2006;13:352–377. [Google Scholar]
- Hertzog C, Lindenberger U, Ghisletta P, Oertzen Tv. On the power of multivariate latent growth curve models to detect correlated change. Psychological Methods. 2006;11(3):244–252. doi: 10.1037/1082-989X.11.3.244. [DOI] [PubMed] [Google Scholar]
- Hertzog C, Oertzen T. von, Ghisletta P, Lindenberger U. Evaluating the power of latent growth curve models to detect individual differences in change. Structural Equation Modeling. 2008;15(4):541–563. [Google Scholar]
- Johnson C, Raudenbush SW. Methodological issues in aging research. Lawrence Erlbaum Associates Publishers; 2006. A repeated measures, multilevel rasch model with application to self-reported criminal behavior; pp. 131–164. [Google Scholar]
- Kendler KS, Prescott CA, Myers J, Neale MC. The structure of genetic and environmental risk factors for common psychiatric and substance use disorders in men and women. Archives of General Psychiatry. 2003;60(9):929–937. doi: 10.1001/archpsyc.60.9.929. [DOI] [PubMed] [Google Scholar]
- Laird NM, Ware JH. Random-effects models for longitudinal data. Biometrics. 1982;38:963–974. [PubMed] [Google Scholar]
- Leue A, Beauducel A. The panas structure revisited: On the validity of a bifactor model in community and forensic samples. Psychological Assessment. 2011;23(1):215–225. doi: 10.1037/a0021400. [DOI] [PubMed] [Google Scholar]
- McArdle JJ. Dynamic but structural equation modeling of repeated measures data. In: Nesselroade JR, Cattell RB, editors. The handbook of multivariate experimental psychology. Vol. 2. New York: Plenum Press; 1988. pp. 561–614. [Google Scholar]
- McArdle JJ. Using multivariate data to structure developmental change. In: Cohen SH, Reese HW, editors. Life-span developmental psychology: Methodological contributions. Hillsdale, NJ: Lawrence Erlbaum Associates; 1994. pp. 223–267. [Google Scholar]
- McArdle JJ, Epstein D. Latent growth curves within developmental structural equation models. Child Psychology. 1987;58:110–133. [PubMed] [Google Scholar]
- McArdle JJ, Nesselroade JR. Using multivariate data to structure developmental change. In: Cohen SH, Reese HW, editors. Life-span developmental psychology: Methodological contributions. Hillsdale, NJ: Lawrence Erlbaum Associates; 1994. pp. 223–267. [Google Scholar]
- Meade AW, Lautenschlager GJ, Hecht JE. Establishing measurement equivalence and invariance in longitudinal data with item response theory. International Journal of Testing. 2005;5(3):279–300. [Google Scholar]
- Meredith W. Notes on factorial invariance. Psychometrika. 1964a;29:177–185. [Google Scholar]
- Meredith W. Rotation to achieve factorial invariance. Psychometrika. 1964b;29:186–206. [Google Scholar]
- Meredith W. Measurement invariance, factor analysis and factor invariance. Psychometrika. 1993;58:525–543. [Google Scholar]
- Meredith W, Tisak J. Latent curve analysis. Psychometrika. 1990;55:107–122. [Google Scholar]
- Millsap RE. Testing measurement invariance using item response theory in longitudinal data: An introduction. Child Development Perspectives. 2009;4(1):5–9. [Google Scholar]
- Millsap RE, Everson H. Methodology review: Statistical approaches for assessing measurement bias. Applied Psychological Measurement. 1993;17:297–334. [Google Scholar]
- Molenaar PCM. Time series analysis and its relationship with longitudinal analysis. International Journal of Sports Medicine. 1997;18:232–237. doi: 10.1055/s-2007-972720. [DOI] [PubMed] [Google Scholar]
- Molenaar PCM. Longitudinal analysis. In: Ader HJ, Mellenbergh GJ, editors. Research methodology in the social, behavioural and life sciences. London: Sage Publications; 1999. pp. 143–167. [Google Scholar]
- Molenaar PCM. A manifesto on psychology as idiographic science: Bringing the person back into scientific psychology – this time forever. Measurement: Interdisciplinary Research and Perspectives. 2004;2:201–218. [Google Scholar]
- Molenaar PCM, Campbell CG. The new person-specific paradigm in psychology. Current Directions in Psychology. 2009;18(2):112–117. [Google Scholar]
- Muthén L, Muthén B. Mplus user's guide. Fifth ed. Los Angeles, CA: Muthén and Muthén; 1998–2007. ( http://www.statmodel.com) [Google Scholar]
- Nesselroade JR, Cable DG. ”Sometimes it's okay to factor difference scores”-The separation of state and trait anxiety. Multivariate Behavioral Research. 1974;9:273–282. doi: 10.1207/s15327906mbr0903_3. [DOI] [PubMed] [Google Scholar]
- R Development Core Team. R: A language and environment for statistical computing [Computer software manual] Vienna, Austria: 2012. Available from http://www.R-project.org (ISBN 3-900051-07-0) [Google Scholar]
- Rasch G. Probabilistic models for some intelligence and attainment tests. Copenhagen: Danmarks Paedagogiske Institut; 1960. [Google Scholar]
- Raykov T. A structural equation model for measuring residualized change and discerning patterns of growth of decline. Applied Psychological Measurement. 1993;17(1):53–71. [Google Scholar]
- Revelle W. psych: Procedures for psychological, psychometric, and personality research [Computer software manual] Evanston, Illinois: 2013. Available from http://CRAN.R-project.org/package=psych (R package version 1.3.2) [Google Scholar]
- Spielberger CD, Gorsuch RL, Lushene R. The State-Trait Anxiety Inventory (STAI) test manual, form x. Palo Alto, CA: Consulting Psychologists Press; 1969. [Google Scholar]
- Stevens SS. On the theory of scales of measurement. Science. 1946;103:677–680. doi: 10.1126/science.103.2684.677. [DOI] [PubMed] [Google Scholar]
- Tan ES, Ambergen AW, Does RJMM, Imbos T. Approximations of normal irt models for change. Journal of Educational and Behavioral Statistics. 1999;24(2):208–223. [Google Scholar]
- Wessman AE, Ricks DF. Mood and personality. New York: Holt, Rinehart, and Winston; 1966. [Google Scholar]
- Wilkinson L Statistical Inference, T. F. on. Statistical methods in psychology journals: Guidelines and explanations. American Psychologist. 1999;54(8):594–604. [Google Scholar]