On the relative role of different age groups in influenza epidemics

Abstract

The identification of key “driver” groups in influenza epidemics is of much interest for the implementation of effective public health response strategies, including vaccination programs. However, the relative importance of different age groups in propagating epidemics is uncertain.

During a communicable disease outbreak, some groups may be disproportionately represented during the outbreak’s ascent due to increased susceptibility and/or contact rates. Such groups or subpopulations can be identified by considering the proportion of cases within the subpopulation occurring before (Bp) and after the epidemic peak (Ap) to calculate the subpopulation’s relative risk, RR=Bp/Ap. We estimated RR for several subpopulations (age groups) using data on laboratory-confirmed US influenza hospitalizations during epidemics between 2009–2014. Additionally, we simulated various influenza outbreaks in an age-stratified population, relating the RR to the impact of vaccination in each subpopulation on the epidemic’s initial effective reproductive number R_e(0).

We found that children aged 5–17 had the highest estimates of RR during the five largest influenza A outbreaks, though the relative magnitude of RR in this age group compared to other age groups varied, being highest for the 2009 A/H1N1 pandemic. For the 2010–2011 and 2012–2013 influenza B epidemics, adults aged 18–49, and 0–4 year-olds had the highest estimates of RR respectively.

For 83% of simulated epidemics, the group with the highest RR was also the group for which initial distribution of a given quantity of vaccine would result in the largest reduction of R_e(0). In the largest 40% of simulated outbreaks, the group with the highest RR and the largest vaccination impact was children 5–17.

While the relative importance of different age groups in propagating influenza outbreaks varies, children aged 5–17 play the leading role during the largest influenza A epidemics. Extra vaccination efforts for this group may contribute to reducing the epidemic’s impact in the whole community.

Introduction

The relative importance of different age cohorts in driving influenza epidemics is not fully understood. One reason for this is the lack of consensus on what makes an age group “important” in transmission, and how this should be quantified. School age children (aged 5–17) were found to have experienced the highest influenza attack rate during the 2009 A/H1N1 pandemic [1], as well as during certain influenza seasons prior to the pandemic [2], though for other seasons, age-specific attack rates for influenza A infection were relatively similar for different age groups [3]. Studies have shown that influenza transmission decreases during school closure periods [4] and increases when schools are opened [5], suggesting the importance of schoolchildren in propagating influenza. However, estimates of the magnitude of change in transmission dynamics of influenza during time periods when schools are open vs. periods when they are closed are variable [6,7]. Studies based on transmission modeling have also suggested the key role of school age children in driving influenza epidemics [8,9]. However, conclusions of those studies hinge on certain assumptions behind transmission models that are rarely calibrated against data from specific influenza seasons, particularly in the non-pandemic context. Earlier peaks of influenza epidemics in younger age groups have been documented, but their interpretation has been controversial. In one study [10], they were cited as evidence of the importance of these groups in transmission, yet it has been argued on the contrary [11] that small magnitude of the differences in peak times in different age groups “casts doubt on the hypothesis that younger school-age children actually lead influenza epidemic waves”. One could further counter that assertion, suggesting that transmission in different age groups is strongly interconnected, leading to so-called “slaved” dynamics in which incidence grows at a similar rate in all age groups [12]. In this scenario, the peak incidence in the driver groups – that is, groups for which depletion of susceptibles has the largest relative impact on the epidemic’s reproductive number [13,14] – corresponds with peak incidence in the community.

In previous work [13] we defined a measure of the importance of a particular age (or other demographic) group as follows: importance in transmission is proportional to the (negative) change in the epidemic’s effective reproductive number that would result from successfully immunizing a small, fixed number of persons randomly chosen from within this group. While this definition is clearly relevant to vaccination policies (vaccinating the most “important” groups yields the highest impact on the epidemic’s dynamics in the whole community), estimating the potential impact of vaccination for a particular epidemic is quite difficult due to a variety of data limitations. Here, we hypothesized that a simple, heuristic but precisely defined measure that is readily estimated for each age group from age-stratified epidemiologic data would be highly predictive of importance defined above, and that it should in general be possible to estimate relative importance of different groups in driving transmission of an infection even when probabilities of case-reporting vary systematically across groups, a common feature in surveillance data. This measure, which for influenza can be estimated separately for each of the circulating (sub) types, A/H1, A/H3 and B, is a simple relative risk (RR) of cases in a particular age group before the peak of the epidemic compared to after the peak of the epidemic. The rationale for this choice is the idea that the key age groups in transmission will experience a disproportionate depletion of susceptible individuals (attack rates) relative to the whole population during the ascent stages of influenza epidemics. This would translate into a lower proportion of such age groups in overall influenza incidence (or other influenza-associated outcomes that can be measured from data) during the descent stages of epidemics.

Estimating incidence of influenza infections in different age groups before and after the epidemic peak is challenging with the available data. At the same time, our proposed summary statistic RR requires only the relative change in such incidence before vs. after the epidemic peak. This relative change can be assessed by considering the corresponding relative change for a surrogate measure (proxy) of influenza incidence. Such a proxy would need to represent a fixed (but not necessarily high) proportion of the true incidence during those periods (Supporting Information). This requires high specificity, which, for example, precludes the ILI data stream from serving as such proxy because the frequency of other conditions causing a nonspecific diagnosis like ILI will change through the season. It does not require high sensitivity, only time-invariant (or more precisely, equally time-varying) sensitivity for each age group. In our analysis, such a proxy is provided by laboratory-confirmed, (sub)typed influenza hospitalizations in the Influenza Surveillance Hospitalization Network (FluSurv-NET). Importantly, interpreting this statistic does not require prior knowledge of either the overall or the group-dependent reporting rate (in this instance, case-hospitalization rate). This means that when laboratory-confirmed hospitalizations, representing only a small, age-specific fraction of all incident cases, are used as a surrogate measure of infections for the estimation of RR, it will estimate the importance of particular age groups in transmitting infection.

Here we report the estimation of the RR from data on laboratory-confirmed US influenza hospitalizations during epidemics associated with influenza A/H1N1, A/H3N2 and B between 2009–2014. This recent period is particularly interesting as influenza vaccination coverage rates have increased following the 2009 pandemic, at least in the US, potentially resulting in different distributions of susceptibility compared to what has taken place in the pre-pandemic period, and the impact of that on the relative roles of the different age groups has not been assessed in the literature. We then go on to test the hypothesis that the group identified as most important by the RR statistic is predictably the one with the highest importance by our definition -- the group for which immunization of a fixed number of persons would cause the greatest reduction in the reproduction number of the epidemic in the population as a whole. In order to investigate this correspondence, we simulated influenza epidemics in an age-stratified population with contact rates between the age groups borrowed from the POLYMOD study [15] and explored a variety of scenarios for the relative susceptibility to infection for the different age groups to reflect the diversity of influenza epidemics.

Materials and Methods

Data

We used the Influenza Surveillance Hospitalization Network (FluSurv-NET) data for the 2009 pandemic and the 2010–2011 through 2012–2013 influenza seasons collected between October-April (with no data on sub-typing of influenza A hospitalizations available prior to 2009). This network conducted population-based influenza-associated hospitalization surveillance in over 80 selected counties located in California, Colorado, Connecticut, Georgia, Idaho, Maryland, Michigan, Minnesota, New York, Oklahoma, Ohio, Oregon, Rhode Island, Tennessee and Utah. The surveillance area encompassed a total of 276 reporting hospitals serving over 29 million children and adults and representing about 9% of the US population. Laboratory testing for influenza was ordered at the discretion of clinicians providing clinical care. Laboratory confirmation was defined as a positive result from viral culture, direct or indirect fluorescent antibody staining, rapid antigen test, or reverse transcription polymerase chain reaction (rt-PCR). Aggregate hospitalization counts were used in the study.

This activity was determined to be routine public health surveillance by the US Centers for Disease Control and Prevention and by state and local institutional review boards and no informed consent from the participants was sought. This study, based on the analysis of aggregated existing data, was determined to be not “Human Subjects Research”.

Hospitalization data analysis

For each season and influenza (sub)type, we determine the periods before and after the peak of that (sub)type’s epidemic as follows: For each age group g (g = 1,‥,5) and week t, let $X{1}_t^g,X{3}_t^g,X{B}_t^g$ be the counts for the number of confirmed hospitalizations in that group on that week with the (sub)types A/H1N1, A/H3N2, and B respectively, and $X{A}_t^g$ be the number of un-subtyped influenza A hospitalizations. We estimate the number of hospitalizations due to influenza A/H1N1 in a group g on week t as

$$H{1}_t^g=X{1}_t^g+X{A}_t^g·\frac{X{1}_t^g}{(X{1}_t^g+X{3}_t^g)}$$ (1)

with a similar correction for A/H3N2. For influenza B, $H{B}_g^t=X{B}_g^t$. To estimate the epidemic’s ascent and descent periods we address the potentially disproportionate impact of the elderly (aged 65+) on hospitalizations compared to their share in incidence by looking at the peak of the weekly hospitalizations among the four non-elderly age groups, defining the before and after the peak periods correspondingly. The total number of nonelderly hospitalizations for (sub)type S on week t is

$$H{S}_t^{NE}=\sum _{g=1}^{4}H{S}_t^g\hspace{1em}(S=1,2,B)$$

The peak week for each subtype is defined as the week t_p for which $H{S}_t^{NE}$ is maximal. To account for the uncertainty of the peak week due to noise in the data, and to avoid misclassification of counts as before or after-the-peak, we excluded weeks t_p − 1 and t_p + 1, and define the period before the peak to be weeks up to t_p − 2 (inclusive), and the period after the peak are weeks starting t_p + 2.

The estimation of RR (described below for an influenza A (sub)type) is performed as follows. We assume that the actual number of infected cases in each age group due to each subtype is large, and the probability of resulting in a confirmed hospitalization is small, with the number of detected hospitalizations well approximated by a Poisson variable. Moreover for each hospitalization in the surveillance system in the chosen age group, there is a probability p_g for this hospitalization to be subtyped, and we assume that this probability is the same for both influenza A subtypes (further details in the Discussion). The observed counts for the number of hospitalizations in a group g due to the chosen influenza A subtype, the other subtype and the un-subtyped ones are therefore independent and Poisson distributed with means

$$({\lambda }_1^g,{\lambda }_2^g,{\lambda }_3^g)=({\lambda }_X^g·p_g,{\lambda }_Y^g·p_g,({\lambda }_X^g+{\lambda }_Y^g)·(1-p_g))$$

Here ${\lambda }_X^g,{\lambda }_Y^g$ are the Poisson parameters, proportional to incidence rates due to the chosen subtype and the other subtype in the age group g. The estimation for ${\lambda }_X^g,{\lambda }_Y^g$ is performed in a Bayesian framework, with posterior samples for those parameters for the periods before and after the epidemic peak in different age groups used to produce a posterior sample of estimates of RR for each age group for which the mean and the 95% credible interval are reported. More details are provided in the Supporting Information. We note here that the point estimates on RR obtained (Tables 1–3) are virtually identical to the “intuitive” estimate one would get using the hospitalization rates given by eq. 1. The purpose of this more elaborate procedure is to produce appropriate uncertainty estimates for the composite parameters of interest. We also note (see Supporting Information) that the relative magnitudes of the RR estimates for the different age groups are independent of (the age-specific) case hospitalization rates.

Table 1.

Peak week for A/H1N1 hospitalizations, and the relative risk for being in a given age group among A/H1N1 hospitalizations for the before-the-peak period vs. after-the-peak period.

Relative risks (RR) in different age groups for periods before vs. after the epidemic peak for influenza A/H1N1
Season	Peak Week	Aged 0–4		Aged 5–17		Aged 18–49		Aged 50–64		Aged 65+
		RR	95% CIa	RR	95% CI	RR	95% CI	RR	95% CI	RR	95% CI
2009	42	1.06	0.91,1.23	1.84	1.58,2.14	1.02	0.94,1.11	0.67	0.58,0.77	0.67	0.54,0.82
2010–2011	8	1.22	0.80,1.84	1.37	0.74,2.45	1.28	1.05,1.58	0.75	0.60,0.93	0.74	0.46,1.13
2011–2012	13	3.03	0.89,9.53	1.21	0.47,2.91	1.62	0.97,2.74	0.81	0.48,1.36	0.39	0.18,0.76
2012
2013–2014	2	1.26	1.03,1.52	1.31	1.00,1.68	1.23	1.13,1.34	0.86	0.79,0.94	0.81	0.72,0.90

^aCI: Confidence Interval

Table 3.

Peak week for influenza B hospitalizations, and the relative risk for being in a given age group among influenza B hospitalizations for the before-the-peak period vs. after-the-peak period.

Relative risks (RR) in different age groups for periods before vs. after the epidemic peak for influenza B
Season	Peak Week	Aged 0–4		Aged 5–17		Aged 18–49		Aged 50–64		Aged 65+
		RR	95% CIa	RR	95% CI	RR	95% CI	RR	95% CI	RR	95% CI
2010–2011	8	1.00	0.78,1.25	0.99	0.70,1.35	1.43	1.09,1.85	1.21	0.82,1.76	0.69	0.54,0.87
2012–2013	8	1.32	1.08,1.61	0.97	0.78,1.21	0.84	0.69,0.99	0.99	0.82,1.18	1.00	0.88,1.13

^aCI: Confidence Interval

Simulations

We simulated influenza outbreaks in a stratified population with 5 age groups (0–4,5–17,18–49,50–64,65+). Transmission dynamics is modeled in the stratified mass action SIR framework. Contacts between the different age groups (strata) are described by a symmetric matrix C = (c_ij), where c_ij is the average number of contacts per unit of time (day) between a pair of individuals in strata i and j. We estimate the matrix C using the POLYMOD study data [15], averaging out the estimates for eight European countries. Additionally, for each age group i, we have

1. Population size n_i (extracted from http://wonder.cdc.gov/Bridged-Race-v2013. HTML)

2. Time-varying number of susceptible individuals h_i (t), with h_i = h_i (0) being the initial number of susceptibles.

3. Individual relative susceptibility s_i ≤ 1 (per contact with an infected individual) for each susceptible individual in stratum i (with s_i = 1 indicating the maximal possible susceptibility).

Based on previous work [27], we assume that infectivity is age-independent. The rate of infection between an infected individual in stratum j and all of stratum i at time t is then

$$M_{ij}(t)=\lambda ·s_i·h_i(t)·c_{ij}$$ (2)

with the constant λ fixed as described below. The natural history of influenza is assumed to have an exponential distribution for the serial interval with a mean of 2.6 days [16]. As such, the initial next generation matrix is

$$(N_{ij})=2.6·(M_{ij}(0))$$ (3)

and its leading eigenvalue is the initial effective reproductive number R_e (0).

The average initial susceptibility in age group i is $\overline{s_i}=\frac{s_i·h_i}{n_i}$. We consider three possibilities for the distribution of susceptibility in each age group:

• SD1. Uniform: $\overline{S_i}=S_i$. Everyone in stratum i is equally susceptible with susceptibility s_i.

• SD2. All-or-nothing: s_i = 1. A fraction $\frac{h_i}{n_i}$ of individuals in stratum i is fully susceptible, the rest have zero susceptibility.

• SD3. Balanced $s_i=\sqrt{{\overline{s}}_i}$. This is an intermediate scenario between SD1 and SD2 where a fraction $\frac{h_i}{n_i}=\sqrt{\overline{s_i}}$ of individuals in stratum i has susceptibility $s_i=\sqrt{\overline{s_i}}$, the rest have zero susceptibility.

We present the results for the intermediate scenario SD3 in the main body of the text, with the results for distributions SD1 and SD2 deferred to the Supporting Information.

Results of the hospitalizations data analysis suggest that the highest estimate of RR for the different epidemics belongs to one the first three age groups (0–4, 5–17, 18–49), while the lowest estimate (both on average, as well as for all influenza A epidemics) belongs to the elderly (aged 65+), followed by individuals aged 50–64. Motivated by those results, we consider the following 5³ = 125 scenarios for the average initial susceptibilities in the different age groups:

$$\overline{s_i}=0.5,0.6,0.7,0.8,0.9\text{for}i\le 3;\overline{s_4}=0.6;\overline{s_5}=0.45$$ (4)

We fix λ in eq. 2 so that R_e (0) = 1.35 when $\overline{S_1}=\overline{S_2}=\overline{S_3}=0.9$ (the largest possible R_e (0) corresponding to the largest allowed average initial susceptibilities). Any scenario given by eq. 4 in which the epidemic doesn’t take off (R_e (0) ≤ 1) is ignored. Otherwise, we compute the relative risks RR_i for cases during the ascent vs. descent stages of the simulated outbreak for each age group i. Additionally, we compute, for each age group i, the relative reduction of the value of the initial effective reproductive number R_e (0) if vaccine of quantity q equaling 2% of the US population is given entirely to group i. In the main body of the text we present those results for a perfect vaccine (offering complete protection of the vaccinated individual). While that does not reflect the reality of influenza vaccination, perfect vaccine amounts to removing individuals from the transmission process, and the group for which a fixed quantity of a perfect vaccine has the largest impact on R_e (0) can be thought of as having the largest relative impact on propagating the epidemic during its initial stages. In the Supporting information, we exhibit the corresponding results for a leaky vaccine whose efficacy (reduction in the susceptibility of each vaccinated individual) is assumed to be 60% for the non-elderly and 50% for the elderly (those numbers reflect the average estimates of vaccine efficacy for influenza A and B epidemics during the recent years).

Results

Hospitalization data: identifying the age group with the highest RR by influenza (sub)type and year

Tables 1–3 give estimates for RR for various age groups, influenza (sub)types and seasons. Combinations of season/(sub)type for which hospitalization counts had been very low were excluded from the analysis. For epidemics associated with influenza A subtypes, children 5–17 had the highest estimates of RR among all age groups for the five largest epidemics during the time period under study (as assessed by combining data on influenza-like illness consultations with data on the percentages of respiratory specimens testing positive for a particular (sub)type, http://www.cdc.gov/flu/weekly/pastreports.htm): 2009 A/H1N1, 2012–2013 A/H3N2, 2013–2014 A/H1N1, 2010–2011 A/H3N2 and the 2010–2011 A/H1N1 epidemics. Adults aged 50–64 and 65+ had the lowest estimates of RR except for the small, 2011–2012 A/H3N2 epidemic. For influenza B outbreaks, children 0–4 had the highest estimate of RR (1.32 (1.08,1.61)) during the 2012–2013 epidemic, while adults 18–49 had the highest RR during the 2010–2011 epidemic (RR=1.43 (1.09,1.85)).

Simulations

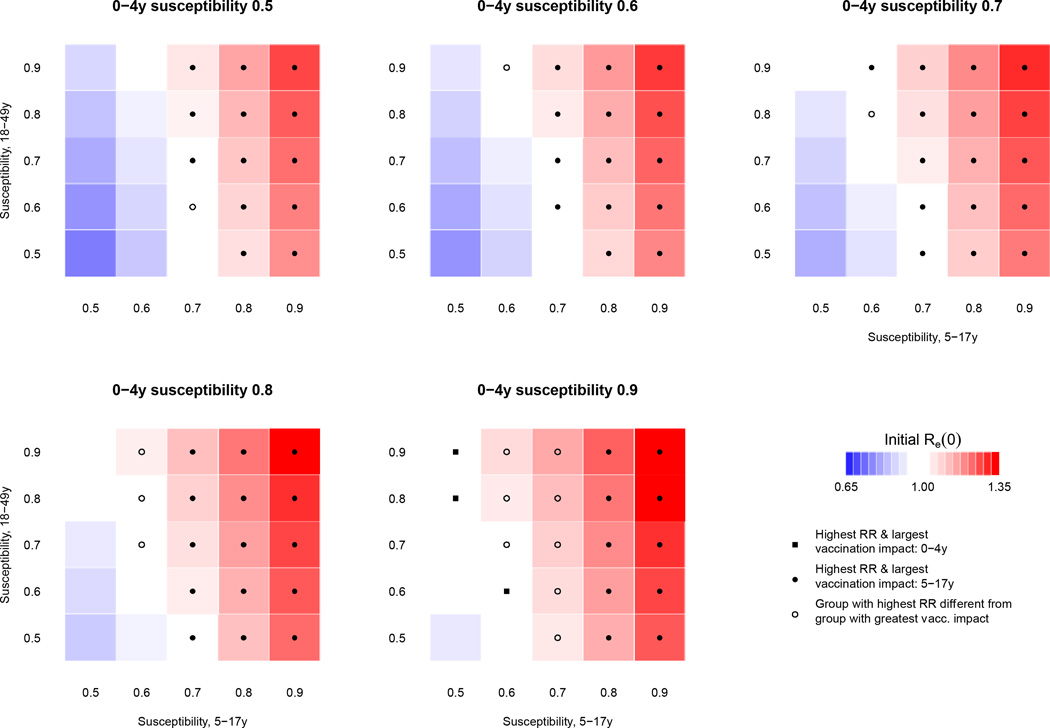
The results of simulations described in the Methods for the balanced susceptibility distribution SD3 are displayed in Figure 1. The symbol in each square indicates whether the group with the highest RR and the group for which distribution of a perfect vaccine would have the largest impact on R_e (0) are both children 5–17, or both children 0–4, or are different from one another. Tables S1–S3 in the Supplementary Information provide the numerical estimates of RR and reduction in R_e (0) for each group under each scenario. Results for susceptibility distributions SD1 and SD2 were similar, and are provided in the Supporting information (Figures S1 and S2, tables S4–S9).

Figure 1.

Simulated epidemics for a range of susceptibility profiles described by eq. 4 for susceptibility distribution SD3. For each of the 125 simulated scenarios, the shaded color indicates the initial R_e (0) value, while symbols denote whether the group with the highest RR and the group for which distribution of a perfect vaccine would have the largest impact on R_e(0) are both children 5–17, or both children 0–4, or are different from one another; absence of a symbol suggests that the epidemic hasn’t taken off.

Among the different scenarios involving varying susceptibility distributions and levels of susceptibility in the younger age groups (0–4, 5–17, 18–49) a total of 255 epidemics took off (R_e (0) > 1). For 233 (91%) of those epidemics, children 5–17 had the highest RR. For 214 (84%) of those epidemics, the group with the highest RR was also the group for which distribution of a perfect vaccine (offering complete protection to a vaccinated individual) quantity equaling 2% of the US population would have the highest impact on the reduction of R_e (0); for a leaky vaccine (partial protection to every vaccinated individual, with his/her susceptibility reduced by a given fraction), this number reduced slightly to 211 (83%) epidemics (Tables S10–S18). Additionally, for both the perfect and the leaky vaccine allocations, children aged 5–17 were the group with both the highest RR and the largest impact on reducing R_e (0) through vaccination for each of the 100 epidemics with the largest R_e (0), as well as for all epidemics where 5–17 year-olds had relative susceptibility ≥ 0.8.

Discussion

The relative impact of different age groups on influenza epidemics is not fully understood; indeed, like the notion of “core group” in the epidemiology of sexually transmitted infections, there is no precise and widely agreed upon definition of the importance of an age group in transmission of influenza. Furthermore, the relative impact may vary by season, influenza (sub)type, vaccination coverage and other factors. There is no consensus among previous studies into children's role in driving influenza epidemics. We hypothesized that the RR summary statistic, a heuristic but precisely defined measure, could reliably identify the age group that plays the largest relative role in transmission during a particular epidemic. This hypothesis revolves around the following idea: groups that experienced a disproportionate depletion of susceptibles due to influenza infection relative to the whole population during the epidemics’ ascent would have their proportion in overall incidence (or any other influenza-associated outcomes) decline during the epidemics’ descent compared to the ascent period. Change in a group’s representation over the course of the epidemic is captured by the summary statistic RR, which is the ratio of its proportion among cases during the epidemic’s ascent to that in the descent. A key utility of this statistic lies in the fact that it can be readily measured from the appropriate epidemic data (in our case, data on influenza-confirmed hospitalizations) serving as surrogate measure for the age-specific influenza incidence;, the latter being generally difficult to estimate. Moreover, even if groups differ in the proportion of incident cases of influenza infection that enter the data set (e.g. the proportion of cases hospitalized), the ordering of groups by RR will reflect the ordering of the proportional change in infection incidence in these groups (see Supporting Information). Here we estimate RR for the 2009–2014 US data on laboratory-confirmed influenza hospitalizations for epidemics associated with the major influenza (sub)types: A/H1N1, A/H3N2 and B.

For epidemics associated with influenza A subtypes, our analysis indicates that except for the small 2011–2012 season, children aged 5–17 had the highest estimated RR among all age groups while adults aged 50–64 and 65+ had the smallest RR estimates. Those results are related to the notion supported by several studies [8,17,18,19] that attaining high vaccination rates among children can have a major impact on mitigation of an influenza epidemic in the whole community. Our results also suggest that the importance of targeting mitigation efforts to the older adults increases during an epidemic’s decline stage compared to the ascent stage [20].

For the influenza B epidemics, children aged 0–4 had the highest estimated RR among all age groups during the 2012–2013 epidemic, while adults aged 18–49 had the highest estimated RR during the 2010–2011 epidemic. This is likely indicative of an increased relative susceptibility of those age groups to the corresponding influenza B strains in those seasons and suggests potential differences in driver groups for influenza B vs. influenza A.

For epidemics associated with influenza A/H1N1, the role of school-age children decreased significantly in the post-pandemic period compared to the pandemic itself, presumably due to the immunity acquired during the pandemic when attack rates among 5–17 year-olds were very high [1]. Moreover in the post-pandemic period, the role of 5–17 year olds as drivers of H1N1 epidemics is of less magnitude than the role 5–17 years olds as drivers of H3N2 epidemics. Compared to the 2010–2011 A/H1N1 season, the moderately severe 2013–2014 A/H1N1 outbreak saw an increase in the role of children aged 0–4, presumably due to the limited immunity to this virus in that age group relative to other age groups.

In order to explore to what extent a higher value of RR in the hospitalization data is indicative of a driver role in an influenza epidemic for a particular age group, and what potential impact increased vaccination efforts in a group with a high RR would have on the dynamics of influenza transmission in the population, we performed a variety of simulations of influenza transmission in the community. We found a strong correspondence between the group with the highest value of RR in the simulated data and the group for which distributing a small, fixed quantity of a vaccine would result in the largest reduction of the epidemic’s initial effective reproductive number R_e (0). For epidemics with the largest R_e (0), school age children had the highest values of RR and vaccination of this group resulted in the largest reduction of the epidemics effective reproductive number R_e (0). We note that this conclusion about the vaccination of school-age children is consistent with results of previous work [13,14,17,21].

Our analysis is based on the assumption that higher values of RR estimated from the hospitalization data correspond to stronger depletion of susceptibles. That depletion might have occurred both due to natural infections and vaccination. Compared to adults, children had higher vaccination rates [22], and generally higher vaccine effectiveness [23,24], and one may wonder to what extent the decline in the share of children in incidence after the epidemic’s peak is explained by vaccination. We note that for the 2009 season, the epidemic had largely subsided by the end of November [25]. Vaccine coverage levels at that point were quite modest, and vaccine coverage differences between children and non-elderly adults were even smaller [26], suggesting a minor relative impact of vaccination on post-peak attack rates in children compared to adults. For the other seasons during our study period for which data are available, most vaccine administration took place by the end of November [22], before the peak in influenza activity (see http://www.cdc.gov/flu/weekly/pastreports.htm, particularly the Influenza-Like-Illness curves), with additional, more limited levels of vaccine administration taking place in all age groups during the winter. Thus comparison of the share of children among hospitalizations before vs. after the epidemic peak largely refers to two time periods during which not many individuals were vaccinated; moreover there is no evidence in the data that during those periods of limited vaccine administration, children were specifically overrepresented in coverage during the epidemics’ ascent compared to the descent. Altogether, vaccination alone is unlikely to explain the high estimates of RR among 5–17 year-olds, particularly for the largest epidemics in the data.

While there is a strong correspondence between an age group with the highest value of RR and the highest impact of vaccination on R_e (0), this correspondence was violated for certain simulated epidemics with a medium-to-small R_e (0). We note that for all the simulated epidemics with 5–17 year-olds either not having the highest RR or the largest impact on R_e (0) through vaccination, these children had a smaller relative susceptibility than one of the other age groups. Our analyses suggest that the latter might be relevant to influenza B epidemics, and possibly to the fairly sizeable 2013–2014 A/H1N1 outbreak during which children 0–4 had very limited prior exposure and immunity to that virus. Additional considerations, such as those based on the pre-seasonal collection of serological data or information on previous circulation of certain viruses might provide further insights into the relative roles of the different age groups during future influenza outbreaks.

It is uncertain to what extent the proposed simulation framework reflects the reality of influenza transmission in the community. Our primary aim in using these simulations was to examine to what extent groups having the highest values of RR (that can be found from the epidemic data) are also the groups for which vaccination would have the largest impact on reducing the epidemic’s initial effective reproductive number R_e (0). This issue was assessed for a wide range of relative susceptibilities across the different age groups in an attempt to capture the spectrum of possible scenarios for influenza transmission dynamics in the population. The proposed framework might still not be able to capture the full spectrum of those scenarios. For example, the group with the highest RR was children aged 5–17 in the vast majority of simulated epidemics, and never adults aged 18–49. This does not agree with the hospitalization data for influenza B epidemics, which may be affected by additional factors such cross-immunity from concurrent or immediately prior influenza A epidemics [27] and initial susceptibilities in the different age groups lying outside the range considered in our simulations. At the same time, for the influenza A epidemics in the hospitalization data, RR was highest for children aged 5–17 except for the very small, 2011–2012 A/H1N1 season, for which our estimate was associated with considerable uncertainty.

Our method has some additional limitations. Spatial heterogeneity could lead to variation in the local timing of the epidemic peak across locations. We note that such heterogeneity should bias the estimates toward the null hypothesis (making the RR estimates in different age groups closer to each other). There is some uncertainty regarding the estimation of the hospitalization burden due to particular subtypes of influenza A, given the presence of un-subtyped cases, and the potential differences in the likelihood of an influenza A infection being subtyped between A/H1N1 and A/H3N2 due to a possible spatial asynchrony in their circulation and differences in laboratory facilities. We note that the impact of the latter on the dominant subtype estimates is minor if the dominant subtype’s circulation levels are significantly higher than that of the other subtype. Finally, while our inference does not require the likelihood of a detection of a hospitalized influenza case to be constant throughout each influenza season, we assume that it scales with time in the same manner for all age groups. The latter assumption may be violated for an age group that has a sub-population with both a different risk of infection and a different case-hospitalization rate compared with the whole age group. We note that violation of this assumption for a particular age group would have no impact on the relative magnitude of RRs for other age groups.

Conclusions

Despite certain limitations, our results provide a cross-seasonal comparison of the relative roles of different age groups during epidemics associated with the major influenza (sub)types. Our estimates and simulation results both exhibit the variability in these relative roles during different influenza epidemics, and yield consistent evidence for a leading role of school age children in propagating the major influenza A epidemics.

Table 2.

Peak week for A/H3N2 hospitalizations, and the relative risk for being in a given age group among A/H3N2 hospitalizations for the before-the-peak period vs. after-the-peak period.

Relative risks (RR) in different age groups for periods before vs. after the epidemic peak for influenza A/H3N2
Season	Peak Week	Aged 0–4		Aged 5–17		Aged 18–49		Aged 50–64		Aged 65+
		RR	95% CIa	RR	95% CI	RR	95% CI	RR	95% CI	RR	95% CI
2010–2011	8	1.44	1.08,1.90	1.83	1.07,3.05	1.64	1.28,2.10	1.10	0.86,1.40	0.74	0.68,0.81
2011–2012	12	1.29	0.87,1.86	1.63	0.87,2.92	0.88	0.63,1.19	1.06	0.76,1.46	0.94	0.83,1.07
2012–2013	1	1.22	1.01,1.46	1.86	1.41,2.40	1.47	1.30,1.66	1.21	1.07,1.37	0.75	0.71,0.80

^aCI: Confidence Interval

Manuscript Highlights.

• -Epidemics are often ‘driven’ by subgroups with higher contact/transmission rates
• -We propose a simple statistic to identify such groups using surveillance data
• -Vaccine distribution to such ‘driver’ groups usually the most effective strategy
• -Children aged 5–17 played most important role in largest influenza A outbreaks