Model-Based Reconstruction of Undersampled Diffusion Tensor K-Space Data

Abstract

The practical utility of diffusion tensor imaging (DTI), especially for 3D high resolution spin warp experiments of ex vivo specimens, has been hampered by long acquisition times. To accelerate the acquisition, a compressed sensing framework that employs a model-based formulation to reconstruct diffusion tensor fields from undersampled k-space data was presented and evaluated. Accuracies in brain specimen white matter fiber orientation, fractional anisotropy (FA) and mean diffusivity (MD) mapping were compared to alternative methods achievable using the same scan time via reduced image resolution, fewer diffusion encoding directions, standard compressed sensing or asymmetrical sampling reconstruction. The efficiency of the proposed approach was also compared to fully-sampled cases across a range of the number of diffusion encoding directions. In general, the proposed approach was found to reduce the image blurring and noise, and provide more accurate fiber orientation, FA and MD measurements compared to the alternative methods. Moreover, depending on the degree of undersampling used and the DTI parameter examined, the measurement accuracy of the proposed scheme was equivalent to fully sampled DTI datasets that consist of 33% to 67% more encoding directions and require proportionally longer scan times. The findings show model-based compressed sensing to be promising for improving the resolution, accuracy or scan time of DTI.

Introduction

Diffusion Tensor Imaging (1) (DTI) is an MRI technique that allows quantitative characterization of the geometry and organization of tissue microstructures such as fiber orientation. DTI has been applied in the brain (2,3) to, for example, trace white matter tracts (4–6), map connectivity and characterize damage caused by stroke (7–9). The method has also been applied to ex-vivo specimens of the heart (10–12) to map structural changes due to fibrosis or infarction (13–17).

Because the diffusion tensor is a rank 2, symmetric matrix (1), a unique solution of the diffusion tensor requires a minimum of six diffusion weighted images sensitized in non-collinear diffusion encoding directions, plus a non-diffusion weighted image. In this sense, the minimum scan time required for a DTI dataset, which spans both the spatial and diffusion dimensions, is seven times that of an anatomical scan acquired using the same sequence and settings. DTI suffers from low SNR because diffusion is measured as signal attenuation and from increased echo time necessary to accommodate the use of diffusion sensitizing gradients. In practice, the loss of signal is often compensated for by additional signal averaging in forms of acquisition repetition or increasing the number of encoding directions, which further prolongs the scan time. Consequently, methods to accelerate the acquisition, especially those that minimize further SNR loss, are highly desirable.

Perhaps the most obvious method to accelerate acquisition would be to either scan at a lower resolution or simply encode fewer diffusion directions. Scanning at a lower resolution would introduce blurring and make it more difficult to discern fine structures in an image. In contrast, although the resolution is maintained, encoding in fewer diffusion directions would sacrifice the accuracy of the diffusion tensor estimation. A possible solution to both of these problems is to accelerate acquisition by partially sampling k-space, and apply reconstruction in such a way that fine structure and diffusion tensor accuracy are preserved. When not reconstructed properly, partially sampling k-space introduces artifacts in image space, such as ghosting, field of view (FOV) overlap or additional noise, depending on the undersampling pattern employed. Techniques have been introduced to reduce the effects of partial- or under-sampling when DTI is acquired using multiple receive coils (18–23).

Rather than reconstructing each image of the multi-image acquisition separately, compressed sensing techniques (24–26) are capable of jointly estimating multiple acquisitions by sharing sparsely sampled data. Compressed sensing can be particularly attractive for DTI, due to the high degree of similarity or redundancy (e.g., the size and shape of the brain, including the white matter) among the acquisitions at different diffusion directions that can be leveraged to represent a transform of the data sparsely. Previously, compressed sensing based on undersampling in the diffusion encoding or q-space has been applied to High Angular Resolution Diffusion Imaging (HARDI) (27,28), which is a more general form of diffusion imaging that allows resolution of crossing fibers. A possible alternate way to undersample DTI or HARDI data is in k-space (29) or spatial frequency domain. Intuitively, the nature of the desired information in the DTI dataset and the well known relationship between image- and k-space may offer flexibility that can be exploited for effective undersampling. For example, the fiber orientation of the brain white matter or myocardium varies relatively slowly and, therefore, the relevant information can be captured even when the outer k-space is sampled with a lower density.

Regardless of the scheme of undersampling, it is important that the performance of any reconstruction method be evaluated on not only the acquisition time acceleration, but also on its ability to capture the desired information. In DTI, fiber orientation, fractional anisotropy (FA) (30) and mean diffusivity (MD) are the often sought-after parameters for assessing tissue microstructure. Therefore, ideally the performance of any compressed sensing acceleration needs to be evaluated in terms of accuracy loss in measuring these parameters with respect to a “ground truth” or “gold standard”. Moreover, to be considered effective, any proposed technique should retain more accuracy than alternative methods using, for example, lower resolution or fewer diffusion encoding directions to achieve the same acceleration.

The goal of the current study is to investigate the validity of a compressed sensing framework for DTI that, in addition, uses the signal intensity model to directly estimate diffusion tensor fields from undersampled k-space data. The formulation bypasses the usual intermediate step of estimating diffusion weighted images. By estimating the diffusion tensor directly, the number of variables to be solved is reduced from N×dim1×dim2×dim3 to 6×dim1×dim2×dim3 (excluding the non-weighted volume) where dim1, dim2, dim3 are the spatial dimensions of a 3D acquisition and N is the number of diffusion weighted images acquired. In a noise dominated system, reducing the number of unknowns can provide more accurate estimates of the fitted parameters. As well, the model-based formulation provides a convenient platform that numerous practical considerations involved in DTI (e.g., phase errors) can be addressed in a single step. Model-based approaches have been proposed previously to compensate for eddy currents, field inhomogeneities and motion in DTI (31,32) and to reconstruct diffusion tensor tomography data (33), but not for accelerating acquisition. Other compressed sensing techniques using exponential models have been proposed for T1 and T2 mapping (34,35).

The current model-based algorithm is demonstrated on a 3D DTI acquisition, which is used for high resolution characterization of fixed specimens (36,37). Three dimensional DTI, especially one acquired with a spin echo sequence, can take many hours for ex-vivo acquisitions and thus can benefit greatly from acquisition acceleration. Also, 3D acquisitions have a higher degree of data redundancy and can be undersampled in more than one dimension. For the sake of brevity, in the following sections, and unless otherwise noted the term DTI strictly refers to 3D spin-warp spin echo DTI. The effectiveness of the model-based compressed sensing algorithm is validated against other means to achieve comparable scan-time reduction. Part of the current work has been presented previously in a conference abstract (38).

Theory

Compressed sensing basically finds the target images by subjecting the estimates to a set of reconstruction constraints and minimization of the associated penalty or cost function. One form of a cost function for compressed sensing (24,39) reconstruction of a series of N undersampled MRI k-space data, d_n, is given as

$$C(\tilde{m})={\displaystyle \sum _{n=1}^N\left({\Vert \overrightarrow{F}({\overrightarrow{m}}_n,n)-{\overrightarrow{d}}_n\Vert }_2^2+\alpha TV({\tilde{m}}_n)\right)}$$ [1]

where ‖ ‖₂ represents the L2-norm, which produces the least squares solution (25) and can be substituted by any other type of measure of deviation between images (40), and m̃_n are the estimated magnitude images. The terms m⃗_n and d⃗_n are the vectorized versions of m̃_n and d_n, such that for image resolution dim1 by dim2, the vectors m⃗_n and d⃗_n have dim1×dim2 elements. The first term in Eq. [1] is a fidelity term that forces the solution to adhere to the acquired k-space data. The second term in Eq. [1] is a total variation (TV) operator (41) applied in image space to constrain the solution to generate piecewise-constant images, hence reducing erratic points due to undersampling k-space. The scalar regularization weight factor α controls the relative contributions of the fidelity and total variation terms. The j^th k-space element of the k-space signal model, F⃗ (m⃗_n, n), is

$$F_j({\tilde{m}}_n,n)=W_n({\overrightarrow{k}}_j){\displaystyle \sum _{\overrightarrow{x}}{\tilde{m}}_n}(\overrightarrow{x})·e^{i{\varphi }_n(\overrightarrow{x})}·e^{-i\overrightarrow{x}·{\overrightarrow{k}}_j}$$ [2]

where W_n is the binary undersampling function for the diffusion direction n, ϕ_n is the image phase which is estimated and fixed from the acquired low-resolution data from each diffusion weighted image, x⃗ is the position in image space and k⃗_j is the position in k-space. The series of images, m̃_n, can be obtained simultaneously by minimizing the cost function in Eq. [1] with respect to m̃_n.

In the current model-based DTI reconstruction, to allow direct estimation of the diffusion tensor, m̃_n is replaced with the standard diffusion tensor intensity equation (1). This allows direct estimation of the diffusion tensor. The relationship between m̃_n and the DTI signal is given by,

$${\tilde{m}}_n=I_o{e}^{-b{\mathit{g}}_b^T\mathit{D}{\mathit{g}}_n}$$ [3]

where I_o is the image without diffusion weighting, b is the diffusion weighting factor and g_n = (g_xn, g_yn, g_zn)^T is the diffusion encoding directional vector in the 3D space spanned by the readout (x), phase (y) and slice (z) encoding directions. D is the rank 2, symmetric tensor defined as

$$\mathit{D}=\left[\begin{array}{ccc}{D}_{xx}& D_{xy}& D_{xz}\\ D_{xy}& D_{yy}& D_{yz}\\ D_{xz}& D_{yz}& D_{zz}\end{array}\right]$$ [4]

Replacing m̃_n yields the new k-space signal model

$$F_j(\mathit{D},n)=W_n({\overrightarrow{k}}_j){\displaystyle \sum _x{I}_o(\overrightarrow{x})}·e^{-b{\mathit{g}}_n^T\mathit{D}(\overrightarrow{x}){\mathit{g}}_n}·e^{i{\varphi }_n(\overrightarrow{x})}·e^{-i\overrightarrow{x}·{\overrightarrow{k}}_j}$$ [5]

For the current formulation, the total variation can be defined as

$$TV(\mathit{D})={\Vert \sqrt{{({\tilde{m}}_n)}_y^2+{({\tilde{m}}_n)}_z^2}\Vert }_1$$ [6]

where (m̃_n)_y and (m̃_n)_z are the partial derivatives of m̃_n with respect to y and z. TV is not calculated in the x-direction since it is already fully-sampled.

Maps corresponding to each diffusion tensor element can be estimated by minimizing Eq. [1] simultaneously with respect to each element of the tensor, D, via, for example, gradient descent optimization. In order to perform gradient descent, computational equations for the derivative of Eq. [1] are needed with respect to each diffusion tensor element, D_s (s ∈ {xx, yy, zz, xy, xz, yz})

$$\begin{gathered} \frac{\partial C(\mathit{D})}{\partial D_s}={\displaystyle \sum _{n=1}^N-2b{({\mathit{g}}_n{\mathit{g}}_n^T)}_s{I}_o{e}^{-b{\mathit{g}}_n^T\mathit{D}{\mathit{g}}_n}\mathit{\text{Real }}\left\{e^{-i{\varphi }_n}{\displaystyle \sum _j(F_j(\mathit{D},n)-d_{jn})e^{i\overrightarrow{x}{\overrightarrow{k}}_j}}\right\} \\ -\alpha b{({\mathit{g}}_n{\mathit{g}}_n^T)}_s{\tilde{m}}_n}\left(\frac{\partial }{\partial y}\left(\frac{{({\tilde{m}}_n)}_y}{\sqrt{{({\tilde{m}}_n)}_y^2+{({\tilde{m}}_n)}_z^2+{\beta }^2}}\right)+\frac{\partial }{\partial z}\left(\frac{{({\tilde{m}}_n)}_z}{\sqrt{{({\tilde{m}}_n)}_y^2+{({\tilde{m}}_n)}_z^2+{\beta }^2}}\right)\right) \end{gathered}$$ [7]

where ${\mathit{g}}_n{\mathit{g}}_n^T$ is a 3 × 3 matrix and the (·)_s operator extracts the s^th element corresponding to the D_s parameter map. The full derivation of this equation can be found in the attached appendix. The diffusion tensor elements are then updated iteratively using the derivative in Eq. [7]

$${\tilde{D}}_s^{r+1}={\tilde{D}}_s^r-\lambda \frac{\partial C(\mathit{D})}{\partial D_s}$$ [8]

where λ is the step size used in the gradient descent and r is the iteration number.

Methods

Data Set

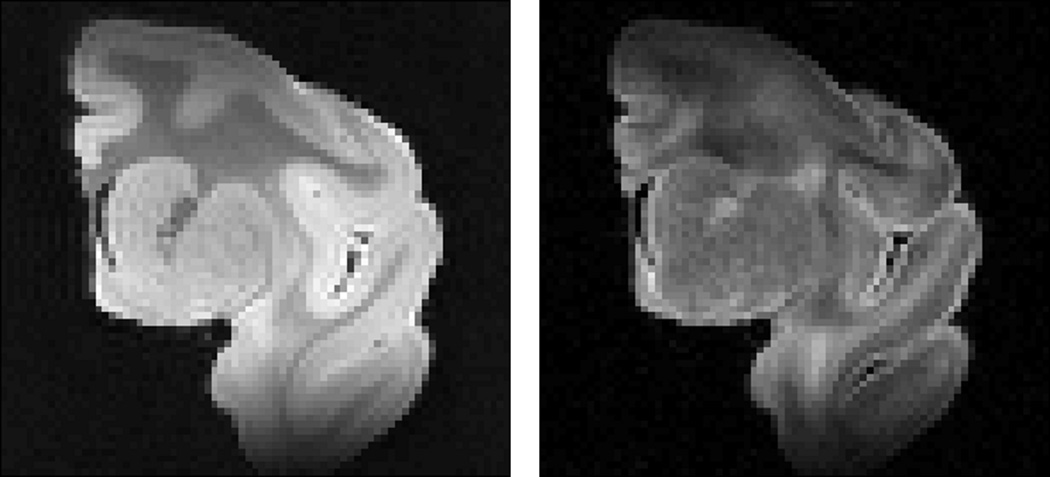
Fully-sampled 3D, Cartesian k-space, DTI spin echo data consisting of diffusion-weighted scans in a relatively high number of encoding directions (96 in all) and 4 non-diffusion weighted “b0” images (100×75×70 matrix size, 0.5×0.5×0.5 mm³ isotropic voxel size, TE = 39ms, TR = 500ms, NEX = 1) were acquired on a fixed, excised macaque brain hemisphere using a Bruker Biospec 7T scanner (Bruker Biospin Inc., Billerica, MA) equipped with a high performance gradient system (max gradient amplitude capable of 600 mT/m). The acquisition time for the entire diffusion MRI dataset was ~72 hrs. Figure 1 shows the “b0” and diffusion weighted images of a representative 2D slice, for reference. The diffusion tensor solution to the entire fully-sampled dataset was used as the “gold-standard” for subsequent performance assessments.

Figure 1.

Two-dimensional MRI coronal view of the macaque brain hemisphere used in this study. Left, nondiffusion-weighted “b0” image, b = 0 s/mm². Right, diffusion-weighted image, b = 5000 s/mm² in a single diffusion direction, scaled up for better display. There is notable shading due to coil inhomogeneity.

Undersampling Schemes

To simulate more typical DTI acquisitions, 10 test datasets each comprised of a subset of diffusion-weighted images encoded in 24 gradient directions were retrospectively selected from the original 96-direction set. The first direction of each subset was randomly chosen, and the remaining directions were selected based on maximizing the angular distance between each successive encoding direction (42). In order to have distinct datasets, precaution was taken to avoid excessive overlap of gradient directions between any two datasets. When the gradient directions overlapped by more than 45%, alternative gradient directions were substituted. Among the final test datasets, the amount of overlap ranged from 8% to 45%, with 20% being the average.

Undersampling was subsequently applied to the above test datasets, which was mathematically equivalent to multiplying the k-space data with appropriate binary masks. k-space was undersampled in the phase (y) and slice (z) directions, while sampled fully in the readout (x) direction for the 3D data. Two different degrees of undersampling were examined, 50% and 75%, which are equal to the acceleration factor R of 2 and 4, respectively. Figure 2 shows examples of the binary masks used with R of 2 and 4. To take advantage of the low-frequency nature of DTI data, the center k-space was fully-sampled, whereas the remaining k-space was sampled randomly, using a uniform distribution, to achieve the desired overall acceleration factor. The reference image, I_o, was sampled fully and reconstructed separately using an IFFT. The reference image was fixed throughout the reconstruction.

Figure 2.

Two-dimensional representation of sampling masks in the phase-slice plane for 50%, left, and 75%, right, undersampling. The data was sampled fully in the readout direction.

Reconstruction

All computation was performed using Matlab (Mathworks, Natick, Mass; version R2011a). Two steps were taken in preparation for the iterative compressed sensing reconstruction. First, an inverse Fourier transform was applied to the k-space data along the readout direction, which was fully sampled. The procedure permitted the reconstruction of data in each subsequent 2D ky-kz plane perpendicular to the readout direction to be performed separately and in parallel. Second, the phase map, ϕ_n needed in Eq. [5] was approximated from the central fully-sampled k-space block and low-pass filtered using a 2D Hann window.

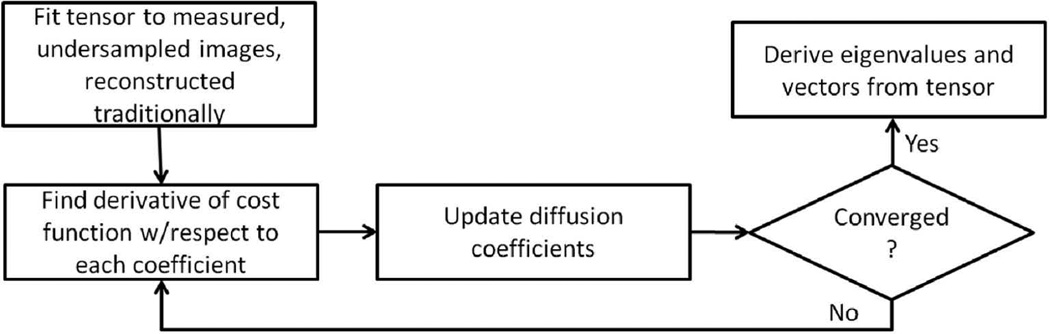
Implementation of the compressed sensing reconstruction is summarized in the flowchart shown in Fig. 3. The estimation was initialized by the linear least squares fit of the diffusion tensor to the images generated by direct reconstruction (inverse Fourier transform) of the undersampled k-space data. The initialization of the diffusion tensor is important, but the optimization solution can withstand a wide range of initial conditions (e.g., initializing DTI parameters to the tensor solution of using the b0 image plus identical DWIs). The algorithm then enters a loop, the first step of which is to determine the derivative of the cost function with respect to each of the diffusion coefficients, according to the procedure outlined in the Theory section. A value of 1×10⁻⁶ was used for β in Eq. [7]. The derivatives were used to update the diffusion tensor elements according to Eq. [8]. The loop was repeated until convergence was achieved, which was determined to occur when the value of the cost function changed by less than 1×10⁻⁴ percent from iteration to iteration.

Figure 3.

Flowchart of the model-based reconstruction algorithm.

Optimal values of the computational parameters, TV weight α and step size λ from Eqs. [7] and [8], were determined empirically by reconstructing an arbitrarily selected test dataset with a range of values of α and λ. The values that yielded the most accurate tensor eigenvector estimation with respect to the gold standard, 0.00025 and 0.00001 for α and λ, respectively, were used in the remaining test datasets. The parameters were found to be relatively robust and when changed by a factor of 10, increased the estimation errors by only about 10%. The reconstruction of each undersampled 24-direction test dataset typically converged within 1000 iterations and took approximately 1.0 hr on a computer with a quad-core processor, 8 GB of RAM and Matlab’s Parallel-Computing toolbox.

Assessment of Performance

The effectiveness of the proposed model-based compressed sensing DTI technique was evaluated by comparing its performance to those of two other reconstruction techniques and two control experiments all of which required equal total scan time:

1. Conventional compressed sensing. The compressed sensing reconstruction estimated individual diffusion weighted images by minimizing the cost function defined in Eq. [1] with respect to m̃_n, as in (29), utilizing a TV weight, α, equal to 0.025 and performing 300 iterations. The data was undersampled in the same manner as the proposed model-based approach.

2. Asymmetrical sampling. In the asymmetrical sampling case, a modified iterative partial Fourier method (43) was employed to fill in the missing k-space. k-Space was sampled asymmetrically in the phase (ky) direction to get an overall acceleration factor, R, of 2 and 4. Ten phase-encodes of negative k-space were sampled for R = 2 and five phase encodes for R = 4. To maintain the same acceleration factor as the other techniques, the same number of phase-encoding steps were not sampled at the high, positive frequencies, but were estimated in the reconstruction to maintain the original resolution.

3. Low resolution. In the lower resolution control scheme, the center half (which is $1/\sqrt{2}$ in each phase and slice dimensions for R = 2) or center fourth (1/2 in each phase and slice dimensions for R = 4) of k-space for each test dataset was taken and zero-padded. The diffusion weighted images were obtained by using the inverse Fourier transform.

4. Fewer Directions. The fewer directions control scheme used fewer encoding directions to achieve the same R factor (12 and 6 fully-encoded images for R = 2 and R = 4, respectively). The directions used for R = 2 and 4 were found by iterating over every 12- and 6-direction combination in each 24-direction test dataset to find the combination that minimizes the fiber orientation deviation angle for each test dataset. Again, the diffusion weighted images were obtained by using the inverse Fourier transform.

In each of the reconstruction and control experiments, the diffusion tensors and their derived parameters were obtained using conventional means (linear least squares fitting on a pixel-by-pixel basis).

The performances of the acquisition schemes in capturing the essential DTI information were quantified along three error metrics: the fiber orientation deviation angle (Δθ, in degrees), fractional anisotropy difference (ΔFA, dimensionless), and mean diffusivity difference (ΔMD, cm²/s) with respect to the gold standard. Fiber orientation, fractional anisotropy and mean diffusivity are parameters commonly derived from DTI results, which are useful in tractography and detection of pathology. The fiber deviation angle, Δθ, was calculated by finding the angular difference (arccosine of the vector dot product) between primary eigenvectors of the gold standard and the model-based estimate. Δθ was averaged over the brain white matter, which was defined as regions with FA greater than 0.3. In low-FA areas, such as the brain gray matter, where diffusion is relatively isotropic, noise can lead to wide fluctuations of the primary eigenvector and skew the error metric. In contrast, root-mean square (RMS) of the FA difference, ΔFA, and MD difference, ΔMD, were calculated over the entire specimen. The mean Δθ, RMS ΔFA and RMS ΔMD metrics obtained for the proposed and alternate schemes in all 10 test datasets were compared using one-way repeated measurement analysis of variance (ANOVA). When significant group difference (i.e., F-test with p < 0.05) was found, post-hoc multiple comparisons based on the Bonferroni criterion with overall P < 0.005 were conducted to identify the group pairings that were significantly different.

Whereas the above comparisons were intended largely to assess the relative advantages of the proposed scheme, to offer guidance in the design of future DTI studies, and as an alternative way to evaluate the performance, it is instructive to determine the fully-sampled DTI experiment that offers equivalent performance as the proposed scheme. To this end, the performance metrics, mean Δθ and RMS ΔFA, were obtained as described above for DTI experiments that comprised fully-sampled diffusion-weighted images encoded over a range of the number of gradient directions (N, 6 ≤ N ≤ 24, 10 experiments for each N). The DTI experiments (i.e., N) that yielded the same performances as the proposed schemes for each R = 2 and R = 4 case were then identified. As an additional reference, the performance metrics obtained for N = 24 were extrapolated to lower values of N via the $1/\sqrt{N}$ relationship, which approximated DTI experiments that are SNR-limited. The same analysis was not carried out for ΔMD since the deviations were found to be small across all schemes and, therefore, improving its measurement efficiency was less critical.

Results

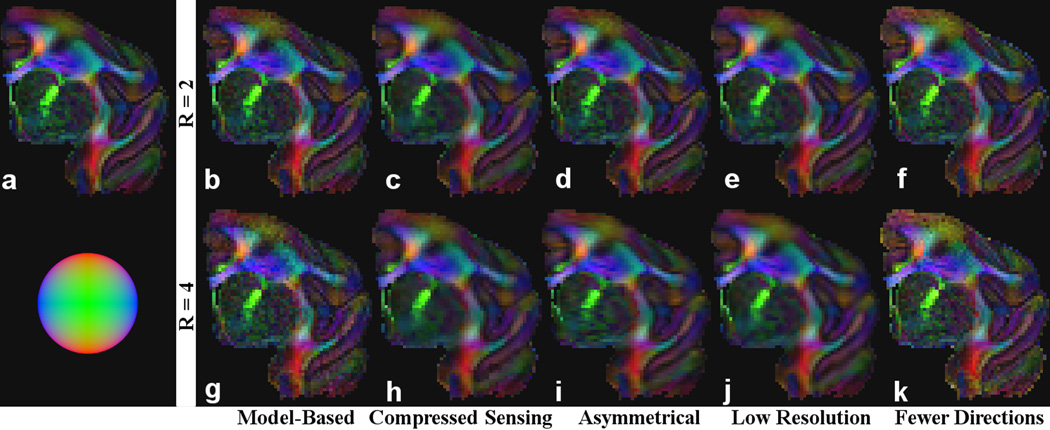
Figure 4 shows the FA-weighted, red-green-blue (RGB) color coded primary eigenvector maps for the model-based, compressed sensing, asymmetrical, low-resolution and fewer direction cases, for R = 2 and 4, obtained for a representative test dataset. Qualitatively, compared to the “gold standard” (also shown in Fig. 4), all five schemes produced progressively worse DTI maps as the acceleration factor R increased, which was expected. The limitations of each of the low resolution and fewer directions control schemes were more conspicuous at R = 4. There was considerable blurring in the low-resolution scheme, whereas the noise was markedly higher in the reduced-direction scheme. In contrast, the issues were clearly improved or avoided in the model-based compressed sensing approach.

Figure 4.

FA-weighted, primary eigenvector RGB maps for the “gold standard” obtained from diffusion-weighted images encoded in 96 directions (a), test dataset comprising of 24 diffusion images reconstructed using the model-based algorithm (b and g), compressed sensing (c and h), asymmetrical sampling (d and i), low resolution scans (e and j), 12 fully-encoded images (f) and 6 fully-encoded images (k). The results from each row (b-f and g-k) require the same scan time. The results from b-e and g-j were derived from undersampled k-space in order to accelerate scan time. The sphere in the lower-left corner indicates the direction of the fibers according to their color in RGB (e.g., red indicates a fiber traveling in the up-down direction).

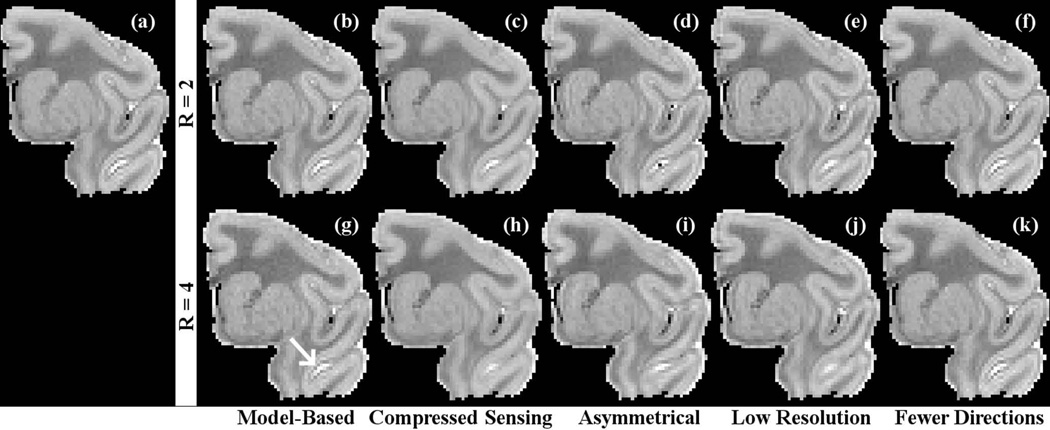
Figure 5 shows the mean diffusivity maps for the five test cases. The degradation in quality due to image acceleration was less apparent for the mean diffusivity maps than it was for the FA maps shown in the previous figure, although there was more blurring in the low-resolution scheme than in the model-based case. The MD maps had more in common with each other than did the FA maps.

Figure 5.

Mean diffusivity maps for the “gold standard” obtained from diffusion-weighted images encoded in 96 directions (a), test dataset comprising of 24 diffusion images reconstructed using the model-based algorithm (b and g), compressed sensing (c and h), asymmetrical sampling (d and i), low resolution scans (e and j), 12 fully-encoded images (f) and 6 fully-encoded images (k). Note the lack of blurring in the model-based case indicated by the arrow.

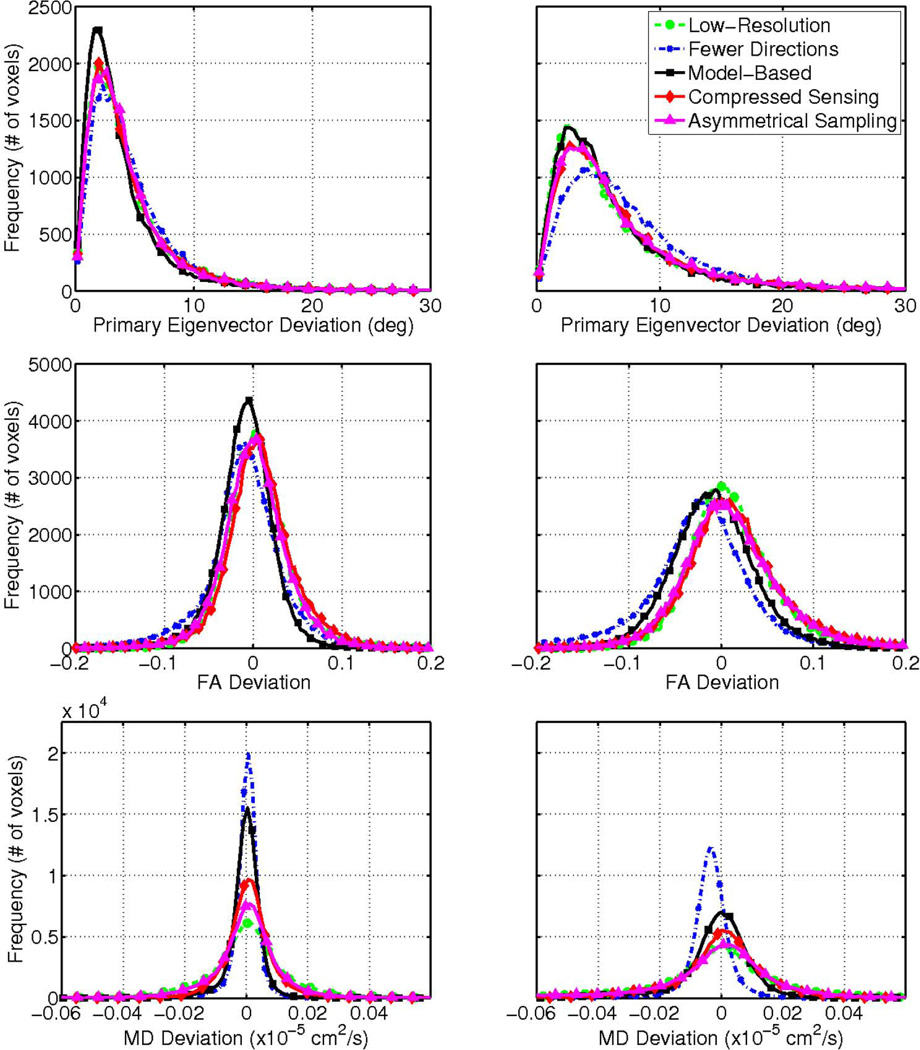
The above qualitative observations are supported by the histograms of the performance metrics shown in Fig. 6, for the same test dataset. In each R = 2 and R = 4 case, the distributions of Δθ, ΔFA and ΔMD for the model-based compressed sensing scheme were generally not only narrower, but also closer to zero, compared to those of the other reconstruction and control schemes, with the exception of ΔMD in the fewer directions case. An exception to the observed trends in the histograms was in the R = 4 case, where the Δθ distributions between the proposed and low-resolution schemes were similar. However, this may be due to the noise-smoothing effect inherent to lowering the scan resolution and the absence of a penalty for blurring in the performance metrics. The similarity likely reflects artifacts of the experimental methodology, and not actual benefits of the low-resolution scheme. Also, there appears to be a slight bias in ΔFA for the proposed model-based technique, the cause of which is currently unclear.

Figure 6.

Distribution of primary eigenvector (top row), FA (middle row) and mean diffusivity deviation (bottom row) for 50% (left) and 75% (right) undersampling for the same test dataset shown in Figs. 4 and 5. The model-based approach (solid squares) was compared against compressed sensing (solid diamonds) and asymmetrical reconstructions (solid triangles) and comparable low-resolution (dashed circles) and fewer-direction (dash dot x’s) cases. The bias in FA deviation (e.g., in the fewer directions case for R = 4) indicates that the FA was underestimated as compared to the gold standard.

The quantitative performance comparisons among the schemes are summarized in Tables 1 and 2, which contain the means of Δθ, ΔFA, and ΔMD for each R = 2 and R = 4 case, respectively. Once again, the results were consistent with the above qualitative observations. Among the test datasets examined, the model-based approach at R = 2 produced a mean Δθ of 4.11 ± 0.05° (n = 10, ± SEM), RMS ΔFA of 3.22 ± 0.07 × 10⁻² and RMS ΔMD of 1.09 ± 0.01 × 10⁻⁷ cm²/s, which were better than those respectively obtained by compressed sensing and asymmetrical reconstructions and the low-resolution scheme. The model-based approach performed better than the fewer-direction case in terms of mean Δθ and RMS ΔFA (4.93 ± 0.12° and 4.35 ± 0.01 × 10⁻²) but not RMS ΔMD (0.57 ± 0.03 × 10⁻⁷ cm²/s). Similarly, at R = 4, the proposed scheme outperformed the compressed sensing and asymmetrical reconstructions and, again, the low-resolution scheme and the fewer-direction scheme in terms of mean Δθ and RMS ΔFA (8.89 ± 0.14° and 7.22 ± 0.03 × 10⁻²) but not RMS ΔMD (0.89 ± 0.05 × 10⁻⁷ cm²/s).

Table 1.

Performance of DTI acceleration schemes in terms of fiber orientation, FA, and MD errors for an acceleration factor R = 2.

Metric		Mean Δθ	RMS ΔFA	RMS ΔMD
Scheme		(deg)	(10−2)	(10−7 cm2/s)
Model-Based		4.11 ± 0.05	3.22 ± 0.07	1.09 ± 0.01
Compressed Sensing		4.81 ± 0.06	3.98 ± 0.06	1.18 ± 0.01
Asymmetrical Sampling		4.77 ± 0.07	4.12 ± 0.07	3.58 ± 0.03
Low Resolution		4.83 ± 0.06	3.98 ± 0.05	1.88 ± 0.01
Fewer Directions		4.93 ± 0.12	4.35 ± 0.01	0.57 ± 0.03

Entries are mean ± SEM for the 10 test datasets examined.

Table 2.

Performance of DTI acceleration schemes in terms of fiber orientation, FA and MD errors for an acceleration factor R = 4.

Metric		Mean Δθ	RMS ΔFA	RMS ΔMD
Scheme		(deg)	(10−2)	(10−7 cm2/s)
Model-Based		6.63 ± 0.04	4.86 ± 0.07	1.90 ± 0.02
Compressed Sensing		7.74 ± 0.04	5.71 ± 0.04	2.27 ± 0.01
Asymmetrical Sampling		8.05 ± 0.08	6.00 ± 0.05	3.73 ± 0.02
Low Resolution		7.17 ± 0.04	5.43 ± 0.03	2.93 ± 0.01
Fewer Directions		8.89 ± 0.14	7.22 ± 0.03	0.89 ± 0.05

Entries are mean ± SEM for the 10 test datasets examined.

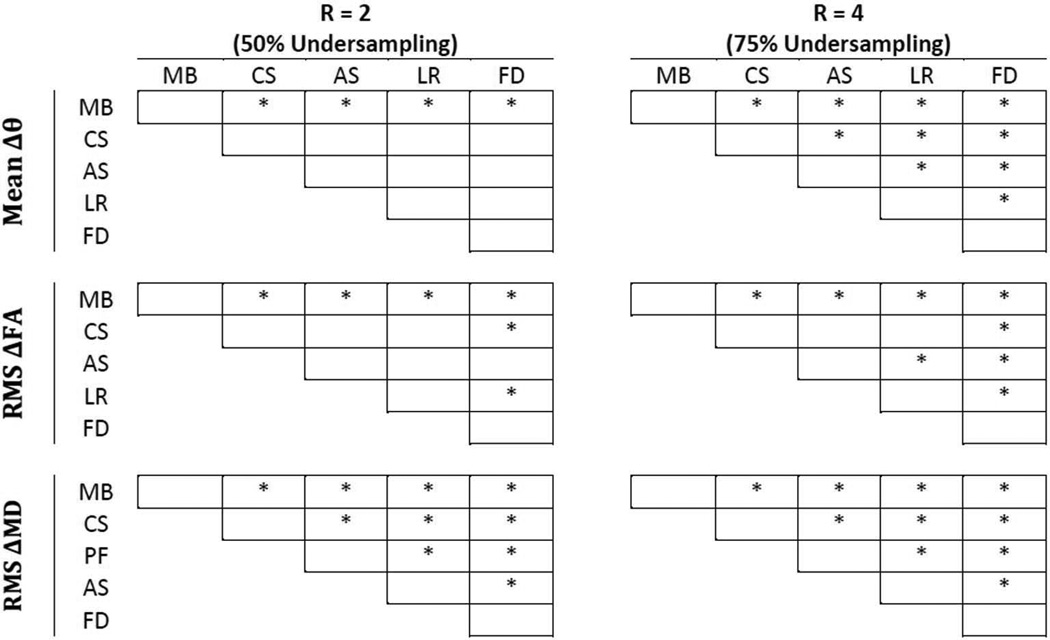
Figure 7 shows the results of the repeated-measurement ANOVA post-hoc comparisons. The results indicate that the performance of the proposed model-based compressed sensing scheme, in terms of Δθ and ΔFA, was significantly better than any of the other reconstruction or control methods. Moreover, between the two control schemes, lowering the scan resolution performs significantly better, in terms of mean Δθ and RMS ΔFA, than reducing the number of diffusion encoding directions in all cases except for mean Δθ at R = 2. Again, this may be due to the noise-smoothing effect of lowering the scan resolution. Nevertheless, the results point out that, for a given total scan time, more relevant DTI information was captured by the proposed model-based compressed sensing scheme than by realizing the acquisition acceleration via reducing the scan resolution or the number of diffusion encoding directions.

Figure 7.

Results of pair-wise, post hoc analysis of the five DTI acceleration schemes from Tables 1 and 2. Asterisks denote a significant difference between the pairs, which was determined by P <0.005 for each post hoc comparison by Bonferroni criterion. MB = model-based, CS = compressed sensing, AS = asymmetrical sampling, LR = low resolution and FD = fewer directions. The model based approach was shown to be statistically different than the other four acceleration approaches.

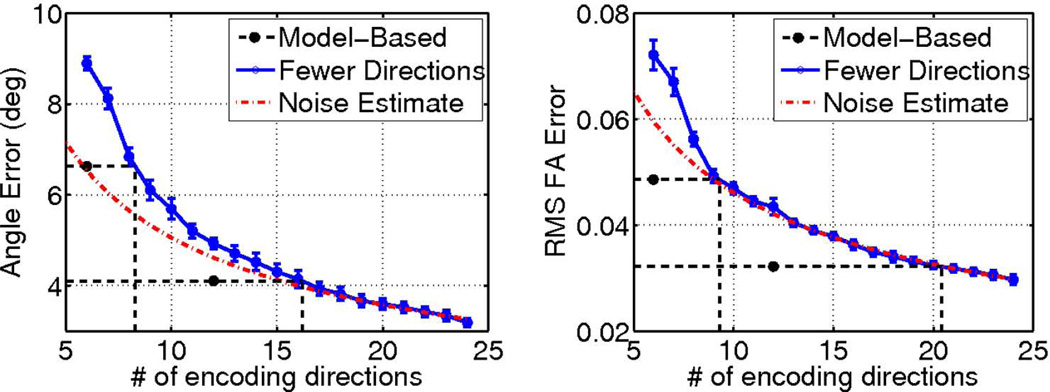
Results of the diffusion encoding gradient direction number and equivalent model-based reconstructed DTI experiment analysis are illustrated in Fig. 8, from which several observations can be made. First, in general and as expected, the number of diffusion encoding directions was inversely proportional to the error. Second, as the number of diffusion encoding directions was reduced from 24, ΔFA closely follows the performance of a noise-dominated DTI experiment where the RMS ΔFA error metric was proportional to ${(\sqrt{N})}^{-1}$. However, mean Δθ deviates more from the ${(\sqrt{N})}^{-1}$ curve, suggesting that the accuracy of the diffusion tensor eigenvector (the fiber orientation) can easily suffer from unoptimized placements of the diffusion encoding gradient directions. Third, at low numbers of gradient directions (less than 9), both mean Δθ and RMS ΔFA dramatically depart from the noise-dominated behavior. And last, depending on the reduction factor R used and the DTI parameter being measured, the proposed model-based compressed sensing scheme can achieve performances that are equivalent to a longer DTI experiment using a higher number of gradient directions. Specifically, instead of a DTI experiment using fully sampled diffusion-weighted images encoded in 12 gradient directions, using a nominal R = 2 to encode in 24 gradient directions in the same acquisition time, the proposed scheme would produce equivalent fiber orientation accuracy that is otherwise achievable by a longer DTI scan using 16 gradient directions. In the case of FA mapping, the accuracy is equivalent to using 20 gradient directions. Similarly, instead of a 6-direction fully-sampled DTI acquisition, using a nominal R = 4 to encode in 24 gradient directions, the proposed model-based approach would produce equivalent fiber orientation and FA mapping accuracy of 8 and 9-direction fully-sampled DTI experiments, respectively.

Figure 8.

DTI fiber orientation, left, and FA, right, measurement errors plotted as a function of the scan time in terms of the number of fully-sampled diffusion scans included in the dataset. The dash dotted lines represent the $1/\sqrt{\mathrm{N}}$ dependence of the errors based on the 24-direction case. The performances of the proposed model based approach are plotted at their equivalent scan times, and are extrapolated (dotted lines) to determine the number of fully-encoded diffusion weighted images needed to achieve the same measurement accuracy.

Discussion

The results from the present study show that the proposed model-based compressed sensing approach for DTI was generally more accurate and produces less blurring than spatial TV compressed sensing and iterative asymmetrical reconstruction methods. Also, the proposed method was better for fiber orientation and FA estimation than either the lower-resolution or fewer-direction control experiments of equal scan time, as seen in Fig. 6. These trends are shown quantitatively in Table 1 and 2, and are statistically significant (Fig. 7). Combined, these results demonstrate the validity of the proposed approach for accelerating DTI, obtaining more accurate DTI, or a combination of both.

One possible exception to the relative performance of the proposed scheme was in the ΔMD metric when compared to the fewer-direction control case, where the deviation of the former was about twice that of the latter (1.09×10⁻⁷ vs. 0.57×10⁻⁷ cm²/s, for R=2). It is noted that both ΔMD values represent only 1–2% deviation from the actual MD value for the entire specimen (0.58×10⁻⁵ cm²/s). In contrast, the percentages of ΔFA values of the same schemes (3.22×10⁻² and 4.35×10⁻²) were an order of magnitude larger, or about 15% of the whole-specimen FA (0.26). Moreover, unlike all other schemes examined, the fewer-direction scheme was based on datasets that were unaltered image subsets of the gold-standard. The overlap of image data would have made not only the ΔMD error but also the ΔFA error artificially lower than its true value, but the effect was less apparent because of the larger error associated with ΔFA. Combined, the observed ΔMDs for the fewer-direction control scheme as seen in Fig. 5 and 6 and Tables 1 and 2 were likely artificial underestimations of already low deviation values.

The data undersampling and scan time savings afforded by the model-based reconstruction can be exploited to include more DTI diffusion encoding gradient directions. Typically DTI employing more encoding directions is better than simply signal averaging in the same directions, especially when the number of directions used is relatively low (44). The proposed compressed sensing technique in effect allows more DTI encoding directions to be used without requiring a proportional increase in the scan time. A second factor that contributed to the performance of the proposed approach was in its use of model-based reconstruction, where fewer parameters were involved in the estimation. When the model-based DTI estimation was applied to the non-undersampled test datasets (data not shown), the mean Δθ and RMS ΔFA performance metrics improved from 3.23° and 3.01×10⁻² to 2.77° and 2.48×10⁻², respectively. Although spatial smoothing, such as in the case of lower-resolution scans, can produce artificially improved metrics, it is unlikely that the model-based compressed sensing method added smoothing, since a very low weighting factor α = 0.00025 was used for the spatial TV constraint in Eq. [7]. As well, in Fig. 4, the model-based result contained little or no evidence of blurring.

Practical implications of the current work for designing DTI acquisition schemes can be extrapolated from the results summarized in Fig. 8. With either R = 2 or 4 undersampling, the proposed approach was equivalent to fully-sampled DTI scans using 1.33 (8/6 for R = 4 or 16/12 for R = 2) times more encoding directions, in terms of the required scan time and the performance in fiber orientation mapping. For FA mapping, the equivalence factors were even greater, 1.5 (or 9/6) and 1.67 (or 20/12) at R = 4 and R = 2, respectively. On the one hand, for acquisitions designed to improve the accuracy of DTI measurements for given scan times, these factors readily provide estimates of the improvements that can be practically realized. On the other hand, for experiments aimed at shortening the scan time while preserving the measurement accuracy, these factors provide a basis to reduce the DTI scan time. For example, to measure FA, a fully sampled DTI scan using 20 encoding directions can be replaced with one that uses 24 directions with R = 2 compressed sensing, which could be obtained in only 62% of the required scan time (including the b0 scan).

It should be noted that the acquisition efficiency improvement factors were determined in the current work for the particular 3D spin echo DTI experiment chosen. Although improvements are also expected when the proposed approach is applied to other DTI studies, the specific gains will necessarily depend on the nature and settings of the experiments, including but not limited to the sample being imaged, pulse sequence and the diffusion encoding gradient direction set used. Moreover, improvements in the implementation of the reconstruction framework may lead to further performance gain. For example, in the current study the phase term, ϕ_n in Eq. [5], was estimated based on lowpass-filtered central k-space data. When phase maps were obtained from fully-sampled k-space data (results not shown), which represent idealized estimates of ϕ_n, the performance metrics mean Δθ, RMS ΔFA and RMS ΔMD improved by approximately 20% to 3.43 ± 0.06, 2.85 ± 0.07 × 10⁻² and 1.00 ± 0.01×10⁻⁷ cm²/s for the R = 2 case.

In this work, the proposed method was demonstrated for the case of uniform RF coil sensitivity (e.g., when imaging is performed using a single coil). The proposed approach can be easily extended for multi-coil parallel imaging (45,46) by adding a coil sensitivity term, c⃗_l, to Eq. [1] and summing over all coils, L,

$$C(\mathit{D})={\displaystyle \sum _{l=1}^L{\displaystyle \sum _{n=1}^N\left({\Vert \overrightarrow{F}({\overrightarrow{c}}_l·{\overrightarrow{m}}_n,n)-{\overrightarrow{d}}_{nl}\Vert }_2^2+\alpha TV({\tilde{m}}_n)\right)}}$$ [9]

Similarly, the model-based approach can be extended to deal with other MRI corrections, such as eddy current distortion or T2 blurring in fast spin echo or T2* blurring in echo-planar imaging (EPI), by adding these terms to the signal model in Eq. [3]. This would require acquisition of additional data to determine a T2* map, for example. Application of the model-based algorithm to EPI could increase SNR by shortening TE, but would not significantly shorten acquisition time. Although currently demonstrated only for 3D spin echo DTI experiments, the proposed model-based compressed sensing reconstruction methodology can potentially serve as a framework to improve other diffusion-based characterizations of ordered tissues such as those involving higher-order tensor representations (47,48) for resolving crossing fibers or rapid-acquisition techniques using fast spin echo (FSE), echo planar (EPI), or multi-coil parallel imaging. These extensions, which will necessarily involve additional technical considerations, are beyond the scope of the current study.

Conclusions

The present study demonstrated a model-based compressed-sensing reconstruction approach for undersampled DTI k-space data acquired using a spin echo readout. The methodology can be applied to enhance the acquisition efficiency of 3D spin echo DTI, including shortening the overall scan time, improving the measurement accuracy, or a combination of both. The performances of the proposed approach in fiber orientation, FA and mean diffusivity mapping were quantified, which serve as practical guides for applying to other DTI experiments. The model-based method was shown to outperform asymmetrical and compressed sensing reconstructions and using lower resolution or fewer diffusion directions to accelerate acquisition. Beyond 3D spin echo DTI, with additional work, the current methodology can potentially be extended to FSE or EPI acquisitions, or higher-order diffusion tensor imaging.

Appendix

The derivative of the cost function in Eq. [1] with respect to the diffusion tensor, D, is derived in this appendix. The derivative of the fidelity term

$$S(\mathit{D};\overrightarrow{\mathit{d}})={{\displaystyle \sum _{n=1}^N\Vert \overrightarrow{F}(\mathit{D},n)-{\overrightarrow{d}}_n\Vert }}_2^2$$ [10]

will be demonstrated first, modeled after the derivation presented in (39). The first step is to expand the L2-norm

$$\begin{gathered} S(\mathit{D};\overrightarrow{\mathit{d}})={\displaystyle \sum _{n=1}^N{\Vert \overrightarrow{F}(\mathit{D},n)-{\overrightarrow{d}}_n\Vert }_2^2={\displaystyle \sum _{n=1}^N{\displaystyle \sum _j(F_j(\mathit{D},n))-d_{jn})\overline{(F_j(\mathit{D},n)-d_{jn})}}} \\ ={\displaystyle \sum _{n=1}^N{\displaystyle \sum _j{F}_j(\mathit{D},n)\overline{F_j(\mathit{D},n)}+d_{jn}\overline{d_{Jn}}-d_{jn}\overline{F_j(\mathit{D},n)}-\overline{d_{Jn}}{F}_j(\mathit{D},n)}}} \end{gathered}$$ [11]

where $\overline{(\cdot )}$ is the complex conjugate. The derivative can be taken in a generalized sense for the diffusion tensor, D, at a spatial location, x⃗_a, such that

$$\begin{array}{c}\frac{\partial S(\mathit{D};\overrightarrow{\mathit{d}})}{\partial D_s({\overrightarrow{x}}_a)}={\displaystyle \sum _{n=1}^N{\displaystyle \sum _j{F}_j(\mathit{D},n)}\frac{\partial }{\partial D_s({\overrightarrow{x}}_a)}}\overline{F_j(\mathit{D},n)}+\overline{F_j(\mathit{D},n)}\frac{\partial }{\partial D_s({\overrightarrow{x}}_a)}\overline{F_j(\mathit{D},n)}-d_{jn}\frac{\partial }{\partial D_s({\overrightarrow{x}}_a)}\overline{F_j(\mathit{D},n)}-\overline{d_{jn}}\frac{\partial }{\partial D_s({\overrightarrow{x}}_a)}{F}_j(\mathit{D},n)\hfill \\ ={\displaystyle \sum _{n=1}^N{\displaystyle \sum _j(F_j(\mathit{D},n)}-d_{jn})\frac{\partial }{\partial D_s({\overrightarrow{x}}_a)}}\overline{F_j(\mathit{D},n)}+\overline{F_j(\mathit{D},n)}-\overline{d_{jn}}\frac{\partial }{\partial D_s({\overrightarrow{x}}_a)}{F}_j(\mathit{D},n)\hfill \\ ={\displaystyle \sum _{n=1}^N{\displaystyle \sum _j(F_j(\mathit{D},n)}-d_{jn})\frac{\partial }{\partial D_s({\overrightarrow{x}}_a)}}\overline{F_j(\mathit{D},n)}+\overline{(F_j(\mathit{D},n)-d_{jn})\frac{\partial }{\partial D_s({\overrightarrow{x}}_a)}\overline{F_j(\mathit{D},n)}}\hfill \\ ={\displaystyle \sum _{n=1}^N{\displaystyle \sum _{j}2\mathit{\text{Real }}\left\{(F_j(\mathit{D},n)-d_{jn})\frac{\partial }{\partial D_s({\overrightarrow{x}}_a)}\overline{F_j(\mathit{D},n)}\right\}}}\hfill \end{array}$$ [12]

Therefore, the general derivative can be found by inputting the derivative of the complex conjugate of Eq. [5] at x⃗_a

$$\begin{gathered} \frac{\partial S(\mathit{D};\overrightarrow{\mathit{d}})}{\partial D_s({\overrightarrow{x}}_a)}={\displaystyle \sum _{n=1}^N{\displaystyle \sum _{j}2\mathit{\text{Real }}\left\{(F_j(\mathit{D},n)-d_{jn})(-W_n(k_j)·b·{({\mathit{g}}_n{\mathit{g}}_n^T)}_s·I_o({\overrightarrow{x}}_a)·e^{-b{\mathit{g}}_n^T\mathit{D}({\overrightarrow{x}}_a){\mathit{g}}_n}·e^{-i{\varphi }_n({\overrightarrow{x}}_a)}·e^{i{\overrightarrow{x}}_a·{\overrightarrow{k}}_j})\right\}} \\ =-2b{\displaystyle \sum _{n=1}^N{({\mathit{g}}_n{\mathit{g}}_n^T)}_s·}{I}_o({\overrightarrow{x}}_a)·e^{-b{\mathit{g}}_n^T\mathit{D}({\overrightarrow{x}}_a){\mathit{g}}_n}·\mathit{\text{Real }}\left\{e^{-i{\varphi }_n({\overrightarrow{x}}_a)}·{\displaystyle \sum _j(F_j(\mathit{D},n)-d_{jn})}{e}^{i{\overrightarrow{x}}_a·{\overrightarrow{k}}_j}\right\}} \end{gathered}$$ [13]

Next, the derivative of the TV term, Eq. [6], is derived. The first step is to express Eq. [6] in the continuous case

$$TV(\mathit{D})={\displaystyle \iint {\displaystyle \sum _{n=1}^N|\nabla {\tilde{m}}_n|dydz=}}{\displaystyle \iint {\displaystyle \sum _{n=1}^N\sqrt{{({\tilde{m}}_n)}_y^2+{({\tilde{m}}_n)}_y^2}dydz}}$$ [14]

where

$${({\tilde{m}}_n)}_y=\frac{\partial {\tilde{m}}_n}{\partial y}$$ [15]

and m̃_n is the DTI signal intensity expressed in Eq. [3]. Next, a new function is defined by examining one spatial location, x⃗_a,

$$U({({\tilde{m}}_n({\overrightarrow{x}}_a))}_y,{({\tilde{m}}_n({\overrightarrow{x}}_a))}_z)={\displaystyle \sum _{n=1}^N\sqrt{{({\tilde{m}}_n({\overrightarrow{x}}_a))}_y^2+{({\tilde{m}}_n({\overrightarrow{x}}_a))}_z^2}}$$ [16]

The Euler-Lagrange equation states that

$$\begin{array}{cc}\hfill \frac{\partial U}{\partial {\tilde{m}}_n({\overrightarrow{x}}_a)}-\frac{\partial }{\partial y}\frac{\partial U}{\partial {({\tilde{m}}_n({\overrightarrow{x}}_a))}_y}-\frac{\partial }{\partial z}\frac{\partial U}{\partial {({\tilde{m}}_n({\overrightarrow{x}}_a))}_z}=& 0\hfill \\ \hfill \frac{\partial U}{\partial {\tilde{m}}_n({\overrightarrow{x}}_a)}=& \frac{\partial }{\partial y}\frac{\partial U}{\partial {({\tilde{m}}_n({\overrightarrow{x}}_a))}_y}-\frac{\partial }{\partial z}\frac{\partial U}{\partial {({\tilde{m}}_n({\overrightarrow{x}}_a))}_z}\hfill \end{array}$$ [17]

The derivative with respect to the diffusion tensor parameters at x⃗_a in a general sense is desired, therefore, the derivative with respect to D_s(x⃗_a) can be found using the chain rule on the above expression

$$\begin{array}{cc}\hfill \frac{\partial U}{\partial {\tilde{m}}_n({\overrightarrow{x}}_a)}\frac{\partial {\tilde{m}}_n({\overrightarrow{x}}_a)}{\partial D_s({\overrightarrow{x}}_a)}=& \left(\frac{\partial }{\partial y}\frac{\partial U}{\partial {({\tilde{m}}_n({\overrightarrow{x}}_a))}_y}+\frac{\partial }{\partial z}\frac{\partial U}{\partial {({\tilde{m}}_n({\overrightarrow{x}}_a))}_z}\right)\frac{\partial {\tilde{m}}_n({\overrightarrow{x}}_a)}{\partial D_s({\overrightarrow{x}}_a)}\hfill \\ \hfill \frac{\partial U}{\partial D_s({\overrightarrow{x}}_a)}=& \left(\frac{\partial }{\partial y}\frac{\partial U}{\partial {({\tilde{m}}_n({\overrightarrow{x}}_a))}_y}+\frac{\partial }{\partial z}\frac{\partial U}{\partial {({\tilde{m}}_n({\overrightarrow{x}}_a))}_z}\right)\frac{\partial {\tilde{m}}_n({\overrightarrow{x}}_a)}{\partial D_s({\overrightarrow{x}}_a)}\hfill \end{array}$$ [18]

The previous expression can be found to be

$$\frac{\partial U}{\partial D_s({\overrightarrow{x}}_a)}={\displaystyle \sum _{n=1}^N\left(\frac{\partial }{\partial y}\frac{{({\tilde{m}}_n({\overrightarrow{x}}_a))}_y}{\sqrt{{({\tilde{m}}_n({\overrightarrow{x}}_a))}_y^2+{({\tilde{m}}_n({\overrightarrow{x}}_a))}_z^2}}+\frac{\partial }{\partial z}\frac{{({\tilde{m}}_n({\overrightarrow{x}}_a))}_z}{\sqrt{{({\tilde{m}}_n({\overrightarrow{x}}_a))}_y^2+{({\tilde{m}}_n({\overrightarrow{x}}_a))}_z^2}}\right)}(-b{({\mathit{g}}_n{\mathit{g}}_n^T)}_s{\tilde{m}}_n({\overrightarrow{x}}_a))$$ [19]

Therefore, the generalized derivative of the total variation term can be expressed as

$$\frac{\partial TV(\mathit{D})}{\partial D_s({\overrightarrow{x}}_a)}=-{\displaystyle \sum _{n=1}^{N}b{({\mathit{g}}_n{\mathit{g}}_n^T)}_s{\tilde{m}}_n({\overrightarrow{x}}_a)\left(\frac{\partial }{\partial y}\frac{{({\tilde{m}}_n({\overrightarrow{x}}_a))}_y}{\sqrt{{({\tilde{m}}_n({\overrightarrow{x}}_a))}_y^2+{({\tilde{m}}_n({\overrightarrow{x}}_a))}_z^2+{\beta }^2}}+\frac{\partial }{\partial z}\frac{{({\tilde{m}}_n({\overrightarrow{x}}_a))}_z}{\sqrt{{({\tilde{m}}_n({\overrightarrow{x}}_a))}_y^2+{({\tilde{m}}_n({\overrightarrow{x}}_a))}_z^2}+{\beta }^2}\right)}$$ [20]

where β is introduced to avoid singularities in the calculation. The product rule needs to be carried out on the above expression to be implemented in the discrete case since m̃_n is a function of I_o (x,y,z) and D(x,y,z). This is not shown explicitly. The overall expression for the derivative of the cost function can be found by combining the results of Eq. [13] and [20]

$$\frac{\partial C(\mathit{D})}{\partial D_s}={\displaystyle \sum _{n=1}^N-2b}{({\mathit{g}}_n{\mathit{g}}_n^T)}_s{I}_o{e}^{-b{\mathit{g}}_n^T\mathit{D}{\mathit{g}}_n}\mathit{\text{Real }}\left\{e^{-i{\varphi }_n}{\displaystyle \sum _j(F_j(\mathit{D},n)-d_{jn})e^{i\overrightarrow{x}{\overrightarrow{k}}_j}}\right\}-\alpha b{({\mathit{g}}_n{\mathit{g}}_n^T)}_s{\tilde{m}}_n\left(\frac{\partial }{\partial y}\left(\frac{{({\tilde{m}}_n)}_y}{\sqrt{{({\tilde{m}}_n)}_y^2+{({\tilde{m}}_n)}_z^2+{\beta }^2}}\right)+\frac{\partial }{\partial z}\left(\frac{{({\tilde{m}}_n)}_z}{\sqrt{{({\tilde{m}}_n)}_y^2+{({\tilde{m}}_n)}_z^2+{\beta }^2}}\right)\right)$$ [21]