A single word in a population of words

Abstract

Carey and Bartlett introduced a new method for studying lexical development, one of presenting the child with a word and a single context of use and asking what was learned from that one encounter. They also reported a then new finding: By using what they already knew about previously learned words, young children could narrow the range of possibilities for likely meanings in a single encounter. This papers honors that original contribution and the robust literature and set of phenomena it generated by considering how newly learned categories must fit into a population of already learned categories. This paper presents an overview of Packing Theory, a formal geometrical analysis of how local interactions in a large population of categories create a global structure of feature relevance such that near categories in the population of have similar generalization patterns. The implications of these ideas for learning from a single encounter, their relation to the evidence of artificial word learning studies, and new predictions are discussed.

Carey and Bartlett’s (1978) paper “Acquiring a single new word” (along with a closely related paper by Katz, Baker & McNamara, 1974) changed research on lexical development. The paper introduced the method of teaching the child a single new word used to refer to a single referent, and then examining –through generalization tests –what the child had learned from that single encounter. In this way, Carey and Bartlett brought the moment of word learning into the laboratory and this method (and the many variants it spawned) has over the past 30 years led to remarkable discoveries and insights, about how word learning grows on itself (Smith, 1995), and about the conceptual (Booth & Waxman, 2002), linguistic (Landau, Smith, & Jones 1992), social (Bloom, 2000; Tomasello, 1992), and pragmatic (Tomasello & Akhtar, 1995) knowledge that children bring to lexical development. Forms of this task, teaching a child a novel word and asking what is learned from that encounter, are now also used to measure cross-linguistic differences (Imai & Gentner, 1997; Yoshida & Smith, 2003), to diagnose atypical developmental patterns (Jones, 2003), and to assess the effectiveness of interventions designed to enhance early word learning (Gershkoff-Stowe & Smith, 2004).

In honor of this seminal paper and all the advances that it spurred, we return to one of the issues that motivated Carey and Bartlett’s specific word-learning experiment: how a newly learned word must “fit in” with the already learned words in that domain. Carey and Bartlett’s experiment was about the learning of color words, and how the child might use already known color words to narrow in on the meaning of a novel label. The learning moment in their naturalistic approach consisted of the experimenter pointing to (for example) an olive-colored tray amidst other trays, and asking the child to “Bring me the chromium tray, not the blue one, the chromium one.” From this single encounter, children only sometimes were able to choose a “chromium” (that is, olive colored) tray when later asked. But that one encounter clearly did result in that lasted: the children to appear to have learned, for example, that “chromium” referred to a color and, more specifically, to an odd color of the murky desaturated kind. In brief, in the context of color words and color categories already known, a single encounter with the word was enough to narrow the search space and limit the range of its extension. Whatever the precise meaning of “chromium” is, it has to “fit in” with the known color words. By having to fit words into an already forming lexicon, the structure of already learned words provides useable information about the kinds of words yet to be learned.

This paper is about one possible mechanism through which “fitting in” a semantic space may yield more rapid honing in on the possible extension of a word. The proposed mechanism is a general one in two senses, First, it is based on general processes relevant to any form of category learning: the discrimination of instances that belong in different categories and the inclusion of experienced instances within a category. Second, a formal analytic proof (Hidaka & Smith, 2008, 2009) shows that –within a space of many known instances and categories -- the joint optimization of discrimination and inclusion is sufficient to create a space of lexical categories that constrains the possible extensions of a new category as it “fits in” to that space. One goal of this paper is to bring the insights of that mathematical analysis to researchers of children’s word learning.

The organization of the paper is as follows: We begin with a brief review of the literature on what children seem to know from a single encounter with a noun used to name one thing. These findings are direct descendants of those reported in the Carey and Bartlett paper. We then present a conceptual overview of Packing Theory, a geometrical theory about how categories must “fit in” to other nearby categories and how the joint optimization of discrimination and inclusion create a higher order structure, or domains of lexical categories. The theory is an extension of exemplar-based accounts of category learning (see, especially, Ashby and Townsend’s, 1986, Generalized Recognition Theory). The new contributions of the mathematical proofs that comprise Packing Theory is the idea that given simply the experienced instances (the extensions) of a system of categories and the optimization of discrimination and inclusion, a highly organized semantic structure emerges. This theoretical ideas, even without considering the formalizations, provide potentially useful insights into early word learning, insights that return us to Carey and Bartlett’s original point.

Novel noun generalizations and categories in a feature space

When 2- and 3- year old children are given a novel never-seen-before thing, told its name (“This is a dax”), and asked what other things have that name, they systematically extend the name to new instances in ways that seem right to adults. Moreover, they generalize names for different kinds of things in different ways which indicates both that they know there are different kinds of things and also that they know something about the kinds of similarities that are relevant to those different kinds. Particularly germane to this paper are findings showing that children extend the names for things with features typical of animates (e.g., eyes) by multiple similarities, for things with features typical of artifacts (e.g., solid and angular shapes) by shape, and for things with features typical of substances (e.g., nonsolid, rounded flat shape) by material (Jones, Smith & Landau, 1991; Kobayashi, 1998; Jones & Smith, 2002; Yoshida & Smith, 2001; Markman, 1989 Booth and Waxman, 2002; Gathercole & Min, 1997; Imai & Gentner, 1997; Landau, Smith & Jones, 1988, 1992, 1998; Soja, Carey, & Spelke, 1991;. see also, Gelman & Coley, 1991; Keil, 1994). Considerable research shows that the systematicity of these generalizations increase with vocabulary growth (Samuelson & Smith, 1999; Gershkoff-Stoew & Smith, 2004) and that they are modulated (in smart ways) by linguistic and task context (Imai & Gentner, 1997; Landau, B., Smith, L. B., & Jones, S., 1992; Yoshida & Smith, 2003).

Packing Theory (as currently formulated, Hidaka & Smith, 2008,2009) my provide new insights into a some aspects of these results: How children use the perceptual features of things, such as having eyes, being angular, being solid to select other features such as similarity in shape or in texture, thereby enabling children to systematically generalize names for different kinds of things in different ways. The applilcability of Packing Theory to this developmental phenomenon begins with the fact that children’s novel noun generalizations for eyed and non-eyed things and solid and nonsolid things appear to directly reflect the feature distributions within the noun categories that children typically learn early. A number of studies that have asked adults to characterize the features and similarities relevant to specific early-learned basic-level categories (Samuelson and Smith, 1999; Colunga & Smith, 2005; 2008; Smith, Colunga and Yoshida, 2003; also Rosch, 1976) show that (by adult judgment), many basic-level artifact categories, for example “chair”, consist of instances that vary greatly in color and material but less so in shape. In contrast, basic-level substance categories (e.g., cheese) consist of instances that vary widely in shape but less so in material and color. Finally, many basic-level animal categories (by adult judgment) are well-organized by many overlapping similarities, such that within a basic-level animal category (e.g., cat) instances are similar in many properties including shape, texture, and color. These regularities mean that the similarities and differences among the instances of any category, including novel ones, can be predicted by the presence of certain perceptual properties: Being solid, rigid, and constructed in shape predicts with-in category similarities in shape; being nonsolid, or flat, or simply shaped predicts with-in category similarities in material; having eyes or feet or a body shape predicts a consortium of within category similarities across several dimensions.

This state of affairs can be theoretically represented in terms of instances and categories in a feature space as illustrated in Figure 1. The real feature space, of course, would be a high-dimensional one, but for ease of thinking about the problem, we show in Figure 1 a 2-dimensional hypothetical space (perhaps a 2-dimensional projection of the higher dimensional space). The two theoretical dimensions are shape (itself a complex dimension, see Pereira & Smith, 2009) and surface properties (texture/material). Within this space, each possible instance is a point, the combination of a particular texture-material and a particular shape. The distribution of experienced instances for individual categories, that is, the frequencies of experienced instances at each feature combination in the space, is represented in the figure by ellipses and shading. A narrow distribution in one direction suggests the increased importance of that particular feature to category membership, that is, that feature varies little within that category.

Figure 1.

A schematic illustration of a smooth space of noun categories. Each ellipsis indicates equal-likelihood contours of instance membership in the category. Generalization patterns (shapes of ellipses) change along with their location in the feature space with near categories having similar generalization patterns.

The figure illustrates a particular hypothesis: that there is a correlation between the location of a category in the feature space and its generalization pattern such that nearby categories are generalized in similar ways and there is a gradient in these generalization patterns across the feature space. The figure specifically suggests that instances with highly constructed shapes are in categories that minimize within-category variation in shape, that things with animal-like shapes are in categories that minimize variation in both texture/material and shape, and that things that are simply shaped are in categories that minimize variation in texture/material. Although there is reason to believe that this description is roughly right (Colunga & Smith, 2005, 2008), there is also a much more general idea here: This more general hypothesis is the feature space of categories in general, like that in Figure 1, is smooth: nearby categories have similar generalization patterns and far categories have dissimilar ones, and there is a gradient of changing category organizations across the feature space. This conceptualization of the space of categories has potentially powerful consequences for explaining 2- and 3- year olds’ ability to systematically generalize a category from a single instance: If near categories have similar generalization patterns then the location of a single instance in the feature space will provide information about the likely distribution of the other instances of that category.

Why would a space of categories be smooth?

Packing Theory (Hidaka & Smith, 2008, 2009) is an answer to the question of why categories that are near each other in some feature space might have similar generalization patterns. The first insight is that this does not have to be the case, but is likely to be the case under some simple geometric constraints. Figure 2 shows three different sets of categories in their respective feature spaces. As in figure 1, the ellipses indicate the probabilistic boundary of instances included in the category. Figure 2a shows a smooth geometry like that proposed by Packing Theory; near categories have similar patterns of feature distributions and far categories have different ones. Figure 2b shows another possible distribution of categories in the feature space; each category has its own organization unrelated to those of near neighbors. The two spaces of categories illustrated in Figure 2a and b are alike in that in both of these spaces, there is little overlap at the edges among instances that might belong in the two categories. That is, in both of these cases, the categories discriminate among instances. However, the categories in 2b are not smooth in that near categories have different generalization patterns. Moreover, this structure leads to gaps in the space, empty regions with no categories. The categories in Figure 2b could be pushed close together to lessen the gaps. But given the nonsmooth structure, there would always be some gaps, unless the categories are pushed so close that they overlap as in Figure 2c. Figure 2c, then, shows a space of categories with no gaps but also one in which individual categories do not discriminate well among instances.

Figure 2.

A cartoon of populations of categories in a feature space illustrating three different ways those might categories might fit into the space. Each ellipsis indicates equal-likelihood contour of category. The broken enclosure indicates the space of instances to be categorized.

The main point is that if the instance distributions of neighboring categories are dissimilar –if, for example, shape can vary widely in one category but is tightly constrained in the adjacent category – then there either have to be gaps in the space (possible instances that do not belong to any category) or categories have to overlap (some instances will have to fall into more than one category.). Thus, we have a first answer to where the smoothness of categories in the feature space might come from: a feature space will be smooth –nearby categories will have similar distributions of instances in that space – if the space of categories is biased against both gaps and overlapping distributions.

Joint optimization of discrimination and inclusion

Packing Theory (Hidaka & Smith, 2008,under review) is a formal proof showing that the joint optimization of discrimination (minimizing the overlap of categories) and inclusion (minimizing gaps) leads to a smooth space of categories. Here we consider Packing Theory at a conceptual level with respect to the simple case of two categories as illustrated in Figure 3. Each category has a distribution of experienced instances for some particular learner; these are indicated by the squares for one category and the crosses for the other. It is assumed that the learner is more certain about some instances than others because of the repeated experiences of some (or the ambiguity of the context in which an instance is encountered). Thus, for the learner, the probability that each of these instances is in the category varies. If each category is considered alone, the extension of the category might be well described in terms of its central tendency and its estimated distribution (or covariance of the features over the instances). This is illustrated by the solid lines that indicate the confidence intervals for instance inclusion around each category.

Figure 3.

Two categories and their instances on two-dimensional feature space. The dots and crosses show the respective instances of the two categories. The broken and solid ellipses indicate equal-likelihood contours with and without consideration to category discrimination respectively.

Packing Theory proposes that the learner’s assessment of the probability that an instance (or possible instance as a location in the feature space) is a member of a category is determined not just by the experienced frequency of that one instance or of similar instances in that category, but also by the experienced frequency of nearby instances in neighboring categories. The assumption is that there is a local competition among categories for instances. This kind of competitive process is common to many psychological theories (Huttenlocher et al., 2007; Ashby & Valentin, 2005, Kohonen, 1995). Packing Theory also proposes that because of this competition, the learner decreases the probability that an instance is in a category in relation to its ambiguity with respect to neighboring categories (see Hidaka & Smith, 2008, 2009, for the formal specification of this joint optimization of inclusion and discrimination). The local competition results in an estimated category distribution that distorts the experienced distribution as shown by the dotted lines: there is a shift in the psychological distribution of instances that optimizes inclusion of experienced instances and the discrimination of instances associated with different categories. This shift effectively makes the generalization patterns for the two categories more aligned and thus more similar than when the experienced instances for each category are considered alone.

Adults know thousands of categories; 3-year-olds year know many hundreds. It is not intuitive to describe the whole structure formed by dozens, hundreds, and thousands of categories when they locally interact across all categories at once. N categories have N(N-1)/2 possible pairs of categories in local competition. Moreover, two categories that compete with each other in a local region in a feature space influence the whole structure by chains of category interactions. The mathematical formulation of Packing theory considers the dynamics of category inclusion and discrimination in a general N-category case and specifies the stable optimal state (see Hidaka & Smith, 2008, 2009, for the formal analysis). The key fact is that the result is a space of categories much like that in Figure 1; there is a global gradient of changing alignments of the generalization pattern such that nearer categories are more similar in their alignment but farther categories are less similar in their distribution of instances in the feature space.

Packing Theory is a general theory, about any distribution of many instances in many categories across any set of features and dimensions. However, the formal analyses show that for the bias inherent in the joint optimization of discrimination and inclusion to play out in aligning categories in the feature space, there need to be relatively many categories (crowding) and relatively many instances in these categories. Interesting empirical predictions follow directly from this idea. First, in the space of all categories, there might well be crowded dense regions and also sparse regions. Smoothness should characterize the dense regions, not the sparse ones. Thus, adults and children should show the ability to infer a roughly right category from a single instance in dense but not sparse regions of the feature space of categories. Further, crowding should emerge with development, with the learning of a increasing number of categories and an increasing number of instances of those categories. Making precise predictions might seem to depend on knowing more about the dimensions and feature space that contemporary evidence provides. This is partially true as crowding is more likely in a lower than in a higher dimensional space, and we do not know the dimensionality of the feature space for human category judgments. However, the specific dimensions selected by the theorist (or learner) do not matter since the optimization depends only on distance relations in the space (and thus on the number of orthogonal, that is uncorrelated, dimensions but not on any assumptions about what orthogonal directions in that space constitute the dimensions). Further, the predictions are general; along any direction in that space (a direction that might consist of joint changes in two psychological dimensions, angularity and rigidity, for example), one should see near categories having more similar generalization patterns and far categories having more different generalization patterns. and will be the same one measured the density of categories in different region If this h

Are common noun categories smooth?

Figure 1 and Packing Theory are hypotheses about the structure of populations of categories (and the processes that create structure). The formal proof that underlies Packing Theory shows that the assumed processes do create a smooth space of categories (and also specify the limits of the theory with respect to the density of categories in the space, Hidaka, under review). But Packing Theory does not show that the space of human categories is smooth in the way proposed, nor, if it is, that that smoothness results from the joint optimization of inclusion and discrimination. Determining whether the space of common noun categories is smooth is thus a critical first step for determining the relevance of this form of “fitting in” to lexical learning. That is, Packing Theory and the idea of a smooth space of categories is at present a candidate explanation about how “fitting” a new category into a population of already learned categories constrains learning. As we discuss later, this candidate explanation also offers new, and empirically testable hypotheses, about some perhaps under-examined aspects of early noun learning, predictions we will consider subsequently. Here, we consider initial psychological evidence that there are at least some regions in the feature space feature space of early-learned noun categories that are smooth. The key empirical question for determining whether natural noun categories have a smooth structure is whether there is a gradient of instance distribution patterns of categories as a function of the similarity of those instances on some set of features. Such a gradient implies correlation between the location of a category in the feature space and its generalization gradient.

Colunga and Smith (2005; 2008) found evidence for a gradient of generalization patterns within one local region of feature space of early-learned noun categories. Figure 4 presents the rationale under the conceptualization of Packing Theory (which was nnot the specific motivation for their studies). The cube represents some large hyperspace of categories on many dimensions and features. Within that space we know from previous studies of adult judgments of category structure and from children’s noun generalizations (e.g., Soja et al, 1991; Samuelson & Smith, 1999; Colunga & Smith, 2005) that solid, rigid and constructed things, things like chairs and tables and shovels) are in categories in which instances tend to be similar in shape but different in other properties. This category generalization pattern is represented by the ellipses in the bottom left corner; these are narrow in one direction (constrained in their shape variability) but broad in other directions (varying more broadly in other properties such as color or texture). We also know from previous studies of adult judgments of category structure and from children’s novel noun generalizations (e.g., Soja et al, 1991; Samuelson & Smith, 1999; Colunga & Smith, 2005), that nonsolid, nonrigid things with accidental shapes (things like sand, powder, and water) tend to be in categories well organized by material. This category generalization pattern is represented by the ellipses in the upper right corner of the hyperspace; these are broad in one direction (wide variation in shape) but narrow in other directions (constrained in material and texture).

Figure 4.

A hyperspace of categories. The elipses represent categories with particular. generalization patterns (constrained in some directions but allowing variability in othes). Packing Theory predicts that near categories in the space will have similar generalization patterns and that there should be a smooth gradient of changing category generalizations as one moves in any direction in the space. Past research shows that categories of solid, rigid and constructed things are generalized by shape but categories of nonsolid, nonrigid, and accidentally shaped things are generalized by material. Packing Theory predicts a graded transition in feature space between these two kinds of category organizations.

The question concerns the categories in between these two regions. Do such categories exist, and if so, what is their pattern of generalization? Categories in between do exist, though they be sparser. Colunga and Smith (2005, 2008) examined adult judgments of 300 common noun categories. Adults were asked to judge objects on various properties of constructedness, rigidity, and solidity as well as to judge the similarity of instances within each category on shape, material and color. They found strong correlations between the degree to which these rigidity, solidity and shape properties characterized category instances categories and the dimensions adults say were important for determining membership in the categories. This is exactly what would be expected by Packing Theory, a smooth and incremental gradient generalization patterns from one region of the space to another.

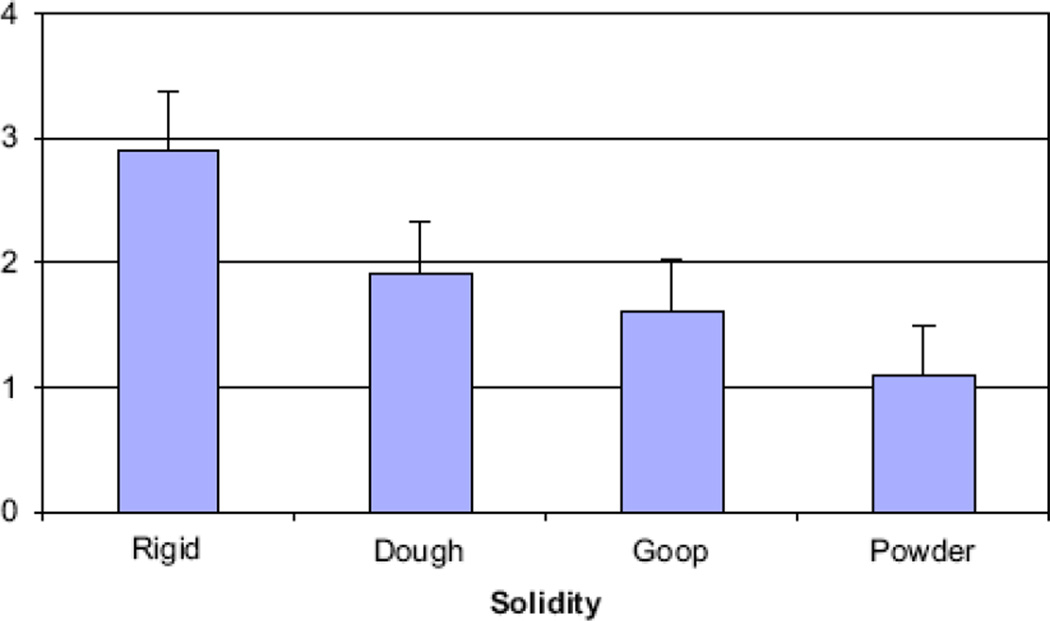
Studies of children’s novel noun generalizations also provide support for a gradient of generalization patterns in the feature space (Colunga & Smith, 2005; 2008; also Sandhofer & Smith, 1999; Yoshida & Smith, 2003). In one experiment (Colunga & Smith, 2008), 2 ½ year old children participated in a novel noun generalization task using exemplars at four degrees of solidity: (1) rigid -- does not change shape when pressed, for example a brick, (2) dough -- changes shape when pressed, but doesn’t take shape of its container, for example playdough, (3) “goop” -- viscous material that flows when touched and takes shape of its container and is contiguous, for example pudding, (4) powder---takes shape of its container, but is not contiguous, for example rice. All the shapes and materials used in the experiment were novel to the children. Each child saw one exemplar at each of the four levels of solidity and was told its unique name, “Look at the dax.” Then in a 2-choice generalization task, the child was asked (“Where is the dax here?” to choose between a novel object that matched the exemplar in material or in shape. Both choice objects were at the same degree of solidity as the exemplar. Figure 5 shows the results: children’s attention to shape and material depended –in a graded way -- on the degree of solidity—on average, the more solid the exemplar, the more shape match choices, the more non-solid the exemplar and the more material match choices were made. These results fit the correlation between judgments of solidity and relevance of shape found in adult descriptions of natural categories. They are also consistent with Packing Theory’s predictions about the smoothness of the space of categories with respect to the feature distribution of instances in the categories.

Figure 5.

Mean proportion of shape choices by 3 year olds in a novel noun generalization task as a function of the solidity and rigidity of the shape (Colunga & Smith, 2008).

Hidaka and Smith (2008, 2009) provide more direct evidence on the smoothness of basic categories. They also used adult judgments of the properties of instances of categories to examine the geometric structure of the feature space. Their analyses focused on the key mathematical relation predicted by Packing Theory: a correlation between the location of a category in the feature space and the distribution of instances. The location of a category is given by the mean of its features for all the known instances. The distribution of instances may be measured by the covariance matrix of the features across those instances. To test this, Hidaka and Smith collected adult judgments of the features relevant to early categories. Their approach differed in an important way from that of Colunga and Smith. Colunga and Smith’s analyses were based on adults judgments along dimensions already believed to be relevant to these categories – shape, material, rigidity, nonsolidity, and so forth. The similar generalization patterns observed for near categories could be specific to solid versus nonsolid things and to the specific (and conceptual important) distinction between objects and substances and not be a general truth about categories anywhere in the feature space. Hidaka and Smith sought to make the more general case predicted by Packing Theory: that the location of categories in a high-dimensional feature space is correlated with their generalization pattern in that space.

Accordingly, the features examined were drawn from a broad set of polar dimensions that were unlikely to be specifically offered by anyone as particularly important to any of these categories. If Packing Theory is right, these features should nonetheless define an n-dimensional space of categories which shows some degree of smoothness: categories with instances similar to each other on these features should also show similar distributions of features across instances. More specifically, adults were asked to judge 48 early-learned basic level categories (drawn from the MCDI, Fenson et al, 1994) along 16 polar dimensions (e.g., wet-dry, noisy-quiet, weak-strong) that broadly encompass a wide range of qualities (see Osgood, 1957; Hidaka & Saiki, 2004) and that are also (by prior analyses) statistically uncorrelated (Hidaka & Saiki, 2004). Adults were given an early-learned noun, e.g., “butterfly” and asked to judge, one at a time on a 1 to 5 scale whether it as wet or dry, noisy or quiet, weak or strong, and so forth. These judgments were then used to infer the location and instance distribution of the categories in the 16-dimensional feature space. The assumption is that the mean features offered by adults will approximate the mean features of instances in the category and that the variance of adult feature judgments will reflect the variance of the instances in these categories.

To assess the smoothness of this space of categories, Hidaka & Smith (2006, 2009) examined whether the distance between any two categories in the space (as measured by the Euclidean distance of the mean feature values) was correlated with the (Euclidean) distance of the covariance patterns for the two categories. If near categories have similar patterns of instance distributions, these two measures should be correlated. Consistent with this prediction, across multiple samplings of independent pairs of categories, the distances of the means and variance patterns was strongly positive (R = 0.54). These positive correlations between the distances of central tendencies and the distances of the covariance in adult judgments provide a first indication that the space of early-learned noun categories may be smooth in the specific way proposed by Packing Theory. Critically, the features analyzed in this study were not pre-selected to particularly fit the categories and thus the observed smoothness seems unlikely to have arrived from the choice of features or a priori notions about the kind of features that are relevant for different kinds of categories. Instead, the similarity of categories on any set of features (with sufficient variance across the category) may be related to the distribution of those features across instances. As such, the results suggest that category location in a feature space and instance variability may be systematically and generally related within a geometry of categories. Categories whose instances are generally similar in terms of their mean features also exhibit similar generalization patterns.

“Fitting in” and children’s novel noun generalizations

In series of simulations, Hidaka & Smith (2008, 2009) have shown that the joint optimization of inclusion and discrimination such processes are sufficient to enable apparent one-encounter learning of a whole category. Given a set of known categories, Packing Theory can –from a single instance of an unknown category --match its actual distribution in adult judgments. These simulations also show that these estimations of an unknown category’s instance distribution from a single instance emerge given a sufficient number of known categories, a sufficient number of known instances for those categories, and sufficient density of the categories in the feature space. Exactly how to translate “sufficient” numbers of categories, numbers of instances, and density is into terms testable in children is the difficult and open question. However, at a qualitative level, Packing Theory makes clear that if this account is right, what children might learn from a first single encounter with a word will depend in subtle but important ways on exactly what they know about neighboring categories.

According to Packing Theory, the smooth structure of natural categories is due to the local interactions –inclusion and discrimination –of the instances of neighboring categories. Because these local competitions depend on the frequency distributions over known instances and the local neighborhood of known categories, there should be observable and predictable changes as children’s category knowledge “scales up” that depend on numbers of categories, numbers and diversity of instances for those categories, and the numbers and diversity of categories in particular regions of the space. Although considerable developmental work has related changes in the words children know to what they can learn from a single encounter with a word and referent, assessments of “knowing” a word have been considered only at the macro level with little attention to what exactly is known about instances or to the neighborhood density of categories. With respect to these issues, Packing Theory makes a number of interesting predictions that suggest there is much to be learned from taking this population approach.

For example, very early in noun learning, when children know very few categories, inclusion (the particular instances that have been experienced) will matter more in joint optimization than discrimination (competition among ambiguous instances at the edges). This, in turn, suggests, that at the earliest stages of learning, there may be possibly dramatic effects on children’s generalizations as a function of the specific exemplars (or number of exemplars) experienced for a category. This prediction might be tested by analyses of individual differences in children’s generalizations in novel noun learning tasks as a function of the number and ranges of specific instances that they have experienced for nearby categories. One should also see expertise differences: if a young learner is a vehicle expert and knows a particular group of categories in this local region of feature space far better than nouns in some other region, say tools, then that child should show more generalizations more aligned to neighboring categories (and more adult-like) in the vehicle region than in the tools region. If the local neighborhood matters (and not just the larger category artifacts), than such a child, for example, might show an earlier or more robust shape bias for vehicles than for tools. Alternatively, to test these ideas, one might exploit the natural ecology of children’s category learning within a culture; for example, children in the U.S. experience many more dog instances than donkey instances or that animal categories are more densely packed early than tool categories, for example. In brief, detailed studies of the numbers and diversity of known categories and instances are predicted by Packing Theory to be fertile ground for testing specific predictions about the growth of local competition among categories, smoothness, and smart novel noun generalizations.

Examining closely the changing geometry of early categories may also bring much deeper insights into gradients of feature relevance in natural category formation. The extant work on children’s knowledge about different kinds of categories has focused on what are called ontological distinctions between, for example, animates, objects and substances (e.g., Colunga & Smith, 2005; Kemp, Perfors & Tenenbaum, 2007; Imai & Gentner, 1997; Soja, Carey & Spelke, 1991). But Packing Theory suggests that there might be useable structure –smoothness – in other regions of the feature space and at other levels of granualarity, about vehicles versus tools versus dishes, for example. The packing model may also offer new insights into previous findings such as Xu & Tennebaum’s (2007) result showing narrower generalizations by young children given three exemplars but broader generalizations given one exemplar. This result (which was predicted by their hypothesis of pre-existing or innate levels in a hierarchy of categories) should, by the packing metric, depend on the local structure, density, and category overlap, of the region from which the instances are drawn. To capitalize on the insights of Packing Theory, we need better empirical evidence on how category knowledge scales up, in terms of the number and range of instances and in the crowding or sparseness of categories in feature space.

Relations to other theories

One of the most remarkable facts about children’s word learning –a fact that is known because of Carey and Bartlett’s then new method – is that children often have a pretty good (partial, but nonetheless mostly correct) idea about the extension of a whole category from a single or very few instances. Thus, a 2 ½ year old who is shown his very first tractor, perhaps a green John Deere in a corn field, is highly likely to generalize the name “tractor” from that day forward to all varieties of tractors –red ones, new ones, antique ones—with few errors. Accordingly, the question of what children know, how they know it, and how it develops has rightly been a major focus of early noun learning (e.g., Swingley, 2005; Booth & Waxman, 2002; Gelman & Markman, 1986; Imai & Gentner, 1997; Jones et al., 1991; Landau et al., 1988; Markman & Hutchinson, 1984; Markman & Markin, 1998; Soja et al., 1991). One key fact is that this rapid and nearly right generalization of a noun category from a very few instances emerges as names for common categories “scales up” and thus appears to be, at least in part, a product of learning a population of categories.

Two types of theoretical approaches, like Packing Theory, have also sought to explain children’s systematic noun generalizations from minimal instances as product of children’s previously acquired categories: connectionist (Colunga and Smith, 2005; Roger and McClelland, 2004) and rationalist-probabilistic approaches (Kemp, Perfors and Tenenbaum, 2007; Xu and Tenenbaum, 2007). Packing Theory is like connectionist accounts in that it views knowledge about the different organization of different kinds as emergent and graded. Packing is like a rationalist account in that it is not specifically a process model. Moreover, since the Packing Theory is built upon a statistical optimality, it could be formally classified as a rationalist model (Anderson, 1990). Despite these differences there are important similarities across all three approaches. We begin with the common ground.

All three accounts, connectionist, Bayesian, and Packing Theory consider category learning and generalization as a form of statistical inference. Thus, all three models are sensitive to the feature variability within a set of instances. All agree on the main idea behind Packing Theory that feature variability within categories determines biases in category generalization. All three also agree that the most important issue to be explained is higher order feature selection, called variously second order generalizations (Smith et al., 2002; Colunga & Smith, 2005), overhypotheses (Kemp, Perfors & Tenenbaum, 2007), and smoothness (Packing Theory). Using the terms of Colunga and Smith (2005), the first order generalization is about individual categories and it is a generalization over instances. The second order generalization is a generalization of distribution of instances over categories. The central goal of all three approaches is to explain how people form such higher-order generalizations and how they might be used in learning new categories from minimal information.

There are also important and related differences among these approaches. The first set of differences concern whether or not the different levels of categories are explicitly represented in the theory. Colunga and Smith’s (2005; see also Rogers & McClelland, 2004) connectionist account represents only input and output associations, the higher order representations of kind -- that shape is more relevant for solid things than for nonsolid things, for example – are implicit in the structure of the input-output associations. They are not explicitly represented and they do not pre-exist in the learner prior to learning. In contrast, the Bayesian approach (Kemp, Perfors & Tenenbaum, 2007; Xu & Tenenbaum, 2007) assumes categories structured as a hierarchical tree. The learner knows from the start that there are higher order and lower order categories in a hierarchy and then needs to learn what the hierarchy is and how different properties matter within that hierarchy. Although the packing model is rationalist in its formal nature; it is emergentist in spirit: Smoothness is not an a priori expectation and is not explicitly represented as a higher order variable but is an emergent and graded property of the population as a whole.

The second and perhaps most crucial difference between packing theory and the other two accounts is the ultimate origin of the higher order knowledge about kinds. For connectionist accounts, the higher order regularities are latent structure in the input itself. If natural categories are smooth, by this view, it is solely because the structure of the categories in the world is smooth and the human learning system has the capability to discover that regularity. But if this is so, one needs to ask (and answer) why the to-be-learned categories have the structure that they do. For the Bayesian accounts, a hierarchical representational structure (with variabilized over-hypotheses) is assumed and innate. These over-hypotheses create a tree of categories in which categories near in the tree will have similar structure. But again, why the system would have evolved to have such an innate structure is not at all clear.

Packing Theory provides an answers and new insights to these issues that neither puts smoothness in the data nor as a pre-specified outcome. Instead, smoothness is emergent in the local interactions of fundamental processes of categorization, inclusion and discrimination. The joint optimization of discriminability and inclusion leads to a smoother space of categories than is in the input and will do so regardless of the starting point. Packing Theory thus provides an answer as to why categories are they way they are and why they are smooth. The answer is not to help children learn categories; it is not a pre-specification of what the system has to learn; although the smoothness of the geometry of categories is clearly exploitable. Rather, the answer as to why categories have the structure they do lies in the local function of categories, in the first place: to include known and possible instances but to also discriminate among instances falling in different categories. The probabilistic nature of inclusion and discrimination, the frequency distributions of individual instances in a category, the joint optimization of discrimination and inclusion in a connected geometry of many categories creates a gradient of feature relevance that is then useable by learners. For natural category learning, for categories that are passed on from one generation to the next, the optimization of inclusion and discrimination over these generations may make highly common and early learned categories particularly smooth. Although the packing model is not a process model, processes of discrimination and inclusion and processes of competition in a topographical representation are well studied at a variety of levels of analysis and thus bridges between this analytic account and process accounts also appear attainable.

Conclusion

The big lesson from the phenomena uncovered by researchers building on Carey and Bartlett’s method, the lesson so clearly evident in that first experiment on chromium, the lesson that Packing Theory (along with connectionist and Bayesian accounts) attempt to address, is this: Words are not learned as islands but in a population of other words. One’s knowledge of other lexical categories –no matter how incomplete or partial – will influence what one learns from any single encounter with an unknown word, and that learning will of course play a role in and constrain future learning. The processes considered here by Packing Theory are most likely just one of many processes of “fitting in,” processes through which lexical learning builds on itself, being constrained not by the population characteristics of already learned words.