Abstract
Genome-wide association studies (GWAS) for non-syndromic cleft lip with or without cleft palate (CL/P) have identified multiple genes as important in the etiology of this common birth defect. We performed a candidate gene/pathway analysis explicitly considering gene-gene (G×G) interaction to further explore the etiology of CL/P. Animal models have shown the WNT signaling pathway plays an important role in mid-facial development, and various genes in this pathway have been associated with non-syndromic CL/P in previous studies. We propose a combined approach to search for possible G×G interactions using machine learning and regression-based methods to test for interactions between genes in the WNT family, and between these genes and other genes identified by genome-wide association studies (GWAS) in case-parent trios. Using this combined approach of regression-based and machine learning methods in CL/P case-parent trios, we found robust evidence of G×G interaction between markers in WNT5B and MAFB (empiric p-values =0.0076 among Asian trios and =0.018 among European trios). Additional evidence for epistatic interaction between markers in WNT5A, IRF6 and C1orf107 was seen among Asian trios, and markers in the 8q24 region and WNT5B among European trios.
Keywords: complex disease, family based study, machine learning
Introduction
Genome-wide association studies (GWAS) have identified many common risk alleles for various complex diseases and traits, but the apparent risk alleles generally exert a modest effect on risk and cannot explain all of the heritability for these complex traits. It has been suggested that undetected gene-gene (G×G) interactions [Van Steen et al. 2012; Moore et al. 2010] and/or the cumulative effects of multiple, independent rare variants (which could have individual large effect sizes) may account for this “missing heritability” [Cantor et al., 2010; Manolio et al., 2009].
Non-syndromic cleft lip with or without cleft palate (CL/P) is the most common craniofacial birth defect in humans. Several genes in the WNT signaling pathway, in particular WNT3A, WNT5A, WNT9B and WNT11, are recognized candidate genes for non-syndromic CL/P [Chiquet et al., 2008]. WNT3 and WNT9B are highly expressed during midfacial formation in mice, suggesting these genes could play a major role in normal development of the lip and palate [Lan et al., 2006]. WNT9B also plays an important role in epithelial development from mesenchymal cells [Caroll et al., 2005]. In an A/WySn mouse model for human CL/P, disruption of WNT9B by the transposon clf1 was shown to cause CL/P [Juriloff et al., 2005; Juriloff et al., 2006]. Recently, Pbx has been shown to affect the joint regulation of WNT-P63-IRF6 through epithelial apoptotic promotion in the midface [Ferretti et al., 2011]. Several WNT signaling genes are expressed in the human embryo between fetal ages 4 to 8 weeks, the critical period for development of CL/P [Ferretti et al., 2011].
Recent GWAS have identified regions of the genome that are significantly associated with risk of CL/P. Rahimov et al. [2008] showed evidence that a variant in IRF6 was associated with increased risk of cleft lip. Association of variants in this gene was later confirmed by Mangold et al. [2010] and Beaty et al. [2010]. Mangold et al. [2010] also detected genome-wide significant association of CL/P near VAX1 and NOG. Beaty et al. [2010] also detected genome-wide significant associations near the MAFB and ABCA4 genes and in the 8q24 region. A subsequent meta-analysis of these 3 studies [Ludwig et al., 2012] supported all of these significant associations and detected significant association to 6 additional regions near the PAX7, THADA, EPHA3, SPRY2 and TPM1 genes and in the 8q21.3 region. See Supplementary Table 2 for more details of these regions.
This study was aimed at detecting risk loci that may not have had large enough marginal effects on CL/P risk to exhibit genome-wide significant marginal effects in the data from the Beaty et al. [2010] GWAS but which might have larger gene-gene interaction effects. This study concentrated on variants in candidate loci to make this problem more tractable. The candidate loci were the 12 regions previously shown to have genome-wide significant association to CL/P (Supplementary Table 2), 18 genes in the WNT pathway, and 65 additional regions which showed suggestive evidence of association to CL/P (genotypic transmission disequilibrium test (TDT) p-values < 10−5) in the Beaty et al. [2010] study. We used 895 trios of Asian ancestry and 681 trios of European ancestry ascertained through a case with an isolated non-syndromic CL/P [Beaty et al, 2010]. We tested for potential G×G interaction between 153 SNPs with genotypic TDT p-values < 10−5 from the 4 genome-wide significant regions and the 65 suggestive regions from the previous GWAS of these trios [Beaty et al., 2010], plus eight SNPs, each representing one of the 8 other regions showing genome-wide significant association with CL/P in the Ludwig et al. [2012] meta-analysis, and 360 SNPs from 18 genes in the WNT pathway.
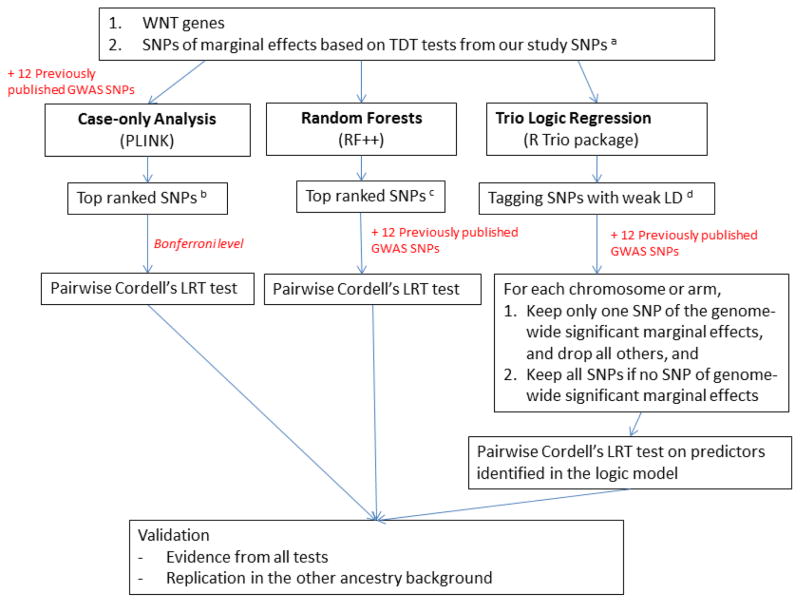
Even when using a candidate locus approach, the multiple testing penalty would be large if we were to model and explicitly test all possible two-way and three-way interactions among the 521 SNPs in these candidate loci. In addition, assumptions concerning additivity of effects and type of epistatic interaction add further complexity to parametric modeling of G×G interactions. Therefore, we used a multi-pronged approach, first applying two machine learning methods, Random Forest (RF) [Breiman, 2001] and Logic Regression (LR) [Ruczinski et al., 2003] adapted to trio data [Li et al. 2010], as well as a parametric, pair-wise case-only interaction test available in PLINK [Purcell et al., 2007]. Results from the three methods (RF, trio LR and case-only) were used to select a set of genes that were further tested for epistatic interaction using conditional logistic regression models in case-parent trios [Cordell, 2002]. Finally, we compared the evidence for interaction across methods and across ancestry groups (Figure 1).
Figure 1. Flow chart of analytical methods for trio design.
a. The threshold was set as genotypic TDT p-values < 10−5.
b. The threshold was set as case-only test p-values < 10−4, excluding pairs in non-negligible LD (r2 < 0.01). The lists of selected SNPs were shown in supplementary table 5 and 6.
c. The threshold was set as the cut-point (“elbow”) along the curve for importance scores from all SNPs. The procedure proposed by Goldstein et al. [2010] is a heuristic approach to identify the top SNPs that have much higher importance scores than the rest. The lists of selected SNPs were shown in supplementary table 3 and 4.
d. The threshold of pairwise LD is set as r2< 0.1 to select the tagging SNPs.
Machine learning methods are data mining tools for high dimensional data. Some machine learning tools, such as Random Forest [Breiman, 2001], rely heavily on bootstrapping to control false-positive rates and relax assumptions regarding the exact relationship between underlying factors (e.g. genes) and outcomes. These methods have the advantage of exploiting potential non-linear relationships, which is more realistic for any complex biological system, as well as unifying the analysis of very large numbers of predictors into a comprehensive framework. We used two machine learning methods: Random Forests (RF) [Breiman, 2001] and trio Logic Regression (trio LR) [Li et al., 2010].
RF is a collection of classification and regression trees (CART), which each can include multiple SNPs to predict the trait. These CARTs are created using bootstrap samples with replacement and random subsets of variables (i.e., predictors, often called “features”) for explaining the occurrence of a dichotomous trait or variation of a quantitative trait. This method has the advantage of not assuming additivity or any specific parametric model, thus avoiding the risk of model mis-specification and its resultant biases. Various bootstrap-based metrics are used to rank these variables in order of importance as potential predictors of the trait. The SNPs that best account for the prediction of disease risk across many thousand trees are considered the most important. The non-parametric, tree-based design of RF allows it to determine whether a feature is an important predictor of the trait even when the marginal effect of the feature is minimal but it acts through a strong interaction effect. Dasgupta et al. [2014] have recently developed a method to estimate the size of such interaction effects using RF and Holzinger et al. [2015] have shown RF can determine that SNPs with interaction effects but zero marginal effects are important risk factors for a trait. RF++ [Karpievitch et al., 2009] is an extension of RF appropriate for trio data (affected case-parent) and provides greater prediction accuracy for individual SNPs compared to all other SNPs included in the analysis. However, its result does not reveal which set of SNPs, as a whole, affects the disease risk.
Logic Regression (LR) is a generalized regression method utilizing logic terms to capture all possible interactions among variables [Ruczinski et al., 2003]. Embedded in this method, the underlying regression model can be any regression model appropriate for the study design. The logic terms were used as covariates fitted to the regression model. Since logic terms can represent different combinations of genotypes from multiple SNPs, LR employs a simulated annealing algorithm to control the searching for the optimal logic term producing the best goodness-of-fit measure from the regression model. Trio LR [Li et al., 2010] is an extension of LR for the case-parent trio design, which uses conditional logistic regression as its regression model.
In addition to the machine learning analyses, we also performed a case-only analysis to identify genes interacting to increase risk to CL/P without considering controls. Two interacting genes, when examined only in cases, will appear to be correlated. If the logistic model is appropriate for this trait, then a parametric model may be more powerful to detect strong two-way interactions.
Here, we propose a combined approach to search for possible G×G interaction using machine learning and regression-based methods in a case-parent trio study, and apply this approach to CL/P case-parent trios focusing on genes in the WNT pathway and specific genes/regions identified as influencing risk to CL/P in GWAS studies [Ludwig et al., 2012]. RF and LR are two supervised machine learning methods with the potential to identify high-order, non-linear interactive relationships within a data set. The two methods are complementary to each other and different from other model-based two-way interaction tests. Therefore, our approach serves as an example, on this small set of SNPs, of using both methods to facilitate the test and interpretation of high-order interaction in more general genome-wide settings.
Methods
Samples
We used data from a GWAS of isolated, non-syndromic CL/P [Beaty et al., 2010], where case-parent trios were drawn from an international consortium. We used 895 trios of Asian ancestry and 681 trios of European ancestry. During data quality control (QC), a SNP was dropped if its missing rate was >1% or if Mendelian errors occurred in more than one trio (5 SNPs in European and 2 SNPs in Asian samples, respectively were dropped for Mendelian errors). Further, monomorphic SNPs within each population were dropped [Beaty et al., 2010]. From the cleaned set of GWAS SNPs, we extracted the 360 markers belonging to the 18 genes in the WNT pathway, plus 152 markers with p<10−5 from GWAS results based on a genotypic TDT [Beaty et al., 2010] (shown in Supplementary Table 1). To remove effects of linkage disequilibrium (LD) among SNPs in WNT genes, we kept only markers with pairwise r2 < 0.1, estimated from the founder population for each ancestry group, resulting in 346 SNPs for the Asian samples and 395 SNPs for the European samples. Of these, 319 SNPs overlapped in the ancestry groups, 27 SNPs were unique to the Asian samples and 76 SNPs were unique to the European samples. In addition, eight SNPs previously identified as significantly associated with CL/P in other published GWAS studies [Rahimov et al., 2008; Mangold et al., 2010; and Ludwig et al., 2012] (Supplementary Table 2) were added to the list considered for each ancestry group when searching for 2-way G×G interactions.
Imputation and pseudo-controls
Both RF and trio LR require complete genotypes for cases and pseudo-controls. We used the R-package Trio [Schwender et al., 2014] to create pseudo-controls and impute missing genotypes in cases. This imputation method first estimated haplotype blocks and haplotype frequencies from the parents, then estimated the joint frequencies of diplotypes in both parents and the case for each case-parent trio. Principal components analysis was conducted using parents from the original GWAS (see Murray et al., 2012), and the largest genetic distances in this data set were between Asian and European ancestry groups. Therefore, we estimated haplotypes within each ancestral group and used their respective haplotype distributions to impute genotypes for these two groups separately. The purpose of using pseudo-controls in the RF++ and trio LR analyses is to control for the effects of population stratification within each of the Asian and European samples, thus retaining the advantage of the trio study design.
Statistical Analyses
The following sections describe details of each method: RF, trio LR, case-only analyses and epistatic tests using conditional logistic regression.
Random Forests
RF is an ensemble method where decision trees are used to rank variables in their order of importance when explaining variation in a trait of interest. Here, decision trees are trained using bootstrap samples of CL/P cases and pseudo-controls (selected with replacement) and random subsets of predictor variables, and tested on out-of-bag (OOB) samples (i.e. those cases and pseudo-controls left-out of the bootstrap sample during the training phase). For a dichotomous trait such as CL/P, prediction error rates for cases and pseudo-controls from tested OOB samples are calculated across all such trees (i.e. the entire forest). The importance of each variable is also estimated using OOB samples by permuting variables and comparing the prediction ability of the forest based on the original values and the permuted values. Each vote on predicted case-control status of the OOB individuals from each tree is aggregated across all trees in a forest, and the prediction error rate is compared for the forest trained using the real data for all variables versus the forest trained using permuted values for one predictor variable. This process is repeated, permuting one predictor variable at a time, and results are used to rank the predictor variables in terms of their contribution to prediction of case-control status. The end product of RF is an ordered list of variables, ranked by the importance of each variable in predicting the outcome based on their marginal effects and G×G (or higher order) interaction effects. These ranked variable lists can be used to select sets of important variables; hence, we should have fewer variables of interest for further analyses after applying RF to a data set.
For the case-parent trio design, an extended RF developed by Karpievitch et al. (2009) can be employed after generating matched case-control sets. This method implements an algorithm to boost correlated data by subject-level strata together using cluster (family) information, and to provide subject- and replicate-level classification and error rates. Using three imputed pseudo-controls per trio per haplotype block, one pseudo-control was randomly selected to match to the case in each trio, for the purpose of controlling effects of population stratification within each ethnic group. As a training dataset for growing trees, 2/3 of matched case-control pairs were randomly selected in each ancestral group, and 1/3 of matched case-control pairs were used as an OOB sample to test grown trees. We calculated the training and testing errors using OOB sampling.
We used the RF++ program version 1.0 [Karpievitch et al., 2009] to select top ranked variables. To perform RF++ in an optimized setting, we pre-tuned two parameters, the number of trees to grow and the number of randomly selected variables to be examined at each node of a tree (“mtry” value). As suggested in the previous literature [Liaw et al., 2002], we tried all combinations of two tree numbers (5,000 and 10,000) and three mtry values (the square root of the total number of variables (p), half of p, and double of p). The combination resulting in the lowest training/testing errors (0.288/0.2836 for the Asian ancestral group, and 0.325/0.2863 for the European ancestral group, respectively) was selected for the analyses. In each random forest, we grew 10,000 trees, and we used the square root of the total number of variables for the mtry parameter (mtry values of 19 and 20 for the Asian and European ancestral groups respectively). To rank variables as potential predictors of the trait, permutation based variable importance scores were calculated. The importance score for the vth predictor was calculated using two proportions of correctly classified individuals in the OOB sets, one obtained from the original data and one after permuting the values of the vth predictor in the OOB data, and repeating the classification of the OOB data using the original tree and the permuted data. For this purpose, among all the trees fitted in the random forest, only a subset of trees will be used in the calculation of importance of the vth predictor variable, i.e. those trees where the variables available to build the tree included the vth variable. The importance score is defined as the difference between these two proportions of OOB correctly classified individuals, averaged over all the applicable trees. One can express this as follows,
where pc,t is the proportion of correctly classified individuals out of the total number of OOB individuals in a given tree t; is the proportion of OOB individuals correctly classified after variable v was randomly permuted across all OOB individuals for tree t; and T is the total number of trees in the forest where the variable v was among the subset of variables which could have been included in the tree.
Trio logic regression for multi-way gene-gene interactions
The LR method has two components making it a flexible framework to analyze trio data. The logic term uses Boolean operators to transform multiple levels of combinations of many binary predictors into just two levels, one corresponding to the logic expression, and its corresponding opposite (i.e. the compliment) of the logic expression. For example, let F1, F2, and F3 stands for three binary predictors. There are 23=8 levels representing whether each factor is present. However, if the logic expression is “F1 and F2 and F3”, only two levels remain, which is also true for expression such as “F1 or (F2 and F3)”. Each logic term is then used as a single predictor in a regression model. The second flexible component of the LR method is its underlying regression model. It can take any form that is appropriate for the study design. LR uses a regression model to fit data using all possible logic terms, and uses the corresponding goodness-of-fit measures, i.e., the score function from the regression model, to determine the optimal logic term. At each step of fitting the regression model with a new logic term, this new term is accepted not only based on how much the goodness-of-fit changes from the old term to the new term, but also based on a probability related to the stage of the search. The probability is determined by the simulated annealing algorithm [Ruczinski et al., 2003], which gives a higher chance of acceptance at the beginning of a search rather than at the end. Logic regression was originally developed for case-control data, or quantitative outcome analysis, but has been extended to the case-parent trio design [Li et al. 2010].
The conditional logistic regression test is often used in lieu of a genotypic TDT for its ability to include covariates and account for population stratification. The trio LR employs the conditional logistic regression model as its underlying regression model and uses the deviance from the conditional regression as the goodness-of-fit measure [Li, et al., 2010]. This method generates genotypes for the pseudo-controls to match with observed genotypes of cases (to control for population stratification), then converts those genotypes into binary predictors under either dominant or recessive coding. A logic term of multiple predictors, i.e., some combination of either dominant or recessive coding at multiple loci were treated as the dependent variable in the underlying conditional logistic regression model. The trio LR method tests whether the relative risk of any combination of transmitted variants, in terms of a logic term representing dominant or recessive coding at multiple markers, is higher than the non-transmitted variants at these same markers.
We initially applied trio logic regression to all selected SNPs. Within each ancestral group, we allowed the logic term to have a maximum of two or three predictors, to identify potential G×G interaction between two or three SNPs. Then, we increased the total number of predictors up to 5, to check whether higher order interactions could be detected. Although the method can detect large main effects of individual SNPs, it is designed, and therefore is more powerful than single marker TDT, to detect G×G interaction when no individual SNP has strong marginal effects. Although it adjusts for the LD among markers (SNPs) within the same haplotype block, this method assumes markers in different haplotype blocks are completely independent. When proposing a new logic term to fit the data, logic regression randomly selects predictors to include in the logic term, with the possibility of adding one predictor in high LD with another predictor already included in the logic term. When we fitted this model using all SNPs, we found markers in adjacent haplotype blocks were picked up as if they interactively affected disease risk, although we had already pruned out all markers in high LD (using a threshold of r2≥0.1) among those without significant marginal effects. This may be due to long-range, low LD rather than a true epistatic interaction. Interestingly, two different sets of two markers, each with very strong marginal effects and physically close to each other, were identified as representing 2-SNP interactions in both Asian and European trios.
To detect possible interactions between markers showing significant marginal effects and other markers in the WNT pathway, preferably on a different chromosome or chromosomal arms from the marker of significant marginal effect, we kept the two markers previously identified as having a 2-way interaction in the analysis, as they had strong marginal effects. Then, we further screened the rest of the SNPs to generate a “strictly pruned set” of SNPs. Initially, we had SNPs in marker set A, which included those SNPs with significant or suggestive marginal effects (TDT test p<10−5) in a GWAS, and SNPs in marker set B, which are SNPs in the WNT genes (which did not have significant marginal effects in our original GWAS). To screen marker set A, we only kept the most significantly associated SNP on the whole chromosome. On chromosomes with only SNPs from marker set B, we kept all of the marker set B SNPs in the G×G interaction analysis. This resulted in our “strictly pruned set” of SNPs, which contains at most one marker per chromosome which has a significant or suggestive marginal effect, and all candidate SNPs (negligible marginal effects) in the WNT genes on the chromosomes without a marker set A SNP. This strictly pruned set of candidate SNPs was used to rule out the possibility of spurious cis-cis interactions that are purely due to inter-marker LD.
Case-only interaction tests
The case-only interaction test available in PLINK tests whether any pair of SNPs assumed to be independent shows excessive correlation in the cases, and relies on a χ2 statistic with 1 degree of freedom to calculate statistical significance. To minimize false positive signals due to SNPs in high LD, or with low minor allele frequency (MAF) in the founder population, we filtered out any SNP in the WNT genes with MAF<5% (leaving 301 SNPs for Asian trios, and 378 SNPs for European trios), and only pairs of SNPs separated by at least 1 Mb and with r2<0.01 (estimated from the founder population) or on a different chromosome were considered (pruning was done separately in the two ethnic groups). Similarly pruned SNPs from the significant GWAS association regions were combined with this pruned set of SNPs in the WNT genes resulting in 351 SNPs for the Asian group and 400 SNPs for the European group. We used a more stringent r2 threshold (r2<0.01) than was used to prune the data for RF and trio LR analysis (r2<0.1) and included the physical distance requirement, because the case-only analysis is not robust to the presence of LD. We observed an excessive number of extremely significant pair-wise results if we set the threshold higher (data not shown). While it is possible SNPs in LD do exhibit a true pair-wise interaction affecting disease risk, it is more likely that most such apparent interactions are false positives due to a violation of the assumption of this test. We used the PLINK [Purcell et al., 2007] --fast-epistasis option (http://pngu.mgh.harvard.edu/purcell/plink/) to perform a case-only analysis using only proband genotypes. In brief, this approach tests whether any pair of SNPs assumed to be independent show excessive correlation between them among cases, and a χ2 statistic with 1 degree of freedom is used to test for statistical significance. Bonferroni correction was used to correct for multiple testing of the actual number of pairwise interactions taken into consideration at the final step.
Epistatic tests using conditional logistic regression for 2-way G×G interactions
All SNP pairs selected from each result of RF, trio LR and case-only analyses were further tested for 2-way G×G interactions using conditional logistic regression [Cordell, 2002] as implemented in the ‘trio’ R package v1.4.24 [Li et al., 2010].
These epistatic tests represent departure from predicted effects under a log-linear model for alleles at two independent genes [Fisher, 1918]. Because this epistatic test is based on a parametric regression model, the number of possible pairwise G×G interactions is virtually unlimited and would quickly create severe issues with multiple testing. To reduce the number of tests, we applied these parametric regression methods only after each data mining method had reduced the number of candidate SNPs. We first used Random Forest (RF) [Breiman, 2001] method to identify a subset of plausible SNPs associated with the disease risk. We also tested high-order interaction using trio Logic regression (LR) [Li et al., 2010], as well as pair-wise interaction using a case-only interaction test available in PLINK. We applied this two-SNP conditional logistic regression epistatic test [Cordell, 2002] to all SNPs or SNP-pairs identified by any of the methods, i.e., RF, LR or case-only analysis, to validate those findings, as well as to compare evidence produced by various approaches.
The basic idea behind case-parent trios in the conditional logistic regression framework is to generate ‘pseudo controls’ from the untransmitted alleles in each parental mating type (where the case is the affected child), thus yielding a matched case-control design. For a single SNP in one gene, these matched sets consist of one case and three pseudo-controls fitted in a conditional logistic regression model. When considering two SNPs from independent genes, this method considers the genotypes at these two SNPs in the one observed case and15 matched pseudo-controls [Cordell, 2009]. Fifteen matched pseudo-controls were generated for each CL/P case, and used in a conditional logistic regression model. We permuted case-control status 10,000 times to obtain empiric p-values for the most plausible pairs of SNPs (nominal p < 0.05) in both ancestral groups for validation.
Results
Random Forests
From the RF analysis, we obtained permuted importance scores for every SNP and ranked them by their scores. Importance scores were ranked from the highest to lowest (Supplemental Figures 1–2) for Asian and European samples separately. To obtain a list of top-ranked candidate SNPs for use in the pairwise conditional logistic regression test [Cordell, 2009], we employed a procedure proposed by Goldstein et al. [2010]. On each plot, we located the cut-point (“elbow”) on the curve, where importance scores started to decrease slowly among the top-ranked SNPs. By doing this, we identified 25 top SNPs in the Asian samples and 32 top SNPs in the European samples with importance scores higher than their corresponding cut-points. This gives us a list of plausible SNPs worth following up. Although somewhat ad hoc, this procedure is reasonable for filtering the SNPs for further testing given the limitations on power in our small dataset. These top SNPs are listed in Supplementary Tables 3–4. Five SNPs: rs3789451, rs11802196, rs6686599, rs813218, and rs6065259, were among these top SNPs in both ethnic groups. Pairs of these top SNPs plus the most significant GWAS SNPs yielding evidence of significant interaction in the pairwise conditional logistic regression tests are shown in Table 1.
Table 1.
G×G (SNP×SNP) interaction between WNT genes and CL/P GWAS genes: Most significant results of the conditional logistic regression epistatic test and corresponding case-only test results for the top ranked SNPs from Random Forests analysis and CL/P GWAS significant SNPs (SNPs pruned to have r2 < 0.1)
| Gene1 | Gene2 | SNP1 (CHR) | SNP2 (CHR) | Case-only test P-value | Epistatic test P-value In Asians | Epistatic test P-value In Europeans |
|---|---|---|---|---|---|---|
| Asian | ||||||
| WNT5B | MAFB | rs4765835 (chr12) | rs11696257 (chr20) | P = 0.7237 (P = 0.00078)a | 0.0085* Empiric P** = 0.0076* |
0.017† Empiric P** = 0.018† |
| WNT2 | IRF6 | rs2023708 (chr7) | rs1044516 (chr1) | P = 0.023 | 0.019† | 0.65 |
| WNT2 | ABCA4 | rs2023708 (chr7) | rs6686599 (chr1) | P = 0.012 | 0.015† | 0.29 |
| European | ||||||
| WNT5A | ABCA4 | rs1499890 (chr3) | rs3789451 (chr1) | P = 0.03 | 0.84 | 0.037† |
| WNT4 | MAFB | rs2807376 (chr1) | rs13041247 (chr20) | P = 0.017 | 0.44 | 0.044† |
| FILIP1L | chr8q24 | rs813218 (chr3) | rs12546523 (chr8) | P = 0.017 | 0.19 | 0.0011* Empiric P** = 0.0017* |
P-value < 0.01
P-value < 0.05
Empiric P value used 10,000 permutations.
In Asian trios using the case-only test, rs4765835 and rs11696257 did not show evidence of interaction (P = 0.7237) but rs4765835 showed strong evidence of interaction with another SNP in MAFB, rs6102085 (P = 0.00078).
Trio logic regression
When all SNPs with large marginal effects from each candidate region and all pruned SNPs from the WNT genes (r2<0.1) were analyzed, the logic regression method detected evidence of G×G interactions between two markers in high LD which both showed significant marginal effects in our discovery GWAS [Beaty et al., 2010]. In the Asian ancestry samples, two markers (rs2013162 in gene C1orf107 and rs126280 in IRF6), spanning about 0.1 MB region on chr. 1 showed evidence of G×G interaction. In the European ancestry samples, rs2395855 and rs1850889 in the 8q24 region showed evidence of G×G interaction. In the analysis of these significant SNPs plus the strictly pruned set of SNPs, we found additional interactions. In the Asian ancestry samples, we identified G×G interactions between 3 SNPs (including rs126280 in IRF6, rs2013162 in C1orf107, and rs7640326 in WNT5A on chr. 3). In the European ancestry samples, the best 3-way interaction model included rs2395855 and rs1850889 (both in 8q24), and rs2240507 (in WNT5B on chr. 12). To confirm this observation, we used the 3-way interaction models identified by trio logic regression to generate a single “combined risk factor”, and then used this combined factor to run a single marker TDT test and estimate genetic effects. For example, for the Asian samples, the optimal logic term is “(rs126280R and rs2013162R) or rs7640326R”, where superscript R means the genotype had two copies of the minor allele at a particular SNP. This logic term means if one person had two minor alleles at both rs126280 and rs2013162, or had two minor alleles at rs7640326, then that person was at elevated risk. For each of the cases and pseudo-controls, we applied that logic term on the genotypes for those three SNPs to generate a binary value as the “single combined risk factor”. Among Asian trios, the log Odds Ratio (OR) estimated for this “single combined risk factor” was 1.43 (p = 10−44). Among European trios, the corresponding log OR was estimated as 1.37 for the “single combined risk factor” (p = 2*10−44). Based on 105 permutation tests, no p-values from the permuted datasets were more significant than these observed p-values. The pairwise conditional logistic epistatic test [Cordell, 2009] for every SNP pair identified in the 3-way interaction models failed to converge, possibly because all of these SNPs were perfectly correlated with case status in these data.
Case-only analysis
Table 2 and Supplementary Tables 5 and 6 show results of the case-only analyses using the candidate SNPs with MAF<0.05, separated by at least 1 Mb and with r2<0.01 or were on a different chromosome. After Bonferroni correction, two pairs of SNPs show significant p-values within each of the Asian and European ancestral groups: two SNP pairs involving markers in WNT9A and COL8A1 among Asian cases (p < 2.09×10−5), and two SNP pairs in WNT2B and WNT5A among European cases (p < 1.45×10−5). Results are shown in Table 2. In addition, supplementary Table 5 and 6 show the pairwise interaction test results with p < 10−4 within each ancestral group respectively. While not significant at the Bonferroni threshold, the case-only approach also found evidence of interaction between SNPs in WNT5B and MAFB, which is consistent with findings from the RF analyses (Table 1).
Table 2. Case-only analysis results passing Bonferroni correction in Asian and European cases.
(SNPs pruned to have r2 < 0.01)
| Sample | GENE1 | GENE2 | SNP1 | SNP2 | Case Only | Epistatic Test* |
|---|---|---|---|---|---|---|
| Asian | WNT9A | COL8A1 | rs681239 (chr1) | rs704574 (chr3) | 1.63E-06 | 3.85E-04 |
| WNT9A | COL8A1 | rs681239 (chr1) | rs792835 (chr3) | 2.26E-06 | 6.46E-04 | |
| European | WNT2B | WNT5A | rs3790604 (chr1) | rs358817 (chr3) | 4.08E-06 | 2.94E-04† |
| WNT2B | WNT5A | rs3790604 (chr1) | rs3856709 (chr3) | 1.15E-05 | 6.35E-04† |
Wald test results provided when epistatic method failed.
Wald test for interaction term fitting a full model with one parameter for each SNP and one interaction term.
Epistatic tests and comparison among methods
The reduced list of candidate SNPs resulting from the RF, trio LR and case-only analyses were further tested for 2-way G×G interactions using the conditional logistic regression epistatic test [Cordell et al., 2002]. From the RF analysis, we identified 25 top-ranked SNPS in Asians and 32 top-ranked SNPs in Europeans, respectively. In addition, 12 genome-wide significant SNPs from the four regions found by Beaty et al. [2010] and from 8 other regions from other published GWAS studies [Rahimov et al., 2008; Mangold et al., 2010; Ludwig et al., 2012] (Supplementary Table 2) were added to the list of top SNPs for pair-wise G×G testing. Since one SNP was both significant in Beaty et al. [2010] and was among the “top” SNPs in the current RF analysis of 630 Asian case-parent trios, we used 36 SNPs in the conditional logistic regression epistatic analysis. For the 841 European case-parent trios, two SNPs significant in Beaty et al. [2010] analyses were also in the “top” list from RF, so only 42 SNPs were used in this epistatic analysis. Table 1 shows significant results of the conditional logistic regression analyses for these SNPs and the corresponding case-only association results. There were 2,390 pairs of SNPs tested in the Asian samples, and 3,415 pairs tested in the European samples.
In the Asian group, the SNP pair composed of rs4765835 (in WNT5B) × rs11696257 (in MAFB) was significant (p=0.0085, empiric p=0.0076). This finding, reported in Table 1, was supported by a significant interaction in Europeans (p=0.017, empiric p=0.018). Additional marker pairs (WNT2/IRF6 and WNT2/ABCA4) also were nominally significant, but showed no evidence of epistasis among European trios. Among European trios, 3 pairs of SNPs yielded consistent results across all methods (nominal p<0.05 in the epistatic test of top RF SNPs, candidate SNPs and the case-only test); WNT5A (rs1499890) × ABCA4 (rs3789451), WNT4 (rs2807376) × MAFB (rs13041247), and FILIP1L (rs813218 on chromosome 3; 101.08MB) × 8q24 region (rs12546523). However, only the FILIP1L × 8q24 pair attained significance in permutation tests (empiric p=0.0017). None of these pairs were significant among Asian trios.
From the case-only analysis, we applied the epistatic test on SNP pairs with the most significant p-value (these SNP pairs are listed in Supplementary Table 5 and 6). The conditional logistic regression epistatic test results are shown in Table 2 for the two pairs of SNPs in each population yielding significant case-only results after Bonferroni correction. However, none of those pairs exhibited significant interaction in the conditional logistic regression test after Bonferroni correction.
The trio LR methods produced evidence for one 3-way interaction, which is hard to test in the epistatic test designed for 2-way interaction. We attempted to perform these 2-way interaction tests on every-pair of SNPs identified in these 3-SNPs interaction models. However, these tests failed to converge, possibly because all three SNPs were perfectly correlated with case status in these data.
We observed some overlapping findings among these methods. Top ranked SNPs from RF, the case-only test, and the epistatic tests, showed fairly strong evidence of interaction between SNPs in WNT5B and MAFB (Table 1) in both Asian and European trios. The empirical p-value of the epistatic tests was 0.0076 in Asian samples and 0.018 in European samples. Case-only analysis reported p=0.00078 in Asian samples. In addition, the trio LR method identified WNT5B in its 3-way interaction model, which included rs2240507 (in WNT5B), plus rs2395855 and rs1850889 (in 8q24) in the European samples.
The partial overlap as well as differences in results across multiple methods revealed the possibility of complex interactions among genes influencing risk to CL/P. At a nominal significance level (p<0.05), both epistatic and case-only analyses detected additional pair-wise interactions, but these involved different pairs in the different ancestral groups. In Asians, we found evidence for WNT2(rs2023708) × IRF6(rs1044516) and WNT2(rs2023708) × ABCA4(rs6686599) interactions, while in Europeans, we found evidence for WNT5A(rs1499890) × ABCA4(rs3789451), WNT4(rs2807376) × MAFB(rs13041247), and FILIP1L(rs813218 chromosome 3) × 8q24 region (rs12546523) interactions. Among these pairs, only the FILIP1L × 8q24 pair attained significance in permutation tests (empiric p =0.0017) in Europeans. Interestingly, WNT5A, together with IRF6 and C1orf107, was identified in a 3-way interaction model using the trio LR method.
Furthermore, none of the most significant pairwise interactions found in the case-only analysis yielded strong evidence of any effect in either the RF or the trio LR analyses. In RF, no SNPs in WNT9A, COL8A1 (on chromosome 3) or WNT2B were highly ranked based on the importance scores in either Europeans or Asians (Supplementary Tables 3–4). However, trio LR did not support the interactions identified from the case-only analysis.
Discussion
Combined approaches of regression-based and machine learning methods for case-parent trio data were used in a search for evidence of G×G interactions between 18 genes in the WNT family and SNPs attaining genome wide significant evidence of association in a family-based study of non-syndromic CL/P from an international collaboration (consisting largely of Asian and European groups). Although different pairs of genes were identified via different methods, the genes WNT5B on chromosome 12 and WNT5A on chromosome 3 showed no significant marginal effects but were identified as interacting with other genes in all three methods. In addition, three regions previously shown to have significant marginal effects on risk of CL/P were also involved in the observed G×G interactions: the IRF6 region, the 8q24 region, and a region on chromosome 20q11.2 - q13.1 containing MAFB [Beaty et al. 2010]. Our RF analyses followed by conditional logistic regression epistatic tests and the case-only analyses showed some evidence for G×G interaction between SNPs in MAFB with markers in WNT5B on chromosome 12p13.3 among both Asians and Europeans. Our trio logic regression results also suggested markers in WNT5B may interact with markers in the chromosome 8q24 region among Europeans, while markers in WNT5A may interact with markers in IRF6 and the nearby open reading frame C1orf107 among Asians. The WNT5B gene is a ligand for members of the frizzled family of 7 transmembrane receptors in the WNT pathway. WNT5B may be a signaling molecule affecting development of different tissues. Also, WNT5B has been reported to show differential expression compared to WNT5A, but WNT5A and WNT5B play an essential role in regulating the longitudinal bone growth during chondrocyte transition between different zones controlled by each gene [Yang et al., 2003]. Since WNT5A has already been reported to be associated with CL/P risk, our evidence of statistical interaction between WNT5B and MAFB is consistent with previous findings.
Based on our results, a combined approach using regression-based and machine learning methods found evidence for G×G interactions among WNT genes and GWAS signals for CL/P. Overall, these results agreed with each other and should provide robust evidence to support further biological investigation. RF methods using matched cases and pseudo-controls successfully prioritized the list of genes for further pairwise tests for G×G interaction tests using regression based methods, and thus minimized multiple testing issues. Logic regression can test for higher order G×G interactions and, its underlying conditional logistic regression model can estimate specific interaction terms. The resulting coefficient gives an estimate of the log odds ratio of the combined effect of putative interacting SNPs. Case-only analysis provides another way to look at the available data among cases, and is computationally fast compared to these other approaches. However, over-representation of pairs of genetic variants among cases could be a result of LD. Hence, case-only results corroborated by additional results from formal tests for epistasis (with permutation testing) should be more robust to false positive findings.
The limitations of our study were small study sample sizes and low power to detect modest effects of G×G interactions compared to the main marginal effect of any individual marker in the presence of LD. In case-only analysis, the method depends heavily on the MAF of markers, which is harder to estimate with great precision in a small sample. When a set of markers collectively is the most appropriate proxy for the causal gene or genes, we will lose power if we only consider a single SNP from the set in the analysis. Furthermore, two markers far away from each other that appear to interactively increase risk, may simply have weak LD between them. Therefore we decided to only follow-up those pairs located on different chromosomes or at least on different chromosomal arms. LD is also a challenge when generating haplotype data for imputing missing genotypes. Since both RF and logic regression analyses require complete genotype data, we had to impute missing genotypes and then created a pruned list of SNPs in linkage equilibrium (LE) with one another. For case-only analysis, since the statistical tests aim to detect correlation between pairs of SNPs, pairwise LD will result in a flood of false positive interaction signals. By default, PLINK’s case-only test analyzes pairs of SNPs located at least 1Mb apart. However, even pruning by 1Mb inter-marker distance yielded false positive signals driven solely by long distance LD. Using a more stringently pruned set of uncorrelated SNPs and filtering the results of case-only analysis down to SNP pairs with r2<0.01 reduced the number of false positive signals caused by LD. Logic regression models are useful to detect interaction when no SNP shows a strong marginal effect. However, this approach cannot fully adjust for LD between markers from different haplotype blocks, making it impossible to differentiate LD from interaction among markers. LD among markers competes with the G×G interaction signal, and cannot be eliminated without dropping many informative markers.
RF++ can test millions of SNPs in parallel, but the LR/trio LR program has a computational restriction. LR can accommodate a maximum of 1000 predictors in one analysis. Fortunately, the number of SNPs in our analysis fell well below this limit; therefore, we directly applied the trio LR on the completed set of SNPs without further filtering the number of SNPs beyond removing SNPs in high LD. However, to use LR or trio LR to test for interactions between larger numbers of candidate SNPs, one might adopt a strategy of choosing the most important SNPs selected by RF or RF++ as input to LR.
Although not all evidence of G×G interactions among European trios replicated in Asian trios, some of our results remain intriguing. Markers in FILIP1L and the8q24 region showed evidence of G×G interaction in Cordell’s epistatic test (p=0.0011). The 8q24 region is a gene desert and its genetic elements remain undefined. Since our analysis was limited to candidate regions from association studies and the genes in the WNT pathway, we may have missed some important gene-gene interactions. However, our analytical approach is promising and could be expanded to other candidate pathways. In practice, for G×G interaction studies for a trio design, RF could prioritize a set of SNPs of interest among many thousands of SNPs, and researchers could then focus on these to ameliorate the multiple testing problem. Downstream tests could use a combination of the conditional logistic regression epistatic test and case-only analysis for 2-way G×G interactions among a preliminary set of SNPs. Trio logic regression could subsequently test for 2-way or higher order interactions.
Finally, the most consistent evidence from this study supports possible interactions between MAFB on chromosome 20q11.2 - q13.1 and WNT5B on chromosome 12q13.3 in both Europeans and Asians. Since WNT5A has already been reported to be associated with CL/P risk, our evidence of statistical interaction between WNT5B and MAFB is especially interesting. In Europeans, there is also some evidence of interactions between these two genes and SNPs in the 8q24 region. In Asians, interactions between WNT5A, IRF6 and the nearby open reading frame C1orf107 were observed. All these results are worthy of follow-up in additional studies of CL/P and suggest that G×G interactions may indeed explain some of the “missing heritability” in the risk of non-syndromic oral clefts.
Supplementary Material
Acknowledgments
The data for this international cleft consortium was a collaborative effort among many groups, and we acknowledge the invaluable contributions of J.C. Murray (Univ. of Iowa), R.G. Munger (Utah State Univ.), A.J. Wilcox (NIEHS), R.T. Lie (Univ. of Bergen), Y-H Wu-Chou (Chang Gung Mem. Hospital), H. Wang (Peking Univ), X. Ye (Wuhan Univ.), S. Huang (Peking Med. College), V. Yeow (KKWCH), S.S. Chong (Natl. Univ. Singapore), S.H. Jee (Yonsei Univ.), B. Shi (West China Schl. Stomatology, Sichuan Univ.) and A.F. Scott (Johns Hopkins). We sincerely thank all of the families at each of the original recruitment sites for participating in this study, and we gratefully acknowledge the invaluable assistance of clinical, field and laboratory staff who contributed to making this work possible. Funding to support data collection, genotyping and analysis came from several sources, some to individual investigators and some to the consortium itself. The consortium for GWAS genotyping and analysis was supported by the National Institute for Dental and Craniofacial Research through U01-DE-018993; “International Consortium to Identify Genes & Interactions Controlling Oral Clefts”, 2007–2009; TH Beaty, PI. This project was part of the gene, environment association studies consortium (GENEVA) funded by NHGRI to enhance communication and collaboration among investigators conducting genome-wide studies for a variety of complex diseases. The current analyses were also supported in part by the Intramural Research Program of the National Human Genome Research Institute, National Institutes of Health. Our group benefited greatly from the work of the Coordinating Center (directed by B. Weir and C. Laurie of the Univ. of Washington) in data cleaning and preparation of these case-parent trios for submission to the Database for Genotypes and Phenotypes (dbGaP: http://www.ncbi.nlm.nih.gov/). We also acknowledge the leadership of T. Manolio of NHGRI and E. Harris of NIDCR. Genotyping services were provided by the Center for Inherited Disease Research (CIDR), funded through a federal contract from NIH to Johns Hopkins University (contract number HHSN268200782096C). Funding for individual investigators and the replication studies include: R01-DE-014581 (THB); R37-DE08559 (JCM, MLM), R01-DE09886 (MLM), R01-DE012472 (MLM), R01-DE014677 (MLM), R01-DE016148 (MLM), P50-DE016215 (JCM, MLM), R21-DE016930 (MLM), R01-HD390661 and R01-DE016877 (RGM). Smile Train Foundation supported data collection in Chengdu. This research was supported in part by the Intramural Research Program of the NIH, National Institute of Environmental Health Sciences (AJW).
Footnotes
The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of Dental and Craniofacial Research, nor the National Institutes of Health.
References
- Beaty TH, Murray JC, Marazita ML, Munger RG, Ruczinski I, Hetmanski JB, Liang KY, Wu T, Murray T, Fallin MD, Redett RA, Raymond G, Schwender H, Jin SC, Cooper ME, Dunnwald M, Mansilla MA, Leslie E, Bullard S, Lidral AC, Moreno LM, Menezes R, Vieira AR, Petrin A, Wilcox AJ, Lie RT, Jabs EW, Wu-Chou YH, Chen PK, Wang H, Ye X, Huang S, Yeow V, Chong SS, Jee SH, Shi B, Christensen K, Melbye M, Doheny KF, Pugh EW, Ling H, Castilla EE, Czeizel AE, Ma L, Field LL, Brody L, Pangilinan F, Mills JL, Molloy AM, Kirke PN, Scott JM, Arcos-Burgos M, Scott AF. A genome-wide association study of cleft lip with and without cleft palate identifies risk variants near MAFB and ABCA4. Nat Genet. 2010 Jun;42(6):525–9. doi: 10.1038/ng.580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breiman L. Random forests. Mach Learn. 2001;45:5–32. [Google Scholar]
- Cantor Rita M, Kenneth Lange, Sinsheimer Janet S. Prioritizing GWAS results: A review of statistical methods and recommendations for their application. Am J Hum Genet. 2010;86(1):6–22. doi: 10.1016/j.ajhg.2009.11.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carroll TJ, Park JS, Hayashi S, Majumdar A, McMahon AP. Wnt9b plays a central role in the regulation of mesenchymal to epithelial transitions underlying organogenesis of the mammalian urogenital system. Dev Cell. 2005 Aug;9(2):283–92. doi: 10.1016/j.devcel.2005.05.016. [DOI] [PubMed] [Google Scholar]
- Chiquet BT, Blanton SH, Burt A, Ma D, Stal S, Mulliken JB, Hecht JT. Variationin WNT genes is associated with non-syndromic cleft lip with or without cleft palate. Hum Mol Genet. 2008 Jul;17(14):2212–8. doi: 10.1093/hmg/ddn121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordell HJ. Epistasis: what it means, what it doesn’t mean, and statistical methods to detect it in humans. Hum Mol Genet. 2002 Oct;11(20):2463–8. doi: 10.1093/hmg/11.20.2463. [DOI] [PubMed] [Google Scholar]
- Dasgupta A, Szymczak S, Moore JH, Bailey-Wilson JE, Malley JD. Risk estimation using probability machines. BioData Min. 2014 Mar;7(1):2. doi: 10.1186/1756-0381-7-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher R. The correlation between relatives on the supposition of Mendelian inheritance. Transactions of the Royal Society Edinburgh. 1918;52:399–433. [Google Scholar]
- Goldstein BA, Hubbard AE, Cutler A, Barcellos LF. An application of Random Forests to a genome-wide association dataset: methodological considerations; new findings. BMC Genet. 2010 Jun;:11–49. doi: 10.1186/1471-2156-11-49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holzinger ER, Szymczak S, Dasgupta A, Malley JD, Li Q, Bailey-Wilson JE. Variable Selection Method for the Identification of Epistatic Models. Pacific Symposium on Biocomputing. 2015;20:195–206. [PMC free article] [PubMed] [Google Scholar]
- Juriloff DM, Harris MJ, McMahon AP, Carroll TJ, Lidral AC. Wnt9b is the mutated gene involved in multifactorial nonsyndromic cleft lip with or without cleft palate in A/WySn mice, as confirmed by a genetic complementation test. Birth Defects Res A Clin Mol Teratol. 2006 Aug;76(8):574–9. doi: 10.1002/bdra.20302. [DOI] [PubMed] [Google Scholar]
- Juriloff DM, Harris MJ, Dewell SL, Brown CJ, Mager DL, Gagnier L, Mah DG. Investigations of the genomic region that contains the clf1 mutation, a causal gene in multifactorial cleft lip and palate in mice. Birth Defects Res A Clin Mol Teratol. 2005 Feb;73(2):103–13. doi: 10.1002/bdra.20106. [DOI] [PubMed] [Google Scholar]
- Karpievitch YV, Hill EG, Leclerc AP, Dabney AR, Almeida JS. An introspective comparison of random forest-based classifiers for the analysis of cluster-correlated data by way of RF++ PLoS One. 2009 Sep;4(9) doi: 10.1371/journal.pone.0007087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lan Y, Ryan RC, Zhang Z, Bullard SA, Bush JO, Maltby KM, Lidral AC, Jiang R. Expression of Wnt9b and activation of canonical Wnt signaling during midfacial morphogenesis in mice. Dev Dyn. 2006 May;235(5):1448–54. doi: 10.1002/dvdy.20723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Q, Fallin MD, Louis TA, Lasseter VK, McGrath JA, Avramopoulos D, Wolyniec PS, Valle D, Liang KY, Pulver AE, Ruczinski I. Detection of SNP-SNP Interactions in Trios of Parents with Schizophrenic Children. Genet Epidemiol. 2010;34:396–406. doi: 10.1002/gepi.20488. [DOI] [PubMed] [Google Scholar]
- Liaw Andy, Wiener Matthew. Classification and Regression by random Forest. R news. 2002;2.3:18–22. [Google Scholar]
- Ludwig KU, Mangold E, Herms S, Nowak S, Reutter H, Paul A, Becker J, Herberz R, AlChawa T, Nasser E, Böhmer AC, Mattheisen M, Alblas MA, Barth S, Kluck N, Lauster C, Braumann B, Reich RH, Hemprich A, Pötzsch S, Blaumeiser B, Daratsianos N, Kreusch T, Murray JC, Marazita ML, Ruczinski I, Scott AF, Beaty TH, Kramer FJ, Wienker TF, Steegers-Theunissen RP, Rubini M, Mossey PA, Hoffmann P, Lange C, Cichon S, Propping P, Knapp M, Nöthen MM. Genome-wide meta-analyses of nonsyndromic cleft lip with or without cleft palate identify six new risk loci. Nat Genet. 2012 Sep;44(9):968–71. doi: 10.1038/ng.2360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangold E, Ludwig KU, Birnbaum S, Baluardo C, Ferrian M, Herms S, Reutter H, de Assis NA, Chawa TA, Mattheisen M, Steffens M, Barth S, Kluck N, Paul A, Becker J, Lauster C, Schmidt G, Braumann B, Scheer M, Reich RH, Hemprich A, Pötzsch S, Blaumeiser B, Moebus S, Krawczak M, Schreiber S, Meitinger T, Wichmann HE, Steegers-Theunissen RP, Kramer FJ, Cichon S, Propping P, Wienker TF, Knapp M, Rubini M, Mossey PA, Hoffmann P, Nöthen MM. Genome-wide association study identifies two susceptibility loci for nonsyndromic cleft lip with or without cleft palate. Nat Genet. 2010 Jan;42(1):24–6. doi: 10.1038/ng.506. [DOI] [PubMed] [Google Scholar]
- Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ, McCarthy MI, Ramos EM, Cardon LR, Chakravarti A, Cho JH, Guttmacher AE, Kong A, Kruglyak L, Mardis E, Rotimi CN, Slatkin M, Valle D, Whittemore AS, Boehnke M, Clark AG, Eichler EE, Gibson G, Haines JL, Mackay TF, McCarroll SA, Visscher PM. Finding the missing heritability of complex diseases. Nature. 2009 Oct;461(7265):747–53. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore JH, Asselbergs FW, Williams SM. Bioinformatics challenges for genome-wide association studies. Bioinformatics. 2010 Feb;26(4):445–55. doi: 10.1093/bioinformatics/btp713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray T, Taub MA, Ruczinski I, Scott AF, Hetmanski JB, Schwender H, Patel P, Zhang TX, Munger RG, Wilcox AJ, Ye X, Wang H, Wu T, Wu-Chou YH, Shi B, Jee SH, Chong S, Yeow V, Murray JC, Marazita ML, Beaty TH. Examining markers in 8q24 to explain differences in evidence for association with cleft lip with/without cleft palate between Asians and Europeans. Genet Epidemiol. 2012 May;36(4):392–9. doi: 10.1002/gepi.21633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MAR, Bender D, Maller J, Sklar P, de Bakker PIW, Daly MJ, Sham PC. PLINK: a toolset for whole-genome association and population-based linkage analysis. Am J Hum Genet. 2007 Sep;81(3):559–75. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rahimov F, Marazita ML, Visel A, Cooper ME, Hitchler MJ, Rubini M, Domann FE, Govil M, Christensen K, Bille C, Melbye M, Jugessur A, Lie RT, Wilcox AJ, Fitzpatrick DR, Green ED, Mossey PA, Little J, Steegers-Theunissen RP, Pennacchio LA, Schutte BC, Murray JC. Disruption of an AP-2alpha binding site in an IRF6 enhancer is associated with cleft lip. Nat Genet. 2008 Nov;40(11):1341–7. doi: 10.1038/ng.242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruczinski I, Kooperberg C, LeBlanc ML. Logic Regression. Journal of Computational and Graphical Statistics. 2003;12:475–511. [Google Scholar]
- VanSteen K. Travelling the world of gene-gene interactions. Brief Bioinform. 2012 Jan;13(1):1–19. doi: 10.1093/bib/bbr012. [DOI] [PubMed] [Google Scholar]
- Yang Y, Topol L, Lee H, Wu J. Wnt5a and Wnt5b exhibit distinct activities in coordinating chondrocyte proliferation and differentiation. Development. 2003 Mar;130(5):1003–15. doi: 10.1242/dev.00324. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.