Abstract
Purpose
To investigate the effect of dose level and anatomical site of injection on the pharmacokinetics of rituximab in mice, and to evaluate the utility of a pharmacokinetic model for describing interspecies differences in subcutaneous absorption between mice and rats.
Methods
Rituximab serum concentrations were measured following intravenous and subcutaneous administration at the back and abdomen of mice. Several approaches were compared for scaling model parameters from estimated values in rats.
Results
The bioavailability of rituximab following subcutaneous injection was inversely related to the dose level and was dependent on the site of injection in mice. The overall rate of absorption was faster in mice as compared to rats. Subcutaneous absorption profiles were well described using the proposed structural model, in which the total receptor concentration, the affinity of rituximab to the receptor, and the degradation rate constant were assumed to be species independent.
Conclusions
Subcutaneous absorption processes show similar trends in rats and mice, although the magnitude differs between species. A mathematical model that combines the absorption of free and bound antibody with presystemic degradation successfully captured rituximab pharmacokinetics in both species, and approaches for sharing and scaling parameters between species were identified.
Keywords: biotherapeutics absorption, interspecies scaling, mathematical modeling, monoclonal antibodies, protein therapeutics
INTRODUCTION
Subcutaneous (SC) injection is a strategic route of administration for chronic delivery of therapeutic proteins, including monoclonal antibodies (mAbs), which provides several advantages over intravenous (IV) injection. However, its clinical implementation can be challenging owing to incomplete bioavailability and restrictions on the volume of single SC injection (1–3). Optimization of the absorption rate and enhancement of the extent of absorption might be required for successful development of SC formulations for human use.
Overall absorption kinetics of proteins and mAbs reflects a complex interplay of multiple processes, including absorption through blood and lymphatic capillaries, transport through the interstitial space, specific and nonspecific binding, and presystemic degradation (1,4–6). Prediction of SC absorption of biotherapeutics in humans from preclinical experiments is largely unsatisfactory, mainly due to the limited understanding of the mechanisms of SC absorption and considerable interspecies differences (1,7). In particular, the structure of the skin and SC space might have a major impact on drug absorption. Although the systemic clearance of mAbs in humans can be predicted relatively well from cynomolgus monkeys (8), no apparent relationships have been established for SC bioavailability among animals and humans. The bioavailability of mAbs in humans is often overestimated based on non-human primate data (1), and examples of scaling absorption kinetics between species are scarce (9,10). Nonlinearities frequently observed in systemic pharmacokinetics and absorption of therapeutic proteins may further complicate data analysis and require the application of more mechanistic models (11,12).
A mathematical model has been developed to study absorption mechanisms of mAbs in rats using rituximab as a model drug (12,13). The bioavailability of rituximab following SC administration decreases inversely with the dose level, and this nonlinear behavior is assumed to manifest from saturation of FcRn-mediated protective binding at the absorption site (14). Co-administration of rituximab with a relatively large dose of nonspecific IgG (both given SC) produces a significant decrease in the extent of rituximab absorption, which further corroborates this hypothesis. Moreover, pharmacokinetic modeling suggests that this binding might serve as one of the absorption mechanisms for mAbs. The important role of FcRn in the SC absorption of mAbs has been shown using FcRn-deficient mice and mAb variants engineered to exhibit altered affinity to FcRn (14,15). In addition to dose-dependence, the anatomical site of injection has a major impact on the rate of absorption of rituximab in rats and also affects the bioavailability, which is in agreement with other therapeutic proteins (16–18). The aim of this study is to investigate the effect of dose and anatomical site of injection on the pharmacokinetics of rituximab in mice. A secondary aim is to evaluate the utility of a previously developed pharmacokinetic model for describing interspecies differences in rituximab absorption between mice and rats.
METHODS
Animals
Male C57BL/6 mice, weighing 18–22 g, were purchased from the Jackson Laboratory Inc. (Bar Harbor, ME). This study was conducted in accordance with an approved protocol by the Institutional Animal Use and Care Committee at the University at Buffalo, State University of New York. Two or three animals were housed in each cage during the study with free access to standard food and water and maintained on a 12/12 h light/dark cycle. Mice were allowed to acclimate for 1 week before study initiation.
Experimental Procedure
Animals were divided into eight groups (n=8–10 each) according to the route of administration and dose level. Each animal received a single injection of rituximab (Rituxan®, 10 mg/mL; Genentech, Inc., San Francisco, CA) by either IV (1 and 40 mg/kg; tail vein) or SC routes (1, 10 and 40 mg/kg; mid back or mid abdomen). The volume of injection was 4 mL/kg (80 μL for 20 g mouse), and the commercially available formulation (10 mg/mL) was diluted with sterile normal saline for low doses. All injections were performed using 29 G needles.
Serial blood samples (15–20 μL) were obtained following drug administration (up to 5 weeks) from the submandibular vein under isoflurane anesthesia using nonheparinized micro-hematocrit tubes (Fisherbrand®, Fisher Scientific, Pittsburgh, PA). Four to six animals were sampled at each time point. Blood was allowed to clot at room temperature for 30–60 min, and serum was separated by centrifugation at 2000 g for 20 min at 4°C. Serum was divided into aliquots and stored at −80°C until analysis.
Analytical Assay
Quantification of rituximab in mouse serum samples was performed using ELISA. The method was used previously for rat serum (12) and was validated for mouse serum in this study. Briefly, rat anti-rituximab IgG2a (clone MB2A4; AbD Serotec, Raleigh, NC) and goat anti-human IgG—peroxidase conjugate (Fc specific; Sigma-Aldrich, St. Louis, MO) were used as capturing and detection antibodies. Plates were developed using o-phenylenediamine (SigmaFast™ OPD, Sigma-Aldrich, St. Louis, MO) and optical density was measured at 492 nm. Samples and standards were prepared at 1:100, 1:1,000, or 1:10,000 dilution using PBS+1%BSA and analyzed in duplicate. The working range of the assay was between 0.25 and 62.5 ng/mL. The calibration curves were fitted with a four-parameter logistic equation.
Pharmacokinetic Modeling
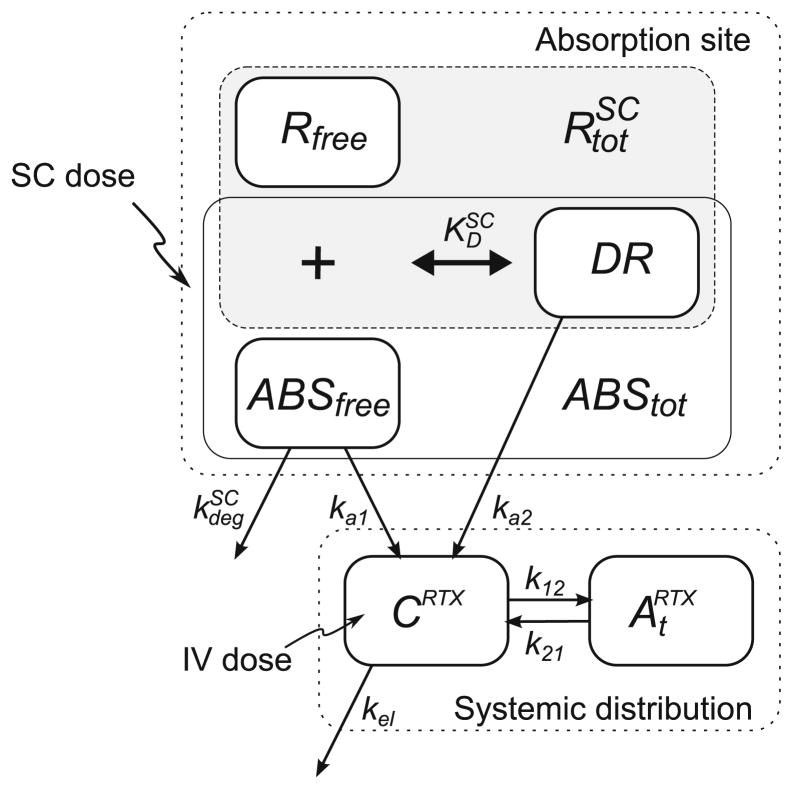
The model used to evaluate the pharmacokinetics of rituximab is based on a model previously developed for rats (Fig. 1) (12). The systemic disposition of rituximab is described by a two-compartment model with linear elimination. The dose is assumed to be administered directly into an absorption compartment (ABS). This differs from the original model, in which an injection compartment precedes the absorption compartment to describe an apparent absorption delay in rats. Such a delay was not observed in mice, and this component was removed from the mouse model. At the absorption site, free antibody (ABSfree) can bind to a receptor (R) to form a complex (DR=ABStot−ABSfree), which is assumed to occur rapidly and characterized by the equilibrium dissociation constant ( ). Free antibody (ABSfree) can also undergo degradation or absorption by first-order processes ( and ka1). The drug-receptor complex delivers antibody to the systemic circulation (CRTX) by a first-order process (ka2). The amount of total receptor at the absorption site was assumed to remain constant with time. Systemic disposition of rituximab includes nonspecific distribution ( ) and first-order elimination (kel). The system is defined by the following differential equations:
| (1) |
| (2) |
| (3) |
| (4) |
with CRTX as the rituximab concentration in the central compartment (with volume Vc), is the amount of rituximab in the peripheral distribution compartment, and k12 and k21 are the first-order transfer rate constants between the central and peripheral compartments. For intravenous administration, CRTX(0) was set equal to Dose/Vc, and initial conditions for Eqs. 1 and 4 were set to zero. For SC administration, ABStot (0) was set equal to the rituximab dose, and initial conditions for Eqs. 3 and 4 were set to zero.
Fig. 1.
Pharmacokinetic model of rituximab following IV and SC administration in mice. The model structure is adapted from Kagan et al. (12) and includes rituximab absorption of both free and bound drug. The systemic distribution follows a standard two-compartment model with linear elimination. ABSfree free drug, R free receptor, and DR drug-receptor complex (DR=ABStot−ABSfree).
Data Analysis
A standard noncompartmental analysis was performed for initial data evaluation using mean rituximab concentration-time profiles. The maximum plasma drug concentration (Cmax) and time to reach Cmax (Tmax) were obtained directly from the experimental data. Terminal half-life, area under the concentration time curve from time zero to infinity (AUC, calculated by linear trapezoidal method), and mean residence time (MRT) were calculated for all data sets. Volume of distribution at steady state (Vss) and clearances were calculated for the IV data sets. Noncompartmental analysis was performed using Phoenix™ WinNonlin® 6.1 (Pharsight, Mountain View, CA).
Several modeling iterations were evaluated to assess the use of the pharmacokinetic model for describing the absorption behavior of rituximab in mice. First, interspecies scaling of systemic disposition parameters was evaluated by applying the power law equation:
| (5) |
with P representing the parameter of interest, BW is body weight, and b is an allometric exponent. Mean body weights of 20 g and 375 g were used for mice and rats. The value of b was fixed to 1 for Vc. For the first-order rate constants kel, k12, and k21, values of 0 and −0.25 were evaluated for the exponent (b). Results were compared to an independent fit of the mouse IV data using the two-compartment model. At the next stage, the absorption in mice was evaluated using two sets of parameters for systemic disposition: 1) the best scaling approach, and 2) the independently fitted parameter set. For the absorption model, the total receptor concentration ( ), the affinity of rituximab to the receptor ( ), and the degradation rate constant ( ) were assumed to be species independent. The rate constants for the absorption of free and bound drug were estimated. Similarly to the rat model (13), a separate rate constant for absorption of the free drug was used for the abdomen and back injection sites; the rate constant for absorption of receptor bound-drug was shared between injection sites.
Model fitting and parameter estimation were performed using MATLAB R2012b (The MathWorks, Natick, MA) with the maximum likelihood method. The variance model was defined as VARi=(σ1+σ2·Y(θ, ti))2, with VARi as the variance of the ith data point, σ1 and σ2 are the variance model parameters, and Y(θ, ti) is the ith predicted value from the pharmacokinetic model. The goodness-of-fit was assessed by system convergence, Akaike Information Criterion, estimator criterion value for the maximum likelihood method, and visual inspection of residuals and fitted curves.
RESULTS
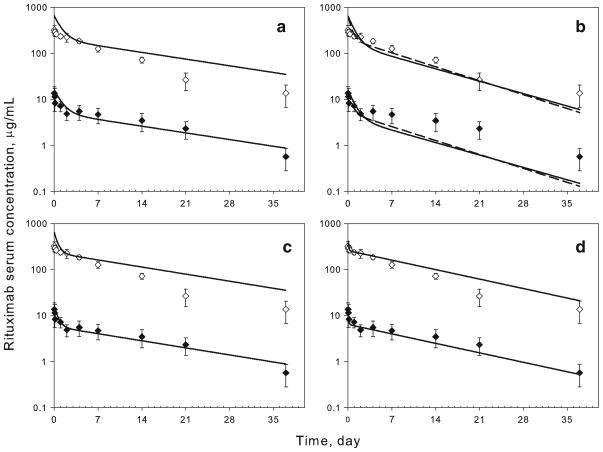
Serum concentration-time profiles of rituximab following intravenous administration to mice (1 and 40 mg/kg) are shown in Fig. 2, and the corresponding pharmacokinetic parameters obtained by noncompartmental analysis are listed in Table I. A slight nonlinearity was observed between the profiles, and dose-normalized concentrations at times 7, 14, and 21 days were statistically different (Student’s two-tailed t-test, p<0.05). The resulting values for the AUC are not dose proportional (Table I). The half-lives of 8 and 11 days is shorter than the half-life observed in rats after IV administration (14 days) (12). Noncompartmental clearance and volume of distribution at steady-state values are similar to values reported for rats (12).
Fig. 2.
Time-course of serum rituximab in mice following IV administration of 1 (filled diamond) and 40 mg/kg (empty diamond). Symbols are mean measured concentrations for rituximab, and error bars represent S.D. (n=4–6). For panels A–C, lines represent model-simulated profiles based on parameters reported previously in rats (12). Volume of the central compartment is set proportional to body weight (Vc ∝ BW1). (a) First-order rate constants were scaled according to the classic power law equation (5) with b=0 for kel, k12, and k21. (b) b=−0.25 for kel, k12, and k21 (solid line) or b=−0.25 for kel and b=0 for k12 and k21 (dashed line). (c) b=0 for kel and b=−0.25 for k12 and k21. (d) Lines represent model fitted profiles
Table I.
Pharmacokinetic Parameters of Rituximab Following IV Administration to Mice
| Parameter | Units | 1 mg/kg | 40 mg/kg |
|---|---|---|---|
| AUC | μg·Day/mL | 121 | 2889 |
| CL | mL/Day/kg | 8.3 | 13.8 |
| Vss | mL/kg | 122 | 156 |
| T1/2 | Day | 11.0 | 8.3 |
| MRT | Day | 14.8 | 11.3 |
Parameters were calculated using noncompartmental analysis of the mean concentration-time profiles. AUC – area under the plasma concentration-time curve; CL clearance; T1/2 terminal half-life; MRT mean residence time; Vss steady-state volume of distribution
Mean serum concentration-time profiles of rituximab injected SC at the back (1, 10, and 40 mg/kg) and abdomen (1, 10, and 40 mg/kg) regions are presented in Fig. 3. The corresponding pharmacokinetic parameters obtained by noncompartmental analysis are listed in Table II. For each of the injection sites, the dose-normalized profiles were not superimposable (data not shown). Injection at the abdomen resulted in a faster absorption as compared to the back injection site.
Fig. 3.
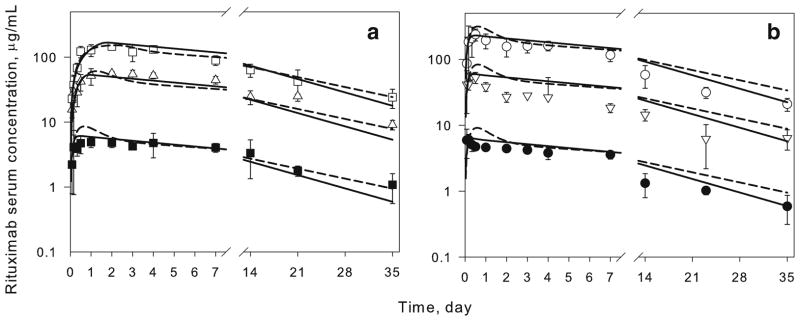
Time-course of serum rituximab in mice following SC administration of 1, 10, and 40 mg/kg at the back (a) and abdomen (b) injection sites. Symbols are mean measured drug concentrations. Lines are model fitted profiles using the final model (Fig. 1) with scaled parameters (dashed lines) or model estimated parameters (solid lines) for systemic rituximab disposition in mice. Error bars represent S.D. (n=4–6).
Table II.
Pharmacokinetic Parameters of Rituximab Following SC Administration to Mice
| Parameter | Units | Back
|
Abdomen
|
||||
|---|---|---|---|---|---|---|---|
| 1 mg/kg | 10 mg/kg | 40 mg/kg | 1 mg/kg | 10 mg/kg | 40 mg/kg | ||
| AUC | μg·Day/mL | 118 | 1166 | 2651 | 75 | 610 | 2742 |
| Cmax | μg/mL | 4.9 | 56.1 | 146 | 6.1 | 56.4 | 239 |
| T1/2 | Day | 14.8 | 12.8 | 13.2 | 10.9 | 13.8 | 10.3 |
| MRT | Day | 21.1 | 18.4 | 19.3 | 15.5 | 20.4 | 14.7 |
| Tmax | Day | 1.0 | 2.0 | 2.0 | 0.17 | 0.33 | 0.50 |
Parameters were calculated using noncompartmental analysis of the mean concentration-time profiles. AUC area under the plasma concentration-time curve; Cmax maximal serum concentration; T1/2 terminal half-life; MRT mean residence time; Tmax time to achieve Cmax
Several approaches for scaling the systemic disposition parameters of rituximab from the values estimated in rats were evaluated. The volume of the central compartment was assumed to be directly proportional to body weight in all cases (i.e., allometric exponent b=1). In Fig. 2a, all rate constants were kept identical between rats and mice, which corresponds to scaling of elimination and distribution clearances directly proportional to changes in body weight. Figure 2b shows two simulations, in which the elimination rate constant was scaled using an allometric exponent of −0.25 (corresponds to scaling of elimination clearance using exponent of 0.75) and distribution rate constants were scaled with an exponent of either −0.25 or 0. Both simulations demonstrate very similar profiles that underestimate the terminal half-life. The best prediction was obtained in the case in which the elimination rate constant was kept identical between species and the distribution rate constants were scaled using an allometric exponent of −0.25 (Fig. 2c). The parameter values are listed in Table III. A better prediction of rituximab concentrations during the first 4 days was obtained as compared to using identical parameter values for mice and rats (Fig. 2a). This combination of scaled parameters was utilized for assessing the absorption of rituximab in mice.
Table III.
Final Pharmacokinetic Model Parameters of Rituximab in Rodents
| Parameter | Units | Rat | Mouse (scaled disposition terms)
|
Mouse (fitted disposition terms)
|
|||
|---|---|---|---|---|---|---|---|
| Mean | Mean | %CV | Mean | %CV | |||
| Vc | 10−2 L/kg | 6.10 | 6.10 | –a | 8.40 | 16 | |
| k12 | day−1 | 0.479 | 0.997 | –a | 4.30 | 69 | |
| k21 | day−1 | 0.305 | 0.635 | –a | 5.14 | 49 | |
| kel | day−1 | 0.137 | 0.137 | –a | 0.125 | 16 | |
|
|
day−1 | 0.513 | 0.513 | –b | 0.513 | –b | |
|
|
nmol | 10.9 | 10.9 | –b | 10.9 | –b | |
|
|
nmol | 3.00 | 3.00 | –b | 3.00 | –b | |
| ka2 | day−1 | 0.295 | 3.19 | 12 | 6.90 | 13 | |
| ka1 back | day−1 | 6.30·10−2 | 0.335 | 17 | 0.474 | 22 | |
| ka1 abdomen | day−1 | 0.242 | 2.38 | 13 | 4.68 | 17 | |
In addition to scaling approaches, a two-compartment model with linear elimination was independently fitted to the mouse data (Fig. 2d). The fitted profiles were superior to any of the scaling approaches in describing the IV data. The final parameter values are listed in Table III, and these values were utilized in evaluating the absorption behavior of rituximab in mice as compared to using the scaled disposition terms (Fig. 2c).
Model-fitted rituximab concentration-time profiles following SC administration at the back and abdomen injection sites are compared with the experimental data in Fig. 3. Both disposition models resulted in similarly good descriptions of the SC experimental data. The estimated values for the rate of absorption of free and bound rituximab are similar (Table III). Utilization of independently fitted parameters for systemic disposition (solid lines) resulted in a slightly lower objective function as compared to the model with scaled parameters for systemic distribution, suggesting an improvement in model performance.
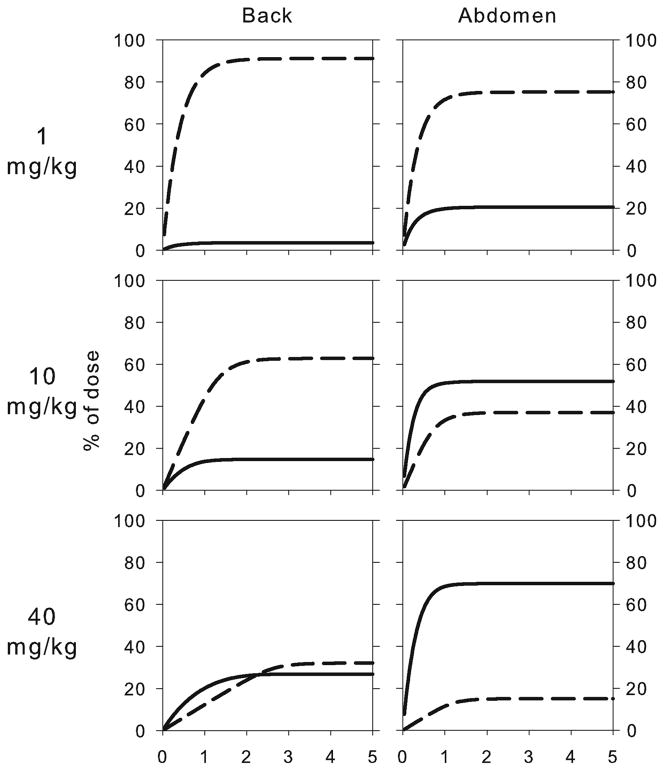
The final pharmacokinetic model (Fig. 1) with scaled systemic disposition parameters was used to simulate the relative contribution of the two absorption pathways to rituximab SC bioavailability following administration at three dose levels at two absorption sites (Fig. 4). In addition, the overall apparent bioavailability of rituximab after SC injection was calculated based on model projections (Table IV). Similar to the rat study, the bioavailability was inversely related to the dose level and was also affected by the anatomical site of injection.
Fig. 4.
Simulated percent of the rituximab dose absorbed as free (solid line) or bound (dashed line) drug following SC administration at the back and abdomen. Simulations were performed using the final model (Fig. 1) with scaled parameters for systemic disposition (Table III).
Table IV.
Model-Based Calculation of Mean Rituximab SC Bioavailability
| Site of injection | Dose, mg/kg | Bioavailability, % | |
|---|---|---|---|
| Model with disposition terms scaled | Model with disposition terms fitted | ||
| Back | 1 | 95 | 97 |
| 10 | 77 | 87 | |
| 40 | 59 | 71 | |
| Abdomen | 1 | 96 | 98 |
| 10 | 88 | 94 | |
| 40 | 85 | 92 | |
DISCUSSION
Mice and rats are the most commonly used animals in preclinical drug development, and it is important to understand the differences and similarities in the absorption behavior of mAbs in these rodent species for proper interpretation and integration into the development process. Development of common mathematical models and approaches for sharing (or scaling) of parameters among species may provide an efficient way for reconciling data from different species and predicting pharmacokinetic and pharmacodynamic properties in humans, as shown in recent studies with exenatide and amphotericin B (9,19). The binding of mAbs to their pharmacological targets can affect their pharmacokinetics (so called target-mediated drug disposition) (20). Since rituximab targets CD20 on human B cells, the utilization of species that lack the pharmacological target can be advantageous for investigating kinetic processes that are regulated by common mechanisms for this class of compounds (e.g., large size and Fc region).
The final structural model for rituximab pharmacokinetics in mice (Fig. 1) is almost identical to the previously developed model in rats. The only difference in the structural model is the removal of a delay compartment for SC injections. Although the rat model included linear first-order disposition and neither rats nor mice express the pharmacological target for rituximab (i.e., human CD20), there is a slight nonlinearity in the IV pharmacokinetic profiles in mice (Fig. 2). Hence, additional model permutations were evaluated in an attempt to improve model performance, such as incorporating FcRn-mediated endosomal recycling of mAbs at the systemic level (21). This modification did not improve the fitted profiles for mouse pharmacokinetics after IV administration (data not shown), which is in agreement with a prior evaluation of this process in rats, in which the endosomal-recycling model provided fits that were similar to the those obtained using the standard two-compartment model and did not influence subsequent estimation of the absorption model parameters (13). The pharmacokinetics of rituximab was also linear in nude mice following IV administration of 0.1, 1 and 10 mg/kg (Zhao, Kagan, Ovacik, and Mager unpublished data). Thus, for simplicity, further data analysis was performed using a standard two-compartment model with linear elimination to describe the systemic pharmacokinetics of rituximab.
Several common rules for scaling parameters of the two-compartment model were evaluated for predicting the IV pharmacokinetic profiles of rituximab in mice. The best projection of both the terminal slope and initial concentration was obtained with scaling the volume of distribution directly with body weight and setting the allometric exponent to −0.25 for the distribution rate constants (Eq. 5, Fig. 2c). The elimination rate constant was shared between the two species. This is equivalent to scaling the systemic clearance directly proportional to body weight (i.e., CL=kel•Vc and Vc ∝ BW1). The degradation of mAbs is an intracellular process (within the endosomal space), and so the clearance of the drug through this pathway may be species independent and proportional to body size. A similar approach was applied for scaling the internalization rate constant (a cellular process) for interferons and exenatide (9,11). This hypothesis is further supported by the independent fitting of the model to the mouse data (Fig. 2d), which resulted in an estimate of kel that is similar to the prior estimated value in rats (0.125 vs. 0.137 day−1, Table III). Interestingly, scaling of the distribution rate constants (k12 and k21 ∝ BW−0.25) did improve model performance, which is in contrast to findings for interferons and exenatide that exhibit species independent terms (9,11).
Overall, the SC absorption of rituximab in mice shows similar tendencies to the behavior of rituximab in rats. At both tested injection sites (back and abdomen), the extent of absorption was inversely related to the dose level (Table IV); however, the magnitude of the nonlinear absorption was less pronounced as compared to rats (12). In addition, the absorption of rituximab from the abdomen was faster than at the back (Tmax values of 0.17–0.5 vs. 1–2 days), with a similar trend found in rats (1.5–2.2 vs. 2.5–4.6 days, respectively (12)).
Traditional allometric and model-based projections of interspecies pharmacokinetics of proteins and antibodies are usually focused on total systemic clearance and volume of distribution (8,22,23). The scalability of the absorption kinetics has not been fully investigated, and available information is limited. The first-order absorption rate constant for pegylated erythropoietin following SC administration was estimated to scale with an allometric exponent of −0.147 (based on four species) (24). The allometric exponent was calculated as −0.349 for the unmodified recombinant human protein (using erythropoietin data from rats, monkeys, and humans) (10). Such conventional allometric relationships, however, do not account for dose-dependent pharmacokinetic processes (e.g., rituximab absorption). Sometimes separate values for the absorption rate constant or bioavailability are estimated for each dose level (25,26). Although useful for capturing observed data, this approach provides little insight into the mechanisms of drug absorption and cannot be effectively applied for interspecies scaling. Another approach is to scale model parameters that define a nonlinear process. For example, although the exact mechanism is unknown, the SC absorption of exenatide can be described using a Michaelis-Menten function, and species-dependent Vmax and Km terms were required (9). Correlations between these parameters and body weight (for mice, rats, and monkeys) were successfully used to predict the SC pharmacokinetic profiles of exenatide in humans. In contrast to exenatide, involvement of the specific binding mechanism (i.e., FcRn) in the absorption of mAbs has been suggested (13–15), which supports the use of the proposed model structure for rituximab (Fig. 1).
The final pharmacokinetic model structure (Fig. 1) provided good descriptions of the SC absorption of rituximab in mice (Fig. 3). Due to the high degree of homology (91%) in the FcRn peptide sequence between mice and rats (27), it was assumed that the binding affinity of FcRn to rituximab ( ) was similar between the species. Furthermore, the amount of binding receptor and the first-order degradation rate constant at the absorption site were assumed to be the same. Utilization of scaled or independently estimated parameters for systemic disposition resulted in a minimal change in estimates of the absorption rate constants for free and bound rituximab (within 2-fold, Table III). Utilization of the model allowed for prediction of the relative contribution of the two absorption pathways into overall bioavailability at the two injection sites and for different dose levels (Fig. 4 and Table IV). Receptor-mediated transport accounts for approximately 91, 63, and 32% of the absorption for the 1, 10, and 40 mg/kg doses injected at the back. The corresponding values for the abdomen injection site are 75, 37, and 15%.
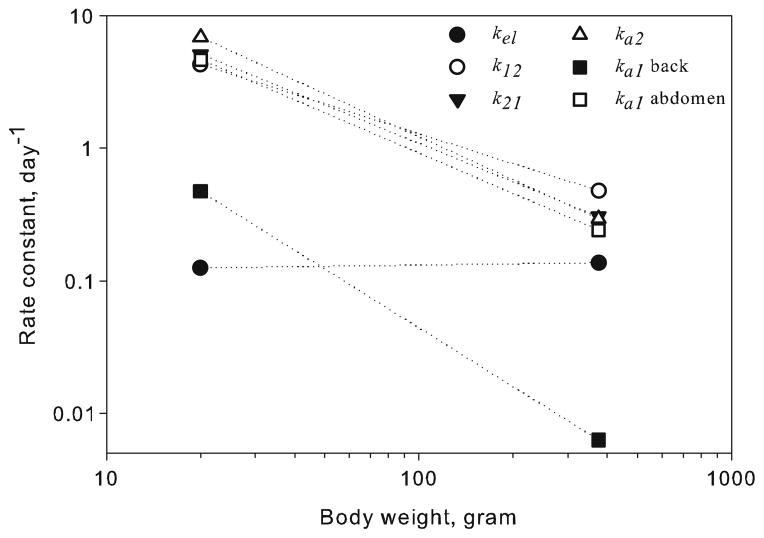
A comparison of independently estimated first-order rate constants in mice and rats is shown in Fig. 5. Interestingly, the absorption rate constants for free (ka1) and bound (ka2) rituximab at both injection sites scale similarly to the distribution rate constants. Data from additional species are required to qualify the interspecies relationships identified in this study. Only limited data on rituximab given by the SC route in humans is available, and several studies are ongoing (3,28,29). However, these results can be potentially expanded for describing the absorption of other mAbs in rodents.
Fig. 5.
Comparison between the model-estimated first-order rate constants in rats and mice as a function of body weight. Rat data were obtained from Kagan et al. (12), and the mouse parameters are from estimating parameters associated with systemic disposition (Table III).
Some methodological differences and limitations between this study and the prior analysis in rats must be considered. In the rat studies, the highest dose (40 mg/kg) was only tested after SC injection at the back site. Due to a limitation of the amount of blood that can be collected from a single animal, a staggered sampling design was used in the present mouse study (i.e., not all animals were sampled at each time point). Sampling limitations might have introduced additional variability in this mouse study as compared to the rat, in which repeated measurements are more feasible. Finally, the amount of endogenous IgG at the absorption site is considered to be negligible and does not interfere with the absorption process.
In summary, we evaluated the SC absorption of rituximab in mice and differences and similarities in absorption and systemic disposition between mice and rats. The SC bioavailability of rituximab in mice decreases with increasing dose levels, although the extent of nonlinearity was less pronounced as compared to rats. The anatomical site of SC injection also significantly affects the rate of absorption. A mathematical model that combines the absorption of free and bound antibody (presumably to FcRn) with pre-systemic degradation successfully captured rituximab pharmacokinetics in both species, and approaches for sharing and scaling parameters between species were identified. This study further emphasizes that a single dose level may not be sufficient for investigation of species differences in the SC absorption of mAbs. Further research is needed to define suitable ranges of dose levels and standardization of study designs for assessing the SC pharmacokinetics of mAbs in preclinical experiments.
Acknowledgments
This work was supported, in part, by the Center for Protein Therapeutics, University at Buffalo, State University of New York.
ABBREVIATIONS
- FcRn
Neonatal Fc receptor
- IV
Intravenous
- mAbs
Monoclonal antibodies
- SC
Subcutaneous
Contributor Information
Leonid Kagan, Email: lkagan@pharmacy.rutgers.edu, Department of Pharmaceutics, Ernest Mario School of Pharmacy Rutgers, The State University of New Jersey, 160 Frelinghuysen Road Piscataway, New Jersey 08854, USA.
Jie Zhao, Department of Pharmaceutical Sciences University at Buffalo, State University of New York, Buffalo, New York, USA.
Donald E. Mager, Department of Pharmaceutical Sciences University at Buffalo, State University of New York, Buffalo, New York, USA
References
- 1.Richter WF, Bhansali SG, Morris ME. Mechanistic determinants of biotherapeutics absorption following SC administration. AAPS J. 2012;14(3):559–70. doi: 10.1208/s12248-012-9367-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bittner B, Schmidt J. Subcutaneous administration of monoclonal antibodies in oncology as alternative to established intravenous infusion. Pharm Ind. 2012;74(4):638–43. [Google Scholar]
- 3.Aue G, Lindorfer MA, Beum PV, Pawluczkowycz AW, Vire B, Hughes T, et al. Fractionated subcutaneous rituximab is well-tolerated and preserves CD20 expression on tumor cells in patients with chronic lymphocytic leukemia. Haematologica. 2010;95(2):329–32. doi: 10.3324/haematol.2009.012484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Swartz MA. The physiology of the lymphatic system. Adv Drug Deliv Rev. 2001;50(1–2):3–20. doi: 10.1016/s0169-409x(01)00150-8. [DOI] [PubMed] [Google Scholar]
- 5.Porter CJ, Charman SA. Lymphatic transport of proteins after subcutaneous administration. J Pharm Sci. 2000;89(3):297–310. doi: 10.1002/(SICI)1520-6017(200003)89:3<297::AID-JPS2>3.0.CO;2-P. [DOI] [PubMed] [Google Scholar]
- 6.Kagan L, Gershkovich P, Mendelman A, Amsili S, Ezov N, Hoffman A. The role of the lymphatic system in subcutaneous absorption of macromolecules in the rat model. Eur J Pharm Biopharm. 2007;67(3):759–65. doi: 10.1016/j.ejpb.2007.04.002. [DOI] [PubMed] [Google Scholar]
- 7.McDonald TA, Zepeda ML, Tomlinson MJ, Bee WH, Ivens IA. Subcutaneous administration of biotherapeutics: current experience in animal models. Curr Opin Mol Ther. 2010;12(4):461–70. [PubMed] [Google Scholar]
- 8.Deng R, Iyer S, Theil FP, Mortensen DL, Fielder PJ, Prabhu S. Projecting human pharmacokinetics of therapeutic antibodies from nonclinical data: What have we learned? MAbs. 2011;3(1):61–6. doi: 10.4161/mabs.3.1.13799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chen T, Mager DE, Kagan L. Interspecies modeling and prediction of human exenatide pharmacokinetics. Pharm Res. 2013;30(3):751–60. doi: 10.1007/s11095-012-0917-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Woo S, Jusko WJ. Interspecies comparisons of pharmacokinetics and pharmacodynamics of recombinant human erythropoietin. Drug Metab Dispos. 2007;35(9):1672–8. doi: 10.1124/dmd.107.015248. [DOI] [PubMed] [Google Scholar]
- 11.Kagan L, Abraham AK, Harrold JM, Mager DE. Interspecies scaling of receptor-mediated pharmacokinetics and pharmacodynamics of type I interferons. Pharm Res. 2010;27(5):920–32. doi: 10.1007/s11095-010-0098-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kagan L, Turner MR, Balu-Iyer SV, Mager DE. Subcutaneous absorption of monoclonal antibodies: role of dose, site of injection, and injection volume on rituximab pharmacokinetics in rats. Pharm Res. 2012;29(2):490–9. doi: 10.1007/s11095-011-0578-3. [DOI] [PubMed] [Google Scholar]
- 13.Kagan L, Mager DE. Mechanisms of subcutaneous absorption of rituximab in rats. Drug Metab Dispos. 2013;41(1):248–55. doi: 10.1124/dmd.112.048496. [DOI] [PubMed] [Google Scholar]
- 14.Wang W, Wang EQ, Balthasar JP. Monoclonal antibody pharmacokinetics and pharmacodynamics. Clin Pharmacol Ther. 2008;84(5):548–58. doi: 10.1038/clpt.2008.170. [DOI] [PubMed] [Google Scholar]
- 15.Deng R, Meng YG, Hoyte K, Lutman J, Lu Y, Iyer S, et al. Subcutaneous bioavailability of therapeutic antibodies as a function of FcRn binding affinity in mice. MAbs. 2012;4(1):101–9. doi: 10.4161/mabs.4.1.18543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kota J, Machavaram KK, McLennan DN, Edwards GA, Porter CJ, Charman SA. Lymphatic absorption of subcutaneously administered proteins: influence of different injection sites on the absorption of darbepoetin alfa using a sheep model. Drug Metab Dispos. 2007;35(12):2211–7. doi: 10.1124/dmd.107.015669. [DOI] [PubMed] [Google Scholar]
- 17.Beshyah SA, Anyaoku V, Niththyananthan R, Sharp P, Johnston DG. The effect of subcutaneous injection site on absorption of human growth hormone: abdomen versus thigh. Clin Endocrinol (Oxford) 1991;35(5):409–12. doi: 10.1111/j.1365-2265.1991.tb03557.x. [DOI] [PubMed] [Google Scholar]
- 18.Macdougall IC, Jones JM, Robinson MI, Miles JB, Coles GA, Williams JD. Subcutaneous erythropoietin therapy: comparison of three different sites of injection. Contrib Nephrol. 1991;88:152–6. doi: 10.1159/000419525. discussion 7–8. [DOI] [PubMed] [Google Scholar]
- 19.Kagan L, Gershkovich P, Wasan KM, Mager DE. Dual physiologically based pharmacokinetic model of liposomal and nonliposomal amphotericin B disposition. Pharm Res. 2014;31(1):35–45. doi: 10.1007/s11095-013-1127-z. [DOI] [PubMed] [Google Scholar]
- 20.Mager DE. Target-mediated drug disposition and dynamics. Biochem Pharmacol. 2006;72(1):1–10. doi: 10.1016/j.bcp.2005.12.041. [DOI] [PubMed] [Google Scholar]
- 21.Hansen RJ, Balthasar JP. Pharmacokinetic/pharmacodynamic modeling of the effects of intravenous immunoglobulin on the disposition of antiplatelet antibodies in a rat model of immune thrombocytopenia. J Pharm Sci. 2003;92(6):1206–15. doi: 10.1002/jps.10364. [DOI] [PubMed] [Google Scholar]
- 22.Dong JQ, Salinger DH, Endres CJ, Gibbs JP, Hsu CP, Stouch BJ, et al. Quantitative prediction of human pharmacokinetics for monoclonal antibodies: retrospective analysis of monkey as a single species for first-in-human prediction. Clin Pharmacokinet. 2011;50(2):131–42. doi: 10.2165/11537430-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 23.Wang W, Prueksaritanont T. Prediction of human clearance of therapeutic proteins: simple allometric scaling method revisited. Biopharm Drug Dispos. 2010;31(4):253–63. doi: 10.1002/bdd.708. [DOI] [PubMed] [Google Scholar]
- 24.Jolling K, Perez Ruixo JJ, Hemeryck A, Vermeulen A, Greway T. Mixed-effects modelling of the interspecies pharmacokinetic scaling of pegylated human erythropoietin. Eur J Pharm Sci. 2005;24(5):465–75. doi: 10.1016/j.ejps.2005.01.002. [DOI] [PubMed] [Google Scholar]
- 25.Mager DE, Neuteboom B, Efthymiopoulos C, Munafo A, Jusko WJ. Receptor-mediated pharmacokinetics and pharmacodynamics of interferon-beta1a in monkeys. J Pharmacol Exp Ther. 2003;306(1):262–70. doi: 10.1124/jpet.103.049502. [DOI] [PubMed] [Google Scholar]
- 26.Gao W, Jusko WJ. Target-mediated pharmacokinetic and pharmacodynamic model of exendin-4 in rats, monkeys, and humans. Drug Metab Dispos. 2012;40(5):990–7. doi: 10.1124/dmd.111.042291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rath T, Kuo TT, Baker K, Qiao SW, Kobayashi K, Yoshida M, et al. The immunologic functions of the neonatal Fc receptor for IgG. J Clin Immunol. 2013;33 (Suppl 1):S9–17. doi: 10.1007/s10875-012-9768-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Salar A, Bouabdallah R, McIntyre C, Sayyed P, Bittner B. A two-stage phase Ib stufy to investigate the pharmacokinetics, safety and tolerability of subcutaneous rituximab in patients with follicular lymphoma as part of maintenance treatment. 53rd American Society of Hematology Annual Meeting and Exposition; December 10–13, 2011; San Diego, CA. 2010. [Google Scholar]
- 29.Assouline S, Buccheri V, Delmer A, Doelken G, Gaidano G, McIntyre C, et al. Subcutaneous rituximab in combination with fludarabine and cyclophosphamide for patients with CLL: initial results of a phase Ib study (SAWYER [BO25341]) show non-inferior pharmacokinetics and comparable safety to that of intravenous rituximab. 54th American Society of Hematology Annual Meeting and Exposition; December 8–11, 2012; Atlanta, GA. 2012. [Google Scholar]