The Generalization of Visuomotor Learning to Untrained Movements and Movement Sequences Based on Movement Vector and Goal Location Remapping

Abstract

The planning of goal-directed movements is highly adaptable; however, the basic mechanisms underlying this adaptability are not well understood. Even the features of movement that drive adaptation are hotly debated, with some studies suggesting remapping of goal locations and others suggesting remapping of the movement vectors leading to goal locations. However, several previous motor learning studies and the multiplicity of the neural coding underlying visually guided reaching movements stand in contrast to this either/or debate on the modes of motor planning and adaptation. Here we hypothesize that, during visuomotor learning, the target location and movement vector of trained movements are separately remapped, and we propose a novel computational model for how motor plans based on these remappings are combined during the control of visually guided reaching in humans. To test this hypothesis, we designed a set of experimental manipulations that effectively dissociated the effects of remapping goal location and movement vector by examining the transfer of visuomotor adaptation to untrained movements and movement sequences throughout the workspace. The results reveal that (1) motor adaptation differentially remaps goal locations and movement vectors, and (2) separate motor plans based on these features are effectively averaged during motor execution. We then show that, without any free parameters, the computational model we developed for combining movement-vector-based and goal-location-based planning predicts nearly 90% of the variance in novel movement sequences, even when multiple attributes are simultaneously adapted, demonstrating for the first time the ability to predict how motor adaptation affects movement sequence planning.

Introduction

Although every voluntary movement is shaped by motor learning, the mechanisms underlying this adaptability remain unclear. A reductionist approach to understanding these mechanisms would entail the identification of the features used for motor planning, followed by an examination of how those features adapt. Along these lines, a central theory in motor control posits that the key feature of motor planning is the movement vector (MV); that is, the plans for point-to-point reaching movements are internally represented as movement vectors from start locations (SLs) to movement goals, and the adaptive changes in motor planning are driven by the remapping of movement vectors (Georgopoulos et al., 1986; Caminiti et al., 1991; Gordon et al., 1994; Shadmehr and Mussaivaldi, 1994; Rossetti et al., 1995; Krakauer et al., 2000; Sober and Sabes, 2003, 2005; Wang and Sainburg, 2005; Tanaka et al., 2009). Correspondingly, neurophysiological and behavioral studies have shown that adaptive changes in motor planning can often be explained by the remapping of movement vectors (Wise et al., 1998; Krakauer et al., 2000; Paz et al., 2003; Wang and Sainburg, 2005; Tanaka et al., 2009). The movement vector planning hypothesis is further supported by the generalization of sensorimotor learning to movements with similar movement vectors, even when other attributes, such as start or goal locations (GLs), are altered (Krakauer et al., 2000; Wang and Sainburg, 2005).

However, several previous studies have shown that adaptation to visuomotor transformations is not limited to movement vector learning (Simani et al., 2007; Malfait et al., 2008; Cressman and Henriques, 2009; Izawa and Shadmehr, 2011; Salomonczyk et al., 2011). These studies have found a small but significant proprioceptive recalibration of hand position following adaptation to visuomotor transformations that directly affect movement planning because the motor system weighs visual and proprioceptive sensory information to estimate the start location of movements (Rossetti et al., 1995; Sober and Sabes, 2003, 2005). Moreover, it would be surprising if visuomotor adaptation was based entirely on the remapping of a single feature, either movement vectors or goal locations, given what we know about the richness and diversity in the neural coding of movement representations. In particular, movement vectors, start locations, and goal locations are all represented in motor planning areas and any or all of these features could be remapped during motor adaptation (Graziano et al., 1994; Lacquaniti et al., 1995; Duhamel et al., 1997; Batista et al., 1999; Avillac et al., 2005; Buneo and Andersen, 2006; Pesaran et al., 2006). In line with this idea, previous findings have suggested that location-based and movement-vector-based control may be distinct processes that are differentially remapped by motor adaptation (Lackner and Dizio, 1994; Dizio and Lackner, 1995; Kurtzer et al., 2005; Ghez et al., 2007; Scheidt and Ghez, 2007; Simani et al., 2007). However, the way in which these features are combined during motor planning is not yet well understood.

Here we hypothesize that, during motor adaptation, the target location and movement vector are differentially remapped, and that these features contribute to motor planning with weightings independent of the amount of remapping. If this were the case, motor adaptation would depend on three distinct factors: the amount of movement vector remapping, the amount of goal location remapping, and the differential weighting of movement-vector-based planning and goal-location-based planning. We begin by designing a series of experiments that dissociate the effects of motor adaptation on movement-vector-based and goal-location-based planning, allowing us to quantify the contributions of these three factors for both individual movements and movement sequences. We then test the idea that these three factors can be used to characterize the planning of goal-directed movement sequences by building and testing a combined remapped feature (CRF) model that quantitatively predicts the effects of motor adaptation based on separate contributions from these factors. Remarkably, we find that this model can predict nearly 90% of the variance introduced by the effects of motor adaptation on novel movement sequences.

Materials and Methods

Participants.

Ninety-three naive neurologically intact adults (53 female, three left-handed) between the ages of 18 and 59 participated in this study. Data from three subjects were not included because they could not perform the task consistently. One could not consistently move with the requested rapidity, one was unable to consistently perform movement sequences, and one subject failed to show consistent adaptation to the trained visuomotor rotations. All experimental procedures were approved by Harvard's Committee on the Use of Human Subjects, and all subjects provided informed written consent before the experiment began.

Apparatus.

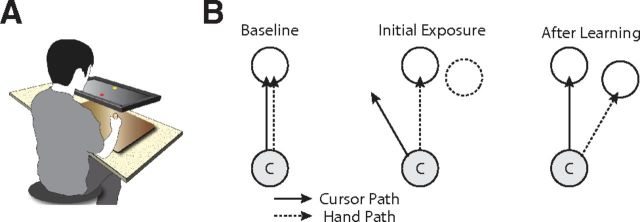
The same apparatus was used in all three experiments in this study (See Fig. 1A). Subjects sat at a desk facing a horizontal LCD monitor. The height of the chair was adjusted at the start of each experiment so that the subject was in a comfortable position for viewing and reaching under the LCD monitor. Underneath the monitor, using a standard power grip as illustrated in Figure 1A, subjects grasped and moved a vertically oriented foam handle (cylindrical with a 25 mm diameter) that contained an embedded stylus. Movements were performed on top of a digitizing tablet that recorded hand position (12 inches by 19 inches; Intuos3, WaCom), and the foam cylinder was lined from below with Teflon tape so that it could slide smoothly over the tablet's surface. The subject's midline was aligned with the center of the digitizing tablet which corresponded to the center of the workspace and the LCD monitor. Vision of the tablet and the subject's arm were obstructed by the LCD monitor for the duration of the experiment.

Figure 1.

Basic experimental setup. A, Illustration of the experimental apparatus. B, Visuomotor rotation learning. During the baseline period, the cursor path matches the hand path. On initial exposure to a visuomotor rotation, the subject's hand movements continue as in baseline, but the cursor movements are rotated. The subject learns to rotate his hand movements so that the cursor moves straight to the target.

General experiment protocol.

This study included three different experiments in which subjects made arm reaching movements while grasping a foam handle with their dominant hand. During each experiment, a digitizing tablet recorded hand position, and a 0.25 cm diameter cursor represented this position on the monitor. A +30% visual magnification was applied to the cursor such that a 1.0 cm hand movement resulted in a 1.3 cm cursor movement; this magnification was present from the very first movement throughout the duration of the experiment, independent of applied visuomotor rotations and should not affect rotation learning or its transfer. Subjects were instructed to perform two types of visually guided movements: individual point-to-point movements 9.0 cm in length and movement sequences that consisted of two point-to-point submovements, each 9.0 cm in length. The individual movements were either performed from the center circle to one of the six peripheral targets, as shown in the left column of Figure 2A, or between two adjacent peripheral targets. The center circle and all six peripheral target circles were 1.2 cm in diameter in hand space. For movement sequences, the first submovement began at the center circle and was directed at one of the six peripheral targets, and the second submovement started at the end of the first submovement and was directed toward one of the two adjacent peripheral targets.

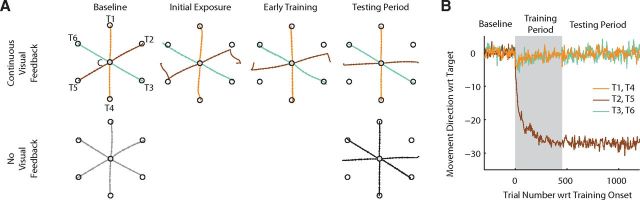
Figure 2.

Motor performance during the baseline, training, and testing periods. A, Top, Hand paths for movements to each of the six peripheral targets with continuous visual feedback during baseline, initial exposure to rotation, early training, and the testing period. Thirty degree rotations were applied on movements from C to T2 and from C to T5 during the training and testing periods. Bottom, Hand paths for no-visual-feedback probe trials to each target. Note that targets are drawn to scale; in subsequent figures targets are drawn larger for ease of viewing. Hand paths in the baseline and testing periods are across-subject averages; however, individual movements are shown for the initial exposure and early training epochs to avoid unnecessary smoothing. B, Learning curves showing the average movement direction measured 100 ms after movement onset over the course of an experiment. Trace colors match the movement colors in A.

The targets shown in Figure 2A illustrate the location of the six targets and center circle (C), drawn to scale. At the start of each trial, a target was displayed for 250 ms before the go cue. During this waiting interval, the center circle was colored yellow, and subjects were instructed to continue holding the cursor inside the center circle. After 250 ms, the color of the center circle changed to purple, cueing subjects to move to the displayed target. Auditory rewards were provided following individual movement trials based on two criteria, movement duration and movement end point. Movement duration was defined as the amount of time during which hand velocity exceeded 5.0 cm/s. The time of movement onset was determined as the time at which hand velocity first exceeded and remained above 5.0 cm/s for 100 ms, while the time of the movement end point was defined as the time at which hand velocity first decreased below and remained below 5.0 cm/s for 300 ms. Subjects received auditory reward following movements with 200–400 ms duration with locations of movement end points inside the presented target. Movement direction was measured as the angle between the vector from hand position at movement start to that at 100 ms into the movement and the vector from the center of the start location and the center of the intended target. Note, however, that we focused our analysis on the end points rather than the movement directions of the no-visual-feedback probe trials because, compared to analysis of movement direction, this allowed for two-dimensional rather than one-dimensional information about adaptive changes in movement planning. Following each trial, the subject returned the cursor to the center circle. We assessed the feedforward movement plan by removing visual feedback of the cursor on selected individual movement trials, which we refer to as probe or test trials (Fig. 2A, bottom row), and on all movement sequence trials. Movements from the center circle to each of the peripheral targets were administered with visual feedback on ∼50% of the trials during the baseline and testing periods. In contrast, individual movements between peripheral target locations and movement sequences used to probe the effects of adaptation were never administered with visual feedback. Visual feedback was restored before the start of the following trial when the cursor was within 2.0 cm of the center circle so that subjects could position their hands for the next trial.

All experiments followed the same general paradigm (Fig. 2B), which consisted of 1950 trials spread over four experiment periods. First, subjects were administered a 300 trial familiarization period, which consisted entirely of individual movements with visual feedback so that they could become accustomed to the task instructions and learn the required movement speed (data not shown in Fig. 2). Following the familiarization period, subjects performed 300 trials during which movement sequences and no-visual-feedback trials (Fig. 2A, bottom left) were intermixed with continuous visual-feedback trials (Fig. 2A, top left) to gauge the baseline performance of the feedforward motor system, before the onset of visuomotor rotation learning.

The training period, which followed the baseline period, consisted of 450 continuous visual-feedback trials during which subjects were exposed to one of several possible patterns of visuomotor rotations (Krakauer et al., 1999, 2000; Wang and Sainburg, 2005; Mazzoni and Krakauer, 2006; Ghez et al., 2007; Scheidt and Ghez, 2007; Cressman and Henriques, 2009; Izawa and Shadmehr, 2011). The visuomotor rotations that we used in this study were either +30° (counterclockwise), −30° (clockwise), or 0° (no rotation). On initial exposure to a nonzero visuomotor rotation, subjects make a hand movement directly to the target, resulting in a cursor movement that is rotated off course around the center circle by ±30°, as shown in the middle panel of Figure 1B. However, with practice, subjects reduce the errors in the cursor movements by performing hand movements that are rotated in the opposite direction of the applied visual rotation (Fig. 1B, right). In Experiments 1 and 2, nonzero rotations were trained to two of the six peripheral target locations, and in Experiment 3, nonzero rotations were trained to four of the six peripheral target locations.

The testing period, which followed the training period, consisted of 900 trials of which approximately half were no-visual-feedback movement sequence, probe, or test trials used to assess the transfer of motor adaptation. The remaining trials were pseudorandomly intermixed continuous visual feedback trials used to reinforce the visual rotations that were trained for each target location. In each experiment, the same visuomotor rotation pattern was applied during the training and testing periods; the specifics of these patterns will be described later. The experiment was performed in 150 trial blocks with rest breaks of 1–5 min between blocks. Thus there was always a rest break at the end of each experimental period and a single rest break was provided in the familiarization and baseline periods, whereas two breaks were provided in the training period, and five in the testing period.

Design principles for Experiments 1–3.

The experiments we conducted in this study were inspired by a computational model of motor planning that we develop in Results for characterizing the effects of visuomotor learning. In short, this model encapsulates the idea that motor planning is jointly dependent on GL-based and MV-based movement plans by representing the effects of visuomotor learning as a weighted average of GL and MV remapping. Experiments 1 and 2 were designed to determine the parameterization of this model for individual movements and movement sequences, respectively, whereas Experiments 3a and 3b were designed to rigorously test the model. The basic idea behind the experimental designs is that probing untrained conditions can yield considerable insight into the internal representations for learning (Krakauer et al., 2000; Wagner and Smith, 2008; Gonzalez Castro et al., 2011; Izawa and Shadmehr, 2011; Joiner et al., 2011; Brayanov et al., 2012; Sing et al., 2013). The details about how we designed experiments to achieve these goals are presented below and detailed in the sections that follow.

The model we develop for characterizing motor planning that is jointly dependent on GL-based and MV-based motor plans is parameterized by different weightings (W_GL and W_MV) for these individual plans, and by different remapping gains (R_GL and R_MV) that characterize the extent to which GL-based and MV-based adaptations are learned. Since the final plan is a weighted average of the individual GL-based and MV-based plans, W_GL and W_MV must sum to one, and therefore together represent only one free parameter. The model thus has three free parameters, one for weightings and two for the remapping gains. As shown in Equations 4 and 5 in Results, where the model is formally presented, these parameters combine into coefficients that multiply experimentally accessible movement attributes: the start location, movement vector, and goal location of the hand. We therefore designed Experiments 1 and 2, the attribute-isolating experiments, to individually measure these coefficients, K_SL, K_MV, and K_GL, with the idea that the W and R parameters, and thus the full model, could be recovered from the experimentally measured K values, allowing the model to be rigorously tested in Experiments 3a and 3b. However, visuomotor adaptation typically affects multiple movement attributes simultaneously, and it is thus difficult to dissociate the effects of adapting each individual attribute. To address this issue, we designed Experiments 1 and 2 with specific test movements (Experiment 1) and test sequences (Experiment 2), distinct from the movements in which adaptation was trained. These test movements were chosen so that the trained motor adaptation would affect only one attribute of each test movement or test sequence. This allowed the adaptation of individual movement attributes to be examined independently of one another so that K_SL, K_MV, and K_GL could be individually measured.

Similarities and differences between Experiments 1 and 2.

In Experiment 1, test movements proceeded as follows: subjects first moved from the center circle to a displayed target with continuous visual feedback, but as the cursor approached this target, a second target appeared, adjacent to the first. Subjects completed the initial movement and held the cursor within the first target for an additional 300 ms. After this period, subjects moved toward the second target, while visual feedback of the cursor was removed at movement onset. In contrast, in Experiment 2, subjects made a movement sequence by performing two submovements in rapid succession, without any additional delay. Visual feedback was withheld at the onset of the first submovement for the duration of the entire movement sequence, and was only restored when subjects returned to C for the start of the next trial.

Since Experiments 1 and 2 were both designed to examine the effects of adapting each movement attribute independently, and only differed in the types of test trials being used (individual movements vs movement sequences), we used the same rotation pattern for both experiments. Specifically, we applied a +30° counterclockwise rotation on movements from C to the peripheral targets T2 and T5, while movements from C to the other four targets (T1, T3, T4, and T6) were trained with 0° rotation.

Design of Experiments 1 and 2: the attribute-isolating experiments.

We designed the test movements and test sequences so that each of them shared only a single movement attribute (MV, GL, or SL) with the movements for which a nonzero visuomotor rotation was trained. The amount of adaptation associated with each individual attribute (SL, MV, and GL) of a test movement or test sequence was assessed by examining the differences between baseline and adapted attribute-matched movements. An MV-matched movement shares its movement vector with the test movement in Experiment 1, or the second submovement of the test sequence in Experiment 2, as shown in Figures 3 and 4. The vector differences in the end points of the baseline and adapted MV-matched movements define the MV adaptation vectors (ΔMV). Similarly, GL-matched movements share a goal location with test movements, and SL-matched movements end at the start location of the corresponding test movements. Correspondingly, vector differences in the end points of the baseline and adapted GL-matched movement and SL-matched movement define the GL-adaptation vector (ΔGL) and SL-adaptation vector (ΔSL), respectively, as shown in Figures 3 and 4.

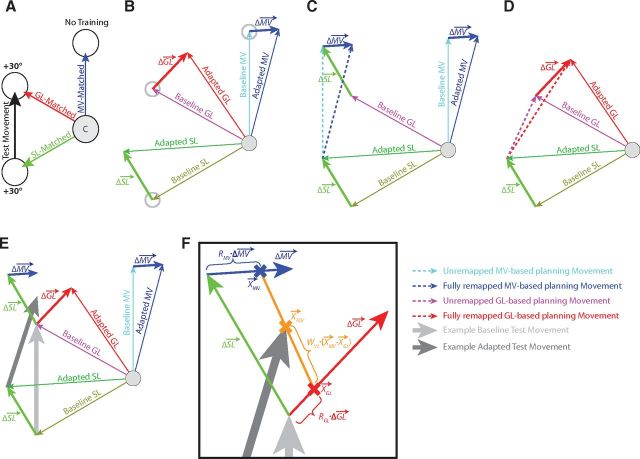
Figure 3.

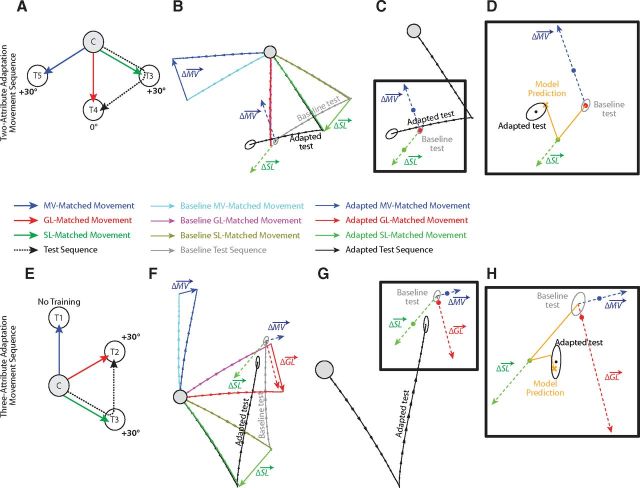
Illustration of the CRF model. A, Illustration of an example test movement (black arrow) that is to be affected by visuomotor adaptation. The effects of the CRF model on the test movement can be described in terms of the adaptation associated with three attribute-matched movements. The movement-vector-matched movement (MV-Matched; blue arrow) shares the same visual displacement as the test movement. The goal-location-matched movement (GL-Matched; red arrow) shares a goal location with the test movement. The start-location-matched movement (SL-Matched; green arrow) is aimed at the start location of the test movement. B, Motor adaptation produces changes in each attribute-matched movement. These changes can be represented in terms of the attribute adaptation vectors (Δ$\overrightarrow{MV}$, Δ$\overrightarrow{GL}$, and Δ$\overrightarrow{SL}$) defined as the differences between the baseline and adapted attribute-matched movements. C, Pure MV-based motor planning with full remapping would predict an adapted movement with a displacement matching the adapted MV-matched movement (blue dashed arrow). However, pure MV-based motor planning with zero remapping would predict an adapted movement with a displacement matching the baseline MV-matched movement (light blue dashed arrow), and intermediate remapping would predict an end point lying along the translated ΔMV. D, Pure GL-based motor planning with full remapping would predict an adapted movement directed toward the adapted goal location (red dashed arrow). In contrast, pure GL-based motor planning with zero remapping would predict an adapted movement directed toward the baseline goal location (magenta dashed arrow), and intermediate remapping would predict an end point lying along ΔGL. E, Extremal points associated with the CRF model. Note that the adapted test movement begins at the Adapted SL, and that the MV-based motor plan is affected by Δ$\overrightarrow{SL}$, while the GL-based motor plan is not. F, Mixing of the MV-based and GL-based motor plans in the CRF model in line with the form of this model shown in Equation 4. Note that the illustration in F is a zoomed-in version showing the top left area of E. The adapted test movement (dark gray arrow) is predicted by a weighted combination of an MV-based plan and a GL-based plan. In this illustration we used a GL-based plan ($\overrightarrow{X}$_GL depicted as the thick red X) with 25% remapping (R_GL = 0.25), and an MV-based plan ($\overrightarrow{X}$_MV depicted as the thick blue X) with 70% remapping (R_MV = 0.70). The net motor output ($\overrightarrow{X}$_TOT, depicted as the thick orange X) is based on weighted combination (W_VL = 0.55) of 55% MV-based planning and 45% GL-based planning. Note that the adapted test movement should always lie inside the quadrilateral defined by the start and end points of the Δ$\overrightarrow{GL}$ vector (red arrow) and the displaced Δ$\overrightarrow{MV}$ vector (blue arrow).

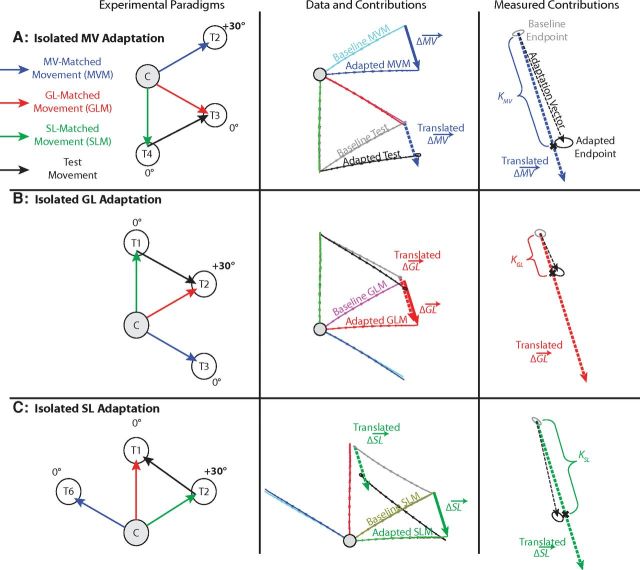
Figure 4.

Design of the attribute-isolating experiments. A, The effects of movement vector adaptation can be isolated for a test movement (T4 to T3) when the MV-matched movement (C to T2) is trained with rotation while the GL-matched (C to T3) and SL-matched (C to T4) movements are trained with zero rotation. When this is the case, the difference in end points of the baseline and adapted MV-matched movements define a nontrivial ΔMV (middle column, thick solid blue arrow). ΔGL and ΔSL can be defined analogously, but are both essentially zero because the SL-matched and GL-matched movements were trained with zero rotation. If ΔGL and ΔSL are essentially zero, the adaptation vector, which indicates the difference in end points between the baseline test movements and the adapted test movements, will depend only on ΔMV, and the gain associated with it (K_MV) can be estimated by comparing the adaptation vector with the translated version of ΔMV as shown in the third column, which is a zoomed in depiction of the lower right area in the second column. B, C, Analogously, test movements with isolated GL adaptation (B) and with isolated SL adaptation (C) can be trained when visuomotor rotations are applied in isolation to the GL-matched and the SL-matched movements, respectively, to estimate K_GL and K_SL. Note that the traces shown in the second and third columns are across-subject-averaged movements based on experimental data from three of the movement configurations studied in Experiment 1. Note that the ellipses drawn on the hand path plots in this and the subsequent figures all represent 1 SEM for movement end points.

The effect of MV adaptation was isolated by examining test movements and test sequences with MVs that were adapted during the training period, while the SL and GL of the test movement were unadapted (ΔSL = 0 and ΔGL = 0). Since movements from C to T2 and C to T5 were rotated during the training period, the 30° and −150° MVs were adapted (note that these directions are with respect to the positive x-axis). Since the movements between T3 and T4 and between T1 and T6 shared these adapted MVs, they served as test movements for evaluating the effect of MV adaptation. Figure 4A shows an example test movement that measures the effect of MV adaptation. Here, we focus on the test movement, illustrated in the left column of Figure 4A, from the SL of T4 to the GL of T3 (black arrow), with an MV-matched movement (blue arrow) of C to T2, a GL-matched movement (red arrow) of C to T3, and an SL-matched movement (green arrow) of C to T4. Note that in the middle column of Figure 4A, the adapted MV-matched movement (blue trace) is rotated relative to the baseline MV-matched movement (cyan trace), while the baseline and adapted GL-matched movements (magenta/red traces) lie on top of each other, as do the baseline and adapted SL-matched movement (yellow/green traces); hence, ΔMV ≠ 0, whereas ΔSL = 0 and ΔGL = 0. The difference between the end points of the adapted and baseline MV-matched movements define ΔMV, and is represented as the solid blue arrow in the middle column of Figure 4A.

If the movement vector adaptation of the MV-matched movement fully transfers to the test trial, we would expect the adapted test end point to be shifted by ΔMV relative to the baseline end point (dashed blue arrow). Since only the MV was adapted, changes in the test trial must be due to the adaptation of MV (ΔMV), and the effects of movement vector adaptation can be evaluated in isolation. In other words, movement vector adaptation of the test trial induced changes in its end point (Fig. 4A, right column, black ellipse, black dashed test adaptation vector arrow), and the coefficient K_MV represents the gain on ΔMV that best approximates this change. We computed K_MV by finding the magnitude of the scalar projection of the test adaptation vector onto ΔMV (black X). The same analysis was conducted for each of the four movement configurations with an adapted movement vector.

Corresponding analyses were conducted to isolate the effects of GL adaptation (Fig. 4B) and SL adaptation (C). In the GL-adaptation cases, ΔGL ≠ 0, whereas ΔMV = 0 and ΔSL = 0, allowing learning-related changes in the test trials to be attributed specifically to ΔGL. Correspondingly, changes in the test trials could be specifically attributed to ΔSL in the SL-adaptation cases in which ΔSL ≠ 0, whereas ΔMV = 0 and ΔGL = 0. This allowed us to calculate the gains (K_GL, and K_SL) on ΔGL and ΔSL that best approximate the difference between the baseline and adapted test end points in each of the GL-isolating and SL-isolating movement configurations.

Design of Experiments 3a and 3b: the attribute-combination experiments.

Experiment 3 (n = 40) investigated how movement sequences were affected by simultaneous adaptation of MV, GL, and SL, whereas Experiments 1 and 2 examined the effects of adapting only one of these attributes at a time. This experiment allowed us to compare the effectiveness of pure MV-based, pure GL-based, and combined MV–GL-based models. In Experiment 3a (n = 20), we examined the effects of adapting two attributes on movement sequences, either SL and GL or SL and MV. Movements from C to the peripheral targets T2, T3, T5, and T6 were all trained with the same rotation (11 subjects trained with +30° rotations, while 9 subjects trained with −30° rotations) while movements from C to T1 and T4 were trained with no rotation. On movement sequences during the testing period, subjects made a first submovement to one of the targets trained with rotation (T2, T3, T5, or T6) followed by a second submovement to an adjacent target. SL adaptation affected each movement sequence because the first submovement in each sequence had always been trained with rotation. In addition to the SLs, GLs were adapted on half of the movement configurations (those with second submovements made between T2 and T3 or between T5 and T6), while MVs were adapted on the other half (those with second submovements made from T2 or T6 to T1 or from T3 or T5 to T4).

Experiment 3b (n = 20) investigated the effects of simultaneously adapting all three attributes. The training paradigm was similar to that in Experiment 3a; however, there was no training given on movements from C to T1 and C to T4 because visual feedback of the cursor was withheld on all movements made to T1 and T4. Again, 11 subjects trained with +30° rotations to T2, T3, T5, and T6, while 9 subjects trained with −30° rotations to those targets. We expected partial adaptation of the C to T1 and C to T4 MVs and target locations due to the generalization from training rotations on movements to the other four targets, similar to the results observed in a previous study (Krakauer et al., 2000). Experiment 3b had the same movement configurations as Experiment 3a, but all three attributes were adapted on each sequence. Since the first target (T2, T3, T5, T6) had been trained with rotation, SL was fully adapted adaptation in each movement sequence. When the location of the second target was also adapted (second submovements between T2 and T3 or T5 and T6), the GL of the test sequence was fully adapted, while the MV was only partially adapted. However, when the second target was T1 or T4, the GL was only partially adapted, while MV of the submovement was fully adapted.

Data analysis.

The adaptation vectors associated with each movement attribute (ΔMV, ΔGL, and ΔSL) were determined by examining the adaptive changes of attribute-matched movements (Figs. 3, 4). We focused our analysis on the end points of these attribute-matched movements because, compared to analysis of movement direction, this allowed for two-dimensional information about adaptive changes in movement planning. The adaptive change in movement vector (ΔMV) was computed as the difference in end points between the baseline and adapted MV-matched no-feedback probe trials. These probe trials began at the center location (C) and had the same visual displacement as the test trial. Similarly, the adaptive change in start location (ΔSL) was defined as the difference in end points between the average baseline and average adapted SL-matched probe trials, and the adaptive change in goal location (ΔGL) was defined as the difference in end points between the average baseline and average adapted GL-matched probe trials. The SL-matched probe trials were no-visual-feedback movements from C to the first target, whereas the GL-matched probe trials were no-visual-feedback movements from C to the second target.

In Experiments 1 and 2, four different movement configurations were used to probe each of the gains that we estimated (K_MV, K_GL, and K_SL). On average, each subject repeated each configuration 25 times during the testing period and 10 times during the baseline period. To compute ΔMV, ΔGL, and ΔSL for each individual, we determined the gains based on the average movements for each configuration and then averaged the gains across the four configurations. Note that the confidence ellipses for movement end points in Figures 4–8 represent SEs across subjects.

Figure 5.

Results of the attribute-isolating experiment for individual movements. A, Four different movement configurations with isolated MV adaptation from Experiment 1. Dashed blue arrows indicate the shifted ΔMV, as shown in Figure 2. All hand paths display across-subject average movements with SE ellipse at the end point. The blue X indicates the best fit location of K_MV over all four movements. Note that analysis of the lower right configuration was detailed in Figure 4A. B, Test movements with isolated GL adaptation. Red arrows indicate the shifted ΔGL. C, Test movements with isolated SL adaptation. Green arrows indicate shifted ΔSL.

Figure 6.

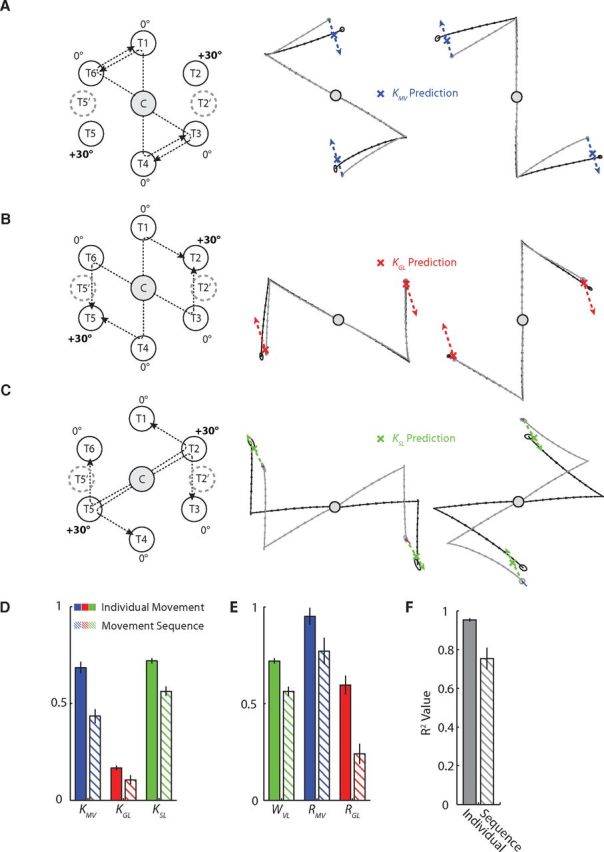
Results of the attribute-isolating experiments for movement sequences. A–C, Same as in Figure 5, but for the movement sequence data studied in Experiment 2. D, Mean and SEM across subjects for K_MV, K_GL, and K_SL found in Experiments 1 and 2. E, Mean and SEM for W_VL, R_MV, and R_GL found in Experiments 1 and 2. F, Mean and SEM for the fraction of variance accounted for by the CRF model in Experiments 1 and 2.

Figure 7.

Predictions of the CRF model when two or three movement attributes are adapted simultaneously. A–D, A movement sequence with two adapted attributes from Experiment 3a. A, Experimental paradigm. B, Baseline and adapted movements. The color scheme is the same as in Figures 3 and 4. Two attributes, MV and SL, are adapted during the training period, while the GL-matched movement was trained with zero rotation. As a result, ΔMV and ΔSL are nonzero, whereas ΔGL is essentially zero. C, Test-movement sequence shown with the contributions of ΔMV, ΔSL, and ΔGL as predicted by the CRF model (colored dots). D, A zoomed in version of C showing the model prediction (orange X) generated by the addition of the ΔMV and ΔSL contributions in line with the form of the CRF model shown in Equation 5. The orange lines in D and H show a graphical depiction of the model prediction as the sum of contributions from ΔMV, ΔSL, and ΔGL. E–H, A movement sequence with three adapted attributes from Experiment 3b, where ΔMV, ΔSL, and ΔGL are all nonzero. E, Experimental paradigm. F, Similar to B, but with adaptation of all three attributes. G, Same as in C. H, Same as in D, but the model prediction now has nonzero contributions from ΔSL, ΔMV, and ΔGL. Average test movements are shown, with across-subject SE ellipses around movement end points.

Figure 8.

Experimental results and evaluation of model predictions for movement sequences with multiple simultaneously adapted movement attributes. A, Adapted test-movement sequences from the two-attribute adaptation experiment (Experiment 3a). Note that 16 different movement configurations are shown. Colored dots indicate the contributions from ΔMV, ΔGL, and ΔSL as predicted by the coefficients predetermined in Experiment 2, and the orange Xs indicate the corresponding predictions of the predetermined CRF model. Purple Xs indicate the predictions of the CRF model with parameters refit to best account for the Experiment 3 data (best-fit CRF model). B, Same format as A but for the three-attribute adaptation experiment (Experiment 3b). Note that the average test movements are shown with across-subject SE ellipse around movement end points. C, The prediction error of the pure GL-based, pure MV-based, best-fit CRF, and predetermined CRF models, computed using leave-one-out cross-validation. D, The fraction of variance (R²) accounted for by each model shown in C relative to the baseline test sequence end point. E, F, The same as C and D but for repeated twofold cross-validation to reduce noise across subjects. Error bars represent SEM across subjects.

In Experiment 3, we evaluated the goodness of fit for MV-based, GL-based, and combined MV–GL-based models on movement sequences with multiple simultaneously adapted movement attributes. Since a value of W_VL = 1 produces pure MV-based planning, the MV-based model constrained W_VL = 1 and had one free parameter, R_MV. This corresponded to fitting K_MV as a free parameter with K_SL = 1 and K_GL = 0. Similarly, since a value of W_VL = 0 produces pure GL-based planning, the GL-based model constrained W_VL = 0 and had one free parameter, R_GL. This corresponded to fitting K_GL as a free parameter with K_SL = 0 and K_MV = 0. For the combined MV–GL-based model, all three parameters (W_VL, R_GL, and R_MV or K_SL, K_MV, and K_GL) had nontrivial values. These parameters were either fit on the Experiment 3 data (CRF best-fit model, with three free parameters) or predetermined based on the across-subject averages from Experiment 2 (CRF predetermined model, with no free parameters). The ability of these models to account for the data observed in Experiment 3 was quantified by computing the prediction error defined as the mean Euclidean distance between the end point data and the model prediction.

We performed two types of cross-validation to calculate prediction error and R² for each of the models. Leave-one-out cross-validation was performed by determining the model parameters on the group average data from all but one of the subjects, and then applying a model with those parameters to the remaining subject. Significance levels associated with leave-one-out cross-validation were computed by performing a paired t test comparing the fraction of variance accounted for by each type of model. This form of cross-validation assesses the goodness of fit of the model for each individual subject, but is prone to the noise inherent within single subject data. Thus, we also performed repeated twofold cross-validation to reduce the effect of noise originating from each subject. To perform this kind of cross-validation, we recursively divided each of the four subgroups (±30° training in Experiment 3a and ±30° training in Experiment 3b) in half and determined the model parameters by fitting on the average data from one half of the subjects, and then evaluating the resulting model on the average data from the other half of the subjects. This analysis was then repeated after swapping the fitting and testing groups, and iterated 1000 times based on different randomly chosen subject groupings, with the two resulting error and R² values being averaged on each iteration. This generated a distribution from which the mean and SE plotted in Figure 8, E and F, can be determined. Significance levels associated with repeated twofold cross-validation were computed by totaling the number of iterations on which one model outperformed the other. Note that since each of the subgroups in Experiment 3 had an odd number of subjects, either 9 or 11, the fitting and testing groupings were not exactly equal in size. Instead they contained 4 or 5 subjects in the case of 9 person subgroups, and 5 or 6 subjects in the case of 11 person subgroups. We can think of the variance associated with each subject's data as arising from two components: one reflecting how the entire population of neurologically intact participants would hypothetically perform, and one reflecting individual subject-specific noise. The latter component should average out if data from multiple subjects are combined. Since the average data from approximately five subjects was used to evaluate the goodness of fit for the cross-validated model, repeated twofold cross-validation would be expected to eliminate ∼80% of the noise variance, thus allowing us to back-calculate an estimate of the total intersubject variance present during the leave-one-out cross-validation. Subtracting this intersubject variance from the residual of the leave-one-out cross-validation produces an estimate of the “true” R² values for each of the models in the absence of intersubject noise.

Results

We performed a series of experiments to determine how motor adaptation affects the planning of untrained visually guided movements and movement sequences, focusing on how the effects of motor adaptation could be accounted for by planning movements in terms of two key features: the GL and the MV. We began by developing a computational framework for understanding how these two features affect the adaptive planning of goal-directed reaching movements. We then experimentally characterized the simplest cases in which motor adaptation affected only one movement attribute at a time, to isolate the specific effects that each attribute had on movement planning for both individual movements and movement sequences. Using these results, we were able to parameterize a computational model we developed so that it could make specific predictions for the end points of movement sequences. We then proceeded to test these predictions on complex movement sequences for which multiple attributes were simultaneously adapted.

Computational framework

We hypothesized that motor plans based on movement vector (X_MV) and goal location (X_GL) are averaged, and that the weighting of these two features (W_VL) determines the extent to which the remapping of each feature affects the net motor output (X_TOT):

Note that W_VL is the weighting of the vector versus the location plan, such that when W_VL = 1, the motor output depends only on the MV-based plan, whereas when W_VL = 0, the motor output depends only on the GL-based plan. Also note that we use Cartesian coordinates to describe the spatial locations and displacement vectors in our model; however, the experiments in this study were conducted in a single workspace, and thus cannot dissociate whether the various spatial locations and displacement vectors are represented in intrinsic coordinates, extrinsic coordinates, or a combination of the two (Brayanov et al., 2012).

We considered the effects of motor adaptation on X_TOT given the relationship expressed in Equation 1. In particular, we examined how three different effects of adaptation might alter X_MV and X_GL. As illustrated in Figure 3B–D, motor adaptation may affect three movement attributes: the movement vector, start location, and goal location associated with a particular movement. Figure 3B shows the geometry of these three adaptations, whereas Figure 3, C and D, shows how they might affect motor planning. Note here that ΔGL, ΔMV, and ΔSL are the overall adaptation vectors affecting goal location, movement vector, and start location, respectively.

As illustrated in Figure 3D, if full goal location remapping were to occur, the GL-based motor plan (the red dashed arrow) would be directed at the adapted GL. In contrast, if no GL remapping were to occur, the GL-based motor plan (the magenta dashed arrow) would be directed at the baseline GL. Note that the adaptation vector associated with the goal location (ΔGL) spans the locus of end points between these two extremal GL-based motor plans. Thus we can define a remapping gain, R_GL, with a value between 0 and 1 that describes the amount of goal location remapping (ΔX_GL) that occurs in terms of ΔGL:

We also hypothesized that during motor adaptation, movement vector and goal location are remapped independently of one another. If full movement vector remapping were to occur, the MV-based motor plan (Fig. 3C, dark blue dashed arrow) would match the displacement of an adapted movement with the same MV (Adapted MV arrow). In contrast, if no MV remapping were to occur, the MV-based motor plan (light blue dashed arrow) would match the displacement of a baseline movement with the same MV (Baseline MV arrow). Note that the adaptation vector associated with the movement vector (ΔMV) spans the locus of end points between these two extremal MV-based motor plans but is offset from the baseline movement end point by the adaptation vector associated with the start location (ΔSL). This offset specifically affects the MV-based plan (X_MV) because this plan is based on a displacement relative to the (adapted) start location, whereas the GL-based plan (X_GL) is based on the intended end point independent of the start location. Therefore, the adaptive change in the movement vector (ΔX_MV) depends on both ΔSL and ΔMV modulated by a remapping gain, R_MV, and can be expressed as follows:

Equations 2 and 3 highlight an important distinction between the effects of GL and MV adaptation. Since MV-based motor plans are derived from a displacement relative to the start location of the movement, ΔSL specifically affects the MV-based plan (X_MV). In contrast, the GL-based plan (X_GL) is based on the intended end point independent of the start location, and so it is unaffected by adaptation of the start location of the movement.

Based on Equations 1–3, the adaptive change in the net motor output (ΔX_TOT) depends on both the weighting coefficient (W_VL) and the remapping coefficients (R_MV and R_GL) for movement vector and goal location, as follows:

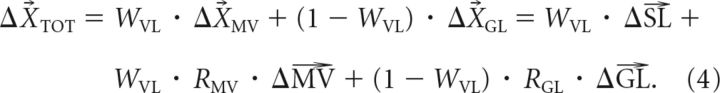Correspondingly, when a single movement is adapted, the learned adaptation could result from remapping of the movement vector (R_MV) or the goal location (R_GL) associated with this movement or a combination of the two.

Design of Experiments 1 and 2: attribute-isolating experiments

It is difficult to dissect the contributions of movement vector and goal location remapping by focusing on trained movements, because their effects are intrinsically coupled in all trained movements. Wang and Sainburg (2005) offered a key insight into dissociating the effects of adaptation on goal location and movement vector. The idea is that the effects of adaptation on these features can be uncoupled by adapting one movement and examining how this adaptation affects another—a test movement. In particular, Wang and Sainburg (2005) designed an experiment to put the effects of movement vector remapping and goal location remapping in opposition for individual test movements.

Here, we refined this approach by training adaptation to a single target (i.e., a single combination of movement vector and goal location) as opposed to a range of targets so that the remapping of these features could be examined independently of one another, thus isolating the effects of R_MV and R_GL rather than oppositely coupling them. We also designed test movements to examine the extent to which goal location and movement vector influence the planning of movements, independently of the extent to which these features are remapped, allowing us to determine W_VL. This weighting coefficient, W_VL, effectively modulates the contribution of each feature to the planning of untrained movements so that, in conjunction with R_MV and R_GL, these three factors collectively determine the effect of motor adaptation on untrained movements. We predict that if W_VL, R_MV, and R_GL are identified, the effect of adaptation on untrained movements and movement sequences can be quantitatively determined from Equation 4.

We thus designed Experiments 1 and 2 to characterize the three factors that determine the effects of motor adaptation on the planning of an untrained movement: the amount of MV remapping (R_MV), the amount of GL remapping (R_GL), and the weighting between an MV-based plan and a GL-based plan (W_VL). We can use Equation 4 as a guide to show how this can be accomplished. Note that this equation describes the adaptive change in the motor output (ΔX_TOT) as a linear combination of the adaptation vectors for three movement attributes, the start location (ΔSL), the movement vector (ΔMV), and the goal location (ΔGL), where their gains are based on W_VL, R_MV, and R_GL and should not change from one movement to the next. This can be made explicit by rewriting Equation 4 in terms of these gains, as follows:

where the gains are K_SL = W_VL, K_MV = W_VL · R_MV, and K_GL = (1 − W_VL) · R_GL. The form presented in Equation 5 makes it clear that if the effects of each adaptation vector (ΔSL, ΔMV, and ΔGL) can be isolated, the corresponding gains can be uniquely determined as follows:

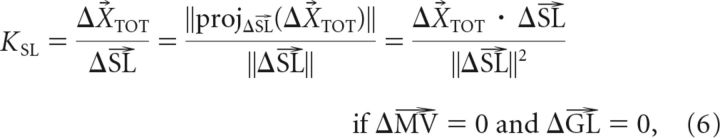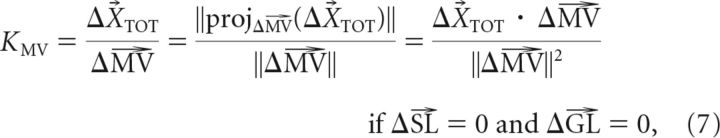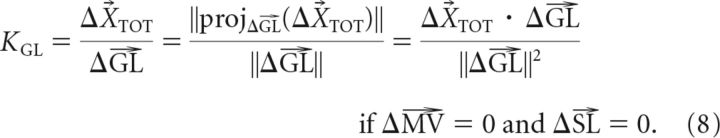We thus designed Experiment 1 to determine each of these gains by independently controlling the magnitudes of the three attribute adaptation vectors, as illustrated in Figure 4. Once these gains (K_MV, K_GL, K_SL) are measured, the weighting and remapping coefficients can be determined from these three gains: W_VL = K_SL, R_MV = K_MV/K_SL, R_GL = K_GL/(1 − K_SL). Motor adaptation generally affects multiple attributes simultaneously, and it is difficult to dissociate the effects of adapting each attribute. To address this issue, we designed these two experiments to use specific test movements (Experiment 1, n = 15) and test sequences (Experiment 2, n = 35) in which the adaptation of these movement attributes could be examined independently of one another.

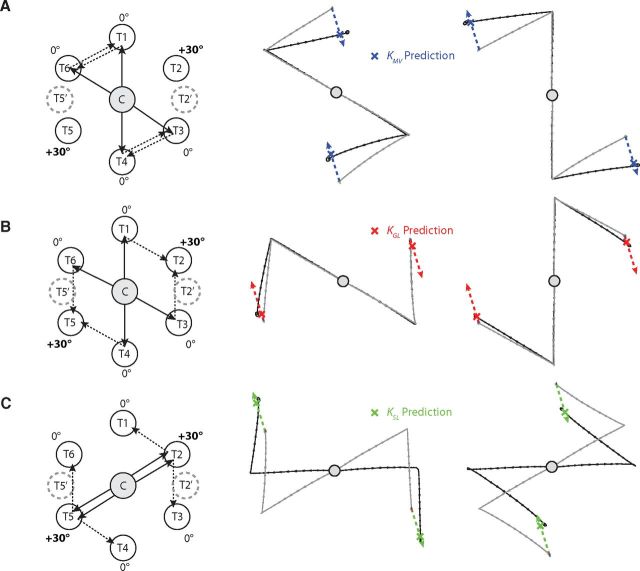
As shown in Figure 2A, subjects were trained on movements from a center circle to six peripheral targets (T1–T6). We trained subjects with +30° visuomotor rotations on movements from C to T2 and from C to T5, while movements from C to the other peripheral targets (T1, T3, T4, and T6) were trained with no rotation (i.e., 0° rotation). We then examined test movements in which only one of the three movement attributes was adapted during training. For each test movement, the start location was one of the peripheral targets (T1–T6), and the goal location was one of the two peripheral targets adjacent to the SL. For example, a test movement from T4 to T3 was affected by only MV adaptation because it shared a MV with the movement from C to T2, which was trained with +30° rotation, while its SL (T4) and GL (T3) were not adapted during the training period because 0° rotation was trained from C to T3 and from C to T4 as illustrated in Figure 4A. Before the test movement, subjects moved to the SL from C and waited an additional 300 ms for the go cue before moving to the GL. In actuality, subjects waited 752 ± 27 ms (note that means ± SEM are provided throughout this paper unless noted otherwise) between the end of the first movement and the start of the test movement. Visual feedback of the cursor was removed at the onset of the test movement and was restored only when the subject returned to C after the test movement. Note that because of the regular hexagonal layout of the peripheral targets, the target displacements for the training (center-out) and test (edge-traversing) movements were identical, as shown in Figures 4 and 5.

Adaptation to visuomotor rotations during the training period in Experiment 1

Before examining how learning visuomotor rotations transferred to untrained movements, we examined the data from the baseline and training periods. During the baseline period, subjects made quick movements (movement duration, 425 ± 3 ms, mean ± SEM; peak speed, 48.44 ± 0.28 cm/s) from C to each of the six peripheral targets. These movements were essentially straight and aimed directly at the targets (Fig. 2A, first column), with no-visual-feedback probe movements and continuous visual-feedback movements to the same targets essentially identical to one another (Fig. 2A, first column, compare colored, gray traces). When a visuomotor rotation was applied during the training period, hand movements were initially directed toward the baseline position associated with the target (Fig. 2A, second column). But gradually, subjects adapted to the visuomotor rotation, and hand movements rotated away from the visual target (Fig. 2A, third column). Ultimately, by the end of the training period and during the testing period, subjects made cursor movements straight to the intended targets with rotated hand paths (Fig. 2A, fourth column, B). Thus, during the testing period, movements to a given target were essentially identical regardless of the availability of visual feedback on cursor position (Fig. 2A, fourth column, compare colored, black traces). Similar to previous visuomotor rotation studies (Krakauer et al., 1999, 2000; Wang and Sainburg, 2005; Ghez et al., 2007; Scheidt and Ghez, 2007; Izawa and Shadmehr, 2011), we found nearly full adaptation on movements trained with rotation (90 ± 1% adaptation), while movements trained with zero rotation showed minimal changes following the training period (3 ± 1% adaptation) as shown in Figure 3B.

Isolating the effects of movement vector, goal location, and start location adaptation

To study the effects of movement vector adaptation independently of SL adaptation and GL adaptation, subjects performed a test movement in which the MV-matched movement was trained with a +30° rotation, while the GL-matched movement and SL-matched movement were trained with 0° rotation. In the example shown in Figure 4A, the test movement (T4 to T3) has an MV-matched movement (C to T2) that was trained with a +30° visuomotor rotation. In contrast, the GL-matched movement (C to T3) and the SL-matched movement (C to T4) were both trained with a 0° rotation. Since neither the GL nor the SL of the test movement is adapted, this manipulation isolates the effect of MV adaptation. This effect can be observed by comparing the difference between the adapted and baseline test movements (Fig. 4A, middle, black vs gray movements). If the rotation learned in the MV-matched movement (C to T2) movement vector fully transfers to the test movement (T4 to T3), the change in MV observed in the test movement would match the change in movement vector (ΔMV) of the MV-matched movement (C to T2). However, the example given in Figure 4A shows ∼21° of rotation (black vs gray data) for the test movement compared to ∼28° of rotation for the MV-matched movement (blue vs cyan data). The gain on this transfer (K_MV) can be quantified as a fraction of the learned change in movement vector (ΔMV) by projecting the test-movement adaptation vector (dashed black arrow) onto the trained adaptation vector (ΔMV), as shown in the right column of Figure 4A. For each subject, we applied this analysis to the four configurations of MV-isolating test movements in Experiment 1 (Fig. 5A) to estimate K_MV from our data and found similar gains for all participants (K_MV = 0.69 ± 0.03, mean ± SEM). The tight error bars on K_MV and the tight confidence ellipses on the test-movement data used to measure it indicate that subjects displayed remarkably consistent generalization of the trained pattern of adaptations in this experiment.

Analogously, to study the effects of goal location adaptation independently of MV adaptation and SL adaptation, subjects performed test movements in which the GL-matched movement was trained with a +30° rotation while the MV-matched movement and SL-matched movement were trained with no rotation. In the example shown in Figure 4B, the test movement (T1 to T2) has a GL-matched movement (C to T2) that was trained with a +30° rotation, while the MV-matched movement (C to T3) and SL-matched movement (C to T1) were trained with 0° rotation. This particular manipulation isolated the effect of GL adaptation from the effects of MV adaptation and SL adaptation, and this effect can be observed by comparing the difference between the adapted and baseline test movements (Fig. 4B, middle, black vs gray movements). The example in Figure 4B shows ∼1.1 cm of shift for the adapted test-movement end point compared to 4.2 cm of shift for the adapted GL-matched movement. We quantified the gain of this transfer (K_GL) by projecting the test-movement adaptation vector (dashed black arrow) onto the trained adaptation vector (ΔGL) as shown in the right column of Figure 4B. To estimate K_GL from our data, we applied this analysis to each of the four configurations of GL-isolating test movements (Fig. 5B) in each subject, finding a significant transfer of goal location adaptation to the untrained test movements in all participants (K_GL = 0.17 ± 0.01, mean ± SEM).

We also isolated the effects of start location adaptation by having subjects perform test movements in which the SL-matched movement was trained with a +30° rotation while the MV-matched movement and GL-matched movement were trained with zero rotation. In the example shown in Figure 4C, the test movement (T2 to T1) has a SL-matched movement (C to T2) that was trained with a +30° rotation, while zero rotation was trained on the MV-matched movement (C to T6) and GL-matched movement (C to T1), thus isolating the effect of SL adaptation. Similarly to the above examples, the difference between the adapted and baseline test movements shows the effect of SL adaptation (Fig. 4C, middle, black vs gray movements). Again, we quantified the gain of this transfer (K_SL) by projecting the test-movement adaptation vector (dashed black arrow) onto the trained adaptation vector (ΔSL), as shown in the right column of Figure 4C. We applied this analysis to each of the four movement configurations of SL-isolating test movements (Fig. 5C) in each subject, to estimate K_SL from our data and found significantly positive gains in all participants (K_SL = 0.72 ± 0.01, mean ± SEM). Note that in Figures 4A–C, all adaptive changes were measured from the same C to T2 movement; thus ΔMV = ΔGL = ΔSL for different test movements, illustrating that adaptation of a single movement can affect different movement attributes of untrained test movements.

Experiment 2: attribute-isolating experiment for movement sequences

In Experiment 2, we studied the transfer of visuomotor adaptation to the planning of movement sequences. In this experiment there were two subgroups of subjects, neither of which participated in Experiment 1. As in Experiment 1, we examined the effects of adaptation for movement vector, goal location, and start location in isolation from one another. However, during the movement sequences in Experiment 2, a second target appeared on the monitor halfway through the first submovement, and subjects were trained to proceed to the second target immediately after completing the first submovement. The dwell time between the end of the first submovement and the onset of the second submovement was thus substantially shorter than in Experiment 1 (311 ± 16 ms vs 752 ± 27 ms, p < 0.0001, when measured using a 5 cm/s speed threshold). During these movement sequences, visual feedback was removed at the onset of the first submovement of the sequence and remained off for the entire duration of the movement sequence. Similarly to Experiment 1, we designed Experiment 2 so that the visuomotor adaptation affected only one of the second submovement's three attributes at a time, with the affected attribute depending on the specifics of the movement sequence. Thus, as in Experiment 1, each of the three attributes was perturbed in isolation. As in the Experiment 1 data, we found that subjects displayed remarkably consistent generalization of the trained pattern of adaptations in Experiment 2, as evidenced by the tight confidence ellipses on the test-movement data shown in Figure 6. The confidence ellipses though small were, however, noticeably larger than in the Experiment 1 data, suggesting greater variability in the execution of movement sequences as would be expected. As in Experiment 1, we found highly significant transfer of adaptation in all three movement attributes (Fig. 6A–C), but the adaptation gains were significantly reduced for each of the three attributes (K_MV = 0.43 ± 0.04, K_GL = 0.11 ± 0.02, K_SL = 0.56 ± 0.02 for Experiment 2 compared to K_MV = 0.69 ± 0.03, K_GL = 0.17 ± 0.01, K_SL = 0.72 ± 0.01 for Experiment 1; p < 0.05 for all three decreases), as shown in Figure 6D. One key difference between Experiments 1 and 2 is the lack of visual feedback at the start location of the test movement. Without visual feedback of hand position, the internal estimate of start location becomes more dependent on proprioceptive information (Sober and Sabes, 2005), which results in reduced transfer of the visuomotor adaptation to the test sequence. A second difference is that the reduced dwell times between submovements that occur in movement sequences are known to result in altered motor planning compared to individual movements (Howard et al., 2012). Thus, compared to the movement sequences studied in Experiment 2, the individual movement test trials studied in Experiment 1 would be expected to elicit greater transfer of adaptation since the original adaptation was also trained in individual movements. This may account for the somewhat reduced, although highly significant R² value for the model in the Experiment 2 data (0.75 vs 0.95), as well as the reduced attribute gains.

Differential weighting and remapping of movement vectors and goal locations

Using Equations 4 and 5, we can compute the differential weighting (W_VL) and remapping of goal locations (R_GL) and movement vectors (R_MV) from the contributions of each attribute's adaptation vectors to the net motor output (K_SL, K_MV, K_GL) determined in Experiments 1 and 2. We find that, in combination, these factors can accurately characterize the planning of both individual movements and movement sequences when movement attributes are adapted in isolation (R² = 0.95 ± 0.01 for individual movements, R² = 0.75 ± 0.06 for movement sequences, mean ± SEM), as shown in Figure 6F. However, in both cases, movement vectors displayed significantly more remapping than goal location (R_MV = 0.95 ± 0.04, R_GL = 0.60 ± 0.05 for individual movements; p < 0.0001; R_MV = 0.77 ± 0.07, R_GL = 0.24 ± 0.05 for movement sequences; p < 0.0001), as shown in Figure 6E. On the other hand, individual movements appear to be predominantly planned based on movement vectors, while movement sequences weigh GL-based plans more evenly with MV-based plans [W_VL = 0.72 ± 0.01 for individual movements, indicating a ratio between MV-based (W_VL) and GL-based planning (1 − W_VL) that is about twice as high (2.6×) as the ratio between MV-based and GL-based planning for movement sequences (1.3×) arising from W_VL = 0.56 ± 0.02; Fig. 6E].

Experiment 3: predicting the planning of movement sequences following the adaptation of multiple attributes

In Experiment 3, we tested the ability of the model presented in Equations 4 and 5 to accurately predict the complex effects of motor adaptation on movement sequences with multiple simultaneously adapted features. We refer to this model as the CRF model because it combines the multiple effects of motor adaptation. As described in Equation 4, the CRF model accounts for the differential remapping of movement vectors (R_MV) and goal locations (R_GL), and modulates the MV-based and the GL-based plans based on a weighting (W_VL). However, this model may also be expressed in terms of the gains (K_SL, K_MV, and K_GL) used to linearly combine the effects of three attribute adaptation vectors (ΔSL, ΔMV, and ΔGL) as shown in Equation 5. Since we have demonstrated that K_SL, K_MV, and K_GL are determined by W_VL, R_MV, and R_GL, both formulations are mathematically equivalent. Critically, because the parameters of the CRF model for movement sequences were individually determined in Experiment 2, we can, without any free parameters, test the ability of this model to predict more complex movement sequences with multiple adapted attributes.

We therefore designed experiments in which subjects performed movement sequences that were affected by the adaptation of either two (Experiment 3a) or three (Experiment 3b) attributes simultaneously. This is in contrast to the attribute-isolating experiments (Experiments 1 and 2) discussed above in which only a single attribute was affected for each individual movement or movement sequence. Separate groups of subjects were recruited for Experiment 3a (n = 20) and 3b (n = 20), and in each of these experiments, subjects performed eight different movement sequences in which multiple attributes were adapted simultaneously. Because approximately half of the subjects in each group learned counterclockwise (+30°) versus clockwise (−30°) visuomotor adaptations that affected the planning of these sequences (see Materials and Methods; see Fig. 8A,B, middle diagrams), we studied a total of 32 adaptation-sequence combinations, 16 each in Experiments 3a and 3b.

Predictions of the CRF model

Figure 7A–D illustrates how the CRF model predicts changes in motor planning in an example movement sequence with two-attribute adaptation. In this example, the second submovement (T3 to T4) is simultaneously affected by start location and movement vector adaptation because both the SL-matched movement (C to T3) and the MV-matched movement (C to T5) received +30° visuomotor rotation training, whereas the GL-matched movement (C to T4) was trained with 0° rotation (Fig. 7B). Here we used the predetermined values for K_MV and K_SL from Experiment 2 to compute the contributions of MV and SL adaptation to this test sequence (Fig. 7C). Figure 7D illustrates how a linear combination of ΔMV and ΔSL can predict the adaptation-induced change in test sequence end point. Note that the blue, red, and green dots represent the individual contributions of MV, GL, and SL to the model prediction, respectively (Fig. 7C,D). In this two-attribute adaptation example, there was no adaptation of the GL of the test sequence and thus no contribution from ΔGL to the model prediction (red dot). The CRF model predicts that the adapted test end point (black dot and error ellipse) will be deviated from the baseline test end point (gray error ellipse) by the vector sum of the ΔSL (green dot) and ΔMV (blue dot) contributions (orange X) as shown in Figure 7D.

An example of a three-attribute adaptation movement sequence is shown in Figure 7E–H. In this example, all three attributes of the test sequence's second submovement (T3 to T2) are adapted. In addition to the +30° training of the SL-matched movement (C to T3) and GL-matched movement (C to T2), rotation learning generalized to the MV-matched movement (C to T1) so that it was also partially rotated, as illustrated in Figure 7F. Consequently, parameterizing the CRF model with the predetermined weights from Experiment 2 generates nontrivial contributions (blue, red, and green dots) from each of the three attributes (ΔMV, ΔGL, and ΔSL). Taking the vector sum of these contributions (orange X) predicts the end point of the adapted test sequence (black dot and SE ellipse) relative to the baseline test sequence (gray SE ellipse), as shown in Figure 7H. Note that this view of the CRF model prediction is analogous to that presented in Figure 3 based on the weighting and remapping of movement vectors and goal locations.

Specifics of the design of the two-attribute and three-attribute adaptation experiments

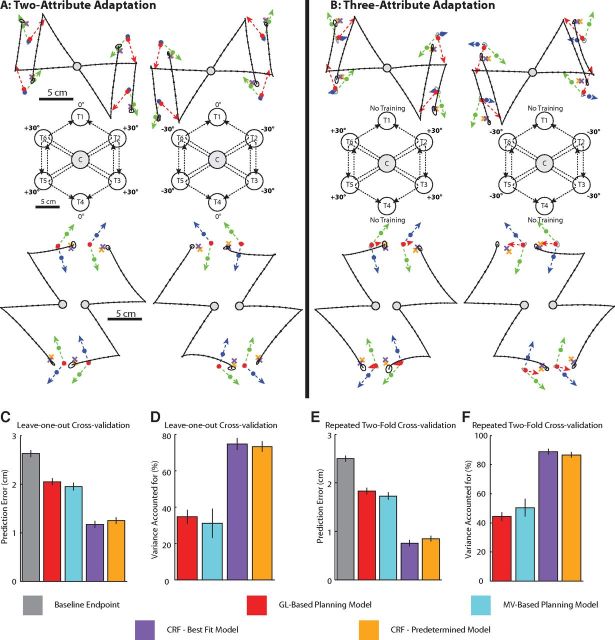
We designed Experiment 3a so that two movement attributes were simultaneously adapted: either start location and goal location or start location and movement vector. To accomplish this, movements from C to the peripheral targets T2, T3, T5, and T6 were trained with ±30° rotations, while movements to from C to T1 and T4 were trained with 0° rotation (Fig. 8A, middle). This training affected the start and goal locations for the four submovements between T2 and T3 and between T5 and T6, but held the movement vectors unchanged (Fig. 8A, top). In contrast, this training affected the start locations and movement vectors for the four test sequences terminating at T1 or T4, but held the goal locations unchanged (Fig. 8A, bottom). Figure 8A shows the predictions of the CRF model (orange and purple Xs) as well as the contributions from ΔMV, ΔGL, and ΔSL (blue, red, and green dots) for all 16 two-attribute adapted sequences examined in Experiment 3a. The predictions of the CRF model with the parameters predetermined from Experiment 2 are shown as the orange Xs, while the predictions from the CRF model with parameters fit to the Experiment 3 data are shown as the purple Xs (Fig. 8A). Note the close similarity between these predictions.

Experiment 3b was similar to Experiment 3a except that T1 and T4 were untrained rather than being trained with zero rotation during the training period. This resulted in noticeable, nonzero generalization of motor learning to T1 and T4 from the trained movements (T2, T3, T5, and T6) as shown in Figures 7F and 8B. This generalization is roughly in line with the findings of a previous study that found that when two movement directions 90° apart are trained with the same visuomotor rotation, ∼55% generalization was observed midway between (Krakauer et al., 2000). Since the trained targets nearest to T1 and T4 were 120° apart from each other in Experiment 3a, we would expect less generalization. In line with this prediction, we found 36 ± 4% (mean ± SEM) generalization on probe trials to T1 and T4 during the testing period. As a result, movements between targets with adapted start and goal locations now had a partially adapted movement vector as well (Fig. 8B, top, blue arrows), and test sequences ending at T1 and T4 had a partially adapted goal location (Fig. 8B, bottom, red arrows). This partial generalization allowed us to examine how test sequences were affected by simultaneously adapting all three attributes of the second submovement, as in the example documented in Figure 7E–H. Thus, whereas single movement attributes were adapted in isolation in Experiments 1 and 2, two or three movement attributes were simultaneously adapted in Experiments 3a and 3b, respectively. In Figure 8, the predictions of the CRF model with the parameters predetermined from Experiment 2 are shown as orange Xs, while the predictions from a fit CRF model which best characterized the data in Experiment 3 are shown as purple Xs (Fig. 8B).

Comparison of the predictions of the CRF model to single-feature-based models

As in the Experiments 1 and 2, we found that subjects displayed remarkably consistent generalization of the trained pattern of adaptations in Experiment 3, as evidenced by the tight confidence ellipses on the test-movement data shown in Figure 8, A and B. Critically, we find that the CRF model with predetermined coefficients from Experiment 2 predicts the movement sequences studied in Experiment 3 significantly better than models which assume pure GL- or MV-based planning (p < 0.0001 for both; Fig. 8C,D), even when these models are fit to the data with free parameters. The net motor output for the purely MV-based plan would entail full weighting for the MV-based plan versus the GL-based plan (W_VL = 1) so that only movement vector remapping (R_MV) would be relevant. In contrast, a purely GL-based plan would entail full weighting for the GL-based plan versus the MV-based plan (W_VL = 0), so that only goal location remapping (R_GL) would be relevant. Correspondingly, each of these models contains one free parameter, R_MV or R_GL, respectively, in the Equation 4 version, or K_MV or K_GL, respectively, in the Equation 5 version.

We compared the pure GL-based and pure MV-based models to a version of the CRF model in which the coefficients were predetermined from Experiment 2 and a version in which the coefficients were fit to the Experiment 3 data. We used leave-one-out cross-validation to characterize the ability of the different model fits to explain individual subject data. This entailed repeatedly fitting the free parameters in each model to the data from all but one of the subjects, and testing this fit on the remaining subject. Because cross-validation entails testing each model on data that were not used in fitting it, the number of free parameters in each model does not bias the assessment of goodness of fit. Thus models with different numbers of free parameters can be compared without specifically accounting for the model complexity or degrees of freedom. Note that there was no fitting in the predetermined CRF model because the same coefficients were used each time.

We found that the pure MV- and GL-based planning models provide similar quality fits to one another, accounting for 31.2 ± 8.1% and 34.8 ± 3.8% of the total variance (mean ± SEM), respectively, in the individual subject data. In contrast, the predetermined CRF model explains the adaptive changes in the movement sequence end points considerably better, accounting for 73.3 ± 2.9% of the total variance and performing better than both the pure MV-based and pure GL-based models for 37 of 40 subjects (Fig. 8D; p < 0.0001 for both the predetermined CRF vs pure MV-based models and the predetermined CRF vs pure GL-based models). Moreover, when the parameters of the CRF model are chosen to best fit the data in Experiment 3 (Fig. 8A,B, purple Xs), this model accounted for essentially the same fraction of variance (74.7 ± 3.3%) as when the parameters were predetermined with 27 of 40 of the subjects better characterized by the single best-fit CRF model and 13 of 40 subjects better characterized by the predetermined CRF model (p = 0.12, paired t test). The close match between the goodness of fit for the predetermined and best-fit CRF models underscores the predictive power of the results from Experiment 2. Interestingly, if the predetermined values from Experiment 1 are used instead of those from Experiment 2, the quality of the fit deteriorates noticeably, accounting for only 62.2 ± 5.4% (mean ± SEM) of the total variance (p < 0.005 for the predetermined parameters from Experiment 2 vs Experiment 1; data not shown in Fig. 8).

We designed Experiments 3a and 3b to test the CRF model over a wide variety of different movement configurations, rather than to maximize the precision of our end point estimate for each configuration. Correspondingly, the movement sequence test data for each subject were divided into eight different sequence types, thus reducing by a factor of eight the number of trials we could average together to estimate each end point position. This resulted in confidence ellipses for each subject's data that were often comparable in size to the errors between each subject's mean data and the CRF model predictions, suggesting that a large fraction of the error in the cross-validated model predictions may be due to noise in estimating the mean data for each subject. If this is the case, the “true” R² values characterizing the ability of the CRF model to explain the effects of motor adaptation on movement sequence planning may be substantially higher than the single-subject R² estimates made above, which are based on noisy data.

One approach to reducing the noise in the mean estimate is to average data across subjects. Thus, to make a better estimate of the true R² value of the CRF models, we performed repeated twofold cross-validation in which the data from a randomly chosen half of the subjects were repeatedly used to fit the model, and the mean data from the other half were used to assess the goodness of the model. With this approach, we find that the CRF model with predetermined coefficients accounts for 86.7 ± 1.9% of the variance (mean ± SEM), while the best-fit CRF model accounts for 89.0 ± 1.9% of the variance. Because there were ∼10 subjects in each of the four subgroups in Experiment 3, the repeated twofold cross-validation allowed us to average across an average of five subjects, thus reducing the mean variability by a factor of about five (∼80%). Extrapolation of this reduction in variability yields estimates for the true R² values of the predetermined and best-fit CRF models of 90.1 and 91.3%, respectively. This suggests that only 9–10% of the total variance arises from factors unrelated to GL-based and MV-based planning, such as biomechanical factors not accounted for by the combined remapped feature model.

Discussion

We examined the adaptive control of individual movements and movement sequences by characterizing how goal location and movement vector contribute to motor planning and how these features are remapped during visuomotor rotation learning. We began by demonstrating that these factors can be represented in terms of scalar gains on the adaptation vectors (ΔSL, ΔMV, ΔGL) of three movement attributes: the start location, movement vector, and goal location (see Equations 1–5). By performing a series of experiments to independently adapt each of these attributes (Experiments 1 and 2), we were able to directly measure the corresponding gains (K_SL, K_MV, K_GL), allowing us to determine the weighting and remapping of movement-vector-based and goal-location-based motor plans. Interestingly, we found that these factors accurately characterized the adaptive changes in motor output for both individual movements (R² = 0.95) and movement sequences (R² = 0.75), with the latter showing increased weighting of goal location compared to movement vector but decreased transfer of adaptation of both GL and MV remapping. We then used the coefficients from the attribute-isolating experiment to parameterize a model that combined remapped features (the CRF model) to predict how movement sequences would be affected when multiple attributes are adapted in combination. Remarkably, we found that this model accounted for nearly 90% of the variance associated with this motor adaptation, significantly more than a best-fit pure movement vector model (partial R² = 0.73, p < 0.0001) and a best-fit pure goal location model (partial R² = 0.76, p < 0.0001). Our results show that multiple features contribute to the planning of both point-to-point and compound reaching arm movements, and that a computational model that takes the remapping of multiple features into account accurately predicts how visuomotor adaptation affects the planning of movement sequences.

Implications for the neurophysiological representation of the CRF model

As noted in the derivation of Equation 5 from Equation 4, the CRF model we propose can be expressed in two distinct forms. Equation 5 expresses the adaptive changes in planning as responses to changes in the SL, MV, and GL. We take advantage of this form by directly measuring the adaptive responses to isolated changes in these three attributes to determine the adaptive gains (K_SL, K_MV, K_GL) associated with each in Experiments 1 and 2, and by directly comparing quantitative predictions based on these gain estimates to experimental data in which multiple movement attributes were simultaneously adapted to test the CRF model in Experiment 3. Equation 4, in contrast, casts the adaptive control of motor planning in terms of the weighting (W_VL) and remapping (R_GL and R_MV) of a goal-location-based plan and a movement-vector-based plan. If interpreted literally, Equation 4 suggests that the motor system makes multiple plans in parallel before weighting them against one another to generate motor output.

Intriguingly, multiple simultaneous neural representations of motor plans are known to arise during the planning of a goal-directed arm reaching movement (Kalaska et al., 1997; Desmurget et al., 1998; Andersen and Buneo, 2002; Andersen and Cui, 2009). A likely source for GL-based planning is the parietal cortex, the hub that integrates both somatosensory (Mountcastle, 1957) and visual information (Robinson et al., 1978; Andersen et al., 1987) for the control of movement (Andersen et al., 1997; Kalaska et al., 1997; Andersen and Buneo, 2002; Buneo and Andersen, 2006; Beurze et al., 2007; Andersen and Cui, 2009). The parietal reach region encodes the goal location of visually guided movements primarily in eye-centered coordinates (Batista et al., 1999; Buneo et al., 2002; Connolly et al., 2003; Pesaran et al., 2006), whereas parietal cortex area 5 encodes target locations relative to both eye position and limb configuration (Lacquaniti et al., 1995; Scott et al., 1997; Buneo et al., 2002). The representation of target locations and movement vectors in an intrinsic, limb-based coordinate frame is essential for generating motor commands and muscle activations, as both GL-based and MV-based planning ultimately require the transformation of visual information into limb configuration space. The ventral premotor area (PMv) is also believed to primarily code target locations (Graziano et al., 1994); however, the dorsal premotor area (PMd) primarily codes movement vectors (Scott et al., 1997; Pesaran et al., 2006), suggesting that MV-based planning may depend on PMd rather than PMv. Even in M1, where neural responses are less related to motor planning and more related to motor execution, both the position and velocity of ongoing movement (which relate to GL-based and MV-based planning, respectively) are simultaneously encoded (Ashe and Georgopoulos, 1994; Paninski et al., 2004; Wang et al., 2007). Future work examining how the neural representations associated with motor planning change during visuomotor adaptation will give further insight into the mechanisms underlying the remapping of movement vector and goal location representations.

Comparison to sequences of eye movements

The adaptive planning of eye movement sequences has been studied more extensively than arm movement sequences (Frens and van Opstal, 1994; Wallman and Fuchs, 1998; Tanaka, 2003; Quaia et al., 2010; Zimmermann et al., 2011), and the neural mechanisms for the planning and control of eye saccades are better understood than for arm movements (Robinson, 1964; Desmurget et al., 1998; Leigh and Zee, 1999). The adaptive control of saccades is highly complex, with learning that is specific to both the kinematic and behavioral context (Deubel, 1995, 1999; Edelman and Goldberg, 2001; Hopp and Fuchs, 2004, 2010; Pélisson et al., 2010). The prevailing theory on the planning of saccadic eye movements states that locations of visual targets are specified by a difference vector in the retinotopic reference frame; this vector is then transformed into a movement vector and then a specific pattern of muscle activations (Wurtz and Goldberg, 1989; Carpenter, 1991; Mazzoni et al., 1996; Leigh and Zee, 1999; Quaia et al., 2010). However, studies examining the adaptive control of saccade sequences have revealed both MV- and GL-based remapping (Frens and van Opstal, 1994; Wallman and Fuchs, 1998; Tanaka, 2003; Quaia et al., 2010; Zimmermann et al., 2011), with different results depending on details of the paradigm and types of saccade sequences elicited. These results are in line with the current findings demonstrating the remapping of both MV and GL during motor adaptation. One study focused on adaptation of SL (Tanaka, 2003), one on GL adaptation (Zimmermann et al., 2011), another compared one condition with GL adaptation to another condition where GL and MV adapted together (Frens and van Opstal, 1994), and two others dissociated GL from MV adaptation (Wallman and Fuchs, 1998; Quaia et al., 2010). However, none of these studies compared the effects of SL, MV, and GL adaptation as in the current study, allowing us to dissociate the weighting from the remapping of the movement vectors and goal locations. Thus, even in the two studies that specifically dissociated adaptation of these features (Wallman and Fuchs, 1998; Quaia et al., 2010), it is unclear whether the differences in GL and MV adaptation are due to differences in the weighting of these two features, the remapping of them, or both.

Remapping of movement vectors or positions?

The current results challenge the conclusions of a previous study that argued for the existence of movement vector remapping without goal location remapping during visuomotor learning (Wang and Sainburg, 2005). Interestingly, the basic methodology in that study is very similar to the current work (which it inspired) in that the effects of visuomotor rotation learning on untrained test movements were examined in both cases. However, instead of fully dissociating MV and GL remapping as in our Attribute-isolating experiments, the experimental design placed MV and GL remapping in conflict. Although post-adaptation movements were not fully aligned with predictions from either type of remapping, the data were clearly better characterized by the MV prediction, and the authors concluded that visuomotor adaptation remaps movement vectors rather than goal locations.

However, the results of Wang and Sainburg (2005) preclude the possibility of GL remapping in lieu of MV remapping, rather than ruling out their coexistence. In line with this idea, the ΔGL-isolation experiment we perform, with an example illustrated in Figure 4B, shows that GL-based remapping clearly contributes to motor planning (p < 0.0001). In fact, the data of Wang and Sainburg (2005) appear to be well explained in retrospect by the dual remapping of both movement vectors and goal locations predicted by the CRF model: the coefficients determined in Experiment 1 for the planning of individual movements indicate a substantially larger effect of movement vector (68%) than goal location (17%), thus predicting the data of Wang and Sainburg (2005) to fall in between the pure MV and pure GL predictions, but much closer to the MV prediction, which is indeed what they found.

Multisensory integration during motor planning

In the current study, movement SL was altered by motor adaptation to dissociate GL-based motor plans from MV-based motor plans and dissect the differential contributions of these two features toward movement planning. Several previous studies have also altered movement start locations, but surreptitiously, thereby creating a mismatch between proprioceptive and visual sensory information (Rossetti et al., 1995; Sober and Sabes, 2003, 2005). As in the current results, these studies found that the change in start location was not fully reflected in the subsequent movement. Instead, the movement end point invariably fell between the baseline end point and the end point resulting from the execution of the baseline movement vector from the altered start location. However, these studies implicitly assumed that motor planning was based purely on movement vectors and explained their results entirely based on a visual–proprioceptive weighting rather than an MV–GL weighting. Correspondingly, they assumed that the motor system's estimate of the start location was the point from which the executed movement vector would have reached the movement goal. However, this need not be the case. Our paradigm alters the start location without creating a visual–proprioceptive mismatch per se, yet results in end point changes similar to those observed previously. This demonstrates that the visual–proprioceptive weighting in estimating the start location is not entirely responsible for the intermediate end point locations observed with visual–proprioceptive mismatch, in line with the idea that motor planning is not purely MV based. Instead, the results are due, at least in part, to the weighting of MV-based versus GL-based motor plans.

A number of previous studies have suggested that motor adaptation may differentially affect postural control and trajectory planning (Lackner and Dizio, 1994; Dizio and Lackner, 1995; Kurtzer et al., 2005; Ghez et al., 2007; Scheidt and Ghez, 2007; Simani et al., 2007). For example, Scheidt and Ghez (2007) demonstrated that trajectory planning and postural control are differentially affected by adaptation in fast out and back movements versus slow end point translations. However, some studies have demonstrated the recalibration of movement control following postural adaptation (Simani et al., 2007; Cressman and Henriques, 2010), and others have conversely demonstrated the recalibration of postural control following movement adaptation (Simani et al., 2007; Cressman and Henriques, 2009; Izawa and Shadmehr, 2011; Salomonczyk et al., 2011), suggesting that postural control and trajectory planning are not entirely distinct. The current study provides a quantitative framework through which these results can be understood, since we show that trajectory control depends on both the weighting of and remapping of GL-based and MV-based motor planning. If this is the case, trajectory adaptation would partially affect location-based postural control and vice versa, in line with what has previously been observed experimentally (Ghez et al., 2007; Simani et al., 2007; Cressman and Henriques, 2009, 2010; Izawa and Shadmehr, 2011; Salomonczyk et al., 2011). Moreover, as Experiment 3 included movement sequences affected by multiple different combinations of trajectory remapping and postural remapping, the ability of the CRF model to predict nearly 90% of the variance induced by motor adaptation indicates the capacity of our framework to quantitatively predict the effects of and interactions between trajectory control and postural control.

Limitations of the current study

Here we demonstrated the ability of a simple three-parameter model to characterize the generalization of visuomotor adaptation to a range of individual movements and movement sequences. In short, the CRF model posits that movement vectors and locations are remapped independently during visuomotor adaptation, predicting that motor commands are based on a weighted average of GL-based plans and MV-based plans. However, in applying the CRF model to both individual movements and movement sequences, we implicitly assumed that they were planned in a similar fashion. Interestingly, the results of Experiments 1 and 2 indicate that the CRF model explains both the individual movement and movement sequence data remarkably well (R² = 0.95 and 0.75; Fig. 6D–F). However, not only were the values of the model parameters different, but also the quality fit was worse for movement sequences with 25% of the variance unexplained versus just 5%, suggesting that the planning of individual movements and movement sequences may differ not only parametrically but structurally.

However, there were differences in the fidelity of the information about the starting point for the test movement in the individual movement data and the analogous submovement in the movement sequence. Thus, it is not entirely clear the extent to which differences between the planning of individual movements and sequences per se were responsible for the differences we observed in Experiments 1 and 2. Moreover, the CRF model accounted for nearly 90% of the variance in movement sequence data in Experiment 3, suggesting that an averaging of MV-based and GL-based plans is the primary determinant of both individual movement and movement sequence planning.