Mechanical restriction of intracortical vessel dilation by brain tissue sculpts the hemodynamic response

Abstract

Understanding the spatial dynamics of dilation in the cerebral vasculature is essential for deciphering the vascular basis of hemodynamic signals in the brain. We used two-photon microscopy to image neural activity and vascular dynamics in the somatosensory cortex of awake behaving mice during voluntary locomotion. Arterial dilations within the histologically-defined forelimb/hindlimb (FL/HL) representation were larger than arterial dilations in the somatosensory cortex immediately outside the FL/HL representation, demonstrating that the vascular response during natural behaviors was spatially localized. Surprisingly, we found that locomotion drove dilations in surface vessels that were nearly three times the amplitude of intracortical vessel dilations. The smaller dilations of the intracortical arterioles were not due to saturation of dilation. Anatomical imaging revealed that, unlike surface vessels, intracortical vessels were tightly enclosed by brain tissue. A mathematical model showed that mechanical restriction by the brain tissue surrounding intracortical vessels could account for the reduced amplitude of intracortical vessel dilation relative to surface vessels. Thus, under normal conditions, the mechanical properties of the brain may play an important role in sculpting the laminar differences of hemodynamic responses.

Graphical Abstract

Introduction

Increases in neural activity in the brain are usually followed by localized increases in blood flow and oxygenation (Raichle and Mintun 2006). Because hemodynamic signals are used to study cognition and perception in humans, it is important to understand the underlying vascular mechanism that causes these changes in blood flow in the awake brain at the level of single vessels (Hillman 2014). Blood is transported to the cortex through a network of interconnected arteries on the surface of the brain (Duvernoy et al. 1981; Blinder et al. 2010) which feed into penetrating arterioles that enter perpendicularly into the cortex. The penetrating arterioles then ramify into the capillary bed (Blinder et al. 2013). Deciphering which components of the cerebral vasculature mediate flow changes is critical for understanding the vascular mechanisms underlying hemodynamic signals (Kim and Ogawa 2012). Specifically, where and to what extent the vessels in the arterial tree dilate will determine the spatial pattern of blood flow changes. This has practical bearing on fMRI imaging, as it is currently a matter of debate whether hemodynamic signals of surface vessels or intracortical vessels are more reliable indicators of local neural activity (Zhao et al. 2006; Kim and Kim 2010; Goense et al. 2012; Huber et al. 2013; Poplawsky and Kim 2014).

Arteries are composed of an inner layer of endothelial cells, and an outer layer of smooth muscle cells which control the diameter of the vessel. Because the endothelial and smooth muscle cells of blood vessels are electrically coupled via gap junctions, extensive studies in the peripheral vasculature (Segal and Duling 1986; Bagher and Segal 2011) and in the vasculature of the brain (Jensen and Holstein-Rathlou 2013) have established that vasodilation and vasoconstriction signals are conducted or propagated through the vascular network. In the brains of anesthetized animals (Iadecola et al. 1997; Erinjeri and Woolsey 2002; Berwick et al. 2008; Chen et al. 2011; Chen et al. 2014), it has been shown that these dilations are conducted through the surface portion of arterial tree. Similarly, in vitro, dilation can be conducted upstream away from the site of initiation (Dietrich et al. 1996). There are no known active conductances in the vasculature, and the voltage-diameter relationship has a saturating non-linearity associated with it (Wölfle et al. 2011), so the propagated dilation decreases with distance from the site of initiation. Because of the long electrotonic length constants of arterioles (Segal and Duling 1986; Bagher and Segal 2011), these dilations propagate without loss of amplitude over hundreds of microns or more. Since intracortical arterioles are embedded in brain tissue composed of astrocytes and neurons that release vasodilatory substances (Attwell et al. 2010), it is thought that vasodilation is initiated in intracortical vessels and then propagates up the vascular tree (Hamel 2006; Tian et al. 2010). Laminar differences in the amplitudes of cerebral blood volume responses have been observed in several MRI studies (Zhao et al, 2006; Kim and Kim 2010; Polimeni et al 2010; Goense et al. 2012; Poplawsky and Kim 2014; Pucket 2014), suggesting that there may be spatially localized hemodynamic signals that could be useful for human neuroimaging. However, all of these experiments were done in anesthetized animals, and anesthesia profoundly decreases the amplitude and slows the dynamics of hemodynamic responses (Martin et al. 2006; Goense and Logothetis 2008; Drew et al. 2011; Pisauro et al. 2013). To better interpret the signals coming from human neuroimaging studies (Gardner 2010; Kriegeskorte et al. 2010), it is important to understand the microvascular basis of hemodynamic in awake animals, preferably those performing voluntary behaviors (Huo et al. 2014; Huo et al. 2015).

Here, we investigated how the amplitudes of the dilations of individual arterioles and venules were affected by cortical location and position in the vascular network. Using two-photon laser scanning microscopy (2PLSM)(Shih, Driscoll, et al. 2012), we quantified the amplitudes of the dilation of arterioles and venules at various cortical depths in the forelimb/hindlimb (FL/HL) representation and neighboring regions of the somatosensory cortex of mice during voluntary locomotion. Voluntary locomotion has been used to study sensorimotor dynamics in the optically accessible limb representations of the cortex (Dombeck et al. 2007; 2009). Because animals naturally and continually engage in voluntary locomotion, it is an ethologically relevant behavior, and gives us insight into neurovascular coupling during normal behavior. Imaging of vessel dilation and neural activity with a genetically-encoded calcium indicator showed that intracortical arteriole dilation was correlated with nearby neural activity. Surprisingly, we found that surface vessels dilated substantially more than intracortical vessels. The difference in dilation amplitudes between surface and intracortical arterioles was not due to the intracortical arterioles being more dilated at baseline, as intracortical and surface arterioles dilated the same amount when the mouse was anesthetized with isoflurane. Histological visualization of smooth muscle and astrocytes revealed that penetrating arteriole enters the brain through a “pial funnel”, a narrowing of the Virchow-Robin space (Cserr et al. 1986; Iliff and Nedergaard 2013) as the vessel goes deeper into the cortex. This implies that any dilation of the intracortical portion of the vessel would entail compression of the surrounding brain tissue. Using mathematical modeling, we showed that the mechanical restriction of dilation by brain tissue could account for the difference in dilation amplitude between surface and intracortical arterioles. Our results suggest that biomechanical constraints interact with vasodilatory signals to drive large surface vessel dilations during natural sensorimotor behaviors.

Materials and methods

Animals and surgery

All surgical and experimental procedures were performed in accordance with NIH guidelines and approved by the Pennsylvania State University Institutional Animal Care and Use Committee (IACUC). Two-photon imaging subjects were 11 (8 male) 2–6 month old C57/BL6 mice (Jackson Labs, Bar Harbor, ME) and 6 (6 male) 2–6 month old Thy1-GCaMP3 mice (Jackson Labs). As we found no differences in vessel dilation amplitudes and fraction of time spent locomoting between C57/BL6 and Thy1-GCaMP3 mice (Table 1), we pooled both groups of mice for analysis. Polished and reinforced thin-skull (PoRTS) windows were implanted over the right somatosensory cortex (Drew et al. 2010; Shih, Mateo, et al. 2012). We purposely did not use craniotomies, because they cause inflammation (Xu et al. 2007; Cole et al. 2011), and change the mechanical properties of the brain tissue, making it more compliant (Hatashita and Hoff 1987). Animals were allowed to recover for at least two days after the surgery before they were habituated on the imaging setup, a spherical treadmill (60 mm diameter) with one degree freedom, equipped with a rotation encoder to detect motion (Nimmerjahn et al. 2009; Gao and Drew 2014). Mice were habituated for several days in 15 minutes sessions, up to 4 times a day. Imaging sessions took place within 1 month of the window implantation surgery.

Table 1.

Number and depth of vessels imaged.

arterioles	Animal	Surface Branch Order0			Surface Branch Order1			0<depth≤50μm			50<depth≤100μm			100<depth≤150μm			150<depth			Vessel groups	Neural areas
		number	peak dilation (%)	run fraction (%)	number	peak dilation (%)	run fraction (%)	number	peak dilation (%)	run fraction (%)	number	peak dilation (%)	run fraction (%)	number	peak dilation (%)	run fraction (%)	number	peak dilation (%)	run fraction (%)
	C57(9)	30	22.0%±7.4%	25.6%±13.6%	36	22.0±7.2%	23.2%±9.5%	19	13.9%±7.3%	23.9%±12.8%	27	9.1%±5.5%	21.3%±7.4%	13	8.0%±4.5%	27.0%±9.56%	9	7.2%±3.9%	25.6%±11.1%	36	--
	Thy1-GCaMP3(6)	9	22.9%±10.3%	24.0%±8.4%	11	20.8%±8.4%	21.2%±6.9%	8	10.4%±4.5%	25.7%±13.5%	12	7.9%±3.6%	23.9%±4.7%	3	7.9%±7.2%	30.0%±5.8%	1	5.60%	20.7%	18	23
	sum	39	22.2%±8.0%	25.2%±12.5%	47	21.8%±7.4%	22.7%±9.0%	27	12.9%±6.7%	24.4%±12.8%	39	8.7%±4.9%	22.1%±6.7%	16	8.0%±4.8%	27.6%±8.9%	10	7.0%±3.7%	25.1%±10.6%	54	23
venules	Animal	Surface Branch Order0			Surface Branch Order1			0<depth≤50μm			50<depth≤100μm			100<depth≤150μm			150<depth			Vessel groups	Neural areas
		number	peak dilation (%)	run fraction (%)	number	peak dilation (%)	run fraction (%)	number	peak dilation (%)	run fraction (%)	number	peak dilation (%)	run fraction (%)	number	peak dilation (%)	run fraction (%)	number	peak dilation (%)	run fraction (%)
	C57(9)	18	8.0%±4.8%	22.4%±10.0%	18	4.8%±5.4%	21.0%±6.5%	7	4.1%±1.4%	24.1%±10.2%	12	3.5%±1.3%	22.7%±9.0%	14	3.4%±1.1%	22.9%±8.1%	6	4.4%±1.2%	29.2%±8.6%	25	--
	Thy1-GCaMP3(6)	4	4.9%±1.2%	22.6%±11.9%	3	3.0%±1.2%	17.6%±7.6%	4	3.9%±1.5%	24.0%±4.9%	6	4.0%±1.4%	25.4%±6.7%	4	3.4%±1.4%	20.8%±6.2%	1	4.0%	21.8%	7	12
	sum	22	7.4%±4.5%	22.5%±10.0%	21	5.1%±1.8%	20.5%±6.6%	11	4.0%±1.3%	24.1%±8.3%	18	3.6%±1.3%	23.6%±8.2%	18	3.4%±1.2%	22.4%±7.9%	7	4.3%±1.1%	28.2%±8.3%	32	12

Two-photon microscopy

Animals were imaged using a two-photon microscope consisting of a Movable Objective Microscope (Sutter Instruments, CA) and a MaiTai HP laser (Spectraphysics, Mountain View, CA), controlled by MPScan software (Nguyen et al. 2006). A 20× 0.5 N.A. (Olympus, Center Valley, PA), or 20 × 1.0 N.A. (Olympus) water dipping objective was used for imaging. Before each imaging session, animals were briefly anesthetized with isoflurane and were infraorbitally injected with 50µL (50mg/mL) fluorescein-conjugated dextran (70 kDa; Sigma, St. Louis, MO) or rhodamineB-conjugated dextran (70 kDa; Sigma). The laser was tuned to 800nm for imaging fluorescein alone, and 910nm for rhodamineB/GCaMP3 imaging. For isoflurane vasodilation experiments, mice were placed on a homoeothermic heating pad while anesthetized with 2% isoflurane in air. Imaging sessions typically lasted ~2 hours. Each vessel was imaged for approximately 15 minutes at ~8 frames/second. Penetrating vessels were imaged 30–250 µm below the pia. We were able to image capillaries clearly down to 200µm through PoRTS windows with no loss of resolution (Supplementary Fig. 6; Supplementary Table 1). Arterioles and venules were identified morphologically (Blinder et al. 2010).

Image processing and data analysis

All reported summary numbers are mean±standard deviation unless otherwise indicated. All error bars or shaded areas in plots show one standard deviation. All data analysis was performed with Matlab (MathWorks) or SAS (SAS 9.3). All peak responses (vessel dilations and neural [Ca²⁺] signals) were taken to be the 95 percentile of diameter or neural activity during an imaging session, and peak-to-peak responses were the difference between the 5th and 95th percentile of diameters.

For surface vessel and neuronal imaging, individual frames were aligned to remove motion artifacts in the x-y plane (Guizar-Sicairos et al. 2008; Drew et al. 2011). Visual inspection of movies, with nearby capillaries as references, indicated that z-axis motion was <5µm. To quantify surface vessel diameter, a rectangular box was manually drawn around a short segment (2–5 µm long) of a vessel. Pixel intensity was averaged along the long axis of the vessel, and the diameter was calculated from the full width at half-maximum. Vessel diameter fractional changes (ΔD/D₀) were calculated by normalizing to the average diameter during a ~10 second-long stationary period.

For penetrating vessels, where the cross-section of a vessel may not be circular and can change shape (Gao and Drew 2014), the Thresholding in Radon Space (TiRS) method (Gao and Drew 2014) was used to obtain a more accurate and robust measure of vessel cross-sectional area. The TiRS algorithm essentially performs a full-width at half maximum measurement along every angle, making it very robust. Briefly, a square region of interest (ROI) enclosing the vessel of interest was manually drawn. The images were first transformed into Radon space, thresholded, and then transformed back to image space, where the vessel cross-sectional area was quantified after a second thresholding. To facilitate comparison, diameters of penetrating vessels were taken to be: $\text{diameter}=2\sqrt{\frac{\text{area}}{\mathrm{\pi }}}$. As with surface vessels, diameters were normalized by the stationary diameter baseline to get ΔD/D₀. The TiRS algorithm has been validated to work well down to signal-to-noise ratios of 1 or less (Gao and Drew, 2014). The signal-to-noise ratio of vessels imaged here were all significantly above this level (Supplementary Table 1).

For neural GCaMP3 signals, a rectangular ROI was manually selected to enclose an area with robust GCaMP fluorescence signals, and a control for background fluorescence ROI was drawn inside a vessel where there was no neural signal. Averaged pixel intensities inside the background ROI were subtracted from the averaged pixel intensities inside the neural ROI. Fluorescence fractional changes (ΔF/F₀) were calculated by normalizing to the same average fluorescence intensity during a ~10 second long stationary period. The ΔD/D₀ and ΔF/F₀ time series were first filtered with a five-point median filter, and then low-pass filtered at 3Hz (3rd order Butterworth) (Huo, et al. 2015).

To detect locomotion events, we first low-pass filtered the velocity signal at 10Hz, calculated the absolute value of acceleration, and then binarized the absolute acceleration signal, using a 10⁻⁵cm/s² threshold. For calculation of the locomotion triggered average, locomotion events separated by <1 second were considered continuous. All locomotion triggered events were >5 seconds in duration, with >2 seconds of quiescence beforehand. Before averaging, dilations or fluorescence changes were normalized to the second before running initiation. The onset time of vessel dilation and neural activity increases were taken to be the x-axis intercept of the line given by the 20% and 80% points of the maximum of the averaged locomotion-triggered response (Tian et al. 2010). We imaged 226 arterioles (138 in FL/HL representation and 88 in other somatosensory regions) and 117 venules (64 in FL/HL representation and 53 in other somatosensory regions) that had at least one five-second long locomotion bout (mean number of bouts for arterioles: 4.4±2.8; venules: 3.8±2.7).

We fitted the dilation amplitude-depth relationship with a linear piece-wise function with three free parameters: a maximal dilation (D_max), a minimal dilation plateau (D_min), and an inflection depth d_I:

$$\frac{\mathrm{\Delta }D}{D_0}=\{\begin{array}{c}-s(D_{\mathit{\text{max}}}-D_{\mathit{\text{min}}})z+D_{\mathit{\text{max}}},z\le d_I\\ D_{\mathit{\text{min}}},z>d_I\end{array}$$ (1)

where $\frac{\mathrm{\Delta }D}{D_0}$ is the vascular dilation amount and cortical depth is z. The slope, s, is determined by the three free parameters. All the parameters were calculated by minimizing the mean-square error between the raw data and estimates of the piece-wise fit using the Matlab function fminserchbnd in which each of the parameter had bounded constraints (10%≤D_max≤40%, 0%≤D_min<20%, 0µm≤d_I≤100µm). To calculate the 95% confidence interval of the depth of the inflection point d_I , 1000 bootstrap estimates were generated. For each bootstrap, the number of points equal to the original data set were randomly re-sampled with replacement.

Histology and anatomical reconstruction

To reconstruct the location of each vessel imaged with 2PLSM in the somatosensory cortex, animals were transcardially perfused with heparin-saline and 4% paraformaldehyde (PFA) at the conclusion of the imaging. Fiduciary marks were made at the corners of the window to reconstruct imaging sites relative to the functional areas. The brain was extracted and sunk in PFA in 30% sucrose. The brain was sectioned and stained for cytochrome oxidase (CO) in order to visualize the forelimb, hindlimb, and vibrissae representations in layer IV (Drew and Feldman 2009).

For anatomical visualization of arterioles and astrocytes we used 4 (2 males) 1–3 months old C57/BL6 mice (Jackson Labs, Bar Harbor, ME). Mice were transcardially perfused with warm heparin-saline, followed by 4% PFA, then were flushed with warm heparin-saline. To prevent the collapse of blood vessels, mice were then perfused with 2% gelatin in PBS and placed in ice-water for 15 minutes (Tsai et al. 2009). The brains were placed in 4% PFA overnight. One brain was kept intact for two-photon imaging and three were coronally sectioned for confocal imaging. The brain and the brain slices were washed in blocking buffer (BB) (5% goat serum and 1% Trition X-100 in 0.1 M PBS) for 1 hour, and then stained with an anti-GFAP antibody (1:500 Anti-Glial Fibrillary Acid Protein, Abcam, Cambridge, MA) in BB at 4°C for 48 hours. The samples were then rinsed for 30 minutes in BB four times, and then stained with a secondary antibody (1:500 Goat Anti-Rabbit Alexa 488, Abcam, Cambridge, MA) and 1:250 dilution of Rhodamine-conjugated phalloidin (Life Technologies, Carlsbad, CA) in BB at 4°C for 48 hours. The brain or brain slices were then rinsed for 30 minutes in BB twice, and 30 minutes in PBS before being imaged using 2PLSM or Olympus Fluoview confocal microscope (Olympus Corporation, Tokyo, Japan).

Mechanical properties of brain tissue and blood vessels

Young’s moduli, E, were calculated from shear moduli, G, using the relationship:

$$E=2G(1+v)$$ (2)

where is v Poisson’s ratio, taken to be 0.45 for brain tissue (Mousavi et al. 2014). The Young’s (or elastic) modulus of a material is a constant that relates an applied pressure to the amount of deformation. Materials with higher Young’s moduli, such as bone, are stiffer than those with low Young’s moduli, such as adipose tissue. Young’s moduli have units of pressure. Published estimates of bulk shear moduli for brain tissue span a wide range, from 1.5 to 19 kPa (Pattison et al. 2010; Weaver et al. 2012), yielding calculated Young’s moduli between 4–55 kPa. We used a value in the middle of this range, the average shear modulus measured in (Pattison et al. 2010), 7 kPa, for our calculations, giving 20.3kPa for the Young’s modulus of brain tissue. The moduli obtained for brain tissue in vivo using magnetic resonance elastography are 10–100× larger than those obtained from ex vivo slices (Franze 2011). While these discrepancies may reflect methodological issues, the differences are likely caused by the confinement by the skull along with the incompressibility of brain tissue, as well as the changes caused by the sacrifice of the animal and damage by the slicing procedure, making the in vivo measurements more applicable for our case.

The pressure-strain modulus of a vessel, E_p, is related to the incremental modulus (equivalent to the Young’s modulus of the vessel wall), E_inc, by the formula (Ethier and Simmons 2008):

$$E_p=E_{\mathit{\text{inc}}}\frac{1-{(1-\frac{2T}{D_0})}^2}{2(1-v^2){(1-\frac{2T}{D_0})}^2}$$ (3)

E_inc is the quantity measured in most experiments examining vessel elasticity. T is the thickness of vessel wall, and D₀ is the vessel diameter at rest. Taking E_inc to be 0.5 ×10⁶ dyne/cm²(Hajdu and Baumbach 1994) for relaxed arteries at <50mm Hg internal pressure (Lipowsky 2005), T/D₀ =0.05 (Hajdu and Baumbach 1994), and v=0.45, we calculate E_p to be 7.4kPa. If we take a higher estimate of E_inc, 2 × 10⁶ dyne/cm²(Coulson et al. 2004), E_p is 29.4kPa. The mechanical properties of brain tissue in vivo have only been measured for bulk tissue, which may differ from microscopic values in the upper cortex.

Results

We performed two-photon imaging of neural activity and vascular responses in the somatosensory cortex of awake mice that were head-fixed on a spherical treadmill (Dombeck et al. 2007; Huo et al. 2014). Voluntary locomotion is a natural sensorimotor behavior that drives a large and robust increase in blood flow and volume (Huo et al. 2015) and neural activity (Chapin and Woodward 1981; Dombeck et al. 2007; Huo et al. 2014) in the limb representations in somatosensory cortex. We imaged a total of 245 arteriole and 124 venule segments in 17 mice through Polished and Reinforced Thin-Skull (PoRTS) windows (Drew et al. 2010; Shih, Mateo, et al. 2012). Using cytochrome oxidase staining (Drew and Feldman 2009), we reconstructed imaging site locations relative to the forelimb/hindlimb (FL/HL) representation, and separated vessels into those located in the FL/HL or other somatosensory representations, allowing us to detect region-specific differences in vessel responsiveness.

Neurovascular coupling during voluntary locomotion

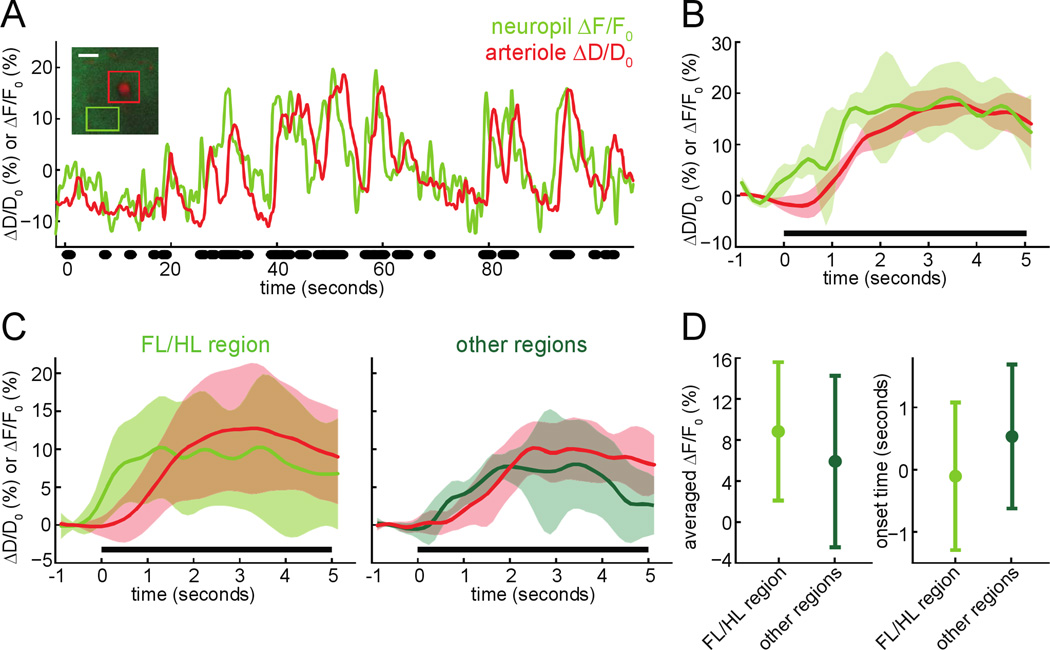
We first asked if increases in neural activity during voluntary locomotion were accompanied by dilation of a nearby penetrating arteriole. To answer this question, we simultaneously imaged penetrating arterioles and neuronal [Ca²⁺] with 2PLSM in Thy1-GCaMP3 transgenic mice (Chen et al. 2012) 50–150µm below the pia. These mice express GCaMP3 primarily in layer V pyramidal neurons, allowing us to detect calcium signals from the apical tufts (Xu et al. 2012) of these neurons in the superficial layers (Fig. 1A, inset). We found that voluntary locomotion drove an increase in neural activity in the somatosensory cortex, followed by dilation of nearby arterioles (Fig. 1A & B). In both the FL/HL region and other surrounding somatosensory regions, locomotion triggered an increase in neuropil fluorescence which was of comparable amplitude as those obtained by other groups using Thy1-GCaMP3 mice (Chen et al. 2012; Issa et al. 2014). The neuropil signal will contain signals from axonal (Lecoq et al. 2009; Glickfeld et al. 2013) and dendritic activity (Tian et al. 2009), which should reflect the local field potential (LFP). The LFP is correlated with hemodynamic signals (Logothetis et al. 2001; Viswanathan and Freeman 2007; Chaigneau et al. 2007). The calcium responses of the neuropil in other somatosensory regions were not significantly different than those in the FL/HL representation (Fig. 1D). The increases in neural activity in both regions were followed by prompt dilation of the nearby arterioles (Fig. 1C), with a 0.35±1.15 second delay relative to neural activity increases in the FL/HL representation and a −0.05±1.26 second delay in the other somatosensory regions. These simultaneous measurements of neural activity and arteriole diameter demonstrated that increases in neural activity were accompanied by dilation of nearby intracortical arterioles. We then investigated how these evoked dilations propagated through the vascular network.

Figure 1. Imaging neurovascular coupling in the somatosensory cortex during voluntary locomotion.

A) Example diameter changes (ΔD/D₀ (%), in red) of an intracortical arteriole and calcium fluorescence changes in nearby neuropil (ΔF/F₀ (%), in green) in the FL/HL region during voluntary locomotion. Locomotion events are denoted by black dots. Increases in neuropil fluorescence preceded the dilation of the arteriole. Inset: 2PLSM image of this example arteriole and its surrounding neuropil, 60µm below the pial surface from a Thy1-GCaMP3 mouse. Green box designates the neuropil ROI in which [Ca²⁺] signals were quantified. Red box encloses the measured penetrating arteriole. Scale bar 20µm. B) Locomotion-triggered average of vessel dilations and neuropil fluorescence increases from the example shown in A. Black bar denotes locomotion period. C) Population locomotion-triggered averages of neuropil fluorescence signal and arteriole dilation in the FL/HL representation (15 neuropil-arteriole pairs, left) and other regions (7 neuron-arteriole pairs, right) of somatosensory cortex from 6 Thy1-GCaMP3 mice. D) Left, comparison of the locomotion-triggered neuropil fluorescence averaged over 1–4 seconds after locomotion onset between the FL/HL region and other regions. Right, Plot of locomotion-triggered neuropil response onset times in the FL/HL region and other regions of somatosensory cortex. The response of the neuropil outside the FL/HL representation was not significantly different from the FL/HL region (averaged ΔF/F₀%: 10.8±6.7% (FL/HL region), 9.2±5.7% (other regions), p=0.14, paired t-test) and had a similar latency (onset time: −0.11±1.19s (FL/HL region), 0.53±1.16s (other regions), p=0.13, paired t-test).

Locomotion-induced vasodilation was dependent on vessel depth, location in the vascular tree, and cortical region

To determine how location in the vascular tree and in the somatosensory cortex affected voluntary locomotion induced vessel dilations, we imaged arterioles and venules from the cortical surface down to 250 µm below the pia, both inside and outside the FL/HL representation. Because conducted dilatory signals have been shown to attenuate when they travel through vessel branch points (Segal and Neild 1996), we segregated the vessels on the pial surface by the number of junctions between them and the penetrating arteriole. We defined penetrating arteriole/ascending venule branches as the part of the pial vessel network that were directly connected to intracortical arterioles or venules without an intervening junction, and a main branch as a portion of vessel that was at least one junction away from the penetrating or ascending vessel (Supplementary Fig. 1).

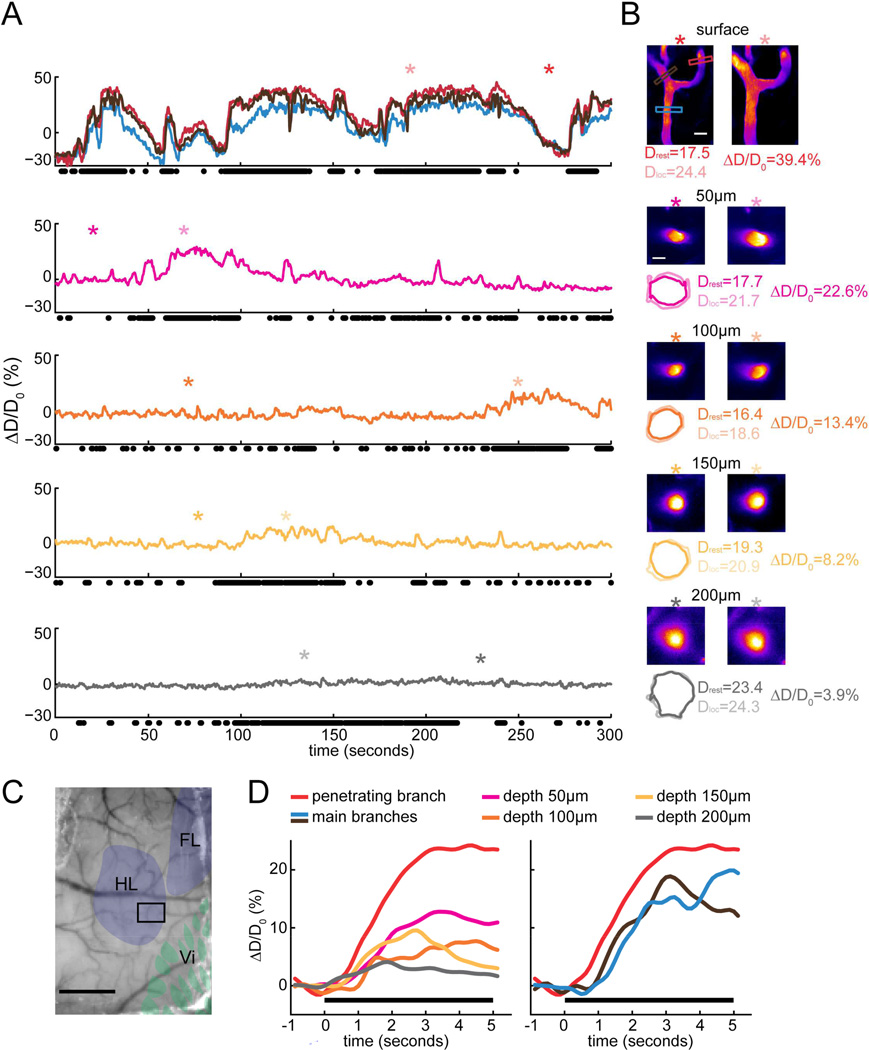
Surprisingly, we found that the locomotion-induced dilations of intracortical arterioles and venules were dramatically smaller than the dilations of surface arterioles and venules. A typical example of the depth-dependence of dilation of an arteriole from a C57/BL6 mouse in the FL/HL region is shown in Fig. 2A. In this example arteriole, locomotion induced dilations throughout the arterial tree, but the amplitude of arteriole dilation decreased with increasing depth below the pia. The evoked dilations were largest at the surface (>20%), decreasing to ~10% at a depth of 50 µm below the pia, and the portion 200 µm below the pia barely responded to locomotion (~5%) (Fig. 2D, left). A similar difference between the response amplitudes of intracortical and surface venules was observed as well (Supplementary Fig. 2). In these example vessels, the deeper portions of penetrating arterioles and ascending venules did not dilate as much during bouts of voluntary locomotion as the more superficial portion of the same vessel and the surface branches.

Figure 2. Locomotion-driven dilations of an example arteriole imaged at multiple depths below the surface.

A) Voluntary-locomotion induced diameter changes of an example arteriole measured at the surface and at multiple depths below the cortical surface. The top panel shows the diameter changes of three surface branches. The penetrating branch (enclosed by red box in B) enters into the brain to become intracortical vessel. The lower panels show the diameter changes of this penetrating arteriole in the brain during locomotion from 50 to 200µm below the pia. Black dots below each panel correspond to locomotion events. The asterisks mark the time points where the images of standing and locomoting in B were taken. Note that imaging at each depth was performed sequentially, so locomotion patterns differ at different imaging depths. B) 2PLSM images of the example arteriole at multiple depths. Asterisks show time points from which images are taken. Scale bars 20µm. Colored boxes in the top image correspond to the colored diameter percentage traces in the top panel of A. Numbers on the top of images are the depth below the surface at which the vessel was imaged. Colored contours show vessel outlines detected with the TiRS algorithm, and are enlarged by a factor of two relative to the images. D_rest and D_loc are the diameters from the above images during rest and locomotion, respectively. ΔD/D₀ is the diameter percentage changes during locomotion relative to rest. C) Photo of PoRTS window with histologically identified somatosensory representations overlaid. HL: hindlimb region, FL: forelimb region, Vi: vibrissae region. The black box encloses the area imaged with 2PLSM that contains the arteriole in A. Scale bar 1mm. D) Locomotion-triggered average of vessel diameter changes at different depth below the cortical surface. Each colored curve was taken from the corresponding time series of the example arteriole in A. Black bars show locomotion.

We quantified the relationship between depth and dilation amplitude across the population of imaged arterioles and venules, both inside and outside the FL/HL representation, in order to reveal vessel-location and somatosensory-region differences. As the vessel dilation amplitudes and fraction of time spent locomoting were similar in both wild-type C57/BL6 and Thy1-GCaMP3 mice (Table 1), we combined the two groups for analysis purposes. Both surface main branches and penetrating branches of arterioles had significantly larger peak dilations during locomotion than intracortical arterioles, both inside and outside the FL/HL representation (Fig. 3A & 3C). This difference in the amplitude of the responses of surface and intracortical arterioles was also apparent if the dilations were averaged 1–4 seconds after the initiation of locomotion (Supplementary Fig. 3), and if the dilations were calculated as peak-to-peak differences over the whole imaging session (Supplementary Fig. 4), indicating that the laminar difference of dilations was a general feature of the cerebral vascular system during locomotion. Lastly, the difference in dilation amplitude was substantial even within the first 100 µm cortex, as the peak dilation of all surface vessels in the FL/HL was significantly larger than intracortical vessels within 100µm of the surface (21.2±7.9% vs. 10.4±6.0%; p<10⁻⁵, paired t-test).

Figure 3. Amplitude of locomotion-evoked dilations depended on vessel location and depth below the surface.

A) Population average of locomotion-triggered arteriole diameter changes inside (left) and outside (right) the FL/HL representation. Insets show the color codes for the location in the vascular tree and depth below the surface (50 µm: 0<depth⩽50µm, 100 µm: 50⩽depth⩽100µm, 150 µm: 100<depth⩽150µm, 200µm: depth>150µm). B) The peak dilation of each arteriole versus the cortical depth along the arteriole that the measurements were made in the FL/HL region (left) and the other regions (right). Only the penetrating branches were included for depth 0µm. Lines are piecewise linear fits. The insets show the locations of these arterioles in the somatosensory cortex relative to the FL/HL representation. Scale bar 1mm. HL: hindlimb region, FL: forelimb region, Vi: vibrissa region. C) Comparison of the peak dilations of the arteriole surface penetrating branches, main branches, and intracortical arterioles in the FL/HL region and the other regions (*: p<0.05, **: p<0.01, ***: p<0.001). At all locations in the vascular tree, vessels in FL/HL region had larger dilations than the corresponding vessels in other regions (penetrating branch: 24.0%±7.5% (FL/HL region), 17.0%±7.1% (other regions), p=0.0019; main branch: 23.9%±7.3% (FL/HL region), 17.8%±5.5% (other regions), p=0.0019; intracortical arterioles: 10.1%±6.3% (FL/HL region), 7.7%±3.7% (other regions), p=0.029, paired t-test). In both regions, the dilation of surface penetrating arterioles was significantly larger than the dilation of intracortical arterioles (FL/HL: p=1.8×10⁻¹⁴, other regions: p=3.9×10⁻⁹, paired t-test). D) Comparison of the onset time of the three arteriole groups as in C. Surface main branches in both regions had significantly delayed onset compared to the surface penetrating branches (FL/HL region: 0.16±0.57s (penetrating branch), 0.46±0.55s (main branch), p=0.043; other regions: 0.30±0.52s (penetrating branch), 0.73±0.39s (main branch), p=0.003, paired t-test), but there was no significant onset difference between surface penetrating and intracortical vessels (intracortical arterioles: 0.34±0.61s (FL/HL region), p=0.20, 0.19±0.80s (other regions), p=0.59, paired t-test). E) The peak dilation of each venule plotted versus its depth below the pia. Venules inside the FL/HL region are purple (left), those outside are light blue (right). The inset shows the locations of these venules in the somatosensory cortex relative to the FL/HL representation. Scale bar 1mm.

In addition to the differences in locomotion-induced vessel dilation amplitude with depth, the dilation amplitude depended on the position in the somatosensory cortex. At all depths, the dilations of vessels in the FL/HL representation elicited by locomotion were significantly larger than those at the same depth in other somatosensory regions (Fig. 3A & 3C). On the surface, both the arteriole main branches and penetrating branches in the FL/HL region exhibited significantly larger peak dilations than their counterparts outside the FL/HL representation (Fig. 3C) and intracortical arterioles showed stronger locomotion-evoked peak dilations in the FL/HL representation than intracortical arterioles in other regions (Fig. 3C). We fit the peak dilation-depth relationship using a piecewise linear model, where the peak dilation was assumed to decrease linearly from a peak D_max, with a slope s, with depth, z, below the cortical surface until an inflection point d_I after which it is assumed to be constant, D_min. For the arterioles in the FL/HL region the best fit was given by: D_max = 24.0%; D_min =8%; s=− 0.21 %/µm; d_I =76.8±19.3µm, with r=0.75. The 95% confidence interval of the inflection depth for arteries in the FL/HL representation obtained by bootstrapping was 36.0µm to 114.3µm. For the arterioles in the other regions, the fit was: D_max = 17.0%; D_min=6.7%; s=−0.14%/µm; d_I =72.0±29.8µm, with r=0.39. For the venules in the FL/HL region, the best fit was: D_max = 7.3%; D_min = 3.7%; s=− 0.06%/µm; d_I = 56.6µm, with r=0.57, while in the other regions, the fit was: D_max = 5.9%; D_min = 3.1%; s=− 0.04%/µm; d_I with r=0.62.

The fitting showed that the peak dilation of the locomotion-triggered average of both arterioles and venules dropped with increasing distance from the pial surface, until it reached an inflection point approximately 50–80µm below the surface, beyond which it was flat (Fig. 3B & 3E).

The significantly larger dilation of arterioles inside the FL/HL representation than those outside the FL/HL representation was surprising, as the large majority of the vessels outside the FL/HL representation were still very close to the FL/HL representation (Fig 3B, average arteriole distance to the border of FL/HL: 0.52±0.27mm, average venule distance: 0.50±0.29mm, 100% arterioles were <1 mm from the border of FL/HL region, and 95.7% venules <1 mm from the border), suggesting that the hemodynamic response was relatively spatially specific. Thus the amplitude of dilation of an arteriole reflected both its position in the vascular tree, as well as its location in the body map in the somatosensory cortex. Similar depth dependencies were seen when the locomotion-triggered response was averaged 1–4 seconds after locomotion initiation (Supplementary Fig. 3) or the differences in the peak-to-peak responses across the entire imaging session were used (Supplementary Fig. 4), again indicating the depth dependence was not due to differences in temporal dynamics of the dilatory response across depths.

Since intracortical arterioles tended to be slightly larger than surface vessels (Supplementary Fig. 5), we wanted to test if this size difference could account for difference in dilation amplitude of surface and intracortical vessels. Smaller surface arterioles are known to be more reactive and dilate more in response to sensory stimulation and hypercapnia (Lee et al. 2001; Drew et al. 2011; Huo et al., 2015), though it is not known if this is the case for intracortical arterioles. We performed a multivariate regression of peak dilation against depth and resting diameter of the arteriole to determine if diameter differences could account for the differences in dilation. The fit yielded the relationship:

$$\frac{\mathrm{\Delta }{D}_{\text{peak}}}{D}=-0.11z-0.36D+0.264$$ (4)

where z was the depth below the surface and D was the vessel diameter. There was no significant interaction between cortical depth and vessel diameter (p=0.3). With resting diameters typically spanning a 20µm range (10–30µm, Supplementary Fig. 5), and depth ranging over 200µm (Fig. 3A), the effect of depth was approximately 3× larger than any diameter-related reactivity effects (0.11/µm × 200µm vs. 0.36/µm × 20µm). From these results, we see that the intracortical part of the vessels dilated substantially less than the surface part of the same vessels, and that this difference was largely attributable to the depth of the vessel, not size differences.

We also quantified the dilation latencies for surface and intracortical arterioles. We found no significant differences in the onset latencies for intracortical and surface vessels in either area (Supplementary Fig. 5, Fig. 3D). As venous dilations were very small (typically ~5% at the peak) and slow, taking tens of seconds to reach their peak (Drew et al. 2011; Huo et al. 2015), we were not able to accurately calculate their onset time. Averaged across all arterioles, the mean onset time was 0.32±0.66 seconds. The near simultaneous dilation of surface and intracortical vessels was consistent with previous studies showing essentially no latency differences between surface and intracortical vessel dilation (Hirano et al. 2011; Nizar et al. 2013; Sekiguchi et al. 2014) (but see (Tian et al. 2010)) and the known rapid (several mm/second) conduction of vasodilation (Hilton 1959; Emerson and Segal 2000; Chen et al. 2011). Our measurement of the variability of vasodilation onset times (standard deviations of 0.55, 0.57, 0.61 seconds for surface main branch, penetrating branch and main intracortical vessels, respectively in the FL/HL representation) was in agreement with other single vessel measurements, as well as with human fMRI studies. Nizar et al. (2013) report a standard deviation of 0.6 seconds in the onset time of vasodilation (calculated from their report of a standard error of 0.1 seconds over 36 wild-type animals). Larger variability in the onset the hemodynamic response, on the order of seconds, has been seen in human and primate fMRI studies (Handwerker et al. 2004; Watanabe et al. 2013).

The smaller dilation of intracortical vessels, relative to surface vessels was surprising and counterintuitive. First, propagated dilations can travel several millimeters with little attenuation (Bagher and Segal 2011), due to the millimeter-scale length constants of vessels. The dilation did not attenuate much in the surface arteriole network (Fig. 3C), and the dilation propagated very rapidly (Fig. 3D), both suggesting that the entire arterial network supplying the somatosensory cortex was strongly electrically coupled (Segal 2005). Secondly, all known anatomical evidence pointed to the vasodilatory signal originating in the cortex (reviewed by Hamel (2006)), so we would expect the intracortical vessels to be dilated more, as they are closer to the origin of the vasodilatory input. Because the dynamics and magnitudes of the dilations we observed in the surface arterioles and venules during voluntary locomotion were very similar to those evoked by passive stimulation (Drew et al. 2011), it is unlikely that this dilation pattern was a unique feature of voluntary locomotion. Because the observed fits of arterial and venous depth dependence of dilation were very similar across cortical regions and vessel types, it is likely that the depth dependence of dilation in arterioles and venules share a common origin.

No difference in maximal dilation between surface and intracortical vessels

One possible origin of the smaller dilation of the intracortical arterioles relative to surface arterioles was that the intracortical portion of the arteriole might have already been dilated by ongoing neural activity in the awake brain, reducing its dilatory range. This saturation of dilation might be caused by the tonic action of vasodilatory substances released from active neurons deep within the brain, where neuronal density is higher (Tsai et al. 2009). If the deep vessels were already dilated during normal wakefulness, then global vasodilation should cause them to dilate proportionally less than surface vessels.

To test the hypothesis that deep vessels were already dilated when the mice were quietly resting between locomotion bouts, we compared the peak diameters of individual vessels during locomotion with their diameters during anesthesia with isoflurane. We used isoflurane rather than CO₂ for vasodilation for several reasons. Isoflurane is a potent vasodilator (Archer et al. 1987, Todd and Drummond 1984; Weeks et al. 1990), directly acting on smooth muscles (Flynn et al. 1992) by blocking calcium channels (Buljubasic et al. 1992; Akata et al. 2003) and opening potassium channels (Kokita et al., 1999). These same pathways are activated in smooth muscles by neural activity (Bolotina et al. 1994; Filosa et al. 2006). At the dose used here (2%), isoflurane completely occludes sensory-evoked vasodilation (Blinder et al., 2013), consistent with isoflurane acting via the same pathway as neural activity. In contrast to isoflurane-induced vasodilation, CO₂-induced dilation has an additive interaction with neurally evoked vessel dilations (Corfield et al. 2001; Martin et al., 2006), meaning that CO₂ dilates cerebral vessels via a different mechanism than sensory-evoked neural activity. Additionally, levels of CO₂ that induce vasodilation cause anxiety in mice (Taugher et al., 2014), which will drive locomotion, confounding the interpretation.

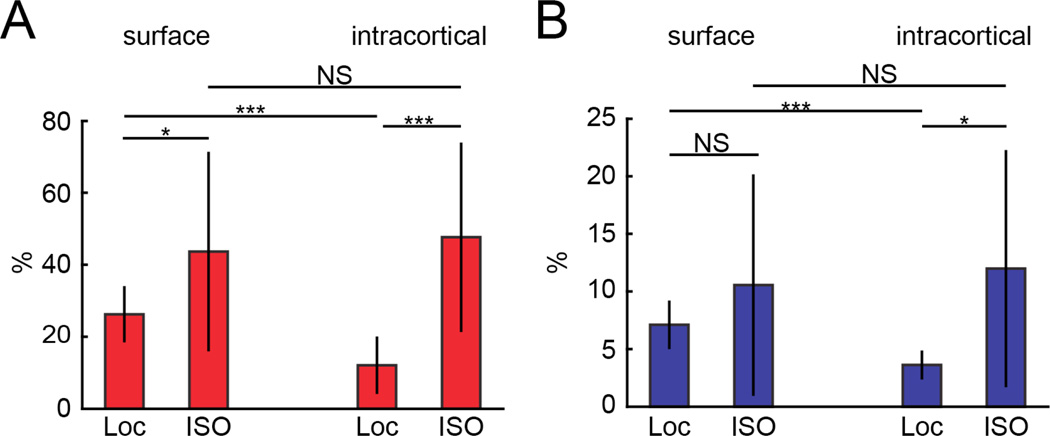
We compared the peak dilations in the locomotion-triggered response to the dilation elicited by isoflurane (Fig. 4). Both surface and intracortical arterioles were significantly more dilated by isoflurane than by locomotion (Fig. 4A). Interestingly, we found that isoflurane dilated surface and intracortical arterioles the same amount (~40%), consistent with the observation that there was smooth muscle on both intracortical and surface arterioles (Supplementary Fig. 7). A similar pattern was found for veins, where intracortical venules dilated by the same amount as surface venules (Fig. 4B). This result has several implications. First, it shows that intracortical and surface vessels have the same maximal dilatory capacity, and the difference in surface and intracortical dilation amplitudes is not due to a baseline dilation or saturation of the intracortical vessels. It is also a positive control of our ability to resolve equivalent changes in intracortical vessels diameter with two-photon microscopy. It is known that isoflurane-induced vasodilation causes a substantial rise in intracranial pressure (Todd and Drummond 1984; Scheller et al., 1988), meaning that this un-physiologically large dilation of cerebral vessels will cause compression of the brain tissue. Since intracortical arterioles in the FL/HL representation were not maximally dilated during locomotion, this suggests that the observed depth- dependence of the dilation was not due to the intracortical arterioles being closer to maximal dilation, or having a more limited range of dilation but rather the dilation of intracortical arterioles was restricted under normal physiological conditions.

Figure 4. Vasodilation by isoflurane reveals that intracortical vessels were not maximally dilated during locomotion.

A) Plot shows the peak percentage change in diameter of arterioles inside the FL/HL region during locomotion and during isoflurane treatment. The percentage change of surface arterioles during locomotion (26.2%±7.8%) was significantly different from that under isoflurane (43.7%±27.7), (n=18, p=0.01, paired t-test). The diameter change of intracortical arterioles during isoflurane treatment (47.7%±26.3) was significantly larger than that during locomotion (12.1%±8.0%), (n=29, p=4×10⁻⁹, paired t-test). Isoflurane caused a similar dilation in surface and intracortical arterioles (p=0.62, paired t-test). B) Plot shows the peak percentage change in diameter of venules inside the FL/HL region during locomotion and during isoflurane treatment. The diameter change of surface venules during locomotion (7.01%±2.2%) was not significantly different from that during isoflurane treatment (10.7%±9.8%) (n=8, p=0.34, paired t-test). However, for the intracortical venules, isoflurane (12.2%±10.5%) dilated the vessels significantly more than locomotion (3.4%±1.17%) (n=11, p=0.02, paired t-test). The dilation caused by isoflurane in surface and intracortical venules was not significantly different (p=0.78, paired t-test).

Intracortical vessels, but not surface vessels, were enclosed by brain tissue

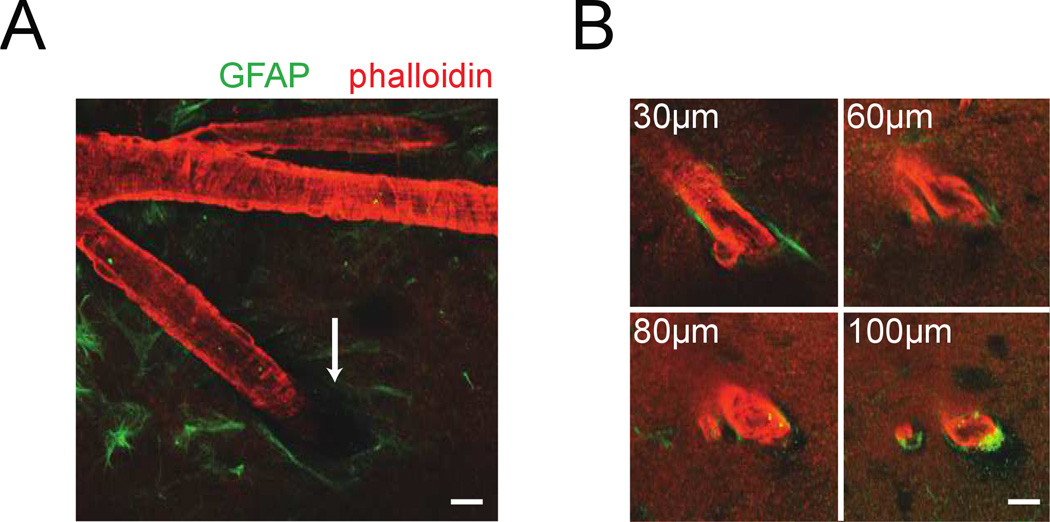
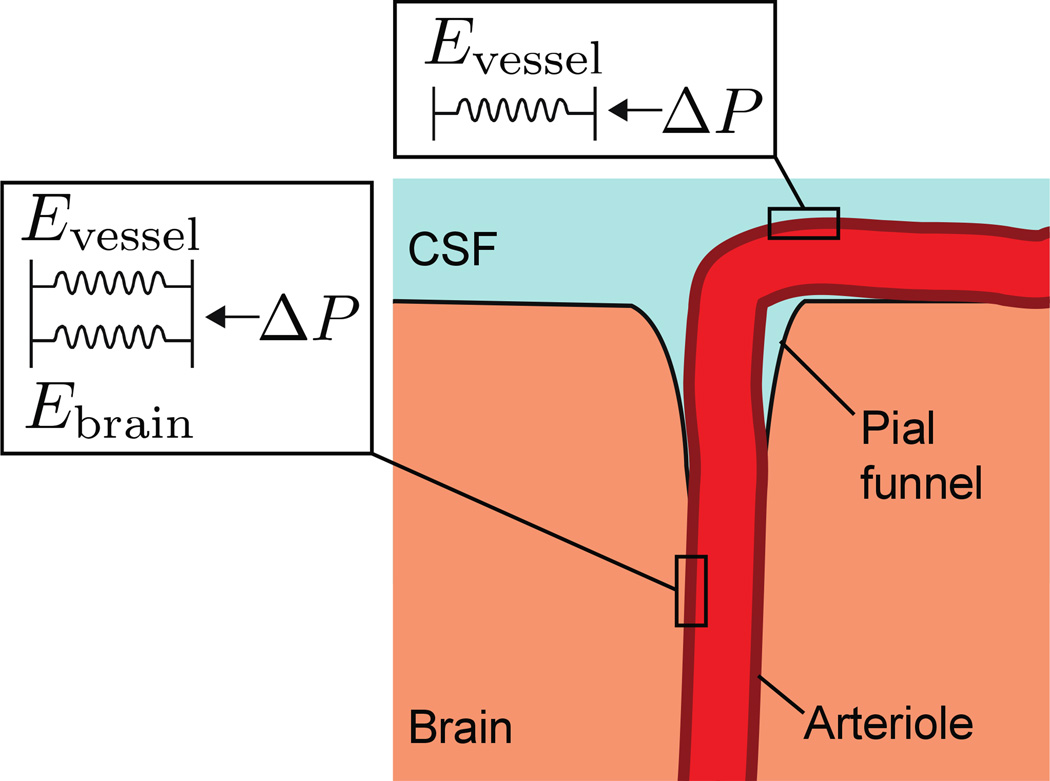
We then asked if the smaller dilations of intracortical vessels could be due to restriction of dilation by the surrounding brain tissue. To test this hypothesis, we visualized smooth muscles and astrocytes in an intact brain ex-vivo. This approach was used in order to maintain the vascular ultrastructure. We filled the vasculature with gelatin to maintain vascular tone (Tsai et al. 2009; Blinder et al. 2013), labeled the actin-rich smooth muscle that surrounds the arterioles with rhodamine-conjugated phalloidin and astrocytes that ensheath the vessel (Abbott et al. 2006; Takano et al. 2006; Koehler et al. 2009) with an anti-GFAP antibody. This allowed us to use 2PLSM to image the interface between brain tissue and the penetrating arterioles up to 100µm below the surface (Fig. 5). The imaging depth was restricted by scattering and the penetration of the antibody (Tsai et al. 2009). Rings of smooth muscle were visible around surface and intracortical arterioles. Consistent with previous studies (Zilles et al. 1991; Drew et al. 2010), we observed GFAP expression on the pial surface. Where the penetrating arteriole enters the brain, we observed a ‘pial funnel’ (Fig. 5A), a narrowing of the Virchow-Robin space between the vessel and the brain that is filled with CSF (Cserr et al. 1986; Iliff et al. 2012). As the vessel went deeper below the pial surface, the space between the brain and vessel was reduced, until the astrocytes were in nearly direct contact with the vessel. This narrowing of the Virchow-Robin space took place less than 100µm below the surface, consistent with the inflection point of the dilation amplitude of vessels (Fig. 3B, Supplementary Figs. 3 & 4). Between the brain tissue and the intracortical vessels (deeper than 50µm) there was a very small (~1µm) perivascular space (Virchow-Robin space) (Zhang et al. 1990; Iliff et al. 2012; Thrane et al. 2013) (Fig. 5B, Supplementary Fig. 7). It seems unlikely that distortion by fixation would cause these effects as the close apposition of glial endfeet and vessels that we observed has been seen in many in vivo imaging studies (Takano et al. 2006; Mccaslin et al. 2011; Iliff et al. 2012; Thrane et al. 2013). These anatomical observations indicate that dilations of the intracortical vessels that we observed would require compression of the surrounding brain tissue, which is not the case for the surface vessels. This mechanical interaction between the intracortical blood vessel and the surrounding brain could be the cause of the difference between the dilation amplitude of surface and intracortical vessels. We next sought to determine if mechanical restriction by brain tissue was physically plausible by using a biomechanical model.

Figure 5. Visualizing arterioles and their interaction with the surrounding brain tissue.

A) 2PLSM image of a penetrating arteriole (red, actin labeled with rhodamine-conjugated phalloidin) and surrounding astrocytes (green, labeled with anti-GFAP antibody) in an ex vivo brain. The pial funnel, a hole in the brain into which the penetrating vessel enters, is marked with the white arrow. B) Four images of the penetrating arteriole in A taken at increasing depths below the pia. The perivascular space between astrocytes and vessel wall below the surface was very small. Any dilation of the intracortical vessel would compress the surrounding brain tissue. Scale bars 20µm.

Mathematical modeling of the mechanical restriction of intracortical vessel dilation by brain tissue

For mechanical restriction of the blood vessels to be a viable explanation for the differences in surface and intracortical vessel dilation, the brain would have to be stiff enough to resist intracortical vessel dilation, but not stiff enough to completely prevent it. While ex vivo measurements of brain tissue mechanical properties have indicated that brain tissue is very soft (having a Young’s modulus of several hundred kiloPascals (Franze et al. 2012)), in vivo measurements have consistently shown that under normal physiological conditions, when the brain is enclosed inside the skull, brain tissue is approximately two orders of magnitude stiffer (Pattison et al. 2010). For this model, we will only address the dilation amplitudes of surface and deep intracortical vessels (those deeper than the inflection point in Fig. 3B), (Fig. 6). We did not model the dilation amplitude of the transition zone between the surface and inflection point, as this would require detailed reconstruction of the Virchow-Robin space, and a substantially more complicated biomechanical model.

Figure 6. Modeling the mechanics of surface and intracortical vessel dilation.

Schematic of the brain-vessel interactions showing that the surface vessel is surrounded by CSF, while the intracortical vessel is enclosed by brain tissue. The mechanical environment of the surface vessel was modeled as a single spring whose elastic modulus was given by the pressure-strain modulus of the vessel (E_vessel). For the intracortical portion of the vessel, the mechanical environment was equivalent to two springs in parallel, with an elastic modulus as the sum of the pressure-strain modulus of the vessel and the Young’s modulus of brain tissue (E_{intracortical} = E_vessel + E_brain). The pressure drop within a short segment of vessel will be small, so both segments were assumed to experience equivalent pressures.

We assumed that the vessel wall experienced a pressure that was the difference between blood pressure and intracranial pressure, and was either surrounded by CSF (in the case of a surface vessel), or by brain tissue (intracortical vessel) (Fig. 6). The forces exerted on the blood vessel wall were assumed to be isotropic. Because blood vessels are roughly cylindrical (Gao and Drew 2014; Tsai et al. 2009), they will experience circularly symmetric forces. Within the physiological range, blood vessel walls can be considered linear elastic solids that obey Hooke’s law (Peterson et al. 1960; Bergel 1961). Using these assumptions, we made an equilibrium 1-D mechanical model where the vessel wall was made of isotropic linear elastic solid. We made the simplifying assumptions that any changes in intracranial pressure caused by vessel dilation were negligible, and only the mechanical properties of the vessel and brain tissue came into play. For a cylinder with elastic walls, such as a blood vessel, the change in diameter is given by:

$$\mathrm{\Delta }P=E_p\frac{\mathrm{\Delta }D}{D_0}$$ (5)

where ΔP is the change in pressure, ΔD and D₀ are the changes in vessel diameter and initial diameter respectively, and E_p is the pressure-strain modulus (Peterson et al. 1960; Bergel 1961), and can be thought of as the “spring constant” of the vessel wall in response to an isotropic force. We assumed that the pressure drop and vessel diameter change were negligible in the short distance (<250µm) over which the vessels are measured, so both the intracortical and surface portions of the vessels experienced the same pressure change, ΔP, and had the same initial diameter, D₀. From our arteriole data where the surface dilations were larger than the intracortical vessels, we can write:

$$\alpha \mathrm{\Delta }{D}_{\text{intracortical}}=\mathrm{\Delta }{D}_{\text{surface}}$$ (6)

where α is the ratio of surface vessel diameter change to intracortical vessel diameter change (Fig. 3B & 3E). Using this model, we then could express the ratio of dilations of the surface vessels as a ratio between the effective Young’s modulus of the surface and intracortical vessels:

$$\frac{E_{\text{intracortical}}}{E_{\text{surface}}}=\frac{\mathrm{\Delta }{D}_{\text{surface}}}{\mathrm{\Delta }{D}_{\text{intracortical}}}$$ (7)

For the surface arteriole, the effective Young’s modulus was taken to be the pressure-strain modulus of the vessel alone, E_vessel. We modeled the mechanical effects of the brain tissue surrounding the vessel as a spring in parallel with the vascular wall (Fig. 6), so the effective Young’s modulus, E_{intracortical}, of the portion of vessel in the brain would be given by the sum of the Young’s modulus of the brain tissue surrounding the vessel E_brain, and the pressure-strain modulus of the vessel, yielding E_{intracorticai} = E_vessel + E_brain From equation (6) and (7), we determined E_{intracortical} = αE_surface and therefore:

$$E_{\text{brain}}=(\alpha -1)E_{\text{vessel}}$$ (8)

In the pressure ranges that cerebral arterioles experience (Lipowsky 2005), cerebral arterioles have effective elastic moduli in the range of ~7 kPa (Hajdu and Baumbach 1994). Elastography measurements of brain tissue indicate that E_brain is ~20kPa (Pattison et al. 2010). Venules have similar elastic properties as arterioles at the physiologically relevant pressures (Baird and Abbott 1977), so brain tissue should restrict the dilation of venules by a similar factor as arterioles, which is consistent with what was seen experimentally (Fig. 3E). Putting these empirically measured quantities into equation (8), our mathematical model predicted that that surface vessel dilations would be approximately 3× larger than intracortical vessels. We calculated average α for the set of vessel segments for which we had both surface (penetrating and main branch) and deep (>100µm) measurements of vessel dilation by taking the ratio of the average surface vessel peak dilation to average deep intracortical vessel peak dilation. From our data we calculate α to be 3.10±1.36 (Fig. 3), very close to the value of 2.9 predicted from the known mechanical properties of brain tissue and blood vessels (Hajdu and Baumbach 1994; Pattison et al. 2010). The intermediate amplitude dilations observed in vessel segments near the surface could be due to extra space afforded by the pial funnel. Both the Young’s modulus of brain tissue and the pressure-strain modulus of the blood vessel are in a range where brain tissue will have appreciable effects on the amplitude of vessel dilation.

Discussion

Spatial specificity of surface and intracortical vascular responses

In the present study, we imaged neural and vascular dynamics in the somatosensory cortex during voluntary locomotion in mice, and found that locomotion drove large increases neural activity followed by local blood vessel dilation in the limb representations (Fig. 1). The significant difference between the amplitudes of arteriole dilation inside and outside the FL/HL representation was surprising, given close proximity of the two populations of measured vessels to each other, and given the relative length constants of arterioles. The differences in arterial dilations between adjacent areas we observed in the somatosensory cortex supports the idea that hemodynamic signals can carry information about activity on a columnar level (Moon et al. 2013).

Our data can also address the issue of spatial and temporal specificity of the vascular response, which has been a contentious issue in fMRI (Kriegeskorte et al. 2010; Gardner, 2010). The voxel size used in fMRI imaging experiments will encompass many vessels, and it is not known if these vessels will respond in a temporally and spatially homogenous manner, or if individual vessels within the voxel exhibit different response dynamics for different stimuli, or reflect non-local activation. If the hemodynamic response is not spatiotemporally separable (Bieβmann et al. 2012), that is, the hemodynamic response is a wave of dilation (Drysdale et al. 2010; Aquino et al., 2012; Aquino et al. 2014a) then the non-separable hemodynamic response should be taken into account when decoding hemodynamic signals (Bieβmann et al. 2012; Aquino et al. 2014b). Surface arteries outside the FL/HL representation had delayed (<0.25 seconds) and smaller dilations to locomotion than surface arteries inside the FL/HL representation. This delay in the dilation corresponds to an effective velocity across the cortical surface of >2mm/second, in agreement with other measures of hemodynamic waves (Aquino et al. 2012). The propagation velocity of the hemodynamic wave across the cortex will be slower than the propagation of the dilation within the arteries, as the arteries do not (usually) form straight-line connections between regions. Thus, our results support the existence of hemodynamics waves (Drysdale et al. 2010; Aquino et al. 2012) during natural behavior, which implies a more detailed hemodynamic response (Kriegeskorte et al. 2010).

Laminar pattern of dilation cannot be accounted for by peripheral innervation of pial vessels

An alternative explanation for the difference between surface an intracortical arteriole dilation seen here is that vasodilatory signals, via peripheral innervation of the large vessels (Hamel 2006) is targeted on surface vessels and conducted down into the intracortical vessels. We think that this is highly unlikely for several reasons. First, targeted optogenetic stimulation of cortical neurons induces increases in blood volume (reflecting vasodilation) that are indistinguishable from sensory stimulation (Vazquez et al. 2013), indicating that the vasodilatory signals are under the local control of cortical neurons, not the peripheral nerves that innervate the large vessels. Second, the known physiology and anatomy of the innervations of pial vessels is inconsistent with vasodilatory signals targeted to the surface vessels (Hamel 2006). Pial vessels receive large sympathetic and parasympathetic innervation, but no direct input from the central nervous system (Hamel 2006). During exercise, such as the voluntary locomotion paradigm studied here (Huo et al. 2014; Huo et al. 2015), sympathetic tone increases (reviewed in (Christensen and Galbo 1983)). Since electrical stimulation of the sympathetic nerves that innervate the pial vasculature causes decreases in cerebral blood flow (Tuor 1990), by constricting the large pial arteries (Baumbach and Heistad 1983), the increased sympathetic tone during locomotion would cause vasoconstriction. Parasympathetic tone decreases during exercise (Arai et al. 1989), so any vasodilatory input from the parasympathetic nerves will be decreased during exercise. Thus, the actions of the peripheral nervous system would oppose any vasodilation in pial arterioles during exercise and tend to cause vasoconstriction, the opposite of what was observed here. Third, a surface-originating vasodilatory mechanism could not explain the differences between surface and intracortical venules, because veins passively dilate in response to changes in pressure (Edvinsson et al. 1983). Since a surface origin of the vasodilatory input is inconsistent with physiological and anatomical evidence, and does not explain the depth dependent responses of venules, the most parsimonious explanation dilation differences between surface and intracortical vessels is that the mechanical properties of brain limit intracortical vessel dilation.

Alternative origins of reduced intracortical vessel dilations

What explanations other than mechanical interactions could account for the smaller dilations of intracortical arterioles and venules relative to those on the surface? Below, we consider several alternative hypotheses.

Given what is known of the anatomy and physiology of cerebral blood vessels, we do not think it is possible that the pial vessels are exposed to higher levels of vasodilators. The intracortical arterioles are ensheathed by astrocyte endfeet, and receive direct projections from neurons that release vasoactive NO, ACh, and peptides (Attwell et al. 2010). In contrast, the pial vessels receive no direct innervation from the nerves of the brain, and are not ensheathed by astrocytes. This would require that vasoactive transmitters diffuse tens to hundreds of microns to the pial vessels. Ngai and Winn (2002) directly tested the hypothesis that surface vessels respond to spillover of vasodilators by flushing the pial vessels with ACSF during sensory stimulation. They found that flushing the pial surface with ACSF had no effect on sensory evoked dilation of pial arterioles, but did reduce CO₂ evoked dilation, supporting the idea that CO₂ dilates vessels via a different pathway than neural activity. This result supports the hypothesis that the pial vessel dilation was due to a hyperpolarization originating in the brain and conducted through the vessel to the pial surface. Lastly, different levels of vasodilatory substances would not explain the difference between intracortical and surface venule dilations.

A second possibility might be that we are unable to detect the dilation of the intracortical vessels due to a resolution or signal-to-noise issue. We think neither of these possibilities is plausible for several reasons. First, under isoflurane, we were able to measure the same dilation in surface and intracortical vessels (Fig. 4), which was a positive control for detection of vessel dilation. Second, we can clearly detect the difference between the dilation amplitudes of surface vessels and intracortical vessels within 100µm of the cortical surface. Within this depth range, single spines can be resolved through a PoRTS window (Drew et al. 2010), so any dilations should be clearly detected. We were also able to clearly visualize microvessels and capillaries at the depths that we measured intracortical arterioles and venules (Supplementary Fig. 6), and there was no differences in the average diameters of the microvessels within the imaged portion of cortex, indicating that our point spread function was not degraded (Supplementary Table 1). Lastly, the TiRS algorithm that we used to quantify vessel cross-sectional area has been validated to work well down the signal-to-noise ratios (S/N) of 1 or less (Gao and Drew, 2014), and our signal to noise ratio was calculated to be >4 for the imaged vessels (Supplementary Table 1). All of these factors suggest that the small dilation of intracortical vessels during locomotion cannot be accounted for by our inability to detect the dilations.

Given that the surface component of the vessels was less than 100µm away from the intracortical portion and that electrical signals propagate passively through arterioles over millimeters due to their large electrotonic length constants (Wolfle et al. 2010; Segal and Duling 1986; Segal 2005), it is unlikely that the smooth muscles of the surface arterioles and intracortical arterioles that we measured from have different intracellular potentials. It is possible that larger dilation of surface vessels could be due to pressure waves traveling upstream (Kim, Khan et al. 2014). One possibility that we cannot rule out is that the surface and intracortical vessels have different contractile properties, specifically that intracortical arterioles require a more hyperpolarized voltage to completely relax relative to the surface arterioles, even if the maximal relaxation of both types of arterioles is the same (Fig. 4). This seems very unlikely for several reasons. First, to our knowledge, no abrupt spatial changes in excitation-contraction coupling have ever been observed in vascular smooth muscle, despite the many studies studying the spatial propagation of vasodilation (Segal, 2005). Second, an abrupt change in the arterioles’ contractile properties as it entered the brain would serve no physiological purpose, as it would reduce blood flow and the specificity of the blood flow to the column-sized area supplied by a single penetrating arteriole (Blinder et al. 2013; Shih et al. 2013). Lastly, this explanation does not explain the differences in dilation of surface and intracortical venules, which have little to no contractile tissue (Edvinsson et al., 1983).

Mechanical limitation of intracortical vessel dilation

Our results showed an unexpected relationship between the position of blood vessels and their dilation during functional activation. During voluntary locomotion, intracortical vessels dilated substantially less than surface vessels, and the depth dependent profile was similar across all vessel types and somatosensory locations (Fig. 3). This difference in dilation amplitude was not due to saturation of dilation, as isoflurane was able to dilate intracortical vessels more than locomotion and to the same degree as surface vessels (Fig. 4), or due to diameter-related reactivity differences (Supplementary Fig. 5), or to a lack of smooth muscle present on intracortical arterioles (Supplementary Fig. 7). The most straightforward explanation of the larger dilation of surface arterioles and venules, was that intracortical arterioles and venules are mechanical restricted by brain tissue (Fig. 5B). Importantly, mechanical restriction of vessel dilation would be consistent with an intracortical origin of vasodilation. It is likely that the vasodilation is conducted throughout the vascular tree, but the dilation is only fully expressed at the surface (Fig. 3C).

Previous studies using two-photon microscopy to investigate single vessel dynamics in response to sensory stimulation have used anesthetized animals (Takano et al. 2006; Tian et al. 2010; Nizar et al. 2013), which attenuates surface arterial and venous dilations by 70 and 100%, respectively (Drew et al. 2011). These studies also used the full-width at half-max to quantify penetrating vessel diameter, which can give erroneously large results for penetrating vessels due to changes of shape during dilation and constriction (Gao and Drew, 2014). These studies also used craniotomies for optical access, and craniotomies cause a decrease in the stiffness of brain tissue by a factor of two (Hatashita and Hoff 1987), which would reduce the mechanical restriction effects present in intact skull preparations. Prior studies of the hemodynamic response in awake animals restricted their measurements to surface vessels (Drew et al. 2011; Huo et al. 2015), or used intrinsic optical signal imaging (Martin et al. 2006; Pisauro et al. 2013; Huo et al. 2014), which could not resolve single vessel dilations. Previous fMRI studies (Zhao et al. 2006; Jin and Kim 2010) have observed the largest fractional cerebral blood volume (CBV) increases in the middle of the cortex. The differences between these previous results and ours are likely due to several factors. First, we only imaged ~250µm below the surface of the cortex, meaning that the entire depth of cortex we imaged over would be lumped together into a single ‘upper layer’ in an fMRI experiment, in which the contribution from intracortical vessels in the upper levels will likely overwhelm any blood volume changes due to pial vessels. In addition, the vascular density on the surface of the brain is ~3× higher than inside the brain, and the pial vasculature is almost entirely composed of large vessels (Tsai et al., 2009), which could cause greatly reduced sensitivity to pial vessel dilation when using supermagnetic particle fMRI techniques, which are sensitive to vessel size (Mandeville, 2012; Kim et al. 2013). Therefore, the CBV signals measured from the pial vessels based on these techniques might be dominated by the signal from intracortical vessels. Additionally, arterioles in the middle layers of cortex have substantially more collateral branches (Blinder et al., 2013), and these branches, as well as capillaries, can themselves dilate (Tian et al. 2010; Hall et al. 2014). It could be that the larger increase in CBV observed in the middle layers of cortex is due to small dilations of many small vessels. It is also possible that the mechanical properties of the layers differ, with the middle layers, having a lower Young’s modulus and thus restrict dilation less than upper layers. Elastography measurements have found that the white matter has a higher Young’s modulus than grey matter (Pattison et al. 2010), and atomic force microscopy measurements have observed that the outer layers of cortex are stiffer than the middle layers (Franze et al. 2013). We might expect the upper layers, which have more neuronal processes and fewer cell bodies, to be stiffer.

As brain tissue resists the dilation of intracortical vessels, why then do surface and intracortical arterioles dilate the same amount under isoflurane? Isoflurane causes large decreases in cerebrovascular resistance via dilation of large cerebral arteries, with little change in the cardiac output (Gelman et al. 1984), which will greatly increase the pressure in the downstream vessels we imaged. Isoflurane relaxes smooth muscle beyond the normal physiological range, dilating the arterioles by >40%. Both arterioles and venules exhibit strain-stiffening (Baird and Abbott 1977; Hadju and Baumbach 1994; Coulson et al. 2004), meaning the vessel become substantially stiffer as it dilates. For arterioles, the pressure-strain modulus rises rapidly for dilations beyond 30%, by a factor of greater than ten between 25% and 35% (Coulson et al. 2004). This means that under the concentrations of isoflurane used here, arterioles are approximately 10× stiffer than in the unanaesthetized animal, making the effective stiffness of the artery several times higher than that of the surrounding brain tissue. Under isoflurane, or any other anesthetic agents that would dilate cerebral blood vessels, the mechanical properties of the vessel, rather than its surroundings, determine the extent of the dilation, which would explain why the intracortical and surface vessel dilations under isoflurane were of the same size.

We anticipate that under anesthetics that have minimal effect on vascular tone, a similar restriction of intracortical vessel dilation should take place as in awake animals, as brain tissue elasticity measurements made under isoflurane (Pattison et al. 2010) are similar to those in awake humans (Mousavi et al. 2014). We think that the restriction of intracortical vessel dilation we see here will not just occur during locomotion, but also generalize in response to other stimuli, since the dynamics and amplitude of surface vessel dilation in response to voluntary locomotion (Huo et al. 2015) are nearly identical to those evoked by stimulation of the vibrissae (Drew et al. 2011). It should be kept in mind that dilation of blood vessels will displace CSF. Since CSF is essentially water, it is incompressible, but is easily displaced. It is thought that CSF either is displaced to remote locations within the brain and spinal cord (Jin and Kim, 2010), and/or enters into the vasculature (Krieger et al. 2012; Iliff et al. 2012) during vasodilation. The pattern of vascular dilation observed here may play a role in the driving the circulation of CSF (Iliff et al. 2013).

Mechanical interactions between tissues in biological systems

If the brain tissue restricts intracortical vessels dilation, changes in the size of the perivascular space may be an important factor in alterations of cerebral blood flow associated with aging and disease (D'esposito et al. 2003). The Virchow-Robin space increases in size with age (Zhu et al. 2010), and can become enlarged or altered in certain neurological diseases (Esiri and Gay 1990; Etemadifar et al. 2011). The perivascular space can be filled with macrophages and other cells, potentially impeding the circulation of CSF (Iliff et al. 2012; Xie et al. 2013) and intracortical vessel dilation. Increases in the size of the perivascular space should permit greater dilation of intracortical vessels, suggesting these changes might be compensatory mechanisms. Interestingly, the mechanical restriction of blood flow by tissue may be a ubiquitous phenomenon that affects blood flow in many organs. The healthy liver has similar mechanical properties to the brain (Glaser et al. 2012), and the stiffness of the liver is dramatically increased by cirrhosis (Sandrin et al. 2003). Consistent with the hypothesis that the mechanical properties of the tissue can reduce vasodilation, postprandial increases in blood flow in cirrhotic patients are substantially reduced relative to healthy controls (Ludwig et al. 1998).

The mechanical properties of cells, tissues and their surrounding environment are important for normal physiological function and play a role in many pathologies (Janmey and Miller 2011), including cancer (Suresh 2007). In the brain, mechanical factors have been postulated to shape cortical folding (Van Essen 1997; Hilgetag and Barbas, 2006), to guide neural development (Siechen et al. 2009; Franze 2013), and to influence the spatiotemporal dynamics of the BOLD signals (Aquino et al. 2012). Our results suggest that the spatial profile of hemodynamic signals depends not only upon neural activity, but it is also sculpted by the mechanical properties of the brain.

Table 2.

depth	0μm<depth≤50μm		50μm<depth≤100μm		100μm<depth≤150μm		150μm<depth		animal #
	diameter (μm)	vessel #	diameter (μm)	vessel #	diameter (μm)	vessel #	diameter (μm)	vessel #
capillary	4.48±0.80	17	4.42±0.60	35	4.70±0.79	12	4.96±0.38	16	4
	ratio	vessel #	ratio	vessel #	ratio	vessel #	ratio	vessel #
SNR	5.70±1.42	38	4.51±1.52	57	4.49±1.40	34	4.30±1.34	17	15

Highlights.

• We imaged locomotion-induced vessel dilation in somatosensory cortex in mice.

• Arterial dilations were larger in the forelimb/hindlimb region than in other areas.

• Surface arterioles and venules dilated more than intracortical vessels did.

• Smaller dilation of intracortical vessels could not be explained by saturation.

• Mechanical restriction by brain tissue could account for the reduced dilation.

Abbreviations

2PLSM

two-photon laser scanning microscopy

CBV

cerebral blood volume

CSF

cerebrospinal fluid

fMRI

functional magnetic resonance imaging

FL/HL

forelimb/hindlimb

GFAP

glial fibrillary acidic protein

LFP

local field potential

PoRTS

Polished and Reinforced Thin-Skull

ROI

region of interest

TiRS

Thresholding in Radon Space