A Temperature-Jump Optical Trap for Single-Molecule Manipulation

Abstract

To our knowledge, we have developed a novel temperature-jump optical tweezers setup that changes the temperature locally and rapidly. It uses a heating laser with a wavelength that is highly absorbed by water so it can cover a broad range of temperatures. This instrument can record several force-distance curves for one individual molecule at various temperatures with good thermal and mechanical stability. Our design has features to reduce convection and baseline shifts, which have troubled previous heating-laser instruments. As proof of accuracy, we used the instrument to carry out DNA unzipping experiments in which we derived the average basepair free energy, entropy, and enthalpy of formation of the DNA duplex in a range of temperatures between 5°C and 50°C. We also used the instrument to characterize the temperature-dependent elasticity of single-stranded DNA (ssDNA), where we find a significant condensation plateau at low force and low temperature. Oddly, the persistence length of ssDNA measured at high force seems to increase with temperature, contrary to simple entropic models.

Introduction

Optical trapping is a useful technique in the field of single-molecule manipulation that is capable of applying forces on dielectric particles in the piconewton range and displacement measurements in the nanometer range. In molecular biology, one of the main uses of optical traps has been to study the mechanical and thermodynamic properties of nucleic acids such as DNA or RNA and proteins (1–3). In nucleic acid thermodynamics, the melting temperature (T_m) of DNA is defined as the temperature at which half of the DNA strands are in the double-stranded DNA (dsDNA) and single-stranded DNA (ssDNA) forms. For other applications, such as PCR and sequencing, it is important to accurately determine the T_m of the DNA.

Traditionally, the thermodynamic properties of DNA have been determined using bulk techniques such as calorimetry (4) and UV absorbance (5,6). In both cases, the T_m has been determined by changing the temperature or pH of the entire sample. Over the past two decades, single-molecule force spectroscopy has been established as a powerful, accurate, and bulk-complementary method to characterize the thermodynamics of nucleic acids. A major advantage of single-molecule methods is that they make it possible to characterize thermally induced fluctuations during thermodynamic transformations in individual molecules and small systems in general (7). In spite of their low number of degrees of freedom, small systems coupled to thermal baths (such as a single DNA molecule embedded in an aqueous environment) are tractable in the standard framework of equilibrium statistical mechanics, where concepts such as equilibrium free energy, enthalpy, and entropy are fully applicable (8). Mechanical melting, or unzipping, is a process that consists of pulling apart the two strands of the dsDNA until the basepairs are disrupted and the molecule converts into ssDNA (9,10). In this case, and in contrast to other techniques, force, rather than temperature, is used to open the molecule. Although force unzipping provides a direct estimate of free-energy differences, extracting the value of T_m always requires one to determine the entropy and enthalpy contributions. In general, the fate of many reactions in molecular biology (i.e., their affinity) is determined by the mutual compensation between the entropy and enthalpy contributions. For molecular weak interactions, such contributions are typically large compared with the affinity value itself: small variations in the entropy and enthalpy terms can modify the sign of the free-energy difference, reversing the direction of such reactions. This important property confers plasticity and adaptability to many regulatory pathways in the cell. For this reason, it is valuable to implement a temperature control function in an optical tweezers instrument, enabling it to measure free-energy differences at different temperatures to extract the enthalpy and entropy contributions.

Previous studies have utilized various methods of temperature control (11–15). Williams et al. (15) first used a Peltier heater-cooler device connected to the microchamber by copper plates and 1.0-NA water-immersion objectives. However, force and distance measurements are less accurate with this type of lens. Mao et al. (12) used water immersion objectives similar to ours (NA = 1.2) with hot-cold circulating water collars in the objectives. The microchamber comes to the same temperature as the objectives because of heat conduction through the water immersion fluid. However, the objective lenses expand or contract by several microns with big changes in temperature, causing the optical trap to shift position by the same amount. A significant time (∼30 min) is required for the instrument to stabilize at each new temperature, making it impractical to test the same individual molecule across a wide temperature range. Resistive heaters placed at the front of the objective lenses were used some time later to reduce the drift generated by fluid circulation (11,13).

As previously discussed (12,16–18), the advantages of using a local heating laser include the minimization of drift effects in the instrument. The wavelength of the heating laser was carefully chosen to generate heat in the bulk solution by infrared (IR) absorption without transmitting unnecessary extra heat to the objective lenses, effectively eliminating drift. Previous studies used the absorption of IR light in water as a method to heat rapidly and locally the surrounding medium (18–20). The use of IR absorption allows for full control of the heated volume as well as temperature changes over short periods of time. The heating laser we chose for our study operates at 1435 nm. It is readily absorbed, so it has a penetration depth of 315 μm in water (21,22). However, for a wavelength of 980 nm, as used in previous studies, the absorption depth is ∼19,920 μm. Therefore, little of the incident light is absorbed in a water cell only 180 μm thick.

Materials and Methods

Instrument design

The instrument used in this study is a miniaturized optical tweezers that uses counterpropagating beams with light-momentum force sensors capable of measuring force directly (23). All experiments were performed according to the scheme of Fig. 1 a, following previous work (10,12,23–26). In this approach, counterpropagating laser beams (Lumics LU845, λ= 845 nm and 150 mW at maximum power) are brought to the same focus through opposite microscope objective lenses (UPLASAPO 60XW, water immersion, NA 1.2; Olympus), generating a single optical trap. The molecular construct is then attached to a polystyrene bead held optically in the trap, which in turn acts as the force sensor, and to a second similar bead affixed by suction on the top of a micropipette. The molecular construct includes the DNA hairpin under study spliced between two dsDNA handles, which act as spacers to prevent nonspecific interactions between the bead and the DNA hairpin (Fig. 1 b). A third laser is introduced coaxially with the trapping lasers to generate heat (Alcatel A1948FBG, λ= 1435 nm and 160 mW at maximum power). The heating laser is a single-mode, fiber-coupled diode laser that is driven by a constant-current power supply. It is worth mentioning that our setup can also operate in the double-trap configuration, which is achieved by steering the trapping beams into two separated foci (27–29), thus avoiding the need to use a micropipette.

Figure 1.

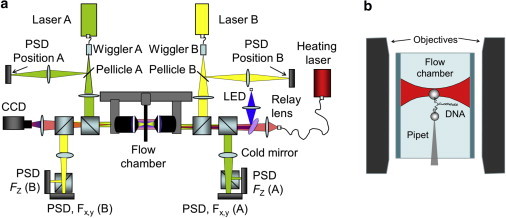
Schematic of the setup. (a) Counterpropagating optical trap with a light-momentum force sensor modified to include a temperature controller. The heating beam passes through a 45° dichroic long-pass filter (Edmund Optics 69-878), which acts as a cold mirror, thus reflecting the blue LED light, which illuminates the experiment, until a CCD camera and allowing the heating wavelength to pass through. (b) Single-molecule experiment. The DNA hairpin under study is attached between two polystyrene beads: one captured in the optical trap and the other held by air suction on the tip of a micropipette (see text for details). To see this figure in color, go online.

To work at low temperatures, we utilize a 1.5 m³ top-opening refrigerator to freeze 20 L of water into a block of ice. The refrigeration is then turned off and the ice melts slowly, thus maintaining the temperature at a constant 4–5°C. The instrument head (10 kg) is lowered into the top of this icebox with a pulley mechanism and is suspended from an extension spring (stiffness 250 N/m) to isolate it from building vibrations. The instrument head does not touch the floor or walls of the icebox. It then takes the head ∼3 h to equalize with the temperature inside the icebox. The head temperature (here designated as ambient) is measured using a thermal sensor installed close to the fluidics chamber. The light from the heating laser (located outside the icebox) to the instrument head is transmitted through 2 m of single-mode optical fiber (Fig. 1 a).

We could increase the temperature by 50°C above ambient by using full laser power (160 mW), and we also focused the heating laser into a small area of ∼10 μm in diameter. However, such a small heated area creates a baseline shift in the light momentum force sensor due to refractive index changes in the heated water at the heating laser focus. That is, the 1435-nm heating beam can deflect the 845-nm trapping beams by heating water locally and changing its refractive index. Such refractive interference also occurs when the trap is empty (not occupied with a bead), indicating that the effect is not a tug-of-war between the heating and trapping beams. Rather, the pseudo-force between beams is repulsive due to the reduced refractive index of hot water.

To reduce such a baseline shift, we spread the heating beam out at the focus and changed its shape. Instead of focusing the heater to a point at the experimental plane, we use the heating equivalent of Köhler illumination (Supporting Material). Thus, the heating laser is focused to a point located at the back focal plane (BFP) of the objective lens so that the beam emerges into the experimental area collimated as a cylinder ∼66 μm in diameter (Fig. S5). By changing to Köhler heating, the typical baseline shift is reduced from ∼3 pN to only ∼0.5 pN at full heating power. However, the maximum temperature increase at the experimental region is reduced to ∼25°C above ambient temperature (Supporting Material). To extend the temperature range and to carry out experiments between 5°C and 30°C (cold measurements), the instrument is placed inside the icebox. For experiments conducted between 25°C and 50°C (hot measurements), the instrument is placed outside of the icebox by operating at room temperature.

The heating laser power is controllable between 0 and 160 mW with wavelength λ = 1435 nm and absorption coefficient, α(λ), between 31.0 and 31.7 cm⁻¹ in water (22). This wavelength is very convenient for our experiments for two reasons: first, λ = 1435 nm does not interfere with the trap-lasers signal of 845 nm in the photodetectors because such silicon detectors have a spectral response between 500 and 1100 nm; second, the absorption coefficient for λ = 1435 nm in water is between 31.0 and 31.7 cm⁻¹ (22). According to Beer’s law, the loss in intensity due to adsorption as light travels through the medium is given by I(x) = I₀ exp(–αx), where α(λ) is the adsorption coefficient and x is the distance the radiation travels through the medium. Thus, we can deposit a significant fraction (27%) of the incident beam power into our water layer, which is ∼100 μm thick.

As noted by Mao et al. (12), one problem with local laser heating is that it generates convective fluid flow, especially in a chamber with a large vertical rise, such as a slide/coverslip oriented edgewise to gravity (so the laser beams can be horizontal). Then the hot water rises in the center and the cold water sinks at the edges in a continuous circuit flow up to 8 μm/s. This flow creates drag forces on tethered beads and also sweeps dirt from around the chamber into the trap, where it accumulates. To reduce such convection, we designed a new microfluidics chamber with reduced water thickness (110 μm instead of 180 μm) and a vertical cul-de-sac domed region that surrounds the pipette (Fig. 2 a). To measure the temperature around the trap, we followed the method described by Peterman et al. (18). By using the Stokes drag test on the trapped bead as a function of the heating laser power, and by knowing how the viscosity of the solution changes with temperature, we could extract the temperature of the surrounding medium (Supporting Material). We performed experiments on a DNA hairpin (Fig. 2 b) by using the new design of the chamber along with Cargille Labs refractive index matching liquid, series AAA, n = 1.330 (30), as immersion fluid between the chamber and objective lenses. This liquid is used on the objectives instead of water because 1) it evaporates much more slowly than water; 2) evaporation does not cool the chamber, so the external ambient temperature probe accurately represents the temperature at the chamber interior when the heating laser is turned off; 3) it absorbs no IR radiation at the heating-laser wavelength (30); and 4) it has lower thermal conductivity than water. Regarding the latter, the thermal conductivity (κ) is inversely related to the increase in temperature produced by a heating source. In particular, the increase in temperature upon heating (ΔT) depends linearly on the power delivered by the heating laser (P) being inversely proportional to the thermal conductivity of the medium (12,18), ΔT ≈ P/κ. The thermal conductivity of the Cargille fluid is 0.1 W/K (30) to be comparable to the thermal conductivity of water (0.6 W/K) and glass (1.1 W/K). The low thermal conductivity of the Cargille fluid contributes to minimize heat flow between the fluidics chamber and the objectives, keeping them isolated from potentially harmful heating effects.

Figure 2.

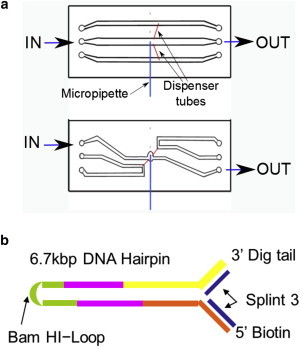
Chamber channels and DNA hairpin designs. (a) Scheme of the old (upper panel) and new (lower panel) microfluidics chamber designed to prevent convection. The new design employs two coverglasses (24 × 60 mm, #2; VWR 48382-139) and one Nescolfilm layer (instead of two as in the old design). With this design, the microchamber thickness is reduced from 180 to 110 μm. The channel design was modified to avoid obstruction of the lower channel by the micropipette (∼80 μm in diameter). The central channel holds the micropipette in the dome (this cavity typically is 2 mm high and 1.8 mm wide). The direction of the flow, which is stopped during an experiment, is marked by IN and OUT labels. The top and bottom channels, connected to the main channel through dispenser tubes, are used to flow different types of beads and to control the concentration and flow speed at their entrance to the dome of the central channel. (b) Design of the 6.8 kb sequence. Details are provided in the Supporting Material. To see this figure in color, go online.

Unfortunately, Cargille fluid has one-quarter the surface tension of water but 1.9 times the density, and thus is difficult to suspend between the objective lens and the coverglass due to gravity forces. To solve this problem, we used thicker #2 coverglasses for the new fluidics chamber. As a result, the distance between the coverglasses and the objective lenses was reduced and the Cargille fluid stabilized over longer times.

Instrument calibration

Smith et al. (23) described several methods to calibrate the light-momentum force sensor, including a light-flux photometric method and a thermal noise force test. However, the simplest calibration is done by using Stoke’s law. Here, we translate the fluid chamber back and forth with a velocity v past a trapped sphere with radius r and measure the drag force F with the momentum sensor, which is then compared with Stokes’ law, F = 6πrηv, where η is the viscosity of the surrounding water. Despite the simplicity of the formula, there are several issues that could affect the accuracy of the test, including 1) multiple peaks in the bead-size distribution, 2) the number of beads tested that are used to get a mean force, 3) deviations from sphericity in the bead distribution, 4) the proximity of chamber walls that affect the ideal behavior of the fluid, 5) viscosity changes due to the presence of salts in the buffers, 6) the temperature of the water, and 7) heating by the trapping lasers.

In brief, to circumvent the bead-related issues, we carried out drag experiments in a chamber with pure water using polystyrene microspheres that are specific for calibration, with a precise diameter of 3.00 ± 0.07 μm (microbead NIST traceable particle size standard, 3.00 μm, Cat. #64060, Polyscience; DISC calibration). We also accounted for wall effects, which become important in our thin chambers. According to Happel and Brenner (31), the drag coefficient is increased by 3% for a 3 μm bead in the center of a 100 μm chamber (Eq. S9). Viscosity changes due to dissolved salts were mainly treated according to measurements in the literature (32,33).

We determined the temperature spatial profile by using water viscosity changes (Fig. 3, left) and analyzing the thermal fluctuations of the optically trapped bead (Fig. 3, right; Supporting Material), and checked the data against a simple 1D heat-flow model (Eq. S8). In this model, the temperature exhibits a parabolic dependence within the heating laser spot and a logarithmic decay outside the spot (the latter trend was previously studied by Mao et al. (12)). Measurements obtained by the two methods are very similar and compatible with this simple model. Experiments with the DNA hairpin were performed across distances of <8 μm near the heating spot center, where temperature is homogeneous within 1°C.

Figure 3.

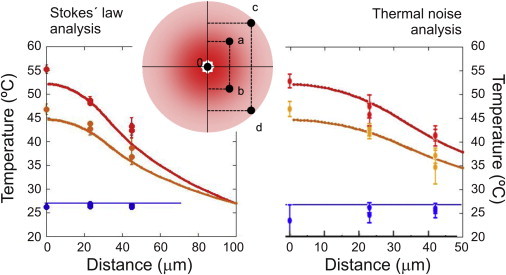
Temperature spatial profile of the heating laser beam. Measurements were taken at five different positions within the heating beam spot (see inset). (a–d) The distances from (a) and (b), and from (c) and (d) to the center of the screen are ∼23 μm and ∼42 μm, respectively. Red dots show the measured temperature at 5.7 mW inside the fluidics chamber (full heating laser power), and orange dots show the measured temperature at 4 mW. Blue dots show the measured temperature with the heating laser off. This measured temperature (∼27°C) is taken as ambient for the 1D heat-flow model (Supporting Material), whose predictions are the red and orange continuous curves for 5.7 and 4 mW, respectively. Left graph: Stokes’ law analysis; right graph: thermal noise analysis. To see this figure in color, go online.

Another possible use for the laser-heating method would be to study single-molecule kinetics after a sudden temperature change. In this case, the temperature rise time after the heating beam is switched on becomes an important parameter. We obtained an estimate for this time by using a finite-element 2D heat-flow simulation (Supporting Material) in which we mimicked the experimental geometry and materials (water, glass, and immersion fluid) with 10,000 discrete ring elements, each with a defined thermal conductivity and specific heat capacity. This simulation generates a steady-state radial profile similar to the 1D model (Fig. S6) even though much of the heat is conducted away laterally through the glass chamber walls rather than radially through the water (Fig. S7 a). The simulation also shows that the temperature reaches 90% of its final equilibrium value within 30 ms after the beam is initiated (Fig. S7 b). Unfortunately, we never achieved such short rise times experimentally because our laser power supply has a low-pass filter to prevent thermal shock to the emitting diode (Fig. S8). Perhaps a fast optical shutter would reveal an inherent 30 ms rise time. Koirala et al. (17) measured a rise time of only 5 ms in their T-jump optical trap, but with a high temperature gradient near their heated bead. In contrast, we needed a larger region of homogeneous temperature in which to unzip our 6.8 kbp hairpin and stretch it into ssDNA with an end-to-end distance of 7 μm.

Heating by trapping near-IR radiation has been examined in previous works (see Mao et al. (12) and references therein). Here, we used viscosity changes to estimate in situ an upper temperature rise of 0.9–1°C at maximum power due to water absorption at 845 nm.

Results and Discussion

DNA as a local thermometer

To demonstrate the capabilities of the temperature-jump instrument, we carried out experiments in which single DNA molecules were unzipped at different temperatures ranging from 3°C to 45°C. Our molecular construct consists of a 6.8 kbp hairpin flanked by two 29 bp handles on the 3′ and 5′ ends (Fig. 2 b; see Supporting Material for details of the molecular construct and for a description of the unzipping setup). In Fig. 4 a, we present force-distance curves (FDCs) obtained during the unzipping process in 1 M NaCl at various temperatures. The unzipping-rezipping cycles show that the curves almost overlap, indicating that the experiments at a 50-nm/s pulling rate were reversible (quasistatic).

Figure 4.

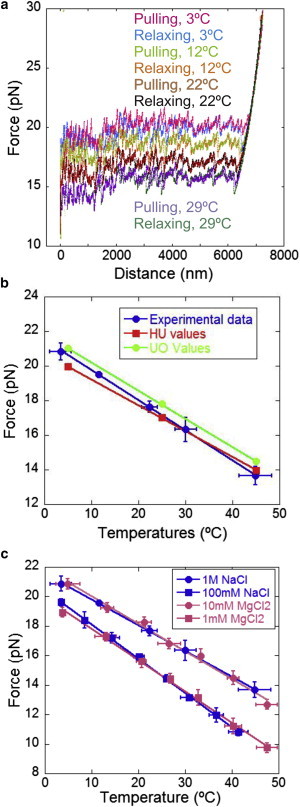
Unzipping experiments at different temperatures. (a) Force-extension curves (FECs) measured at 1 M NaCl + TE, pH 7.5. Here the cold measurements have been aligned to the hot segments, where the position-sensitive photodetectors operate at room temperature, by matching the unzipping measurements at 25°C. See Supporting Material. Unzipping and rezipping traces are almost identical, showing that the experiments were carried out under quasistatic conditions. (b) Mean unzipping/rezipping force versus temperature. Experimental data points, each averaged over four molecules at 1 M NaCl TE buffer, pH 7.5, are shown in combination with two theoretical predictions based on experimental data from (10) (HU) or SantaLucia (4) (UO; see also Table S2). (c) Mean unzipping/rezipping force versus temperature in different ionic conditions. Experimental data represent the average over eight molecules. These results remarkably follow the rule regarding a 1:100 ratio of monovalent to divalent salt, similarly to what has been observed for RNA (33). To see this figure in color, go online.

The stability of dsDNA with respect to ssDNA, as specified by the free-energy difference ΔG(T), is strongly dependent on T (15). Increasing T reduces the stability of dsDNA and promotes the melting process. By measuring the mean unzipping/rezipping force for different molecules and across the above-mentioned temperature range, we observed that the mean force decreased linearly with the temperature (Fig. 4 b). This is explained by the entropic contribution to the free energy of formation of the double helix, which destabilizes the double helix upon an increase in temperature. For each molecule, the temperature was measured and analyzed as described in the Supporting Material. Moreover, the zero force baseline, in any case always lower than 0.5 pN, was corrected for each trace. Using a simulation program (Supporting Material) to reproduce the unzipping experiments, we predicted the change of the mean unzipping/rezipping force versus temperature (Fig. 4 b; Table S2). In this simulation, we used either the nearest-neighbor (NN) basepair free-energy values for ΔH and ΔS (unified oligonucleotide (UO) values) (4) or those reported from unzipping experiments (HU values) (10). The parameters for the extensible freely jointed chain (ext-FJC) model were taken from Bosco et al. (34).

The experimental measurements of the forces are in agreement with the theoretical predictions at room temperature, with a difference in the mean force of ∼2% (Table S2). However, below room temperature the discrepancy between the experimental results and the theoretical values predicted by HU is ∼4%. This is not the case with the UO prediction, which shows a difference of ∼1%. In contrast, at high temperatures, the discrepancy between the experimental results and the theoretical predictions is larger for the UO values, ∼3%. Clearly, the slopes between the experimental data and the simulated data are different in Fig. 4 b.

Experiments were conducted in different buffer solutions (1 M NaCl, 100 mM NaCl, 10 mM MgCl₂, and 1 mM MgCl₂; Fig. 4 c). Unzipping forces are almost the same at 1 M NaCl and 10 mM MgCl₂ at 25°C. The same effect is observed for the solutions at 100 mM NaCl and 1 mM MgCl₂. This shows that the mean unzipping force follows the 1:100 rule regarding the ratio of monovalent to divalent salt, a trend that was also observed for RNA (35). The mean unzipping force is expected to vary proportionally with the logarithm of ionic strength; however, a 100-fold concentration of Na⁺ is required to achieve the same unzipping force as compared with the Mg²⁺ case, indicating strong, nonideal effects in the binding affinity of counterions to DNA in solution.

Average basepair free energies from force melting experiments

Force melting experiments have been used in combination with Monte-Carlo techniques to derive the salt- and sequence-dependent basepair free energies in DNA (10). Here we discuss a simpler model to derive the average (sequence-independent) basepair free energies, enthalpies, and entropies at different temperatures.

We approximate the typical sawtooth pattern of the FDC in unzipping experiments by a horizontal line corresponding to the mean unzipping force, f_p (Fig. 5). In the plateau region, the extension of trap and molecular handles (x_T, x_h in Fig. 5) is approximately constant, so the change in the trap-to-pipette distance when moving from λ₁ to λ₂ corresponds to the increase in ssDNA length (Δx_ss), which is induced by the unfolding of n dsDNA basepairs, λ₂ − λ₁ = Δx_ss= nΔx (where Δx is the length change induced by the unfolding of a single basepair). The configuration of the experimental setup along the FDC at two different distances is depicted in Fig. 5 (top, green circles). The area under the equilibrium FDC curve between the two distances is the reversible work, W = f_p Δλ, that is necessary to bring the system from distance λ₁ to distance λ₂ (W corresponds to the area of the dashed rectangle in Fig. 5). W equals the total free-energy change ΔG, which is the sum of a contribution due to the unfolding ΔG₀ (the average basepair free energy) and a contribution from the stretching of the ssDNA (this stretching free energy corresponds to the area below the blue dotted line in Fig. 5, with the line being the FDC of 2n bases of ssDNA). Equating the work and the free-energy change, we get

$$W=f_p\text{Δ}\lambda =\text{Δ}G=n\text{Δ}{G}_0+\int fdx.$$ (1)

Integrating Eq. 1 by parts and using the fact that Δλ = nΔx yields $n\text{Δ}{G}_0-n\int \text{Δ}xdf=0$ ; hence,

$$\text{Δ}{G}_0=\int \text{Δ}xdf.$$ (2)

This integration by parts can be understood geometrically as the difference between the area of the dashed rectangle and the area under the dotted curve in Fig. 5. This is shown as a purple region in Fig. 5. According to Eq. 2, the average basepair free energy ΔG₀ can be computed from the definite integral of the force-extension curve of an unfolded basepair, taken up to the rezipping/unzipping plateau force. Therefore, to measure ΔG₀, it is necessary (besides measuring the mean unzipping force) to parametrize the temperature- and salt-dependent elasticity of ssDNA.

Figure 5.

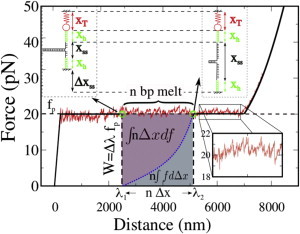
Calculation of mean basepair free energies from unzipping measurements. The configuration of the experimental setup at two different distances (λ₁, λ₂) is shown above the FDC. The sawtooth pattern (inset) is approximated by a straight line corresponding to the mean unzipping force (f_p). The force equals f_p at λ₁ and λ₂, so the extension of trap and molecular handles (x_T, x_h) stays constant. Different distances λ correspond then to different ssDNA extensions. The reversible work necessary to drive the system reversibly from λ₁ to λ₂ corresponds to the area in the dashed rectangle. Along this transition, n basepairs are disrupted, and the corresponding free-energy change involves both the basepairing free energy and the free energy due to stretching 2n bases of ssDNA. The basepair free energy can be recovered once the elastic contribution arising from stretching the ssDNA is subtracted from W (as detailed in the main text). To see this figure in color, go online.

Analyzing the change in molecular extension with temperature

The elasticity of ssDNA can be measured from the unzipping pattern. We use the simulations (Supporting Material) that yield the number of basepairs corresponding to the different force peaks observed along the sawtooth pattern. From the experimental unzipping data, we can measure the distance between consecutive peaks at a given force and temperature, which is due to the difference in ssDNA extension. More in depth, the ratio between the measured distance and the number of basepairs between peaks provides the extension of ssDNA per basepair, Δx. This is a differential extension measurement, i.e., it is based on the measurement of differences in the trap position. As a consequence, it avoids the systematic error associated with the definition of the zero in absolute distance or molecular extension measurements. The zero for extension measurements is difficult to determine precisely in single-trap tweezers because a significant uncertainty results from the fact that the molecule can be attached anywhere on the surface of the immobilized bead in the pipette, a problem that needs to be solved to compare single molecules in different conditions (36–38).

Fig. 6 a shows unzipping traces for one molecule at two different temperatures (5°C and 29°C). After correcting for the experimental drift on the traces, we observe that the unzipping pattern shrinks as the temperature is raised (two horizontal black arrows in Fig. 6 a), implying that the ssDNA extension at the unzipping force changes with temperature. By repeating this measurement for different temperatures, we can determine the change in molecular extension between the helix and the coil state (Δx), and how this parameter varies with temperature. Fig. 6 b shows the extension per basepair versus temperature. Experimental unzipping results show that Δx decreases with increasing temperature. As in Fig. 4 b, the mean unzipping force also decreases with temperature.

Figure 6.

Dependence of the molecular extension of ssDNA on temperature and force. (a) Unzipping/rezipping traces for the same molecule at 5°C and 29°C. By measuring the change in distance between different peaks along an FDC (horizontal black arrows), we determine the molecular extension of the hairpin as a function of the temperature and force. (b) Extension/basepair versus temperature. Each dot represents the average over four molecules in either 1-M NaCl or 100-mM NaCl buffer solution. The force was not held constant; rather, the extensions were taken at the equilibrium zipping force, which varied with temperature, as shown in (a). Although the distance between basepairs does change with T, it does not appreciably change when the salt concentration is varied. (c) Extension/base versus unzipping force. Results were averaged over four molecules in either 1-M NaCl or 100-mM NaCl buffer solution. The distance between bases changes with force in both conditions. To see this figure in color, go online.

Fig. 6 c shows the length change that occurs upon the unfolding of a basepair as a function of the mean unzipping force, which in turn is temperature dependent. Consequently, the change shown in Fig. 4 a is the combined effect of a change in force and temperature. To disentangle the effect of force from that of temperature in the previous measurements, we carried out a second set of measurements using a previously developed experimental methodology (34). In this approach, after the DNA hairpin has been completely unzipped, a 30-base oligo that selectively binds to the loop region of the DNA hairpin is flowed inside the fluidics chamber, blocking the rezipping. The oligo-bound molecule is then kinetically trapped in the ssDNA form. This method allows one to measure the ssDNA FDC down to low forces, where the duplex form would otherwise be preferred.

Fig. 7 a shows the FDC of one ssDNA molecule obtained by this method in the temperature range of 5–25°C. A shoulder is observed at low forces (<10 pN) due to nonspecific secondary structure formation. As previously described (10,23,34), this plateau is observed at low forces (<10 pN) and high salt (>100 mM NaCl). The effect of temperature on this plateau is clearly distinguishable (Fig. 7 a). The plateau height increases at decreasing temperatures. The compaction of ssDNA is apparent in the force shoulder that extends over the range of 5–10 pN. This shoulder indicates the formation of secondary structures that are stabilized by lowering the temperature and increasing the salt. Similar effects on ssDNA were observed in previous works (39,40) and recently quantified for a wide range of monovalent and divalent ionic concentrations (34), but only Danilowicz et al. (41) showed that reducing the temperature produces the same condensation effect as a higher salt concentration.

Figure 7.

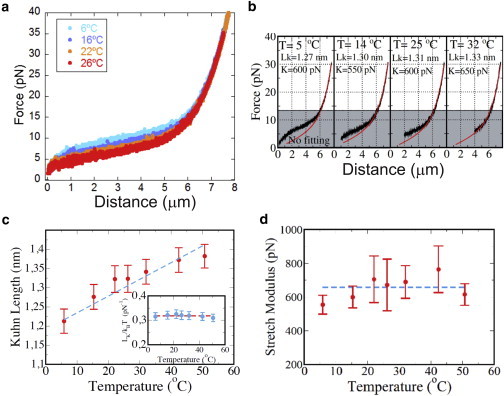
Temperature dependence of the single-stranded elastic response. (a) Cycles of pulling and relaxing curves of ssDNA at four different temperatures (6°C, 16°C, 22°C, and 26°C) and with 1 M NaCl, pH 7.5. The ssDNA was formed by using the oligo method (34). (b) The theoretical fit was obtained by using the ext-FJC model for forces in the range of 13–40 pN outside the dark gray region (labeled as no fitting in the legend). The experimental curves were taken at 1 M NaCl, pH 7.5. (c) Kuhn length (L_K) values for ssDNA at different temperatures and 1 M NaCl as a function of the temperature. Inset: Kuhn length scaled to the thermal energy level, k_BT. (d) Stretching modulus versus temperature for ssDNA measured at 1 M NaCl. In both panels, the dots represent the average at each temperature over six experiments, each with a different molecule. To see this figure in color, go online.

To parametrize the elasticity of ssDNA at different temperatures, one must adopt an elastic model. Commonly used models to investigate the elastic properties of the ssDNA include the ext-FJC model (18), where the Kuhn length (L_K) is the parameter to determine, and the worm-like chain model (42,43), where the elasticity is governed by the persistence length (L_p).

Earlier studies (10,34,40) suggested that the ext-FJC is the best model to fit the parameters at different ionic concentrations, and hence we chose it for our analysis. The ext-FJC model considers the molecule as a chain formed by N rigid segments each of length L_K. The force-extension curve of the ext-FJC model follows the equation

$$x=L_c\left[\text{c}\text{o}\text{t}\text{h}\left(\frac{f{L}_K}{k_{B}T}\right)-\left(\frac{k_{B}T}{f{L}_K}\right)\right]\left(1+\frac{f}{K}\right),$$ (3)

where L_c is the contour length, L_K is the Kuhn length, and K is the stretching modulus. The value of L_c is determined by fixing the contour length of the molecule to 0.57 nm/bp (34). The total contour length is thus L_c = 7857 nm for a hairpin of 13,650 nt. Equation 3 was fitted to the experimental FDC at different temperatures. The fits were constrained with the data obtained from the peak-to-peak distance analysis and performed in the force range of 15–40 pN to avoid secondary structure formation. The results of the fits are shown in Fig. 7 b. The Kuhn length shows an approximately linear dependence on T (Fig. 7 c), whereas the stretch modulus is independent of temperature (Fig. 7 d). Remarkably, the change in Kuhn length is apparently compensated for by the change in temperature (Fig. 7 c, inset), so the ratio k_BT/L_K is constant in the explored temperature range.

Analyzing the T dependence of thermodynamic potentials for DNA melting

The parametrization of the temperature-dependent elastic properties of ssDNA discussed in the previous section can be used to compute the integral in Eq. 2 to derive the average basepair free energy. Experimental measurements enter Eq. 2 both through the mean unzipping force f_p and the elastic parameters, with the uncertainty in the former being the main contribution to the error on ΔG₀.

In Figs. 8 a and S14 a, the ΔG₀ obtained from Eq. 2 is compared with the average of the 16 heterogeneous NN basepair free energies given by the UO and HU predictions. Interestingly, our results interpolate between the UO and HU values, being fully compatible with HU at room temperature. Similar to what was observed for the mean unzipping forces (see above), the measured free energies are in agreement with the UO values at low temperatures and with the HU values at high temperatures.

Figure 8.

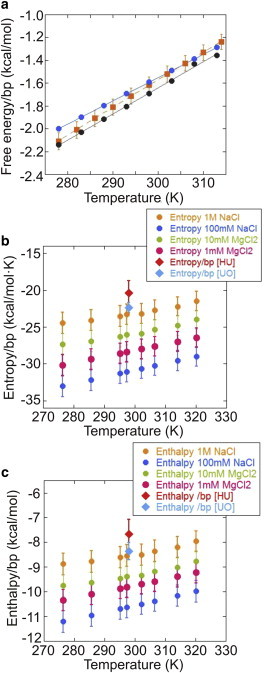
Average thermodynamic potentials versus temperature derived from DNA unzipping experiments. (a) Basepair free energy and comparison with UO (4) and HU (10) predictions at 1 M NaCl, pH 7.0. The orange squares show the experimental results calculated by fitting the elastic parameters as described in Supporting Material. The gray (blue) dots are average UO (HU) values for the free energy/basepair. (b) Basepair entropy as a function of temperature under different salt conditions. (c) Basepair enthalpy under different salt conditions. For comparison with the theoretical predictions, we also show the average of the entropies/enthalpies of the 16 NN motifs under standard conditions (1 M NaCl, 298 K) for the UO (blue diamond) and HU (red diamond) predictions. To see this figure in color, go online.

The thermodynamic stability of the DNA duplex is the result of a compensation of large entropy (ΔS) and enthalpy (ΔH) terms: ΔG = ΔH – TΔS. The new force-jump setup allows for experimental measurements of the entropy change (ΔS) and enthalpy change (ΔH) in the unfolding process. Along the transition line at constant force f_p, Eq. 2 reads $\text{Δ}{G}_0\left(T\right)={\int }_0^{f_p}\text{Δ}xdf$.

The entropy change, computed as the partial derivative of the free energy with respect to the temperature, gets a contribution from the basepair term, $\text{Δ}{S}_0=-\partial \text{Δ}{G}_0/\partial T$ and from the force-dependent ssDNA stretching term, $\text{Δ}{S}_{elas}=-\int \partial \text{Δ}x/\partial Tdf$. Then

$$\text{Δ}S=-\partial \text{Δ}G/\partial T=\text{Δ}{S}_0-\text{Δ}{S}_{elas}.$$ (4)

Calorimetric methods measure ΔS₀, and hence, for a direct comparison of our unzipping measurements with bulk measurements, the total entropy change should be corrected to account for the force-dependent elastic term ΔS_elas. However, as discussed in the previous section, the ratio k_BT/L_K is approximately constant (Fig. 7 c, inset) and the stretching contribution of ssDNA (as given by Eq. 3 and the integral appearing in ΔS_elas) varies slowly with temperature, so ΔS_elas can be neglected: ΔS ≈ ΔS₀.

The entropy change ΔS can be derived directly from the Clausius-Clapeyron relation (40) (Supporting Material). For the mechanical melting transition, the Clausius-Clapeyron equation yields

$$\frac{\partial f_p}{\partial T}=-\frac{\text{Δ}S}{\text{Δ}x}\approx -\frac{\text{Δ}{S}_0}{\text{Δ}x}.$$ (5)

By neglecting ΔS_elas, we can measure the entropy change independently of the ssDNA elastic parameters. Equation 5 combines the slope of the force-versus-temperature curve shown in Fig. 4, b and c, with the Δx measurements shown in Fig. 6 b. The force-temperature curves of Fig. 4 b can then be used to compute entropy changes. Equation 5 implies that the difference in the measured entropy values is due to the different slopes of the lines shown in Fig. 4 b.

Using Eq. 5 to combine data from Figs. 4 c and 6 b yields data for Fig. 8, b and c. These figures show the enthalpy and entropy change as a function of the temperature, and Fig. S14 b shows the ratio between these thermodynamic potentials. The measured free energy, entropy, and enthalpy values at room temperature are shown in Table S3, and can be compared with those previously obtained for ssRNA (14). As far as the free energy is concerned, there is good agreement between our experimental values and those reported in the literature (4,10). On the contrary, SantaLucia’s (4) measurements of entropy and enthalpy do not agree with our results, since our ΔS value is 5% higher than his. It must be noted that SantaLucia (4) derived the entropy from the free energy via T_m measurements (always relying on the two-state assumption and inaccurate determination of the melting point), whereas here we provide a more direct measurement of the entropy change. One problem with our method is that we measure local temperatures indirectly by changes in the hydrodynamic drag coefficient of a bead moving through water. Specifically, we equate the beam-center temperature for stationary water (when we unzip DNA) to the beam-center temperature when water is flowing past a test bead in a Stokes test. However, the introduction of cold water flowing past the Köhler heating beam should cause a small lateral shift in the heating profile and a reduction in temperature at the center of the beam. Therefore, we underestimate the temperature rise for the unzipping experiments, and consequently the slope of our plateau force-versus-temperature data (Fig. 4 b) appears too large. Suppose a flow velocity of 400 μm/s and an equilibration time of 0.03 s (Fig. S7 b) cause a shift of 12 μm in the temperature profile relative to the heating beam. Then, according to Eq. S8A, the temperature at the center beam would drop by 1° (4% of 25°C) and the experimental slope in Fig. 4 b would be 4% too high. Note that reducing the experimental slope by 4% makes it a rather good match to the UO-prediction slope (Table S2). In the future, it should be possible to check the temperature shift during flow more precisely by running a 3D simulation with ∼1 million elements.

Conclusions

To our knowledge, we have developed a novel high-resolution temperature-jump optical tweezers instrument. The instrument covers a range of temperatures between 5°C and 50°C. Following the strategy put forward in previous studies (4,12,18,19), we used a heating laser to minimize the effects of instrumental drift. We carefully chose the laser wavelength to generate maximum heat in the bulk solution and transformed the focused beam geometry of the heating laser into a Köhler configuration to avoid convection effects and minimize force baseline shifts.

Using this strategy, we developed a temperature-jump optical tweezers with great thermal and mechanical stability. To test the viability of our temperature controller, we carried out a full thermodynamic characterization of DNA duplex formation by mechanically unzipping single DNA molecules at different temperatures. FDCs were measured under different temperature and salt conditions. The mean unzipping/rezipping force was found to decrease with temperature, as expected, due to the entropic contribution to the free energy of formation of the double helix, which is known to destabilize the double helix upon an increase in temperature.

We used the instrument to measure the average basepair free energy ΔG₀(T) in a range of temperatures between 5°C and 50°C. It was necessary to determine the temperature-dependent elastic properties of ssDNA because the work of stretching ssDNA appears to make a major contribution to the full reversible work measured along the unzipping FDC. Remarkably, we found that the persistence length of ssDNA appears to increase with temperature. This is at odds with the standard elastic rod model, which predicts that it should be inversely proportional to temperature. The persistence length of dsDNA was shown to decrease with temperature (44), but these two molecules have vastly different mechanics since one is stiffened by stacked basepairs and the other is stiffened mainly by electrostatic repulsion between phosphates. It is difficult to evaluate the full implications and generality of this result; however, it suggests that the elastic behavior of single-chain polymers (such as ssDNA, ssRNA, and polypeptide chains) is mostly determined by electrostatic effects. Throughout this study we compared our experimental results with theoretical predictions given by the UO energies (4) and unzipping (HU) values (10). Our experimental results for the average basepair free energies agree with the theoretically predicted values (HU or UO) at room temperature. In contrast, the analysis of entropies and enthalpies highlighted significant differences with respect to those predictions. These discrepancies are attributed to systematic differences observed for the temperature-dependent free energy above and below room temperature. In fact, below room temperature there is a discrepancy of ∼4% between the experimental results and the theoretical values predicted by HU. This was not the case with the prediction of UO values, which show a difference of ∼1%. However, above room temperature the discrepancy between the experimental results and the theoretical predictions is larger for the UO values. These small but systematic discrepancies in free-energy measurements transduce into large discrepancies in the average entropy and enthalpy between our measurements and both UO and HU predictions.

The temperature-jump optical trap paves the way to obtaining a more detailed characterization of the thermodynamics of duplex formation in nucleic acids by deriving the 10 unique NN basepair free energies, enthalpies, and entropies at different temperatures from single-molecule unzipping experiments. Until now, this task could only be accomplished for basepair free energies via unzipping experiments at room temperature (10), and not for basepair-dependent enthalpies and entropies, which could be derived only indirectly from existing melting data on short (10–50 bp) oligos. The ability to control both force and temperature provided by the temperature-jump optical trap now makes it possible to directly measure basepair-dependent enthalpies and entropies at various temperatures. Our instrument may additionally shed light on two long-standing issues in the field of nucleic acid thermodynamics: measurement of the heat capacity change (and its temperature dependence) and characterization of the entropy-enthalpy compensation across the melting transition.

Promising future research directions include the characterization of the observed strong temperature dependence of secondary structure formation in ssDNA at low forces. Finally, although in this work we have only discussed experiments on DNA, our instrument can be used to manipulate any kind of biopolymer. As an example, we foresee the use of this instrument, in combination with fluctuation relations (27,43), to disentangle the entropic and enthalpic contributions in protein folding from pulling experiments under irreversible conditions. Given the importance of temperature in determining the fate of many chemical reactions and biophysical processes, we anticipate that temperature-jump methods, such as the one presented here, will be of great interest to the single-molecule community.

Author Contributions

S.L. and M.R.-C. performed research. S.L. and S.B.S. built the instrument. S.L., M.R.-C., and S.B.S. analyzed data. M.R.-C., J.R.A.-G., and S.B.S. contributed analytic tools. S.B.S. and F.R. designed research. S.L., M.R.-C., J.R.A-G., S.B.S., and F.R. wrote the article.

Editor: Keir Neuman.

Supporting Citations

References (45–48) appear in the Supporting Material.