Nanoscale Pulling of Type IV Pili Reveals Their Flexibility and Adhesion to Surfaces over Extended Lengths of the Pili

Abstract

Type IV pili (T4P) are very thin protein filaments that extend from and retract into bacterial cells, allowing them to interact with and colonize a broad array of chemically diverse surfaces. The physical aspects that allow T4P to mediate adherence to many different surfaces remain unclear. Atomic force microscopy (AFM) nanoscale pulling experiments were used to measure the mechanical properties of T4P of a mutant strain of Pseudomonas aeruginosa PAO1 unable to retract its T4P. After adhering bacteria to the end of an AFM cantilever and approaching surfaces of mica, gold, or polystyrene, we observed adhesion of the T4P to all of the surfaces. Pulling of single and multiple T4P on retraction of the cantilever from the surfaces could be described using the worm-like chain (WLC) model. Distinct peaks in the measured distributions of the best-fit values of the persistence length L_p on two different surfaces provide strong evidence for close-packed bundling of very flexible T4P. In addition, we observed force plateaus indicating that adhesion of the T4P to both hydrophilic and hydrophobic surfaces occurs along extended lengths of the T4P. These data shed new light, to our knowledge, on T4P flexibility and support a low-affinity, high-avidity adhesion mechanism that mediates bacteria-surface interactions.

Introduction

Type IV pili (T4P) are very thin protein filaments produced by a large number of bacterial and archaeal species. They play key roles in a wide variety of processes including attachment to surfaces, bacteriophage attachment, twitching motility on surfaces, and virulence (1–4). In the model organism Pseudomonas aeruginosa, T4P are composed of many repeats of a 15 to 20 kDa PilA pilin subunit (5–8). The conserved N-terminal α-helices of the pilin subunits are highly hydrophobic and, when assembled, form a tightly packed filament core with considerable tensile strength (6). Connecting to the N-terminal helix by the αβ loop, more variable C-terminal β-sheet domains ending (with rare exceptions) in disulfide-bonded loops (DSL) form the outer surface of the T4P (7,8). Based on structural data obtained using electron microscopy, T4P have been modeled as left-handed three-start helices (with a 12.3 nm pitch) or as right-handed one-start helices (with a 4.1 nm pitch) (8). Kinks in the N-termini of PilA caused by proline/glycine at positions 22 and 42, coupled with cavities and grooves on the T4P surface between subunits, allow for pronounced flexibility of T4P.

The major subunit PilA serves as the subunit of T4P but has also been proposed to function as an adhesin at the distal tip of the pilus (9). The conserved C-terminal DSL in PilA has been implicated as the pilus adhesinotope, as well as being involved in intersubunit interactions within the pilus (10). Harvey et al. showed that single-residue changes in the C-terminal disulfide-bonded loop of the P. aeruginosa T4P pilin influenced pilus assembly and twitching motility (11). The assumption that PilA is the adhesive component of T4P (12) has been challenged by studies showing that minor pilins and the large nonpilin PilY1 protein are also pilus-associated (13,14) and thus could contribute to pilus-mediated adhesion.

The extension and retraction of T4P that results in twitching motility arises from the assembly and disassembly of pilin subunits at the inner membrane, powered in P. aeruginosa by the ATPases PilB and PilT, respectively (2,6,7). Using total internal reflection fluorescent (TIRF) microscopy to visualize P. aeruginosa T4P tagged with Cy3 fluorophores, retraction rates of ∼0.5 μm/s (∼10³ subunits/s) have been reported (15). T4P retraction dynamics have also been studied using optical tweezers (16–20), showing that the retraction of a single pilus by a PilT motor can generate a force as large as 100 pN, representing the strongest linear protein motor discovered to date (17). This magnitude of retraction force allowed the bacteria to move toward the anchored portion of the pilus at a speed of several μm/s.

The mechanical stiffness of a pilus can be specified by its persistence length; the distance along the pilus within which it remains essentially straight (21). Two studies reported very different results for the persistence length of T4P. Skerker et al. (15) estimated a persistence length of ∼5 μm for T4P of P. aeruginosa, based on thermal fluctuations in shape that were observed in TIRF images of isolated pili with one end anchored to a glass surface. This large value of the persistence length indicated that T4P were almost as stiff as actin filaments (22). However, this is likely an overestimate because of the association of the pili with the underlying substrate as well as labeling of the T4P with the fluorescent Cy3 dye, leading to reduced flexibility. In contrast, Touhami et al. (23) used atomic force microscopy (AFM) to pull on T4P of wild-type P. aeruginosa bacteria that were adhered to the tip of AFM cantilevers. Because forces are directly applied to T4P using AFM, it is a more direct technique to measure the mechanical properties of T4P compared with estimating their mechanical stiffness from static optical microscopy images. In the experiments of Touhami et al., T4P were allowed to adhere to an underlying surface during a short dwell time, and the AFM cantilever was then retracted from the surface. To analyze force peaks in their AFM force-separation data, they used a worm-like chain (WLC) model modified with a linear elastic spring term that was interpreted as the elastic modulus of the bacterial cell wall. This analysis yielded a very small value for the persistence length of 0.8 nm—over a factor of 1000 less than that inferred by Skerker et al.—suggesting that T4P are very flexible. This very small value of the persistence length is problematic, however, because it is considerably smaller than the length of a single pilin subunit (8 nm) (24). In addition, the use of wild-type P. aeruginosa adds a complication, because the T4P can retract in the presence of a large applied force (17,25). Therefore, it is possible that the forces applied to the T4P are large enough to go beyond the entropic force regime, invalidating the use of the WLC model. In addition, retraction of the T4P would result in variations in the contour length during T4P pulling, complicating the data analysis.

Recently, Beaussart et al. (26) presented an AFM study of various aspects of T4P of P. aeruginosa PAO1: AFM pulling on isolated T4P, on T4P on wild-type cells, and the interaction of T4P on bacterial cells with eukaryotic cells. They observed a high occurrence of force-separation curves in which the force was a linear function of the separation, and interpreted this observation as a reversible stretching of the individual T4P. They also observed force plateaus that they interpreted as the elongation of T4P, as suggested by Biais et al. (27).

In our study, we used AFM to focus on the mechanical and adhesive properties of T4P in the absence of T4P retraction forces. To eliminate T4P retraction, we used a P. aeruginosa PAO1 mutant that is unable to retract its T4P because of the deletion of the gene encoding the retraction motor protein PilT. We observed distinct force peaks in the AFM force-separation curves corresponding to pulling on T4P that we interpreted in terms of the WLC model. Similar measured distributions of the persistence length for two different surfaces provide strong evidence for the bundling of T4P in a close-packed geometry. The most prominent, fundamental value of the persistence length is very small (∼1 nm), in agreement with the value obtained in the study by Touhami et al. (23), which is significantly less than the ∼8 nm length of the PilA subunit. We can interpret this result either as attributable to bundling of intact T4P, each with a persistence length of ∼1 nm, or as attributable to bundling of single, highly flexible strands of the PilA subunit, because of the unraveling of the three strands of the T4P at high pulling forces. This second interpretation implies that the persistence length of a relaxed T4P consisting of three close-packed strands would be ∼3² × 1 nm ∼9 nm.

In addition to the presence of force peaks in the AFM force-separation curves, we observed distinct force plateaus in curves collected on three different surfaces (two hydrophilic—mica and gold—and one hydrophobic—polystyrene). Because of distinct differences between force plateaus measured on different surfaces, we can attribute the force plateaus to adhesion along extended lengths of the T4P with the underlying surface, supporting a role for PilA itself as an adhesinotope. The distributions of force plateau values and plateau lengths could be understood in terms of a statistical mechanical model and indicated that T4P adhesion was largest with the gold surface.

Collectively, our results provide direct evidence for a high degree of flexibility of T4P, their tendency to form close-packed bundles, and their ability to adsorb onto both hydrophilic and hydrophobic surfaces over extended portions of their length rather than just at the distal end of the pilus. This combination of T4P properties allows P. aeruginosa PAO1 cells to establish contact with and colonize a broad range of surfaces.

Materials and Methods

Growth of Pseudomonas aeruginosa PAO1

The Pseudomonas aeruginosa PAO1 bacterial cells (pilA pilT double mutant containing pBADGr-pilA, hereafter referred to as the PAO1 pilT mutant) from frozen stocks were streaked on trypticase soy agar (TSA) plates in which both gentamicin (30 μg/mL) and L-arabinose (0.2% by mass) were incorporated, which helped to maintain the plasmid pBADGr. After growing for 2 days at room temperature, the cultures were maintained on TSA plates and used within 2 weeks. For use in AFM experiments, a single colony of cells from the TSA plate was transferred to trypticase soy broth (TSB) medium in which both gentamicin (30 μg/mL) and L-arabinose (0.2% by mass) were incorporated to induce PilA expression. The bacterial colony was then cultured at 37°C overnight (15 to 16 h) on a rotary shaker (150 rpm) to the late-exponential growth phase. An equal amount of TSB medium was added to the bacterial culture, and the mixture was maintained under the same growth conditions for an additional 3 h to reach the midexponential growth phase of the bacteria. The bacterial cells were then harvested by centrifugation at 2200 × g for 5 min, and then resuspended either in phosphate-buffered saline (PBS, pH = 7.4, 0.01 M phosphate buffered saline, 0.138 M NaCl, 0.0027 M KCl, from Sigma-Aldrich, St. Louis, MO) or Milli-Q water (resistivity of 18.2 MΩ·cm). The washing procedure was performed only once for T4P pulling experiments to avoid the loss of the pili from the bacterial cells. Because of the deletion of pilT, T4P of this mutant can extend but cannot retract, and these cells were used both for AFM imaging and for the AFM T4P pulling experiments.

Wild-type P. aeruginosa PAO1 cells and P. aeruginosa PAO1 fliC pilT mutant cells, which do not have flagella, were also prepared. For these cells, we used the same growth and harvesting conditions as for the P. aeruginosa PAO1 pilT mutant cells complemented with pBADGr-pilA, without the addition of gentamicin and L-arabinose to the TSA plates and the TSB medium. These cells were used in AFM imaging experiments performed in air.

Preparation of substrates

Three different surfaces were used for the T4P pulling experiments. Mica surfaces were prepared by cleaving 1 × 1 cm pieces of muscovite mica. Gold surfaces were prepared by flame annealing a thin gold foil (Sigma-Aldrich; 99.99% purity, 0.5 mm thickness) for 5 to 10 s. Polystyrene surfaces were prepared by spin-coating a 1.5% (by mass) solution of polystyrene (PS, Polymer Source (Montreal, Quebec, Canada), Sample No. P3856-S, M_w/M_n = 1.10, M_w = 16,000) in toluene using a spin speed of 1500 rpm onto a 1 × 1 cm oxidized Si (100) wafer.

Sample preparation for AFM imaging

After bacteria were harvested by centrifugation, they were resuspended in Milli-Q water (resistivity of 18.2 MΩ·cm). 75 μL of the bacterial suspension was adsorbed onto a freshly cleaved 1 × 1 cm mica surface for 10 min at room temperature. The mica surface with adsorbed bacterial cells was rinsed with 100 μL of Milli-Q water twice and dried in air for another 30 min. The resulting surfaces were then imaged in air using contact mode AFM with a low value of the applied force (1.0 to 2.0 nN) to observe the T4P surrounding the bacterial cells.

Adhesion of bacterial cells to AFM cantilevers

For the AFM T4P pulling experiments, cells of the P. aeruginosa PAO1 pilT mutant were immobilized either onto V-shaped silicon nitride cantilevers with sharp pyramidal tips (OTR4, Bruker Nano Surface, Santa Barbara, CA), which have a tip height of 2.5 to 3.5 μm and a cantilever length of 200 μm, or onto V-shaped silicon nitride cantilevers with a 600 nm diameter SiO₂ colloidal tip (spring constant of 0.06 N/m, Novascan Technologies, Inc., Ames, IA). Several AFM probes were incubated overnight in a 0.1% aqueous poly-L-lysine solution (Sigma Aldrich). The probes were then placed onto Kimwipe tissue to dry in air for 2 h, and then immersed in freshly harvested bacterial suspension either with Millipore water or PBS buffer for an additional 2 h. One of the bacteria-modified AFM cantilevers was then transferred to the liquid cell of the AFM for T4P pulling experiments without allowing the cantilever to dry. The additional AFM cantilevers were kept in PBS buffer solution at 4°C for subsequent experiments.

AFM pulling of type IV pili (T4P)

AFM force-separation curves were collected in PBS buffer using a Multimode AFM (Veeco Instruments) with a Nanoscope IV controller. Typically, AFM cantilevers with a sharp pyramidal tip were used, but experiments were also performed using cantilevers with a 600 nm diameter SiO₂ colloidal tip. The speed during approach and retraction of the AFM cantilever was 7.9 μm/s, and contact between the AFM tip and surface was maintained for between 0.3 and 5 s to allow nonspecific bonding to occur between the T4P on the adhered bacterial cells and the underlying surface. Retraction of the AFM cantilever from the surface resulted in stretching of T4P. The spring constant of the AFM cantilevers was measured before and after the pili pulling experiments using the thermal tuning function of the Nanoscope software (Veeco Instruments). For both types of AFM cantilevers, the tip height was sufficiently large to ensure that direct contact between the bacteria attached to the cantilever and the underlying substrate could be avoided in most cases.

Analysis of AFM force-separation curves

The force peaks observed in AFM force-separation curves were analyzed using the worm-like chain (WLC) model that describes semi-flexible polymer elasticity (28):

$$F\left(z\right)=\frac{k_{B}T}{L_p}\left[\frac{1}{4}{\left(1-\frac{z}{L_c}\right)}^{-2}-\frac{1}{4}+\frac{z}{L_c}\right],$$ (1)

where F is the force applied by the AFM cantilever, L_p is the persistence length of the T4P, k_B is Boltzmann’s constant, T is the absolute temperature, z is the end-to-end distance of the T4P corresponding to the separation between the surface and the AFM tip in the force-separation curves, and L_c is the contour length of the T4P. In Eq. 1, the adjustable fitting parameters are the persistence length L_p and the contour length L_c. In fitting the force-separation curves to Eq. 1, we have assumed that each peak begins at z = 0. We enforced this condition because the bacteria and T4P have to be very close to the underlying surface for the T4P to adhere to the surface, as discussed in the Supporting Material. Although each peak is assumed to start at z = 0, the range of data used for fitting each peak was limited to the data leading up to each peak but not including the data corresponding to previous peaks in the force-separation curves. Because T4P adhesion can occur at a contact point along the length of the pilus, as discussed below and indicated schematically in Fig. 1, we have also defined the rupture length as the vertical distance between z = 0 and the separation value at which the force reaches its maximum value. By definition, the rupture length is less than or equal to the contour length of the T4P.

Figure 1.

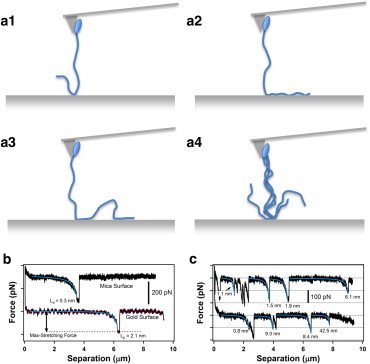
(a1–a4) Schematic diagrams of side views of the experimental geometry used for AFM pulling measurements of T4P. Cells of a pilT mutant of P. aeruginosa PAO1 (ellipses) are adhered near the end of the tip on the AFM cantilevers, and T4P were pulled away from an underlying surface. Four of the different possible scenarios for contact between the T4P and the surface are indicated: (a1) a single contact point, (a2) an adsorbed segment, (a3) multiple contacts along the length of a single T4P, and (a4) multiple T4P. (b) Single force peaks in typical AFM force-separation curves measured for pulling on single T4P from a mica surface (upper curve) and from a gold surface (lower curve) using a sharp AFM tip. Both curves were measured for T4P on the P. aeruginosa PAO1 pilT mutant. The solid curves correspond to the best fit of each force peak to the WLC model (Eq. 1). The best-fit values of the persistence length L_p are indicated on the plots. (c) Multiple force peaks in typical AFM force-separation curves measured for the pulling of T4P on a P. aeruginosa PAO1 pilT mutant strain from a mica surface using a sharp AFM tip. The solid curves correspond to best fits of individual force peaks to the WLC model. The best-fit values of the persistence length L_p are indicated on the plots. To see this figure in color, go online.

A detailed description of the analysis of force plateaus observed in the AFM force-separation curves is presented in the Supporting Material.

Results and Discussion

Single molecule pulling measurements

AFM force peaks

When we began our AFM pulling experiments on T4P, we often observed force-separation curves in which the force depended linearly on the separation, as observed by Beaussart et al. (26). We found that subsequent rinsing of the AFM tips resulted in the observation of conventional nonlinear force peaks, which could be accurately described by the WLC model. These results led us to conclude that the observation of linear force-separation curves was attributable to the pulling on a large number of T4P, averaging the individual force peaks to produce an approximately linear curve. This interpretation is consistent with the large values of the linear spring constants reported in (26) (∼2 pN/nm) that, for the maximum separation value of 10 μm in our experiments, would correspond to a force of 20 nN, which is 70 times larger than the maximum force of ∼300 pN measured in our study. For all of the measurements in this study, we used the improved protocol in which the AFM tips were rinsed following bacterial adhesion, and this resulted in the observation of either force peaks or force plateaus as the sample-separation distance was increased.

For contact between a T4P and the underlying surface at a single point (Fig. 1 a1), retraction of the AFM cantilever produced a force peak in the AFM force-separation curves, i.e., an increase in the force experienced by the AFM cantilever with increasing separation (Fig. 1 b). Attachment of a single T4P at multiple locations on the surface (Fig. 1 a3) as well as attachment of multiple T4P to the surface (Fig. 1 a4) resulted in a series of force peaks in AFM force-separation curves (Fig. 1 c). In all cases, we found that each force peak could be fit to the WLC model (Eq. 1) without the need to include the spring constant term that was used by Touhami et al. (23). This result indicates that stretching of the T4P occurred within the entropic elasticity regime. The maximum value of the pulling force (rupture force) corresponds to the loss of contact between the T4P and the surface, with the force dropping abruptly to the baseline value.

In the force peaks corresponding to the pulling of single T4P, such as those shown in Fig. 1 b, the pulling force increases significantly only when the separation between the AFM tip and the surface is close to the contour length of the T4P. Therefore, in AFM force-separation curves containing multiple force peaks (Fig. 1 c), each force peak represented the stretching of a T4P with a different contour length.

We also performed AFM T4P pulling experiments in which the AFM cantilevers were modified with P. aeruginosa PAO1 fliC pilT mutant cells, which have several long pili composed of PilA subunits expressed from their native locus on the chromosome, but no flagella. The AFM force-separation curves collected for the fliC pilT mutant strain were very similar to those recorded for the PAO1 pilT mutant expressing PilA from a plasmid (data not shown), indicating that the force peaks observed corresponded to pulling on T4P, and that expression of the pilin from an inducible vector versus from its chromosomal locus did not affect the results.

To improve the reliability of the data fitting procedure, we selected force peaks that contained a relatively flat portion of the AFM force-separation curve before the sharp increase in force. Specifically, we required a considerable range (> 0.5 μm) of tip-sample separation values with force values close to zero to establish a reliable baseline for the fitting procedure. In force-separation curves containing single peaks, this was straightforward to achieve. In force-separation curves containing multiple peaks, the range of tip-sample separation values was extended from the peak down to, but not including, the separation value corresponding to the previous peak. This provided sufficient separation between successive force peaks such that the fit of each peak to the WLC model (Eq. 1) could be performed with a well-defined force baseline. These fits yielded best-fit values of the contour length L_c, the persistence length L_p, and the force baseline. We expected to measure a common value of L_p because this is a fundamental property of the T4P. However, we found that the values of L_p varied considerably for the different force peaks even within the same AFM force-separation curve, as shown in both curves in Fig. 1 c. The remarkable difference in the L_p values, ranging from ∼1 to ∼40 nm, prevented us from fixing the value of L_p, which has been done in previous studies (23). As discussed below, we interpret this large variation in the L_p values as attributable to pulling on bundled T4P.

Statistical analysis of the mechanical properties of T4P

Because of the statistical nature of the AFM force pulling experiment, it is necessary to collect and analyze a large number of AFM force-separation curves to obtain an understanding of the mechanical properties of T4P. In Fig. 2, we show histograms of the T4P rupture length and rupture force values obtained from a large number of AFM force-separation curves collected on mica (Fig. 2, a and d, 980 curves), gold (Fig. 2, b and e, 1060 curves), and polystyrene (Fig. 2, c and f, 609 curves).

Figure 2.

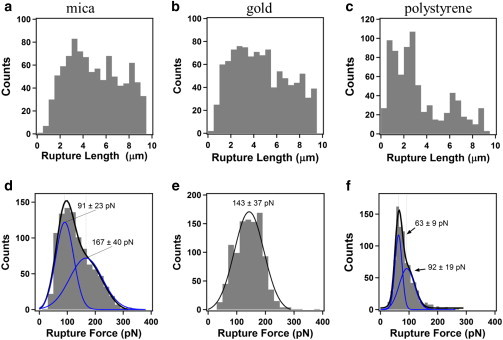
Histograms of the rupture length (a–c) and rupture force (d–f) measured by pulling on T4P of a P. aeruginosa PAO1 pilT mutant during retraction of the AFM cantilever with sharp pyramidal tips from different surfaces: (a) and (d) correspond to mica surfaces (N = 980); (b) and (e) correspond to gold surfaces (N = 1060); and (c) and (f) correspond to polystyrene surfaces (N = 609). The solid lines in (d)–(f) correspond to best fits to the rupture force data using either one or two Gaussian functions, with the best-fit center positions and standard deviation values indicated on the plots. To see this figure in color, go online.

The large rupture lengths measured for T4P for the PAO1 pilT mutant relative to those measured for PAO1 wild-type cells (1 to 2 μm) (23) are reasonable because the T4P in the pilT mutant can extend but cannot retract. The distributions measured for the T4P rupture lengths for the mica and gold surfaces shown in Fig. 2 were quite similar: the distributions were broad, with values ranging from 0 to 10 μm, which is the upper vertical displacement limit of the AFM piezoelectric transducer. The rupture length values measured for the polystyrene surface showed a considerable peak at a smaller value of ∼2 μm, indicating that shorter segments of the T4P adhere more readily to this surface. The distribution of rupture lengths for the polystyrene surface was very similar to that of the separation values corresponding to the start of AFM force plateaus for this surface, as discussed below.

In contrast, the rupture force histograms were significantly different for the different surfaces (Fig. 2), with either two peaks (mica and polystyrene) or a single peak (gold) and the rupture force corresponding to the primary peak ranging from 60 to 140 pN. Because the rupture forces measured for the three different surfaces were significantly different, it is likely that the rupture event occurs between the T4P and the underlying surface, rather than within the T4P or at the point of attachment of the T4P to the cell.

The rupture forces measured in our study are comparable with the rupture forces measured in optical tweezers experiments with carboxylated latex beads (17,18) and previous AFM experiments (23). Moreover, the smaller rupture forces measured on the hydrophobic polystyrene film (∼60 pN peak in Fig. 2 f), compared with the larger values measured on the hydrophilic surfaces of mica (∼90 pN peak in Fig. 2 b) and gold (∼140 pN peak in Fig. 2 d), are consistent with the physical structure of T4P, in which hydrophilic residues decorate the outer surface. Because of this arrangement, T4P are likely to bond more strongly with hydrophilic surfaces.

Determination of T4P persistence length

The large variation in the best-fit values of the persistence length L_p for force peaks prevented us from choosing a common value of L_p. Fig. 3 shows histograms of the T4P persistence length L_p for the mica surface (Fig. 3 a) and the gold surface (Fig. 3 b), measured for bacterial cells adsorbed onto an AFM cantilever with a sharp pyramidal tip. The two histograms have similar distributions, with a dominant peak at a small value of L_p (∼1 nm), and additional, less prominent peaks at larger values of L_p (∼4.5, ∼9, ∼17, and ∼25 nm). The insets in Fig. 3, a and b show expanded views of the histograms for L_p values ranging from 0 to 6 nm, using a smaller bin size of 0.1 nm that is justified because the uncertainties in the best-fit L_p values were typically less than 10%. The high degree of similarity of the L_p distributions for the two surfaces validates our measurements of the mechanical properties of T4P, because the persistence length is a parameter that is intrinsic to the pili rather than the nature of the underlying surface. The multiple discrete peaks within the L_p histograms in Fig. 3, which occur at the same values of the persistence length for both surfaces, provide strong evidence for bundling of T4P, forming higher-order, stiffer structures with larger values of L_p. This concept of bundling is consistent with negatively stained electron microscopy images of T4P bundles (25), in which bundling of a large number of T4P (up to 8 to 10 T4P) was proposed to explain retraction forces as large as 1.0 nN, more than ten times larger than the retraction force of ∼70 pN for a single pilus.

Figure 3.

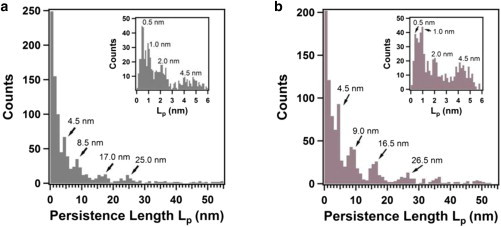
Histograms of the best-fit values of the persistence length L_p for T4P of a P. aeruginosa PAO1 pilT mutant for (a) mica surfaces and (b) gold surfaces, using a bin size of 1.0 nm, and measured using a sharp pyramidal AFM tip. The insets in (a) and (b) are expanded views of the L_p distributions ranging from 0 to 6 nm using a smaller bin size of 0.1 nm. To see this figure in color, go online.

The effect of bundling on the measured value of the persistence length depends on the packing geometry of the T4P. Two packing mechanisms have been proposed for multistranded helical protein fibrils: in the close-packing filament model (29), the persistence length scales with the square of the number of filaments packed, according to $L_p=n^{2}E{A}_0^2/k_{B}T$, where E is Young’s modulus of the T4P, A₀ is the cross-sectional area of a single strand of a pilus, k_B is Boltzmann’s constant and T is the absolute temperature; for the ribbon-like packing model (30), the persistence length increases linearly with the number of filaments packed into a ribbon, according to $L_p=nE{A}_0^2/k_{B}T$. The distributions shown in Fig. 3 provide strong evidence that the T4P occur as close-packed bundles because the peak L_p values increase as the square of the number of T4P, e.g. ∼1 nm, ∼4 nm (2² × 1 nm), ∼9 nm (3² × 1 nm), and so on.

There are two possible scenarios for the close packed bundling that we cannot distinguish based on the data: 1) the bundling of intact T4P, each with a persistence length of ∼1 nm, which is consistent with previously published values of T4P persistence lengths (23); and 2) the application of large pulling forces on the T4P leads to an unraveling of the three intertwined helical strands (as shown schematically in Fig. 4 c), analogous to that observed in double-stranded DNA pulling measurements (31), such that the force is (typically) supported by a single flexible strand at high forces. Because the value of L_p is determined by the high-force portion of the force-extension curves, the smallest (and most dominant) value of L_p ∼1 nm in the histograms in Fig. 3 would correspond to the stretching of a single strand of the T4P (Fig. 4 c). This would imply that the persistence length of T4P consisting of three intertwined strands in the absence of a stretching force is given by their closed-packed arrangement, corresponding to a T4P persistence length of ∼3² × 1 nm ∼9 nm. Scenario (2) is appealing in that it resolves the puzzling result that the fundamental persistence length value of ∼1 nm is significantly less than the ∼8 nm length of a single PilA subunit of the T4P. However, the absence of a distinctive unraveling feature in the measured force-separation curves, as was observed in (31), does not allow us to commit to this interpretation. It is also possible that the application of large forces induces reversible stretching of T4P, as inferred recently from the results of optical tweezer measurements, AFM, and molecular combing experiments on N. gonorrheae T4P (27). The exposure of hidden epitopes could also be accompanied by a change in the mechanical properties of T4P at large stretching forces.

Figure 4.

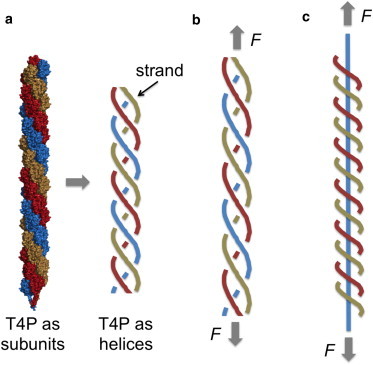
Schematic diagrams of a type IV pilus (T4P), with and without the application of a stretching force. In (a), the relaxed form of the T4P (PDB entry 2HIL, rendered using MacPyMol (Delano Scientific, San Carlos, CA)) (left) and, for simplicity, is also shown as three continuous, close-packed, intertwined helical strands (right). In (b), the application of a pulling force F to the ends of the T4P results in stretching of the three-helix molecule. In (c), a large value of F has resulted in the (hypothesized) release of two of the three strands such that a single strand carries the stretching force. To see this figure in color, go online.

In AFM experiments in which they pulled on T4P of wild-type P. aeruginosa PAO1, Touhami et al. (23) suggested that it was necessary to account for the deformation of the cell membrane that is caused by pulling on T4P anchored in the cell envelope, and introduced a linear spring term into the WLC equation to account for this effect. Given that the effective spring constant k₁ of the cell membrane for P. aeruginosa PAO1 cells is relatively large (∼0.2 nN/nm), as measured in AFM force-indentation curves (32), application of a stretching force of 200 pN would deform the cell membrane by only ∼1 nm (assuming that extension and compression of the cell membrane have equivalent stiffness). Therefore, deformation of the bacterial cell envelope is not an important effect in our measurements.

In the Supporting Material, we show that adhesion between the T4P and the underlying surface will occur only if the bacteria are close to the end of the AFM tip, as illustrated in Fig. 1. As a result, there are only small uncertainties in the best-fit values of L_c and L_p. In addition, in the Supporting Material, we discuss the effect of lateral offsets between the location of the adhered cells on sharp pyramidal tips and the adhered segments of T4P on the underlying surface, and we show that this also results in only small average shifts in the best-fit values of L_c and L_p.

AFM force plateaus

We also observed distinct force plateaus in the AFM force-separation curves when the AFM cantilever was retracted from the surface, as shown in Fig. 5 a for a mica surface. In these AFM force-separation curves, an increase in the force was observed, followed by an extended range in which the force remained essentially constant as the cantilever was retracted from the surface at constant speed. The extent of the force plateaus ranged from tens of nanometers to several micrometers. Although Lee et al. (9) and Giltner et al. (12) suggested that the C-terminal disulfide-bonded loop (DSL) region of the pilin subunit of P. aeruginosa is exposed only at the distal tip of the pilus where it serves as a nonspecific adhesin, the force plateaus observed in the AFM force-separation curves in Fig. 5 are not consistent with tip adherence. Instead, the force plateaus can be interpreted as forced desorption or peeling of an extended length of the T4P from the underlying surface (Fig. 1 a2), as observed using AFM for other semi-flexible polymer chains (33–36). If the major pilin subunit mediates adherence, the adhesive force between the T4P and the surface should be constant along the length of the pilus, and the peeling force should remain constant over an extended range of tip-sample separations, producing a force plateau in the AFM force-separation curve (Fig. 5 a).

Figure 5.

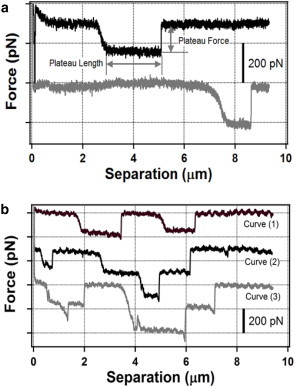
(a) AFM force-separation curves showing single force plateaus for pulling of T4P on a P. aeruginosa PAO1 pilT mutant during retraction of an AFM cantilever with a sharp pyramidal tip from a mica surface. (b) AFM force-separation curves showing multiple force plateaus for pulling of T4P on a P. aeruginosa PAO1 pilT mutant during retraction of an AFM cantilever with a sharp pyramidal tip from a gold surface. To see this figure in color, go online.

Fig. 5 b shows AFM force-separation curves that contain force plateaus measured on a gold surface. Curve (1) contains two force plateaus with a similar value (∼200 pN), showing that multiple adsorbed T4P segments can be peeled from the gold surface, one after the other. These two plateaus could represent desorption of either two different portions of the same pilus or single portions of two different T4P. Curves (2) and (3) in Fig. 5 b contain several force plateau levels that are multiples of ∼200 pN. We interpret this as multiple T4Ps being peeled from the substrate simultaneously, such that the peeling forces are additive. For example, for curve (3), the second plateau at a force of 400 pN within the plateau at a force of 200 pN corresponds to forced desorption of two different T4Ps of different lengths from the underlying surface: the longer plateau corresponds to forced desorption of a longer adsorbed T4P and, adding to this, is the forced desorption of a second shorter T4P that is pulled in parallel with the first T4P within the range 4.5 to 5.0 μm, which produces a plateau force that is double that of the single T4P.

We observed similar force plateaus for T4P pulling on hydrophobic polystyrene surfaces (data not shown). The force plateaus start at random separation distances and extend for considerable distances, showing the same general behavior as seen on the mica and gold surfaces. However, the magnitude of the plateau force (∼50 pN) observed on polystyrene surfaces is typically smaller than on mica and gold surfaces (see below).

Plateau forces and distribution of plateau lengths for different surfaces

During the peeling of T4P from a surface, the plateau force gives a measure of the strength of the T4P-surface interaction (36). We can understand the relationship between the peeling force f and the adhesion energy per unit length ε through the use of an equilibrium statistical model for the peeling of a freely-jointed-chain (FJC, Kuhn length a = 2L_p for the relaxed T4P) that is allowed to slide freely on a flat surface (35). A detailed analysis of this model is presented in the Supporting Material. The T4P are modeled as polydisperse linear chains, with part of each chain adsorbed to the surface and the remainder of that chain in the surrounding liquid. We show that the plateau length distribution W(L) follows an exponential decay law:

$$W\left(L\right)\propto e^{-L/L_d},$$ (2)

with a decay length L_d given by the following:

$$L_d=\frac{a}{\text{ln}\left[\frac{2\text{sinh}\left(\beta fa\right)}{\beta fa}\right]-\beta \epsilon a}.$$ (3)

By substituting measured values of the plateau force into Eq. S11 from the Supporting Material, we show that the adhesion per unit length of T4P on the surface is nearly equal to the measured plateau force.

The distributions of force plateau lengths measured for the mica, gold, and polystyrene surfaces using AFM cantilevers with sharp pyramidal tips are shown in Fig. 6, a–c, respectively. All of the force plateau length distributions have maxima at the smallest plateau lengths, decrease with increasing plateau length, and can be well described by a single exponential decay, consistent with the results of the statistical mechanical model discussed above (Eq. 2). We obtained best-fit values for the exponential decay length L_d of 0.76 ± 0.04 μm (mica), 1.7 ± 0.3 μm (gold), and 0.97 ± 0.06 μm (polystyrene). Intuitively, the significantly larger value of L_d obtained for the gold surface indicates that T4P adhere most strongly to the gold surface.

Figure 6.

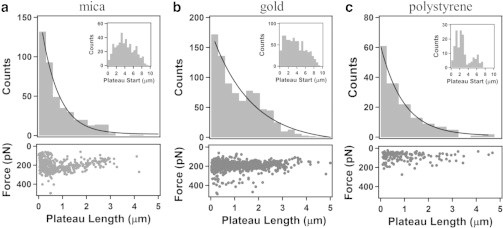
Histograms of the length of force plateaus for the peeling of T4P from (a) mica (434 values), (b) gold (838 values), and (c) polystyrene (155 values) using sharp pyramidal AFM tips. For each histogram, the solid line corresponds to the best fit of the data to a single exponential function. The insets show distributions of the separation values corresponding to the start of the force plateaus (plateau start) for the different surfaces. The lower plots in (a)–(c) show distributions of the plateau force values versus plateau length for force plateau events obtained on the different surfaces.

The insets to Fig. 6, a–c show that the force plateaus began at tip-sample separations that varied from 0 to 10 μm, with distributions that were similar to those measured for the pili rupture lengths in Fig. 2. The peaks obtained at smaller values of ∼2 μm in the rupture force (Fig. 2) and plateau start (Fig. 6) distributions for the polystyrene surface are consistent with significant adhesion occurring only for shorter segments of T4P for this surface. This is perhaps because of reduced adhesion of T4P to the hydrophobic surface such that the flexibility associated with longer pili is sufficient to prevent their adhesion to the surface. In addition, there was no significant dependence of the plateau forces on the length of the plateaus, as can be seen in the lower plots in Fig. 6.

Histograms of the force plateau values measured on different surfaces are shown in Fig. 7, a–d. The large adhesion of the T4P to the gold surface can be seen from the well-defined distribution (average value of ∼180 pN; Fig. 7 b). Although the plateau forces measured on the mica surface using an AFM cantilever with a sharp pyramidal tip are large (broad distribution with an average value of ∼200 pN; Fig. 7 a), measurements performed using a colloidal AFM tip with fewer bacterial cells attached to the cantilever revealed a much smaller force plateau value (narrow distribution with an average value of ∼70 pN; Fig. 7 d). This interpretation is reasonable because—with a smaller number of bacteria are adhered to the colloidal tips than to the sharp pyramidal tips—the probability of pulling single T4P is correspondingly higher. The broad distribution measured using the sharp pyramidal tips is likely because of the simultaneous peeling of multiple T4P from the surface, which resulted in the superposition of plateau forces that were multiples of the fundamental peeling force of ∼70 pN, because the plateau forces are additive for simultaneous pulling of multiple T4P (Fig. 5 b). This would lead to a considerably broader distribution extending to larger plateau force values, as observed Fig. 7 a. The force plateau distribution measured for the polystyrene surface exhibits a maximum at a relatively small value (∼50 pN).

Figure 7.

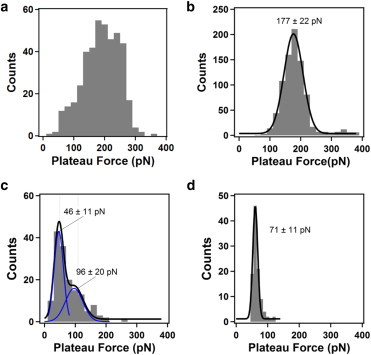
Histograms of plateau forces measured for the peeling of T4P from (a) mica (434 values), (b) gold (838 values), and (c) polystyrene (155 values) using AFM cantilevers with sharp pyramidal tips. (d) Histogram of plateau forces measured for the peeling of T4P from mica (103 values) using AFM cantilevers with a 600 nm diameter colloidal tip. For the histograms in (b)–(d), the solid lines correspond to best fits of Gaussian functions to the data, with the best-fit center positions and standard deviation values indicated on the plots. To see this figure in color, go online.

A direct comparison of the rupture forces (Fig. 2) and plateau forces (Fig. 7) reveals that we have obtained reasonable agreement for the different surfaces: the gold surface has a rupture force ∼150 pN and a plateau force ∼180 pN; the polystyrene surface has a rupture force ∼60 pN and a plateau force ∼50 pN; and the mica surface has a rupture force ∼80 pN (for the 600 nm colloidal tip) and 90 pN (main peak for the pyramid sharp tip) and a plateau force ∼70 pN (for the 600 nm colloidal tip). Although the distributions of rupture forces and plateau forces are broader for the mica surface, which we interpret as being because of multiple, additive events (rupture or desorption), the distribution measured using 600 nm colloidal tips with less bacteria and T4P provides similar results for the rupture force (80 pN) and the plateau force (70 pN).

As noted above, substitution of typical measured plateau force f values into Eq. S11 shows the plateau force is nearly equal to the adhesion energy per unit length ε. Therefore, our results show that T4P adhere better to the gold surface than the mica and polystyrene surfaces, and this is consistent with the trends observed in the measured distributions of rupture forces measured in force peaks (Fig. 2, b, d, and f). It is interesting to note that the values of f, and therefore ε, are similar to the ∼70 pN force generated by a single pilus motor (25), which should have implications for bacterial motility on different surfaces.

Maier et al. showed that large forces applied to T4P of Neisseria gonorrheae with low levels of PilT expression induced extension of T4P (18). To determine the contribution of force-induced T4P extension to the force plateaus observed in our study, we considered the amount of T4P extension that might occur during the force plateaus. Maier et al. measured the rate of T4P retraction and extension for forces greater than 110 pN to be 0.35 μm/s. For an average force plateau length of 1 μm (Fig. 6) and an AFM tip retraction speed of 7.9 μm/s, the average time corresponding to a force plateau is 0.12 s. During this time, the T4P could extend from the bacterial cell surface by only 36 nm, which is a very small percentage (4%) of the average plateau length. Therefore, force-induced pilus extension likely does not contribute significantly to the observed force plateaus. We conclude that the force plateaus are attributable to peeling of the T4P from the surface, indicating that T4P adhere to both hydrophilic and hydrophobic surfaces over significant portions of their length.

Miller et al. observed force plateaus for force pulling of type I pili, which they attributed to a force-induced transition in the pilus structure (37). We note that the structure of a type IV pilus is very different from that of a type I pilus: type IV pili are three intertwined helical strands (Fig. 4), whereas the type I pilus is a single helix with a central hollow channel. The structural change that occurs in type I pili produces a force plateau (37) that corresponds to the reversible unraveling of the hollow helix and this type of unraveling cannot occur for the intertwined helices of the type IV pilus.

Conclusions

We used AFM-based pulling to study the mechanical properties and adhesion of Type IV pili (T4P) of a pilT mutant of P. aeruginosa PAO1 unable to retract its T4P, and found that the WLC model is sufficient to describe the force peaks observed in the AFM force-separation curves. Our data support a low-affinity, high-avidity model of T4P attachment to surfaces, where each major subunit PilA exposes a nonspecific adhesinotope and adhesion occurs along the length of the pili. We have also obtained clear evidence for bundling of T4P by the observation of distinct peaks corresponding to different close-packed bundling combinations in the L_p distributions for both mica and gold surfaces. In addition to the presence of force peaks in the AFM force-separation curves, we observed force plateaus that we attribute to the forced desorption or peeling of extended lengths of T4P from both hydrophilic and hydrophobic substrates, consistent with the low-affinity, high-avidity model. The significant differences between the rupture force distributions on the mica, gold, and polystyrene surfaces lead us to conclude that rupture occurred primarily between the pili and the underlying surface, as the last of a series of low-affinity interactions is lost.

The small values of the T4P persistence length L_p, and hence large flexibility of the pili, obtained in our study are consistent with the small values of L_p reported by Touhami et al. (23) rather than the large values reported by Skerker et al. (15). High T4P flexibility provides the bacteria with several distinct advantages. First, it facilitates contact of the T4P with surfaces over extended lengths of the T4P, enhancing avidity and thus adhesion of the T4P to the surfaces, which is consistent with our observation of distinct force plateaus in AFM force-separation curves. In addition, bundling of T4P, which we inferred from the distributions of the persistence length values in our study, should occur more readily for flexible pili and provides a mechanism for bacteria to use T4P cooperatively to generate large forces. By adhering to both hydrophilic and hydrophobic surfaces along extended portions of their length, T4P allow P. aeruginosa PAO1 cells to establish contact with and colonize a broad range of surfaces.

Author Contributions

S.L. contributed to the design of the experiments, performed the experiments, performed the data analysis, and contributed to the interpretation of the experimental results and the writing of the article. M.G. contributed to the data analysis and the writing of the article. H.H. generated the bacterial mutants used in the experiments. L.L.B. provided the bacterial mutants and contributed to the interpretation of the experimental results and the writing of the article. R.A.W. performed the calculation of the statistical model presented in the Supporting Material and contributed to the writing of the article. J.R.D. contributed to the design of the experiments, the interpretation of the experimental results, and the writing of the article.

Editor: Keir Neuman.