Design and Testing of a Simulation Framework for Dosimetric Motion Studies Integrating an Anthropomorphic Computational Phantom into Four-dimensional Monte Carlo

Abstract

We have designed a simulation framework for motion studies in radiation therapy by integrating the anthropomorphic NCAT phantom into a 4D Monte Carlo dose calculation engine based on DPM. Representing an artifact-free environment, the system can be used to identify class solutions as a function of geometric and dosimetric parameters. A pilot dynamic conformal study for three lesions (~ 2.0 cm) in the right lung was performed (70 Gy prescription dose). Tumor motion changed as a function of tumor location, according to the anthropomorphic deformable motion model. Conformal plans were simulated with 0 to 2 cm margin for the aperture, with additional 0.5 cm for beam penumbra. The dosimetric effects of intensity modulated radiotherapy (IMRT) vs. conformal treatments were compared in a static case. Results show that the Monte Carlo simulation framework can model tumor tracking in deformable anatomy with high accuracy, providing absolute doses for IMRT and conformal radiation therapy. A target underdosage of up to 3.67 Gy (lower lung) was highlighted in the composite dose distribution mapped at exhale. Such effects depend on tumor location and treatment margin and are affected by lung deformation and ribcage motion. In summary, the complexity in the irradiation of moving targets has been reduced to a controlled simulation environment, where several treatment options can be accurately modeled and quantified The implemented tools will be utilized for extensive motion study in lung/liver irradiation.

Introduction

In the treatment of moving tumors, different strategies may be applied to mitigate the effects of breathing motion on external beam dose delivery. These include the irradiation of the internal target volume (ITV) (1), respiratory gating (2, 3) and tumor tracking (4–8). Such techniques entail an increasing level of complexity in terms of treatment planning and technology needed for accurate targetry. It is still unclear though what is the dosimetric gain in using complex motion mitigation strategies for different tumor location, size, motion amplitude. Furthermore, the level of geometrical uncertainty in targeting the tumor, due to setup error and residual motion, translates into the use of safety margins around the CTV. As a matter of fact, the potential benefit of one strategy over the other results from the complex interaction of multiple variables.

4D CT is a clinically available option to perform patient specific analysis, aiming at defining the best treatment modality in a case specific way (9, 10). Such analysis is labor intensive, involving target and normal tissue segmentation over multiple respiratory phases, the application of deformable registration techniques and extensive 4D planning (11). Furthermore, one has to deal with motion artifacts due to irregular breathing and/or inaccuracies in phase binning of 4D CT images (12, 13).

In this scenario, computational models may play a complementary role in providing insights into action thresholds. Several anthropomorphic computational models for radiation dosimetry have been developed since the 1960s, ranging from stylized to voxel-based models (14, 15). These latter have reached sub-millimeter anatomical detail relying on tomographic images of real subjects (15). Recent developments have extended the capabilities of computational models to incorporate 4D motion, namely respiration and heartbeat (16–18). These features make latest 4D anthropomorphic models extremely valuable for extensive dosimetric studies of the effects of motion.

Motion studies can be performed by integrating 4D models into a dose calculation engine. Monte Carlo emerges as the best solution, given the intrinsic accuracy, especially for low density materials and in presence of heterogeneities (19). This specifically applies to motion studies in the lung (20). The use of 4D Monte Carlo dose calculations for time dependent geometries, including variations in patient anatomy due to organ motion, has proven to be highly efficient (21–23). Moreover, 4D Monte Carlo has been shown to have the same computational time of a 3D dose calculation featuring the same statistical uncertainty (21).

Consequently, we applied Monte Carlo dose calculations on an anthropomorphic 4D computational patient model to understand the effects of motion on dose deposition. Our approach to 4D Monte Carlo dose calculation in patient data is described in detail in a previous publication (24). We extended the use of our 4D Monte Carlo calculation engine to integrate an anthropomorphic 4D computational phantom in a unique simulation framework. This represents a framework where the interactions of multiple variables can be conveniently modeled to quantify the dosimetric effects due to motion. The advantage of this approach is the availability of a controlled environment, where no inaccuracies in 4D CT acquisition, deformable registration and workload in data processing exist.

In this work, implementation and testing of the simulation framework for 4D Monte Carlo motion studies are reported. Conformal and IMRT treatment plans were generated and applied to coin size moving tumors in order to examine the accuracy in tracking and delivering dose in 4D. Dosimetric results were correlated to the anatomical changes induced by breathing, as a function of tumor motion, ribcage expansion and lung deformation.

Materials and Methods

4D Anthropomorphic Computational Model

NCAT (NURBS-based Cardiac-Torso) (17) is a spline-based anthropomorphic model created on the Visible Human Data-set (25). It includes a spline-based description of 3D human anatomy and dynamic 4D modeling of breathing (18) and heartbeat (16). The computational model can be used to generate 4D attenuation and/or activity medical images. Hereafter, we will focus on the use of NCAT to obtain artificial 4D CT images for radiotherapy planning studies.

In the standard NCAT release, the user can edit functional variables that control respiration and heart pulse, in order to generate deformable 4D CT models according to specific criteria (18). The main control variables include:

• Motion option: beating heart only/respiration only/combined mode

• Maximum diaphragm motion in the superior-inferior (SI) direction

• Maximum anterior-posterior (AP) expansion of the chest wall applies to motion studies in the lung (20).

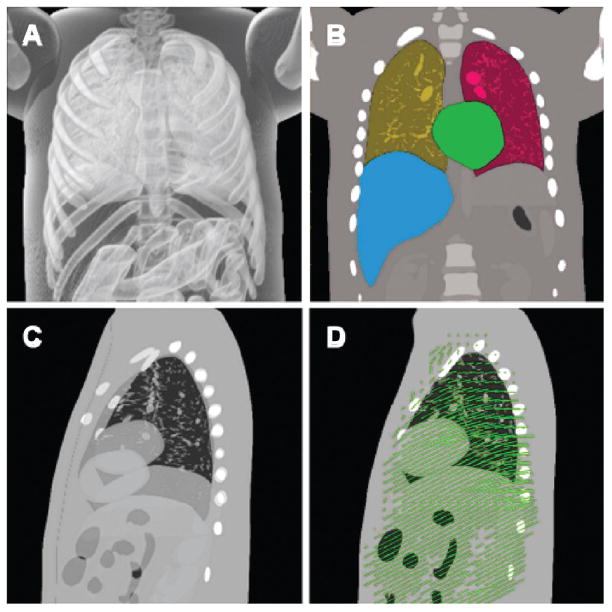
Though the spline-based representation can provide a continuous model in space and time, the spatial resolution and phase binning of NCAT-generated 4D CT images can be adjusted. Spherical tumors of arbitrary location and size can be inserted into the NCAT 4D CT dataset, and contours of all organs and a deformable registration map can be extracted from the spline-based representation (Figure 1) (26).

Figure 1.

Panel A: NCAT based 3D rendering at exhale, where the anatomical details inside the lung are visible. Panel B: segmented NCAT model showing the right/left lung, heart, and liver. Panel C: sagittal view with exhale and inhale superimposed in transparency. Panel D: deformation vector field mapping exhale to inhale.

4D Monte Carlo Dose Calculation

According to the approach proposed by Vanderstraeten et al. (27), 14 tissue subsets (materials) were utilized for Monte Carlo dose calculations. In our case, stoichiometric calibration was not necessary as density values for each voxel were provided by the NCAT model (28). Table I reports the properties of the 14 materials used for Monte Carlo dose calculations.

Table I.

Material composition and properties for Monte Carlo dose calculations.

Material	Composition							Z	A [Da]	Medium toH20 Stopping Power	Density Range [g/cc]
	H	C	N	O	P	Ca	Ar				Min	Max
1	-	0.000	0.784	0.211	-	-	0.005	7.262	14.548	1.110	− ∞	0.095
2	0.130	0.105	0.031	0.749	0.002	-	-	6.999	13.872	0.996	0.095	0.879
3	0.117	0.697	0.001	0.189	-	-	-	5.826	11.544	0.995	0.879	0.997
4	0.107	0.120	0.024	0.755	0.001	-	-	7.050	13.996	1.013	0.997	1.057
5	0.097	0.465	0.025	0.355	0.019	0.041	-	7.010	13.951	1.024	1.057	1.152
6	0.089	0.424	0.027	0.365	0.030	0.064	-	7.479	14.910	1.040	1.152	1.247
7	0.075	0.357	0.031	0.384	0.049	0.106	-	8.355	16.695	1.054	1.247	1.342
8	0.066	0.314	0.033	0.396	0.061	0.131	-	8.886	17.779	1.068	1.342	1.437
9	0.059	0.277	0.035	0.406	0.071	0.154	-	9.348	18.721	1.079	1.437	1.533
10	0.052	0.245	0.037	0.414	0.080	0.173	-	9.753	19.548	1.090	1.533	1.628
11	0.046	0.216	0.039	0.422	0.087	0.191	-	10.111	20.279	1.100	1.628	1.723
12	0.041	0.190	0.040	0.429	0.094	0.206		10.430	20.930	1.117	1.723	1.818
13	0.036	0.167	0.042	0.435	0.101	0.220		10.716	21.513	1.125	1.828	1.913
14	0.044	0.200	0.054	0.559	0.132	0.029		8.657	17.403	1.129	1.914	+ ∞

Monte Carlo dose calculation was done in three steps (24):

1. transport of electron and photons from the electron target to the flattening filter, performed with EGSnrc (29). The VARIAN 2100C/D treatment head was modeled based on manufacturer’s information, in order to characterize the beam as a phase space distribution at the level of the flattening filter

2. transport of electrons and photons from the flattenning filter to after the MLC (multileaf collimator) using the variance reduction method published by Siebers et al. (30). The method was expanded to incorporate the variations in the MLC and jaws during beam delivery or between different beams (24). This represents an efficient method of transporting photons through MLC/jaws and accounts for beam hardening and tongue-and-groove effect by using multiple Compton scatter in the MLC/jaws medium. The Compton scatter is sampled based upon the total thickness of MLC traversed. Pair production and electron interaction within the MLC are ignored.

3. Simulation of patient dose deposition using the DPM algorithm (31). DPM was used in favor of EGSnrc because it allows a more time efficient computation of dose in a patient/phantom geometry. The standard DPM parameters were used in the DPM simulations and the time variations were accounted for using a 4D CT data set (24). DPM and EGSnrc were benchmarked against each other showing agreement to within 1%. The various Monte Carlo algorithms used separately in either of the two methods were extensively studied by Kawarakow et al. (32).

Step (a) using EGSnrc software is only performed once during the commissioning of the Monte Carlo code to the linac present at our hospital. It is then unchanged for all the simulations of IMRT or non-IMRT field with Monte Carlo. Steps (b) and (c) are performed for all simulations of IMRT fields used in the present manuscript. The statistical uncertainty was calculated using the method of Walters et al. (33). The uncertainty in the present results are, for the target area approximately, 3% per beam, which corresponds to an overall uncertainty of below 2%.

Conformal Study

Three 4D anthropomorphic computational models were generated with NCAT. The spatial resolution of the resulting 4D CT images was set to 1.5625 mm (256 × 256 × 256 voxels). The same input parameters were applied to define breathing: 4 cm diaphragm motion and 2 cm chest wall expansion. This allowed us to test the implemented simulation framework in a case with large motion. The respiratory cycle was binned into 10 phases, with the exhale phase encompassing 60% of the total duration.

The models differed in the location of the tumor (~ 2.0 cm): three spherical lesions (LOW, MED, UP) were placed in the right lung (Figure 2). Given the spatial resolution of the generated 4D CT images, the lesions resulted in 12–14 voxels thick spherical objects. Tumor motion changed according to the motion model implemented in NCAT as a function of tumor location. Though the lung is modeled as a deformable object, the spherical lesion is assumed as a rigid object (18), being the motion defined by the center of mass. The peak to peak motion in the SI direction measured 3.8 cm, 2.8 cm, and 1.2 cm for the LOW, MED, and UP lesion, respectively. The corresponding motion amplitude in the AP direction was 0.9 cm, 0.9 cm, and 0.2 cm, correspondingly.

Figure 2.

Anatomical location of the three lesions (LOW, MED, UP) located in the right lung (left panel). Only one lesion was used for a given simulation setup. The right panel shows the exemplifying beam arrangement for the conformal study.

A conformal study was performed with Monte Carlo dose calculations, assuming a prescription dose of 70 Gy (95% coverage). The beam arrangement included 6 beams (0°, 22°, 180°, 228°, 270°, 334°) as shown in Figure 2. Beam weights were optimized at 50% inhale (phase 3).

Tumor tracking was simulated for each 4D phantom, relying on the NCAT breathing model to shift the beams in order to follow tumor motion over the respiratory cycle. Monte Carlo dose calculations were performed separately on each phase, considering 5 · 10⁷ simulated photons (5 · 10⁸ total). The number of photons was selected to achieve less than 3% error in the dose calculation per beam in the target area, as specified in the previous section. Conformal plans were simulated with different margins added to the GTV: 0 cm, 1 cm, 2 cm. An additional 0.5 cm margin was applied to account for beam penumbra. The resulting dose distributions were mapped to the exhale phase as described in the previous section. The composite 4D dose allowed us to quantify the dosimetric effects of tumor tracking as a function of the applied margin. The rationale of using different margins in this study was to investigate and quantify the effect of rigid tumor motion vs. lung deformation on target coverage and normal lung irradiation.

Finally, ideal respiratory gating was simulated through the calculated dose distribution at exhale.

IMRT Case

The implemented simulation framework was used for Monte Carlo dose calculations in IMRT on a static case. This was obtained by making use of optimized MLC sequences calculated by a commercial treatment planning software. The extension of our 4D Monte Carlo framework to IMRT delivery is straightforward, as the dose mapping procedure applied in the conformal study is independent of the simulated irradiation technique. The same applies to accounting for variable density values in the lung as a function of the breathing phase: one can easily overwrite density values in any structure relying on 4D NCAT segmentation. On the other hand, potential interplay effects between organ motion and leaf motion (34) are currently not considered in our model.

The LOW lesion at exhale with 0 cm PTV margin was selected for Monte Carlo IMRT dose calculations. The same additional margin for beam penumbra used in the dynamic conformal study was applied. The NCAT generated 3D CT images were converted into the DICOM format and imported into XiO^® treatment planning (CMS Inc.). This latter was used to generate optimized leaf-sequence for the MLC in five beams (0°, 180°, 228°, 270°, 334°). The MLC leaf-sequence files, featuring 6–12 segments for each beam, were then exported to the Monte Carlo dose calculation engine. The conversion from DICOM plan obtained using the XiO^® treatment planning system to Monte Carlo was performed using the MATLAB^® toolbox, which reads DICOM format. A total number of 5 · 10⁷ photons were simulated for IMRT dose calculations.

Results and Discussion

Conformal Study

Monte Carlo dose calculation takes approximately under 1 hour of computational time per phase to achieve 3% error per beam in PTV dose prediction. Figure 3 depicts an exemplifying dynamic sequence of conformal dose distributions over the breathing cycle.

Figure 3.

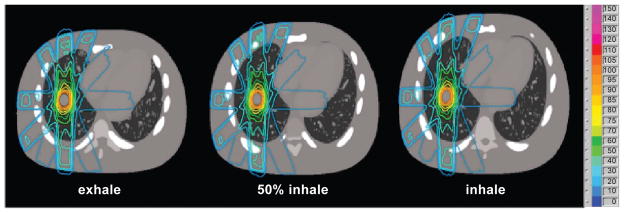
Monte Carlo dose distribution at exhale, 50% inhale, and inhale during tumor tracking with no additional margin except for penumbra (LOW lesion).

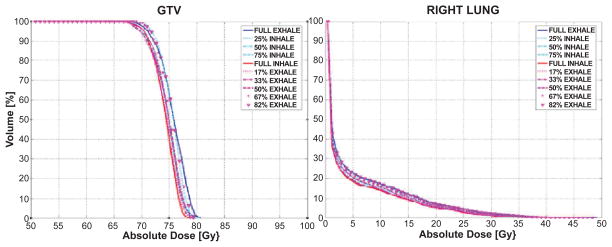
Dose volume histograms (DVHs) for the same tumor tracking case are shown in Figure 4. Results show dosimetric variations as a function of the breathing phase. Though accurate geometric tracking was achieved, as shown in Figure 3, target underdosage at inhale and overdosage at exhale were found (Figure 4).

Figure 4.

DVHs for GTV and right lung (0 cm margin) over the breathing cycle for the LOW lesion.

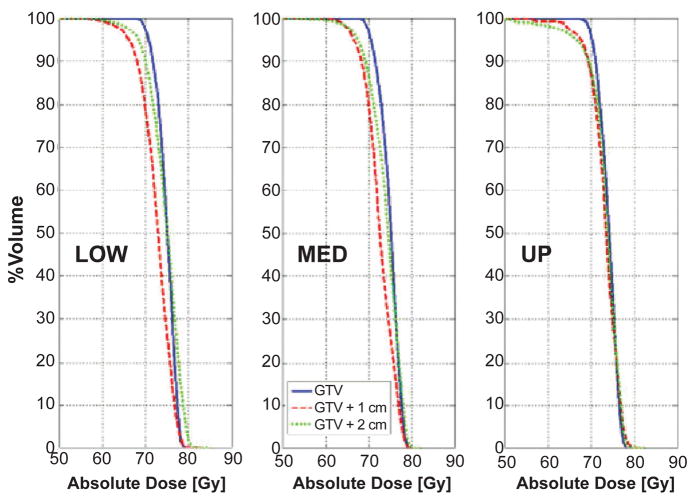
Figure 5 shows target coverage as a function of margin for the three lesions, where the composite dose distribution over the breathing cycle is mapped to the exhale phase. With increasing margin the influence of the tumor location (LOW to UP) on the motion DVH becomes more pronounced. Target underdosage was highlighted for 1 cm and 2 cm margin, ranging from 1.58 Gy (LOW lesion, 2 cm margin) to 3.67 Gy (LOW lesion, 1 cm margin); results are expressed in terms of variation in the dose delivered to 95% of the target volume (D95).

Figure 5.

DVHs of 4D Monte Carlo dose calculations over the breathing cycle, mapped at exhale. Results are shown as a function of tumor location and margin.

Ideal tumor tracking on a rigidly moving tumor in the lung results in perfect target coverage when no margin is used. The same conclusion does not hold when a non zero margin is applied, due to the deformable anatomy of the lung (Figure 5). As a matter of fact, margins are a geometric concept that is used to define the aperture in order to cover a volume encompassing the tumor. When deformable anatomy is involved, the aperture defined on a specific breathing phase includes voxels of normal tissue that will be moving in or out, according to the local amount of deformation. Therefore, though one can effectively track over the breathing cycle any geometric volume around the tumor, dose coverage is not ensured for each single voxel included in the original target. Figure 5 also shows that such effect is dependent on tumor location (i.e., motion amplitude) and the applied margin. The maximum variation was measured for the LOW lesion, i.e., where deformation is larger. Target underdosage was found to be higher for the 1 cm than the 2 cm margin. This is consistent with the observation that, when the margin is wide enough, lung deformation has reduced effects, as the aperture effectively includes the portion of lung volume that is deforming the most. When comparing the target dose for different margins, results may be affected by the uncertainties in DVH estimation, that are larger for the zero margin case compared to 1 cm and 2 cm margin. Though this was not quantified in our simulations, results are in keeping with the anatomo-physiological changes induced by breathing in the anthropomorphic phantom, indicating that the effect has a significantly smaller magnitude.

Figure 6 compares tumor tracking and respiratory gating showing DVHs for the right lung for the LOW and UP lesion. It is worth stressing that these results were obtained considering constant lung density over the breathing cycle. Recent studies show that such approximation results in minor effects if compared to motion and heterogeneities correction (20, 35). Normal lung DVHs illustrate that tracking has a dosimetric advantage vs. gating, at least in a large motion case. This can be explained by the fact that the radiation beam intersects the normal lung at different locations when tumor tracking is performed, thus locally reducing dose deposition in the healthy lung. Such effect was also found to be dependent on the applied margin, with an increasing trend for larger margins. Figure 6 shows that the actual gain is negligible as long as the margin can be reduced to a minimum (ideally zero). This should be accurately considered, as the technological and methodological effort to reduce the uncertainties in tumor tracking is definitely of higher magnitude than the one needed for respiratory gating. On the other hand, tumor tracking can significantly increase the duty cycle, thus reducing the overall treatment time in the irradiation of a moving target.

Figure 6.

Normal tissue irradiation (right lung) for the LOW and UP lesion, where respiratory gating is compared to tumor tracking.

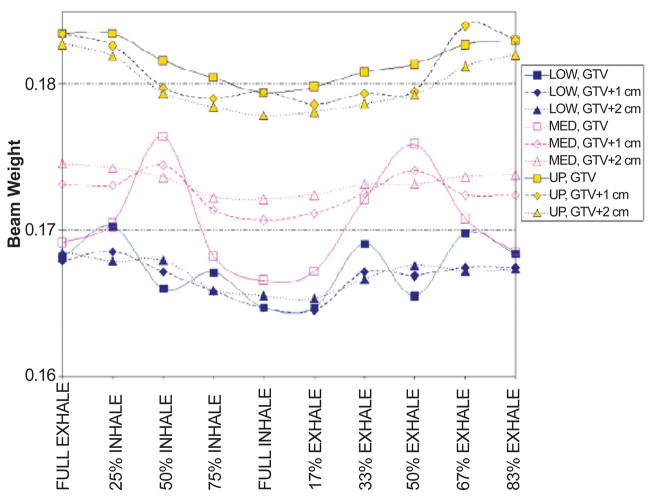
The change in beam weight to ensure optimal target coverage over the breathing cycle was also investigated. Results for the beam at 0° are shown in Figure 7. Variations in optimal beam weights over the breathing cycle are highly dependent on the amount of bone tissue within the aperture, especially for lesions in the medium/lower lung when small margins are applied (Figures 7, 8). With larger apertures (1–2 cm margin) bone tissue variations were averaged out, and beam weights showed a higher correlation with the amount of lung tissue. Therefore, beam weight changes are sensitive to tumor location on one hand, and ribcage bony structures moving in and out of the aperture on the other. Consequently, deriving a reliable model of weight variations over the breathing cycle is not a trivial task, as anatomy variations need to be site specifically quantified. Conversely, this emphasizes the need for an accurate simulation framework where such effects can be conveniently and quantitatively studied.

Figure 7.

Beam weight variation over the breathing cycle for the beam at 0° (AP) as a function of tumor location (LOW, MED, UP) and margin (0, 1, 2 cm).

Figure 8.

Beam weight variation for the MED lesion as a function of margin for the beam at 0° (upper panel); the lower panel shows the relative decrease in lung/bone tissue in the aperture with respect to the average value over the breathing cycle.

IMRT Case

The 3D dose distribution when IMRT was simulated is depicted in Figure 9, compared to the corresponding 3D conformal case.

Figure 9.

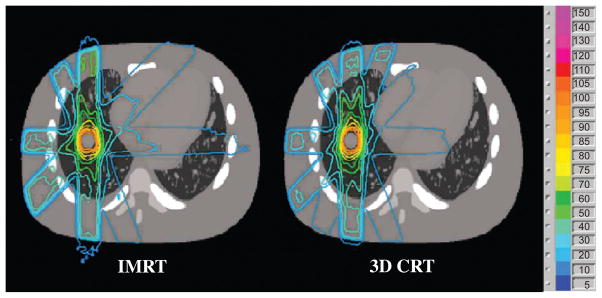
IMRT vs. 3D conformal (3D CRT) dose distribution.

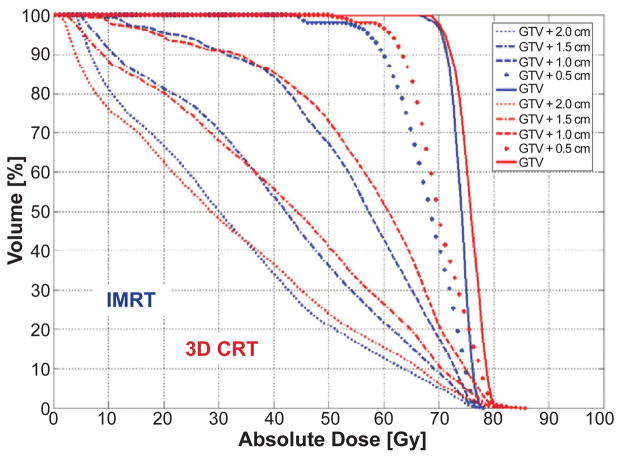
Figure 10 shows the variations in the dose gradient outside of the GTV. The advantage of IMRT vs. 3D CRT is visible from the considerably steeper DVH for the GTV (thick lines in Figure 10). Also, concentric volumes encompassing the GTV highlight a reduction in dose deposition, signifying higher conformality in the dose distribution.

Figure 10.

DVHs of multiple volumes encompassing the GTV for IMRT (blue) and 3D CRT (red) at exhale.

Conclusion

A simulation framework comprising a 4D anthropomorphic computational model and a 4D Monte Carlo dose calculation engine has been implemented. This study shows that the simulation framework can model tumor tracking in deformable anatomy with high accuracy. Furthermore, the absolute dosimetry provided by 4D Monte Carlo dose calculations effectively quantifies variations due to anatomical structures moving in and out of the radiation beam pathway. The implemented tools have been applied to a dynamic conformal study for three lesions in the right lung.

The complexity in the irradiation of moving targets has been reduced to a controlled 4D simulation environment for dosimetric motion studies. Anatomical changes due to breathing need to be carefully considered even though perfect tumor tracking can be achieved. When large motion occurs, the anatomical structures moving in and out of the radiation beam pathway alter dose deposition over the breathing cycle. The dosimetric advantages of tumor tracking vs. respiratory gating in normal lung irradiation seem negligible, when high accuracy in tumor localization leads to small safety margins.

The implemented 4D Monte Carlo tools have been successfully tested and will be applied for extensive motion study in lung/liver irradiation. Future developments will extend the implemented tools to include lung density variations and particle beam Monte Carlo dose calculations.

Abbreviations

3D

Three-dimensional

4D

Four-dimensional

AP

Anterior posterior

CRT

Conformal radiotherapy

CT

Computed tomography

CTV

Clinical target volume

DVH

Dose volume histogram

GTV

Gross target volume

IMRT

Intensity modulated radiotherapy

ITV

Internal target volume

MLC

Multi-leaf collimator

NCAT

NURBS-based cardiac torso

NURBS

Non uniform rational B-splines

PTV

Planned target volume

SI

Superior inferior