The dynamic deformation of a layered viscoelastic medium under surface excitation

Abstract

In this study the dynamic behavior of a layered viscoelastic medium in response to the harmonic and impulsive acoustic radiation force applied to its surface was investigated both theoretically and experimentally. An analytical solution for a layered viscoelastic compressible medium in frequency and time domains was obtained using the Hankel transform. A special incompressible case was considered to model soft biological tissues. To verify our theoretical model, experiments were performed using tissue-like gel-based phantoms with varying mechanical properties. A 3.5 MHz single-element focused ultrasound transducer was used to apply the radiation force at the surface of the phantoms. A phase-sensitive optical coherence tomography (OCT) system was used to track the displacements of the phantom surface. Theoretically predicted displacements were compared with experimental measurements. The role of the depth dependence of the elastic properties of a medium in its response to an acoustic pulse at the surface was studied. It was shown that the low-frequency vibrations at the surface are more sensitive to the deep layers than high-frequency ones. Therefore, the proposed model in combination with spectral analysis can be used to evaluate depth-dependent distribution of the mechanical properties based on the measurements of the surface deformation.

I. Introduction

Acoustic radiation force is widely used in elasticity imaging as an external load for remote tissue palpation (Nightingale, 2011, Palmeri and Nightingale, 2011, Sarvazyan et al., 1998, Greenleaf et al., 2003, Sarvazyan, 2010). This approach is based on focusing an acoustic beam in tissue and converting acoustic energy into tissue motion. Acoustic radiation force-based methods offer significant advantages over other external excitations because the force can be more precisely controlled in terms of space and time and directly applied to the region of interest. The small tissue deformation induced by acoustic stimulation is safe and highly localized. Tissue motion at the ultrasound beam focal point and propagation of the induced elastic waves are related to tissue mechanical properties. The radiation force can be generated not only inside the tissue but also at the tissue surface or at the tissue boundaries where there is a significant difference in the acoustic impedance. Tissue excitation and surface deformation measurements have been used in elastography of skin (Li et al., 2012a, Li et al., 2012b, Coutts et al., 2006, Kirkpatrick et al., 2006), cornea (Tanter et al., 2009, Twa et al., 2014), crystalline lens (Wang et al., 2013, Manapuram et al., 2011, Wu et al., 2015), bladder wall (Li et al., 2014, Nenadic et al., 2013) and other potential applications (Sarvazyan, 2010). However, in all of these applications, the depth inhomogeneity of the tissue plays an important role in its mechanical response. The overall goal of our study is to develop a reconstruction method to estimate the depth dependence of the mechanical properties of a medium based on surface motion measurements.

In previous studies, we used acoustic radiation forces generated by the reflection of an ultrasound wave to probe a laser-induced gas micro-bubble as a way to remotely measure the localized viscoelastic properties of the crystalline lens (Yoon et al., 2012, Yoon et al., 2013, Aglyamov et al., 2012). This approach did not depend on the amplitude of the radiation force and was based on the time characteristics of the bubble displacement. Here, we extend this approach to the case where the acoustic radiation force is applied to the surface of a multi-layered tissue. For example, to evaluate the mechanical properties of the ocular tissues, such as the lens and cornea, the short acoustic radiation force can be focused on the anterior surface of the lens or cornea to noninvasively create a spatially localized deformation (Manapuram et al., 2011, Tanter et al., 2009, Wang et al., 2013). Both the lens and cornea have a layered structure and inhomogeneous distribution of mechanical properties (Hollman et al., 2002, Weeber et al., 2007, Yoon et al., 2013).

Combining the acoustic radiation force and optical coherence tomography (OCT) is a promising diagnostic technique for many biomedical applications (Li et al., 2012a, Kirkpatrick et al., 2006, Manapuram et al., 2012a, Manapuram et al., 2012b, Manapuram et al., 2011, Wang et al., 2013). In comparison with other imaging techniques, such as ultrasound and magnetic resonance imaging, OCT has significant advantages in resolution and accuracy of motion estimation, but limited by the low penetration depth of light. Therefore, OCT is an ideal imaging technique for surface measurements after a deformation force is applied to the sample surface; this emerging technique is optical coherence elastography (OCE) (Wang and Larin, 2014).

From a mathematical point of view, the problem of the elasticity evaluation based on the excitation and measurement on the tissue surface is similar to the problems of mechanical impedance measurements (Skovoroda and Aglyamov, 1998, Zhang et al., 2001) and surface wave propagation (Royston et al., 1999, Royston et al., 2003, Zhang et al., 2011). The influence of the temporal and spatial profiles of the stress source (radiation force) was studied previously (Hachemi et al., 2006). A model based on the elastodynamic Green’s function formalism was considered to describe displacements at the surface of the elastic homogeneous half-space after a short acoustic pulse. There was good agreement between the results of phantom studies and theory (Hachemi et al., 2006). Nevertheless, to describe a mechanical response of biological tissues to an acoustic radiation force, depth inhomogeneity should also be taken into account.

In the current study, we present a model of a layered, viscoelastic medium excited by the harmonic or short acoustic load on its boundary. We consider the influence of depth dependence of the mechanical properties of a medium to vibrations at the focal point of the transducer on the surface. This model was verified in phantom studies using an ultrasound-based OCE system. We demonstrated that the spectral analysis of the surface motion permits differentiation of the mechanical response of different layers to surface perturbation. Therefore, the developed model could be used in the model-based reconstruction of the distribution of mechanical properties throughout the tissue.

II. METHOD

1. A Viscoelastic Layer

Consider an infinite viscoelastic layer of thickness H where the mechanical properties depend only on the depth, i.e. change in the direction of the z-axis of the cylindrical system of coordinates (r, θ, z). An external acoustic load is considered as an axisymmetric force applied to the upper surface of the layer. No volumetric forces are considered in an assumption that all acoustic energy is ideally transferred into stress on the surface. Therefore, no additional reflections of the ultrasound wave inside the medium are considered. Because the problem is axisymmetric, the θ-component of the displacement vector U = (U_r, 0, U_z) is zero, and dependence on the angle θ is not considered. The equation of motion is given by:

$$\begin{array}{l}\frac{\partial S_{rr}}{\partial r}+\frac{\partial S_{rz}}{\partial z}+\frac{S_{rr}-S_{\theta \theta }}{r}=\rho \frac{{\partial }^2{U}_r}{\partial t^2},\\ \frac{\partial S_{rz}}{\partial r}+\frac{\partial S_{zz}}{\partial z}+\frac{S_{rz}}{r}=\rho \frac{{\partial }^2{U}_z}{\partial t^2},\end{array}$$ (1)

where t is time, ρ is medium density, and S_mn are stress tensor components. The viscoelastic stress-strain constitutive relation in terms of the relaxation functions λ̄(t) and μ̄(t) can be expressed as (Christensen, 1971):

$$\begin{array}{l}{S}_{mn}={\delta }_{mn}\underset{-\infty }{\overset{t}{\int }}\overline{\lambda }(t-\tau )\frac{\partial \gamma }{\partial \tau }d\tau +2\underset{-\infty }{\overset{t}{\int }}\overline{\mu }(t-\tau )\frac{\partial {\epsilon }_{mn}}{\partial t}d\tau ;m,n=r,\theta ,z;\\ {\epsilon }_{rr}=\frac{\partial U_r}{\partial r},{\epsilon }_{\theta \theta }=\frac{U_r}{r},{\epsilon }_{zz}=\frac{\partial U_z}{\partial z},{\epsilon }_{rz}=\frac{1}{2}(\frac{\partial U_r}{\partial z}+\frac{\partial U_z}{\partial r}),{\epsilon }_{r\theta }={\epsilon }_{\theta z}=0\\ r=\mathit{div}\mathbf{U}={\epsilon }_{rr}+{\epsilon }_{\theta \theta }+{\epsilon }_{zz};\end{array}$$ (2)

Where ε_mn are strain tensor components, δ_mn is the Kronecker symbol, and γ is the divergence of the displacement vector. The relaxation functions λ̄(t) and μ̄(t) are analogous to the Lame constants in elasticity and their specific form is defined by the chosen viscoelastic rheological model (Christensen, 1971). We assume fixed boundary conditions for the bottom (z = H), and normal P(r, t) and shear Q(r, t) stresses given on the top surface (z = 0):

$$\begin{array}{l}{U}_r(r,H,t)=U_z(r,H,t)=0,\\ S_{zz}(r,0,t)=-P(r,t),S_{rz}(r,0,t)=-Q(r,t).\end{array}$$ (3)

2. Harmonic Excitation of a Multi-Layered Medium

Let us now consider a multi-layered medium with N layers, where mechanical parameters λ^j(ω), μ^j(ω), and ρ_j are constants for every layer, as shown in Fig. 1. We consider the problem in the frequency domain assuming harmonically applied force with angular frequency ω. The equation of motion (1) for every layer in the frequency domain is given by:

$$\begin{array}{l}\frac{\partial {\sigma }_{rr}^j}{\partial r}+\frac{\partial {\sigma }_{rz}^j}{\partial z}+\frac{{\sigma }_{rr}^j-{\sigma }_{\theta \theta }^j}{r}+{\rho }_j{\omega }^2{u}_r^j=0,\\ \frac{\partial {\sigma }_{rz}^j}{\partial r}+\frac{\partial {\sigma }_{zz}^j}{\partial z}+\frac{{\sigma }_{rz}^j}{r}+{\rho }_j{\omega }^2{u}_z^j=0,\end{array}$$ (4)

where ${\sigma }_{mn}^j$ and ( $u_r^j$, 0, $u_z^j$) are the Fourier transforms of the components of stress tensor and displacement vector, respectively, and index j = 1…N refers to the number of the layer. Boundary conditions and conditions of continuity for displacement and stress on the layer boundaries z=h_j are:

$$\begin{array}{l}{\sigma }_{zz}^1(r,0,\omega )=-p(r,\omega ),{\sigma }_{rz}^1(r,0,\omega )=-q(r,\omega ),\\ {\sigma }_{zz}^j(r,h_j,\omega )={\sigma }_{zz}^{j+1}(r,h_j,\omega ),{\sigma }_{rz}^j(r,h_j,\omega )={\sigma }_{rz}^{j+1}(r,h_j,\omega ),\\ u_z^j(r,h_j,\omega )=u_z^{j+1}(r,h_j,\omega ),u_r^j(r,h_j,\omega )=u_r^{j+1}(r,h_j,\omega ),\\ u_z^N(r,H,\omega )=0,u_r^N(r,H,\omega )=0,j=1:N-1,\end{array}$$ (5)

where p(r, ω) and q(r, ω) are the Fourier transforms of the stress functions on the surface P(r, t) and Q(r, t). The relationship between stress ( ${\sigma }_{mn}^j$) and strain ( ${\epsilon }_{mn}^j$) spectral components for layer j has a form:

$${\sigma }_{mn}^j={\delta }_{mn}{\lambda }^j(\omega ){\gamma }^j+2{\mu }^j(\omega ){\epsilon }_{mn}^j;m,n=r,\theta ,z.$$ (6)

where γ^j is the divergence of the displacement vector in the frequency domain for layer j.

Fig. 1.

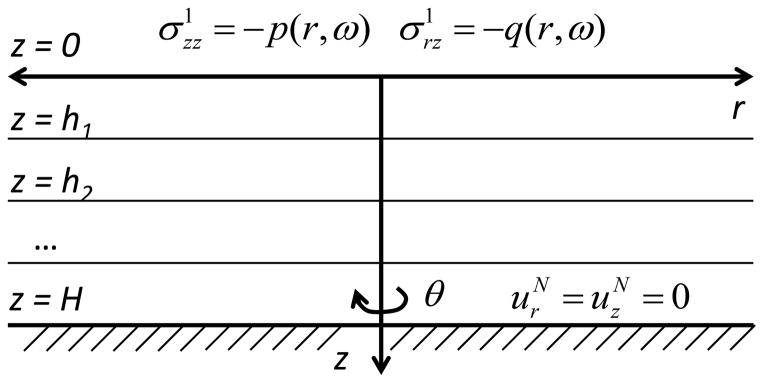
The multi-layered viscoelastic medium under the axisymmetric surface excitation.

This viscoelastic stress-strain relation, therefore, is exactly the same as for a purely elastic medium except that the Lame moduli are replaced by the complex moduli λ^j(ω) and μ^j(ω) (Christensen, 1971). These moduli are specified as functions of frequency for a particular viscoelastic material. For example, for Kelvin-Voigt solid ${\lambda }^j(\omega )={\lambda }_1^j+i\omega {\lambda }_2^j$ and ${\mu }^j(\omega )={\mu }_1^j+i\omega {\mu }_2^j$, where ${\lambda }_1^j$ and ${\lambda }_2^j$ are coefficients of volume compressibility and viscosity, respectively, while ${\mu }_1^j$ and ${\mu }_2^j$ are the coefficients of shear elasticity and viscosity. In the Maxwell solid ${\lambda }^j(\omega )={\lambda }_1^j{\lambda }_2^j\omega ({\lambda }_2^j\omega +i{\lambda }_1^j)/({\lambda }_1^{j2}+{\omega }^2{\lambda }_2^{j2})$ and ${\mu }^j(\omega )={\mu }_1^j{\mu }_2^j\omega ({\mu }_2^j\omega +i{\mu }_1^j)/({\mu }_1^{j2}+{\omega }^2{\mu }_2^{j2})$.

Applying the Helmholtz decomposition to the displacement vector $(u_r^j,0,u_z^j)=\nabla {\phi }_j+\nabla \times {\mathbf{\Psi }}_j$ and combining it with equations (4) result in two independent equations for the compressional φ_j and shear ψ_j wave potential functions:

$$\begin{array}{l}({\lambda }^j(\omega )+2{\mu }^j(\omega ))(\frac{{\partial }^2{\phi }_j}{\partial r^2}+\frac{1}{r}\frac{\partial {\phi }_j}{\partial r}+\frac{{\partial }^2{\phi }_j}{\partial z^2})+{\rho }_j{\omega }^2{\phi }_j=0,\\ {\mu }^j(\omega )(\frac{{\partial }^2{\psi }_j}{\partial r^2}+\frac{1}{r}\frac{\partial {\psi }_j}{\partial r}+\frac{{\partial }^2{\psi }_j}{\partial z^2})+{\rho }_j{\omega }^2{\psi }_j=0,\end{array}$$ (7)

where ∇× is the curl operator, ∇ is the gradient operator, and Ψ_j = (0, ∂ψ_j /∂r, 0). Using inverse Hankel transform we seek a solution of the equations (7) in the form:

$$\begin{array}{l}{\phi }_j=\underset{0}{\overset{\infty }{\int }}\alpha J_0(\alpha r)(A_1^j{e}^{-{\nu }_1^{j}z}+A_2^j{e}^{{\nu }_1^{j}z})d\alpha ,\\ {\psi }_j=\underset{0}{\overset{\infty }{\int }}\alpha J_0(\alpha r)(B_1^j{e}^{-{\nu }_2^{j}z}+B_2^j{e}^{{\nu }_2^{j}z})d\alpha ,\end{array}$$ (8)

where J₀ is the Bessel function of the order 0, and the coefficients A^j₁, A^j₂, B^j₁, B^j₂ are the functions of α and yet to be determined using the boundary conditions and the conditions of continuity for displacement and stress on the layer boundaries z=h_j (5). After combining the Helmholtz decomposition and (8) we find that the solution of the equations (4) for every layer in terms of the spectral components of displacements is given by

$$\begin{array}{l}{u}_z^j(r,z,\omega )=-\underset{0}{\overset{\infty }{\int }}\alpha J_0(\alpha r)[{\nu }_1^j(A_1^j{e}^{-{\nu }_1^{j}z}-A_2^j{e}^{{\nu }_1^{j}z})+{\alpha }^2(B_1^j{e}^{-{\nu }_2^{j}z}+B_2^j{e}^{{\nu }_2^{j}z})]d\alpha ,\\ u_r^j(r,z,\omega )=-\underset{0}{\overset{\infty }{\int }}{\alpha }^2{J}_1(\alpha r)[A_1^j{e}^{-{\nu }_1^{j}z}+A_2^j{e}^{{\nu }_1^{j}z}+{\nu }_2^j(B_1^j{e}^{-{\nu }_2^{j}z}-B_2^j{e}^{{\nu }_2^{j}z})]d\alpha ,\\ {\nu }_1^j=\sqrt{{\alpha }^2-{(k_1^j)}^2},{\nu }_2^j=\sqrt{{\alpha }^2-{(k_2^j)}^2},{(k_1^j)}^2={\rho }_j{\omega }^2/({\lambda }^j(\omega )+2{\mu }^j(\omega )),{(k_2^j)}^2={\rho }_j{\omega }^2/{\mu }^j(\omega ).\end{array}$$ (9)

The components of stress tensor (6) give

$$\begin{array}{l}{\sigma }_{zz}^j(r,z,\omega )={\mu }^j(\omega )\underset{0}{\overset{\infty }{\int }}\alpha J_0(\alpha r)[(2{\alpha }^2-{(k_2^j)}^2)(A_1^j{e}^{-{\nu }_1^{j}z}+A_2^j{e}^{{\nu }_1^{j}z})+2{\alpha }^2{\nu }_2^j(B_1^j{e}^{-{\nu }_2^{j}z}-B_2^j{e}^{{\nu }_2^{j}z})]d\alpha ,\\ {\sigma }_{rz}^j(r,z,\omega )={\mu }^j(\omega )\underset{0}{\overset{\infty }{\int }}{\alpha }^2{J}_1(\alpha r)[2{\nu }_1^j(A_1^j{e}^{-{\nu }_1^{j}z}-A_2^j{e}^{{\nu }_1^{j}z})+(2{\alpha }^2-{(k_2^j)}^2)(B_1^j{e}^{-{\nu }_2^{j}z}+B_2^j{e}^{{\nu }_2^{j}z})]d\alpha ,\end{array}$$ (10)

where J₁ is the Bessel function of the order 1.

Combining equations (5), (9) and (10) and using Hankel transform p̃(α, ω) and q̃(α, ω) of stresses on the top surface p(r, ω) and q(r, ω) :

$$\stackrel{\sim }{p}(\alpha ,\omega )=\underset{0}{\overset{\infty }{\int }}sp(s,\omega )J_0(s\alpha )ds,\stackrel{\sim }{q}(\alpha ,\omega )=\underset{0}{\overset{\infty }{\int }}sq(s,\omega )J_1(s\alpha )ds$$ (11)

give a system of 4xN linear equations for the coefficients A^j₁, A^j₂, B^j₁, B^j₂. After solving equations (5) spectral components of displacements can be calculated using equations (9). Note that if a half-space is considered, i.e. the thickness H is going to infinity, the boundary conditions (5) lead to the condition $A_2^N=B_2^N=0$ to limit displacements for large z. For single layer, when N=1, and only the boundary conditions should be satisfied explicit expression of these coefficient is:

$$\begin{array}{l}{A}_1^1=-\left\{\stackrel{\sim }{p}[g+{De}^{{\nu }_1^{1}H}(f_1{e}^{{\nu }_2^{1}H}-f_2{e}^{-{\nu }_2^{1}H})]+2\stackrel{\sim }{q}\alpha {\nu }_2^1[D-e^{{\nu }_1^{1}H}(f_1{e}^{{\nu }_2^{1}H}+f_2{e}^{-{\nu }_2^{1}H})]\right\}/M(\alpha )\\ A_2^1=-\left\{\stackrel{\sim }{p}[g+{De}^{-{\nu }_1^{1}H}(f_1{e}^{-{\nu }_2^{1}H}-f_2{e}^{{\nu }_2^{1}H})]-2\stackrel{\sim }{q}\alpha {\nu }_2^1[D-e^{-{\nu }_1^{1}H}(f_2{e}^{{\nu }_2^{1}H}+f_1{e}^{-{\nu }_2^{1}H})]\right\}/M(\alpha )\\ B_1^1=-\left\{2\stackrel{\sim }{p}{\nu }_1^1[D-e^{{\nu }_2^{1}H}(f_1{e}^{{\nu }_1^{1}H}+f_2{e}^{-{\nu }_1^{1}H})]-\stackrel{\sim }{q}[{De}^{{\nu }_2^{1}H}(f_2{e}^{-{\nu }_1^{1}H}-f_1{e}^{{\nu }_1^{1}H})-g]/\alpha \right\}/M(\alpha )\\ B_2^1=-\left\{2\stackrel{\sim }{p}{\nu }_1^1[-D+e^{-{\nu }_2^{1}H}(f_1{e}^{-{\nu }_1^{1}H}+f_2{e}^{{\nu }_1^{1}H})]-\stackrel{\sim }{q}[{De}^{-{\nu }_2^{1}H}(f_2{e}^{{\nu }_1^{1}H}-f_1{e}^{-{\nu }_1^{1}H})-g]/\alpha \right\}/M(\alpha ),\end{array}$$ (12)

where

$$\begin{array}{l}{f}_1={\alpha }^2-{\nu }_1^1{\nu }_2^1,f_2={\alpha }^2+{\nu }_1^1{\nu }_2^1,g=4{\alpha }^2{\nu }_1^1{\nu }_2^1,D=2{\alpha }^2-{(k_2^1)}^2,\\ M(\alpha )={\mu }^1(\omega )[4gD+(D^2-g)f_1(e^{({\nu }_1^1+{\nu }_2^1)H}+e^{-({\nu }_1^1+{\nu }_2^1)H})-(D^2+g)f_2(e^{({\nu }_1^1-{\nu }_2^1)H}+e^{({\nu }_2^1-{\nu }_1^1)H})].\end{array}$$

In the case of a half-space, when H → ∞ equations (12) transform to

$$A_1^1=\frac{-D\stackrel{\sim }{p}+2\alpha {\nu }_1^2\stackrel{\sim }{q}}{{\mu }^1(\omega )(D^2-g)},B_1^1=\frac{2\alpha {\nu }_1^1\stackrel{\sim }{p}-D\stackrel{\sim }{q}}{\alpha {\mu }^1(\omega )(D^2-g)},A_2^1=B_2^1=0.$$ (13)

For multi-layered medium and arbitrary N, solution of the 4xN system of linear equations (5), (9–11) can be solved for every α numerically to find the coefficients A^j₁, A^j₂, B^j₁, B^j₂ for each layer. To find the time-domain response of a viscoelastic layered medium to specified normal P(r, t) and shear Q(r, t) stresses, inverse Fourier transform should be applied to the displacements (9).

3. Modeling tissue dynamic response

To model a tissue dynamic response to acoustic radiation pulse we consider several additional assumptions for the model. Because most soft tissues are nearly incompressible, we consider an incompressible medium when λ(ω) is real and going to infinity, such that ${\nu }_1^j=\alpha$ in (9). We assume also that density is the same for all layers. To specify the stress-strain relationship, we consider the Kelvin-Voigt model, when ${\mu }^j(\omega )={\mu }_1^j+i\omega {\mu }_2^j$, where ${\mu }_1^j$ and ${\mu }_2^j$ are the coefficients of shear elasticity and viscosity, respectively. In incompressible medium Young’s modulus E_j, is three times its shear modulus, ${\mu }_1^j$, i.e., $E_j=3{\mu }_1^j$ for each layer. It has been demonstrated that this model adequately describes tissue and tissue-mimicking phantom behavior under short acoustic radiation force (Aglyamov et al., 2007, Urban and Nenadic, 2011, Yoon et al., 2012, Yoon et al., 2013, Yoon et al., 2011). We assume that shear stress applied on the tissue surface is zero, i.e. Q(r, t)=0, and the acoustic radiation force generates only normal stress during short pulse of duration t₀:

$$P(r,t)=\{\begin{array}{ll}{P}_0(r),\hfill & 0\le t\le t_0\hfill \\ 0,\hfill & t>0\hfill \end{array}$$ (14)

where P₀(r) is the amplitude of the acoustic pressure, as a function of space. Note here, that we consider P₀(r) as the time-averaged pressure, assuming that the pulse duration t₀ is much larger than the period of acoustic wave. The Fourier transform of this function is:

$$p(r,\omega )=-\frac{{iP}_0(r)}{\omega }(e^{i\omega t_0}-1).$$ (15)

If a constant harmonic pressure p₀ is applied in the area of the radius R on the surface of the medium, and no pressure applied for r > R, i.e.:

$$P_0(r)={\overline{P}}_0(R,p_0,r)=\{\begin{array}{ll}{p}_0,\hfill & r\le R\hfill \\ 0,\hfill & r>R\hfill \end{array},$$ (16)

The Hankel transforms of P₀(r) has a form (Abramowitz and Stegun, 1972):

$${\stackrel{\sim }{P}}_0(\alpha )=\frac{p_{0}R}{\alpha }{J}_1(\alpha R).$$ (17)

In our experimental studies axial displacements were measured on the surface of tissue-mimicking phantom. For the points on the surface z = 0, expression for axial displacement in frequency domain is:

$$u_z^1(r,0,\omega )=-\underset{0}{\overset{\infty }{\int }}{\alpha }^2{J}_0(\alpha r)[A_1^1-A_2^1+\alpha (B_1^1+B_2^1)]d\alpha =\underset{0}{\overset{\infty }{\int }}F(\alpha )d\alpha$$ (18)

where unknown constants were found using representations (15–16) after solving 4xN linear equations (5). This integral was numerically evaluated and axial displacements in time domain for z = 0 were obtained after inverse Fourier transform.

Since the problem is a linear one, arbitrary space distribution of the pressure on the upper surface P₀(r) can be approximated by a set of functions (16) with different radii R and amplitudes p₀, assuming that the pressure is zero for large r. If P₀(r) is approximated by a sum of L functions ${\overline{P}}_0(R^{\beta },p_0^{\beta },r)$:

$$P_0(r)\approx \sum _{\beta =1}^L{\overline{P}}_0(R^{\beta },p_0^{\beta },r),\beta =\mathrm{1..}L,$$ (19)

the solution ${\overline{u}}_z^j(r,z,\omega )$ for that pressure distribution can be approximated by a sum of solutions $u_z^j(R^{\beta },p_0^{\beta },r,z)$ obtained for the radius R^β of and amplitude $p_0^{\beta }$ of the pressure:

$${\overline{u}}_z^j(r,z,\omega )\approx \sum _{\beta =1}^L{u}_z^j(R^{\beta },p_0^{\beta },r,z,\omega ),\beta =\mathrm{1..}L.$$ (20)

In the calculations, double-weep method was used to solve 4xN system of linear equations (5) for the constants A^j₁, A^j₂, B^j₁, B^j₂. For numerical integration of (18), the integral was presented as a sum of two integrals:

$$u_z^1(r,0,\omega )=\underset{0}{\overset{{\alpha }_1}{\int }}F(\alpha )d\alpha +\underset{{\alpha }_1}{\overset{\infty }{\int }}F(\alpha )d\alpha =F_1+F_{\infty }$$ (21)

Simpson’s rule was used for the numerical approximation of the integral F₁. To evaluate integral F_∞, an approximation for half-space (13) was used, where the mechanical parameters of the top layer were substituted in (13). Taking into account the asymptotic forms of the Bessel functions for large argument $J_0(\xi )\approx \sqrt{2/\pi \xi }cos(\xi -\pi /4)$ and $J_1(\xi )\approx \sqrt{2/\pi \xi }cos(\xi -3\pi /4)$ (Abramowitz and Stegun, 1972), the approximation of the integral F_∞ has a form:

$$\begin{array}{l}{F}_{\infty }\approx \sqrt{\frac{R}{r}}\frac{p_0}{\pi {\mu }^1(\omega )}\underset{{\alpha }_1}{\overset{\infty }{\int }}\frac{sin\alpha (R-r)-cos\alpha (R+r)}{2{\alpha }^2}d\alpha ,\text{for}r\ne 0,\\ F_{\infty }\approx \sqrt{\frac{R}{\pi }}\frac{p_0}{{\mu }^1(\omega )}\underset{{\alpha }_1}{\overset{\infty }{\int }}\frac{sin\alpha R-cos\alpha R}{2{\alpha }^{3/2}}d\alpha ,\text{for}r=0.\end{array}$$ (22)

The integral (22) can be integrated explicitly (Abramowitz and Stegun, 1972). The choice of the parameter α₁ is based on the closeness of the integrands in (18) and (22), and depends on the specific geometry and frequency.

III. EXPERIMENTAL SET-UP

To verify our theoretical model, the experiments were performed using two homogeneous and two two-layered gelatin-based phantoms with a different concentration of the gelatin in each layer. During phantom preparation, the same gelatin solution was used to prepare test samples. These samples were used to independently measure elastic properties of the phantom material. Both phantoms and samples were constructed at the same time and underwent the same procedures to minimize any possible differences in elastic properties. Young’s moduli of the samples were obtained by direct uniaxial load-displacement measurements using an In-Spec 2200 benchtop portable tester (Instron, Inc., Norwood, MA). Uniaxial tests were performed before and after acoustic radiation force experiments (about 2 hours interval) and no significant changes in the elastic properties with time were found. Two homogeneous phantoms with 6% and 18% gelatin concentrations had Young’s moduli of E = 8 kPa and E = 48 kPa, respectively. The layered phantoms had a top layer made of 6% gelatin concentration (E₁ = 8 kPa) and bottom layer made of 18% gelatin concentration (E₂ = 48 kPa). The thicknesses of the top layers were 5 and 2 mm for the first and the second phantoms, respectively. The overall thickness was 16 mm for all phantoms. No additional ultrasound scatterers were added in the gelation solution.

The integration of acoustic stimulation and the phase-sensitive OCT (PhS-OCT) system for simultaneous excitation and measurement of local displacements is schematically shown in Fig. 2. The spectral-domain OCT system used a superluminescent diode (Superlum Diodes, Ltd., Ireland) as the laser source, which provides a central wavelength of 840 nm and a bandwidth of about 100 nm. A Michelson interferometer was used as an interference comparator between the sample and the reference arms. The fringes of interference were spatially resolved through a high resolution spectrometer with a CCD line scan camera (Basler, Inc., Germany). The line scan rate of the CCD was set as 25 kHz, which represented the A-line acquisition speed of the OCT system. The full width at half maximum of the laser beam at the imaging focal plane was approximately 8 μm. The measured phase stability of the system was about 5 milliradians at maximal SNR from a mirror and about 0.11 radians at SNR of 30 dB from the phantom.

Fig. 2.

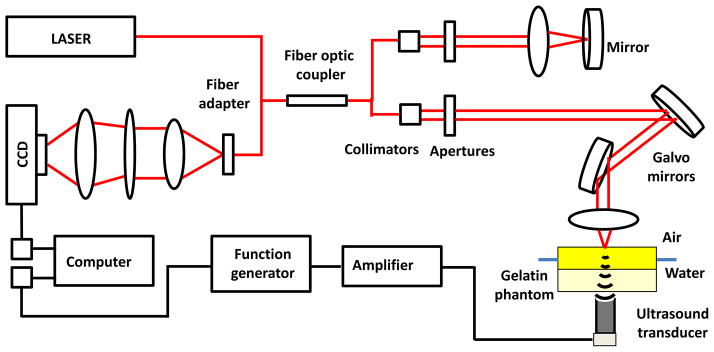
Schematic of the experimental setup which combines the single-element focused ultrasound transducer and the phase-sensitive OCT system.

A 3.5 MHz single-element focused ultrasound transducer (ValpeyFisher Corp., Hopkinton, MA) was attached to the bottom of a water-filled tank to generate acoustic radiation force on the upper surface of tissue-mimicking phantom (Fig. 2). The upper surface of the phantom was placed above the water level. The transducer had a diameter of 13 mm and a focal length of 19 mm. The function generator was used to provide gated 3.7 MHz sinusoidal signal applied through a 55 dB power amplifier (A150, ENI, Rochester, NY) to the transducer. The duration of acoustic radiation force pulse was varied from 54 μs to 13 ms. Prior to the experiment, the foci of both the ultrasound transducer and the OCT system were aligned. In the experiments the pre-amplified voltage was varied from 5 mV to 20 mV to control the amplitude of displacement and avoid the artifacts of phase wrapping which accompany OCT measurements of relatively large and fast displacements.

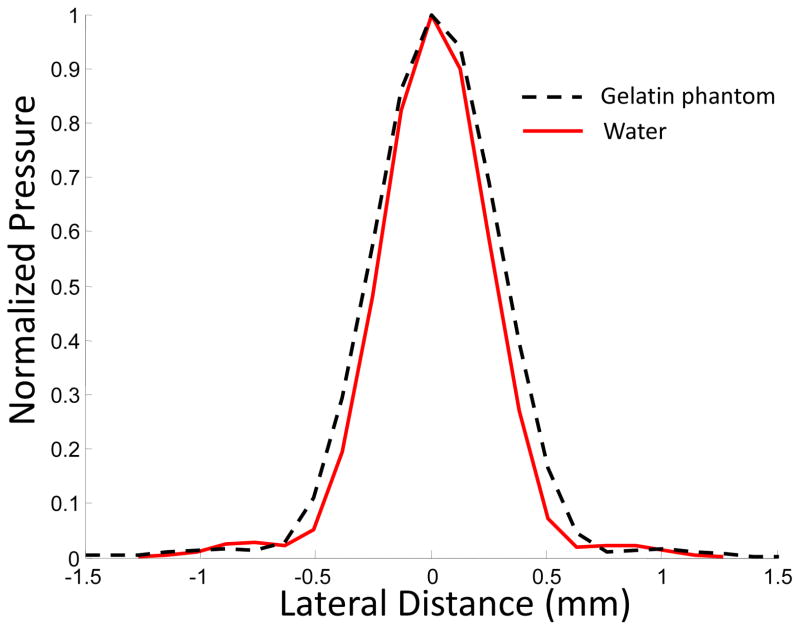
The ultrasound field in the focal point of the transducer was measured using a needle hydrophone with a sensor diameter of 0.2 mm (Precision Acoustics Ltd, Dorchester, UK). For the pre-amplified voltage signal of 100 mV, the peak positive and negative pressures at the focal point were 12 and 8 MPa, respectively. The corresponding spatial peak pulse average (SPPA) intensity was 2600 W/cm². The normalized distributions of the time-averaged pressure in the focal zone of the transducer in water and in a phantom are shown in Fig. 3. As seen in Fig. 3, in a gelatin-based phantom, the focal size is slightly increased.

Fig. 3.

Normalized pressure distribution in the focal zone of a 3.5 MHz transducer in water and gelatin-based phantom.

IV. RESULTS AND DISSCUSSION

1. Model calculations

To illustrate the influence of the depth dependence of the elasticity distribution in the medium, calculations were performed for homogeneous and inhomogeneous media. In these calculations, the medium was assumed to be incompressible, while the overall thickness of the layer H = 10 mm, density ρ_j = 1000 kg/m³, and shear viscosity coefficients ${\mu }_2^j=0.1$ Pa s and ${\mu }_2^j=1.0$ Pa s were used. The pressure distribution on the top surface was defined by equations (16–17), where the radius of the ultrasound beam R = 0.5 mm, and the pressure amplitude p₀=100 Pa were selected. The integral in (18) was calculated numerically to find the spectral component of axial displacement $u_z^1(r,0)$ on the surface of the medium. Using the fast Fourier transform, the axial displacement in the time domain was found.

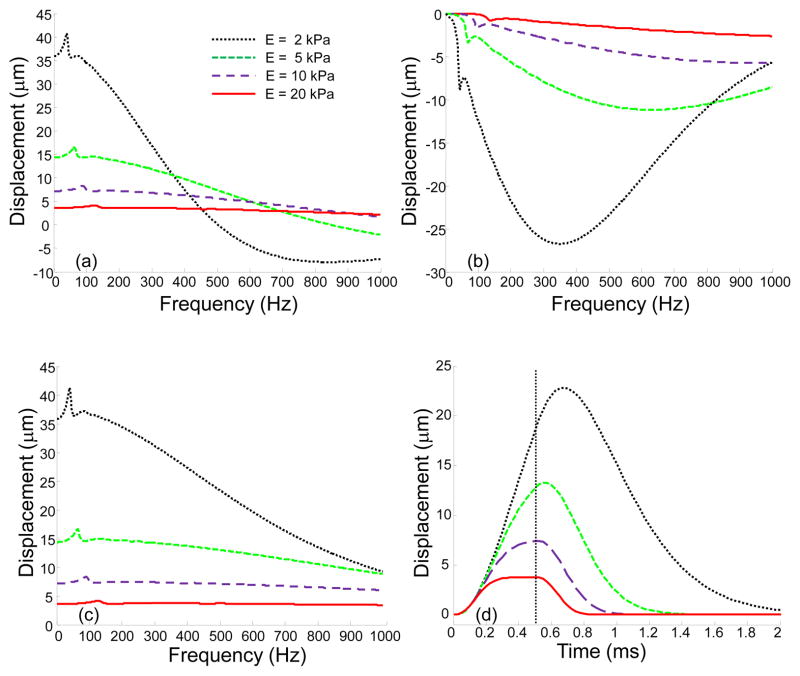
Figure 4 presents the displacements in frequency and time domains for homogeneous viscoelastic layers of different elasticity. Figures 4(a) and (b) shows real and imaginary parts of the axial displacements, respectively, as functions of frequency for different values of Young’s modulus. Real and imaginary parts represent the vibration in-phase and out-of-phase with the external force. For low frequencies, the vibrations are mostly in-phase with the external force and the imaginary part of the displacement is close to zero. When frequency increases, the impact of viscosity also increases, and the phase shift between the external load and the displacement appears. Zero frequency corresponds to a static load when there is no influence of viscosity. As shown in Fig. 4(c), the absolute value of the displacement decreases with frequency, however this decay is more pronounced for soft materials. The increase in elastic modulus results in two effects: a decay in the displacement amplitude and a shift of the resonance frequency to the high frequency region. Figure 4(d) demonstrates the influence of elasticity in the time domain, when the duration of the external force t₀ =0.5 ms (see Eq. (14)). In the stiffer media, the magnitude of the displacement as well as the time necessary to reach the maximum displacement decrease. In addition, in the stiff medium, the displacement reaches a state of equilibrium, where external force is compensated by the elastic response of the medium, much faster than in the soft medium. The magnitude of the displacement in the equilibrium position corresponds to the static case, i.e. zero frequency. For example, for E = 20 kPa, the maximum displacement in Fig. 4(d) corresponds to the real part and the absolute value of the displacement at zero frequency in Figs. 4(a) and (c). These results are in agreement with our previous studies for a homogeneous medium, where acoustic radiation force was used to move hard spheres and laser-induced microbubbles in a viscoelastic medium (Aglyamov et al., 2007, Karpiouk et al., 2009, Yoon et al., 2012, Yoon et al., 2013, Yoon et al., 2011).

Fig. 4.

(a) Real part; (b) imaginary part; and (c) absolute value of the axial displacements $u_z^1(0,0)$ on the surface of viscoelastic layer for different values of Young’s modulus (2 kPa, 5 kPa, 10 kPa, and 20 kPa) in the frequency domain; (d) axial displacement in the time domain for 0.5 ms pulse of the acoustic force. A dash vertical line represents the end of the acoustic pulse.

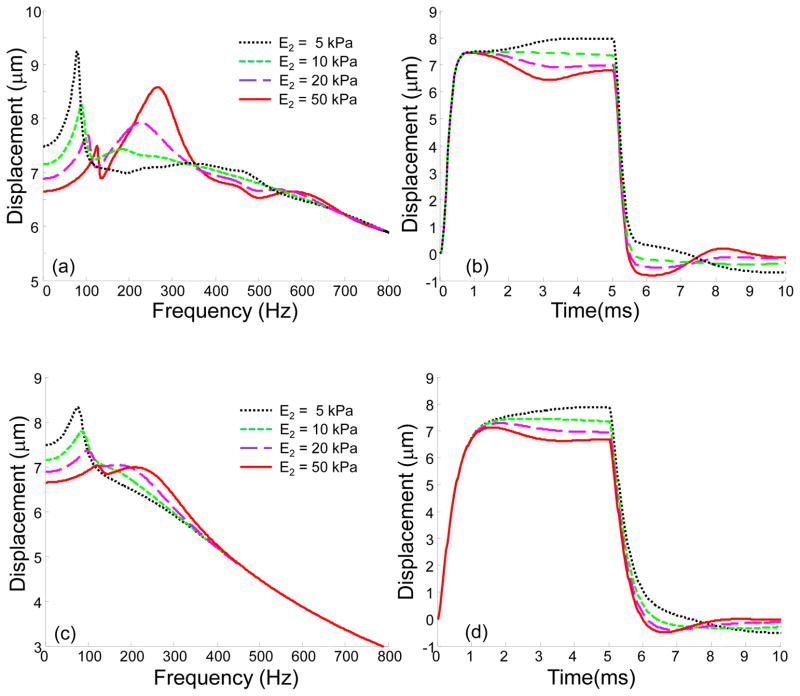
To investigate the role of different layers in the tissue response to an acoustic pulse, a simulation of a three-layered medium was performed, where the stiffness of the second layer was varied, while the stiffness of the first and third layers was kept the same (E₁ = E₃ = 10 kPa). Shear viscosity was constant for all layers. To investigate the influence of viscosity, two different values of shear viscosity was considered: ${\mu }_2^j=0.1$ Pa s and ${\mu }_2^j=1.0$ Pa s. The 3 mm thick layer was placed at a depth of 3 mm (h₁ =3 mm, h₂ =6 mm) and the total thickness was H = 10 mm. Note here that h₁ and h₂ are boundary positions and the thickness of the second layer is h₂-h₁ = 3 mm. Figure 5 presents the results of this simulation in the frequency and time domains, where Young’s modulus of the second layer was varied from 5 kPa to 50 kPa. As shown in Figure 5(a, c), a stiffer second layer results in a shift of the spectrum to the high frequency region and the appearance of additional resonance frequencies. However, the differences in spectral components disappear with an increase in frequency, where the upper layer is mostly responsible for the tissue reaction. Figure 5(b, d) presents displacement profiles in the time domain for t₀ = 5 ms. As seen in Figure 5(c) high viscosity leads to drop of the displacement amplitude, especially for the high frequency components. As a result, high frequency components become less sensitive to the deep layers.

Fig. 5.

(a), (c) Absolute value of the axial displacements in frequency domain and (b), (d) displacements in the time domain for a three-layered medium, where Young’s modulus of the second layer (E₂) is varied from 5 kPa to 50 kPa. Shear viscosity is (a–b) 0.1 Pa s ( ${\mu }_2^1={\mu }_2^2={\mu }_2^3=0.1$ Pa s); and (c–d) 1 Pa s ( ${\mu }_2^1={\mu }_2^2={\mu }_2^3=1.0$ Pa s) for all layers. Other parameters are: E₁ = E₃ = 10 kPa, h₁ = 3 mm, h₂ = 6 mm, H = 10 mm. The case E₂ =10 kPa corresponds to a homogeneous medium. In the time domain solution the time of excitation is 5 ms.

After that, the Young’s modulus of the second layer was fixed (E₂ = 50 kPa). This stiff layer was placed at the different depths h₁ from 1 to 6 mm, while other parameters were the same, including the thickness of the second layer (3 mm), as in the previous case. The results of this simulation are shown in Fig. 6. High-frequency vibrations are mostly sensitive to the upper layers, and there is no significant difference in the frequency response for frequencies higher than 1500 Hz. Conversely, the low-frequency vibrations depend on both deep and superficial layers. As shown in Fig. 6(a) the resonance frequency is shifted from 135 Hz to 750 Hz when the depth of occurrence of the stiff layer decreases from 6 mm to 1 mm. Therefore, while in the low frequency region the displacement amplitude for h₁=6 mm is higher than that of h₁ = 1 mm, in the high frequency region it could be the reverse. The change in the frequency response is also seen in Fig. 6(b), where displacements in the time domain are shown.

Fig. 6.

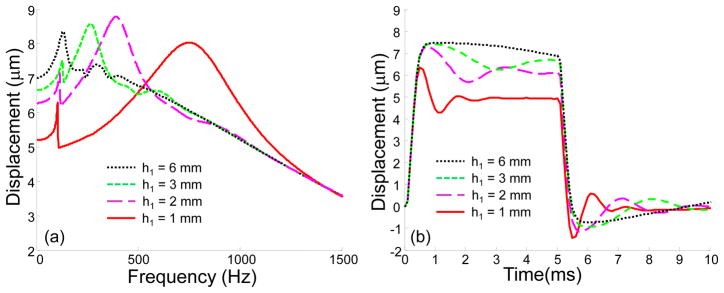
(a) Absolute value of the axial displacements in the frequency domain and (b) displacements in the time domain for a three-layered medium, where stiff second layer (E₂=50 kPa) is placed at different depths h₁ in the medium. Shear viscosity is 0.1 Pa s for all layers. Other parameters are the same as in Fig. 5.

Figure 7 shows the surface wave propagation for a homogeneous and inhomogeneous three-layered medium. The parameters and geometry of the model are the same as in Fig. 6 for h₁ = 1 mm. As seen in Fig. 7, the presence of the stiff layer results in decreasing the amplitude and increasing the speed of the surface wave propagation, due to an increase of overall stiffness. In addition, there is also a change in frequency content, i.e. the shift to the high frequency region, similar to the displacements at the focal point.

Fig. 7.

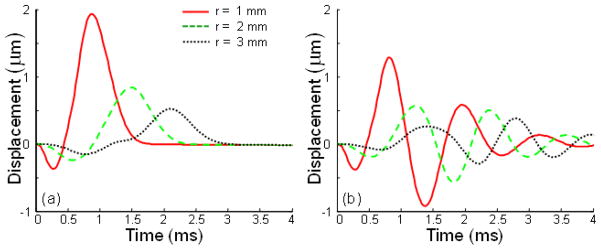
Surface axial displacements in the time domain for different radial positions in (a) a homogeneous medium (E₂ = 10 kPa) and (b) a medium with a hard layer (E₂ = 50 kPa) placed at a depth of h₁ = 1 mm. Shear viscosity is 0.1 Pa s. The time of excitation is 0.5 ms for both cases.

2. Comparison of the model predictions with experimental data

The results of the developed model were compared with the experimental results obtained in phantom studies. Because the acoustic radiation pressure on the surface of the gelatin-based phantoms is difficult to estimate, the spatial distribution was taken from the phantom calibration experiments (see Fig. 3). To approximate this distribution, Eqs. (19–20) were used with L= 6. The amplitude of radiation pressure was obtained by fitting the experimental data to theoretical predictions, and used in theoretical calculation to compare with experimental data. Note here that the purpose of such consideration is comparison of the frequency and time characteristics of the surface vibrations, but not the amplitudes of the displacements, which linearly depend on the pressure magnitude. Because shear viscosity was not measured independently in the experiment, it was fixed as 0.2 Pa·s for all layers. In accordance with theoretical analysis, the influence of shear viscosity in this range is not significant and the behavior of the medium is largely defined by elasticity. The density was assumed to be 1000 kg/m³.

At first, the results of theoretical modeling were compared with the results of the experiments on the homogeneous phantoms. Figure 8(a) shows the displacements at the focal point of the ultrasound transducer on the surface of two homogeneous phantoms with Young’s moduli of 8 kPa and 48 kPa for a short acoustic pulse of 0.054 ms. Similar to our model calculations (see Fig. 4(d)), in the stiffer phantom, the magnitude of the displacement as well as the time of maximum decrease, and the experimental displacements are in good agreement with the results of the theoretical predictions shown in Fig. 8(b), where the maximum pressure P_max = 51 Pa was assumed for both phantoms.

Fig. 8.

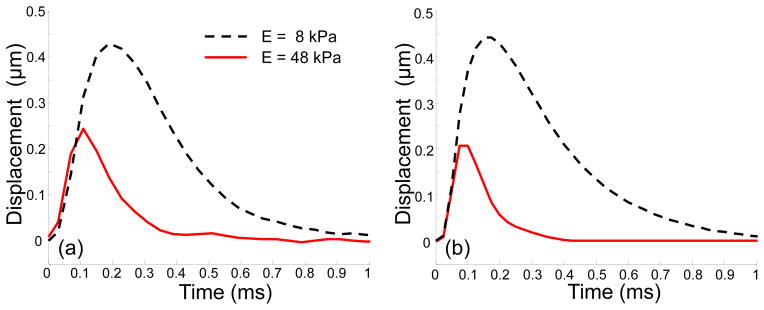
(a) Experimentally measured and (b) theoretically predicted displacements on the surface of homogenous soft (E=8 kPa) and hard (E=48 kPa) media at the point of excitation. Durations of the acoustic pulse t₀ = 0.054 ms. In calculations P_max = 51 Pa for both phantoms.

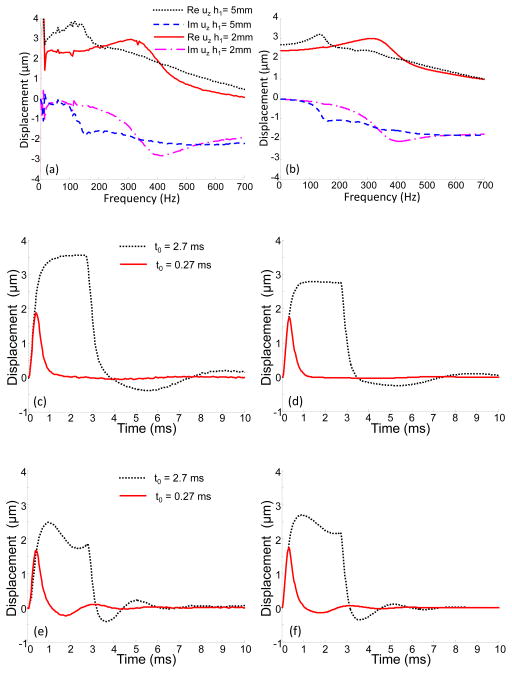
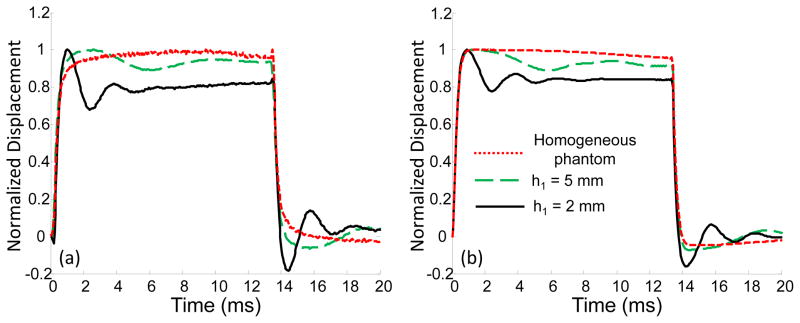
The comparison of experimental results and model predictions for two inhomogeneous phantoms in the frequency and time domains is shown in Fig. 9. The only difference between these phantoms is the thickness of the top layer (h₁ = 5 mm and h₁ = 2 mm). As shown in Fig. 9(a), in the case of the thinner layer, the dominant frequency is shifted into the high frequency zone, as expected based on the theoretical calculations (Fig. 9(b)), reflecting an increase in the average elasticity of the sample. Overall, there is good agreement between theory and experiment both in the frequency and time domains. Note here that in Fig. 9(b),(c), and (d) we assumed the same acoustic pressure for both samples, P_max = 43 Pa.

Fig. 9.

(a) Experimentally measured and (b) theoretically predicted spectral components of the displacements on the surface of the two-layered medium (E₁ = 8 kPa, E₂ = 48 kPa) at the point of excitation (r=0) with different thicknesses of the top soft layer (h₁ = 5 mm, and h₁ = 2 mm). (c), (e) Experimentally measured and (d), (f) theoretically predicted displacements in the time domain for the first (h₁ = 5mm) and the second (h₁ = 2 mm) phantoms, respectively, when two different durations of the acoustic pulse were used (0.27 ms and 2.7 ms). In calculations P_max = 43 Pa for both phantoms.

Figure 10 shows the experimental and theoretical displacements as functions of time for a long acoustic pulse (t₀ = 13.3ms). Displacements were normalized to avoid the influence of the variations in the amplitude of the radiation force for different samples. The homogeneous sample had the same elasticity as the top layer of inhomogeneous phantoms (E₁=8 kPa). As seen in Fig. 10, inhomogeneity brings additional vibrations to the displacement profile, while the homogeneous sample demonstrates no significant vibrations for both experimental and theoretical curves.

Fig. 10.

(a) Experimentally measured and (b) theoretically predicted displacements on the surface of the two-layered media (E₁ = 8 kPa, E₂ = 48 kPa) for the time of excitation t₀ = 13.3 ms and different thicknesses of the top layer h₁. The displacements were normalized to avoid the influence of variation in the magnitude of the acoustic radiation force. The homogeneous sample had the same elasticity as the top layer of inhomogeneous phantoms (E₁ = 8 kPa).

As shown in Figs. 8–10, the results of the model calculations are in good agreement with the experimental data. Still, some disagreements could result from the experimental conditions and the limitations of the model. It is difficult to control the amplitude of the acoustic radiation pressure on the phantom surface, because even small changes in the experimental conditions lead to significant changes in the force amplitude, and we cannot guarantee that the pressure amplitude was the same for different phantoms even if the same parameters of acoustic excitation were used. In Figs 8 and 9 we assumed the same pressure when we compared the phantoms in pairs, but as seen in Fig. 9 the pressure was likely higher for the first phantom with the top layer thickness of 5 mm. Even in the high frequency region the displacement for this phantom is higher than for another phantom (see Fig. 9(a)).

In the model, no volumetric forces were considered. However, a high intensity ultrasound field could produce additional radiation force comparable with the force generated at the phantom-air boundary, despite the fact that no scatterers were added to the tissue-mimicking phantoms. This effect could be more pronounced for biological tissues. Additional analysis of the radiation force distribution close to the surface of the medium is required. Because no viscosity measurements were performed, and shear viscosity was fixed as 0.2 Pa s for all phantoms, the error in viscosity estimation could result in additional disagreement between simulation and experiment. Also, the motion of the phantom as a whole object was not taken into account. In the experiment, the bottom part of the phantom was not fixed, contrary to the model. We assume that this difference in boundary conditions did not affect our results because of the significant thickness of the phantoms (16 mm). For thin samples, however, boundary conditions on the bottom are more important and should be considered accurately. We don’t expect any significant changes in the elasticity of the phantoms during experiment (about 2 hours), based on the results of the uniaxial tests of gelatin samples performed before and after experiment.

The results of the simulations and the experiments show that while low-frequency vibrations on the surface are sensitive to deep layers of the medium, high-frequency components attenuate rapidly with depth and only the upper layers are involved in the high-frequency response of the medium. Such results are in agreement with the experimental data obtained for surface wave propagation by the other groups (Li et al., 2012b, Li et al., 2014). Therefore, the depth-dependence of the mechanical parameters could be potentially resolved by relying on the spectral analysis concept. Such an approach can be based on the analysis of the frequency and time characteristics of tissue motion rather than on the vibration amplitudes, similar to our approach in the bubble-based acoustic radiation force method (Aglyamov et al., 2012, Yoon et al., 2012, Yoon et al., 2013).

In this work we used the experimental design when ultrasound stimulation and OCT beam were placed in opposite sides. Such design was selected to avoid problems associated with water coupling and to maximize the energy on the surface of the phantom. However, for imaging tissues in situ both ultrasound stimulation and OCT beam are preferable to be on the same side. Such design was incorporated in our recent work to assess the age-related changes in the biomechanical properties of the crystalline lens in situ (Wu et al., 2015).

V. CONCLUSIONS

In this work we proposed a model of a layered viscoelastic medium excited by acoustic radiation force on its surface. The motion at the focal point of the ultrasound beam and surface wave propagation were considered. A significant difference in frequency content for different distributions of the depth-dependent elastic properties was demonstrated. Specifically, low frequency components are more sensitive to the deep layers than high frequencies. The model was tested in phantom studies using a combined ultrasound/OCT system. The results demonstrated good agreement between theoretical calculations and experimental data. The proposed approach has the potential to become a method of elasticity reconstruction based on the measurements on the tissue surface.

Table 1.

Phantoms used in the experimental studies.

	Homogeneous Soft Phantom	Homogeneous Hard Phantom	Two-layered Phantom 1		Two-layered Phantom 2
Gelatin Concentration			Top Layer	Bottom Layer	Top Layer	Bottom Layer
	6%	18%	6%	18%	6%	18%
Young’s modulus	8 kPa	48 kPa	8 kPa	48 kPa	8 kPa	48 kPa
Thickness	16 mm	16 mm	5 mm	11 mm	2 mm	14 mm