Agreement among graders on Heidelberg retina tomograph (HRT) topographic change analysis (TCA) glaucoma progression interpretation

Abstract

Purpose

To evaluate agreement among experts of Heidelberg retina tomography’s (HRT) topographic change analysis (TCA) printout interpretations of glaucoma progression and explore methods for improving agreement.

Methods

109 eyes of glaucoma, glaucoma suspect and healthy subjects with ≥5 visits and 2 good quality HRT scans acquired at each visit were enrolled. TCA printouts were graded as progression or non-progression. Each grader was presented with 2 sets of tests: a randomly selected single test from each visit and both tests from each visit. Furthermore, the TCA printouts were classified with grader’s individual criteria and with predefined criteria (reproducible changes within the optic nerve head, disregarding changes along blood vessels or at steep rim locations and signs of image distortion). Agreement among graders was modelled using common latent factor measurement error structural equation models for ordinal data.

Results

Assessment of two scans per visit without using the predefined criteria reduced overall agreement, as indicated by a reduction in the slope, reflecting the correlation with the common factor, for all graders with no effect on reducing the range of the intercepts between the graders. Using the predefined criteria improved grader agreement, as indicated by the narrower range of intercepts among the graders compared with assessment using individual grader’s criteria.

Conclusions

A simple set of predefined common criteria improves agreement between graders in assessing TCA progression. The inclusion of additional scans from each visit does not improve the agreement. We, therefore, recommend setting standardised criteria for TCA progression evaluation.

Glaucoma is a progressive optic neuropathy disease characterised by progressive loss of retinal ganglion cells with associated visual field (VF) loss. Accurate and sensitive methods to detect disease progression are essential to monitor patients and to evaluate the efficacy of therapy.

Confocal scanning laser ophthalmoscopy (CSLO, Heidelberg retina tomograph (HRT); Heidelberg Engineering, Heidelberg, Germany) has been shown to allow quantification of the optic disc topography, ^1–8 along with topographic changes over time (topographic change analysis (TCA)).⁹ TCA marks changes that exceed the intervisit variability, defined as the variability among baseline visits. A major limitation of the TCA method is the lack of widely accepted progression criteria. We hypothesise that the agreement among clinicians in the interpretation of the TCA report can be improved by evaluating multiple tests obtained in the same visit and by using standardised predefined common criteria compared with the use of individual grader criteria. Observing changes that appear consistently in the same visit might enhance the confidence of the grader in evaluating changes. Similarly, having a common set of criteria for defining progression that all graders obey is expected to improve agreement between the graders. The purpose of this study was to investigate methods to improve intragrader and intergrader agreement in detecting TCA-defined glaucoma progression.

METHODS

Healthy, glaucoma suspects (GS) and glaucoma subjects from the Pittsburgh Imaging Technology Trial (PITT) were selected for this observational longitudinal study. The PITT study is a prospective longitudinal study designed to assess ocular structure longitudinally carried out at the University of Pittsburgh Medical Center Eye Center. The study was approved by the institutional review board and ethics committee, and informed consent was obtained from all subjects. This study followed the tenets of the Declaration of Helsinki and was conducted in compliance with the Health Insurance Portability and Accountability Act.

All participants underwent a complete baseline ophthalmic examination, which included a full medical history, intraocular pressure (IOP) measurements, undilated and dilated biomicroscopy, VF testing and CSLO scans. Both eyes from each subject were included if they were eligible.

Subjects were excluded from the study if they had history of diabetes mellitus or posterior pole pathology other than glaucoma. Additionally, subjects were excluded for use of systemic steroids, any other systemic medications known to affect the retina and neurological conditions known to affect the VF.

Subjects included in this study had a best-corrected visual acuity of 20/60 or better and a refractive error of +6.00 to −6.00 dioptres with cylinder of <+3.00 dioptres. All subjects had at least 2 years of follow-up, with >5 visits that included reliable VF tests and two good quality CSLO scans at each visit.

Healthy eyes had full VFs, IOP between 8 and 21 mm Hg and normal appearing optic nerve head (ONH). GS had IOP≥22 mm Hg, asymmetrical cupping (>0.2 difference in cup to disc ratio (CDR) between eyes), large cupping (>0.6 CDR) or were the fellow eye of a glaucomatous eye, all in the presence of full VF. Glaucomatous eyes had reproducible and characteristic VF defect (see below) in at least 2 consecutive visits with any of the structural changes present in the GS criteria.

VFs were assessed by a Humphrey field analyser (Zeiss, Dublin, California, USA) using the Swedish interactive threshold algorithm 24-2 standard program. VFs were considered reliable if fixation losses, false positives or false negatives were <30%. Glaucomatous VFs were defined as three adjacent depressed points on the pattern deviation plot at p<5%. None of the points could be edge points unless they were located immediately above or below the nasal horizontal meridian.

CSLO

Only high-quality CSLO images (HRT 3; software V.1.5.10.0) with pixel SDs <50 qualified for the study. Progression analysis was performed using the TCA method, which has been previously described.⁹ Briefly, the expected level of variability for each superpixel for each subject is defined from the baseline visits. If the change exceeds the subject-defined variability, the superpixel is marked. Probability symbols (red and green marks) indicate locations with statistically significant change.

TCA evaluation

For each subject, two sets of HRT scans were used: set (A) one image randomly chosen from each visit to be used in the TCA; set (B) both images from each visit included in the TCA. The TCA printouts were downloaded into a customised viewing program.

Three glaucoma experts independently examined the two sets, which were randomly ordered, to determine the presence of glaucoma progression using their own individual criteria. A week later, the experts re-evaluated the two sets of printouts using the following common criteria of progression:

• Reproducible clusters of red spots.

• Red clusters must be within the ONH margin.¹⁰

• Red spots located along blood vessels should be ignored.^11,12

• Red spots occurring on steep slopes along the optic rim edge should be judged with caution as the reliability of the surface detection of the device is low at these locations (figure 1, left).¹¹

• Alternating clusters of red and green areas that do not correspond to any anatomical feature and, therefore, are typically artefacts and should not be considered progression (figure 1, right).

Figure 1.

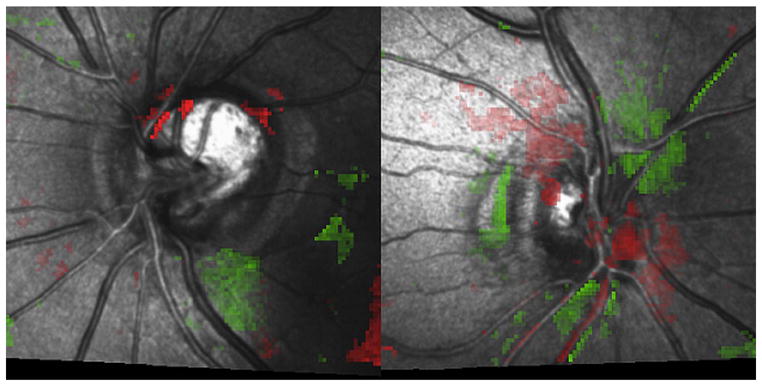
Criteria for assessing topographic change analysis (TCA) report. (Left) A TCA report with red spots occurring on steep slopes along the optic rim and along or immediately adjacent to blood vessels. These were judged with caution because the reliability of the surface detection of the device is low at these locations. (Right) Alternating clusters of red and green areas, which are typically artefacts.

Statistical analysis

Two separate models were fitted to assess TCA progression detection for each grader: (1) one scan versus two sets of scans per visit while using each individual grader’s criteria, and (2) one scan per visit evaluated with each individual grader’s criteria versus the use of common criteria.

Agreement is evaluated by assuming a latent common progression factor (μ) that is on a continuous scale, as illustrated in the simplified path diagram (figure 2). Because ratings on both eyes were used, the model accounts for the correlation (ρ) between the latent progression of each eye. The model for agreement includes a slope parameter (β) that measures the correlation between the common factor (μ) and each unobserved (latent) continuous rating (χ), while simultaneously describing the variance of the random error (imprecision) as 1–β². In this model, a steeper slope (higher correlation) simultaneously indicates better precision (repeatability) and higher correlation between true progression (μ) and the grader’s only indirectly observed continuous judgement (χ). An intercept α is used to convert the unobserved χ into the dichotomous categories of non-progressor (below the intercept) and progressor (above the threshold). The lower the threshold, the higher the probability the grader will assign the status of progression. Finally, differences in βs indicate that graders differ in terms of precision while differences in αs indicate graders tend to disagree as to the boundary between non-progressor and progressor. Graders with markedly different α are using different criteria for making judgements. β values closest to one are representing higher repeatability.

Figure 2.

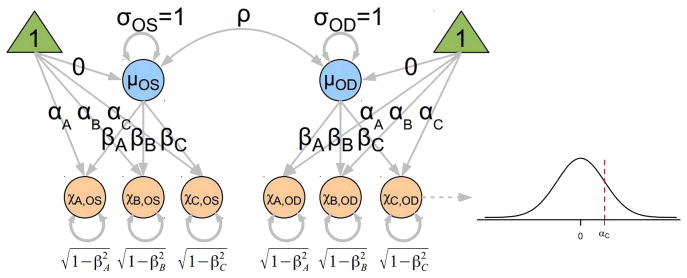
Simplified path diagram illustrating the common factor agreement model used in this study. Double-ended curved arrows denote correlations. The ‘true’, but unobserved, progression (μ) for the right (μ_OD) and left (μ_OS) eyes is assumed to be on a continuous scale, normally distributed with mean of zero and SD of one. The orange circles denote the unobserved judgements χ made by each grader on a continuous scale. The grader bias is described by the intercept α and the scale factor (slope) β. A nonlinear transformation (denoted by the dashed path pointing from χ_C,OD to the normal distribution) converts the continuous measurement into the dichotomous observation—values below the intercept α are non-progressors and those above the intercept are progressors. The true progression for eyes is correlated as denoted by ρ. Because the latent variables for progression (μ) and the unobserved continuous ratings (χ) are constrained to have variances of one and means of zero, the factor loadings β can be interpreted as tetrachoric correlation coefficients. As a consequence of these constraints, the variance of the residual error is constrained to be equal to one minus the corresponding squared correlation coefficient (1–β²).

The OpenMx package in the R Language and Environment for Statistical Computing software (V.2.15.1)¹³ was used to construct structural equation models and estimate the model parameters using full information maximum likelihood.

RESULTS

Fifty-nine subjects (109 eyes) were qualified for the study. The mean baseline age of all the participants was 58.8 (SD=8.5) years, the mean VF index was 96.7 (9.4) and the mean follow-up was 3.7 (0.9) years (table 1).

Table 1.

Participants’ demographics reported as mean (SD)

	Healthy	Glaucoma suspects	Glaucoma
N	21	50	38
Follow-up days	1355 (201)	1295 (346)	1465 (303)
Baseline visual field mean deviation dB	−0.23 (1.03)	−0.65 (1.42)	−2.13 (2.85)
Baseline visual field index	99.4 (0.4)	97.0 (12.7)	94.8 (6.3)

The repeatability within each grader in assessing the TCA printouts when using one or two sets of images per visit (table 2) and when the grader used the individual grader criteria or the common criteria (table 3) is represented by the slope (β) value. The use of two images per visit reduced the repeatability of all graders in comparison with their repeatability when assessing only one set of images per visit (table 2). The reduction in repeatability for grader A was statistically significant, as the 95% CI for the slope ratio did not include one.

Table 2.

Slopes and intercepts (SEs) for each grader using their individual criteria for topographic change analysis progression comparing one image for assessment versus two sets of images for each visit

Grader	One image	Two images	Slope ratio (two images/one image)
			Estimate	Lower limit	Upper limit
Slope (β)
A	0.958 (0.051)	0.841 (0.069)	0.879	0.697	0.904
B	0.819 (0.063)	0.740 (0.078)	0.903	0.743	1.169
C	0.966 (0.036)	0.896 (0.048)	0.928	0.780	1.075

Grader	One image	Two images	Intercept difference (two images—one image)
			Estimate	Lower limit	Upper limit
Intercept (α)
A	1.099 (0.158)	0.781 (0.140)	−0.319	−0.593	−0.068
B	0.035 (0.130)	−0.050 (0.158)	−0.085	−0.200	0.178
C	0.449 (0.135)	0.431 (0.133)	−0.018	−0.222	0.183

Differences in intercepts where the CI does not include zero and ratios of slopes where the CI does not include one are statistically significant (shown in bold).

Table 3.

Slopes and intercepts (SEs) for each grader in detecting topographic change analysis progression with individual grader criteria and with predefined common criteria on a single image for each visit

Grader	Individual criteria	Common criteria	Slope ratio (Common criteria/Individual criteria)
			Estimate	Lower limit	Upper limit
Slope (β)
A	0.972 (0.036)	0.956 (0.035)	0.983	0.893	1.127
B	0.791 (0.068)	0.863 (0.067)	1.091	0.853	1.404
C	0.990 (0.039)	0.786 (0.087)	0.794	0.578	0.932

Grader	Individual criteria	Common criteria	Intercept difference (Common criteria/Individual criteria)
			Estimate	Lower limit	Upper limit
Intercept (α)
A	1.100 (0.153)	0.999 (0.148)	−0.100	−0.250	0.103
B	0.020 (0.129)	1.041 (0.150)	1.022	0.738	1.334
C	0.434 (0.136)	1.037 (0.149)	0.603	0.350	0.892

Differences in intercepts where the CI does not include zero and ratios of slopes where the CI does not include one are statistically significant (shown in bold).

The use of predefined common criteria improved the repeatability of the grader with the worst repeatability (B, table 3). However, for the graders with high repeatability when assessing TCA printouts with their own criteria (A and C), the use of the predefined common criteria lowers their repeatability. For grader C, the reduction in the repeatability was statistically significant.

The raw percentages of pairwise agreement between graders showed little difference when the progression assessment was made based on evaluation of one image per visit compared with two images (table 4a). However, applying the predefined common criteria showed improvement in agreement throughout (table 4b).

Table 4.

Percentage agreement among graders (A, B and C) assessing progression using one or two images per visit using individual grader criteria (a) and for assessing one set of images from each visit with individual grader criteria and with predefined common TCA progression criteria (b)

(a)
Individual criteria	One image	Two images	Difference
A vs B	59.1	58.2	0.9
A vs C	77.3	75.5	1.8
B vs C	78.2	77.3	0.9

(b)
One image	Individual criteria	Common criteria	Difference
A vs B	59.1	86.4	−27.3
A vs C	77.3	86.4	−9.1
B vs C	78.2	83.6	−5.5

TCA, topographic change analysis.

The agreement between the graders with one versus two images per visit and using the individual grader progression criteria showed a minimal reduction in the intercept (α) for graders B and C (table 2). For grader A, there was a substantial decrease in the intercept using two images compared with one image per visit, and the corresponding 95% CIs for the differences excluded zero and thus the difference was statistically significant. The end result of going from one image to two images per visit, while using the individual grader criteria, was to diminish the repeatability of all graders while all of the thresholds still tended to differ substantially from each other.

Agreement between graders in assessing progression with individual grader criteria and with predefined common criteria is represented by the intercept (table 3). Graders B and C had significantly higher intercepts with predefined common criteria compared with individual grader criteria. Using the predefined common criteria resulted in very similar intercepts among all graders. This implies that the graders will tend to use the same category for a given level of progression. Using the individual grader criteria, graders A and C had similar levels of repeatability and both were more precise than B while having substantially different thresholds. Using the predefined common criteria, the precision of C substantially dropped and increased somewhat for B so that A was most precise and C least precise, yet all having substantially similar thresholds.

DISCUSSION

TCA has been suggested as the primary method for detecting glaucoma progression with CSLO based on topographical changes in the ONH. In this study, we investigated methods to improve agreement among graders in detection of TCA progression. We demonstrated that the use of two images from each visit did not improve the performance of any measure. However, there was an improved agreement among graders by using a set of predefined common criteria for progression.

Repeatability of a grader is often assessed by evaluating a set of samples multiple times. However, one can artificially influence the outcome by consistently providing the same response. Since we included three graders, the statistical approach we used allows us to establish the ‘true’ decision whether a subject is progressing or not. Comparing the performance of each individual grader to this ‘true’ definition enables us to accurately determine the repeatability for each grader. Furthermore, agreement between graders is frequently expressed as raw percentage agreement or by calculating κ. However, these methods do not consider the systematic error (bias) versus random error (imprecision), and therefore it is impossible to identify the relative precision of each grader or to examine how the rating categories differ among graders. Additionally, pairwise comparisons fail to use all the available information that could be used to describe agreement. Our statistical approach considers these factors and, therefore, provides a more comprehensive analysis. Consequently, it is difficult to compare our results with those reported in previous studies.

In this study, we hypothesised that the use of two scans per visit would improve the performance of the graders on declaring progression, but our results did not show any advantage compared over using a single scan per visit (table 2). The repeatability for all three graders was lower (significantly lower for grader A) with two images per visit compared with one image. The threshold for grader A significantly decreased but overall the range of the thresholds was not reduced by the use of two images per visit. This finding might be explained by differences between the two scans in each visit that led to uncertainty in the interpretation. It should be noted that for other methods of assessing progression, the acquisition of more than one scan per visit might be advantageous.¹⁴

The predefined common criteria we introduced aimed to improve the agreement between graders, as we observed limited agreement among the graders when individual grader criteria were used. These criteria were established based on the clinical experience of the investigators and previous studies, and are not necessarily the optimal set of criteria for TCA progression analysis. Nevertheless, we demonstrated that these criteria could improve the agreement in detecting progression between graders. Our analysis demonstrated that the use of predefined common criteria leads to a significantly lower slope (worst repeatability) to one grader while for the other graders the change was not significant with higher slope (better repeatability) to one grader and lower slope to the other (table 3). Therefore, the use of the predefined common criteria did not consistently improve the correlation between the individual graders and the common factor of progression, as we expected. However, using the common criteria the graders have more similar thresholds with a significant increase in grader B and C thresholds. This finding explains the improvement observed in percentage agreement between graders when using the predefined common criteria (table 4).

We observed a slight difference in the repeatability when assessing one image per visit with individual grader criteria in the two testing scenarios, as appearing in tables 2 and 3. We chose to construct a separate model for each testing scenarios to allow comparison with and without the use of the additional feature, which otherwise was not possible. As the grader’s decision varied in the different scenarios, the ’true’ decision with which each grader is compared is slightly different, leading to the discrepancy. Nevertheless, the difference in the actual repeatability values was small, and the overall trend among the graders was maintained.

A possible limitation of this study was that the graders in this study were also those who introduced the criteria, and therefore part of the predefined common criteria were already used by the individual observers while evaluating the images. However, the clinical reality is that every experienced grader uses their own set of criteria when evaluating the TCA report. As this type of evaluation leads to poor agreement among graders, our goal in this study was to test the hypothesis that setting common criteria between graders can improve the agreement, as we confirmed by our results. Therefore, even when the same graders define the common criteria, the agreement between the graders improves, thus allowing better use of the TCA analysis.

Although the set with predefined common criteria was always evaluated second, all the graders in this study were highly experienced in evaluating TCA reports, so there was no learning effect involved in this assessment. Moreover, we took several measures to prevent any potential bias by presenting the testing sets to the graders a week apart, and by including a relatively large number of images that were randomly ordered.

In conclusion, the use of predefined common criteria improved agreement among graders in assessing TCA progression, while the use of multiple images from the same visit did not improve agreement among graders. We, therefore, recommend the use of the predefined common criteria for routine clinical assessment of TCA reports. Future study might further refine these criteria.