Adaptive shaping of cortical response selectivity in the vibrissa pathway

Abstract

One embodiment of context-dependent sensory processing is bottom-up adaptation, where persistent stimuli decrease neuronal firing rate over hundreds of milliseconds. Adaptation is not, however, simply the fatigue of the sensory pathway, but shapes the information flow and selectivity to stimulus features. Adaptation enhances spatial discriminability (distinguishing stimulus location) while degrading detectability (reporting presence of the stimulus), for both the ideal observer of the cortex and awake, behaving animals. However, how the dynamics of the adaptation shape the cortical response and this detection and discrimination tradeoff is unknown, as is to what degree this phenomenon occurs on a continuum as opposed to a switching of processing modes. Using voltage-sensitive dye imaging in anesthetized rats to capture the temporal and spatial characteristics of the cortical response to tactile inputs, we showed that the suppression of the cortical response, in both magnitude and spatial spread, is continuously modulated by the increasing amount of energy in the adapting stimulus, which is nonuniquely determined by its frequency and velocity. Single-trial ideal observer analysis demonstrated a tradeoff between detectability and spatial discriminability up to a moderate amount of adaptation, which corresponds to the frequency range in natural whisking. This was accompanied by a decrease in both detectability and discriminability with high-energy adaptation, which indicates a more complex coupling between detection and discrimination than a simple switching of modes. Taken together, the results suggest that adaptation operates on a continuum and modulates the tradeoff between detectability and discriminability that has implications for information processing in ethological contexts.

we live in a complex sensory environment, where different sensory cues are important for perception and decision-making in different contexts. Not only is there evidence for different information being parsed into different pathways (Goodale and Milner 1992), sensory information processing within a pathway may also be context dependent, where competing coding schemes coexist (Crick 1984; Sherman 2001a). Specifically, sensory pathways may switch from conveying information for detecting novel features in the environment, to conveying information for discerning fine details (Adibi et al. 2013; Lesica et al. 2006; Lesica and Stanley 2004; Moore 2004; Sherman 2001b; Wang et al. 2010), setting the stage for a complex and dynamic coding scheme that may be particularly important for interacting with the natural environment (Stanley 2013).

One mechanism that modulates sensory information processing is adaptation, a ubiquitous and cross-modal phenomenon where the pathway shifts its dynamic range in response to persistent external stimuli, resulting in both perceptual and electrophysiological manifestations. Adaptation can occur on a variety of time scales and at different stages of the sensory pathway. We focus on rapid adaptation in the cortex on the time scale of hundreds of milliseconds. During rapid adaptation, neurons decrease firing rate in response to repeated stimuli in hundreds of milliseconds and recover on a similar time scale (Webber and Stanley 2006). It has long been posited that adaptation is not simply fatigue of the neural system, but changes how information is encoded, processed, and eventually extracted (Ahissar et al. 2000; Chung et al. 2002; Clifford et al. 2007; Ego-Stengel et al. 2005; Fairhall et al. 2001; Higley and Contreras 2006; Khatri et al. 2009; Maravall et al. 2007; Wang et al. 2010). In somatosensation, psychophysical studies have shown that adaptation heightens spatial acuity in tactile discrimination tasks (Goble and Hollins 1993; Tannan et al. 2006; Vierck and Jones 1970), while electrophysiological studies qualitatively show a spatially constrained cortical representation of repetitive stimuli, proposed as a potential mechanism for enhanced acuity (Lee and Whitsel 1992; Moore 2004; Sheth et al. 1998; von Bekesy 1967). Despite the potentially profound implications for sensory coding, however, this phenomenon has not been extensively quantified.

Analogous to the spatial acuity enhancement observed in humans, we recently demonstrated that both awake rats and the ideal observer of the cortex can better discriminate the spatial location of a whisker stimulus (i.e., which one of two adjacent whiskers was deflected) following sensory adaptation. However, the detectability (i.e., the probability that the animal reports the sensation of a whisker deflection or the probability that the ideal observer classifies the trial as a detected signal as opposed to noise) is degraded at the same time, suggesting a fundamental change in spatial acuity that has implications for texture processing (Ollerenshaw et al. 2014). Although a range of electrophysiological studies have demonstrated the effects of adaptation on cortical activation in the rodent vibrissa pathway (Adibi et al. 2013; Boloori and Stanley 2006; Chung et al. 2002; Ganmor et al. 2010; Higley and Contreras 2007; Khatri et al. 2004, 2009; Moore 2004; Sheth et al. 1998; Webber and Stanley 2004), the extent to which the nature of the adapting stimulus shapes the spatial activation in the cortex is unknown, as is the ultimate effect on detectability and discriminability.

We used voltage-sensitive dye (VSD) imaging to measure cortical activation in the anesthetized rat and explicitly tested spatially distributed primary sensory cortex (S1) vibrissa representations for a range of adapting stimuli. The VSD imaging enables simultaneous recording from multiple cortical columns to capture the spatially distributed representation, while possessing the temporal characteristics requisite for capturing the transient temporal dynamics of the cortical response. We specifically modulated the energy in the adapting stimulus through covariation of the frequency and velocity, two primary parameters comprising the kinetic signature (Arabzadeh et al. 2005) of whisker motion in whisking behavior and texture contact (Wolfe et al. 2008). Increasing amounts of adaptation resulted in cortical representations that were increasingly degraded in the overall activation and constrained spatially. Single-trial-based ideal observer analysis revealed a decrease in detectability of the whisker input with increasing adaptation and an increase in spatial discriminability for moderate levels of adaptation but degraded discriminability for more extreme levels of adaptation. Taken together, the results suggest that adaptation operates on a continuum and modulates the tradeoff between detectability and discriminability in an ethologically relevant way that emphasizes the competing demands that different tasks place on the system.

MATERIALS AND METHODS

Using VSD imaging in anesthetized rat barrel cortex, we analyzed the effect of sensory adaptation on the detectability and spatial discriminability of adjacent whisker stimulation on single-trial basis. As illustrated in Fig. 1A, in the rat vibrissa system, each vibrissa uniquely evokes the strongest response in its corresponding column (primary barrel) in the S1, and the vibrissae topographically align with the cortical columns. We used computer-controlled piezo-electric actuators to deflect the facial vibrissae of anesthetized rats, while recording the activation of a large population of neurons in cortical layer 2/3 using VSD imaging (Wang et al. 2012). Figure 1B illustrates the experimental setup, and Fig. 1C shows an example of the cortical response to a punctate deflection of a single vibrissa over time. The approximate map of cortical columns was functionally registered onto the image, as previously described (Wang et al. 2012; see Barrel Mapping below). The stimulus in this example was a punctate deflection of 1,200°/s in the rostral-caudal plane (exponential rise and decay). All responses across all stimulus conditions were time-averaged from signal onset to peak (10–25 ms poststimulus) for further analyses (see Data Analysis and discussion below). We then performed ideal observer analysis and classified each single trial based on fluorescence signals in the primary and adjacent barrels.

Fig. 1.

Voltage-sensitive dye (VSD) imaging of the rat barrel cortex in vivo. A: the rat vibrissa pathway is a well-suited model for somatosensory processing, as the primary cortical columns (barrels) are topographically mapped to the whiskers on the snout. Each whisker deflection evokes the strongest response in its corresponding barrel (primary barrel). B: in the anesthetized rat, computer-controlled piezoelectric actuators stimulated the whiskers, while the VSD camera system simultaneously collected the fluorescence signal from layer 2/3 of the primary somatosensory cortex. C: an example response to a single punctate whisker deflection of 1,200°/s on whisker E3, averaged over 30 trials. Top of image corresponds to the medial side of the animal or row E; right side of the image corresponds to the posterior of the animal or arc 1. Upon the onset of the response at ∼10 ms poststimulus, the VSD signal was constrained in the primary barrel-related column, but quickly spread to adjacent columns, and peaked at ∼20–25 ms. An outline of the barrel map functionally registered using the responses to different whisker deflections was overlaid on the VSD images. ΔF/F₀, change in the fluorescence relative to the background. D: the corresponding time course for the response shown in C. The adjacent barrel-related column was the E4 column.

Surgery

All procedures were approved by Institutional Animal Care and Use Committee at Georgia Institute of Technology and in agreement with the National Institutes of Health guidelines. Seven female albino rats (Sprague-Dawley; 250–330 g) were sedated with 4% vaporized isoflurane, then anesthetized with pentobarbital sodium (50 mg/kg ip, initial dose). Supplemental doses were administered as needed to maintain a surgical level of anesthesia, confirmed by monitoring heart rate, respiration and eyelid/pedal reflexes to adverse stimuli (toe or tail pinch). Following the initial pentobarbital sodium dose, the animal was mounted on a stereotaxic device (Kopf Instruments, Tujunga, CA) on a vibration isolation table. Atropine (0.09 mg/kg sc) was administered subcutaneously to keep the lungs clear of fluid. Lidocaine was injected subcutaneously into the scalp before the initial incision on the head. In all experiments, saline was administered (2 ml·kg⁻¹·h⁻¹) to prevent dehydration. Body temperature was maintained at 37°C by a servo-controlled heating blanket (FHC, Bowdoinham, ME). After the midline incision on the head, skin and tissue were resected, and connective tissue was removed. A craniotomy (∼3 mm × 4 mm) was drilled on the left hemisphere over the S1 (stereotaxic coordinates: 0–4.0 mm caudal to the bregma, and 4.0–7.0 mm lateral to the midline; Paxinos and Watson 2007). The dura was left intact. A dental acrylic dam was constructed around the craniotomy. At the end of the surgical procedures, a light level of anesthesia was maintained with pentobarbital sodium. The animal was euthanized with an overdose of pentobarbital sodium solution after VSD imaging.

Staining

The dura was cleaned using a gentle flow of saline (0.9%), then dried with a gentle air blow for about 10–15 min or until it appeared “glassy” (Lippert et al. 2007). VSD (VSD RH1691, Optical Imaging) was diluted in saline to ∼1.5 mg/ml. The dye solution (∼200 μl) was carefully placed into the dam using a micropipette. The craniotomy was covered to prevent the dye from photo-bleaching. The dye solution in the dam was circulated and replenished with fresh dye solution every 5–10 min (Lippert et al. 2007). After ∼2 h of staining, the unbound dye was washed out with saline. Saline was applied to the brain surface after washing. Imaging was performed through saline on the brain surface. Saline was replenished throughout the experiment.

Optical Imaging

The excitation light source was a 150-W halogen lamp filtered at 621–643 nm. The fluorescence signals were collected with a MiCam02 camera system (BrainVision). The camera was focused onto layer 2/3, at ∼300 μm below the pia surface (Petersen et al. 2003a). The frame was 184 × 123 pixels, at 200 Hz (frame rate = 5 ms). Prior to each trial, a background image of the craniotomy (F₀) was recorded. The objective lens was 1× and the condenser lens was 0.63×. The magnification was ×1.6. The field of view was 3.5 mm × 2.3 mm, and the pixel size was 18.9 μm × 18.9 μm. All individual frames of 25–50 single trials were recorded.

Vibrissa Stimulation

Vibrissa deflections were generated by a multilayered piezo-electric bending actuator (range of motion: 1 mm, bandwidth: 200 Hz; Polytec PI, Auburn, MA), which was calibrated using a photo-diode circuit, by determining the relationship between command voltage steps and the resulting deflection amplitudes and velocities. Calibration of the two stimulators was performed with a slotted infrared switch (QVA11134, Fairchild Semiconductor), analogous to the methods described in other studies (Andermann et al. 2004; Arabzadeh et al. 2005). As the tip of the actuator interrupts the path of the infrared beam, the change in the output voltage of the optical switch is directly proportional to that of the tip displacement. The voltage change was then transformed to the corresponding actuator displacement change using the linear relationship between small changes in beam occlusion and output voltage (also determined experimentally). The vibrissae were each inserted into a 4-cm section of a 20-μl glass pipette (inner diameter of ∼0.65 mm) fixed to the end of an actuator. The ends of the glass pipettes were then situated 10 mm from the face. Actuator inputs were controlled by a programmable, real-time computer.

Vibrissae were deflected with an exponentially rising (τ = 2 ms) and decaying saw-tooth waveform of 17 ms in duration in the rostral-caudal plane. Each trial had 200 ms of prestimulus recording. Under the nonadapted condition, a single deflection, referred to as the test probe, was delivered to a single vibrissa. In adapted trials, the same probe was preceded immediately by an adapting stimulus train of 1,000 ms on the same vibrissa, with no additional time between the adapting train and the test probe. The same protocol described above was presented to an adjacent vibrissa in the next trial. In our laboratory's previous study (Ollerenshaw et al. 2014), we varied the stimulus protocol in imaging experiments such that, for some animals, the adapting stimulus was delivered onto both whiskers at the same time, and for others onto a single whisker. We found no qualitative differences. Because of the physiological variations, the adjacent pair of vibrissae stimulated was not always the same pair across animals. Typically, our surgery technique allowed us to open the craniotomy centered around D2; barrels with good VSD staining and devoid of bleeding were chosen (for animal 1: E3 and E4; animal 2: D2 and D3; animal 3: E1 and E2; animal 4: C2 and C3; animals 5 and 6: C1 and C2; animal 7: D1 and D2).

Each trial was 5,000 ms, and there was at least 3,800 ms of rest between the last deflection and the next trial. Stimulation protocols were presented in random order and repeated 25–50 times. Therefore, a test probe under the same adapting condition was separated from its next presentation by at least 120 s. The design to interleave adapting stimulus conditions controls for physiological state changes over time, such as those related to anesthesia and spontaneous cortical activity.

The frequency of the adapting stimulus train was 4, 10, 20, or 40 Hz, and the deflection velocity was 100, 500, 1200, 2500, or 3,500°/s. The total energy in the adapting stimulus was the square of whisker displacement integrated over time. To evoke a robust nonadapted response in each animal, the test probe ranged from 1,200°/s to 3,500°/s among seven animals.

Data Analysis

All analyses of VSD data were conducted using Matlab (MathWorks, Natick, MA). The analyses were based on the change in the fluorescence relative to the background, or ΔF/F₀. Specifically, the VSD frames were divided by the background image F₀ pixelwise. Additionally, to account for nonstationarities and physiological effects (cardiovascular and respiratory motions) in the images, a baseline frame was subtracted from all subsequent frames to form ΔF. For nonadapted trials and prestimulus frames, the baseline was the average of the first 50 ms of prestimulus frames. For adapted trials, the baseline was the first 50 ms immediately preceding the probe. The resulting frames were divided by the background F₀, to produce the primary measure ΔF/F₀. Note that we report this as a percent change. The response frames were time-averaged from the typical onset to peak frame of cortical response (10–25 ms poststimulus) for all stimulus conditions. Numerous studies have asserted that sensory detection can be modeled as temporal integration of the ongoing neural response (Carpenter 2004; Chen et al. 2008; Cook and Maunsell 2002; Fridman et al. 2010; Gold and Shadlen 2001, 2007; Huk and Shadlen 2005; Mazurek et al. 2003; Roitman and Shadlen 2002; Schall and Thompson 1999; Smith and Ratcliff 2004; Stüttgen and Schwarz 2010). Therefore, we integrated from a typical VSD signal onset time of 10 ms (consistent with the cortical response latency in this pathway), to a typical VSD signal peak time of 25 ms. The prestimulus frames within each nonadapted trial (150 ms preceding the first stimulus), excluding those used as the baseline, were also time-averaged every four frames. To normalize each dataset, the nonadapted response was trial-averaged and spatially-filtered (a 5 × 5-pixel or ∼0.1 mm × 0.1 mm median, then a 5 × 5-pixel average spatial filter). The filtered image was then fitted a two-dimensional Gaussian function by the least squared error algorithm. All ΔF/F₀ pixel values were normalized to the amplitude of this Gaussian function for each vibrissa. We quantified the magnitude and area of the response for each adapting stimulus condition. The response for each stimulus condition was trial-averaged and spatially filtered as described above. To produce more accurate Gaussian fits, the filtered image was rotationally averaged, using the elliptical parameters produced by the nonadapted Gaussian fit, meaning they were centered around the same pixel and had the same major and minor axes ratio. A pixel value threshold (see Adaptation Intensity below) was applied to the image, then the least square algorithm was used to derive a two-dimensional Gaussian fit. The magnitude of the response was the amplitude of the Gaussian fit, and the area was represented by the pixels within +1 SD of the Gaussian center.

Barrel Mapping

The method for barrel mapping was adapted from our laboratory's previous studies (Millard et al. 2013; Wang et al. 2012). A barrel map was obtained from cytochrome-c oxidase staining of one animal. The barrels were outlined in Neurolucida software (MBF Bioscience, Williston, VT). This barrel map serves as a generic template for all other animals. In previous studies, we have found the barrel map to be relatively well conserved across animals. For each animal, the initial VSD responses to several individual whisker deflections were superimposed to form a response map, as the initial responses are relatively constrained within the primary barrel (Petersen et al. 2003a). The template barrel map was then linearly scaled, translated, and/or rotated, so that the centroids of the responses to several individual whisker deflections and the geometric centers of the barrels produce minimal squared errors.

Adaptation Intensity

To quantify the extent of cortical adaptation for each stimulus condition, an adaptation intensity was defined as follows. First, we calculated the response ratio for a given stimulus condition, which is the total fluorescence in the trial-averaged adapted response divided by that in the trial-averaged nonadapted response. For each stimulus condition, the trial-averaged image was filtered with a 5 × 5 pixel (∼0.1 mm × 0.1 mm) median then a 5 × 5 pixel average spatial filter. Total fluorescence was the sum of all pixels above the prestimulus noise threshold, defined as the mean + 1 SD of all pixel values from the trial-averaged prestimulus frames. Adaptation intensity equals 1 minus the response ratio, so that intuitively, the most intense adaptation condition corresponds to an adaptation intensity of 1, while an adaptation intensity of 0 signifies nonadapted condition.

Ideal Observer Analysis

Response variables.

For each animal, two regions of cortex were defined so that each highlighted the center of the response to the corresponding whisker stimulation. The region corresponding to whisker 1 stimulation was referred to as region 1 and so on. For trials from whisker 1 stimulation, region 1 was the center of the cortical response to its primary whisker stimulation (hereon referred to as the primary region), and region 2 was the center of the cortical response to the adjacent whisker stimulation (hereon referred to as the adjacent region). For whisker 2 stimulation trials, region 2 was the primary region, and region 1 was the adjacent region (see Fig. 5A). To obtain the region for each whisker stimulation, the trial-averaged nonadapted response was spatially filtered with a 5 × 5 pixel (∼0.1 mm × 0.1 mm) median filter and a 5 × 5 pixel average filter, then fitted with a two-dimensional Gaussian function. The corresponding activation region was defined as the 98% height contour of the Gaussian fit. The two regions were non-overlapping and approximately the size of a cortical column (∼300–500 μm in diameter; Bruno et al. 2003). Once defined, the two regions were applied to the unfiltered, single-trial frames. The average fluorescence within each region was defined as a response variable.

Fig. 5.

Ideal observer analysis of spatial discrimination. A: the average fluorescence signals in the two stimulated barrels (highlighted with black ellipses) were collected to represent each single trial. The average fluorescence in the barrel corresponding to whisker 1 (W₁) was designated as R₁ and so on. For whisker 1 stimulation, R₁ was the primary barrel variable, and R₂ the adjacent variable. B: for each adaptation intensity, the response variables above the detection threshold were collected from all single trials across animals (see Data Analysis in materials and methods). The response variables R₁ and R₂ were the average fluorescence in the two adjacent barrels [with R₁ corresponding to the primary barrel of whisker 1 and R₂ to that of whisker 2 (W₂)], normalized to amplitude of trial-averaged nonadapted response (see materials and methods). The brown ellipse outlines the trials from whisker 1 stimulation, and the green ellipse whisker 2. A single trial was classified as a response to either whisker 1 or whisker 2 stimulation using the LRT (see materials and methods). The discrimination performance was defined as the percentage of trials correctly classified. The outcome of the LRT was directly related to the separability of the two clusters, which was determined by the distance between the centers of the clusters (indicated by the plus signs), standard deviation (in both horizontal and vertical directions), and correlation of the clusters. C: a cartoon illustration of improved discriminability by the increased distance between the centers of the clusters. D: a cartoon illustration of improved discriminability by decreased standard deviations. E: a cartoon illustration of improved discriminability by increased noise correlation.

Detection.

The primary region response variable was defined as the decision variable (DV) for this analysis. For each stimulus condition, the DVs from all single trials were binned and fitted with a Gaussian probability function, referred to as the signal distribution. A prestimulus noise distribution was formed by the DVs extracted from prestimulus frames (150 ms preceding the first stimulus) in all nonadapted trials, referred to as the noise distribution. From the perspective of an ideal observer of cortical activation, each single trial in the signal distribution and noise distribution was classified as either signal or noise using the Likelihood Ratio Test (LRT). Given a single trial response variable R, the log ratio of the probability (P) that the response was a signal (S), P(S|R), to the probability that the response was noise (N), P(N|R), was used to classify the trial. A nonnegative log likelihood ratio classifies the trial as signal and otherwise noise. With an equal probability of signal and noise, Bayes' rule expresses the log likelihood ratio as follows:

$$\ln \left[\frac{P\left(S\mid R\right)}{P\left(N\mid R\right)}\right]=\ln \left[P\left(R\mid S\right)\right]-\ln \left[P\left(R\mid N\right)\right]$$ (1)

For normal distributions, this expression becomes

$$-\frac{1}{2}\left(R-{\mu }_S\right)\mathrm{\prime }{{\sum }_S}^{-1}\hspace{0.17em}\left(R-{\mu }_S\right)-\frac{1}{2}\ln \mid {\sum }_S\mid -\left[-\frac{1}{2}\left(R-{\mu }_n\right)\mathrm{\prime }{{\sum }_n}^{-1}\hspace{0.17em}\left(R-{\mu }_n\right)-\frac{1}{2}\ln \mid {\sum }_n\mid \right]$$ (2)

where μ_s is the mean of the signal response variables, ∑_s is the covariance (variance in this one-dimensional variable case), and μ_n and ∑_n are the mean and covariance, respectively, of the noise response variables (Duda et al. 2001). The LRT is validated with the “leave-one-out” method, where a detection decision for a single trial is made based on the model (average and variance) calculated using the rest of the trials. The fraction of correctly classified trials was the final measure for detectability. The same noise distribution was used in all adapting conditions. To ensure the results were not sensitive to the choice of prestimulus time frames, we repeated the analysis using noise distributions derived from the time frame following the adapting stimulus. Briefly, for each adapting condition, we used the set of frames in the 25-ms period preceding the test probe (after the adapting stimulus) to form its own “adapted noise distribution.” Using adapted noise distributions for each corresponding adapted signal, the detection performance still showed a monotonic decrease with adaptation (see Fig. 4F).

Fig. 4.

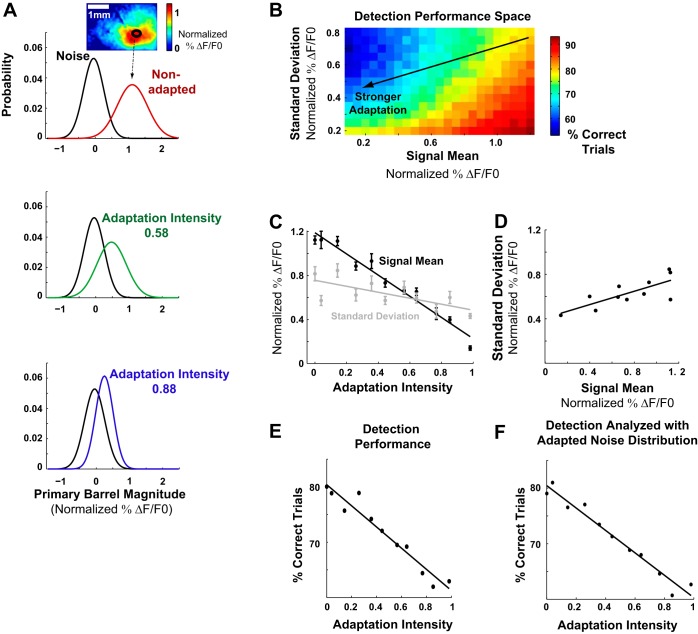
Detectability of the stimulus was degraded with adaptation. A: detection performance of an ideal observer measures the separation of the signal distribution from the noise distribution. This was defined as the percentage of trials correctly classified as signal or noise using the likelihood ratio test (LRT; see materials and methods). As the three examples demonstrated, the mean and standard deviation of the signal distribution both decreased with adaptation, which would have opposite effects on the separation of signal from noise. B: the optimal detection performance increased with larger signal mean but smaller standard deviation. The change in standard deviation and mean induced by adaptation is indicated by the black line. The arrow indicates the direction of stronger adaptation. C: the mean (r = −0.98, P < 0.0005) and standard deviation (r = −0.7, P = 0.017) of the signal distribution decreased with adaptation intensity. D: the standard deviation of the signal distribution is correlated with its mean (r = 0.76, P = 0.0068). E: as signal mean and standard deviation both decreased with stronger adaptation, the detection performance on the line shown in B also decreased with stronger adaptation. F: detection performance is qualitatively the same when analyzed using the noise distribution following the adapting stimulus.

Discrimination.

As the animal likely further distinguishes the stimulus features only after it is detected, only detectable trials were considered for discrimination analysis. The primary response variable of a single trial must be above the detection threshold, which was calculated from the noise distribution of each whisker stimulation data where the threshold value yielded the 10% false alarm rate observed in previous behavioral studies (Ollerenshaw et al. 2012; Stüttgen et al. 2006; Stüttgen and Schwarz 2008). The noise distribution was formed as described in the detection analysis. The detection threshold is a value such that the probability of obtaining a prestimulus noise value above the threshold, thus resulting in a misclassification of noise as a signal (false alarm rate), is 10%. To ensure that the discrimination result does not solely depend on a particular level of detection threshold, we repeated the analysis for a range of assumed thresholds. Specifically, we performed the discrimination analysis with the threshold set to 0, 25, 50, 75, and 100% of the detection threshold. Regardless of the detection threshold value, including the 0% level, which essentially constituted no threshold, the discrimination result was qualitatively the same (see Fig. 6E). We repeated the analysis using noise distributions after the adapting stimulus. We derived detection thresholds specific to each adapting condition, using the adapted noise distributions described above (see Detection above). We again found that the discrimination performance was qualitatively similar (see Fig. 6F).

Fig. 6.

Discrimination performance peaked at an intermediate adaptation intensity. A: discrimination performance was strongly influenced by variability within column and noise correlation across columns. Discrimination performance increased with higher noise correlation but lower standard deviation of the variable clusters. The change in standard deviation and noise correlation induced by adaptation is indicated by the black curve. The arrow indicates the direction of stronger adaptation. For simplicity, the combined primary and adjacent barrel variable standard deviation is shown on the map because they were well correlated (r = 0.87, P = 0.0005). The distance between the cluster centers was not included as a factor because it did not demonstrate correlation with adaptation intensity (r = −0.17, P = 0.61) or the cluster mean (r = 0.46, P = 0.16, data not shown). B: the standard deviation of the primary barrel variables and that of the adjacent barrel variables were correlated (r = 0.87, P = 0.0005). C: correlation across columns was maximal at an intermediate within-column variability (combined primary and adjacent barrel standard deviation). D: the values on the performance map along the black curve in A were extracted and plotted against adaptation intensity. Similar to Fig. 4, C and D, the combined standard deviation decreased with stronger adaptation (data not shown). The discrimination performance peaked at an intermediate adaptation intensity. E: the discrimination performance is relatively insensitive to the detection threshold. Each discrimination performance was evaluated using a fraction of the detection threshold value that yielded 10% false alarm rate (see materials and methods). F: discrimination performance was qualitatively the same when analyzed using the noise distribution following the adapting stimulus. G: a possible computational mechanism for the overall nonlinear noise correlation. Each axis represents a component of correlated neural activity, and each square is the overall noise correlation that is the sum of the two components. The black curve represents a possible scenario where one component increases its noise correlation with adaptation, while the other decreases its noise correlation, thus creating an overarching effect for the overall noise correlation. The arrow indicates the direction of stronger adaptation.

As with all electrophysiological studies, the data are impaired by limited trials. The duration of data collection in an average VSD experiment is limited to ∼2 h, mainly due to photo-bleaching. Thus the number of trials for each stimulus condition is low. To rectify this, all response variables from seven animals were normalized (see Data Analysis above), merged, and grouped according to their adaptation intensity. We first tested normality on the data sets collected, and the majority of data sets were normally distributed. We then fitted Gaussian probability functions to the merged data to obtain estimates of the parameters (mean, variance, and covariance). As the raw data are limited and noisy samples, we used unlimited samples from the fitted parametric model.

In detail, for each stimulus condition, the adaptation intensity was calculated from its trial-averaged image. For each detected trial within that stimulus condition, the response variables in the two adjacent barrels, R (R₁, R₂), were extracted and normalized (see Data Analysis). Because the responses from two adjacent whisker deflections were approximately symmetric, for each adaptation intensity, all primary and adjacent variables were designated as trials from whisker 1 stimulation, duplicated with reversed primary and adjacent values, and designated as trials from whisker 2 stimulation. All response variables across seven animals (14 whisker deflections) with the same adaptation intensity were merged, and the mean μ (μ₁, μ₂), standard deviation σ (σ₁, σ₂) and covariance σ₁₂ were calculated. The centers of the response variable cluster, marked with black crosses (Fig. 5B), represent the trial-average responses μ (μ₁, μ₂). The ellipses outline 2 SDs. The eccentricity of the ellipse represents the noise correlation (Pearson correlation coefficient) between R₁ and R₂.

Regression analysis was used to determine the relationship between these parameters and adaptation intensity, and to determine the simplest and most appropriate perspective for the subsequent analyses. The difference between the primary and adjacent means, which determines the distance between the cluster centers, did not show any correlation with adaptation intensity (r = −0.17, P = 0.61, data not shown) or with the mean of the cluster (r = 0.46, P = 0.16, data not shown). Because the standard deviation of primary barrel variables is correlated with that of the adjacent barrel variables (r = 0.87, P = 0.0005, see Fig. 6B), they are presented as a combined standard deviation, $\sqrt{({\sigma }_1^2\hspace{0.17em}+\hspace{0.17em}{\sigma }_2^2)\hspace{0.17em}/\hspace{0.17em}2}$. The combined standard deviation is highly correlated with primary (r = 0.97, P < 0.0005) and adjacent (r = 0.97, P < 0.0005) standard deviation and the covariance (r = 0.99, P < 0.0005). The noise correlation was defined as the ratio of the covariance to the product of the primary and adjacent standard deviations, which is the Pearson correlation coefficient between R₁ and R₂.

Trials (n = 1,000) were drawn from a two-dimensional Gaussian distribution with the parameter values indicated in Fig. 6, B and C. Because the distance between the cluster centers did not change with adaptation, the values shown here all used a typical value from the nonadapted state. Each single trial was then classified using the LRT. Similar to the detection analysis in Fig. 4, the direction of stronger adaptation on the map was determined by the decreasing combined standard deviation with adaptation intensity (for adaptation intensity and μ₁, r = −0.73, P = 0.011; for μ₁ and the combined standard deviation, r = 0.62, P = 0.043, data not shown). For the observed response R on a given trial, the log ratio of the probability that the response resulted from whisker 1 (W₁) stimulation, P(W₁|R), to the probability that the response resulted from whisker 2 (W₂) stimulation, P(W₂|R), was used to classify the trial. A nonnegative log-likelihood ratio classifies the trial as whisker 1 stimulation, and otherwise as whisker 2 stimulation. The likelihood ratio is:

$$\ln \left[\frac{P\left({\text{W}}_1\mid R\right)}{P\left({\text{W}}_2\mid R\right)}\right]=\ln \left[P\left(R\mid {\text{W}}_1\right)\right]-\ln \left[P\left(R\mid {\text{W}}_2\right)\right]$$ (3)

For normal distributions, this expression becomes:

$$-\frac{1}{2}\left(R-{\mu }_1\right)\mathrm{\prime }{{\sum }_1}^{-1}\hspace{0.17em}\left(R-{\mu }_1\right)-\frac{1}{2}\ln \mid {\sum }_1\mid -\left[-\frac{1}{2}\left(R-{\mu }_2\right)\mathrm{\prime }{{\sum }_2}^{-1}\hspace{0.17em}\left(R-{\mu }_1\right)-\frac{1}{2}\ln \mid {\sum }_2\mid \right]$$ (4)

where μ₁ is the mean of the whisker 1 stimulation response vectors, ∑₁ is the covariance matrix, and μ₂ and ∑₂ are the mean and covariance matrix, respectively, of the whisker 2 stimulation response vectors (Duda et al. 2001). The LRT is validated with the “leave-one-out” method, and the fraction of correctly classified trials was the final measure for discriminability. Because the data satisfy the condition that, μ₁ σ₂² > μ₂ σ₁², the outcome of the LRT was directly determined by the unity line. That is, for whisker 1 deflection data points, any trial that is below the unity line would be correctly classified as whisker 1 deflection, and any trial that is above the unity line (meaning the adjacent barrel fluorescence is greater than the primary barrel value) would be misclassified as whisker 2 deflection.

RESULTS

To investigate how the dynamics of sensory adaptation mediate the spatiotemporal activation of the cortex and the possible implications for the cortical code, we employed VSD imaging of the cortex in response to a range of tactile inputs in the rat vibrissa system.

The VSD imaging captures the spatially distributed activation of cortex at a relatively high temporal resolution (see materials and methods), enabling the simultaneous measurement across cortical columns. Figure 1C shows an example of the cortical response to a punctate deflection of a single vibrissa over time. The response initially appeared constrained in the primary cortical barrel-related column at 10 ms after the stimulus onset, quickly spread to adjacent columns, peaked at ∼25 ms, and gradually decayed back to baseline at ∼100 ms, consistent with previous findings (Lustig et al. 2013; Petersen et al. 2003a). Figure 1D shows the corresponding time courses of the single trials and the averaged trial of the response in Fig. 1C. The fluorescence was averaged within the primary and adjacent barrels. It should be noted that the VSD signal has been shown to be approximately linearly proportional to the underlying subthreshold membrane potential in the rat barrel cortex (Petersen et al. 2003a, 2003b). We then performed ideal observer analysis to analyze the potential effects of sensory adaptation on cortical information coding. For a detection task, each trial was classified as detected signal or noise based on the average fluorescence in the primary barrel; for a discrimination task, each trial was classified as whisker 1 or whisker 2 deflection, based on the average fluorescence in both primary and adjacent barrels.

Frequency and Velocity of Adapting Stimuli Differentially Shape Cortical Response

It is well established that the barrel cortex is highly sensitive to the frequency and velocity of whisker deflections, which are primary parameters comprising the kinetic signature of whisker motion (Arabzadeh et al. 2004, 2005; Chung et al. 2002; Khatri et al. 2004; Moore 2004; Ritt et al. 2008; Temereanca et al. 2008; Wolfe et al. 2008). Therefore, we investigated to what extent these properties of the adapting stimulus shape the cortical response, particularly the spatial activation, through VSD imaging. An example of this characterization is shown in Fig. 2. We compared the cortical responses to a 1,200°/s punctate deflection, referred to here as the test probe, recorded under different conditions. First, in the absence of any prior adapting deflections of the vibrissae, the recorded cortical response to the test probe was referred to as the nonadapted response, a typical example of which is shown in Fig. 2, top. For the adapted responses, the cortical activation was recorded in response to the test probe stimulus following an adapting stimulus of varying frequency and velocity (see materials and methods). In this example, nine different adapting trains were derived from the combination of three frequencies (4, 10, and 20 Hz) and three deflection velocities (100, 500, and 1,200°/s), while the test probe remained a single deflection of 1,200°/s on either one of two adjacent whiskers before and following adaptation. Each image in the grid shows the response to the test probe following an adapting stimulus of a certain frequency and velocity. The responses shown are time-averaged from signal onset to peak (10–25 ms poststimulus, see discussion).

Fig. 2.

Cortical responses to separate deflections on two adjacent whiskers. Whiskers deflected were E3 and E4; responses were averaged over 30 trials. Top: nonadapted response, stimulus protocol consisted of two separate single deflections on the two adjacent whiskers. Bottom: adapted responses. An adapting stimulus train was applied on either one of two adjacent whiskers for 1,000 ms at 4, 10, or 20 Hz, and each deflection within the adapting stimulus was 100, 500, or 1,200°/s, resulting in 9 combinations of adapting stimuli. A single deflection followed on the same whisker as a probe, at a fixed velocity across all adapting stimulus conditions. Images were trial-averaged and time-averaged from signal onset to peak (10–25 ms after stimulus onset). The cortical response became increasingly suppressed with increasing frequency and/or velocity.

The nonadapted state showed significant qualitative overlap of the cortical responses to adjacent whisker stimuli. Adaptation tended to attenuate the magnitude of the cortical responses, while also spatially localizing the response, consistent with previous studies describing the spatial “sharpening” of the cortical response following adaptation (Kleinfeld and Delaney 1996; Lee and Whitsel 1992; Moore 2004; Moore et al. 1999; Ollerenshaw et al. 2014; Sheth et al. 1998; Simons et al. 2005; von Bekesy 1967). This effect, however, was very dependent upon the nature of the adapting stimulus. At any given velocity of the adapting stimulus, as the frequency of the adapting stimulus increased (top to bottom), the cortical response to the test probe decreased in magnitude and in area. Similarly, at any given frequency, as the velocity increased (left to right), the cortex was also increasingly suppressed. Most importantly, different adapting stimulus trains led to similar cortical responses. For example, an adapting stimulus with low frequency but high velocity (such as 4 Hz and 1,200°/s) and one with higher frequency but lower velocity (such as 10 Hz and 500°/s) had qualitatively similar effects on the response to the same probe stimulus. Note that, in this experiment, we additionally tested the entire range of velocities coupled with a frequency of 40 Hz, but the resulting cortical response was largely suppressed, even more so than for the 20-Hz case (not shown). These same qualitative effects were noted across all experiments (n = 7 animals, 14 whiskers), although the exact combinations of the velocities and frequencies of the adapting stimuli were slightly different across different animals (see materials and methods).

This qualitative observation, coupled with previous findings (Arabzadeh et al. 2004) suggested that the total energy in the adapting stimulus might be the relevant determinant of the degree of adaptation. Here, we define the total energy in the stimulus as the square of the whisker deflection angle, integrated over the duration of the adapting stimulus, as in Fig. 3A, top. Although this would be analytic for purely sinusoidal inputs, for the pattern of exponentially rising and decaying deflections we presented, the energy was computed numerically (see materials and methods). Figure 3A shows that the adapting stimulus energy increased with higher frequency and/or velocity. An adapting stimulus with higher frequency but lower velocity had a similar energy as one with lower frequency but higher velocity. In terms of the cortical response, the adaptation intensity was derived as a metric for the degree of adaptation, similar to those commonly used in studies characterizing adaptation in spiking activity (Chung et al. 2002; Higley and Contreras 2007; Khatri et al. 2004). It was defined as 1 minus the ratio of the total fluorescence in the trial-averaged image of the adapted response to that of the corresponding nonadapted response (see materials and methods). Figure 3B shows that the adaptation intensity increased with increasing adapting stimulus energy (r = 0.96, P < 0.0005), demonstrating that a continuum of adapted responses exists, and that the degree of adaptation is shaped by the temporal feature of the adapting stimulus. Note that each data point is the average of all adaptation intensities within a range of adapting stimulus energy. Thus different frequency and velocity combinations can result in similar adaptation intensities.

Fig. 3.

Cortical response decreased in both magnitude and area with stronger adapting stimulus energy. A: the total energy in the adapting stimulus increased with frequency and/or velocity such that a high-frequency/low-velocity adapting stimulus contained similar energy as a low-frequency/high-velocity stimulus, as shown in the grid on log scale. B: adapting stimulus energy determined the extent of cortical suppression. Adaptation intensity, defined as 1 minus the ratio of total fluorescence in the trial-averaged adapted response to that of the corresponding nonadapted response (see materials and methods), was used to quantify the extent of cortical response suppression. A higher adaptation intensity indicated stronger adaptation. Average adaptation intensity was correlated with the total energy in the adapting stimuli. Error bars represent ±1 SE of the mean. C: both magnitude and area of the response decreased with adaptation. With stronger adaptation, or higher adaptation intensity, both the magnitude and the area of the response decreased. An example of this phenomenon is shown on the right. In the nonadapted state (adaptation intensity of 0), the trial-averaged image (over 30 trials) had a strong magnitude and a large area spread. The contour of a two-dimensional Gaussian fit was superimposed (black) to show the quantification of area. With stronger adaptation, there was a gradual decrease in magnitude and area spread. The Gaussian contour of the response to the corresponding adjacent whisker deflection was superimposed (gray outline), demonstrating that stronger adaptation reduced area overlap between the responses from the adjacent barrels. Scale bar, 1 mm.

As shown qualitatively in Fig. 2, as the cortex adapts, both the magnitude and the area of the response tend to decrease together. To quantify the above observations in detail, a two-dimensional Gaussian model was fitted to the trial-averaged image (see materials and methods). The magnitude of the response was defined as the amplitude of the Gaussian fit, and the response area was defined as the area of the Gaussian contour at 1 SD (examples of which are shown in Fig. 3C, right). Figure 3C shows the trial-averaged magnitude (black curve) and the area (gray curve) spanning the adapting stimulus energy range. The trial-averaged magnitude and area for each stimulus condition were binned according to their adaptation intensity; thus each data point represents the mean and SE of multiple trial-averaged responses in the same range of adaptation intensity. As an example, the right side shows the trial-averaged responses at three different adaptation intensities. As adaptation intensified, the response magnitude decreased (correlation between average magnitude and adaptation intensity r = −0.93, P < 0.0005), as demonstrated in the example images. At the same time, the area of the response also decreased (r = −0.97, P < 0.0005), as shown by the bold black outlines in the example images. When the contour of the response to the corresponding adjacent whisker deflection was superimposed (gray outlines), it was evident that the responses to the two adjacent whisker deflections became less overlapped as adaptation intensified. Qualitatively, this seems to suggest that, as the magnitude decreased, the response may become harder to detect; however, as the area also decreased, it may become easier to discriminate between the responses to adjacent whisker deflections. Although many studies have posited that a spatially sharpened response at the level of cortex may be a potential mechanism for enhanced spatial acuity observed in psychophysical studies (Lee and Whitsel 1992; Moore 2004; Moore et al. 1999; Sheth et al. 1998; Simons et al. 2005; von Bekesy 1967), the relationship between average response and quantitative information conveyed trial to trial is not trivial (Averbeck et al. 2006; Pouget et al. 1999). Only recently has the cortical response been analyzed on a single-trial basis in terms of what information is available for detection and discrimination tasks (Ollerenshaw et al. 2014; Wang et al. 2010). However, these studies investigated the cortical information and detection-discrimination tradeoff in a binary manner, in either the presence or absence of an adapting stimulus. How the properties of the adapting stimulus and the continuum of cortical responses may shape the detectability and spatial discriminability of the whisker inputs, therefore, is unknown. Furthermore, it is also the case that accurately determining the cortical area of activation involves several assumptions and is itself nontrivial. We, therefore, turn to ideal observer analysis as a simpler and more powerful description of the information conveyed by the cortical signals.

Adaptation Degrades Detectability of the Stimulus

To assess the potential significance of the changes in the cortical activation following adaptation, we evaluated the ability of an ideal observer to discern between the spatially disparate whisker stimuli. Because the adaptation affects not only the area of cortical activation, but also the magnitude of cortical activation above the intrinsic noise level, we considered both the discriminability of spatially disparate stimuli as well as their detectability, as the coupling between these two aspects of cortical activation suggested a tradeoff between detectability and discriminability. In the detection task, the ideal observer of the cortical recordings was required to report whether a whisker had been deflected; in the discrimination task, the ideal observer reported which of the two adjacent whiskers was deflected.

Figure 4 shows the detection performance on a single-trial basis from the ideal observer's perspective. Figure 4A shows examples of signal and noise probability distributions from one animal at zero (nonadapted), medium, and high adaptation intensities. The signal distribution consisted of all single-trial responses, where each trial was represented by the average fluorescence in the primary barrel (Fig. 4A, inset; see materials and methods). Both the noise and signal distributions were characterized as Gaussian distributions (see materials and methods). In the framework of conventional signal detection theory, the detectability of a signal is a function of the separation between the signal distribution and the noise distribution, a correct classification of an observation as signal depends on attributing the observation to the signal distribution and not to the noise distribution, and vice versa (Macmillan and Creelman 2004). The separation between the signal distribution and the noise distribution is determined by two factors: the distance between their means and their SDs. Qualitatively, a smaller distance between the means obscures the distinction between two distributions, and a smaller standard deviation has the opposite effect (Macmillan and Creelman 2004).

To fully quantify the effects of the mean and standard deviation on detectability in this framework, we calculated the optimal classification performance for a range of these parameters (Fig. 4B). For each mean and standard deviation (corresponding to a single square in the color map in Fig. 4B), we drew 1,000 single trials from a normal distribution with the given signal mean and standard deviation designated as “signal” trials, and 1,000 single trials from a normal distribution with the constant prestimulus noise mean and standard deviation designated as “noise” trials. Any given single-trial response R was optimally classified by the LRT, where the probability that R was a signal trial, P(S|R), was compared with the probability that it was a noise trial, P(N|R). A single trial was correctly identified as a signal if P(S|R) > P(N|R), but misclassified as noise if P(S|R) < P(N|R). Any given single noise trial was similarly classified. The percentage of trials correctly classified was defined as detectability. Therefore, each square on the color map represents the theoretical optimal classification performance given a noise distribution and a signal distribution, where chance is 50%. We show that, for a given noise distribution, detectability decreased with smaller mean of the signal distribution, but increased with smaller standard deviation.

However, as shown in Fig. 4A, both the mean and the standard deviation of the signal distribution decreased with more intense adaptation, making the possible effects of adaptation on detection ambiguous. Thus we quantified the relationship between the mean and the standard deviation of the signal distribution as the system adapts. As shown in Fig. 4, C and D, with increasing adaptation intensity, both the mean and standard deviation of the signal distribution decreased (for mean r = −0.98, P < 0.0005, for standard deviation, r = −0.7, P = 0.017), and the standard deviation decreased with smaller mean (Fig. 4D; r = 0.76, P = 0.0068). Mean and standard deviation were averaged across animals (n = 14). The linear relationship between the mean and the standard deviation in Fig. 4D was traced by the black line on the LRT color map in Fig. 4B, with the arrow indicating the direction of stronger adaptation (same as the direction of decreasing mean with stronger adaptation, as quantified in Fig. 4C). Extracting the LRT results along the line, detection performance decreased nearly 20% monotonically with stronger adaptation (Fig. 4E).

For simplicity in the analysis, the same noise distribution was used in all adapting conditions. To ensure the result was not sensitive to the choice of prestimulus time frames, analyses were repeated using noise distributions derived from the time period following the adapting stimulus (see materials and methods). The detection performance still showed a monotonic decrease with adaptation from ∼80% to 60%, as shown in Fig. 4F.

Moderate Extent of Adaptation Enhances Discriminability of the Stimulus

Figures 5 and 6 show the discrimination performance on a single-trial basis from the ideal observer's perspective. Each single trial was represented with a two-dimensional variable, consisting of the average fluorescence in the cortical barrel-related columns corresponding to the two adjacent whiskers (denoted R₁ for barrel 1 and R₂ for barrel 2, Fig. 5A, see materials and methods). The response of barrel 1 to deflection of whisker 1 is denoted R₁|W₁, while the response of barrel 2 to deflection of whisker 1 is denoted R₂|W₁, and so on. For each stimulus condition, all trials form a scatter plot (Fig. 5B).

As it is unlikely that either the animal or the ideal observer could distinguish the stimulus features without detecting the stimulus first, only detectable trials were considered for discrimination analysis. Because behaving animals are observed to respond to ∼10% of stimulus-absent trials in a detection task (Ollerenshaw et al. 2012; Stüttgen et al. 2006; Stüttgen and Schwarz 2008), we utilized a detection threshold value that yielded 10% false-alarm rate (see materials and methods).

Due to experimental constraints in the VSD imaging, the trials available for discrimination were limited. Thus all detectable trials across all animals were normalized to the maximum value in the nonadapted response (see materials and methods), merged, and grouped according to their corresponding adaptation intensity (n = 7 animals). The responses to either whisker deflection were approximately symmetric, in that the response in the primary and adjacent barrels to a single whisker stimulus mirrored the analogous responses when the adjacent whisker was stimulated. Under this assumption, the responses were further combined, reducing the responses to the primary, (R₁|W₁), (R₂|W₂), and adjacent barrel, (R₂|W₁), (R₁|W₂), responses. Adjacent whisker stimulation responses were mirrored from the combined result.

An example of the response clusters is shown in Fig. 5B. The trials from whisker 1 deflection are outlined by the brown ellipse, and the trials from whisker 2 deflection (mirrored from whisker 1 deflection) are outlined in green. The overlap of the two response clusters directly determines the level of performance to expect in discriminating between the deflections of either of the two whiskers. Qualitatively, the overlap of the two-dimensional clusters is determined by the distance between the cluster means (black plus signs), their overall standard deviations, and the noise correlation between R₁ and R₂. Noise correlation is computed as the Pearson correlation between R₁ and R₂, as the correlation across trials is not dependent on the average responses to the stimulus, but on the trial-to-trial variability (Averbeck et al. 2006). Figure 5, C–E, provides illustrations of how these key parameters influence the degree of overlap and thus the level of discriminability. As shown in Fig. 5C, if the centers of the clusters are farther apart (compare with the original cluster outlines in Fig. 5B) while variability and noise correlation were held constant, then the ellipses are farther away from each other. Similarly, if the variability of the individual column response is smaller while the centers and noise correlation remained unchanged (Fig. 5D), the area overlap between the ellipses also decreases. Finally, if the noise correlation of the responses across columns is higher with the same centers and variability (Fig. 5E), the ellipses become more elongated, and the ellipses are thus less overlapped.

The theoretical optimal classification performance in relation to its determinants is quantified in the color map in Fig. 6A. The distance between the cluster means was not strongly influenced by adaptation, and was thus not included (see materials and methods, data not shown). Furthermore, because the variability along the horizontal axis (σ₁, standard deviation of primary barrel variable) and that along the vertical axis (σ₂, standard deviation of adjacent barrel variable) were correlated (r = 0.87, P = 0.0005; Fig. 6B), they were jointly presented as a combined standard deviation (see materials and methods) for a clearer visualization. Thus, assuming a fixed distance between the cluster means, for each given standard deviation and noise correlation combination, we quantified the optimal discrimination performance by classifying 1,000 single trials drawn from a normal distribution with the given parameters, which essentially approximates the area overlap between the ellipses. The discrimination performance was evaluated with the LRT. Given a particular single-trial response R = (R₁, R₂), the probability that it resulted from whisker 1 stimulation, P(W₁|R), was compared with the probability that it resulted from whisker 2 stimulation, P(W₂|R). A single trial that was truly drawn from whisker 1 deflection was correctly classified if P(W₁|R) > P(W₂|R), but otherwise misclassified as whisker 2 stimulation. Discrimination performance increased with higher noise correlation at a given standard deviation, and with smaller standard deviation at any given noise correlation.

Next, we located where the experimental observations reside in the theoretical optimal performance map in Fig. 6A. We expected the standard deviation to decrease with adaptation, as shown in Fig. 4. However, it was not immediately clear how the noise correlation covaried with standard deviation, and how this would affect discriminability. We found that, similar to data presented in Fig. 4, C and D, the combined standard deviation decreased with stronger adaptation, and that noise correlation was maximal at an intermediate standard deviation (Fig. 6C; see materials and methods). This nonlinear relationship between the combined standard deviation and the noise correlation is indicated by the black curve on the color map in Fig. 6A. The arrow indicating the direction of stronger adaptation in Fig. 6A is in the direction of decreasing standard deviation. Extracting the LRT results along the curve, we show that discrimination performance followed a similar trend as the noise correlation and reached a maximum at an intermediate adaptation intensity (Fig. 6D). This nonlinearity could arise from multiple mechanisms that have opposing effects on correlated activity (see discussion and Fig. 6G). Note that relatively modest changes in the noise correlation resulted in a nearly 10% increase in discrimination performance.

Although the choice of detection threshold was based on animal task performance from previous studies (Ollerenshaw et al. 2012; Stüttgen et al. 2006; Stüttgen and Schwarz 2008), to ensure that the discrimination result does not solely depend on a particular level of detection threshold, we repeated the analysis for a range of assumed thresholds in Fig. 6E. Specifically, we performed the discrimination analysis with the threshold set to 0, 25, 50, 75, and 100% of the detection threshold. Regardless of the detection threshold value, including the 0% level, which essentially constituted no threshold, the discrimination result was qualitatively the same, where the discriminability was the highest at a moderate adaptation intensity of ∼0.5, but lower at either end of the adaptation spectrum.

In these analyses, the noise distributions were derived from the nonadapted cases for simplicity. It is, however, possible that the adaptation influences the noise distributions against which signals would be compared. To directly test whether this produced a significant effect, we derived detection thresholds specific to each adapting condition, using the adapted noise distributions described above (see Detection above). We found that the discrimination performance was qualitatively the same (Fig. 6F).

Taken together, the results thus far suggest that varying degrees of adaptation shape detectability and discriminability in distinctly different ways. The detection and discrimination performances as a function of adaptation intensity are summarized in Figs. 4E and 6D. The fact that the detectability decreased monotonically with increasing amounts of adaptation implies that a stimulus is most detectable in the nonadapted state (adaptation intensity = 0). In contrast, the probability of correctly discriminating a stimulus given that it was detected was the highest at an intermediate adaptation intensity. As described in Fig. 3B, the adaptation intensity is a function of the overall energy in the adapting stimulus. As a result, the intermediate adaptation intensity corresponds nonuniquely to a range of velocities and frequencies that lead to a stimulus energy of ∼500 degrees² × ms. For the experimental conditions here, this corresponds to a low velocity adapting stimulus that is in the 10- to 20-Hz range, or one that has a lower frequency of 4 Hz but a higher velocity. These different modes of vibrissa motion with complementary frequency and velocity could be related to natural whisking behavior that is thought to adapt the sensory pathway in behaving rats and speculated to improve tactile discrimination (Fanselow and Nicolelis 1999; Moore 2004; Semba and Komisaruk, 1984; also see discussion).

DISCUSSION

Rats can reliably discriminate between stimulation of adjacent whiskers, further enhanced by adaptation (Ollerenshaw et al. 2014). Although, as in most behavioral studies, this was an artificial task, the performance reflects spatial acuity, much like two-point tactile discrimination in humans. As the rodents palpate objects with their whiskers, the spatial resolution at which the sensors are represented centrally affects information transmitted. If adjacent whiskers cannot be distinguished, they likely convey redundant information, even though they contact different parts of the object. Furthermore, the form of adaptation here carries ethological relevance. Moderate adaptation resulted from either a low-velocity adapting stimulus at a high frequency (10–20 Hz), or one of high velocity but low frequency (4 Hz). In behavioral studies, different frequencies of natural whisking have been observed (Fanselow and Nicolelis 1999; Semba and Komisaruk 1984). Importantly, similar to what was demonstrated with passive adaptation here, the higher frequency range whisking exhibited smaller amplitude and vice versa. We speculate that the frequency-amplitude switch in whisking behavior likely conserves energy in whisking movements, producing similar effects on spatial acuity. With high-energy adaptation, both detectability and spatial discriminability degrade, resulting from high-frequency, high-velocity adapting stimuli not observed in natural whisking. Our observations are thus consistent with a continuous modulation of information processing to facilitate the tradeoff between detectability and spatial acuity in the natural environment.

Although adaptation has been widely studied, there is no consensus as to a single hallmark effect or biophysical mechanism, likely pointing to a range of mechanisms and manifestations. Particularly, although a range of studies have shown consistent decreases in firing with adaptation, recent studies have suggested more nuanced effects, with diverse functional consequences across cortical laminae and cell types (Heiss et al. 2008; Higley and Contreras 2006; Khatri et al. 2004). Demonstrated here with VSD, which captures the aggregate subthreshold activity across cell types within layer 2/3, is a net suppressive effect of adaptation, but the relative contributions of different cell types and mechanisms cannot be determined with this approach. However, the most prominent feature of adaptation, the reduction in cortical activity, is linked to thalamocortical synaptic depression (Chung et al. 2002) and reflects a weaker thalamic drive due to thalamic desynchronization (Temereanca et al. 2008; Wang et al. 2010), as we demonstrated in awake animals (Ollerenshaw et al. 2014). One possible explanation for the cortical spatial sharpening here is that cortical cells with direct ventral posterior medial nucleus (VPm) inputs adapt less than those without (Chung et al. 2002); VPm cells project primarily to barrels, while medial posterior nucleus cells project primarily to septa and exhibit more prominent adaptation than VPm cells, creating a sharpened spatial response (Diamond 1995; Diamond et al. 1992; Moore et al. 1999). The response modulation by adaptation likely reflects a complex combination of these mechanisms and others. The fact that the cortical response is continuously modulated suggests that at least one mechanism may also operate on a continuum. Finally, it is likely that the adaptive effects observed here are affected by anesthesia. However, it is clear from our laboratory's previous work (Ollerenshaw et al. 2014) that, in the awake state, adaptation results in similar trends in the tradeoff between detectability and discriminability. It further demonstrated in the awake animal clear adaptation effects on the thalamic inputs that drive the cortical activation, strikingly similar to those observed under anesthesia (Chung et al. 2002; Ganmor et al. 2010; Khatri et al. 2004; Temereanca et al. 2008; Wang et al. 2010). Thus the fundamental findings here likely reflect how similarly adapting stimuli would shape activation in the awake animal.

Adaptation-induced spatial sharpening has long been speculated as a mechanism for enhanced spatial acuity in psychophysical studies (Sheth et al. 1998; von Bekesy 1967). However, average responses do not dictate the information conveyed (Averbeck et al. 2006; Pouget et al. 1999). In fact, we found that the main factor shaping the discriminability was the noise correlation of activation across cortical columns. Although many studies point out the peril of noise correlation in coding efficiency (Abbott and Dayan 1999; Adibi et al. 2013; Middleton et al. 2012; Zohary et al. 1994), it should be noted that noise correlation can have different effects on coding efficiency, depending on the relationship between the average responses (Averbeck et al. 2006). For neurons sharing functional feature selectivity, such as those in the same column, a stimulus evokes similar average responses in the units recorded. That is, the average responses to two separate stimuli would both be located along the unity line (see Averbeck et al. 2006, Fig. 1). In contrast, in the context of the spatial discriminability here, the functional units recorded are two adjacent columns, where a stimulus evokes dissimilar average responses, with the primary barrel having the stronger average response. Thus increased noise correlation results in an increase in the separability of the responses (see Fig. 5E).

To explore population correlation and its impact on neural coding, we measured the correlation between the averaged population activity in the primary and adjacent barrels. As briefly discussed in materials and methods, the neural signal that supports the detection of a sensory input can be temporally integrated. In particular, decision making often requires integration of information over time (Gold and Shadlen 2007; Huk and Shadlen 2005). In addition, it is unlikely that an animal makes multiple decisions every few milliseconds on a simple stimulus over a very short period of time, as the VSD signal decays after 100 ms. After the peak frame, the VSD signal decays in the primary barrel and spatially spreads throughout the cortex. We infer that these later time frames are not used by the animal in this context, since the spatially homogeneous cortical activation in later frames would preclude spatial discrimination, inconsistent with our laboratory's previous behavioral observations (Ollerenshaw et al. 2014). Therefore, the response in each barrel was further time-averaged from the typical onset time (10-ms poststimulus, consistent with the cortical response latency in this pathway) to peak of cortical response (25 ms). Although VSD measures population activity, the local VSD signal corresponds well with single-unit subthreshold whole cell recording, indicating an overall high level of synchrony in subthreshold population activity in the cortex (Petersen et al. 2003a). This is consistent with our result of relatively high noise correlation and with findings in cat and monkey visual cortex (Chen et al. 2006; Lampl et al. 1999). However, action potentials in the whole cell recordings are not detected in the VSD signals. Possibly due to the diverse receptive field properties of layer 2/3 neurons (Simons 1978), the low firing rate correlation measured in single-neuron pairs (Gawne and Richmond 1993; Lee et al. 1998; Middleton et al. 2012; Romo et al. 2003; Zohary et al. 1994) is likely a nonlinear transformation of the population subthreshold correlation measured with VSD. Nevertheless, consistent with part of our findings, Adibi and colleagues (2013) also demonstrated that adaptation increased noise correlation, albeit of firing rates in both single-unit pairs and populations.

Furthermore, we found that adaptation nonmonotonically influenced the noise correlation. It has been shown that, regardless of stimulus condition, noise correlation in single-unit firing rates is inversely proportional to the mean (Adibi et al. 2013). Here, adaptation monotonically decreased the magnitude of the response to the subsequent whisker deflection. The little-to-moderate range of adaptation was thus consistent with observations from Adibi et al. (2013). The more extreme range of adaptation deviates from this prediction, however, likely due to exceedingly strong suppression of activity in this regime. This nonlinearity could arise from several mechanisms having opposing effects on correlated activity. The prestimulus noise correlation indicates stimulus-independent correlated activity, likely mediated by internal brain state (Arieli et al. 1996; Kohn et al. 2009; Middleton et al. 2012). The stimulus likely induces another stimulus-dependent noise correlation, which could be mediated by multiple and opposing mechanisms, such as background synaptic field and feed-forward inhibition (Middleton et al. 2012). Similar to whisking, adaptation likely places the cortex into a desynchronized state, thus decreasing the noise correlation (Poulet and Petersen 2008). On the other hand, adaptation decreases the firing rate in response to the probe stimulus, increasing the noise correlation. Additionally, adaptation has been shown to shift the excitation-inhibition balance (Heiss et al. 2008), which is implicated in high-frequency gamma, thus possibly increasing the noise correlation in the spontaneous state. The nonlinearity in noise correlation likely arises from these diverse mechanisms. Figure 6G illustrates the simplest case where the overall cortical activity is the linear sum of stimulus-independent and stimulus-dependent components. Adaptation could potentially increase the noise correlation of one component while decreasing that of the other (traced by the black curve, arrow indicates more profound adaptation), making the overall noise correlation initially increase but decrease with more profound adaptation. However, further investigation is needed to fully elucidate this issue.

Although the results here relate to the effects of passive, bottom-up adaptation on sensory processing, there are potential ties to top-down, internally regulated processing. It is proposed that, in an awake but quiescent animal, thalamic bursting leads to a large sensory-evoked cortical response, favoring detection; in an active animal, thalamic tonic firing results in cortical activities more selective of fine features (Crick 1984; Sherman 2001; Lesica et al. 2006; Lesica and Stanley 2004). Relatedly, rodents move their whiskers rhythmically when exploring the environment, speculated to enhance tactile discrimination (Carvell and Simons 1995; Fanselow and Nicolelis 1999; Harvey et al. 2001; Moore 2004). Active whisking suppresses S1 response to a single stimulus (Crochet and Petersen 2006; Fanselow and Nicolelis 1999; Ferezou et al. 2007), similar to what has been demonstrated through passive adaptation (Ollerenshaw et al. 2014). Although the direct effects of centrally regulated, active whisking and the indirect effects of the associated brain states on cortical representations are not the same as the effects of passive adaptation, the functional similarities of the modulation in activity suggest that these aspects may synergistically reinforce the continuous control of information transmission described here.

GRANTS

This work was supported by the National Institute of Neurological Disorders and Stroke (R01-NS-48285).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: H.J.Z., Q.W., and G.B.S. conception and design of research; H.J.Z. performed experiments; H.J.Z. analyzed data; H.J.Z. and G.B.S. interpreted results of experiments; H.J.Z. prepared figures; H.J.Z. drafted manuscript; H.J.Z. and G.B.S. edited and revised manuscript; H.J.Z., Q.W., and G.B.S. approved final version of manuscript.