Co-localized confocal Raman spectroscopy and optical coherence tomography (CRS-OCT) for depth-resolved analyte detection in tissue

Abstract

We report the development of a combined confocal Raman spectroscopy (CRS) and optical coherence tomography (OCT) instrument (CRS-OCT) capable of measuring analytes in targeted biological tissues with sub-100-micron spatial resolution. The OCT subsystem was used to measure depth-resolved tissue morphology and guide the acquisition of chemically-specific Raman spectra. To demonstrate its utility, the instrument was used to accurately measure depth-resolved, physiologically-relevant concentrations of Tenofovir, a microbicide drug used to prevent the sexual transmission of HIV, in ex vivo tissue samples.

1. Introduction

To maximize their effectiveness, many therapeutic and prophylactic drugs must be delivered to specific tissue sites. For example, the target of vaginally-applied Tenofovir, a topical microbicide drug used to prevent the transmission of HIV, is primarily the stromal tissue underlying the superficial epithelium, which is where HIV-infectible cells reside [1]. The current gold-standard method used to measure Tenofovir concentrations in tissue is liquid chromatography-tandem mass spectrometry (LC-MS/MS) [2]. Although it is highly sensitive, LC-MS/MS is destructive, expensive, and labor intensive. LC-MS/MS is also applied to homogenized tissue, and therefore cannot delineate the spatial concentration profiles of drugs, which drive both diffusion and delivery to specific tissue sites [1].

Optical imaging and spectroscopy methods offer an attractive, potentially noninvasive and less-expensive alternative for evaluating drug delivery to targeted tissues. For instance, optical coherence tomography (OCT) can measure depth-resolved tissue morphology up to one millimeter below the tissue surface [3,4] depending upon the type of tissue and its associated optical properties. Chemically-sensitive optical methods, such as Raman spectroscopy (RS) [5–11], can measure spatiotemporal distributions of analytes with up to micron-level spatial resolution when utilizing confocal detection [12]. In fact, confocal Raman spectroscopy has been recently applied, using commercially-available instrumentation, to detect Tenofovir in tissue samples ex vivo [13]. Combining confocal RS (CRS) with OCT in a single instrument could provide an accurate method to evaluate drug delivery to specific tissue sites or analyze the morphological and chemical properties of potentially pathologic tissues.

A number of groups have previously developed combined RS and OCT instruments to characterize biological tissue. The first RS-OCT device combined a time-domain OCT system with a near-infrared Raman spectrometer to guide acquisition of Raman spectra from a localized malignancy in breast tissue [14]. Other RS-OCT instruments have varied in technical detail and application: a combined instrument that utilized spectral-domain OCT was developed for retinal imaging and spectroscopy [15]; a combined Raman and spectral-domain OCT system was built using a single spectrometer with a common detection path and was used to sequentially acquire Raman and OCT data from rodent calvaria and retina and human skin [16]; a clinical instrument with a hand-held probe was developed to characterize cancerous skin lesions [17]; and a depth-sensitive Raman spectrometer was combined with OCT to analyze the epithelial and stromal layers of goat tissue [18].

Although the depth-sensitive instrument described above was used to acquire distinct Raman spectra from epithelial and stromal tissues [18], none of the previously-reported RS-OCT instruments have been capable of measuring analytes on the sub-200-micron scale. High spatial resolution is desirable to accurately translate concentration gradients into fundamental molecular transport parameters such as diffusion coefficients. Here, we report the development of a combined CRS-OCT instrument capable of measuring co-localized morphological and chemical information with sub-100-micron resolution. This performance was achieved by independently adjusting the effective illumination numerical aperture (NA) of each subsystem as discussed in section 2.1. The axial resolution of the Raman subsystem was also measured as a function of sampling depth in two-layer, biological-tissue phantoms as described in section 2.3. As expected, the resolution degraded with increasing sampling depth, but remained better than 100 µm over the entire practical depth range. Finally, the utility of the instrument was demonstrated by combining co-localized CRS and OCT data to accurately measure depth-resolved, physiologically-relevant concentrations of Tenofovir in epithelial and targeted stromal layers of intact, ex vivo tissue samples.

2. Materials and methods

2.1 Instrumentation

Cross-sectional OCT images and co-localized Raman spectra were acquired with the instrument depicted in Fig. 1. The OCT subsystem consists of a fiber-based Michelson interferometer. Light from a superluminescent diode (SLD-371-HP3, Superlum, Moscow, Russia) is passed through a Faraday isolator (AC Photonics, Inc., Santa Clara, CA) and split into reference and sample arms with a 50:50 fiber coupler. A galvanometer mirror and 4F lens system scan the beam in the sample arm across the back aperture of a long working distance objective lens (HCX PL Fluotar L50X/0.55, Leica Microsystems Inc., Buffalo Grove, IL). The interference signal generated by combining the light returned by the sample with that returned by the reference arm is dispersed with a custom-built spectrometer onto a line scan camera (AViiVA UM2, e2v Inc., Milpitas, CA) achieveing a spectral resolution of 0.07 nm over the 810 – 860 nm spectral range. Polarization controllers in the source, sample, and detection arms are used to optimize the splitting ratio at the fiber coupler as well as the detected interferometric signal.

Fig. 1.

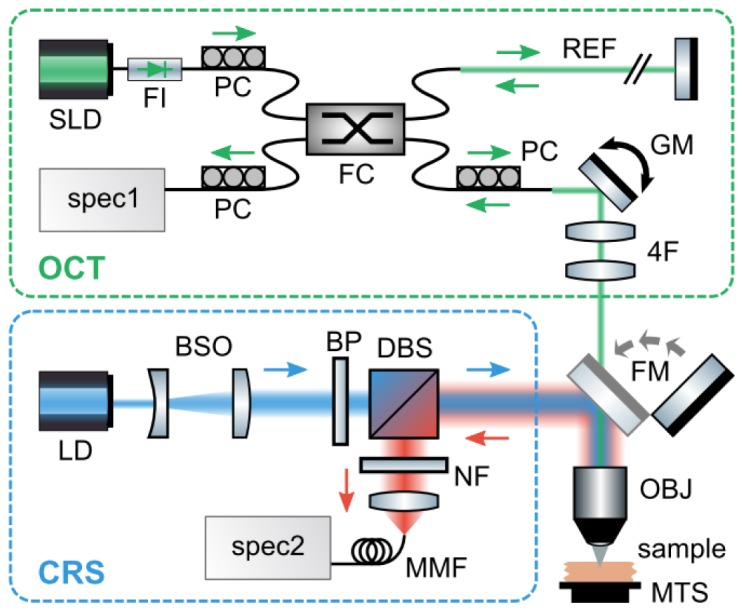
Diagram of the instrument used to acquire cross-sectional OCT images and co-localized Raman spectra through a common objective lens. Abbreviations: SLD, superluminescent diode; FI, faraday isolator; FC, fiber coupler; REF, reference arm; PC, polarization controller; GM, galvanometer mirror; 4F, 4F lens system; spec1, spectrometer #1; LD, laser diode; BSO, beam shaping optics; BP, bandpass filter; DBS, dichroic beamsplitter; NF, notch filter; MMF, multimode fiber; spec2, spectrometer #2; FM, flip mirror; OBJ, objective lens; MTS, motorized translation stage.

The RS subsystem utilizes a laser diode (LD785-SH300, Thorlabs Inc., Newton, NJ) for excitation. The output from the laser is circularized with a cylindrical and spherical lens set. The light is then filtered with shortpass (FES0800, Thorlabs Inc., Newton, NJ) and bandpass (LD01-785/10-12.5, Semrock Inc., Rochester, NY) filters and focused onto the sample with the objective lens described above. This configuration delivers about 30 mW of power to the sample plane, which is approximately equal to the maximum permissible continuous exposure limit set by the American National Standards Institute for skin illuminated with 785-nm light [19]. A dichroic beamsplitter (LPD01-785RS-25, Semrock Inc., Rochester, NY) and a notch filter (NF03-785E-25, Semrock Inc., Rochester, NY) in the collection path reject the elastically scattered light and an achromatic tube lens (f = 40 mm) focuses the Stokes-shifted, Raman scattered light into a 100-µm-core-diameter, multimode optical fiber, which acts as a confocal pinhole. The fiber delivers the light to a spectrometer (BIGBLOCK, Wasatch Photonics Inc., Durham, NC) where it is dispersed onto a 1340 × 400 pixel array, back-illuminated, deep-depletion, charge coupled device camera (PIX400BR-SF-Q-F-BB-A-US-D, Princeton Instruments, Trenton, NJ). A flip mirror is used to switch between the OCT and Raman modes of operation and a motorized translation stage (Newport Corp., Irvine, CA) is used to accurately position the sample. The subsystems were coaligned with a 1951 USAF resolution target, which provided high spatial contrast in both Raman and OCT data.

One of the benefits of OCT relative to other imaging modalities is that the axial and lateral resolutions are decoupled; the axial resolution is determined by the coherence length of the source while the lateral resolution depends upon the size of the focused beam waist [20]. The depth of focus, however, remains linked to the lateral resolution of the instrument. In conventional OCT, lateral resolution is often sacrificed to achieve a larger depth of focus by using a low NA objective lens. Conversely, confocal Raman microscopes typically utilize high NA objectives in order to acquire depth-resolved spectra with high spatial resolution. To satisfy these conflicting design parameters (i.e., a low NA objective for OCT imaging and a high NA objective for confocal Raman measurements), the OCT illumination beam diameter is reduced to approximately 0.25 mm in order to underfill the back aperture of the objective lens (NA = 0.55). With this approach, the effective NA of the OCT illumination beam was approximately 0.03 while the NA of the Raman illumination remained 0.55.

Detailed instrument properties are listed in Table 1. For the OCT portion of the instrument, the signal-to-noise ratio (SNR) was calculated as

$$\text{SNR}=20\times \left[{\log }_{10}\left(E_M/E_N\right)+\text{ND}\right]$$ (1)

where $E_M$ is the maximum peak height of an axial scan (i.e., the magnitude of the Fourier-transformed spectrum) acquired from a mirror with an exposure time of 100 µs, $E_N$ is the standard deviation of the noise in the axial scan, and $\text{ND}$ is the optical density of a neutral density filter placed in the sample arm to prevent saturation of the detector. The axial resolution was determined by measuring the full-width at half maximum (FWHM) of the mirror peak in the axial scan and the lateral resolution and field of view were established by imaging a 1951 USAF resolution target. The imaging depth was quantified by recording the falloff in $E_M$ as the mirror was translated in the sample arm. The SNR of the CRS subsystem was characterized by acquiring a spectrum of a silicon wafer with an exposure time of 1 second and dividing the height of the peak near 520 cm⁻¹ by the standard deviation of the noise. The resolution of the CRS subsystem was calculated as the FWHM of the signal acquired from the silicon wafer as it was translated through the focal volume. Finally, the spectral resolutions of both the OCT and Raman spectrometers were quantified by measuring the FWHMs of the spectral lines emitted from a mercury-argon gas-discharge lamp.

Table 1. Detailed instrument properties.

		OCT		CRS
Illumination power		3.0 mW at sample plane		30.0 mW at sample plane
Illumination wavelength		λ0 = 830 nm, Δλ = 45 nm		λ0 = 785 nm, Δλ = 0.5 nm
SNR		94 dB		36 dB
Axial resolution (in air)		8 µm		19 µm
Lateral resolution (in air)		40 µm		3 µm
Spectral resolution		0.07 nm		3.3 cm−1
Spectral range		810 – 860 nm		150 – 1950 cm−1
OCT imaging depth		1.6 mm (−3 dB falloff)		-
OCT field of view		900 µm		-

A description of the procedures used to measure these properties can be found in section 2.1.

Note that the axial resolution (i.e., round-trip coherence length, $l_c$) of the OCT subsystem is about 10% larger than the theoretical prediction for a Gaussian source with a center wavelength (λ₀) of 830 nm and bandwidth (Δλ) of 45 nm $[l_c=(2 \text{ln}(2)/\pi )\times ({{\text{λ}}_0}^2/\text{Δλ})=7 \text{µm}]$ [21]. This difference is attributed to incomplete dispersion compensation between the sample and reference arms as well as the non-Gaussian spectral shape of the source.

2.2 Data processing

The signal recorded by the OCT spectrometer, $I(k)$, is given by

$$I(k)=I_S(k)+I_R(k)+2\sqrt{I_S(k)I_R(k)}\times \cos \left(2\text{Δ}zk\right),$$ (2)

where $I_S(k)$ and $I_R(k)$ are the intensities of the light returned from the sample and reference arms at absolute wavenumber k, respectively; and $\text{Δ}z$ is the difference in optical path length between the sample and reference arms. Prior to acquiring OCT images, a pair of shutters was used to sequentially record $I_S(k)$ and $I_R(k)$ while blocking the light from the other arm of the instrument. These measurements were subracted from all subsequent ones in order to isolate the interference term. Next, the interference spectrum was remapped onto a linear wavenumber axis and a phase correction was applied to compensate for any dispersion imbalance between the sample and reference arms [22,23]. Finally, the processed interference spectrum was Fourier transformed to determine the depth-resolved reflectivity of the sample.

A number of routines were used to process Raman spectra. Background signal, including laser-induced fluorescence from the system optics, was removed by subtracing a separately-acquired background spectrum. The Raman shift axis was calibrated with polystyrene to correct for spectral instabilities in the laser diode and fluorescence lineshapes were modeled and removed with an iterative polynomial fitting routine [24, 25]. Impulsive noise (e.g., noise due to high-energy cosmic rays) was removed by (1) acquiring multiple frames per acquisition; (2) calculating the median absolute deviation among these frames on a pixel-by-pixel basis; and (3) replacing outliers with the median value at that pixel. Finally, the spectra were smoothed with a Savitzky-Golay filter [26] over a 5 cm⁻¹ window, which was chosen to approximately match the resolution of the spectrometer. Although Raman data were acquired over the full spectral range of the instrument (150 – 1950 cm⁻¹), the processed spectra were cropped for display purposes in Figs. 2, 4, and 6 below. All data acquisition and processing routines were executed in LabVIEW (version 2012, National Instruments, Austin, TX) or MATLAB® (version 8.1, MathWorks, Natick, MA).

Fig. 2.

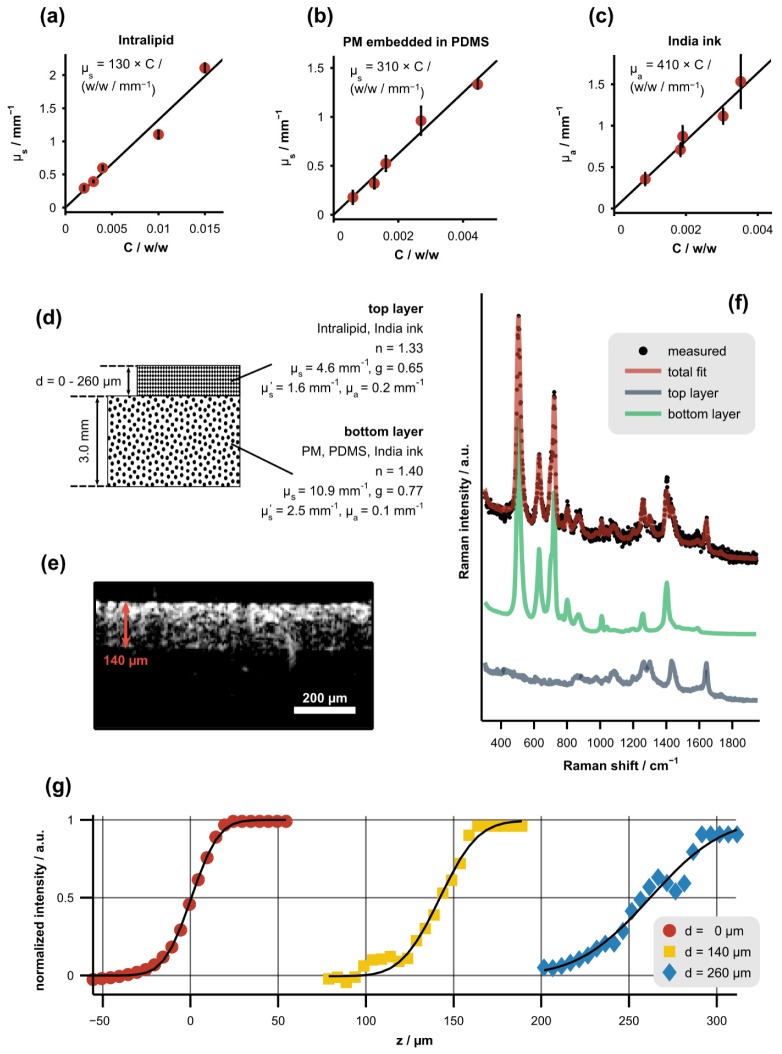
Procedure used to measure the axial resolution of the CRS subsystem as a function of sampling depth in tissue phantoms. (a)-(c) Scattering or absorption coefficient of phantom constituents versus concentration, C, along with least-squares linear fits. Error bars represent the standard deviation of each measurement. (d) Diagram depicting the optical properties (determined with 785-nm illumination) and physical dimensions of the two-layer tissue phantoms. The top layer was a mixture of Intralipid and India ink while the bottom layer was a mixture of PM, PDMS, and India ink. (e) Representative, cross-sectional OCT image of a tissue phantom with a top-layer thickness of 140 µm. (f) Representative Raman spectrum of a tissue phantom acquired near the boundary between the layers along with the corresponding least-squares fit showing the underlying spectral components (offset for clarity). (g) Normalized signal intensity of the bottom-layer spectrum versus focal position (z) for varying top-layer thicknesses, d. Each data set was fit with a Gaussian cumulative distribution function (black lines).

Fig. 4.

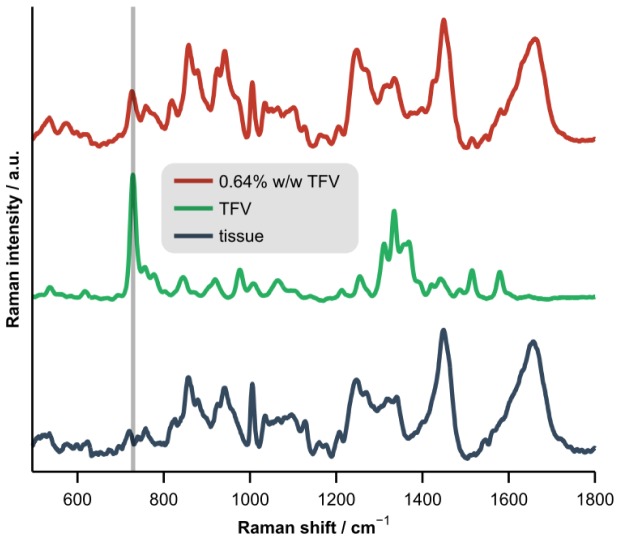
Representative Raman spectra of porcine vaginal tissue, pure tenofovir (TFV), and tissue homogenized with 0.64% w/w TFV (offset for clarity). The vertical bar highlights the spectral location of the adenine ring breathing mode near 730 cm⁻¹.

Fig. 6.

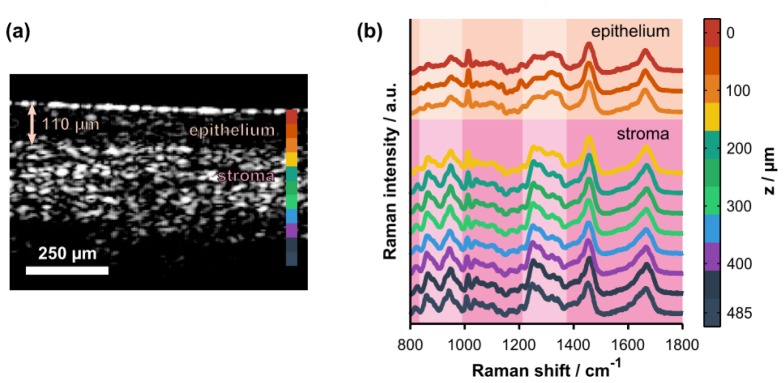
(a) Representative cross-sectional OCT image of intact, ex vivo porcine vaginal tissue. The arrow highlights the thickness of the superficial epithelium. The colorbar shows the axial locations where Raman spectra were acquired. (b) Co-localized, depth-resolved Raman spectra acquired from the same tissue sample (offset for clarity). Spectroscopic differences due to natural biochemical variation (e.g., collagen content) in the epithelium versus the stroma are highlighted by the pale-colored columns. The highlighted spectral regions include hydroxyproline and proline bands (800 – 1000 cm⁻¹) and the amide III protein band (1200 – 1400 cm⁻¹). Note that the Raman data were cropped to the 800 – 1800 cm⁻¹ spectral range for display purposes only; the full spectral range was retained for quantitative analyses.

2.3 Determination of axial resolution in biological tissue

The resolutions listed in Table 1 were measured in non-scattering samples. In turbid media (e.g., biological tissue) resolution degrades as a function of sampling depth because scattering both attenuates the ballistic signal (the primary component measured by both confocal microscopy and OCT) and obscures it with a diffuse background. Spherical aberration due to the refractive index mismatch at sample surface also degrades resolution [27].

In order to characterize the effects of scattering and spherical aberration on axial resolution, two-layer tissue phantoms were constructed and the edge response of the CRS subsystem was measured across the boundary between the layers as a function of the top-layer thickness. A diagram depicting the phantoms, including the optical properties of each layer, is presented in Fig. 2(d). The top layer was a mixture of Intralipid (Liposyn II, Hospira, Lake Forest, Illinois) and India ink while the bottom layer was a mixture of polydimethylsiloxane (PDMS), polystyrene microspheres (PM), and India ink. To fabricate the bottom layer, PM (0.25-µm radius, Duke Scientific, Microgenics Corporation, Fremont, CA) were stirred into a PDMS base agent (Dow Corning, Midland, MI) and mixed with a curing agent at a 10:1 base-to-curing-agent ratio. The solution was vortexed and sonicated to create a homogenous mixture and placed in a vacuum chamber for 45 minutes to remove air bubbles. The mixture was cured at room temperature for 24 hours.

The scattering and absorption coefficients of the phantom constituents were determined as a function of concentration by measuring the on-axis, narrow solid-angle transmission of each component [Fig. 2(a)-2(c)] in the single-scattering regime as described previously [8]. Reduced scattering coefficients were determined based upon scattering anisotropy values reported in the literature or calculated from Mie theory [28]. All optical properies were measured at the illumination wavelength of the CRS subsystem (785 nm). After determining the relationship between the concentration of each constituent and the resulting optical properties of the mixture, the final concentrations in the tissue phantoms were chosen to match the average optical properties of esophageal tissue [29–33]. We chose to model esophageal tissue because the optical properties of vaginal tissue have not been well established in the literature. Both of these tissues also have non-keratinized stratified squamous epithelia suggesting that the optical properties of esophageal tissue are a reasonable representation of those associated with vaginal tissue.

Prior to measuring each edge response, the thickness of the top layer was measured with the OCT subsystem [Fig. 2(e)]. Cross-sectional OCT images were also used to verify that the optical properties of the phantoms were homogeneous and that the layer thicknesses were constant over the entire measurement area. Next, Raman spectra were acquired as the focal position was adjusted across the boundary between the layers. The normalized signal from the bottom layer (PM, PDMS, and India ink mixture) was determined by least-squares fitting and is plotted in Fig. 2(g). This subfigure shows that the edge response broadens as the sampling depth increases. Finally, each edge response was fit with a Gaussian cumulative distribution function,

$$F\left(z\right)=\frac{1}{2}\left[1+\text{erf}\left(\frac{z-d}{\sigma \sqrt{2}}\right)\right],$$ (3)

where erf is the error function, z is the focal position or sampling depth, d is the thickness of the top layer, and $\sigma$ is the standard deviation of the underlying Gaussian function. The relationship between sampling depth and axial resolution, defined as the full-width at half maximum $[\text{FWHM}=2\sqrt{2\ln \left(2\right)}\sigma ]$, is shown in Fig. 3(b).

Fig. 3.

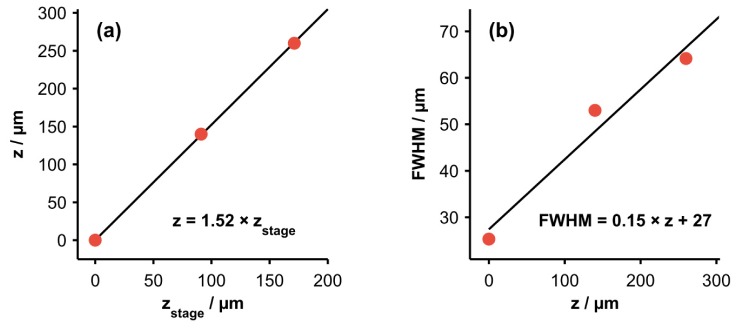
(a) Relationship between the height of the motorized translation stage, $z_{\text{stage}}$, and the CRS focal position or sampling depth, z. (b) Relationship between the axial resolution (FWHM) of CRS measurements and z. Least-squares fits suggest that both relationships are approximately linear over this range.

Because of the refractive index mismatch at the sample surface as well as light attenuation within the sample, there is not a one-to-one correspondence between axial translation of the motorized stage and the resulting change in the sampling depth of the CRS measurements [27]. In order to determine the relationship between the sampling depth, z, and the height of the motorized translation stage, $z_{\text{stage}}$, the boundary in each measured CRS edge response (defined as the point where the bottom-layer spectral intensity reached 50% of the maximum value) was compared to the known thickness of the top layer of the phantom. The relationship between z and $z_{\text{stage}}$ is displayed in Fig. 3(a). This relationship was used to calibrate the depth axis displayed in Fig. 2(g) and all subsequent figures. It should be noted that both the spherical aberration induced by the sample and the lack of one-to-one correspondence between z and $z_{\text{stage}}$ could be mitigated by utilizing a water immersion objective that reduces the refractive index mismatch at the tissue surface.

2.4 Porcine tissue samples

Fresh porcine vaginal tissue obtained from a local abattoir were used for all biological tissue measurements. First, serial dilutions of Tenofovir in homogenized tissue samples were prepared to evaluate the sensitivity of the Raman spectrometer and build a concentration prediction model. The tissue was placed in a small volume of isotonic Ringer’s solution (Hospira Inc., Lake Forest, IL), homogenized with an Omni General Laboratory Homogenizer (Omni International, Kennesaw, GA), and then stored for 24 hours in Ringer’s solutions containing different concentrations of Tenofovir. Eleven total dilutions of Tenofovir in homogenized tissue were prepared with nominal mass fractions ranging from 0 to 0.0064 (i.e., 0 to 0.64% w/w or 0 to 6.4 mg/mL) corresponding to the predicted range of concentrations delivered to the vagina by a standard-formulation gel loaded with 1% Tenofovir [1]. Each sample was separated into two homogenates: one analyzed with our CRS-OCT instrument and the other stored at −80°C and subsequently measured with gold-standard LC-MS/MS to determine the true concentration of Tenofovir. A Raman spectrum of pure Tenofovir was also constructed by measuring a sample of 2% w/w Tenofovir in Ringer’s solution and subtracting a separately-acquired spectrum of the Ringer’s solution alone.

The tissue samples measured with LC-MS/MS were diluted with water and mixed with isotopically-labeled Tenofovir (Tenofovir-IS) as an internal standard. An analytical column (XBridge C₁₈, 2.1 × 20 mm, 5 μm, Waters Corp., Milford, MA) was used to retain analytes, which were then eluted under gradient conditions. Concentration measurements were acquired with a triple quadrupole mass spectrometer (Agilent 6410, Agilent Technologies, Inc., Santa Clara, CA) using electrospray ionization and positive ion m/z transitions of 288/176 (Tenofovir) and 293/181 (Tenofovir-IS).

The Raman spectrum acquired from each homogenized sample was normalized to the spectral contribution from the tissue alone, which was determined by least-squares fitting with separately-acquired spectra of tissue and of pure Tenofovir. Next, the area under the peak near 730 cm⁻¹ (adenine ring breathing mode) [13] was calculated to predict the concentration of Tenofovir in the sample. A leave-one-out cross-validation approach based upon linear regressions of the LC-MS/MS data on the Raman-derived peak areas was used to generate the predictions. Figure 4 presents representative Raman spectra of porcine vaginal tissue, pure Tenofovir, and tissue homogenized with 0.64% w/w Tenofovir.

Following the experiments on homogenized samples, data were acquired ex vivo from intact porcine vaginal tissue. A gel layer loaded with either 0% (control) or 1% Tenofovir was placed over the tissue and the entire sample was placed in a Transwell insert (Corning, Inc., Corning, NY) as described previously [13]. The samples were incubated for 5, 60, or 120 minutes allowing Tenofovir to diffuse out of the gel and into the underlying tissue. At the end of the incubation period, the gel layer was removed, the tissue surface was cleaned with a sterile wipe, and the intact tissue was then immediately measured with the CRS-OCT system. The Raman-based prediction model developed with the homogenized samples was applied to estimate the concentration of Tenofovir in each intact tissue sample as a function of depth. Measurements were acquired up to the maximum practical penetration depth of 300 µm below the surface, which is approximately equal to the transport length or reduced mean free path of near-infrared light in the tissue.

3. Results and discussion

The cross-validated, Raman-based predictions of Tenofovir concentration in homogenized porcine vaginal tissue versus the gold-standard measurements acquired with LC-MS/MS are displayed in Fig. 5(a). The prediction accuracy was quantified by calculating the root mean squared error of cross-validation (RMSECV). Given a 10-minute integration time, the RMSECV was 0.03% w/w, which is also approximately equal to the minimum detectable concentration. More advanced chemometric methods, including partial least squares [34] and hybrid-linear analysis [35], provided modest improvements (RMSECV = 0.02% w/w for both); further improvements in prediction accuracy could potentially be achieved with a calibration set that spans a larger range of the spectroscopic variability observed in biological tissue. For comparison, a recently-developed pharmacokinetic model of drug delivery indicates that the concentration of Tenofovir delivered to the epithelium and superficial stroma by a standard-formulation gel ranges between approximately 0.05 and 0.5% w/w for up to 8 hours after application [1]. This suggests that our instrument is sensitive to physiologically-relevant concentrations of Tenofovir in tissue. The relationship between prediction accuracy and integration time is presented in Fig. 5(b). A power-law fit reveals that the RMSECV is proportional to the inverse square root of integration time, as expected for shot-noise limited detection and linear prediction models [36].

Fig. 5.

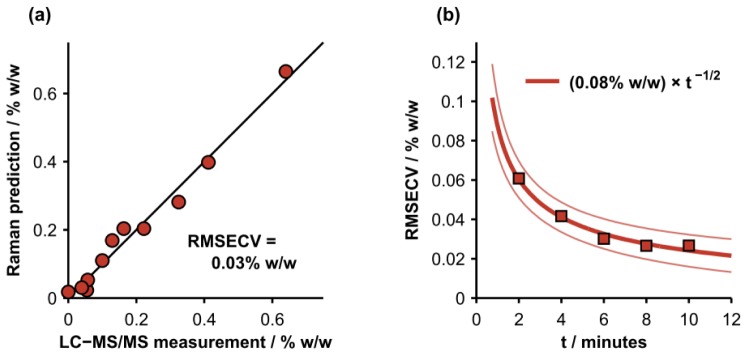
(a) Cross-validated, Raman-based predictions of Tenofovir concentration in homogenized, porcine vaginal tissue versus gold-standard measurements acquired with LC-MS/MS. The root mean squared error of cross-validation (RMSECV) was 0.03% w/w for an integration time of 10 minutes per sample. (b) RMSECV versus total integration time in minutes (t) per sample. The solid lines represent a power-law fit and the 95% confidence interval of the fit.

A representative OCT image of intact porcine vaginal tissue (prior to topical application of Tenofovir gel) along with depth-resolved Raman spectra acquired from the same location are presented in Fig. 6. Figure 6(a) shows the surface of the epithelial layer and also the boundary between the epithelial and stromal layers approximately 110 µm beneath the tissue surface. Spectroscopic differences due to variation in the biochemical properties (e.g., collagen content) of these layers are highlighted in Fig. 6(b). A comprehensive review of the biochemical and spectroscopic differences between epithelial and stromal layers can be found elsewhere [37,38].

Concentration profiles of Tenofovir in intact porcine vaginal tissue, derived from depth-resolved Raman spectra acquired after topical application of the drug, are displayed in Fig. 7. The integration time for each data point was 2.5 minutes, which provided a concentration prediction uncertainty and limit of detection of about 0.05% w/w [see Fig. 5(b)]. The average depth of the interface between the epithelium and stroma was also measured with the OCT subsystem. The combined CRS and OCT data quantify the concentration of Tenofovir delivered to the superficial epithelium versus the targeted stromal layer. The figure also shows that the overall concentration gradient is initially flat, becomes steep at an intermediate time of t = 60 minutes, and then levels at t = 120 minutes as drug equilibrates across the layers due to depletion of drug from the overlying gel layer. Future work will focus on converting these concentration profiles into fundamental molecular transport parameters such as diffusion and partition coefficients.

Fig. 7.

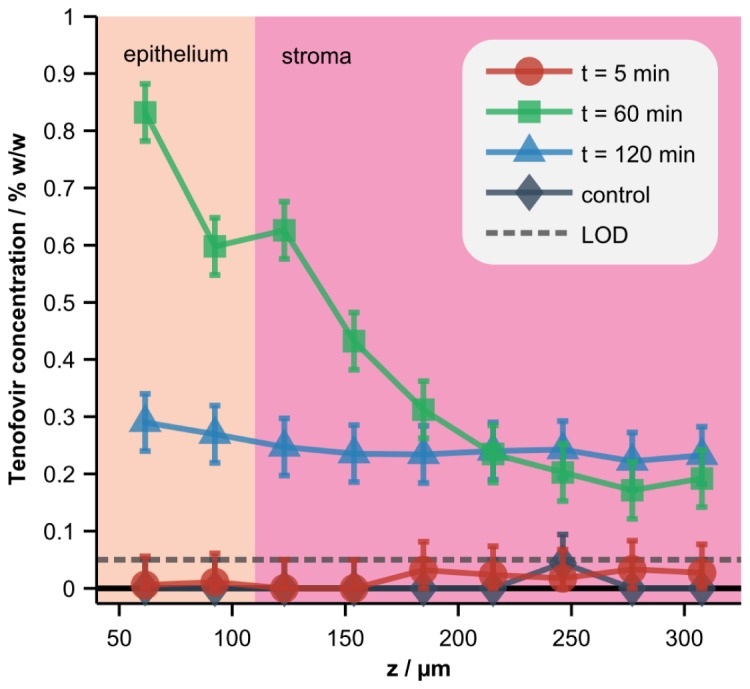
Depth-resolved concentrations of Tenofovir in tissue. A standard-formulation gel loaded with 0% (control) or 1% Tenofovir was applied to the tissue surface in a Transwell assay and the concentration of the drug in the tissue was measured at 5, 60, or 120 minutes (min) post-application. Error bars and the limit of detection (LOD), both defined as the RMSECV calculated with homogenized tissue samples (Fig. 5), are also displayed. Co-localized OCT images were acquired and used to determine the average depth of the interface between the epithelium and stroma.

4. Conclusion

This study presents a combined CRS-OCT instrument capable of acquiring cross-sectional OCT images and co-localized, chemically-specific Raman spectra with sub-100-micron spatial resolution. The instrument uses skin-safe light levels and was utilized to accurately measure depth-resolved, physiologically-relevant concentrations of Tenofovir, a microbicide drug used to prevent the sexual transmission of HIV, in ex vivo tissue samples. These results highlight the unique capacity of high-resolution CRS-OCT to evaluate analytes in targeted biological tissues. Further analysis of depth-resolved concentration profiles acquired with CRS-OCT could also lead to fundamental knowledge about the diffusion of drugs into and through distinguishable tissue layers, and the partitioning of drugs at interfaces between both the drug carrier and the tissue surface and various tissue layers [1,13]. Future applications of this instrument can therefore contribute to anti-HIV microbicide science and development, and to the analysis of drug delivery to tissue more generally.