Mapping conduction velocity of early embryonic hearts with a robust fitting algorithm

Abstract

Cardiac conduction maturation is an important and integral component of heart development. Optical mapping with voltage-sensitive dyes allows sensitive measurements of electrophysiological signals over the entire heart. However, accurate measurements of conduction velocity during early cardiac development is typically hindered by low signal-to-noise ratio (SNR) measurements of action potentials. Here, we present a novel image processing approach based on least squares optimizations, which enables high-resolution, low-noise conduction velocity mapping of smaller tubular hearts. First, the action potential trace measured at each pixel is fit to a curve consisting of two cumulative normal distribution functions. Then, the activation time at each pixel is determined based on the fit, and the spatial gradient of activation time is determined with a two-dimensional (2D) linear fit over a square-shaped window. The size of the window is adaptively enlarged until the gradients can be determined within a preset precision. Finally, the conduction velocity is calculated based on the activation time gradient, and further corrected for three-dimensional (3D) geometry that can be obtained by optical coherence tomography (OCT). We validated the approach using published activation potential traces based on computer simulations. We further validated the method by adding artificially generated noise to the signal to simulate various SNR conditions using a curved simulated image (digital phantom) that resembles a tubular heart. This method proved to be robust, even at very low SNR conditions (SNR = 2-5). We also established an empirical equation to estimate the maximum conduction velocity that can be accurately measured under different conditions (e.g. sampling rate, SNR, and pixel size). Finally, we demonstrated high-resolution conduction velocity maps of the quail embryonic heart at a looping stage of development.

1. Introduction

Cardiac electrophysiology has contributed directly to our understanding of heart diseases (e.g. arrhythmias) in the adult [1, 2]. In addition, cardiac electrophysiology has become an integral part of understanding cardiac conduction system development and cardiac development in general [3–12]. The malformation of the conduction system during development often leads to congenital heart diseases [3, 13]. Cardiac conduction system development starts at heart looping stages, when the tubular heart undergoes rapid structure changes including the formation of the primitive chambers and the emergence of cardiac cushions (precursors for cardiac valves) [14, 15]. At the same time, the conduction pattern also undergoes drastic changes, including a rapid increase of conduction velocity in the primitive atrial and ventricular region [16, 17]. On the other hand, the conduction velocity in the atrioventricular junction (AVJ) remains relatively unchanged and significantly slower than either the atrial or the ventricular region [16]. These changes are believed to be important in maintaining cardiac function during the important transition from the tubular heart to the chambered heart, and failure to establish the proper conduction pattern during these stages can eventually lead to the development of accessory pathways (e.g. Wolff-Parkinson-White syndrome or atrioventricular nodal reentry tachycardia), which can cause sudden death if left untreated [18].

Experimentally, electrophysiological recordings are taken with electrodes. However, unlike adult hearts, embryonic hearts pose many unique challenges for direct electrode recordings due to their small size and fragility. An alternative that is used for both adult and embryonic electrophysiological research is optical mapping (OM). OM uses voltage-sensitive dyes and is contact-free, achieves high spatial resolution, and accommodates a large field-of-view, circumventing many of the difficulties of electrodes and enabling direct measurement of activation time, action potential duration (APD), action potential upstroke velocity, and conduction velocity during cardiac development [11, 16, 19–22].

However, OM of hearts at very early developmental stages (e.g. linear heart tube stage or looping stage) poses some new challenges. The biggest challenge is that OM signals from early embryonic hearts often suffer from low signal-to-noise ratio (SNR). Several factors contribute to the reduced SNR. (1) The myocardium at these early stages is only 1-3 cell layers thick [23–25], which limits the number of cells that contribute to the signal. (2) Each pixel spans a very small region due to a small field of view (< 1 mm²) and therefore magnification is needed, further limiting the number of cells contributing to the signal. Hearts at looping stages have complex internal and external structures [26–28]. High spatial resolutions are preferred and binning pixels to increase SNR may not be ideal. (3) Similar to OM in adult hearts, high temporal sampling rates are required in embryonic hearts. Cardiac action potentials at the looping stages can have relatively fast upstrokes, which is on the order of several milliseconds [29], so improving SNR by increasing the integration time is not a viable option.

Low SNR poses an even greater problem for the measurement of conduction velocity compared to other measurements. Unlike primary measurements such as activation time, APD, or action potential upstroke velocity, conduction velocity is a secondary measurement based on the activation time (essentially a spatial gradient of the activation time). Difference measurements always increase the noise in a signal. The spatial gradient is made by taking a difference between adjacent pixels, which will increase the noise. However, obtaining an accurate conduction velocity map of early embryonic hearts can be very valuable, not only for studying normal conduction system development, but also for diagnosing and phenotyping congenital heart defects where conduction abnormalities may play a role. For example, the Knockout Mouse Project (KOMP) is currently collecting and analyzing roughly 20,000 knockout mice lines, of which 30% are projected to be embryonic lethal, and roughly 26% of the analyzed embryonic lethal mouse lines harbor congenital heart diseases [30]. It is reasonable to assume a subset of these lines with congenital heart defects have defective conduction system development; however, to properly phenotype them we cannot only rely on qualitative assessments such as conduction patterns, which are crude and lack statistical power. A high-resolution, quantitative, and accurate conduction velocity map can offer the statistical power needed for rapid phenotyping, because fewer embryos will be needed to achieve statistical significance. Another potential use for the conduction velocity map is drug screening. Our previous study suggested that ethanol-exposed quail embryos may have compromised conduction patterns [31], and a quantitative map would be a great help for studying the effect of ethanol exposure, and eventually for screening drugs that may rescue the detrimental effects of ethanol, such as folate [32].

The method that is currently commonly used for calculating conduction velocity was developed for OM in adult hearts and has been applied to late-stage embryonic hearts [33, 34]. It relies on temporal and spatial filtering to increase SNR so that action potential features can be accurately extracted [reviewed by 35]. Spatial filtering is generally performed with either uniform binning or a Gaussian kernel [35]. Temporal filtering is most commonly implemented with low pass filtering (e.g. Butterworth, Chebyshev, etc.) [35, 36]. Once the action potential curve is sufficiently smoothed, parameters such as activation time (defined as the mid-point of the upstroke phase) [7, 22, 37] and action potential duration (e.g. APD90, defined as the interval from activation time to 90% repolarization time) can be extracted. We choose the midpoint of the upstroke for our activation time instead of the often used (dV/dt)_max because for non-uniformed conduction, it was shown to be a more reliable parameter for local activation time [7], although in our case, the midpoint of the cumulative normal curve is identical to the time of (dV/dt)_max and both definitions yield the same results. Secondary measurements, such as conduction velocity, can also be calculated from the measured activation time [33]. However, the same method, when applied to the early embryonic heart, is often inadequate for accurate conduction velocity measurements. Generating a sufficiently high SNR signal from embryonic hearts often requires extensive use of filters, which reduces spatial and temporal resolution. Importantly, extensive use of these filters may bias the conduction velocity measurement, and this aspect has not been thoroughly examined.

In this paper, we will present an approach based on least squares optimization as an alternative to image filters. We will discuss the precision of the method in relationship to the measurement parameters, such as SNR, sampling frequency, pixel size, etc. We will also explore the potential bias of the method using a computer-generated digital phantom. We conclude that the high-resolution conduction velocity mapping is achievable for early tubular hearts, despite the low SNR.

2. Algorithm

2.1 Determination of activation time

The first step for measuring conduction velocity is to determine the time of activation at each pixel. We decided to apply a novel approach based on least squares curve fitting, which is usually very robust against noise. A function based on the cumulative normal distribution function is used to fit both the action potential upstroke and the repolarization simultaneously. The general form of the cumulative normal distribution can be expressed as

$$\Phi (x,A,\mu ,\sigma )=\frac{A}{\sigma \sqrt{2\pi }}{\displaystyle {\int }_{-\infty }^x{e}^{-\frac{{(x-\mu )}^2}{2{\sigma }^2}}dx}$$ (1)

where amplitude A, mean µ, and standard deviation σ will be determined by curve fitting later.

To reconstruct the full activation potential, we used two cumulative normal distributions (curves a, c) and a linear function (line b) to bridge the two (Fig. 1). The junction point P₁ is set at 99% of the amplitude on curve a, and P₂ is the point where line b and curve c have the same slope. Overall, the function contains seven parameters, A₁, µ₁, σ₁ for curve a, –A₂, µ₂, σ₂ for curve c, and –s for the slope of line b. All parameters in this setup will be positive and additional constraints can be applied to speed up the fit process. For example, A₁ and A₂ will be close to 1.0 if the signal is normalized, µ₂ is greater than µ₁, and σ₁ is generally small because the upstroke of the activation potential usually take place in a very short time span. After the fit, activation time is determined as µ₁, which is 50% of the maximum value [37].

Fig. 1.

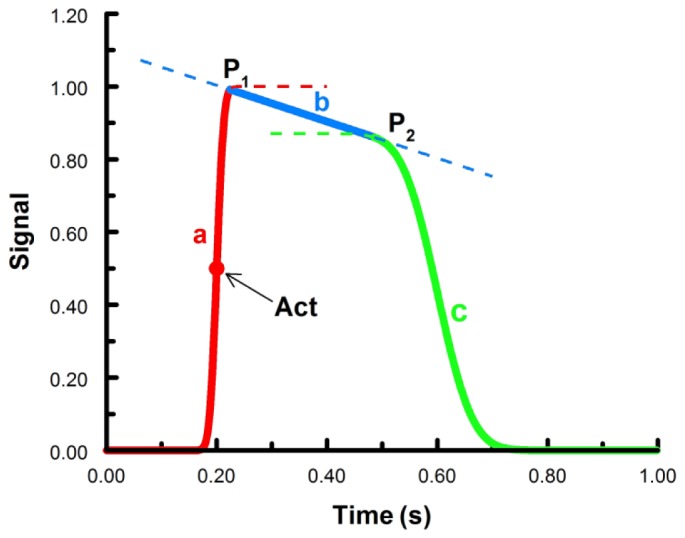
Functions to fit the cardiac action potentials. Curve a (red) and c (green) are cumulative normal distributions, line b (blue) is a linear function. P1 and P2 are junction points connecting the three functions. Together, the solid lines for a, b, and c comprise the fitted action potential. The red dot is the time of activation (arrow), which is 50% of the maximum value of the first cumulative normal. Act – activation time.

It is worth noting that the construct in Fig. 1 is not based on actual electrophysiological changes of ion channels during cardiac cell activation. The primary goal of the function is to accurately resemble actual action potential morphologies with the simplest function possible in order to extract the precise activation time. Other parameters, such as upstroke velocity and action potential duration (APD) can also be estimated from the function. Taking advantage of the built-in function in MATLAB (normcdf), cumulative normal distributions are easy to implement with a small number of parameters and high levels of robustness during fitting.

2.2 Calculation of the spatial gradient of the activation time

There are several established methods for gradient calculation in a digital image. One is the central difference method [33, 38], another is to use an edge detection filter such as the Sobel filter, this is a common method for computer graphics [39], but has not been adopted for OM signal processing. We propose a 2D linear least squares optimization method for our purposes, which is similar to the early attempt of using a second-order polynomial fit to obtain conduction vectors from adult right ventricular epicardium [34].

The central difference method is a simple two-point difference in both x and y dimensions using the immediate neighbors to the pixel under measurement. However, in regions of high conduction velocity, the differences in activation time within the window can be miniscule, especially when the distance between pixels is small. This makes it difficult to accurately determine the gradient when the SNR is low. In addition, the central difference method only utilizes information from four pixels even if a larger window is used for the calculation, leaving a large amount of information unused. Instead, we employ a 2D linear function T = T₀ + G_x⋅x + G_y⋅y to fit the activation time in an n × n window, where T₀, G_x, and G_y are the coefficients to be determined by the fit. This way, the gradients in both the x and y directions can be directly estimated from the fit. In addition, a weight factor (w) is applied to each pixel in the fit window, where w is equal to SNR² when the pixel is inside of the heart, and zero when the pixel is outside of the heart. Here, we define SNR as the amplitude of the signal divided by the root mean square (RMS) of the noise. The rationale for the weight is that activation time is measured more accurately with higher SNR, thus demanding a higher weight. Based on our subsequent analyses, the uncertainty of the activation time (measured by its standard deviation) is inversely proportional to the SNR, and weighting by SNR² will produce the best linear unbiased estimator based on generalized least squares [40]. The pixels not on the heart are weighted zero since they do not contain valid data. This allows an unbiased estimation along the edge of the heart. We also utilized a variable fit window size, where the fit window is progressively enlarged until the fit parameters can be precisely determined (for details, see Material and methods). This is essential for early embryonic heart OM because in regions of fast conduction and low SNR the OM recordings often yield unreliable fit parameters when the fit window is too small.

2.3 Correct the gradient from 2D to 3D based on the 3D structure of the heart

The gradient calculated above is only a 2D projection of the actual gradient in 3D. The details of 3D correction were described in our earlier publication [41]. Briefly, OCT can be used to obtain the 3D contour of the heart, and that information can be used to correct the gradient and conduction velocity, so they will be accurate in regions of the heart that are not parallel to the OM imaging plane.

3. Materials and methods

3.1 Quail embryonic heart preparation

Fertilized quail eggs (Coturnix coturnix, Boyd’s Bird Co Inc, Pullman, WA) were placed in a humidified, forced draft incubator at 38°C (G.Q.F. Manufacturing Co., Savannah, GA) for ~52 hours. Embryos were removed from the egg and staged by somite counting. Embryos at Hamburger-Hamilton (HH) stage 15 (somite number 25-26) were selected for imaging. The hearts were dissected in room temperature Tyrode’s solution (Sigma-Aldrich, St. Louis, MO). The hearts were then stained in Tyrode’s solution containing 10µM of di-4-ANEPPS (Life Technologies, Carlsbad, CA) for 12 minutes at room temperature. The solution was then replaced with Tyrode’s solution containing 10 µM of cytochalasin D (Sigma-Aldrich) to eliminate contraction. The embryonic heart was then placed in the center of the imaging chamber (Warner Instruments LLC, Hamden, CT) on the sample stage. The experiment environment was maintained at 38°C, and a total of two hearts were imaged to demonstrate consistency.

3.2 OM/OCT setup and imaging protocol

The multi-modal OCT/OM system was described in detail previously [41]. Briefly, our combined system included a custom-built spectral domain OCT system with a 47 kHz line rate, a center wavelength of 1310 nm, and an axial resolution of ~10 µm and lateral resolution of ~12 µm in air. The combined system also included an OM system featuring an EMCCD camera (iXon3 860, Andor Technology, South Windsor, Connecticut), which can record at 128 × 128 pixel resolution (0.88 mm × 0.88 mm field of view), with a frame rate of 500 Hz. Each imaging session lasted for 4 seconds, and the OM data sets were saved as TIFF image stacks. The 3D OCT volume (500 lines/frame, 300 frames/volume, total volume 1.5(L) × 1.5(W) × 3.1(H) mm) was recorded at the same time.

3.3 Optical pacing

Details of optical pacing of excised quail hearts are described in our earlier publication [42]. Briefly, the excised heart was exposed to pulsed infrared laser light delivered by a single-mode fiber (wavelength 1465 nm, pulse width 20 ms, spot size 12-µm diameter, radiant exposure 60 J/mm²). The pacing stimuli were delivered to the atrium of the heart, and the pacing frequency was set at 2.5 Hz, which was slightly above the intrinsic heart rate for excised hearts at HH-stage 15.

3.4 Image processing

The image processing steps were performed in MATLAB (MathWorks, Natick, MA) with custom written software. Specifically, the image processing involved the following steps:

• (a). A mask was generated based on the variance of the fluorescence signals at each pixel over the entire imaging session (2000 frames in total) to minimize the total processing time for the subsequent steps. The cutoff was determined based on a histogram-based method to avoid human intervention. A manual inspection was performed and the mask could be eroded if necessary in case the cutoff was not aggressive enough to ensure the conduction velocity measurement along the edge of the heart is accurate.

• (b). With a 4-second imaging session and pacing frequency of 2.5 Hz, there should be 10 heartbeats. Usually, only 9 of these beats are complete beats for further analyses. Data were broken into 9 segments of 200 frames each, by manually identifying the start of the first complete beat.

• (c). Each segment was processed separately to obtain the activation time based on the least squares fit using the double cumulative normal function described earlier (Fig. 1). The activation time was obtained from the fit (µ₁), and the fit SNR was calculated as the amplitude of the signal (the peak of the fitted curve) divided by the standard deviation of the fit residue. To increase the processing speed, we first normalized the signal between 0 and 1, and a prefit using a rectangular pulse function was performed to obtain a closer initial guess of the parameters µ₁ and µ₂. The fit process was performed using parallel processing.

• (d). The activation time and SNR at each pixel were used to perform the weighted 2D linear fit, to determine the spatial gradient of the activation time. The details are described in the previous section. Briefly, for each pixel, the initial weighted fit was performed with a 3 × 3 fit window, and the parameters were obtained from the least squares fit. The 95% confidence intervals for each fit parameter were used to judge if the overall fit was satisfactory (defined as <10% uncertainty for the magnitude of the 2D gradient vector). The fit window was then increased and the step was iterated until the 10% precision requirement was fulfilled, or the maximal window size was reached (maximal window size was arbitrarily chosen at 25 × 25 pixels, or about 166 µm × 166 µm). This window size is smaller than half of the width of the heart tube, and is sufficient for measuring conduction velocities as high as 100 mm/s for our imaging system (detailed discussion is in the Results section).

• (e). (optional) The measured 2D gradient vector at each pixel was averaged over 9 heartbeats, which would increase the dynamic range as long as each of the heartbeats are similar to each other. Alternatively, gradients from any single heartbeat can be processed separately to obtain beat-to-beat variation.

• (f). Gradients in the z direction were calculated based on the 3D geometry of the heart surface. The details were published previously [41].

• (g). The conduction velocity was calculated from the 3D gradient vector, and plotted on the 3D surface of the heart. The magnitude of the conduction velocity is the size of the pixel divided by the magnitude of the time gradient vector, and the direction of the conduction velocity is the same as the direction of the time gradient vector [41].

3.5 Validation of the algorithm

Ideally, the method presented here should be validated against an independent measurement. However, no current approach has the necessary spatial resolution and capability to accurately measure the conduction velocity up to 100 mm/s in the early looping heart. Therefore we used computer simulations for our validation, which is in essence a Monte Carlo approach.

3.5.1 Validation of the double cumulative normal fit

We first downloaded noise-free ventricular and atrial action potential traces from The Physiome Project (http://physiome.org/, an online collection of biophysical and physiological models) [43]. The models are based on the guinea-pig ventricular action potential [44], and the rabbit atrial action potential [45]. These traces had a high temporal sampling rate (100 kHz), which could be down-sampled to simulate different sampling frequencies (500 Hz – 10 KHz). We examined how well our function could be used to fit these traces. Next, we performed a Monte Carlo simulation by adding randomly distributed noise to the trace, to simulate data with different SNR levels. We chose normally distributed noise because the main source of noise in OM experiments is shot noise, which should resemble a normal distribution as long as a sufficiently large number of photons can be recorded. At each SNR level and sampling frequency, 100 independent traces were generated and fit to the function described in Fig. 1. The bias could be measured by comparing the activation time obtained from the fit to the theoretical value, and the precision of the fit was determined as the standard deviation of the activation time among the 100 simulations.

3.5.2 Validation of the 2D linear fit

For comparison, we modified the central difference method [33] for a larger window size rather than using only the adjacent pixels. At any given pixel position (i,j) and window size 2 × k + 1 (k = 1,2,3…), the gradient in both x- and y- direction are given by

$$\begin{array}{ccc}{G}_x=\frac{T_{i+k,j}-T_{i-k,j}}{2k}& & G_y=\frac{T_{i,j+k}-T_{i,j-k}}{2k}\end{array}$$ (2)

where T_i,j is the activation time at pixel position (i,j).

We also compare with gradient estimation using the Sobel filter. The Sobel filter is a traditional 3 × 3 image gradient operator. We modified the filter to accommodate larger window sizes based on the following iterated process [46, 47],

$$sob(1)=\frac{1}{8}\cdot \left[\begin{array}{ccc}-1& 0& 1\\ -2& 0& 2\\ -1& 0& 1\end{array}\right]$$ (3)

$$sob(k+1)=\frac{1}{16}\cdot \left(\left[\begin{array}{ccc}1& 2& 1\\ 2& 4& 2\\ 1& 2& 1\end{array}\right]\otimes sob(k)\right),k=1,2,3,\mathrm{...}$$ (4)

where $\otimes$ denotes the 2D convolution operation. The gradient estimate can be obtained by

$$\begin{array}{ccc}{G}_x=sob(k)\otimes A& & \end{array}\begin{array}{cc}& G_y=sob{(k)}^T\otimes A\end{array}$$ (5)

where T is the transpose operator, A is the original image of the activation time, and k is the desired window size.

Ventricular action potentials were arranged in a 25 × 25 array to establish a uniform conduction pattern (14 mm/s with a 30 degree angle from the x-axis), with the appropriate amount of noise being independently added to each trace. The activation time at each pixel was obtained with the double cumulative normal fit and fed into each method to calculate the spatial gradient of the activation time at the center pixel. After 100 repeats, the results were compared to the theoretical values to determine both accuracy and precision for each method.

3.5.3 Validation of conduction velocity calculations with non-uniform conduction pattern

We first constructed a curved “digital phantom”, which resembled part of the heart tube at the looping stage. The phantom was constructed using two concentric quarter circles as the inner edge and outer edge of the “heart tube”. The conduction velocity at each pixel was parallel to the direction of the “tube” with a magnitude given by the equation V = r × (v₁ × sin(2θ) + v₂), where r is the distance from the upper left corner to the pixel in question, θ is the angle between the x-axis and the line connecting the upper left corner and the pixel in question, and v₁ and v₂ can be adjusted to achieve a minimal conduction velocity of 1.0 mm/s, and a maximal conduction velocity of 100 mm/s. This phantom behaves similarly to the actual heart tube with higher conduction velocity in the middle “ventricle region”, and higher conduction velocity at the outer edge. Noise was added to obtain different simulated SNR levels. Due to long calculation times, we only tested this curved phantom at an SNR of 4.0, which was the typical SNR level for our raw OM signals. A weighted 2D linear fit with an adaptive window size was performed and the resulting conduction velocity map was compared to the theoretical conduction velocity map.

4. Results

4.1 Measuring activation time with a least squares fitting algorithm

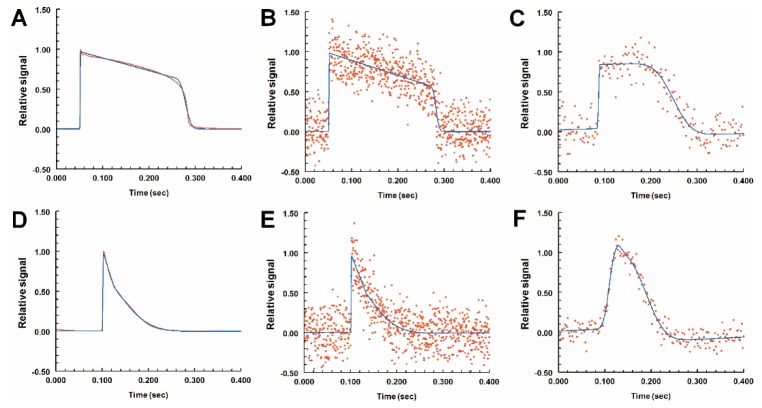
Although the function we used (Fig. 1) resembled a cardiac action potential, we could not properly validate goodness of fit with the actual action potential traces obtained from our OM experiments, since we could not obtain noise-free signals. Published computer simulated models of guinea-pig ventricular [44] and rabbit atrial action potentials [45] were used as an alternative to validate our method. These model action potential traces are noise-free and their activation time can serve as gold standards [48] for comparisons with our measurements. Shown in Fig. 2, both the ventricular action potential (red trace in Fig. 2(A)) and atrial action potential (red trace in Fig. 2(D)) fit quite well to our function (blue traces in Fig. 2(A) and 2(D)). There were minor differences in the ventricular action potential, mostly during the repolarization phase, but the depolarization phase overlapped very well with the fit function, suggesting the fit could measure the activation time with high accuracy.

Fig. 2.

Least squares optimization to fit cardiac action potential curves. Red lines are noise-free action potentials of adult ventricular cells (A) or atrial cells (D). Red dots (B and E) are computer-generated signals based on the noise-free traces from A and D respectively with Gaussian-distributed noise to simulate OM recordings (sampling frequency 2000 Hz, SNR 4.0). Panels C and F are actual recordings from a stage-15 quail heart, at the ventricle and atrium respectively. The signals are displayed as relative fluorescence for comparison purposes. The blue lines (A-F) are the fit lines using the function described in Fig. 1. The added noise did not significantly alter the fit (blue lines, A vs. B, or D vs. E).

Our next step was to simulate the actual OM signal by adding random Gaussian noise to the noise-free traces (red dots in Fig. 2(B) and 2(E)). The trace was down-sampled (500 - 10,000 Hz) to mimic OM imaging at different frame rates. The noise magnitude was adjusted to mimic different SNR levels. Figure 2(B) and 2(E) show such simulated signals (2000 Hz sampling frequency and SNR of 4.0). The blue lines denote the fit function to these noisy data, and they differed from the original signals in Fig. 2(A) and 2(D) only slightly. For comparison purposes, Fig. 2(C) and 2(F) show the actual recordings from a quail embryonic heart and the fit functions. The function fit the data reasonably well. Using simulation, we can also study the influence of random noise to the measurement of activation time. We repeated the procedure of adding randomly distributed noise 100 times at each SNR level and sampling frequency. The activation time was recorded in each case, and the average from the 100-simulations (dots in Fig. 3) could then be compared to the gold standard (dashed lines in Fig. 3). Based on these results, we can conclude that the fit method has very little bias as long as the SNR is above 4. Even at SNRs between 2 and 4, the activation time could be measured very accurately with a bias well below 1.0 millisecond, and always well below the temporal sampling period. Typically, higher frame rates increased the measurement accuracy at lower SNRs. At sampling frequencies of 5 kHz or 10 kHz, the measurements were highly accurate and they were omitted from the plot.

Fig. 3.

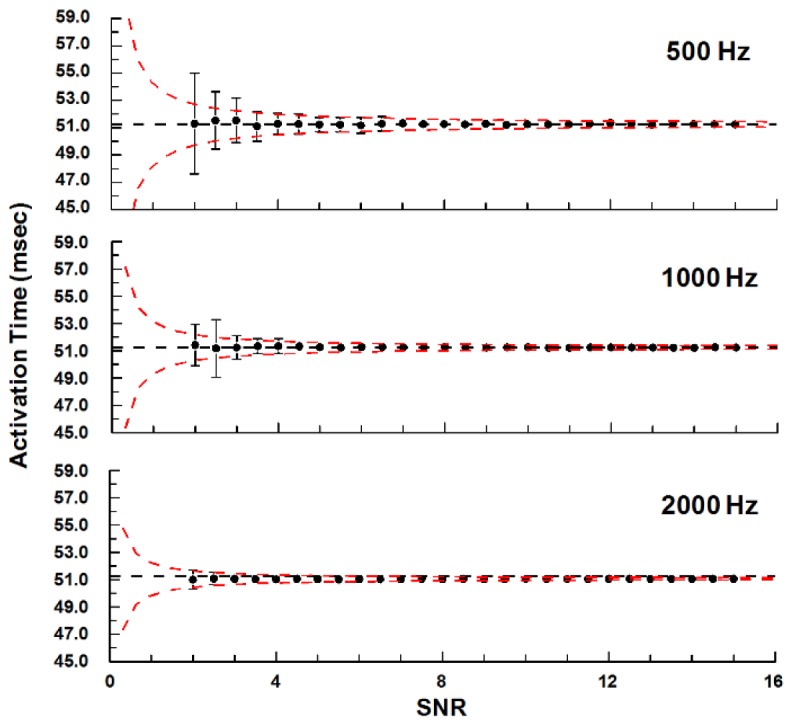
The fit method was accurate for a wide range of SNRs and sampling frequencies. The gold-standard activation time was determined from the noise-free model of a ventricular action potential (Fig. 2(A)) and plotted as the dashed lines. Each dot represents the average of 100 simulations with different random noise patterns, and the error bars are standard deviations. Simulations were performed at SNR levels between 2 and 15 with sampling frequencies of 500, 1000, or 2000 Hz (5k and 10k Hz were omitted from the plot). The red dashed lines are predictions of the fit precision based on power-law equations using the standard deviations from SNRs of 4-15.

In addition, we computed the standard deviation of the measured activation time (error bars in Fig. 3), which represented the level of precision of the method for a particular SNR. This measurement noise was more notable compared to the bias, especially for low SNRs. We compared the standard deviations at SNRs of 4-15 and sampling rates between 0.5 and 10 kHz, and they appeared to follow power laws. Least squares fit to a power-law equation gave us the following empirical equation that could be used to predict the standard deviation of the measurement (r² = 0.96):

$$S.D{.}_{activation\_time}(s)\cong \frac{0.19}{Sampling\_rate{(Hz)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\times SNR}$$ (6)

For our OM system with a sampling frequency of 500 Hz and typical SNR of 4, our measurement precision would be about 0.7 milliseconds based on this estimation. At lower SNR (2-4), the standard deviations were generally larger than what the equation predicted, especially with slower sampling frequency, but the discrepancies were usually no larger than 2-fold.

4.2 Determination of the gradient of activation time

To compare the three algorithms (central difference, Sobel operator and 2D linear fit), we first constructed a computer simulated “phantom” that was 25 × 25 pixels in size. We used the noise-free model action potential trace mentioned earlier, shifting them in time to construct a uniform conduction pattern with a conduction velocity of 14 mm/s at a 30 degree angle from the x-axis. We chose a velocity of 14 mm/s because it is the median velocity based on our previous measurements [41]. Random Gaussian noise was added to each trace independently to simulate different SNRs. Since our pixel size (6.9 µm) is much larger than our optical resolution (1.9 µm), noise from adjacent pixels are likely to be independent from each other. We verified the noise independency by examining 90 randomly selected pixel pairs in actual data collected from our OM experiments and the noise from adjacent pixels were not correlated (data not shown).

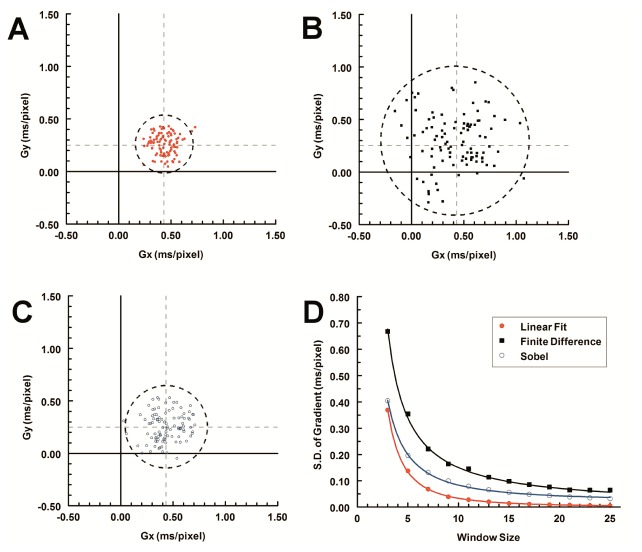
After the activation time was determined based on our fit function, the gradient can be calculated using any of the three methods. They all showed no overall bias when the gradient was uniformly distributed in the fit window (Fig. 4(A)-4(C)), however, the 2D linear fit method showed the highest level of precision. The level of precision is displayed by the circle whose radius represents two times the standard deviation. The 2D linear fit had the smallest S.D. (Fig. 4(A)), S.D. = 0.13 ms/pixel), the central difference had the largest S.D. (Fig. 4(B)), S.D = 0.35 ms/pixel), and the Sobel filter method was in between (Fig. 4(C)), S.D. = 0.20 ms/pixel).

Fig. 4.

2D linear fit method (A, red closed circles) was more precise than the central difference (B, black squares) or Sobel filter (C, blue open circles). Dashed cross-lines are the set value for the gradient (Gx = 0.43 ms/pixel, Gy = 0.25 ms/pixel), and the dashed circles represent mean ± 2 × S.D. (n = 100, 5 × 5 window size, SNR = 4) of each method. Each method became more precise with larger window sizes (D), and solid lines in (D) were trend lines using power-law functions. The linear fit method had the smallest standard deviation in all conditions.

In addition, all three methods became more precise with larger window sizes (Fig. 4(D)). The decrease of the standard deviations followed power laws. The 2D linear fit method had the quickest decline and followed an inverse square relationship with the length of the fit window. The central difference method was only inversely proportional to the length of the fit window, and the Sobel method was in the middle, proportional to the −1.5 power of the length of the window.

Finally, we arbitrarily chose a threshold of 10% as our targeted precision level so that the S.D. of the gradient was no more than 10% of the magnitude of the 2D gradient vector. When the precision is too low (e.g. Fig. 4(B)), the possibility exists that the large range of measurements might overlap the origin and result in an inaccurate gradient amplitude close to zero, which corresponds with a conduction velocity close to infinity. In addition, the conduction direction would be highly inaccurate with a range as large as 180° (Fig. 4(B)). With higher precision (e.g. Fig. 4(A)), both the amplitude and direction can be measured more accurately. For example, a 9 × 9 window is needed with the 2D fit method to reach a precision level of 10% when the activation time gradient is 0.5 ms/pixel (Fig. 4(D)). Comparing the three techniques using a 9 × 9 window the conduction velocity (14.0 mm/s) and angle (30°) were much more accurate and precise using the 2D linear fit (conduction velocity - 14.0 ± 0.7 mm/s, and the direction of conduction - 29.8 ± 3.8°) compared to the Sobel method (conduction velocity - 14.3 ± 2.3 mm/s, and the direction of conduction - 30 ± 10°) and central difference method (conduction velocity - 14.2 ± 3.8 mm/s, and the direction of conduction - 31 ± 15°).

Referring to the curves in Fig. 4(D), the influence of other parameters such as sampling frequency, SNR, or the pixel size on conduction velocity measurement can also be examined. After a least squares fit with the power-law equation, we derived an empirical equation to estimate the maximum conduction velocity that can be accurately measured at a 10% precision level,

$$V_{\max }(mm/s)\cong \frac{0.11\times Sampling\_rate{(Hz)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\times SNR\times {(\max .window(mm))}^2}{pixel\_size(mm)}$$ (7)

In our specific system (frame rate = 500, SNR = 4, and pixel size = 6.9 µm), we chose the maximal window size to be approximately half of the width of the heart tube (166 µm, or 25-pixel window). The maximal conduction velocity we could accurately measure with the aforementioned parameters would be about 110 mm/s, which should accommodate our intended measurements of the early-stage looping heart [16, 41].

4.3 Determine the gradient in a heart-like digital phantom

In the embryo heart, the conduction velocity is spatially non-uniform. If the window size is too large and the conduction velocity is varying significantly within the window area, this could potentially bias the measurement. To test this, we created a different digital phantom that closely resembles the tubular heart with non-uniform conduction velocity ranging from 1 to 100 mm/s (Fig. 5(A)).

Fig. 5.

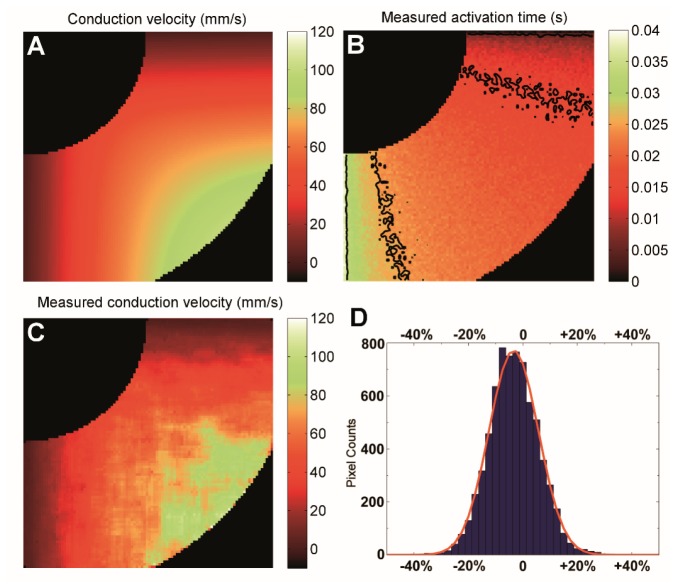
The heart-like digital phantom. The phantom was bordered by two concentric circles with a width of about 0.42 mm. The conduction was from the upper right corner to the lower left corner with a velocity ranging from 1 to 100 mm/s. (A) Preset conduction velocity, (B) Measured activation time with noise added to simulate an SNR of 4 (isochrone lines representing 10 ms spacing without spatial averaging to reflect the influence of noise), (C) Measured conduction velocity, and (D) Histogram of the bias, the red solid line was the fit to a Gaussian distribution.

To obtain the gradient, we first calculated the activation times at each pixel using the fitting function described in Fig. 1. The resulting isochrone map indicated a conduction pattern from the upper right corner to the lower left corner with the expected noise level consistent with an SNR of 4 (Fig. 5(B)). However, it was difficult to directly relate such a time map to the expected conduction velocity map (Fig. 5(A)), and it is particularly difficult to judge the direction of the conduction. Next, we performed the weighted 2D linear fit. When computing the gradient near edges, the fit window may contain pixels outside of the mask. Since those pixels do not contain valid data, a weight of zero was given to any pixels outside of the mask. All other pixels were weighted by SNR² to de-emphasize pixels that have low SNR. Based on Eq. (6), the precision of measured activation time is inversely proportional to SNR. The common method [40] for weighted least squares fits is to use the reciprocal of the variance (1/σ²) of the measurement as the weight factor, and in our case it will be proportional to SNR².

Since the conduction velocity is non-uniform, a smaller fit window is preferred to minimize potential bias, although a larger fit window may sometimes be required for sufficient precision. Therefore, we utilized an iterative approach using a progressively enlarged fit window until the fit precision was less than 10% of the measurement. The fit precision can be estimated based on the 95% confidence intervals for each fit parameter. The final fit window size is generally related to the SNR and the conduction velocity, and because the phantom had a uniform SNR of 4, the window size distribution correlated well with the magnitude of the conduction velocity (data not shown). After the desired window size was reached, the conduction velocity in this phantom was measured (Fig. 5(C)) fairly closely to the expected values (Fig. 5(A)). We compared the measured conduction velocity to the expected value at each pixel and computed the relative bias as a percentage of the expected value. The result was plotted as a histogram (Fig. 5(D)). The measured conduction velocity, when plotted as relative bias to the set values, distributed as a normal distribution (red line in Fig. 5(D)) with a relative bias of −3.3%, and a standard deviation of 9.6%. In other words, the measured conduction velocity was 96.7 ± 9.6% of the set values. The standard deviation was very close to the 10% threshold, indicating the algorithm performed as expected in limiting the precision to within 10%.

4.4 Demonstration of conduction velocity mapping in HH-stage 15 embryonic quail hearts

We next applied the method to OM data obtained from HH stage 15 quail hearts. We optically paced the excised hearts at 2.5 Hz to minimize the effect of heart rate on conduction velocities [42]. Four seconds of data were collected and nine complete heartbeats were analyzed. We first constructed the conventional activation time map using the isochrone display projected on the 3D surface of the heart tube (Fig. 6). Based on the map, we could qualitatively visualize conduction velocity based on how dense the isochrone lines were in any given region. For example, the outer curvature of the ventricle had a less dense population of isochrone lines, suggesting a higher conduction velocity, whereas regions on the inner curvature and regions close to the outflow tract or atrium displayed denser isochrone lines, suggesting slower conduction velocity. However, this visualization is not very quantitative, and when comparing multiple hearts, only large differences in conduction velocity can be identified. A smaller change, for example, a 10-20% change of conduction velocity, would be very difficult to identify. The conventional color scheme of isochrone maps also leads to false impressions of uniformity. For example, the largest block in Fig. 6 was colored solid green, although the conduction velocities within this block were certainly different (the outer rim, for example, would have much higher conduction velocity).

Fig. 6.

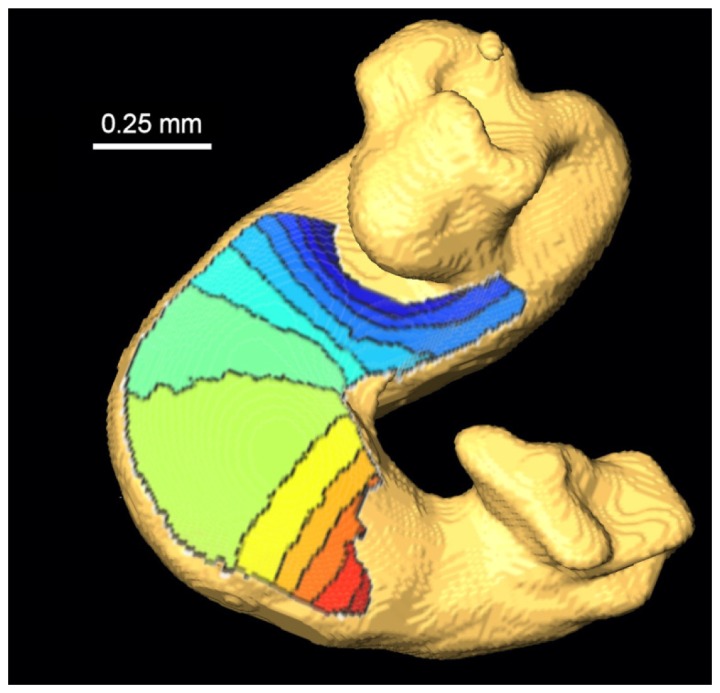
Activation isochrone map of a HH-15 quail embryonic heart. The conduction propagated from blue to red (early to late), with each line representing a 10-ms interval. The plot is the result of the average of 9 consecutive heart beats. The isochrone map was projected on the surface of an OCT volume representing the tubular heart. Regions around the atrium and outflow tract were removed from display due to increased noise levels caused by being out-of-focus.

Next, we computed the conduction velocity of each individual heartbeat. The results are shown in Fig. 7(A), with all 9 heartbeats showing consistent conduction velocity patterns. By having conduction velocity maps for all 9 heartbeats, we could study beat-to-beat variation of conduction, or further reduce the measurement noise by averaging. When averaging multiple heartbeats, pixels with inconsistent gradients among the 9 heartbeats could be removed from the final display, most of which were in regions of the outflow tract and were out-of-focus. The averaged conduction velocities were calculated from the averaged gradient, and the resulting conduction velocity map was smoother (Fig. 7(B)). It is worth noting that the averaging needs to be performed on the gradient, because the velocity is in essence the reciprocal of the gradient and the noise pattern is no longer normally distributed. With this averaging, we could further extend the dynamic range of our conduction velocity measurement (at 10% precision). By modifying Eq. (7), we can derive a similar equation

$$V_{\max }(mm/s)\cong \frac{0.11\times Sampling\_rate{(Hz)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\times SNR\times {(\max .window(mm))}^2}{pixel\_size(mm)}\times \sqrt{n}$$ (8)

where, n is the number of heartbeats (assuming the noise patterns from different heartbeats are independent). This averaging is valid as long as each heartbeat is expected to be identical to the next. This assumption was typically valid for normally developing hearts (Fig. 7(A)). For abnormally developing hearts that exhibit arrhythmia, such averaging may not be valid, depending on the type of arrhythmia. The quiver plot was also generated from the conduction velocity map to illustrate both the magnitude and the direction of the conduction velocity vector (Fig. 7(C) and 7(D)). Without the use of additional spatial averaging, the quivers from nearby pixels showed high levels of consistency both in magnitude and direction.

Fig. 7.

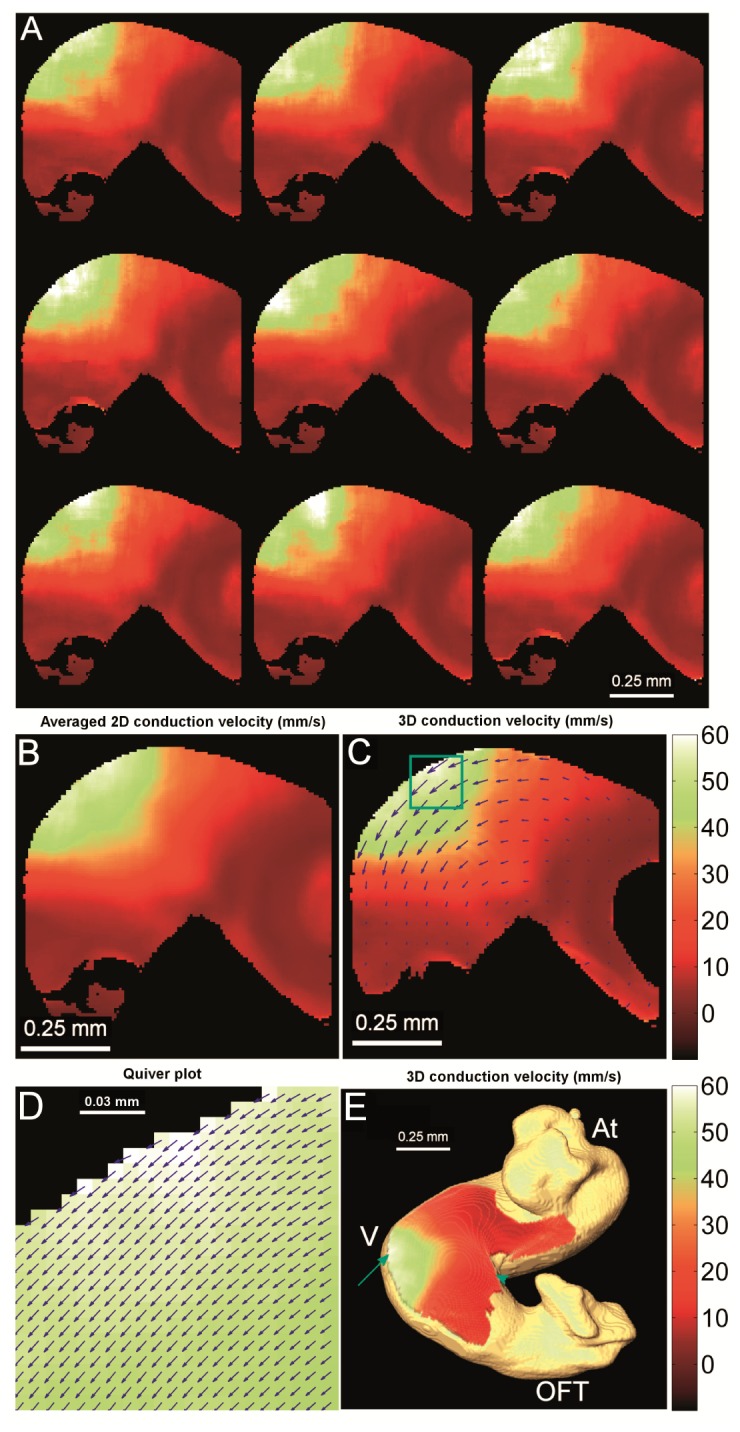
Conduction velocity map of a HH-stage 15 quail heart. (A) Conduction velocity maps calculated from each individual heartbeat, showing consistent conduction velocity patterns. (B) Averaged conduction velocity from all 9 heartbeats. (C) 3D corrected conduction velocity based on the 3D structure obtained from OCT. A quiver plot indicates the direction of conduction, and the length of the quiver was proportional to the 3D corrected conduction velocity. To make the quivers visible, only every eighth pixel horizontally and vertically was displayed. (D) The enlarged view of the quiver plot on every pixel inside of the green box in (C) showed consistent quiver directions. (E) 3D corrected conduction velocity map, projected on the 3D surface of the heart. The colorbars are in mm/s and represent the conduction velocity for all the panels. At – Atrium, V – Ventricle, OFT – outflow tract, red arrow – outer curvature of the ventricle, and blue arrowhead – inner curvature of the ventricle.

We determined the velocity vector direction and magnitude by utilizing the 3D structure of the heart [41]. Standard OM systems can only measure conduction in 2D, essentially a projection of the actual conduction that can happen in 3D. We have developed a method to project the velocity vector back to 3D using structure obtained from OCT. The results are presented in Fig. 7(C)-7(E) and have been shown to be more accurate than standard OM measurements [41].

To demonstrate repeatability, we examined the conduction velocity in two HH-stage 15 hearts. In each heart, the highest conduction velocity was found at the outer curvature of the ventricle (arrow in Fig. 7(C)) as expected from the isochrone map (Fig. 6), while the inner curvature of the ventricle had a much lower conduction velocity. These measurement were consistent between hearts as shown in Table 1 (results are shown as mean ± S.D. over a 3 × 3 pixel region).

Table 1. Conduction velocity (mm/s) at different regions of the tubular heart (HH-stage 15).

	Outer curvature of the ventricle	Inner curvature of the ventricle
Embryo 1	58.9 ± 0.8	6.5 ± 0.3
Embryo 2	68.8 ± 1.2	4.8 ± 0.2

5. Discussion

Optical mapping with voltage-sensitive dyes can record action potentials with high spatial resolution over large regions of interest, which is essential for studying embryonic heart electrophysiology. However, the SNR obtainable from the embryonic heart are much lower in comparison to recordings of the adult heart and conventional image processing algorithms are inadequate for obtaining activation time and conduction velocities. Here, we have presented a technique capable of extracting these measurements in very low SNR conditions. The algorithm relies on least squares fitting to measure the activation time, and the gradient of the activation time. This method is non-biased with high precision over a large range of SNR and sampling frequencies (Fig. 3).

With a Monte Carlo approach, we were able to derive an empirical equation to estimate the precision level of this fitting method (Eq. (6)). The equation accurately estimates precision for SNRs above 4 and slightly underestimates them when the SNR is between 2 and 4. One can improve the precision by raising the SNR, which increases inversely to the standard deviation. Another way to improve precision is to increase the sampling frequency, however, this has less impact since the standard deviation is only inversely correlated to the 2/3 power of sampling frequency. Also, increasing the sampling frequency will often result in decreased SNR due to reduced integration time, Eq. (6) can be used to evaluate the tradeoff to devise an optimal imaging protocol.

For gradient calculations, we employed a progressive window size with the weighted 2D linear fit. Although gradients can be calculated utilizing just the adjacent pixels, noise levels increasingly interfere with obtaining accurate gradient measurements as conduction velocities increase. For example, our activation time precision is ~0.7 ms at an SNR of 4 and a sampling rate of 500 Hz, yet the activation time differential between adjacent pixels can be as low as 0.1 ms for HH-stage 15 quail hearts. A larger window size is therefore sometimes needed to achieve high precision (Fig. 4). More importantly, a larger window size greatly benefits the 2D linear fit because all the information within the window can be utilized unlike the central-difference method that only employs information from four pixels. The Sobel filter, despite also using all the information within the window, was developed in the late 70s when computational power was very low, it was optimized for speed [39] and not necessarily for accuracy. Additionally, the Sobel filter cannot be used when there are missing data (e.g. along the edges of the heart).

Using a larger window size can bias the gradient measurement in regions where the conduction velocity is not uniformly distributed, both in amplitude and direction. We therefore demonstrated that our method could accurately measure conduction velocities on a computer simulated heart-tube-like phantom mimicking the non-uniform conduction velocities present in HH-stage 15 quail hearts (Fig. 5(B) and 5(C)). Specifically, the overall bias was only −3.3% even when utilizing window sizes up to 25 × 25 pixels (Fig. 5(D)). The situation in the real tubular heart can be more complicated and potentially vary from heart to heart. Since the bias is caused by non-uniform conduction velocity, the degree of the bias is therefore knowable and can be corrected if the exact distribution of the conduction velocity is known. In theory, the measured conduction velocity map can be used as an initial step to iteratively correct the bias, but this is beyond the scope of this study.

Similarly, we derived an empirical equation to predict the upper limit of the conduction velocity a particular OM system can accurately measure (Eq. (7)). It is no surprise that increasing SNR or temporal sampling frequency extends the range of conduction velocities that can be measured. Smaller pixel size offers higher spatial sampling frequency, and based on Eq. (7) can also extend the range of measurable conduction velocity. The effects of the maximum fit window size, however, are complicated. On one hand, larger window sizes offer more pixels for the fit, thus reducing the standard deviation of the conduction velocity estimate. On the other hand, it can potentially introduce larger bias when the conduction velocity is not uniform. It therefore becomes a tradeoff of dynamic range and bias, and has to be evaluated on a case-by-case basis.

Quantitative comparisons of conduction velocities among cohorts of embryonic hearts are difficult due to large measurement noise (e.g. 3D geometry, or inaccurate image processing method). The total variances (both biological and technical) are estimated to be about ± 30% for OM of looping-stage hearts [16, 41], and the technical variances are major contributing factors [41, 42]. This greatly limits our ability to compare cohorts of hearts with potentially different conduction velocities unless a large number of hearts are imaged. Limiting the contribution of measurement noise can greatly improve the efficiency when comparing hearts exposed to different conditions (e.g. gene knockout or environmental toxin exposure such as ethanol). To achieve such a goal, we applied two other techniques we developed recently. First, the excised hearts were paced with infrared light at the atrium [49]. We choose optical stimulation because electrical point stimulation is not applicable in early embryos due to difficulty in positioning, tissue fragility, and poor spatial precision and electrical artifacts [42]. Since many electrophysiological parameters (e.g. conduction velocity) have shown a frequency dependency [42], controlling the heart rate with optical pacing makes comparisons between hearts easier and more reliable. Another technique we applied is 3D correction of conduction velocities using structure information supplied by OCT imaging [41] (Fig. 6 and 7(C)). OM, as a 2D imaging method, requires the tissue to be relatively flat. With embryonic hearts, there are always complex 3D structures involved that cannot be flattened easily due to the fragile nature of the sample. This could potentially be a bigger problem when abnormally developed hearts are imaged, because they do not necessarily orient the same way as normal hearts, and comparisons could be difficult until these velocities can be corrected in 3D. In combination with our improved image processing algorithm, we demonstrated great consistency of conduction magnitude and directions among nearby pixels (Fig. 7(C)-7(E)). Our conduction velocity map also showed regions of fast conduction and slow conduction (Fig. 7(E)). The conduction velocity was much higher at the outer curvature of the ventricle (~60 mm/s) than at the inner curvature (~6 mm/s). We verified the pattern in another heart at the same developmental stage (HH-stage 15), and both showed similar values in each of the two regions (Table 1). Overall, by driving down measurement noise, we could detect differences in conduction velocities with limited number of embryos in the future. This could greatly increase the throughput required for large scale phenotyping project, e.g. the knockout mice project (KOMP) [30].

It is difficult to directly validate our measurements with independent experimental approaches. The previous study using an electrode reported a much slower conduction velocity in the ventricle (17 mm/s at HH-stage 13, and 48 mm/s at HH-stage 17) [50]. Recent optical mapping of chicken hearts demonstrated that ventricular conduction velocity increased from 2.3 mm/s at HH-stage 10 to 168 mm/s at HH-stage 18, using a different method [16]. The measured conduction velocity of about 60 mm/s at HH-stage 15 by us is in good agreement to this trend. The earlier electrode recording potentially underestimated the maximum conduction velocity by missing the region with the highest velocity (only two electrodes were used to calculate conduction velocity). Our measurements are also significantly faster than the previously reported ventricular conduction velocity measurements of hearts at similar stages using the central-difference method (17-30 mm/s for HH-stage 15 hearts) [41], although other regions with slower conduction velocity showed similar results. This is possibly due to the inability of the central difference method to obtain an accurate measurement when the conduction velocity is high. Conduction velocity at the ventricle was much noisier using the central-difference method [41], suggesting the 2D linear fit is a significant improvement for measuring fast conductions.

One of the limitations of the fitting approach was the processing speed, especially the initial step of obtaining activation time. Fitting a function with seven independent parameters is computationally intensive. Some steps were taken to increase the processing speed. We limited the search range for each parameter (see Method section), and the program used parallel processing in MATLAB to further decrease the time. The fitting function typically took 5 minutes of computation time for a single heartbeat (128 × 128 pixels) on a computer with Intel Xeon X5650 processors (12-core, 2.67 GHz, 24G RAM). All other steps of the algorithm are significantly faster. A data set consisting of 10 heartbeats would require a total of one hour of post-processing time. However, the complexity involved is linear to the size of the image or the number of heartbeats, therefore it is a tractable problem. With improved computing power, optimization of the algorithm and code, and the possibility of GPU computing, the time could be significantly reduced in the future.

In conclusion, we developed an alternative image processing method based on least squares optimization to calculate cardiac conduction velocity in early embryonic hearts. Coupled with optical pacing to control the heart rate and 3D geometry correction of the conduction velocity, these methods together can deliver accurate measurement of the conduction velocity in the developing heart. Using these tools, we have observed that the conduction velocity in the outer curvature of the ventricle is much faster than the rest of the ventricle. Recently, Bressan et al reported that connexin 40 (Cx40) expression is significantly elevated in the same outer curvature region of the ventricle at a similar developmental stage, while the expression remains very low in the inner curvature of the ventricle or in the atrioventricular junction [16], offering a potential explanation of the observed increase in conduction velocity. The difference in connexin expression could result in large changes in the conduction velocity and this will require further experimentation to confirm. Combined with molecular staining, the conduction velocity map can offer important insights into the development of the cardiac conduction system, which can eventually benefit diagnosis and treatment of congenital heart disease in humans.