Baseline Shape Diffeomorphometry Patterns of Subcortical and Ventricular Structures in Predicting Conversion of Mild Cognitive Impairment to Alzheimer’s Disease

Abstract

In this paper, we propose a novel predictor for the conversion from mild cognitive impairment (MCI) to Alzheimer’s disease (AD). This predictor is based on the shape diffeomorphometry patterns of subcortical and ventricular structures (left and right amygdala, hippocampus, thalamus, caudate, putamen, globus pallidus, and lateral ventricle) of 607 baseline scans from the Alzheimer’s Disease Neuroimaging Initiative database, including a total of 210 healthy control subjects, 222 MCI subjects, and 175 AD subjects. The optimal predictor is obtained via a feature selection procedure applied to all of the 14 sets of shape features via linear discriminant analysis, resulting in a combination of the shape diffeomorphometry patterns of the left hippocampus, the left lateral ventricle, the right thalamus, the right caudate, and the bilateral putamen. Via 10-fold cross-validation, we substantiate our method by successfully differentiating 77.04% (104/135) of the MCI subjects who converted to AD within 36 months and 71.26% (62/87) of the non-converters. To be specific, for the MCI-converters, we are capable of correctly predicting 82.35% (14/17) of subjects converting in 6 months, 77.5% (31/40) of subjects converting in 12 months, 74.07% (20/27) of subjects converting in 18 months, 78.13% (25/32) of subjects converting in 24 months, and 73.68% (14/19) of subject converting in 36 months. Statistically significant correlation maps were observed between the shape diffeomorphometry features of each of the 14 structures, especially the bilateral amygdala, hippocampus, lateral ventricle, and two neuropsychological test scores—the Alzheimer’s Disease Assessment Scale-Cognitive Behavior Section and the Mini-Mental State Examination.

INTRODUCTION

Alzheimer’s disease (AD) is a progressive neurodegenerative disorder that is predominantly diagnosed in people over 65 years of age [1]. It is the most common form of dementia, which is characterized by trouble with thinking and language as well as a loss of long-term memory. The cause and the mechanism of progression for most AD cases are still unknown. AD worsens during its progression until death and currently there are no treatments that can cure or reverse this progression. Definite diagnosis of AD can only be made based on histopathologic evidence obtained from a biopsy or autopsy [2]. Mild cognitive impairment (MCI) is a syndrome that is regarded as a risk state for dementia [3] and is associated with an increased risk of progression to probable AD [4]. More than half of the individuals with MCI deteriorate to dementia within 5 years [3] at a rate of about 10% to 15% per year. Considerable heterogeneity exists among MCI patients: some convert to AD with varying progression rates, and others remain stable for a long period of time or even revert to normal cognitive status. In this article, the former is named MCI converters (MCI-C) and the latter is named MCI non-converters (MCI-NC). Specifically, in this study, the MCI-C subjects converted to the AD status within 36 months from their baseline while the MCI-NC did not.

The ability to identify an MCI patient’s risk of developing AD is important for clinical decision making and timing therapy. Structural neuroimaging measures have been shown to be sensitive to the degeneration that occurs in MCI and AD [5], which may provide robust biomarkers for predicting the conversion from MCI to AD. Methods of detecting MCI that represents prodromal AD would aid clinical practice by allowing attention to be focused on those with the highest risk of conversion. However, accurate prediction of the MCI-to-AD conversion is very challenging [6], especially when utilizing only the baseline information. This difficulty is due to the “lag” between brain atrophy and cognitive decline. The MCI-to-AD prediction can be regarded as a classification problem between the MCI-C and the MCI-NC. During the last decade, there have been many methods developed, using structural imaging, to differentiate between MCI-C and MCI-NC [6–20]. A majority of the studies focusing on the prediction of MCI-to-AD conversion were based on the information from a single scan, the baseline dataset. Recently, longitudinal structural features have been proposed as better biomarkers for the prediction of MCI conversion. For a more comprehensive literature survey of previous work on predicting the MCI-to-AD conversion using structural imaging biomarkers, we refer the reader to [15].

There are typically three different types of structural MCI-to-AD predictors. The most widely used one is the cortical thickness [6,7,13,15,17–20] because this measurement is very sensitive to small structural changes in the cortex. The second measurement is the volume of specific structure of interest, such as the hippocampus [6,14,19] and the amygdala [14]. The third type of predictors is the biomarkers obtained from whole brain based analyses. To be specific, methods such as the voxel-based morphometry analysis have been suggested to locate the most discriminative regions that are then taken as the biomarkers for the MCI-to-AD prediction [6,8,10–12,15].

In recent years, the single-scan based shape diffeomorphometry patterns of subcortical and ventricular structures have been implicated to provide important anatomical information in characterizing the difference between healthy controls (HC) and MCI as well as AD [21–28]. In diffeomorphometry, one utilizes the diffeomorphisms stemming from a fixed coordinate system (the template space) to study the shape morphometrics [29] of the target groups rather than the shapes themselves. In our previous study [28], we have demonstrated the diffeomorphometric abnormalities detected in MCI and AD populations, when compared with HC, of the fourteen subcortical and ventricular structures: the left and right amygdala, hippocampus, thalamus, caudate, putamen, globus pallidus, and lateral ventricle. In a continuation of the previous work, we herein propose a method for the prediction of MCI-to-AD conversion using the diffeomorphometry-based shape features of those same fourteen structures in the baseline data consisting of 210 HC subjects, 175 AD subjects, and 222 MCI subjects, among which 87 MCI subjects did not deteriorate to AD within 36 months from baseline.

The shape features are obtained in the framework of large deformation diffeomorphic metric mapping (LDDMM) [30], in which a diffeomorphism is computed as the end point of an energy-minimizing path (a geodesic) through the group of diffeomorphisms. Given a fixed template, the anatomical variability in the targets is encoded by the geodesics from the template to each target. The fundamental “conservation of momentum” property of these geodesics [31] allows for representing the entire flow of a geodesic with the initial momentum configuration. This means that, once a template is fixed, the space of initial momenta becomes an appropriate linear vector space [32–34] for studying shape. Anatomical patterns that are specific to MCI and AD can therefore be studied by applying linear statistical techniques, such as principal component analysis (PCA), to the initial momentum vectors, which was already demonstrated in [26,28].

In this experiment, the primary training process, including feature extraction and dimensionality reduction, was performed on the baseline HC and AD subjects while the optimization over possible structure combinations utilized the addition of the baseline MCI subjects. The testing process was carried out on the baseline MCI subjects. Such a design comes from the observation that the differences, in terms of the shape diffeomorphometry patterns, between MCI-C and MCI-NC are similar to those detected between AD and HC, which has been shown in [28]. It has also been reported that other patterns of change, within the brain, of MCI-C are similar to those of AD while those of MCI-NC are similar to HC [35]. Predicting the conversion from MCI to AD using classifiers built from HC-versus-AD information has also been successfully demonstrated in [35–38].

In this article, we first describe the procedure for generating the possible HC-versus-AD linear discriminant analysis (LDA) classifiers to be used in the prediction of MCI-to-AD conversion, which are built from the diffeomorphometry-based shape features of subsets of the fourteen subcortical and ventricular structures from 210 HC subjects and 175 AD subjects, all of which come from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) baseline dataset. We then demonstrate the optimization procedure over possible combinations of structure-specific shape features by utilizing data from 222 MCI subjects in a 10-fold cross-validation fashion, thus yielding 10 optimal LDA MCI-to-AD predictors. After that, we cross-validate the predictors on the 222 MCI subjects, including 135 MCI-C subjects and 87 MCI-NC subjects, the conversion of which is determined by a follow-up of 36 months. At the end of this paper, we evaluate the correlation between the vertex-based shape diffeomorphometry patterns of the fourteen structures and two neuropsychological test scores for the Alzheimer dementia – the Alzheimer’s Disease Assessment Scale-Cognitive Behavior Section (ADAS-cog) [39] and the Mini-Mental State Examination (MMSE) [40].

MATERIALS AND METHODS

Data used in the preparation of this article were obtained from the ADNI database (http://adni.loni.usc.edu/). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public-private partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of MCI and early AD. Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials.

The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California – San Francisco. ADNI is the result of efforts of many coinvestigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 adults, ages 55 to 90, to participate in the research, approximately 200 cognitively normal aging individuals to be followed for 3 years, 400 people with MCI to be followed for 3 years and 200 people with early AD to be followed for 2 years. For up-to-date information, see http://www.adni-info.org/. In this study, we included data from 210 HC subjects, 222 subjects with MCI, and 175 subjects with AD. Within the MCI group, 135 subjects converted to AD (MCI-C) within a follow-up of 36 months. The conversion time within the MCI-C group is heterogeneous since an MCI patient may convert at any time over the course of 6 months to 3 years. In the case of this study, 17 subjects converted in 6 months, 40 in 12 months, 27 in 18 months, 34 in 24 months, and the remaining 17 in 36 months. For the group MCI-NC, we only included those MCI subjects that were followed for at least 3 years, yielding a total of 87 subjects in MCI-NC. Clinical and demographic data for the three groups (HC, MCI, and AD) are presented in Table 1. In brief, subjects are 55–92 years old, and are not depressed. The control subjects have MMSE scores of 25–30 and a Clinical Dementia Rating (CDR) score of 0. The subjects with MCI have MMSE scores of 23–30, a CDR of 0.5, preserved ability to perform daily living activities, and an absence of dementia. The subjects with AD have MMSE scores of 20–28, a CDR of 0.5 or 1.0, and meet the criteria for probable AD. The three groups did not differ significantly in terms of age (F = 2.53, p = 0.081). All groups differed on MMSE and CDR-sum of boxes (CDR-SB) as expected based on diagnostic criteria (all p < 0.001). Table 2 lists the demographics of the two sub-groups of MCI: MCI-C and MCI-NC. According to Student’s t-tests, the two MCI sub-groups did not differ significantly in age (p = 0.734), but had statistically significant difference in terms of both MMSE (p = 5.262e⁻⁵) and CDR-SB (p = 2.364e⁻⁴).

Table 1.

Demographic data for the three groups: Healthy controls (HC), mild cognitive impairment (MCI), and Alzheimer's disease (AD). The statistics for age, Mini-Mental State Examination (MMSE), and Clinical Dementia Rating-sum of boxes (CDR-SB) are displayed as mean ± SD

Parameter	HC Group (n = 210)	MCI Group (n = 222)	AD Group (n = 175)
Subject age (y)	76.25 ± 5.01	74.73 ± 7.55	75.28 ± 7.49
No. of male subjects	109	150	94
MMSE score	29.12 ± 1.02	27.57 ± 1.76	23.43 ± 2.01
CDR-SB score	0.03 ± 0.12	1.3 ± 0.60	4.23 ± 1.64

HC, healthy controls; MCI, mild cognitive impairment; AD, Alzheimer's disease; MMSE, Mini-Mental State Examination; CDR-SB, Clinical Dementia Rating-sum of boxes.

Table 2.

Demographic data for the two subgroups of MCI: MCI-C and MCI- NC. The statistics for age, MMSE, and CDR-SB are displayed as mean ± SD

Parameter	MCI-C (135)	MCI-NC (87)
Subject age (y)	74.39 ± 7.04	74.73 ± 7.57
No. of male subjects	81	69
MMSE score	26.68 ± 1.72	27.57 ± 1.76
CDR-SB score	1.84 ± 0.96	1.30 ± 0.60

MCI, mild cognitive impairment; MCI-C, MCI converters; MCI-NC, MCI non-converters; MMSE, Mini-Mental State Examination; CDR-SB, Clinical Dementia Rating-sum of boxes.

Image protocol and volumetric segmentation

The raw MR scans, in the format of DICOM, were downloaded from the public ADNI website (http://adni.loni.usc.edu/data-samples/mri/). Locally, the raw MR data were automatically corrected for spatial distortion due to gradient nonlinearity [41] and B1 field inhomogeneity [42]. Each subject was scanned twice with a 3D MPRAGE protocol at 1.5 Tesla. The two T1-weighted images were rigid-body aligned to each other, averaged to improve the signal-to-noise ratio, and then resampled to isotropic 1-mm voxels. Description of the rigid-body alignment algorithm is detailed in [43], wherein it served as a first step of a longitudinal registration pipeline. Averaging the two scans of the same subject allowed an increase in the signal-to-noise ratio. Volumetric segmentations of the fourteen subcortical and ventricular structures were obtained using FreeSurfer [44]. Based on the transformation of the full brain mask into atlas space, the total cranial vault value was estimated from the atlas scaling factor [45] to control individual differences in head size. The quality of the automated volumetric segmentations has been reviewed by technicians who have been trained by an expert neuroanatomist with more than 10 years of experience. Images that have been degraded due to motion artifacts, technical problems (a change in scanner model or change in the radiofrequency coil during the time-series), or significant clinical abnormalities (e.g., hemispheric infarction) were excluded from our analysis.

Baseline shape processing

The processing of the baseline shapes of all the fourteen structures for each individual subject was detailed in [28], for which we will briefly summarize the steps here. For each structure, the 2-D surface that contours the boundary of the 3-D volume segmentation was approximated by a diffeomorphically deformed atlas surface to ensure correct topology and smoothness. The deformation was created by aligning the atlas segmentations (manually labeled) and the subject segmentations (from FreeSurfer) using a multi-channel LDDMM-image mapping. More details and validation of this surface-generation methodology can be found in [28,46].

To obtain the baseline shape diffeomorphometry features associated with the surface of each structure for each individual subject, we created a common template surface for each structure using the algorithm proposed and validated in [47]. Briefly, for each single structure, every subject surface was first rigidly aligned (rotation and translation) to a common spatial position. The rigid registration algorithm computes an optimal transformation between the vertex sets of two surfaces by minimizing a score which combines registration and soft assignment. After rigid registration, each observed subject surface is modeled as a random deformation of a hidden template plus additive Gaussian noise. Given this model, the template is estimated from the subject surfaces using an approximation of the expectation-maximization algorithm, subject to some topology constraints. It is enacted by ensuring that the hidden template surface is a diffeomorphic deformation of a reference shape, called the hyper-template.

The LDDMM-surface mapping algorithm [48] was then employed to align the common template surface to each subject surface, creating the deformation associated with each structure surface of each subject. The readers are referred to [28] for more details about the mathematical foundations and the experimental steps of this procedure.

Generation of the baseline shape diffeomorphometry features

For each single structure, we generate its baseline shape diffeomorphometry features separately as follows. From each LDDMM-surface mapping, we obtain initial momentum vectors α₀ that are defined at all vertices of the template surface. The initial momentum vectors characterize the shape variations in the subject surface relative to the template surface. Similar to the “conservation of momentum” concept in physics, given the vertices on the template surface and the initial momentum vectors α₀, the evolution of the entire diffeomorphic flow is uniquely determined [31]. The initial momentum vectors α₀ encode the geodesic connecting the template surface to the subject surface. Therefore, we selected the initial momentum vectors α₀ to be our features for prediction. These vectors form an extremely high dimensional space and thus, for each structure, we performed PCA on the initial momentum vectors of all the HC and the AD subjects to construct an orthonormal basis. The initial momentum vectors of all the MCI subjects were projected onto that PCA basis. It is worth noting that, in our context, the inner product used in the PCA is derived from the Riemannian metric that leads to the geodesic equation in LDDMM. Details of PCA on the initial momentum space can be found in [32–34]. To reduce the dimension of the feature space, we retained only the first M principal components (PCs) that account for 95% of the total variance. We then selected only those PCs that show significant group difference between HC and AD. To make this selection, for each PC, we performed a Student’s t-test between the PC coefficients for HC and those for AD, and selected the PCs with a p-value less than 0.05. We also retained the corresponding PC coefficients for all the MCI test subjects. This established our training and testing features for cross-validation.

Selecting the optimal baseline classifier and validation

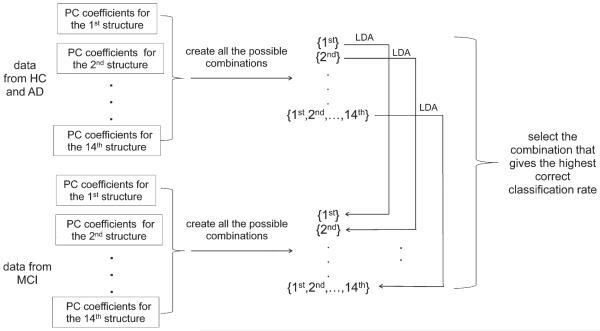
After performing PCA on the initial momentum space and an ensuing selection of PC coefficients, we had feature matrices for fourteen structures. In each feature matrix, every row contains the PC coefficients for a different subject while each column contains the coefficients for all of the projections onto a specific PC basis vector. As we have shown in [28], it is plausible that the combination of features from a subset of structures is the most discriminating. To find the optimal combination, we tested all of the possible classifiers we could build from the PCs of the fourteen structures. We used linear discriminant analysis (LDA) to construct our classifiers. Considering each possible combination, we built a total of 16383 (2¹⁴–1) different classifiers and compared their classification performance with each other. The procedure of sifting the optimal LDA classifier for the MCI-to-AD prediction is demonstrated in Fig. 1.

Fig. 1.

Flowchart demonstrating the procedure of selecting the optimal linear discriminant analysis (LDA) classifier in classifying MCI-C from MCI-NC. PC, principal component.

To estimate the accuracy of our predictor in classifying MCI-C versus MCI-NC, we adopted 10-fold cross-validation; about 22 MCI subjects (8 from MCI-NC and 14 from MCI-C) were excluded before we selected the optimal LDA classifier. To be specific, we excluded those 22 MCI subjects at the very beginning and then sifted the optimal LDA classifier based on the feature information from the other 200 MCI subjects (called “data from MCI” in Fig. 1) and the 210 HC and 175 AD subjects (the “data from HC and AD” in Fig. 1), as described in the previous section. We then used that sifted optimal LDA classifier to determine the subgrouping of the MCI subjects excluded at the beginning. The 10-fold cross-validation procedure is demonstrated in Fig. 2. It is important to notice that we would obtain a unique optimal classifier for each of the 10-fold tests. Since the test subjects were removed from both the initial PCA and the process of selecting the optimal classifier, we avoid any bias or overestimation of the accuracy of the predictor in forecasting the conversion from MCI to AD.

Fig. 2.

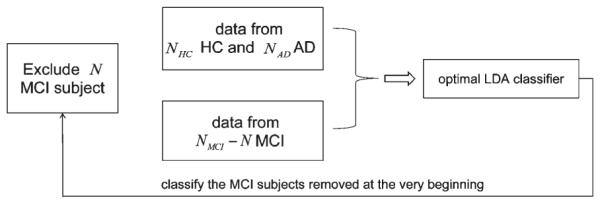
Flowchart demonstrating the procedure of performing 10-fold cross-validation without being biased by the subjects removed at the beginning. This process is repeated for the N MCI subjects in each fold. N_HC indicates the number of HC subjects, N_MCI indicates the number of MCI subjects, and N_AD indicates the number of AD subjects.

Comparison with the hippocampal volume based biomarker

The hippocampal volume has been suggested to play a critical role in predicting the MCI-to-AD conversion [6,14,19]. We therefore treat it as a benchmark for evaluating our shape diffeomorphometry based MCI-to-AD predictor. We compared the prediction accuracy from our shape diffeomorphometry informatics with that from the hippocampal volumes. Following the work presented in [19] and [6], we combined the volumes of the left and right hippocampus together. Furthermore, we did not use the HC and AD hippocampal volumes as the training features. Instead, we performed 10-fold cross-validation with respect to the MCI hippocampal volumes. To be consistent with our shape-based procedure and the two aforementioned works, we again used LDA as the classification technique. It is noticeable that in [19], the hippocampal segmentations were not obtained from FreeSurfer but from the authors’ own approach.

Correlating the shape diffeomorphometrics and neuropsychological test scores

Imaging based biomarkers would not be useful in clinical trials if they could not be significantly associated with cognitive deterioration. In this study, we evaluated the correlation between the shape diffeomorphometrics of each structure and two neuropsychological test scores (ADAS-cog and MMSE). ADAS-cog measures a number of cognitive domains, including components of memory, language, and praxis. This scale is scored from 0 to 70 with higher values indicating greater cognitive impairment. MMSE provides a continuous scale to assess primary cognitive functions that affect the dementia of the Alzheimer type, including orientation, registration, attention, recall, language, and constructional praxis [40]. The MMSE score ranges from 0 to 30. In contrast to ADAS-cog, lower MMSE scores indicate more severe cognitive impairment.

For the correlation analysis, instead of the initial momentum vectors α₀, we used a scalar field—the log-determinant of the Jacobian matrix of the diffeomorphism from the LDDMM-surface mapping. The log-determinant of the Jacobian is defined at each vertex of the template surface, quantifying the factor by which the diffeomorphism expands or shrinks the surface area at each vertex [28]. We calculated the Pearson product-moment correlation coefficients (PCCs) between the scalar field at each vertex and the two cognitive test scores, co-varying for the age, gender, and the estimated intracranial volume. Statistical significance of the correlation at each vertex is measured by a p-value obtained from non-parametric permutation tests, in which a total of 40,000 permutations were performed. Since multiple correlation tests were performed simultaneously at all vertices of the template surface, for each structure, we corrected for multiple comparison by adjusting the p-values in a way that controls the familywise error rate (FWER) at a level of 0.05 based on the “maximum statistic” method described in [49].

RESULTS

The PCA procedure resulted in 48 PCs for the left hippocampus, 49 PCs for the right hippocampus, 21 PCs for the left amygdala, 24 PCs for the right amygdala, 44 PCs for the left lateral ventricle, 39 PCs for the right lateral ventricle, 61 PCs for the left thalamus, 60 PCs for the right thalamus, 45 PCs for the left caudate, 45 PCs for the right caudate, 58 PCs for the left putamen, 59 PCs for the right putamen, 30 PCs for the left globus pallidus, and 29 PCs for the right globus pallidus. After a further reduction via the Student’s t-tests between HC and AD, we retained 9 PCs for the left hippocampus, 11 PCs for the right hippocampus, 5 PCs for the left amygdala, 6 PCs for the right amygdala, 16 PCs for the left lateral ventricle, 15 PCs for the right lateral ventricle, 8 PCs for the left thalamus, 16 PCs for the right thalamus, 5 PCs for the left caudate, 7 PCs for the right caudate, 9 PCs for the left putamen, 15 PCs for the right putamen, 6 PCs for the left globus pallidus, and 7 PCs for the right globus pallidus.

From the 10-fold cross-validation, we obtained 10 optimal LDA classifiers. For 7 out of 10, the optimal LDA classifiers came from the same combination of structures: the left hippocampus, the left lateral ventricle, the right thalamus, the right caudate, and the bilateral putamen. For 2 out of 10, the optimal combination came from four structures: the left hippocampus, the left lateral ventricle, the right thalamus, and the right caudate. For the remaining classifier, the optimal combination came from six structures: the bilateral hippocampus, the left amygdala, the right thalamus, the right caudate, and the left globus pallidus. Applying the optimal LDA selection procedure to the complete MCI sample (all 222 MCI subject), we obtained a combination of the left hippocampus, the left lateral ventricle, the right thalamus, the right caudate, and the bilateral putamen. Based on this experimental result, to predict the conversion for future MCI scans using the shape diffeomorphometry patterns built from the HC and AD population, we consider the combination of those six structures to be the optimal LDA predictor.

According to the 10-fold cross-validation results, we are capable of achieving a total classification accuracy of 74.77%, a sensitivity of 77.04% (classifying MCI-C) and a specificity of 71.26% (classifying MCI-NC). The area under the receiving operating characteristic curve (AUC) is found to be 73.81%. The accuracy of our approach in predicting the outcome for the MCI-C subjects varies depending on the subject’s conversion time. To be specific, we correctly predicted 82.35% (14/17) of the MCI subjects converting in 6 months, 77.5% (31/40) of the MCI subjects converting in 12 months, 74.07% (20/27) of the MCI subjects converting in 18 months, 78.13% (25/32) of the MCI subjects converting in 24 months, and 73.68% (14/19) of the MCI subjects converting in 36 months. Generally, the closer the MCI subject is about to convert, the more accurately the classifier can predict that conversion.

Using the hippocampal volume to predict the MCI-to-AD conversion for our MCI dataset, we successfully predicted the outcome for 57 out of 87 MCI-NC subjects and 83 out of 135 MCI-C subjects, yielding a specificity of 65.52% and a sensitivity of 61.48%. For the MCI-C subjects, the hippocampal volume predicted 58.82% (10/17) of the MCI subjects converting in 6 months, 62.5% (25/40) of the MCI subjects converting in 12 months, 62.96% (17/27) of the MCI subjects converting in 18 months, 68.75% (22/32) of the MCI subjects converting in 24 months, and 47.37% (9/19) of the MCI subjects converting in 36 months. A comparison of the prediction accuracy given by using our shape diffeomorphometry patterns and the hippocampal volumes for the dataset in this study as well as the prediction results reported in [19] and [6] are listed in Table 3. Compared with the hippocampal volume biomarker, our shape diffeomorphometry biomarker boosted the overall prediction accuracy by 12%. Comparing the prediction accuracy from the hippocampal volume biomarker applied to three different subsets of ADNI dataset (the first three rows in Table 3), we observed that all three prediction results are in the same range with only slight differences. These differences may have been caused by variations in the MCI dataset used in each study, especially the MCI-C subjects; [6] only examined MCI-Cs with conversion periods of up to 18 months which are generally considered as relatively easy cases for prediction. Also the hippocampal volumes examined in [19] were not obtained from FreeSurfer but from the authors’ own segmentation approach. This difference in the hippocampal definition may have also contributed to the slight differences in the prediction accuracy of the three works.

Table 3.

Comparisons of the shape diffeomorphometry and the hippocampal volume as biomarkers for the prediction of MCI to AD

Study	Features	Conversion period	N (MCI-NC, MCI-C)	Acc	Sen	Spe
Cuingnet et al. [6]	Hippocampal volume	0-18 months	134, 76	0.67	0.62	0.69
Wolz et al. [19]	Hippocampal volume	0-48 months	238, 167	0.65	0.63	0.67
Proposed	Hippocampal volume	0-36 months	87, 135	0.63	0.66	0.61
	Shape diffeomorphometry	0-36 months	87, 135	0.75	0.77	0.71

MCI, mild cognitive impairment; MCI-C, MCI converters; MCI-NC, MCI non-oonverters; Acc, accuracy, Sen, sensitivity, Spe, specificity.

For each of the 14 subcortical and ventricular structures, the vertex-based correlation maps between the two neuropsychological test scores (ADAS-cog and MMSE) and the shape diffeomorphometry patterns, as quantified by the log-determinant of the Jacobian matrix, are demonstrated in Fig. 3. In that figure, PCCs are assigned non-zero values only for vertices where the shape diffeomorphometry correlated statistically significantly with the corresponding score after performing multiple comparison correction by controlling the FWER at a level of 0.05.

Fig. 3.

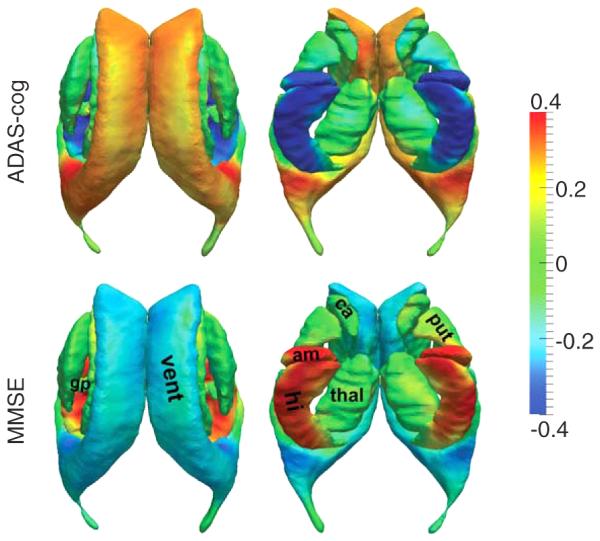
Statistically significant correlation maps between the vertex-based shape diffeomorphometrics of the 14 subcortical and ventricular structures and the values of ADAS-cog (top panel) and MMSE (bottom panel). Colors represent the Pearson product-moment correlation coefficients. For each correlation map, two views are presented. vent, lateral ventricle; am, amygdala; hi, hippocampus; ca, caudate; thal, thalamus; put, putamen; gp, globus pallidus.

As shown in Fig. 3, for a majority of vertices on each structure surface, especially the surfaces of the bilateral hippocampus, amygdala, and lateral ventricle, significant correlations were observed between the shape diffeomorphometrics and the values of ADAS-cog and MMSE. The shape diffeomorphometrics of the bilateral hippocampus and amygdala were mostly negatively correlated with the ADAS-cog value and positively correlated with the MMSE value. The opposite trend was observed for the lateral ventricle; the shape diffeomorphometrics of the bilateral ventricles were positively correlated with the ADAS-cog value and negatively correlated with the MMSE value. This observation implies that the atrophy of a majority of regions on the hippocampus and the amygdala, as well as the ventricular expansion, is indicative of the cognitive deterioration that occurs in the progression toward AD. Inhomogeneous correlation maps were observed across the surface of the basal ganglia structures and the thalamus; some vertices were positively correlated with the ADAS-cog score while others were negatively correlated. This observation may explain why, globally, the basal ganglia and the thalamus are not significantly different in the MCI and AD population when compared to normally aging subjects in general. We also notice that the spatial maps of the ADAS-cog and MMSE correlations are highly consistent with each other, revealing vertex-wise reverse correlation trends on the template surfaces.

DISCUSSION

In this paper, we proposed a new structural imaging based biomarker for the prediction of conversion from MCI to AD. The features were extracted from the shape diffeomorphometry patterns of fourteen subcortical and ventricular structures (the left and right amygdala, hippocampus, thalamus, caudate, putamen, globus pallidus, and lateral ventricle) of baseline HC and AD subjects from the ADNI database. Shape diffeomorphometry patterns offer new biomarkers in addition to the more conventional structural biomarkers: cortical volumes [6,14,18–20,50] and cortical thickness [6,7,17–20,50]. So far, there have been very few studies exploring the possibility of predicting MCI-to-AD conversion via the shape diffeomorphometry patterns in those fourteen subcortical and ventricular structures. That said, the shapes of subcortical and ventricle structures have been shown to be affected by the dementia of Alzheimer type [9,21–26,28,51,52], which may suggest discriminant features for the prediction of MCI-to-AD. The application of diffeomorphometry patterns to the classification of AD from HC has already been successfully demonstrated in several other studies [11,26,27] and one can see the possibility for this given the fact that, for a fixed template, the evolution of the target is completely determined by the deformation. In the same sense, the diffeomorphisms stemming from a single template to different targets can be used to characterize the morphometrics in those targets. Statistical inference based on the metric, the geodesic length of the flows of diffeomorphisms connecting human biological shapes, enables machine learning of the statistical representation of shape [53]. Indeed, we have found that the shape diffeomorphometrics of the 14 structures, especially the amygdala-hippocampus memory circuit and the adjacent lateral ventricles, are statistically significantly correlated with two neuropsychological test scores—ADAS-cog and MMSE (Fig. 3). This clearly suggests that the shape diffeomorphometrics can be indicative of the cognitive impairment in the pathology of AD.

In recent years, compared to single-structure approaches, multi-structure based diffeomorphometry has become widely employed in application to shape abnormality detection in various disorders [28,54,55]. In this study, we developed and validated a shape diffeomorphometry based biomarker from multiple subcortical and ventricular structures to predict the conversion from MCI to AD. To the best of our knowledge, this is the most detailed application of machine learning to diffeomorphometry markers from multiple structures and the first one applied to the MCI-to-AD prediction. Instead of using the shape patterns from all of the fourteen structures, we developed an automated feature selection procedure, as demonstrated in Fig. 1, to select the optimal subset for predicting the MCI-to-AD conversion. In our experiment, the optimal LDA predictor arises from a combination of the shape diffeomorphometry patterns of a subset containing six of the original structures: the left hippocampus, the left lateral ventricle, the right thalamus, the right caudate, and the left and right putamen. In reaching this conclusion, all the shape diffeomorphometry patterns were obtained from the HC and AD baseline datasets while the MCI baseline dataset was used in the optimization procedure to determine which combination yields the highest prediction accuracy. According to a 10-fold cross-validation, our pipeline achieved a classification accuracy of 74.77%, a sensitivity of 77.04%, a specificity of 71.26% and an AUC of 73.81%, which are superior or comparable to results reported in other classification methods (Tables 4 and 5).

Table 4.

A comparison of the success rates of various methods in predicting the conversion of MCI-C patients grouped by conversion times. The total number of MCI-C subjects used in each study is given in parenthesis

	m06	ml2	ml8	m24	m36	m48
Eskildsen et al. [15]
cortical thickness	78.7% (122)	75.2% (128)	-	69.4% (61)	69% (29)	-
cortical thickness+age	77.1% (122)	76.6% (128)	-	70.5% (61)	72.4% (29)	-
Zhang et al. [12]	50% (2)	100% (9)	87.5 (8)	80% (10)	50% (6)	66.67% (3)
Proposed method	82.4% (17)	77.5% (40)	74.07% (27)	78.1% (32)	73.7% (19)	-

MCI-C, mild cognitive impairment converters.

Table 5.

A comparison of the proposed method with previous work on predicting conversion from MCI to AD. Some results are directly obtained from the ones summarized in [15]

Study	Structures	Features	Conversion period	N (MCI-NC, MCI-C)	Acc	Sen	Spe	AUC
Zhang et al. [12]	Whole brain	VBM+PET	0-48 months	50, 38	0.78	0.79	0.78	0.77
Wee et al. [20]	Cortical	Thickness+Volume	0-36 months	111, 89	0.75	0.63	0.84	0.84
Cho et al. [7]	Cortex	Thickness	0-18 months	131, 72	0.71	0.63	0.76	NA
Chupin et al. [14]	Hippocampus and amygdala	Volume	0-18 months	134, 76	0.64	0.6	0.65	NA
Cuingnet et al. [6]	Hippocampus	Atlas based	0-18 months	134, 76	0.67	0.62	0.69	NA
-	Whole brain	VBM (grey matter)		-	0.71	0.57	0.78	NA
-	Cortex	Cortical thickness	-	-	0.7	0.32	0.91	NA
Davatzikos et al. [8]	Whole brain	VBM	0-36 months	170, 69	0.56	0.95	0.38	0.73
Koikkalainen et al. [16]	Whole brain	TBM, combination of  classifiers	0-36 months	215, 154	0.72	0.77	0.71	NA
Misra et al. [10]	Whole brain	VBM, ROIs	0-36 months	76,27	0.82	-	-	0.77
Querbes et al. [17]	Cortex	Cortical thickness	0-24 months	50,72	0.73	0.75	0.69	NA
Westman et al. [18]	Cortical and  subcortical	Thickness and volume	0-12 months	256, 62	0.58	0.74	0.56	NA
Wolz etal. [19]	Hippocampus	Atlas based	0-48 months	238, 167	0.65	0.63	0.67	NA
-	Whole brain	TBM		-	0.64	0.65	0.62	NA
-	Whole brain	Manifold learning		-	0.65	0.64	0.66	NA
-	Cortex	Cortical thickness	-	-	0.56	0.63	0.45	NA
-	Combination	Combination	-	-	0.68	0.67	0.69	NA
Liu et al. [50]	Hippocampus,  amygdala, caudate	Volume	0-12 months	79,21	0.69	0.76	0.68	NA
-	Inferior temporal and  lateral orbitofrontal	Thickness	-	-	0.59	0.62	0.59	NA
Singh et al. [11]	Whole brain	Volume deformation  Pattern	0-48 months	73,54	0.66	0.65	0.67	0.72
Leung et al. [9]	Hippocampus	Shape atrophy rates	0-12 months	128, 86	NA	NA	NA	0.67
Proposed method	Subcortical	Shape  diffeomorphometry	0-36 months	87, 135	0.75	0.77	0.71	0.74
	structure and laterary  ventricle

Acc, accuracy; Sen, sensitivity; Spe, specificity; AUC, area under the receiver operating characteristic curve; MCI-C, MCI converters; MCI-NC, MCI non-converters; VBM, voxel-based morphometry; PET, positron emission tomography; NA, not available; TBM, tensor-based morphometry; ROI, region of interest.

The performance of the LDA classifier, in the prediction of MCI-to-AD conversion, is affected by the conversion times of the MCI-C subjects (82.35% for MCI subjects converting in 6 months, 77.5% for MCI subjects converting in 12 months, 74.07% for MCI subjects converting in 18 months, 78.13% for MCI subjects converting in 24 months, and 73.68% for MCI subjects converting in 36 months). As expected, the accuracy for the prediction of MCI-C subjects that converted within 6 months after the baseline is the highest while the accuracy for those who had not converted until 36 months later from baseline is the lowest. This suggests that it is relatively easier to predict the conversion of MCI subjects who will convert sooner since their patterns have more similarities with those of AD subjects.

In a majority of existing studies on the prediction of MCI-to-AD conversion, we find a lack of details on the variability of prediction accuracy with respect to the conversion times of the MCI-C subjects. This is largely due to the fact that many studies focused entirely on the MCI-C subjects with a follow-up time of no longer than 18 months or had a relatively small number of subjects with longer conversion times. In our study, we presented the prediction results for MCI-C subjects with a variety of conversion times, and compared them with two recently published works that proceeded similarly [12,15]. The comparison is shown in Table 4. Compared with the results reported in [15], our approach is capable of achieving a higher prediction accuracy at each conversion time. However, more subjects were examined in [15]. The small number of MCI-C subjects investigated in [12] at each conversion time (2 MCI subjects that converted within 6 months, 9 MCI subjects that converted with 12 months, 8 MCI subjects that converted within 18 months, 10 MCI subjects that converted within 24 months, 6 MCI subjects that converted within 36 months, and 3 MCI subjects that converted within 48 months) makes it difficult to compare with our proposed method, considering that at least twice as many MCI-C subjects were included in our study at each conversion time. These small numbers of testing subjects are explained by the use of longitudinal and multimodality data in the classification in [12], which largely restricted the number of available subjects. A comprehensive comparison between the proposed methods and recent work on MCI-to-AD predictors is summarized in Table 5.

According to the comparison results illustrated in Table 3 and results from previous publications [6,19], the structural definitions can make a difference to the prediction accuracy; in this case, the hippocampal volumes produced by different segmentation methods vary from each other in terms of the MCI-to-AD prediction accuracy. This observation motivates us in future to adopt more advanced segmentation methods for producing more precise subcortical and ventricular structures [56], which may potentially enhance the prediction power of our shape diffeomorphometry biomarker. Another improvement may be found in looking to the class of structures we analyze. Currently, many studies are focusing on extracting features from whole brain regions [6,8,10,11,15,16,19]. It is thus natural to consider extending the proposed framework to incorporate the shape diffeomorphometry patterns from regions other than the fourteen structures analyzed herein.

In this study, the shape PCs were computed for each structure separately and then combined directly. This may potentially ignore important information since different structures may be correlated. For example, the expansion of the lateral ventricle is directly related with the compression of the hippocampus and the amygdala, which should be taken into consideration when combining the features from those three structures. Future work should focus on taking the correlation between the shape features from different regions into consideration when designing the feature matrix, similar to the work done in [20]. In addition, instead of directly grouping the shape features from different structures and then performing a single LDA, the technique of multi-kernel learning, such as those demonstrated in [57,58], may improve the results. It is likely that the clearest avenue for further exploration in this work lies in our utilization of only the baseline information. In the future, an important extension will be to incorporate longitudinal information [10,12,13,57] into the prediction procedure.

In conclusion, we have developed and validated a novel structural imaging based biomarker, for the prediction of MCI-to-AD conversion, using patterns of shape diffeomorphometry in the framework of LDDMM. These patterns were extracted from a subset of subcortical structures and the lateral ventricles, based on a training dataset of 210 HC and 175 AD subjects. The optimal combination of structure-specific shape diffeomorphometry patterns was determined using 222 MCI subjects. The procedure was validated on a total of 135 progressive MCI subjects and 87 MCI subjects who remained stable after a follow-up of 3 years. The prediction accuracy on each subgroup of MCI-C, grouped according to the conversion time, was demonstrated to be superior or comparable to previously reported results.