Modeling the Dynamics of the U.S. Healthcare Expenditure Using a Hyperbolastic Function

Abstract

In this paper, we investigate the dynamics of the U.S. national healthcare expenditures from 1960 to 2011. The data were obtained from the U.S. Department of Health and Human Services, Center for Medicare and Medicaid Services. The analytical method allows extracting the long-run deterministic trend from the cyclical and the random components. The long-run trend is estimated using six classical growth models and three more recent growth curves called Hyperbolastic growth models of types I, II, and III, denoted by H1, H2, and H3, respectively. The statistical results indicate that the H1 model provides the best fit of the data. The study is complemented by a mathematical analysis of the deterministic long-run component of the national healthcare expenditure (NHE) as modeled by H1. This analysis is performed by examining the behavior of the absolute growth rate (pace of increase curve), the relative growth rate, and the acceleration of the U.S. NHE over the 52-year time frame. To the best of our knowledge, this paper provides the first application of Hyperbolastic models to economics data. This study can be used by researchers and policy makers as a descriptive as well as a predictive tool.

1. Introduction

The U.S. national healthcare expenditure (NHE) has been consistently increasing over the past decades, placing healthcare reform at the center of political and economics debates (Blavin et al., 2012). Given that forcasting healthcare spending is critical to the design of sound fiscal policies as well as effective healthcare cost control strategies, several estimates of future healthcare expenditure have been proposed. In 2007, for instance, under the assumption that healthcare costs continue to grow at historical average relative to the gross domestic product (GDP), the Congressional Budget Office estimated that healthcare spending will reach 99% of the GDP by 2082 (CB0, 2007). In addition to emphasizing the alarming necessity to reduce healthcare spending, these unrealistically large statistics underlie the need for more reliable projections. Designing good forecasting models relies on the understanding of the dynamics of both the past and current costs. Yet, few studies have focused on describing the historical trend of the U.S. NHE. In fact, the lack of rigorous mathematical models that go beyond descriptive statistics to summarize the long run behavior of the U.S. NHE is striking. The contribution of this paper to the healthcare cost literature is twofold.

First, it models the dynamics of the U.S. NHE from 1960 to 2011 using three relatively new growth functions called Hyperbolastic models of types I, II and III and denoted by H1, H2 and H3 respectively. These models have been proven to be very useful to model biological data and describe several growth phenomena (Tabatabai et al., 2005, 2011). To the best of our knowledge, this paper provides their first application in the economics field and demonstrates that Hyperbolastic models are valuable tools in economics modeling. The analysis is based on the decomposition of the U.S. total healthcare expenditure into three distinct components: the deterministic long run trend, the deterministic cyclical trend and the random disturbance. Rather than imposing an additive or multiplicative assumption on the relationship between these different components, our approach relies on the structure of the data trend.

Second, using three criteria (the Akaike Information Criterion corrected for the sample size (AIC_c), the Mean Square Error (MSE), and the adjusted R-squared (R²)), we compare the performance of the three Hyperbolastic models with those of six classical growth functions: Cubic (Riggs et al. 2011, 2012), Logistic, Log-Logistic, Weibull, Gompertz, and Exponential models. The rating of the performance of the nine models is consistent across the criteria and suggests that among the models investigated, the Hyperbolastic growth model of type I (H1) gives the best fit to describe the U.S. NHE. Based on the best model estimated, we derive three measures of the general dynamics of the U.S. NHE: the absolute growth rate, the relative growth rate, and the absolute acceleration. We also compare some statistics calculated from the predicted values of the best model H1 with those calculated directly from the original data. Finally, we discuss the useful applicability of Hyperbolastic models to economics modeling.

Our findings can serve several purposes. First, our model summarizes the historical behavior of the U.S. NHE by presenting a big picture of its growth dynamics over time. It provides a general and rigorous overview of how healthcare expenditure has evolved over time. Furthermore, the estimated deterministic growth function can be used to forecast future values of healthcare spending in different time spans.

The paper is organized as follows. In Section 2, we review studies on the dynamics of the U.S. NHE and discuss some important issues in modeling its trend. Section 3 discusses the data. In Section 4, we describe the method and the models used in this study. Sections 5 and 6 are, respectively, devoted to the statistical estimation and the mathematical analysis of the dynamics of the U.S. NHE. We used Mathematica Version 8.0 for all computer analyses. Finally, Section 7 provides a brief discussion of the usefulness of Hyperbolastic models in economics modeling and Section 8 concludes this investigation.

2. Trend Estimation of the U.S. National Healthcare Expenditure

Previous studies on the trend of the U.S. healthcare expenditure have highlighted the sensibility of the historical behavior of healthcare spending to the time frame considered. The variability of the findings is justified by Getzen (2013) as follows: “As the unit and span of observation change, different phenomena are observed”. For instance, it has been documented that the income elasticity of health expenditure is significantly lower in the short run than it is in the long run (Lago-Peñas et al. 2013; Getzen, 2000a). Another interesting result is that the trend of the U.S. NHE is very morphing: linear in the short-run (month to month), it mutates to a logistic shape over the decades (Getzen, 2013). The variability in the outcomes of the studies is embedded in the multidimensional nature of medical spending. The most important factors explaining this changing behavior are the rapid growth rate, the sluggish adjustment to shocks that can persist for decades, and the presence of unobservable or non-quantifiable major factors such as technological progress, and new public health policies (Getzen, 2013; Friedman, 2010).

Many sophisticated models have been used to investigate the dynamics of the U.S. healthcare spending (Meijer et al., 2013; Moscone and Tosetti, 2010; Smith et al. 2009; Borger et al. 2008; Okunade and Vasudeva, 2002; Gerdtham and Löthgren, 2000). Most of these studies aimed at understanding the relationship between income and medical costs using a transformed variable (eg: healthcare costs growth rate, excess growth of healthcare costs over GDP, healthcare costs share of GDP, etc.) rather than the actual level of spending. Dealing with a transformed variable is compelling in that by reducing the variability in the data, it helps avoid many econometrics challenges (Friedman, 2010). The major drawback of these transformations is that sometimes it is the variability in the costs that needs to be investigated.

Some studies have performed a multivariate analysis of the dynamics of the U.S. NHE using the total expenditure data (Martin et al., 2011; Roehrig et al., 2009; Ginsburg, 2008; Levit et al., 2003). These models, while very useful to understand the effect of different factors at play, can be very limited or even misleading when it comes to describing or predicting healthcare expenditure at a national scale. In fact, many studies have underlined the variability of the determinants of healthcare spending depending on whether the analysis focuses on a macro perspective (global, national or state healthcare spending) or a micro standpoint (individuals, households, hospitals, etc.). For example, it has been shown that the larger the unit of observation, the weaker the association between healthcare expenditure and health status, and the stronger the correlation between medical costs and income (Lago-Peñas et al. 2013; Getzen, 2013; Getzen 2006, Getzen, 2000b). Furthermore, as pointed out by Getzen (2008), more detailed models are not necessarily more accurate to describe and forecast the dynamics of healthcare expenditures. Many good forecasting models only account for the trend and the cyclical variations in the data, with no explanatory variables.

It follows from these studies that little attention has been paid to univariate analysis of the U.S. NHE using expenditure level data. Two papers in the literature performed a univariate analysis of the dynamics of the U.S. healthcare spendings. Riggs et al. (2011, 2012) investigated the long run dynamics of the U.S. national total, private and public healthcare expenditures over forty years (from 1960 to 2000). Their methodology is based on the decomposition of the healthcare expenditures as the product of three linear components: the total population, the consumer price index (CPI), and the per capita CPI-adjusted healthcare expenditure. Each of these three components was estimated using ordinary least squares, with time as the only covariate. The goodness of fit of the regressions is based on the high value of the R-squared (greater than 96% in all their models). Under these assumptions, Riggs et al. (2011, 2012) concluded that the U.S. national total, private and public healthcare expenditure should be modeled with a cubic function of time.

Although the two foregoing studies can provide a quick snapshot of the behavior of the U.S. NHE, they are simplistic and have several weaknesses. First, the assumption that the U.S. population, the CPI and the CPI-adjusted health care expenditure have all been increasing historically at a constant growth rate is very strong and heuristic. Second, although it is well known that when the error terms are correlated, the ordinary least squares method is inefficient and the estimated standard errors are biased (Wang and Jain, 2003), these studies totally ignore the structure of the models residuals. Finally, many studies have shown that relying solely on R² as a goodness of fit measure might be misleading (Spiess and Neumeyer, 2010; Wang and Jain, 2003), and that residuals standard errors provide a better goodness of fit indicator. Our analysis addresses all these issues. First, our study covers a larger time frame (from 1960 to 2011) and, therefore, provides a broader description of the dynamics of the U.S. NHE over the years. Second, our decomposition approach of the data handles autocorrelation in the errors terms by estimating the cyclical component of the data using the product of a linear function and a trigonometric function. Furthermore, we introduce and compare more sophisticated growth models including the cubic model, and Hyperbolastic models, which are absent in the economics literature.

As Riggs et al. (2011) and Riggs et al. (2012), many studies of the dynamics of economics data assume that they have a deterministic linear long-run trend. Sometimes, when the observed data are not linear, non-linearity is removed by applying monotonic transformation to the original data. However, most historical economics time series do not exhibit a constant growth rate. They often begin with a slow growth, follow with an accelerated phase, then stabilize. Growth models have been used to describe such changing behaviors.

Some of the most predominantly used growth models are the Logistic, Gompertz, and Weibull growth models. The logistic curve is symmetric with equal period of slow and fast growth while the Gompertz curve is asymmetric with a shorter period of fast growth (Tabatabai et al., 2005). These two growth curves are characterized by a point of maximum growth rate located at a fixed proportion of their asymptotic values. This lack of flexibility reduces their adequacy to model several time series behaviors. In 2005, a family of three flexible growth models called Hyperbolastic models were introduced in the literature (Tabatabai et al., 2005). Hyperbolastic models are of three types: H1 (which generalizes the Logistic growth model), H2, and H3 (which generalizes the Weibull growth model). The Hyperbolastic growth models have been used to study several biological phenomena including infections disease outbreak (Tabatabai et al., 2005), craniofacial and stem cell growth (Bursac et al., 2006), broiler growth kinetics (Ahmadi and Mottaghitalab, 2007), the progression of cancer (Tabatabai et al., 2005; Eby et al., 2010) and stem cell proliferation (Tabatabai et al., 2011). In all these studies, their ability to accurately estimate parameters has been tested and compared to traditional growth models. In all cases, at least one of the Hyperbolastic growth models has been proven to be superior.

Unlike classical sigmoidal growth models, Hyperbolastic models have not been used to study economics variables. We refer the reader to Ramos (2012) and Jarne et al. (2005) for some applications of sigmoidal functions to business and economics. This study presents the first application of Hyperbolastic growth models to economics data. The following parametric growth functions are estimated and compared in this analysis: Cubic, Logistic, Log-logistic, Exponential, Weibull, Gompertz and Hyperbolastic types I, II, III. Table 1 in Section 4 describes the functional forms of these growth models.

Table 1. Functional forms of growth models.

Growth Model	Functional form: f(t)	Parameters with expected signs
Cubic	α + β * t + γ * t2 + θ * t3	α, β, γ, θ
Exponential	M + α * exp[−β * t]	M, α, β
Logistic	$\frac{\mathrm{M}}{1+\mathrm{\alpha }\ast exp[-\mathrm{\beta }\ast \mathrm{t}]}$	M, α, β (M > 0, β > 0)
Log-logistic	$\frac{\mathrm{M}}{1+\mathrm{\alpha }\ast exp[-\mathrm{\beta }\ast log(\mathrm{t})]}$	M, α, β (M > 0, β > 0)
Weibull	M − α * exp(−β * tγ)	M, α, β,γ (M > 0, β > 0)
Gompertz	M * exp[−α * exp(−β * t)]	M, α, β (M > 0, β > 0)
H1	$\frac{\mathrm{M}}{1+\mathrm{\alpha }\ast exp[-\mathrm{\beta }\ast \mathrm{t}-\gamma \ast arcsin\mathrm{h}(\mathrm{t})]}$	M, α, β, γ (M > 0, β > 0)
H2	$\frac{\mathrm{M}}{1+\mathrm{\alpha }\ast arcsin\mathrm{h}[exp(-\mathrm{\beta }\ast {\mathrm{t}}^{\gamma })]}$	M, α, β,γ (M > 0, β >0)
H3	M−α * exp[−β * tγ − arcsinh(θ * t)]	M, α, β, γ,θ (M>0, β >0)

Recall that $arcsin\mathrm{h}t=ln(t+\sqrt{t^2+1})$ is the inverse hyperbolic sine function of t.

3. Data

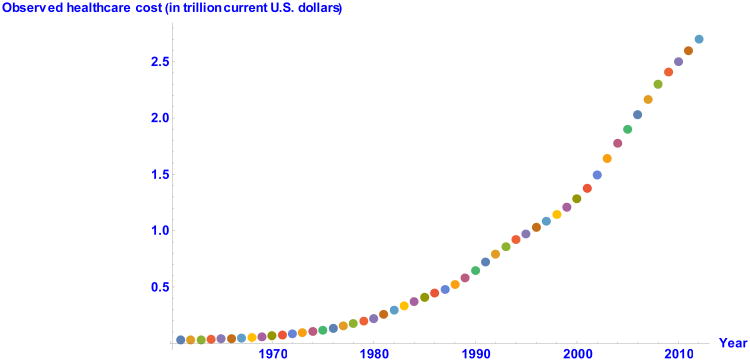
We use official estimates of the U.S. total healthcare expenditure for the years 1960 through 2011. The data were obtained from the U.S. Department of Health and Human Services, Center for Medicare and Medicaid Services¹. Figure 1 shows the dynamics of the U.S. healthcare expenditure over time.

Figure 1.

Scatterplot of U.S. national healthcare expenditure (in trillion current U.S. dollars) between 1960 and 2011. To obtain a better figure, we converted the healthcare cost from million current U.S. dollars to trillion current U.S. dollars.

4. Method and Model

A classic time series analysis decomposes the variation in the data into four components: a deterministic trend pattern, a seasonal variation², a cyclic component and a random disturbance (Chatfield, 2000). These components are usually linked to the original data with additive or multiplicative functional forms. Recall that, unlike multiplicative decomposition, the additive decomposition does not suit series that show variation in the size of the fluctuations with the level of the series.

4.1 Decomposition Method

In this subsection, we identify the different components of the U.S. NHE from 1960 to 2011. The relationship between the series and its different components is data driven and is described below.

The scatter plot of the U.S. NHE (Figure 1) clearly shows a systematic upward movement. To estimate its long-run deterministic trend, we fit the data using nine parametric growth models (these models are presented in Section 4.2). The original series is then detrended by subtracting the estimated deterministic trend from the original data. The visual inspection of the trend-adjusted series displays irregular fluctuations around zero with growing amplitude. A multiplicative model using the sine function is used to capture these fluctuations. The sine function is multiplied by an upward linear trend to account for the increase in the magnitude of the fluctuations. After estimating the cyclical deterministic pattern in all the models, we perform a cyclical adjustment of the detrended data by dividing the trend-adjusted data by the deterministic cyclical pattern. The random component of the series is the residuals obtained after removing both the deterministic trend and cyclical components from the original data. A residual analysis confirms that the random component is white noise and normally distributed. The model is summarized in the following equation:

$$Y(t)=f(t)+C(t)\ast E(t),$$ (1)

where t is the time (in years), Y(t) is the U.S. national healthcare expenditure (in million current U.S. dollars), f(t) is the growth function that models the long-run deterministic trend of, Y(t) C(t) = t * sin t is the cyclical pattern of Y(t) (which is not of interest in this study), and E(t) is the random component that represents the residuals of the time series after the removal of all the other components.

The next subsection describes the different growth functions f(t) used to select the model that best estimates the deterministic long-run trend of the U.S. health care expenditure.

4.2 Growth Models

The following parametric growth functions are estimated and compared in this analysis: Cubic, Exponential, Logistic, Log-logistic, Weibull, Gompertz, and Hyperbolastic of types I, II, and III.

In Table 1, all the parameters are real constants. M represents the maximum healthcare expenditure estimable by the model which is assumed to be constant³ for simplicity. In all the models except the cubic model, the parameter of interest is the intrinsic growth rate β which is the theoretical maximum rate at which the healthcare costs will grow with no perturbation in the economy. This measure assumes that no forces (for examples: policy intervention, recession, technological advance, diseases outbreak, etc.) other than the population growth deviated the costs from its “natural” historical trend β is usually positive for growth models, but can also be negative to model decreasing behaviors. The shape parameters α, γ and θ are nuisance parameters. The H1 model reduces to a general logistic model when γ = 0 while the H3 model reduces to the Weibull model when θ = 0 (Tabatabai et al., 2005).

5. Statistical Analysis

The predictive growth functions for the U.S. healthcare expenditure are derived by fitting the growth models described in Table 1 to the healthcare expenditure data. Using non-linear least squares, we minimize the following expression:

$${\sum }_{t=1}^n{\left[\frac{Y(t)-f(t)}{C(t)}\right]}^2.$$ (2)

The parameter estimates of the nine models are presented in Table 2. The results show that the intrinsic growth rate β is highly significant (p<0.001) in H1, Log-logistic, Gompertz, Logistic models, and has the expected sign. The estimated values are respectively 8.58%, 258.52%, 1.87%, and 10.96% for these models. The computed R² statistics (all greater than 97%) show that the data are well explained by all the models.

Table 2. Parameters estimates for the nine growth models (standard errors in parentheses).

	Models
Parameters Estimates	H1	Cubic	H2	Log-logistic	Weibull	H3	Gompertz	Logistic	Exponential
M	5.67 × 106** (0.63 × 106)	n/a	7.08 × 106** (1.50 × 106)	4.49 × 108 (5.49 × 109)	−7.54 × 106 (5.43 × 106)	0.02 × 106 (0.1 × 106)	5.86 × 107 (2.51 × 107)	3.50 × 106** (0.22 × 106)	0.06 × 106** (0.01 × 106)
α	404.25 (325.29)	16.91** (1.85)	448.57 (316.57)	4.47 × 106 (5.32 × 107)	−7.57 × 106 (5.54 × 106)	−6.02 (0.13 × 106)	7.78** (0.25)	121.23** (13.58)	−0.07** (0.38 × 102)
β	8.58 × 10−2** (0.98 × 10−2)	131.49 (149.15)	29.10 × 10−2 (15.58 × 10−2)	2.58** (0.10)	−1.18 × 10−5 (1.50 × 10−5)	−1.9 (2.5)	1.87 × 10−2** (0.21 × 10−2)	0.10**(0.51 × 10−2)	−5.31 × 10−4 (4.42 × 10−4)
γ	1404.25 (8.58 × 10−2)	1198.24 (3419.6)	10.75 ** (0.11)	n/a	2.58** 0.16	0.30 (0.18)	n/a	n/a	n/a
Θ	n/a	26436.9 (21128.2)	n/a	n/a	n/a	-6.76 (0.14 × 106)	n/a	n/a	n/a
AICC	1092.90	1093.96	1094.29	1161.53	1109.76	1113.85	1116.63	1161.53	1222.51
MSE	1.22 × 109	1.25 × 109	1.25 × 109	4.70 × 109	1.69 × 109	1.78 × 109	1.98 × 109	4.70 × 109	1.51 × 1010
R2	0.9982	0.9982	0.9982	0.9932	0.9976	0.9975	0.9971	0.9932	0.9781

Note:

^*p<0.05,

^**p<0.001

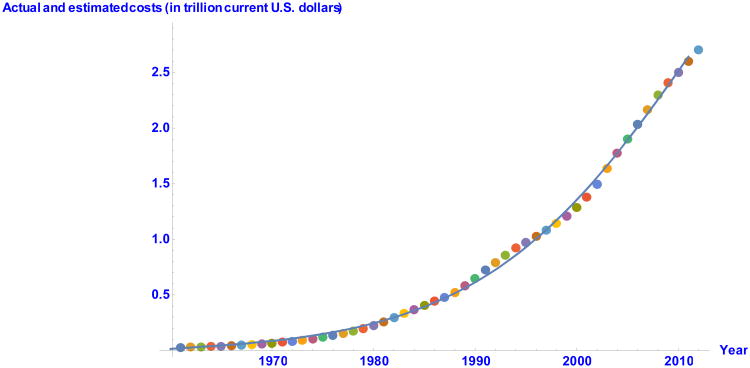
In addition to the R² statistic, we used the Akaike Information Criterion corrected for the sample size (AIC_C) and the Mean Square Error (MSE) to select the best model (see Table 2). We rank the models from the best to the worst based on the two goodness of fit measures. As depicted in Figure 2, the ranking of the models is consistent under the two criteria and is as follows. The H1 growth model provides the best fit of the data followed by the cubic, H2, Log-logistic, Weibull, H3, Gompertz, Logistic, and finally the Exponential growth curves. Figure 3 shows the observed and estimated healthcare costs based on the H1 model.

Figure 2.

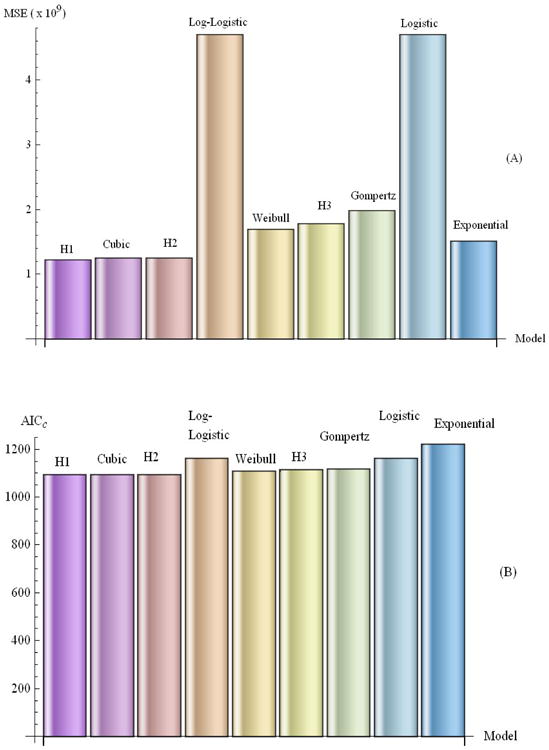
Accuracies of models in estimating healthcare expenditure. Figure 2 (A) gives the Mean Square Error (MSE) in each of the nine models used, while Figure 2 (B) depicts the corresponding Akaike Information Criterion corrected (AIC_C). Hyperbolastic model of type I (H1) ranks first among all the models used.

Figure 3.

Observed U.S. national healthcare expenditure (in trillion current U.S. dollars) compared to the estimated H1 growth curve. Hyperbolastic model of type I (H1) accurately fits the data points. To obtain a better figure, we converted the observed and predicted healthcare costs from million current U.S. dollars to trillion current U.S. dollars.

Table 3 compares some healthcare expenditure statistics calculated from the predicted values of the first two ranked models (H1 and cubic models) with their counterparts calculated from the original data. Two results are worth being mentioned. First, over the 52 years the average healthcare expenditure calculated from the original data is significantly different (at 5% level) from the one derived from the cubic model. Model H1 yields a reversed result, meaning the average healthcare expenditure predicted with H1 are not statistically different from the average healthcare expenditure calculated using the original data. Second, the average relative growth rate calculated from the observed data (8.57 %) is very close to the intrinsic growth rate estimated with the H1 model (8.58%).

Table 3. Summary statistics of actual and estimated NHE using H1 and cubic models.

	Actual Data	Predicted data (H1)	Predicted data (cubic)
Average cost (in million current U.S. dollars)	788654.05	792908.9*	797988.5
Average absolute growth (in million current U.S. dollars per year)	52419.22	53951.84	54813.66
Average relative growth (percent per year)	8.57	9.13	8.63
Average absolute acceleration (in million current U.S. dollars per year per year)	1978.36	2483.68	2953.17
Average relative acceleration (percent per year per year)	0.66	0.58	8.41

Note: All the numbers are our calculations.

^*The average healthcare expenditure calculated from the actual data is significantly different (at 5% level) from the average derived from the cubic model, but is not significantly different from the average calculated using H1. Also, the average relative growth rate calculated from the data (8.57 %) is very close to the intrinsic growth rate estimated with the H1 model (8.58%).

In the next section, we present a mathematical analysis of the dynamics of the long-run trend of the U.S. healthcare costs based on the H1 model.

6. Mathematical Analysis

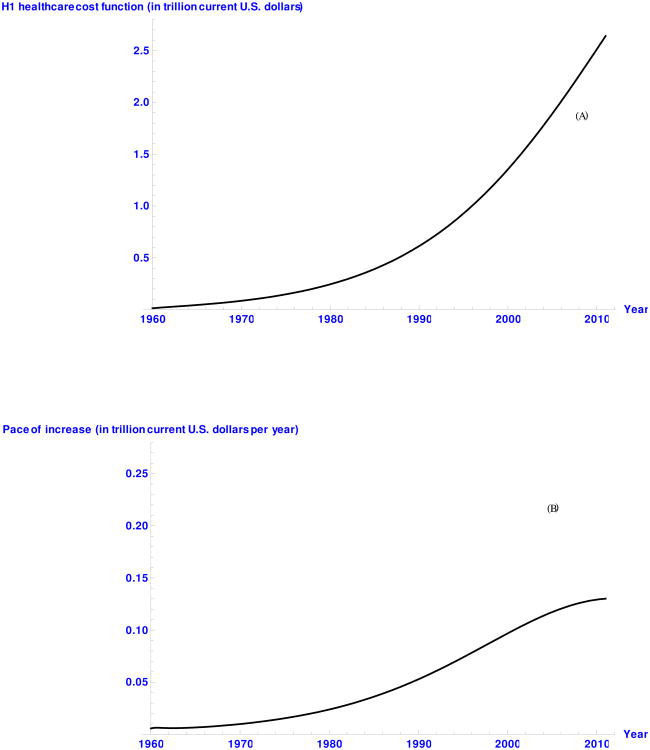
Four functions are used to analyze the growth dynamics of the U.S. NHE: the cost curve estimated in the previous section using the H1 model, the absolute rate, relative growth rate, and the absolute acceleration. The plot of each of these functions⁴ is depicted in Figure 4.

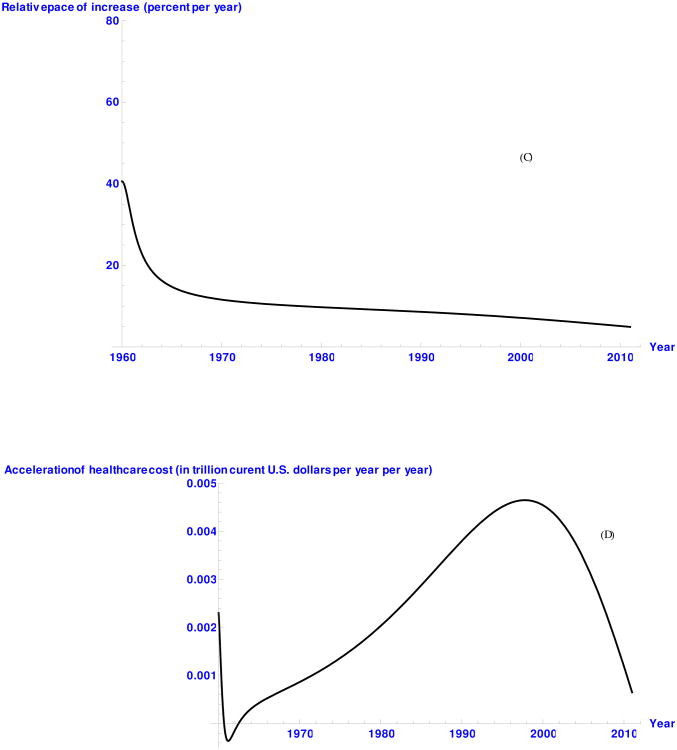
Figure 4. Curves of the growth dynamics of the U.S. NHE from 1960 to 2011: (A) Predicted healthcare cost using H1, (B) Pace of increase, (C) Relative pace of increase, (D) Absolute acceleration.

The U.S. NHE has been increasing over the years at different paces (Figure 4). When modeled with the H1 growth curve (Figure 4 (A)), it seems to have an exponential growth. However, a closer examination of the absolute growth curve (Figure 4 (B)) reveals a more complex structure: an asymmetric S-shape growth with a longer period of fast acceleration. The change in the acceleration rate over time is illustrated by the absolute acceleration (Figure 4 (D)) which helps distinguish two main phases around the point of maximum acceleration. The first phase is longer (1960 - 1997) and is overall characterized by an increasing acceleration of the U.S. total healthcare costs. At the beginning of the 1960's, the acceleration curve slightly trends down, and then rises to its highest point around 1997. The second phase is decelerating and is shorter (1997-2011). It is characterized by a relatively steeper and steadily decreasing acceleration. This suggests that the deceleration process is faster than the acceleration one.

The relative growth rate curve (Figure 4 (C)) measures the percentage change in the U.S. NHE⁵. This measure of the rate of speed of the U.S. healthcare expenditure confirms what was observed on the previous curves: historically, the U.S. total healthcare spending has been consistently increasing (relative growth rate above the t-axis) but at a decreasing proportion of the total costs.

7. Hyperbolastic Functions and Economics Modeling

Hyperbolastic models can be very useful in statistical and mathematical modeling of various increasing and decreasing economics mechanisms. Several characteristics make them suitable for economic modeling. First, two of the Hyperbolastic models generalize some traditional models extensively used in the economics field: the H1 and H3 models respectively generalize the Logistic and the Weibull models. Second, the properties of most traditional growth models make them inadequate to fit many economic variables. For example, the cubic model has a linear acceleration. The Logistic model is symmetric with an equal period of acceleration and deceleration. Although the Gompertz model is not symmetric, its point of maximum acceleration is also at a fixed location. The exponential model assumes an exponential growth and acceleration. Tabatabai et al. (2005) illustrated the flexibility of Hyperbolastic models and demonstrated their ability to fit a wide range of symmetric and asymmetric shapes including linear, exponential, polynomial and sigmoidal shapes. The flexibility of Hyperbolastic models makes them suitable to describe economics data measured by various variables (for examples, level and growth) and in different time frames (short, medium, and long run). This specifically applies to the U.S. healthcare expenditure growth data which has been shown to have different shapes in different time spans.

Hyperbolastic models can also be used to extrapolate future values of economics variables in the short and medium runs. The advantage of the extrapolation method (compared to other forecasting approaches such as micro-simulation and general equilibrium models) is that it relies only on statistical estimations rather than an economics model (Friedman, 2010). Given that the assumption that past patterns will repeat in the long run is unrealistic, Hyperbolastic models might not be appropriate for long-term predictions.

8. Concluding Remarks

The behavior of the U.S. total healthcare expenditure is complex and difficult to model. Although some studies have claimed that in the long-run, its growth curve is sigmoidal (Getzen, 2013), formal models of the historical trend of total healthcare costs are almost absent in the literature. In this work, we investigated the long-run dynamics of the U.S. healthcare expenditures from 1960 to 2011 by introducing the three Hyperbolastic growth models in the economics literature. These models are discussed from the medical biology literature. We compared their performance with those of six well known growth functions (Cubic, Logistic, Log-Logistic, Gompertz, Weibull, and Exponential). We found that the Hyperbolastic model H1 provides the best approximation of the long term behavior of the U.S. healthcare costs. This analysis underlines the potential of Hyperbolastic functions to accurately describe and predict economics phenomena.

For future work, it might be of interest to use the generalized Hyperbolastic growth models to investigate the effects of various economics factors (such as GDP, technological progress) on healthcare spending. Also, future healthcare expenditure could be forecast using the estimated model and the results could be compared with those of classical prediction models.