Statistical methods for association tests of multiple continuous traits in genome-wide association studies

Summary

Multiple correlated traits are often collected in genetic studies. The joint analysis of multiple traits could have increased power by aggregating multiple weak effects and offer additional insights into the etiology of complex human diseases by revealing pleiotropic variants. We propose to study multivariate test statistics to detect SNP association with multiple correlated traits. Most existing methods have been based on the GEE approach without explicitly modeling the trait correlations. In this article, we explore an alternative likelihood based framework to test the multiple trait associations. It is based on the familiar multinomial logistic regression modeling of genotypes, can be readily implemented using widely available software, and offers very competitive performance. We demonstrate through extensive numerical studies that the proposed method has competitive performance. Its usefulness is further illustrated with application to association analysis of diabetes-related traits in the Atherosclerosis Risk in Communities (ARIC) Study.

Introduction

Multiple correlated traits are often collected in genetic studies. The joint analysis of multiple traits could have increased power by aggregating multiple weak effects and offer additional insights into the etiology of complex human diseases by revealing pleiotropic variants. We propose to study multivariate test statistics to detect SNP association with multiple correlated traits.

There are several existing methods for multiple traits association analysis. For example, the canonical correlation analysis proposed by Ferreira and Purcell (2009) is computationally fast but does not accommodate covariates. Liu et al. (2009) proposed GEE model (Liang and Zeger, 1986) for combined analysis of one continuous and one binary trait. Yang et al. (2010) proposed adaptively weighting the univariate test statistics and assessed the P-values via computationally intensive permutations. Rasmussen-Torvik et al. (2010) explored averaging multiple related traits to gain more accuracy and detection power. O’Reilly et al. (2012) proposed a proportional odds regression modeling of genotypes to study multiple traits. van der Sluis et al. (2013) proposed a trait-based association test using an extended Simes procedure (TATES) that combined the univariate trait p-values while correcting for the correlations among the multivariate traits. He et al. (2013) modeled the marginal distributions of multivariate traits with generalized linear models, and empirically accounted for the dependence via the GEE sandwich variance. A closely related and similar approach is the GEE based scaled marginal association test of Schifano et al. (2013), which also works for multiple secondary continuous traits analyses via inverse probability weighting. Dimension reduction methods have also been proposed to linearly combine the multi-traits into a summary score, which is then subject to the traditional likelihood based association testing methods. For example, we can use the first principal component of the responses, which maximizes the trait combination variation. Klei et al. (2008) proposed linearly combining responses based on maximizing the heritability. While the canonical correlation analysis (Ferreira and Purcell, 2009) tried to maximize the correlation of trait combinations with the SNP. Existing GEE based methods typically explicitly avoided modeling the trait correlations. The dimension reduction methods typically incorporated the trait dependence to construct the summary scores, which however were not guaranteed to maximize the multi-trait SNP associations.

In this article, we explore an alternative likelihood based framework to test the multiple trait associations. It is based on the familiar multinomial logistic regression modeling of genotypes, can be readily implemented using widely available software, and offers very competitive performance. We demonstrate through extensive numerical studies that the proposed method has competitive performance. We further illustrate the usefulness of the proposed method through an application to genome-wide association study (GWAS) of diabetes-related traits.

Materials and Methods

We first present the likelihood based framework for association tests with multivariate traits, and derive the genotype based multinomial logistic regression model.

Genotype based multinomial logit model

Consider multivariate traits Y ∈ R^m, a covariate vector X of length p (which could contain both non-ancestry covariates, e.g., age and gender, and ancestry covariates, e.g., ancestry indicator or principal components), and a genotype score G coding the number of minor alleles. Assume the multivariate normal trait model, (Y|G, X) ~ N(γ₀ + γ_XX + γG, Σ), where γ₀ is a vector of length m, γ_X is a m × p matrix, γ is of length m, and Σ is a m × m covariance matrix. Multivariate trait association amounts to testing H₀ : = 0. When assuming the conditional Hardy-Weinberg equilibrium (HWE) and X consists of ancestry covariates (e.g., population indicator or ancestry principal components), we model the genotype with a conditional binomial distribution, (G|X) ~ Binom(2, f₀), where f₀ = 1/(1 + exp(−α₀ − X^Tα₁)), and α₁ is a vector of length p. To model potential deviation from the HWE, we adopt the following multinomial logistic model (see Appendix for details)

$$\text{log}\frac{\text{Pr}(G=1|X)}{\text{Pr}(G=0|X)}={\alpha }_{01}+X^T{\alpha }_1,\text{log}\frac{\text{Pr}(G=2|X)}{\text{Pr}(G=0|X)}={\alpha }_{02}+2X^T{\alpha }_1.$$ (1)

In the simple case of no ancestry covariates, the model is equivalent to fitting the genotype with a three-category multinomial distribution.

Denote the conditional genotype distribution probability π_G = Pr(G|X, Y) for G = 0, 1, 2. We can derive an adjacent-category logit (ACL) model (Agresti, 2013) (see Appendix for technical details)

$$\text{log}\frac{{\pi }_G}{{\pi }_0}={\beta }_{0G}+G{X}^T{\beta }_X+G{Y}^T\beta ,\beta ={\mathrm{\Sigma }}^{-1}\gamma ,G=1,2.$$ (2)

The multivariate trait association amounts to testing H₀ : β = 0, where β is a vector parameter of length m.

A closely related approach is the MultiPhen method (O’Reilly et al., 2012), which assumed the proportional odds model (POM) for analyzing the three genotypes. In general the POM can provide a good approximation to the ACL model for common variants with small effects, while the two models could show large differences for less frequent variants (see Appendix for details). In our numerical studies, the proposed ACL model performs consistently better than the MultiPhen, which has reduced performance and slightly inflated type I errors for less frequent variants.

Conducting multivariate association tests

Consider a study with a total of n unrelated individuals. Denote the maximum likelihood estimator of β under model (2) as β̂ and its associated asymptotic covariance matrix as V. To test the null hypothesis that β = 0, we can use the Wald statistic β̂^TV⁻¹β̂, which asymptotically follows a m degrees of freedom (DF) chi-square distribution. The Wald test is known to have aberrant testing behavior for logistic model (Hauck and Donner, 1977). We propose to use the likelihood ratio test (LRT) for the multivariate trait association based on the proposed model (2).

When genetic effects are similar across traits, we can further improve the multivariate association test power using a test statistic with one degree of freedom following the lines of O’Brien (1984) and He et al. (2013), which performed a Wald test of linear combinations of β. In the appendix we presented similar Wald tests under the proposed models. In the following we derive the corresponding LRT.

When the genotype effects are the same in the multivariate trait model, we can denote γ = η1, where 1 = (1, ⋯, 1)^T. The ACL model simplifies to

$$\text{log}({\pi }_G/{\pi }_0)={\beta }_{0G}+G{X}^T{\beta }_X+G\eta (Y^T{\mathrm{\Sigma }}^{-1}\mathbf{1}).$$ (3)

When the scaled genotype effects are the same in the multivariate trait model, we can denote γ = ηS, where S = (s₁, ⋯, s_m)^T with $s_k=\sqrt{{\mathrm{\Sigma }}_{kk}}$, k = 1, ⋯, m. The ACL model simplifies to

$$\text{log}({\pi }_G/{\pi }_0)={\beta }_{0G}+G{X}^T{\beta }_X+G\eta (Y^T{\mathrm{\Sigma }}^{-1}S).$$ (4)

Under both models, the multivariate trait association reduces to testing H₀ : η = 0 and can be tested using the 1-DF LRT. In practice we use Σ̂ = Cov(Ỹ), where Ỹ are the residuals of regressing Y on X.

When the multivariate traits have a compound covariance matrix Σ = σ²[(1 − ρ)I + ρJ], ρ ∈ [0, 1), where I is an identity matrix and J = 11^T a matrix with all elements equal to 1, we can check that ${\mathrm{\Sigma }}^{-1}\mathbf{1}={\sigma }^{-2}\frac{1}{1+(m-1)\rho }\mathbf{1}$, and hence $Y^T{\mathrm{\Sigma }}^{-1}\mathbf{1}={\sigma }^{-2}\frac{m}{1+(m-1)\rho }\mathrm{Y̅}$, where Ȳ is the average of Y. Therefore when it is reasonable to assume a common effect with compound covariance matrix, the best approach is testing the average of the multivariate traits either by the proposed ACL or the equivalent linear regression model. In the next section, we will discuss one such example of application to a GWAS of diabetes-related traits.

RESULTS

Simulation studies

We consider three forms of LRT: Q_g is the omnibus LRT testing β = 0 under model (2), T_g is the LRT testing η = 0 under model (3), and $T_g^{\prime }$ is the LRT testing η = 0 under model (4). He et al. (2013) conducted extensive numerical studies and has shown that their proposed GEE based approach appropriately controls the type I errors and has the overall best detection power compared to the TATES of van der Sluis et al. (2013), MANOVA and univariate test based methods. Here we compared the proposed methods to their GEE score tests, denoted as (Q, T, T′), which are the m-DF omnibus test and 1-DF tests assuming a common effect or common scaled effect. In addition we also include the closely related MultiPhen approach (O’Reilly et al., 2012), which assumed a proportional odds model for the genotype distribution.

We simulate a standard normal covariate X₁, a binary ancestry indicator X₂ with Pr(X₂ = 1) = 0.5, and a SNP G with minor allele frequency (MAF) p₀ + p₁X₂. We will consider testing m = 2, 4, 8 related traits respectively.

For two continuous traits, we simulated 1,000 individuals based on the bivariate normal distribution: Y₁ = 1 + 0.5X₁ + 0.5X₂ + γ₁G + ε₁ and Y₂ = 1 + X₁ + X₂ + γ₂G + ε₂, where (ε₁, ε₂) are zero-mean normal with variances $({\sigma }_1^2=2,{\sigma }_2^2=1)$ and correlation ρ.

For four continuous traits, we simulated 1,000 individuals with a compound-symmetry correlation matrix: Y₁ = 1 + 0.5X₁ + 0.5X₂ + γ₁G + ε₁, Y₂ = 1 + X₁ + X₂ + γ₂G + ε₂, Y₃ = 1 + 0.5X₁ + 0.5X₂ + γ₃G + ε₃, and Y₄ = 1 + X₁ + X₂ + γ₄G + ε₄, where (ε₁, ε₂, ε₃, ε₄) are zero-mean normal with variances $({\sigma }_1^2=2,{\sigma }_2^2=1,{\sigma }_3^2=1,{\sigma }_4^2=1)$ and correlation ρ.

For eight continuous traits, we simulated 1,000 individuals with a compound-symmetry correlation matrix: Y_i = 1 + 0.5X₁ + 0.5X₂ + γ_iG + ε_i for i = 1, 3, 5, 7, Y_k = 1 + X₁ + X₂ + γ_kG + ε_k for k = 2, 4, 6, 8, where (ε₁, ⋯, ε₈) are zero-mean normal with variances ${\sigma }_1^2=2,{\sigma }_i^2=1$, i = 2, ⋯, 8, and correlation ρ.

We used 10 million experiments under the null to evaluate the type I error, and 10,000 experiments under various combinations of γ_j to evaluate the power. We conducted simulations for p₀ = (0.1, 0.3), p₁ = 0.1, and ρ = (0.2, 0.5, 0.8). Here we report the results for ρ = 0.5. The conclusions remain the same for ρ = 0.2, 0.8 (data not shown).

For two continuous traits, Table 1 summarizes the estimated type I errors, Table 2 and 3 summarize the power for p₀ = 0.1 and p₀ = 0.3 respectively. The MultiPhen has slightly inflated type I errors for less common variant (MAF=0.1). All the other tests appropriately control the type I errors. Overall the GEE score tests are the most conservative. The MultiPhen, Q_g and Q are omnibus tests with reasonable power under all alternatives. Not surprisingly $T_g^{\prime }$ is more powerful than the other tests when γ₁ is close to γ₂, and T_g is the most powerful when γ₁/σ₁ and γ₂/σ₂ are close to each other. The proposed Q_g performs better than MultiPhen especially for less common variant (MAF=0.1). In general the proposed likelihood based tests are better than the corresponding GEE based score tests, and their differences become more pronounced as the MAF decreases. This agrees with the general principle that the likelihood based test is typically more powerful than the GEE based test, and the LRT has better power than the score test especially for relatively large effect sizes.

Table 1.

Type I error of multivariate tests for m = 2 continuous traits with ρ = 0.5 pairwise correlation: the SNP has a MAF of p₀ and p₀ + 0.1 respectively in the two populations. Q_g is the m-DF omnibus LRT, T_g is the 1-DF LRT assuming common effect, and $T_g^{\prime }$ is the 1-DF LRT assuming common scaled effect. (Q, T, T′) are the corresponding GEE based m-DF omnibus test and 1-DF tests assuming a common effect or common scaled effect. MultiPhen assumes a proportional odds model for testing the multivariate traits.

	p0 = 0.3, ρ = 0.5			p0 = 0.1, ρ = 0.5
α	10−5	10−4	10−3	10−5	10−4	10−3
MultiPhen	0.95 × 10−5	1.02 × 10−4	1.02 × 10−3	1.16 × 10−5	1.07 × 10−4	1.02 × 10−3
Qg	0.92 × 10−5	1.02 × 10−4	1.02 × 10−3	1.02 × 10−5	1.02 × 10−4	1.02 × 10−3
Tg	0.93 × 10−5	1.01 × 10−4	1.01 × 10−3	1.02 × 10−5	1.02 × 10−4	1.01 × 10−3
${\mathrm{T}}_g^{\prime }$	1.03 × 10−5	1.00 × 10−4	1.00 × 10−3	0.95 × 10−5	1.02 × 10−4	1.02 × 10−3
Q	0.72 × 10−5	1.00 × 10−4	1.01 × 10−3	0.60 × 10−5	0.76 × 10−4	0.85 × 10−3
T	0.76 × 10−5	0.86 × 10−4	0.95 × 10−3	0.75 × 10−5	0.77 × 10−4	0.89 × 10−3
T′	0.74 × 10−5	0.90 × 10−4	0.95 × 10−3	0.64 × 10−5	0.77 × 10−4	0.88 × 10−3

Table 2.

Power of multivariate tests for m = 2 continuous traits (Y₁, Y₂) with ρ = 0.5 pairwise correlation: the SNP has a MAF of 0.1 and 0.2 in the two populations. Q_g is the m-DF omnibus LRT, T_g is the 1-DF LRT assuming common effect, and $T_g^{\prime }$ is the 1-DF LRT assuming common scaled effect. (Q, T, T′) are the corresponding GEE based m-DF omnibus test and 1-DF tests assuming a common effect or common scaled effect. MultiPhen assumes a proportional odds model for testing the multivariate traits. σ_i is the standard error of Y_i and γ_i is the SNP coefficient, i = 1, 2. The highest powered tests are bold-faced.

		α = 10−4, p0 = 0.1, ρ = 0.5
(γ1, γ2)	(γ1/σ1, γ2/σ2)	MultiPhen	Qg	Tg	${\mathrm{T}}_g^{\prime }$	Q	T	T′
(0.3,0)	(0.21,0)	0.3521	0.3728	0.0266	0.0016	0.3275	0.0216	0.0015
(0.3,0.1)	(0.21,0.1)	0.1943	0.2045	0.1486	0.0478	0.1747	0.1251	0.0411
(0.25,0.18)	(0.18,0.18)	0.1677	0.1842	0.2632	0.2268	0.1522	0.2318	0.1964
(0.3,0.25)	(0.21,0.25)	0.5022	0.5324	0.6248	0.6237	0.4802	0.5865	0.5803
(0.2,0.2)	(0.14,0.2)	0.1719	0.1840	0.2204	0.2622	0.1535	0.1930	0.2339
(0.2,0.25)	(0.14,0.25)	0.3922	0.4220	0.3678	0.5084	0.3740	0.3320	0.4726
(0.25,0.25)	(0.18,0.25)	0.4295	0.4569	0.4985	0.5654	0.4053	0.4574	0.5268
(0,0.25)	(0,0.25)	0.6225	0.6518	0.0527	0.2690	0.6043	0.0420	0.2475
(0,0.3)	(0,0.3)	0.8822	0.9004	0.1192	0.5133	0.8709	0.0931	0.4819
(0.1,0.25)	(0.07,0.25)	0.4406	0.4638	0.1682	0.3844	0.4168	0.1385	0.3580
(0.1,0.3)	(0.07,0.3)	0.7526	0.7766	0.2999	0.6343	0.7334	0.2593	0.6083
(0.2,0.3)	(0.14,0.3)	0.6856	0.7085	0.5494	0.7428	0.6618	0.5034	0.7125

Table 3.

Power of multivariate tests for m = 2 continuous traits (Y₁, Y₂) with ρ = 0.5 pairwise correlation: the SNP has a MAF of 0.3 and 0.4 in the two populations. Q_g is the m-DF omnibus LRT, T_g is the 1-DF LRT assuming common effect, and $T_g^{\prime }$ is the 1-DF LRT assuming common scaled effect. (Q, T, T′) are the corresponding GEE based m-DF omnibus test and 1-DF tests assuming a common effect or common scaled effect. MultiPhen assumes a proportional odds model for testing the multivariate traits. σ_i is the standard error of Y_i and γ_i is the SNP coefficient, i = 1, 2. The highest powered tests are bold-faced.

		α = 10−6, p0 = 0.3, ρ = 0.5
(γ1, γ2)	(γ1/σ1, γ2/σ2)	MultiPhen	Qg	Tg	${\mathrm{T}}_g^{\prime }$	Q	T	T′
(0.3,0)	(0.21,0)	0.4834	0.4971	0.0102	0.0000	0.4495	0.0081	0.0000
(0.3,0.1)	(0.21,0.1)	0.2361	0.2468	0.1394	0.0263	0.2142	0.1197	0.0231
(0.25,0.18)	(0.18,0.18)	0.2037	0.2126	0.2945	0.2406	0.1801	0.2613	0.2091
(0.3,0.25)	(0.21,0.25)	0.6904	0.7043	0.7748	0.7710	0.6573	0.7424	0.7332
(0.2,0.2)	(0.14,0.2)	0.2032	0.2112	0.2336	0.2916	0.1789	0.2059	0.2612
(0.2,0.25)	(0.14,0.25)	0.5414	0.5564	0.4470	0.6391	0.5112	0.4070	0.6007
(0.25,0.25)	(0.18,0.25)	0.5949	0.6101	0.6266	0.7097	0.5598	0.5834	0.6716
(0,0.25)	(0,0.25)	0.8095	0.8220	0.0293	0.2915	0.7849	0.0242	0.2692
(0,0.3)	(0,0.3)	0.9795	0.9813	0.1032	0.6217	0.9752	0.0788	0.5868
(0.1,0.25)	(0.07,0.25)	0.5999	0.6122	0.1615	0.4632	0.5638	0.1350	0.4320
(0.1,0.3)	(0.07,0.3)	0.9178	0.9246	0.3424	0.7785	0.9058	0.2978	0.7567
(0.2,0.3)	(0.14,0.3)	0.8682	0.8768	0.6874	0.8850	0.8475	0.6437	0.8670

For four continuous traits, Table 4 summarizes the estimated type I errors, Table 5 and 6 summarize the power for p₀ = 0.1 and p₀ = 0.3 respectively. The MultiPhen has slightly inflated type I errors for less common variant (MAF=0.1). For all the other tests, the empirical sizes are close to the nominal significance level. Overall the proposed LRT tests are more powerful than the GEE score tests especially for less common variant (p₀ = 0.1) and relatively large effect sizes. When all γ_j are close to each other, the 1-DF tests could have improved power.

Table 4.

Type I error of multivariate tests for four continuous traits

	p0 = 0.3, ρ = 0.5			p0 = 0.1, ρ = 0.5
α	10−5	10−4	10−3	10−5	10−4	10−3
MultiPhen	1.14 × 10−5	1.09 × 10−4	1.06 × 10−3	1.28 × 10−5	1.13 × 10−4	1.10 × 10−3
Qg	1.08 × 10−5	1.04 × 10−4	1.05 × 10−3	1.06 × 10−5	1.07 × 10−4	1.06 × 10−3
Tg	0.92 × 10−5	1.03 × 10−4	1.02 × 10−3	1.05 × 10−5	1.07 × 10−4	1.02 × 10−3
$T_g^{\prime }$	1.02 × 10−5	1.01 × 10−4	1.03 × 10−3	1.06 × 10−5	1.05 × 10−4	1.02 × 10−3
Q	0.75 × 10−5	0.84 × 10−4	0.92 × 10−3	0.56 × 10−5	0.73 × 10−4	0.85 × 10−3
T	0.82 × 10−5	0.88 × 10−4	0.97 × 10−3	0.76 × 10−5	0.89 × 10−4	0.92 × 10−3
T′	0.75 × 10−5	0.90 × 10−4	0.97 × 10−3	0.85 × 10−5	0.84 × 10−4	0.93 × 10−3

Table 5.

Power of multivariate tests for four continuous traits

α = 10−4, p0 = 0.1, ρ = 0.5
(γ1, γ2, γ3, γ4)	MultiPhen	Qg	Tg	$T_g^{\prime }$	Q	T	T′
(0.3,0,0,0)	0.3720	0.3929	0.0026	0.0001	0.3306	0.0016	0.0000
(0.3,0.2,0.1,0)	0.9374	0.9423	0.3047	0.0619	0.9282	0.2728	0.0588
(0.25,0.18,0.18,0.18)	0.5897	0.6003	0.8153	0.7565	0.5670	0.7997	0.7368
(0.2,0.2,0.2,0.2)	0.7224	0.7329	0.8578	0.9017	0.7025	0.8387	0.8891

Table 6.

Power of multivariate tests for four continuous traits

	α = 10−6, p0 = 0.3, ρ = 0.5
(γ1, γ2, γ3, γ4)	MultiPhen	Qg	Tg	${\mathrm{T}}_g^{\prime }$	Q	T	T′
(0.3,0,0,0)	0.5374	0.5522	0.0001	0.0000	0.4916	0.0000	0.0000
(0.3,0.2,0.1,0)	0.7186	0.7322	0.0642	0.0050	0.6782	0.0471	0.0041
(0.25,0.18,0.18,0.18)	0.2319	0.2413	0.4597	0.3787	0.1973	0.4163	0.3355
(0.2,0.2,0.2,0.2)	0.3570	0.3724	0.5206	0.6108	0.3138	0.4795	0.5673

For eight continuous traits, Table 7 summarizes the estimated type I errors. For all the tests, the empirical sizes are close to the nominal significance level. Table 8 and 9 summarize the power for p₀ = 0.1 and p₀ = 0.3 respectively. The proposed LRT tests are more powerful than the GEE score tests especially for less common variant (p₀ = 0.1) and relatively large effect sizes. When all γ_j are close to each other, the 1-DF tests could have much improved power. The proposed Q_g performs better than MultiPhen especially for less common variant (MAF=0.1).

Table 7.

Type I error of multivariate tests for eight continuous traits

	p0 = 0.3, ρ = 0.5			p0 = 0.1, ρ = 0.5
α	10−5	10−4	10−3	10−5	10−4	10−3
MultiPhen	0.95 × 10−5	0.97 × 10−4	1.06 × 10−3	1.16 × 10−5	0.99 × 10−4	1.06 × 10−3
Qg	0.92 × 10−5	1.05 × 10−4	1.03 × 10−3	1.02 × 10−5	0.94 × 10−4	1.03 × 10−3
Tg	0.93 × 10−5	0.93 × 10−4	1.04 × 10−3	1.02 × 10−5	1.06 × 10−4	1.02 × 10−3
${\mathrm{T}}_g^{\prime }$	1.03 × 10−5	1.08 × 10−4	1.00 × 10−3	0.95 × 10−5	1.07 × 10−4	0.99 × 10−3
Q	0.72 × 10−5	0.70 × 10−4	0.81 × 10−3	0.60 × 10−5	0.50 × 10−4	0.70 × 10−3
T	0.76 × 10−5	0.91 × 10−4	0.95 × 10−3	0.75 × 10−5	1.06 × 10−4	0.93 × 10−3
T′	0.74 × 10−5	0.92 × 10−4	0.95 × 10−3	0.64 × 10−5	1.07 × 10−4	0.94 × 10−3

Table 8.

Power of multivariate tests for eight continuous traits

α = 10−4, p0 = 0.1, ρ = 0.5
(γ1, ⋯, γ8)	MultiPhen	Qg	Tg	${\mathrm{T}}_g^{\prime }$	Q	T	T′
γ1 = 0.3, γi>1 = 0	0.2962	0.3157	0.0005	0.0007	0.2336	0.0002	0.0002
(0.3, 0.2, 0.1, 0.05, 0, ⋯, 0)	0.6798	0.7021	0.0071	0.0001	0.6032	0.0049	0.0004
γ1 = 0.2, γi>1 = 0.15	0.0471	0.0508	0.2246	0.1947	0.0331	0.1976	0.1701
γi = 0.15	0.0502	0.0544	0.1970	0.2343	0.0346	0.1699	0.2044

Table 9.

Power of multivariate tests for eight continuous traits

α = 10−6, p0 = 0.3, ρ = 0.5
(γ1, ⋯, γ8)	MultiPhen	Qg	Tg	${\mathrm{T}}_g^{\prime }$	Q	T	T′
γ1 = 0.3, γi>1 = 0	0.4808	0.4965	0.0000	0.0000	0.4045	0.0000	0.0000
(0.3, 0.2, 0.1, 0.05, 0, ⋯, 0)	0.9069	0.9163	0.0012	0.0000	0.8703	0.0009	0.0000
γ1 = 0.2, γi>1 = 0.15	0.0424	0.0452	0.2498	0.2098	0.0298	0.2190	0.1803
γi = 0.15	0.0469	0.0499	0.2089	0.2610	0.0323	0.1779	0.2295

Overall we can see that the proposed LRT is an attractive approach with good power across a wide range of alternatives. It performs better than the GEE score test especially with a large number of related traits and relatively large effect sizes. The GEE score test in general is the most conservative and requires a relatively large sample size especially for testing a large number of traits in order to obtain stable GEE sandwich covariance estimator. Increasing the sample size will result in more accurate size estimates. When prior knowledge about the specific mechanistic hypotheses regarding the underlying architecture of the multivariate traits holds, the 1-DF GEE score test and the proposed 1-DF LRT are more powerful especially for a large number of correlated traits. The MultiPhen approach has reasonable detection power under all alternatives, often performs better than the omnibus GEE score test and only slightly worse than the omnibus LRT test. However, it did not incorporate prior knowledge about the underlying architecture of the multivariate traits.

An interesting scenario is one in which only the first trait Y₁ is marginally associated with the SNP (γ₁ = 0.3) and all the other traits are not related to the SNP (γ_i>1 = 0). Stephens (2013) has reported that joint testing by incorporating correlated null trait could improve the detection power. Table 10 compared the univariate association test of Y₁ versus the joint testing under previous simulation settings. We can see that jointly testing highly correlated traits could have greater power over testing Y₁ alone, which is consistent with the findings of Stephens (2013). In general the larger the trait correlation, the more detection power we have.

In addition we also performed simulation studies under smaller sample size and for non-normally distributed traits. The conclusions remain the same (please see supplementary material for complete results).

ARIC GWAS

The Atherosclerosis Risk in Communities (ARIC) study (The ARIC Investigators, 1989) is a population-based, multi-center prospective investigation of cardiovascular disease. Men and women aged 45–64 years at baseline were recruited from four U.S. communities: Forsyth County, North Carolina; Jackson, Mississippi; suburban areas of Minneapolis, Minnesota; and Washington County, Maryland. A total of 15,792 individuals participated in the baseline examination in 1987–1989. The vast majority of ARIC participants are of European (73%) or African ancestry (26%). We conducted two association analyses of diabetes-related traits in ARIC.

First we analyzed repeated measures of one phenotype (fasting glucose levels) in 5947 non-diabetic ARIC white participants measured at four visits approximately three years apart. The design of the ARIC Study, methods for genotyping, measurement of plasma glucose and other covariates have been described previously (Rasmussen-Torvik et al., 2010). Mean glucose levels were similar across the four visits and the covariance matrix was close to compound symmetry with correlations around 0.55. Therefore we expect that the proposed statistics T_g and $T_g^{\prime }$ will have greater detection power. In addition we applied the averaging approach of Rasmussen-Torvik et al. (2010), which is expected to have improved detection power compared to analysis of a single phenotype. We applied an additive genetic model and adjusted for age, gender and study center (population indicators). When applied to the four fasting glucose measurements, the averaging approach identified 101 significant SNPs, T_g identified 102, $T_g^{\prime }$ identified 101, T and T′ identified 101 each, Q_g identified 96, MultiPhen identified 92, and Q identified 92, at the genome-wide significance level 5 × 10⁻⁸. Analyzing glucose at each glucose measure separately identified 34, 84, 37, 64 genome-wide significant SNPs at visits 1, 2, 3, and 4, respectively. The identified SNPs by all methods are genome-wide significant in a meta-analyses of fasting glucose GWAS conducted by the MAGIC Consortium (Dupuis et al., 2010).

The additional SNP identified as genome-wide significant by $T_g^{\prime }$ but not T, T′, or T_g, rs1260326, had a p-value of 4.3 × 10⁻⁸ using $T_g^{\prime }$, and the individual p-values for separate analyses of glucose at visits 1, 2, 3, and 4 were 1.1 × 10⁻⁶, 2.7 × 10⁻⁵, 3.1 × 10⁻⁵, 9.3 × 10⁻⁵ respectively. The MAGIC meta-analysis reported a p-value of 4.3 × 10⁻¹³ for rs1260326.

Comparing Q_g to MultiPhen, the four additional SNPs identified by Q_g, rs7951037, rs11558471, rs3802177, and rs13266634, had p-values of 4.6 × 10⁻⁸, 3.3 × 10⁻⁸, 2.9 × 10⁻⁸, and 2.3 × 10⁻⁸ using Q_g. Their respective p-values reported by the MAGIC meta-analysis were 7.3 × 10⁻³², 2.6 × 10⁻¹¹, 2.0 × 10⁻¹⁰, 5.5 × 10⁻¹⁰.

Second, we simultaneously analyzed three distinct diabetes-related phenotypes in 5068 non-diabetic white participants measured at visit 4 in ARIC: fasting glucose, fasting insulin and glucose levels 2 hours after an oral glucose challenge. We applied an additive genetic model and adjusted for age, gender and study center (population indicators). To account for the skewed distribution of fasting insulin, we adopted the Box-Cox transformation with an estimated power of 0.35 (Box and Cox, 1964). The three diabetes-related traits had an average pairwise correlation of 0.31. When analyzing fasting insulin and 2 hour glucose levels individually, we did not identify any significant SNPs at a genome-wide significance level (5 × 10⁻⁸). For joint testing of all three phenotypes, T_g, $T_g^{\prime }$, T, T′ identified none, MultiPhen identified 95, Q 96, and Q_g identified 98 genome-wide significant SNPs, among which, 58, 59 and 61 SNPs were reported as genome-wide significant in the MAGIC GWAS meta-analyses of fasting glucose, fasting insulin, and 2 hour glucose levels (Dupuis et al., 2010; Saxena et al., 2010).

Compared to MultiPhen, Q_g identified three additional genome-wide significant SNPs, rs1402837, rs1101533 and rs853780, with p-values of 2.1 × 10⁻⁸, 4.6 × 10⁻⁸, and 4.6 × 10⁻⁸ respectively. Their respective p-values reported by the MAGIC meta-analysis of fasting glucose were 7.4 × 10⁻⁴⁰, 1.0 × 10⁻³⁸, and 2.1 × 10⁻³⁸.

Discussion

In summary, we recommend the proposed likelihood based test or the MultiPhen of O’Reilly et al. (2012) as a complementary approach to enhancing the power of analyzing multiple continuous traits in unrelated individuals, in spite of their increased computational demand relative to the score test. The novel GEE score test approach of He et al. (2013) can be broadly applied to mix of continuous and discrete traits for related or unrelated individuals. We think the likelihood based joint analysis of continuous and discrete traits (e.g., mixed effects modeling approach) is an important direction for further research.

We have implemented the proposed methods in R programs posted at http://www.biostat.umn.edu/~baolin/research/mta_Rcode.html.

Table 10.

Detection power incorporating correlated multivariate traits (γ₁ = 0.3, γ_i>1 = 0)

α = 10−6, p0 = 0.3, ρ = 0.2
m	Uni(Y1)	MultiPhen	Qg	Q
2		0.2640	0.2759	0.2398
4	0.3354	0.1981	0.2035	0.1640
8		0.1271	0.1337	0.0942
α = 10−6, p0 = 0.3, ρ = 0.5
m	Uni(Y1)	MultiPhen	Qg	Q
2		0.4834	0.4971	0.4495
4	0.3354	0.5374	0.5522	0.4916
8		0.4808	0.4965	0.4045
α = 10−6, p0 = 0.3, ρ = 0.8
m	Uni(Y1)	MultiPhen	Qg	Q
2		0.9852	0.9866	0.9813
4	0.3354	0.9985	0.9988	0.9979
8		0.9990	0.9991	0.9979
α = 10−6, p0 = 0.1, ρ = 0.2
m	Uni(Y1)	MultiPhen	Qg	Q
2		0.0388	0.0440	0.0277
4	0.0592	0.0234	0.0263	0.0134
8		0.0117	0.0130	0.0052
α = 10−6, p0 = 0.1, ρ = 0.5
m	Uni(Y1)	MultiPhen	Qg	Q
2		0.0903	0.0994	0.0671
4	0.0592	0.0978	0.1091	0.0659
8		0.0678	0.0756	0.0379
α = 10−6, p0 = 0.1, ρ = 0.8
m	Uni(Y1)	MultiPhen	Qg	Q
2		0.6070	0.6367	0.5414
4	0.0592	0.8021	0.8284	0.7217
8		0.7977	0.8199	0.6741

APPENDIX

Genotype based multinomial logistic regression model

Consider multivariate traits Y ∈ R^m, a covariate vector X of length p, and a genotype score G. Assume the multivariate normal trait model

$$(Y|G,X)~N({\gamma }_0+{\gamma }_{X}X+\gamma G,\mathrm{\Sigma }),$$

where γ₀ is a vector of length m, γ_X is a m × p matrix, γ is of length m, and Σ is a m × m covariance matrix. We can check that

$$\text{log}\frac{\text{Pr}(Y|G,X)}{\text{Pr}(Y|G=0,X)}=G{\gamma }^T{\mathrm{\Sigma }}^{-1}[Y-{\gamma }_0-{\gamma }_{X}X-\gamma G/2].$$

When the SNP follows the HWE, the genotype score G can be modeled with a binomial distribution, Binom(2,f₀), where f₀ is the MAF. Therefore we have log[Pr(G = 0)/ Pr(G = 1)] = log[(1 − f₀)/f₀] − log(2), and log[Pr(G = 1)/ Pr(G = 2)] = log[(1 − f₀)/f₀] + log(2). This is essentially an adjacent category logit (ACL) model when treating log[(1 − f₀)/f₀] as a parameter. We can equivalently write this ACL model as

$$\text{log}\frac{\text{Pr}(G)}{\text{Pr}(G=0)}=\text{log}(2)I(G=1)+G\text{log}\frac{f_0}{1-f_0},G=1,2.$$

When individuals are coming from potentially several ancestry populations, we can assume conditional HWE: within each ancestry population we model the SNP with a binomial distribution, Binom(2,f₀), where the MAF f₀ now depends on the population ancestry. In the case of unknown ancestry but with ancestry covariate included (e.g., computed ancestry principal components), we model f₀ using a logistic regression model, log[f₀/(1 − f₀)] = α₀ + X^Tα₁, which also holds for the case of known ancestry populations, where we just include the population indicators in the covariate X. Therefore when assuming HWE (conditional on X), we have

$$\text{log}\frac{\text{Pr}(G|X)}{\text{Pr}(G=0|X)}={\alpha }_{0G}+G{X}^T{\alpha }_1,$$

where α_0G = log(2)I(G = 1) + Gα₀, G = 1, 2, which can be further relaxed to two separate parameters to allow potential deviation from the HWE. In principle, we just need to include those ancestry informative covariates in the previous model. Some additional environmental variables (e.g., age) can be assumed to be independent of genotype and excluded from the previous model. But as we will show in the following, this does not affect our derived model for Pr(G|X, Y).

Define the conditional genotype distribution probability π_G = Pr(G|X, Y), G = 0, 1, 2. We have

$${\pi }_G=\frac{\text{Pr}(G|X)\text{Pr}(Y|G,X)}{\text{Pr}(Y|X)}=\frac{\text{Pr}(G|X)\text{Pr}(Y|G,X)}{{\sum }_{g=0}^2\text{Pr}(G=g|X)\text{Pr}(Y|G=g,X)}.$$

Note that

$$\text{log}\frac{{\pi }_G}{{\pi }_0}=\text{log}\frac{\text{Pr}(G|X)\text{Pr}(Y|G,X)}{\text{Pr}(G=0|X)\text{Pr}(Y|G=0,X)},G=1,2.$$

Therefore we have

$$\text{log}\frac{{\pi }_G}{{\pi }_0}={\alpha }_{0G}+G{X}^T{\alpha }_1+G{\gamma }^T{\mathrm{\Sigma }}^{-1}[Y-{\gamma }_0-{\gamma }_{X}X-\gamma G/2].$$

Define

$${\beta }_{0G}={\alpha }_{0G}-G{\gamma }^T{\mathrm{\Sigma }}^{-1}{\gamma }_0-\frac{1}{2}{G}^2{\gamma }^T{\mathrm{\Sigma }}^{-1}\gamma ,{\beta }_X={\alpha }_1-{\gamma }_X^T{\mathrm{\Sigma }}^{-1}\gamma ,\beta ={\mathrm{\Sigma }}^{-1}\gamma .$$

We have

$$\log \frac{{\pi }_G}{{\pi }_0}={\beta }_{0G}+G{X}^T{\beta }_X+G{Y}^T\beta ,G=1,2,$$

which can be equivalently written as an adjacent-category logit (ACL) model (Agresti, 2013)

$$\text{log}\frac{{\pi }_g}{{\pi }_{g+1}}=({\beta }_{0g}-{\beta }_{0,g+1})-X^T{\beta }_X-Y^T\beta ,g=0,1,$$

where β₀₀ = 0. The multi-trait genotype association H₀ : β = 0 can be tested using a m-DF chi-square test.

Here we are testing Pr(G|X, Y) = Pr(G|X) (i.e., H₀ : β = 0) for the multi-trait genotype association. While in the multivariate normal trait model, we are testing Pr(Y|X, G) = Pr(Y|X) (i.e., H₀ : γ = 0) for the multi-trait genotype association. In the previous derivation, we have shown that γ and β have one-to-one correspondence, β = Σ⁻¹γ. Therefore these two tests are equivalent. Here the multi-trait genotype association is essentially testing the independence of Y and G conditional on X. Note that the conditional independence has the symmetry property, Pr(G|X, Y) = Pr(G|X) is equivalent to Pr(Y|X, G) = Pr(Y|X), therefore both tests can be used to test the multi-trait genotype association.

Multivariate trait association detection using 1-DF Wald test

We consider the linear combination U = a^T β̂, which follows an asymptotic normal distribution, U ~ N(a^TΣ⁻¹γ, a^TVa). With a common genotype effect across the multivariate traits, we have γ = η1, where 1 = (1, ⋯, 1)^T. The non-centrality parameter of U is then proportional to

$$\frac{a^T{\mathrm{\Sigma }}^{-1}\mathbf{1}}{\sqrt{a^{T}Va}}=b^T{V}^{-1/2}{\mathrm{\Sigma }}^{-1}\mathbf{1},b=\frac{V^{1/2}a}{\sqrt{a^{T}Va}}.$$

Note that b^Tb = 1 and hence taking b ∝ V^−1/2Σ⁻¹1 will maximize the non-centrality parameter. Therefore the test statistic

$$W_g=\frac{{\mathbf{1}}^T{\mathrm{\Sigma }}^{-1}{V}^{-1}\hat{\beta }}{{({\mathbf{1}}^T{\mathrm{\Sigma }}^{-1}{V}^{-1}{\mathrm{\Sigma }}^{-1}\mathbf{1})}^{1/2}}$$

is asymptotically normal with unit variance and maximizes the non-centrality parameter among all linear combinations of β̂. If we have a common scaled genotype effect across the multivariate traits, γ = ηS, where S = (s₁, ⋯, s_m)^T with $s_k=\sqrt{{\mathrm{\Sigma }}_{kk}}$, k = 1, ⋯, m, similarly we can show that the test statistic

$$W_g^{\prime }=\frac{S^T{\mathrm{\Sigma }}^{-1}{V}^{-1}\hat{\beta }}{{(S^T{\mathrm{\Sigma }}^{-1}{V}^{-1}{\mathrm{\Sigma }}^{-1}S)}^{1/2}}$$

is asymptotically normal with unit variance and maximizes the non-centrality parameter among all linear combinations of β̂. In practice we set Σ̂ = Cov(Ỹ) where Ỹ are the residuals of regressing Y on X. Alternatively we can also construct the 1-DF Wald statistics based on the proposed model (3) and (4). In our numerical studies the LRT performed consistently better than the Wald test (data not shown).

Comparison of POM and ACL model

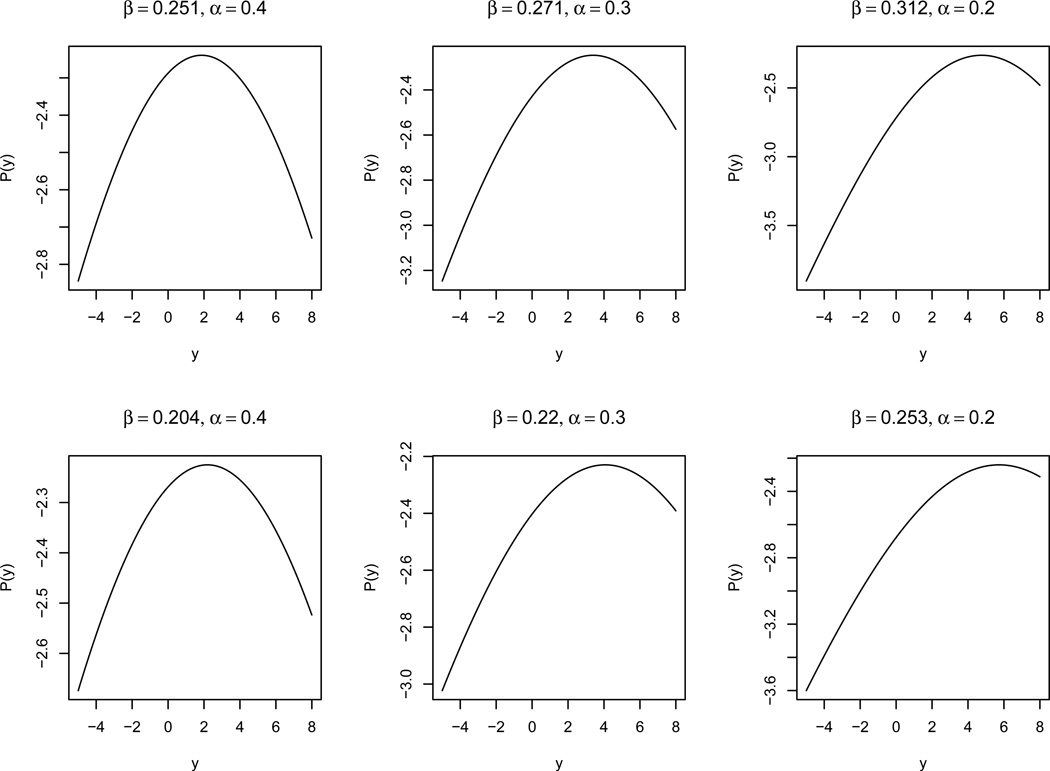
When assuming the trait is normally distributed with an additive genetic effect, we have shown that the conditional genotype distribution can be modeled with an ACL model. Here we explore how well the POM can approximate the ACL model. For simplicity, consider a single trait Y ~ N(βG, 1), where the genotype G has a MAF of α and is assumed to follow the HWE. We can derive the ACL model, log[Pr(G|Y)/ Pr(G = 0|Y)] ∝ GY β. While the POM assumes that P(Y) = log[Pr(G ≥ 1|Y)/ Pr(G = 0|Y)] − log[Pr(G = 2|Y)/ Pr(G ≤ 1|Y)] is a constant independent of Y. Figure 1 plots the function P(Y) under different combinations of genotype effect β and MAF α. The combinations of β and α in the first row have around 50% detection power for POM with 1000 samples under 5 × 10⁻⁸ significance level, and the second row corresponds to around 15% detection power for POM. In general we can see that the P(Y) is nearly constant for large MAF (α = 0.4) and shows increased ranges for reduced MAF and increased genetic effects. Table 11 compares their detection power. The ACL model consistently performs better than the POM/MultiPhen. For MAF of α = 0.4, the POM approximates the ACL model well and they have very similar power. Overall smaller MAF and larger genetic effect lead to more power differences as the POM approximation to the ACL model becomes poor.

Figure 1.

POM approximation to ACL: P(y) as a function of y. The combinations of β and α in the first row have around 50% detection power for POM with 1000 samples under 5 × 10⁻⁸ significance level, and the second row corresponds to around 15% detection power for POM.

Table 11.

Detection power of POM/MultiPhen versus ACL under 5 × 10⁻⁸ significance level with 1000 samples: power estimated with 10⁴ experiments. α is the MAF, and β is the SNP effect.

α	0.4	0.3	0.2	0.4	0.3	0.2
β	0.251	0.271	0.312	0.204	0.220	0.253
POM/MultiPhen	0.494	0.500	0.498	0.152	0.151	0.151
ACL	0.504	0.530	0.538	0.155	0.164	0.173

If the trait Y and some covariate X are both related to the genotype G, e.g., X is ancestry covariate, and we have varying trait means and genotype frequencies under different X, the true null model Pr(G|X, Y) = Pr(G|X) is an ACL model. When using the POM model to approximate the null ACL model Pr(G|X), the POM model could potentially include both X and Y due to their dependence, and lead to inflated type I errors.