Laplacian Dynamics with Synthesis and Degradation

Abstract

Analyzing qualitative behaviors of biochemical reactions using its associated network structure has proven useful in diverse branches of biology. As an extension of our previous work, we introduce a graph-based framework to calculate steady state solutions of biochemical reaction networks with synthesis and degradation. Our approach is based on a labeled directed graph G and the associated system of linear non-homogeneous differential equations with first order degradation and zeroth order synthesis. We also present a theorem which provides necessary and sufficient conditions for the dynamics to engender a unique stable steady state.

Although the dynamics are linear, one can apply this framework to nonlinear systems by encoding nonlinearity into the edge labels. We answer an open question from our previous work concerning the non-positiveness of the elements in the inverse of a perturbed Laplacian matrix. Moreover, we provide a graph theoretical framework for the computation of the inverse of such a matrix. This also completes our previous framework and makes it purely graph theoretical. Lastly, we demonstrate the utility of this framework by applying it to a mathematical model of insulin secretion through ion channels in pancreatic β-cells.

1 Introduction

In recent years, many researchers have devoted significant efforts to developing a systems-level understanding of biochemical reaction networks. In particular, the study of these chemical reaction networks (CRNs) using their associated graph structure has attracted considerable attention. The work led by Craciun and Feinberg on multistationarity (Craciun and Feinberg, 2006; Craciun et al., 2006; Craciun and Feinberg, 2010, 2005) and the work led by Mincheva and Roussel on stable oscillations (Mincheva, 2011; Mincheva and Roussel, 2007a, b) are two particularly influential approaches. For a good overview of the various graph theoretic developments, we direct the interested reader to the review provided in Domijan and Kirkilionis (2008).

In 1956 King and Altman developed a graphical method for deriving steady states of enzyme-catalyzed biochemical reactions. Since then many similar schematic methods have been developed independently in many subbranches of biochemistry (Monod et al., 1965; Ackers et al., 1982; Lean et al., 1980). These schematic methods were simplified and summarized into rules (known as Chou’s graphical rules (Lin and Lapointe, 2013; Zhou and Deng, 1984)) by Chou and coworkers (Chou, 1981; Chou and Min, 1981; Chou, 1983). Gunawardena (2012) unified all those ad hoc schematic methods into a single mathematical “linear framework”. The framework utilizes the Laplacian dynamics associated with a biochemical network and is based on famous Matrix-Tree Theorem (MTT). Subsequently, Mirzaev and Gunawardena (2013) provided a rigorous mathematical foundation for the “linear framework” as well as analysed the time-dependent behavior of the Laplacian dynamics. For more extensive review of “linear framework” and related graphical methods we refer reader to Gunawardena (2014).

Systems described by Laplacian dynamics are created using a weakly connected graph, G, with n vertices, with labeled, directed edges, and without self loops. Henceforth, we refer this type of directed graphs simply as “graph”. Note that by weakly connected we mean that the graph cannot be expressed as the union of two disjoint graphs. If there is an edge from vertex j to vertex i, we label it with e_ij > 0, and with e_ij = 0 if there is no such edge.¹

The Laplacian matrix (hereafter, a Laplacian ) of given graph G is then defined as

$${(\mathcal{L}(G))}_{ij}=\{\begin{array}{ll}{e}_{ij}\hfill & \text{if}i\ne j\hfill \\ -{\sum }_{m\ne j}{e}_{mj}\hfill & \text{if}i=j.\hfill \end{array}$$ (1)

The corresponding Laplacian dynamics are then defined as

$$\frac{d\mathbf{x}}{dt}=\mathcal{L}(G)·\mathbf{x}$$ (2)

where x = (x₁, ···, x_n)^T is column vector of species concentrations at each vertex, 1, ···, n. In a biochemical context one may think of vertices as different species and edges as rate of transformation from one species to another. However, we note that this framework is symbolic in nature in the sense that the mathematical description of the computed steady states is done without the specification of rate constants, i.e., edge weights e_ij. In other words, the only information about an individual e_ij relevant to our approach is whether or not it is zero.

Laplacian matrices were first introduced by Kirchhoff in 1847 in his article about electrical networks (Kirchhoff, 1847). Ever since then Laplacians have been studied and applied in various fields. For an example of studying the applications of Laplacians to spectral theory, we refer the interested reader to Bronski and DeVille (2014) in which they study the class of Signed graph Laplacians (a symmetric matrix, which is special case of above defined Laplacian).

In this article we will extend the framework initially developed in Gunawardena (2012) to investigate behaviors of Laplacian dynamics when zero-th order synthesis and first order degradation are added to the system. Specifically, we will examine the following dynamics,

$$\frac{d\mathbf{x}}{dt}=\mathcal{L}(G)·\mathbf{x}-D·\mathbf{x}+\mathbf{s}$$ (3)

where the degradation matrix D is a diagonal matrix with (D)_ii = d_i ≥ 0 and the synthesis vector s is a column vector with (s)_i = s_i ≥ 0. Hereafter, we refer to these new dynamics as synthesis and degradation dynamics (or simply as SD dynamics). In the biological network literature these types of dynamics are often referred as an inconsistent networks (Marashi and Tefagh, 2014).

For these dynamics, several questions naturally arise. Under what conditions does this system have non-negative, stable steady state solution? Moreover, how can we relate the steady state solution to the underlying graph structure of G as we did for Laplacian dynamics without synthesis and degradation? Our goal is to answer these questions on a theoretical level as well as apply the result to real world CRN examples.

Many biologically important systems cannot be modeled without synthesis and degradation. The main contribution of this work is to build upon the work of Gunawardena (2012); Mirzaev and Gunawardena (2013) making it applicable to a broader range of applications in biochemical networks.

The outline of this work is as follows. We will first briefly review the main results of Gunawardena (2012); Mirzaev and Gunawardena (2013) and present some additional notation (to be used in subsequent sections). In Section 3 we describe our main theoretical results and in Section 4 fully discuss the proof of an important result from Section 3. In Section 5, we illustrate an application of these results to exocytosis cascade of insulin granules in pancreatic β-cells. Lastly, in Section 6, we conclude with a discussion of the implications of these results as well as plans for future work.²

2 Preliminaries

In this section we briefly summarize the important results of (Gunawardena, 2012; Mirzaev and Gunawardena, 2013) and refer the interested reader to those articles for proofs and more extensive discussion and interpretation. For the sake of clarity, we will preserve the original notation while we include some additional definitions that can be found in many introductory graph theory books.

Given a graph G, we denote the set of vertices of G with (G) and for i, j ∈ 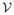(G) such that i ≠ j we write i ⇒ j to denote the existence of a directed path from vertex i to vertex j. If i ⇒ j and j ⇒ i, vertex i is said to be strongly connected to vertex j, and is denoted i ⇔ j. A graph G is strongly connected if for each ordered pair i, j of vertices in G, we have that i ⇔ j. The strongly connected components (SCCs) of a graph are the largest strongly connected subgraphs. Let C[i] denote the SCC containing i, i ∈ 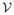(C[i]). Suppose we are given two SCCs, C[i] and C[j], if i ⇒ j we write C[i] ⪯ C[j] to denote that C[i] precedes C[j]. This precedes relation is both reflexive and transitive. Moreover, the relation is also antisymmetric as C[i] ⪯ C[j] and C[j] ⪯ C[i] imply that i ⇔ j and C[i] = C[j]. From this, we can conclude that the precedes relation allows for a partial ordering of the SCCs. Accordingly, this allows us to identify so-called terminal SCCs (tSCC), which are those SCCs C[i] such that, if C[i] ⪯ C[j] then C[i] = C[j]. These tSCCs are used in many other contexts, for example, they are also known as “attractors” of state transition graphs (Bérenguier et al., 2013).

With this terminology, we can devise an insightful relabeling of the vertices of graph G. Such a relabeling will transform the Laplacian matrix into one with a block lower-diagonal structure, which will prove convenient in our theoretical development. Suppose there are q tSCCs out of a total of p + q SCCs. Our goal is to relabel the vertices such that the first p blocks of Laplacian matrix correspond to the p non-terminal SCCs. Since the precedence relation, ⪯, is a partial ordering, there exists an ordering of the SCCs, C₁, …,C_p+q, such that, if C_i ⪯ C_j, then i ≤ j. Since a tSCC cannot precede any other SCC, then the tSCCs will occur in some arbitrary order C_p+1, …, C_p+q (which will not impact our results). We denote a_i as the number of vertices in C_i, and $m_i={\sum }_{k=1}^i{a}_k$ as the partial sum of the a_i’s, (with m₀ = 0). Note that the a_i’s should add up to the number of vertices in graph G, i.e., ${\sum }_{i=1}^{p+q}{a}_i=n$. Then the vertices of C_i are relabeled using only indices m_i−1 + 1, …, m_i−1 + a_i for i = 1, …, p + q. Consequently, the new Laplacian matrix, (G), is constructed using the relabeled vertices. Since i < j implies C_j ⪱ C_i, the Laplacian of G can be written in block lower-triangular form

$$\mathcal{L}(G)=\left(\begin{array}{cccccc}\begin{array}{|c|}\hline {\mathcal{L}}_1\\ \hline\end{array}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \cdots & \mathbf{0}\\ ⋮& \ddots & ⋮& ⋮& ⋮& ⋮\\ +& +& \begin{array}{|c|}\hline {\mathcal{L}}_p\\ \hline\end{array}& \mathbf{0}& \cdots & \mathbf{0}\\ +& \cdots & +& \begin{array}{|c|}\hline {\mathcal{L}}_{p+1}\\ \hline\end{array}& \mathbf{0}& \mathbf{0}\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮\\ +& \cdots & +& \mathbf{0}& \mathbf{0}& \begin{array}{|c|}\hline {\mathcal{L}}_{p+q}\\ \hline\end{array}\end{array}\right)=\left(\begin{array}{cc}N& \mathbf{0}\\ B& T\end{array}\right),$$

where + stands for some matrix with non-negative real entries, the submatrix N is block lower-triangular with nonnegative off-diagonal elements, B is a matrix with non-negative elements, 0 is matrix of all zeros, and T is also a block diagonal matrix such that

$$N=\left(\begin{array}{ccc}\begin{array}{|c|}\hline {\mathcal{L}}_1\\ \hline\end{array}& & \mathbf{0}\\ ⋮& \ddots & \\ +& +& \begin{array}{|c|}\hline {\mathcal{L}}_p\\ \hline\end{array}\end{array}\right),T=\left(\begin{array}{ccc}\begin{array}{|c|}\hline {\mathcal{L}}_{p+1}\\ \hline\end{array}& & \mathbf{0}\\ & \ddots & \\ \mathbf{0}& & \begin{array}{|c|}\hline {\mathcal{L}}_{p+q}\\ \hline\end{array}\end{array}\right).$$ (4)

By the definition of the Laplacian matrix (see (1)) all off-diagonal elements are non-negative real numbers. The blocks in boxes on the main diagonal, denoted by 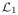, …, , 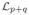are the submatrices defined by restricting (G) to the vertices of the corresponding SCCs, C₁, …, C_p+q. Note that for i = p + 1, …, p + q each 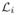is Laplacian matrix in its own, 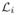= (C_i). However for the non-terminal SCCs, C₁, …, C_p, there is always at least one outgoing edge to some other SCC. This implies that for i = 1, …, p each matrix 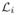is defined as the Laplacian of a corresponding SCC minus some non-zero diagonal matrix corresponding to outgoing edges from this SCC, 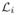= (C_i) − Δ_i for some Δ_i ≢ 0. In this case we call 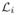a perturbed Laplacian matrix, and note the following property of 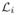(proven in Mirzaev and Gunawardena (2013)).

Remark 1

The perturbed Laplacian matrix of a strongly connected graph G is non-singular.

A directed spanning subgraph of graph G is a connected subgraph of G that includes every vertex of G, so that any spanning subgraph which is at the same time is a tree (an acyclic, undirected graph) is called directed spanning tree (DST) of the graph G. We say that a DST, 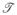, is rooted at i ∈ G if vertex i is the only vertex in 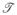without any outgoing edges, and denote the set of DSTs of graph G rooted at vertex i with Θ_i(G). Thus Θ_i(G) is a non-empty set of spanning trees for a strongly connected graph G. However, for an arbitrary graph there maybe no spanning tree rooted at specific vertex, in which case Θ_i(G) = ∅. In this case the corresponding element, (G)_(ji), is zero, where (G)_(ji) denotes the ji-th minor of Laplacian matrix (G) and is the determinant of the (n−1) × (n−1) matrix that results from deleting row j and column i of (G).

Next we review the main theorem, Matrix-Tree Theorem on which the results of this paper are based. The theorem utilizes the graph structure of graph G to calculate minors of a Laplacian. The first statement and proof of the MTT goes back to Tutte (2008) Uno (1996) in his article provided an algorithm for enumerating and listing all spanning trees of a general graph and Ahsendorf et al. (2014) utilized Uno’s algorithm to compute minors of Laplacian matrix using the Matrix-Tree theorem.³ We direct readers to Mirzaev and Gunawardena (2013) for a proof with same notations as in this article.⁴

Theorem 2

(Matrix-Tree Theorem) If G is graph with n vertices then the minors of its Laplacian are given by

$$\mathcal{L}{(G)}_{(ij)}={(-1)}^{n+i+j-1}\sum _{\mathcal{J}\in {\mathit{\Theta }}_j(G)}{P}_{\mathcal{J}},$$

where 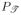is the product of all edge labels in the directed spanning tree .

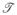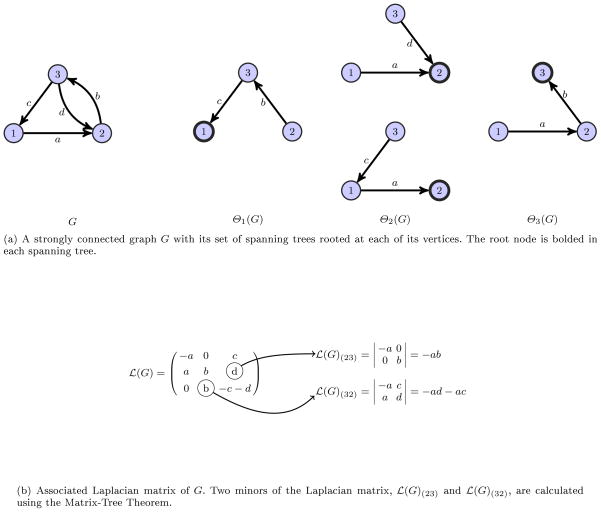
Figure 1 illustrates the theorem above, where the (G)₍₂₃₎ and (G)₍₃₂₎ minors of (G) are computed using spanning trees of the graph G. Consequently, the MTT implies that the ij-th minor of the Laplacian (up to sign) is the sum of all 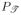for each spanning tree, 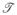, rooted at vertex j. Since all edge labels of the graph G are non-negative numbers (zero only if there is no such edge), then the expression ${\rho }_i^G={\sum }_{\mathcal{J}\in {\mathit{\Theta }}_i(G)}{P}_{\mathcal{J}}$ will always be non-negative.⁵ If G is strongly connected then Θ_i(G) ≠ ∅, so ${\rho }_i^G$ is strictly positive.

Fig. 1.

Illustration of Matrix-Tree Theorem

Having the MTT in hand, one can then calculate the kernel elements of the Laplacian, (G), using the following two fairly well known Propositions.

Proposition 1

If G is strongly connected graph, then ker (G) = span{ρ^G}, where ρ^G is column vector with ${({\mathit{\rho }}^G)}_i={\rho }_i^G>0$.

Here, the kernel is defined in the conventional sense, ker (G) = {x ∈ ℝ^n×1 : (G) · x = 0}. Moreover, Proposition 1 guarantees that a kernel element has all positive elements, a fact which is not immediately obvious using standard linear algebraic methods. When G is not a strongly connected graph, the kernel elements of (G) are constructed using kernel elements of its tSCCs. Specifically, since for i = 1, ···, q each 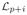= (C_p+i) is a Laplacian matrix on its own, by Proposition 1 there exists a column vector ${\mathit{\rho }}^{C_{p+i}}\in {ℝ}_{>0}^{a_{p+i}}$ such that 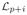· ρ^C_p+i = 0 and a_i is the number of vertices in C_i. Then we can extend this column vector to ${\overline{\mathit{\rho }}}^{C_{p+i}}\in {ℝ}_{>0}^n$ by setting all entries with indices outside the tSCC C_p+i to zero:

$${\left({\overline{\mathit{\rho }}}^{C_{p+i}}\right)}_k=\{\begin{array}{ll}{({\mathit{\rho }}^{C_{p+i}})}_{k-m_{p+i-1}}\hfill & \text{if}{m}_{p+i-1}\le k\le m_{p+i}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (5)

Since (G) has lower-block diagonal structure and since 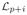· ρ^C_p+i = 0 for each i = 1, ···, q we have (G) · ρ̄^C_p+i = 0. Furthermore, one can also prove that the kernel of Laplacian (G) has exactly q element. These can be summarized in the following Proposition:

Proposition 2

For any graph G,

$$ker\mathcal{L}(G)=\mathit{span}\left\{{\overline{\mathit{\rho }}}^{C_{p+1}},\dots ,{\overline{\mathit{\rho }}}^{C_{p+q}}\right\},$$

and dim ker (G) = q

To prove stability of the steady states we will use the following theorem and corollary, which provides sufficiency conditions for the solution to a dynamical system dx/dt = A · x coupled with initial condition x(0) = x₀ to converge to a steady state (proof in Mirzaev and Gunawardena (2013)). Typically, the stability of the dynamics depends on the sign of the real parts of the eigenvalues of A as well as the algebraic and geometric multiplicities of the zero eigenvalue.

Theorem 3

Suppose that the real matrix A satisfies following two conditions

1. If λ is an eigenvalue of A, then either λ = 0 or Re(λ) < 0

2. alg_A(0) = geo_A(0), where alg_A(0) and geo_A(0) are the algebraic and geometric multiplicities of zero eigenvalue, respectively.

Then the solution of dx/dt = A · x converges to a steady state as t → ∞ for any initial condition.

Corollary 1

The Laplacian of a weakly connected graph satisfies conditions of Theorem 3. Moreover, 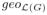(0) = 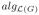(0) = q, where q is number of tSCCs of G.

With these preliminary results in hand we will provide stability analysis for the SD dynamics as well as a graph theoretical algorithm for the computation of steady states.

3 Theoretical Development

In this section we will provide a thorough analysis of the synthesis and degradation dynamics (SD dynamics), (2), that we defined earlier. Suppose now that we add partial labeled edges to core graph, G,

$$\stackrel{s_i}{\to }i,i\stackrel{d_i}{\to }$$

corresponding to zeroth-order synthesis and first-order degradation, respectively. Each vertex can have any combination of synthesis and degradation edges and the dynamics can now be described by the following system of linear ordinary differential equations (ODEs):

$$\frac{d\mathbf{x}}{dt}=\mathcal{L}(G)·\mathbf{x}-D·\mathbf{x}+\mathbf{s}.$$ (6)

Here (G) is the Laplacian matrix of the core graph G, D is a diagonal matrix with (D)_ii = d_i, and s is a column vector with (s)_i = s_i, using the convention that d_i or s_i is zero if the corresponding partial edge at vertex i is absent.

In the presence of synthesis without degradation the steady state does not exist because it becomes infinite. Therefore, whenever we have D ≡ 0 we assume that s ≡ 0. In this case the system reduces to one of Laplacian dynamics, for which a thorough analysis was given in Mirzaev and Gunawardena (2013). From now on we will assume that at least one element of D is nonzero.

Proposition 3

The dynamics defined by Equation (6) have a unique solution for a given initial condition.

Proof

This can easily be verified as the right hand side of the dynamics, f(x) = (G) · x − D · x + s is affine in x and thus also Lipschitz continuous. Thus the existence of unique continuous solution is guaranteed.

The next question to be answered is to identify the conditions under which the SD dynamics poss steady state solution(s). In order to derive the necessary and sufficient conditions for existence of steady state solution we adopt the complementary graph G^★ that was introduced in Gunawardena (2012). The complementary graph is formed by defining new vertex, ★, such that

$$★\stackrel{s_i}{\to }i\text{or}i\stackrel{d_i}{\to }★$$

For the sake of simplicity we will divide our results into two cases: when G^★ is a strongly connected graph and when it is not strongly connected.

3.1 Strongly connected case

Assume that complementary graph G^★ is strongly connected. Note that G^★ can be strongly connected even though core graph G is not strongly connected (see Figure 4A and 4B of Gunawardena (2012) for an illustration). Let F denote the Laplacian of core graph G minus the degradation matrix D:

$$F=\mathcal{L}(G)-D=\left(\begin{array}{cccccc}\begin{array}{|c|}\hline {\mathcal{L}}_1-D_1\\ \hline\end{array}& \cdots & \mathbf{0}& \mathbf{0}& \cdots & \mathbf{0}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ +& \cdots & \begin{array}{|c|}\hline {\mathcal{L}}_p-D_p\\ \hline\end{array}& \mathbf{0}& \cdots & \mathbf{0}\\ +& \cdots & +& \begin{array}{|c|}\hline {\mathcal{L}}_{p+1}-D_{p+1}\\ \hline\end{array}& \mathbf{0}& \mathbf{0}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ +& \cdots & +& \mathbf{0}& \mathbf{0}& \begin{array}{|c|}\hline {\mathcal{L}}_{p+q}-D_{p+q}\\ \hline\end{array}\end{array}\right)$$ (7)

Suppose that there is some index m ∈ {p + 1, …, p + q} for which D_m ≡ 0. Then 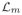− D_m = 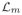= (C_m), which implies that tSCC C_m of core graph G is preserved as a tSCC in the complementary graph G^★. This in turn contradicts the fact that graph G^★ is strongly connected. Thus each matrix 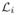− D_i is a perturbed Laplacian matrix of some strongly connected graph, so that from Remark 1 each 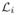− D_i is a non-singular matrix for i = p+1, ···, p+q. For i = 1, ···, p as each of the 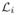’s is already a perturbed Laplacian matrix, “perturb”-ing them further does not change the fact that they are non-singular. Thus the matrix F is a non-singular matrix, since its diagonal components are all non-singular matrices and the unique steady state solution is given algebraically as

$${\mathbf{x}}_s=-{(\mathcal{L}(G)-D)}^{-1}·\mathbf{s}.$$ (8)

Note that steady state does not depend on the given initial condition. In other words, the dynamics reach a unique steady state for any given initial condition.

Next, we prove that for any given initial condition the SD dynamics converge to steady state solution in (8). Towards this end, we define a change of variables

$$\mathbf{x}=\mathbf{y}-{(\mathcal{L}(G)-D)}^{-1}·\mathbf{s}.$$

This substitution transforms the original SD dynamics into

$$\frac{d\mathbf{y}}{dt}=(\mathcal{L}(G)-D)·\mathbf{y}.$$ (9)

From Theorem 3 we know that eigenvalues of the Laplacian, (G), satisfy Re(λ) ≤ 0, where equality holds if and only if λ = 0. The proof of this result follows from applying the Gershgorin theorem to the columns of the matrix (G). Then the matrix D in (G) − D shifts the centers of the Gershgorin discs further to left on the real line without changing their radii, so we will still have Re(λ) ≤ 0 for eigenvalues of the matrix (G) − D. On the other hand, the matrix (G) − D is non-singular, so it follows that Re(λ) < 0. This result in turn implies that solution of the system given in (9) converges to the trivial steady state, y_s = 0. Thus we can now state the following theorem.

Theorem 4

Given core graph G with partial labeled synthesis and degradation edges. If the associated complementary graph G^★ is strongly connected, then the SD dynamics (6) have a unique stable steady state solution.

The symbolic computation of the steady state solution using (8) can be very expensive even for small number of vertices. Therefore we restate an algorithm, given in Gunawardena (2012), which uses graphical structure of graph G^★ to calculate steady state solution given in (8).

Let 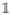= (1, ···, 1)^T be a vector of all ones. At steady state we have $\frac{d\mathbf{x}}{dt}=\mathbf{0}$ and using the fact that 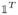· (G) = 0 it follows from (3) that

$$d_1{x}_1+\cdots +d_n{x}_n=s_1+\cdots +s_n.$$ (10)

In other words at steady state we should have an overall balance in synthesis and degradation. The Laplacian (G^★) of the graph G^★ can then be related to the Laplacian (G) of the graph G

$$\mathcal{L}(G^{★})=\left(\begin{array}{cc}\mathcal{L}(G)& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right)+\left(\begin{array}{cc}-D& \mathbf{s}\\ {𝟙}^T·D& -{𝟙}^T·\mathbf{s}\end{array}\right)$$ (11)

Suppose now that we have overall balance in synthesis and degradation then using (11) it is easy to see that (x₁, ···, x_n, 1) is a steady state of

$$\frac{d\mathbf{x}}{dt}=\mathcal{L}(G^{★})·\mathbf{x}$$ (12)

if and only if (x₁, ···, x_n) is a steady state of the SD dynamics given in (6). Since G^★ is strongly connected, the MTT provides a basis element for the kernel of the Laplacian matrix (G^★), ker { (G^★)} = span{ρ^G★} (Gunawardena, 2012). Consequently, the unique steady state x_s is given by

$${({\mathbf{x}}_s)}_i=\frac{{\left({\mathit{\rho }}^{G^{★}}\right)}_i}{{({\mathit{\rho }}^{G^{★}})}_{★}}$$ (13)

Since any steady state solution of (12) can be written as scalar multiple of kernel element, ρ^G★, that single degree of freedom is used to guarantee that (x_s)_★ = 1 (synthesis and degradation vertex, ★). This condition also ensures that overall balance in synthesis and degradation (10) is satisfied.

3.2 General Case

In contrast to the strongly-connected case, the steady state solutions do not always exist in the general case. First, we will derive conditions to assure the existence of a steady state solution. Then, we will show that provided we have a steady state solution x_s, the system converges to this x_s as t → ∞. Third, we provide a framework for construction of x_s using the underlying graph structure of graph G with illustration of results using a hypothetical example.

Consider the matrix F and degradation matrices D_p+1, …, D_p+q corresponding to tSCCs C_p+1, …, C_p+q, respectively. If D_i ≢ 0 for all i ∈ {p + 1, …, p + q}, then for each i ∈ {p + 1, …, p + q} the matrix 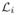− D_i is perturbed Laplacian matrix and thus non-singular. This in turn implies that the matrix F is non-singular. And hence the steady state solution can be given as

$$x_s=-F^{-1}\mathbf{s}.$$ (14)

Since the complementary graph G^★ is no longer strongly connected observe that graph theoretic algorithm described in Section 3.1 cannot be used for computation of the steady state given in (14). In Section 4 we prove that all the entries of inverse matrix F⁻¹ are non-positive numbers. Subsequently, in Section 4.3 we present graph theoretical algorithm, which computes the inverse matrix F⁻¹.

From now on throughout this section we assume that the complementary graph G^★ is not strongly connected, and there is at least one i ∈ {p + 1, …, p + q} such that D_i ≡ 0. Let {i₁, ···, i_k} ⊆ {p + 1, ···, p + q} be a set for which D_i1 = ··· = D_ik ≡ 0, then we can relabel the vertices of G^★ such that matrices 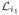, …, 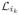are positioned in the lower right of matrix F,

$$\begin{array}{l}F=\mathcal{L}(G)-D=\left(\begin{array}{cccccc}\begin{array}{|c|}\hline {\mathcal{L}}_1-D_1\\ \hline\end{array}& \cdots & \mathbf{0}& \mathbf{0}& \cdots & \mathbf{0}\\ ⋮& \ddots & ⋮& & & \\ +& +& \begin{array}{|c|}\hline {\mathcal{L}}_{p+q-k}-D_{p+q-k}\\ \hline\end{array}& \mathbf{0}& \cdots & \mathbf{0}\\ +& \cdots & +& \begin{array}{|c|}\hline {\mathcal{L}}_{p+q-k+1}\\ \hline\end{array}& \cdots & \mathbf{0}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ +& \cdots & +& 0& \cdots & \begin{array}{|c|}\hline {\mathcal{L}}_{p+q}\\ \hline\end{array}\end{array}\right)\\ =\left(\begin{array}{cccccc}\begin{array}{|c|}\hline {\mathcal{M}}_1\\ \hline\end{array}& \cdots & \mathbf{0}& \mathbf{0}& \cdots & \mathbf{0}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ +& +& \begin{array}{|c|}\hline {\mathcal{M}}_r\\ \hline\end{array}& \mathbf{0}& \cdots & \mathbf{0}\\ +& \cdots & +& \begin{array}{|c|}\hline {\mathcal{L}}_{r+1}\\ \hline\end{array}& \mathbf{0}& \mathbf{0}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ +& \cdots & +& \mathbf{0}& \mathbf{0}& \begin{array}{|c|}\hline {\mathcal{L}}_{r+k}\\ \hline\end{array}\end{array}\right)=\left(\begin{array}{cc}N& \mathbf{0}\\ B& T\end{array}\right)\end{array}$$ (15)

where r = p + q − k, each 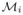= 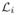− D_i = (C_i) − Δ_i − D_i is a perturbed Laplacian matrix of some SCC C_i and each 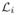corresponds to the Laplacian matrix of some tSCC in graph G^★. This relabeling is always possible because the labeling procedure described in Section 2 does not provide any restriction on individual labeling of vertices located in the set of tSCCs.

Next we present a theorem, which provides the necessary and sufficient conditions in order for a steady state to exist. For that we partition the synthesis vector s such that it matches up with the partition of the matrix F,

$$F=\left(\begin{array}{cc}N& \mathbf{0}\\ B& T\end{array}\right),\mathbf{s}=\left(\frac{{\mathbf{s}}^{\prime }}{{\mathbf{s}}^{″}}\right).$$

Theorem 5

When G^★ is not strongly connected and T ≢ 0, the necessary and sufficient conditions for existence of a steady state solution are

1. s″ ≡ 0

2. B · N⁻¹ · s′ ≡ 0

Proof

Let us first derive the equivalent statements for the existence of a steady state solution. Finding a steady state solution of the system is equivalent to solving the linear system

$$(\mathcal{L}(G)-D)·\mathbf{x}=-\mathbf{s}.$$ (16)

Thus a steady state solution exists if and only if −s ∈ Range { (G) − D}. Let us apply simple row reduction (i.e., Gaussian elimination) to the augmented matrix ( (G) − D ¦ s)

$$\begin{array}{l}\left(\begin{array}{ccccccc}\begin{array}{|c|}\hline {\mathcal{M}}_1\\ \hline\end{array}& \cdots & \mathbf{0}& \mathbf{0}& \cdots & \mathbf{0}& \\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮& -{\mathbf{s}}^{\prime }\\ \ast & \cdots & \begin{array}{|c|}\hline {\mathcal{M}}_r\\ \hline\end{array}& \mathbf{0}& \cdots & \mathbf{0}& \\ & B_1& & \begin{array}{|c|}\hline {\mathcal{L}}_{r+1}\\ \hline\end{array}& \mathbf{0}& \mathbf{0}& -{\mathbf{s}}^{(1)}\\ & ⋮& & ⋮& \ddots & ⋮& ⋮\\ & B_k& & \mathbf{0}& \mathbf{0}& \begin{array}{|c|}\hline {\mathcal{L}}_{r+k}\\ \hline\end{array}& -{\mathbf{s}}^{(k)}\end{array}\right)\\ \to \left(\begin{array}{ccccccc}\begin{array}{|c|}\hline {\mathbb{I}}_{a_1}\\ \hline\end{array}& \cdots & \mathbf{0}& \mathbf{0}& \cdots & \mathbf{0}& \\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮& -N^{-1}{\mathbf{s}}^{\prime }\\ \mathbf{0}& \mathbf{0}& \begin{array}{|c|}\hline {\mathbb{I}}_{a_r}\\ \hline\end{array}& \mathbf{0}& \cdots & \mathbf{0}& \\ & B_1& & \begin{array}{|c|}\hline {\mathcal{L}}_{r+1}\\ \hline\end{array}& \mathbf{0}& \mathbf{0}& -{\mathbf{s}}^{(1)}\\ & ⋮& & ⋮& \ddots & ⋮& ⋮\\ & B_k& & \mathbf{0}& \mathbf{0}& \begin{array}{|c|}\hline {\mathcal{L}}_{r+k}\\ \hline\end{array}& -{\mathbf{s}}^{(k)}\end{array}\right)\\ \to \left(\begin{array}{ccccccc}\begin{array}{|c|}\hline {\mathbb{I}}_{a_1}\\ \hline\end{array}& \cdots & \mathbf{0}& \mathbf{0}& \cdots & \mathbf{0}& \\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮& -N^{-1}{\mathbf{s}}^{\prime }\\ \mathbf{0}& \mathbf{0}& \begin{array}{|c|}\hline {\mathbb{I}}_{a_r}\\ \hline\end{array}& \mathbf{0}& \cdots & \mathbf{0}& \\ \mathbf{0}& \cdots & \mathbf{0}& \begin{array}{|c|}\hline {\mathcal{L}}_{r+1}\\ \hline\end{array}& \mathbf{0}& \mathbf{0}& -{\mathbf{s}}^{(1)}+B_1{N}^{-1}{\mathbf{s}}^{\prime }\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮& ⋮\\ \mathbf{0}& \cdots & \mathbf{0}& \mathbf{0}& \mathbf{0}& \begin{array}{|c|}\hline {\mathcal{L}}_{r+k}\\ \hline\end{array}& -{\mathbf{s}}^{(k)}+B_k{N}^{-1}{\mathbf{s}}^{\prime }\end{array}\right).\end{array}$$

So the above system (16) has a solution if and only if each partial linear system

$${\mathcal{L}}_{r+i}·{\mathbf{z}}^{(i)}=-{\mathbf{s}}^{(i)}+B_i·N^{-1}·{\mathbf{s}}^{\prime }$$ (17)

has a solution. Equation (17) provides an equivalent condition for the existence of a steady state solution for the SD dynamics. At this point we will prove that (17) is satisfied if and only if two conditions of the theorem are satisfied.

Let us assume that (17) holds true. Then each partial linear system has a solution if the following condition is satisfied:

$${𝟙}^T·{\mathcal{L}}_{r+i}·{\mathbf{z}}^{(i)}={𝟙}^T·\mathcal{L}(C_{r+i})·{\mathbf{z}}^{(i)}=\mathbf{0}=-{𝟙}^T·{\mathbf{s}}^{(i)}+{𝟙}^T·B_i·N^{-1}·{\mathbf{s}}^{\prime }i\in \{1,\cdots ,k\}.$$ (18)

To proceed further we need the nontrivial fact that all the entries of the matrix N⁻¹ are non-positive real numbers and so assume it to be true.⁶ All entries of the vector s⁽ⁱ⁾ and matrix B_i are non-negative real numbers, because all edge weights are non-negative real numbers by definition. Therefore, each of the products B_i · N⁻¹ · s′ are the matrices with non-positive entries. This in turn implies that both of the summands in (18) are equal to zero,

$$-{𝟙}^T·{\mathbf{s}}^{(i)}\equiv \mathbf{0}\text{and}{𝟙}^T·B_i·N^{-1}·{\mathbf{s}}^{\prime }\equiv \mathbf{0}i\in \{1,\cdots ,k\}$$

Recall that a sum of non-negative (ℝ_≥0) real numbers is equal to zero if and only if each of the numbers are equal to zero. Hence,

$${\mathbf{s}}^{(i)}\equiv \mathbf{0}\text{and}{B}_i·N^{-1}·{\mathbf{s}}^{\prime }\equiv \mathbf{0}i\in \{1,\cdots ,k\}$$ (19)

which is equivalent to the two conditions of the theorem,

$${\mathbf{s}}^{″}={({\mathbf{s}}_1,\cdots ,{\mathbf{s}}_k)}^T\equiv \mathbf{0}\text{and}B·N^{-1}·{\mathbf{s}}^{\prime }\equiv \mathbf{0}.$$ (20)

Conversely, assume that two conditions of the theorem are satisfied. Then it easy to observe that (19) also holds true. Consequently, it follows that the linear system (17) reduces to

$${\mathcal{L}}_{r+i}·{\mathbf{z}}^{(i)}=\mathcal{L}(C_{r+i})·{\mathbf{z}}^{(i)}=-{\mathbf{s}}^{(i)}+B_i·N^{-1}·{\mathbf{s}}^{\prime }=\mathbf{0}$$ (21)

which always has a solution. Moreover, the solution of the above linear system (21) can be constructed graph theoretically by Proposition 1.

The first condition of the theorem, s″ ≡ 0, can be interpreted as follows: a necessary condition for the existence of a steady state is that if a tSCC does not have degradation edge, it should also not have a synthesis edge. On the other hand, one can also visualize these conditions in terms of chemical reactions. If there is continuous inflow of substrates into the production part of the reaction and a lack of outflow, then reaction will grow without bound. The second condition of the theorem identifies nodes without degradation, which also contribute directly (or indirectly) to tSCCs. Indeed, these types of nodes also cause the SD dynamics to grow without bound.

Next we show that (3) can be transformed into homogeneous system of linear differential equations, provided that both conditions of Theorem 5 are fulfilled. As in the previous section we define the matrix F = (G) − D, and partition F and s as

$$F=\left(\begin{array}{cc}N& \mathbf{0}\\ B& T\end{array}\right)\mathbf{s}=\left(\frac{{\mathbf{s}}^{\prime }}{\mathbf{0}}\right)$$

where F ∈ ℝ^n×n, N ∈ ℝ^m×m, $B\in {ℝ}_{\ge 0}^{m\times (n-m)}$, T ∈ ℝ^{(n−m)×(n−m)} and column vectors $\mathbf{s}\in {ℝ}_{\ge 0}^n,{\mathbf{s}}^{\prime }\in {ℝ}_{\ge 0}^m$. Let us also define a matrix $Q\in {ℝ}_{\le 0}^{n\times n}$

$$Q=\left(\begin{array}{cc}{N}^{-1}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right),$$

to be used in the change of variable x = y − Q · s. This substitution transforms (3) into

$$\frac{d\mathbf{x}}{dt}=\frac{d\mathbf{y}}{dt}=F·\mathbf{y}-F·Q·\mathbf{s}+\mathbf{s}=F·\mathbf{y}-\left(\frac{{\mathbf{s}}^{\prime }}{B·N^{-1}·{\mathbf{s}}^{\prime }}\right)+\left(\frac{{\mathbf{s}}^{\prime }}{\mathbf{0}}\right).$$

Assuming that a steady state solution of the SD dynamics exists, then by Theorem 5 we have that B · N⁻¹ · s′ ≡ 0, from which it follows that

$$\frac{d\mathbf{y}}{dt}=F·\mathbf{y}.$$ (22)

Theorem 6

Under conditions of Theorem 5 and for any given initial condition the dynamics defined in (22) converge to a unique steady state as t → ∞.

Proof

We will prove this theorem by showing that matrix F satisfies both conditions of Theorem 3. First note that by definition, the matrix F is a Laplacian matrix minus a non-negative diagonal matrix, F = (G) − D. Hence, it follows that

$$\sum _{v\ne i}\mid {(F)}_{vi}\mid =\sum _{v\ne i}{(\mathcal{L}(G))}_{vi}=\mid {(\mathcal{L}(G))}_{ii}\mid \le \mid {(\mathcal{L}(G))}_{ii}\mid +d_i=\mid {(F)}_{ii}\mid$$

Therefore, if we apply Gerschgorin’s theorem to the columns of the matrix F, we see that each eigenvalue of F is located in the discs of the form

$$\{z\in \mathbf{C}\mid \mid z+\mid {(\mathcal{L}(G))}_{ii}\mid +d_i\mid \le \mid {(\mathcal{L}(G))}_{ii}\mid \}.$$

A disc touches the y – axis from the left hand side if and only if |( (G))_ii| + d_i = |( (G))_ii|, or d_i = 0. Hence for an eigenvalue, λ, of the matrix F we conclude that Re(λ) ≤ 0, where equality holds if and only if λ = 0. Thus, the matrix F satisfies first condition of Theorem 3.

Conversely, from the lower-block diagonal structure of the matrix F and Corollary 1, it follows that

$$\begin{array}{l}{\mathit{geo}}_F(0)=dim\{kerF\}=dim\{kerN\}+dim\{ker{\mathcal{L}}_{r+1}\}+\cdots +dim\{ker{\mathcal{L}}_{r+k}\}\\ =0+{\mathit{geo}}_{{\mathcal{L}}_{r+1}}(0)+\cdots +{\mathit{geo}}_{{\mathcal{L}}_{r+k}}(0)=k.\end{array}$$

Remember that each matrix 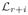is the Laplacian matrix of the tSCC C_r+i, so the dim ker { 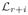} = 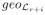(0) = 1 = 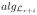(0). Again the block diagonal structure of F suggests that

$$\begin{array}{l}{\mathit{alg}}_F(0)={\mathit{alg}}_{{\mathcal{M}}_1}(0)+\cdots +{\mathit{alg}}_{{\mathcal{M}}_r}(0)+{\mathit{alg}}_{{\mathcal{L}}_{r+1}}(0)+\cdots +{\mathit{alg}}_{{\mathcal{L}}_{r+k}}(0)\\ =0+\cdots +0+1+\cdots +1=k.\end{array}$$

Since each matrix 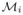is non-singular, none of their eigenvalues are zero. Hence, it follows that the dynamics (22) satisfy the second condition of Theorem 3, alg_F (0) = geo_F (0) = k. Therefore, the matrix F satisfies both conditions of Theorem 3, which in turn implies that the dynamics defined in (22) converge to a unique steady state for any given initial condition.

Now we will provide a framework for finding the steady state solution of the SD dynamics. Define R as an n × k matrix whose columns are a basis elements of the column null space (right kernel) of the matrix F.⁷ Analogously, define L such that is a k × n matrix whose rows are basis elements of the row null space (left kernel) of the matrix F. Then these matrices satisfy

$$F·R=\mathbf{0}\text{and}L·F=\mathbf{0}$$

Naturally, L and R can be chosen so that the following equation holds

$$L·R={\mathbb{I}}_k.$$ (23)

Since matrices L and R are not uniquely defined, equation (23) serves as a normalization condition. In fact, in the subsequent section we discuss an example of such normalization. The following lemma gives a representation of the steady state for the dynamics defined in (22) in terms of matrices R and L. For the proof of this lemma we refer reader to Lemma 3 of Mirzaev and Gunawardena (2013).

Lemma 1

Assume that F is a matrix for which (23) holds and when coupled with the initial condition y(0) = y₀ the solution of system (22) converges to a steady state y_s as t → ∞. Then y_s = R · L · y₀.

Once the steady state solution of the dynamics (22) is found, the steady state solution of the SD dynamics (6) can be found using back substitution:

$$x_s={\mathbf{y}}_s-Q·\mathbf{s}=R·L·{\mathbf{y}}_0-Q·\mathbf{s}=R·L·{\mathbf{x}}_0+(R·L-{\mathbb{I}}_n)·Q·\mathbf{s}.$$ (24)

3.2.1 Construction of the matrices R and L

We next discuss the graph theoretical procedure to construct matrices R and L that satisfy (23). The general strategy is to calculate matrix R using Proposition 2, then construct the uniquely defined matrix L that satisfies (23). Consider the block decomposition of matrix F given in (15), decompose matrices R and L such that

$$F=\left(\begin{array}{cc}n-u& u\\ N& \mathbf{0}\\ B& T\end{array}\right)\begin{array}{c}n-u\\ u\end{array},L=\left(\begin{array}{cc}n-u& u\\ X& U\end{array}\right)k,R=\left(\begin{array}{c}k\\ Y\\ V\end{array}\right)\begin{array}{c}n-u\\ u\end{array}$$ (25)

where k is the number of tSCCs of complementary graph G^★, u is number of vertices that are in tSCCs C_r+1, …, C_r+k, X is k × (n − u), U is k × u, N is (n − u) × (n − u), B is u × (n − u), T is u × u, Y is (n − u) × k and V is u × k.

Consequently, the kernel elements of the matrix F are constructed using Proposition 2, ker{F} = span{ρ̄^C_r+1, ···, ρ̄^C_r+k} using the tSCCs, {C_r+1, ···, C_r+k} and thus we have F · ρ̄^C_r+i = 0, i = 1, …, k. Let ρ̂^C_r+i be normalized version of ρ̄^C_r+i such that

$${𝟙}^T·{\widehat{\mathit{\rho }}}^{C_{r+i}}=1.$$ (26)

Then the i^th column of R is defined as R_i = ρ̂^C_r+i such that

$$F·R_i=\mathbf{0}.$$

As a result we have matrix R which satisfies

$$F·R=\mathbf{0}.$$ (27)

In other words, for any vertex j ∉ 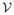(C_r+i), (R_i)j = 0. This in turn implies that Y ≡ 0 and V is non-zero matrix corresponding to the tSCCs of complementary graph G^★.

Then we can construct the matrix L using the following process. Let U be the matrix given by first transposing V and then replacing each nonzero element of V by 1. Since 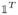· (C_r+i) = 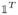· 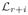= 0, we have that U · T = 0 and by (26) we have that U · V = 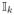. Let the matrix X be constructed as X = −U · B · N⁻¹. With this definition and (25), we can see that the matrix L satisfies the criteria L · F = 0,

$$L·F=(X\mid U)·\left(\begin{array}{cc}N& \mathbf{0}\\ B& T\end{array}\right)=(X·N+U·B\mid U·T)=(-U·B·N^{-1}·N+U·B\mid U·T)=\mathbf{0}$$ (28)

Moreover, by definition, (25), the matrices L and R also satisfy (23) as illustrated by

$$L·R=(X\mid U)·\left(\frac{Y}{V}\right)=X·Y+U·V=0+{\mathbb{I}}_k={\mathbb{I}}_k$$ (29)

Therefore by (27), (28) and (29) we can conclude that constructed matrices R and L satisfies (23) and so the steady state of the SD dynamics (6) is given by (24).

3.3 Illustration of Results

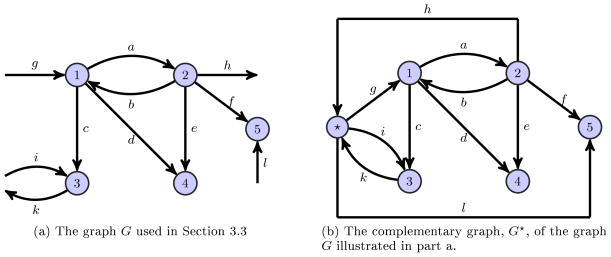
Consider the directed graph G with 5 vertices, given in Figure 2a with its complementary graph G^★ in Figure 2b.

Fig. 2.

A graph with its corresponding complementary graph.

We have labeled vertices according to the labeling procedure described in Section 2. We note that the complementary graph G^★ of graph G is not strongly connected, with non-terminal SCC C₁ with 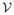(C₁) = {1, 2, 3, ★} and two tSCCs, C₂ with 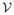(C₂) = {4} and C₃ with 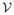(C₃) = {5}. The Laplacian matrix for the core graph G is

$$\mathcal{L}(G)=\left(\begin{array}{ccccc}-(a+c+d)& b& 0& 0& 0\\ a& -(b+e+f)& 0& 0& 0\\ c& 0& 0& 0& 0\\ d& e& 0& 0& 0\\ 0& f& 0& 0& 0\end{array}\right).$$ (30)

The degradation and synthesis are given by D = diag (0, h, i, 0, 0), s = (g, 0, k, 0, l)^T, respectively. The associated SD dynamics are given by a system of ODEs as in (6). So the matrix F = (G) − D with its corresponding partitioning is given by

$$F=\left(\begin{array}{cc}N& 0\\ B& T\end{array}\right)=\left(\begin{array}{ccccc}-(a+c+d)& b& 0& 0& 0\\ a& -(b+e+f+h)& 0& 0& 0\\ c& 0& i& 0& 0\\ d& e& 0& 0& 0\\ 0& f& 0& 0& 0\end{array}\right)$$ (31)

Then we partition the vector s such that it matches with the partitioning of F, so that we have

$$\mathbf{s}=\left(\frac{{\mathbf{s}}^{\prime }}{{\mathbf{s}}^{″}}\right),\text{where}{\mathbf{s}}^{\prime }=\left(\begin{array}{c}g\\ 0\\ k\end{array}\right)\text{and}{\mathbf{s}}^{″}=\left(\begin{array}{c}0\\ l\end{array}\right).$$

In order for an steady state to exist, the vector s should satisfy the necessary and sufficient conditions given in Theorem 5. By the first condition we have that s″ ≡ 0, and thus 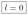implying that we cannot have synthesis on vertex 5. Next, we check the second condition of Theorem 5,

$$\mathbf{0}=B{N}^{-1}{\mathbf{s}}^{\prime }={𝟙}^{T}B{N}^{-1}{\mathbf{s}}^{\prime }=\left(-\frac{a(e+f)+d(b+e+f+h)}{b(c+d+(a+c+d))(e+f+h)}-\frac{bd+(a+c+d)(e+f)}{b(c+d)+(a+c+d)(e+f+h)}0\right)\left(\begin{array}{c}g\\ 0\\ k\end{array}\right),$$

and conclude that 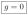. Hence, the steady state solution exists if and only if g = l = 0. The graphs G and G^★ which are compatible with having a steady state are depicted in Figure 3. In a comparison with Figure 2a, we note the absence of synthesis on nodes 1 and 5.

Fig. 3.

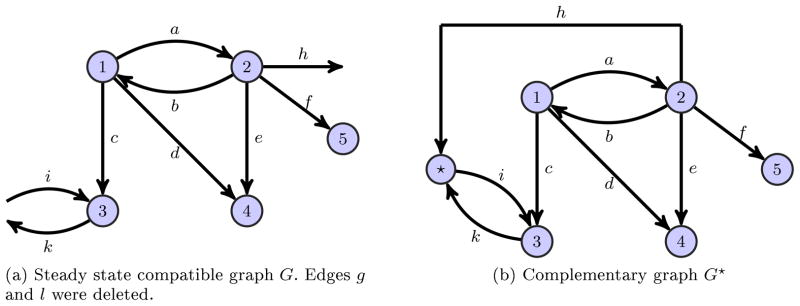
Steady state compatible graph with its corresponding complementary graph. The graph G illustrated in Figure 2a was tested for the conditions of Theorem 5 and conflicting edges were deleted.

Every matrix is defined as in (31) except for the vector s = (0, 0, k, 0, 0)^T. As before G^★ has two tSCCs, C₂ with (C₂) = {4} and C₃ with (C₃) = {5}. Now with the necessary and sufficient conditions in hand, we will follow the construction process for the matrices R and L described in Section 3.2.1. Since tSCCs, C₂ and C₃, each have only one vertex, we have normalized vectors ρ̂^C₂ = (0, 0, 0, 1, 0)^T and ρ̂^C₃ = (0, 0, 0, 0, 1). So the columns of the matrix R are defined as R₁ = ρ̂^C₂, R₂ = ρ̂^C₃,

$$R=\left(\begin{array}{cc}0& 0\\ 0& 0\\ 0& 0\\ 1& 0\\ 0& 1\end{array}\right)=\left(\frac{Y}{V}\right)$$

Therefore, $V=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$, then transposing V and writing 1’s instead of its non-zero elements we get $U=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)$. And so the matrix X is

$$X=-U·B·N^{-1}=\frac{1}{b(c+d)+(a+c+d)(e+f+h)}\left(\begin{array}{ccc}af& (a+c+d)f& 0\\ ae+d(b+e+f+h)& bd+(a+c+d)e& 0\end{array}\right)$$

So

$$L=(X\mid U)=\left(\begin{array}{ccccc}\frac{af}{b(c+d)+(a+c+d)(e+f+h)}& \frac{(a+c+d)f}{b(c+d)+(a+c+d)(e+f+h)}& 0& 0& 1\\ \frac{ae+d(b+e+f+h)}{b(c+d)+(a+c+d)(e+f+h)}& \frac{bd+(a+c+d)e}{b(c+d)+(a+c+d)(e+f+h)}& 0& 1& 0\end{array}\right)$$

Accordingly, by (24) the steady state, x_s, is given by

$${\mathbf{x}}_s=R·L·{\mathbf{x}}_0+(R·L-{\mathbb{I}}_n)·F^{+}·\mathbf{s}=R·L·{\mathbf{x}}_0+{(\begin{array}{ccccc}0& 0& \frac{k}{i}& 0& 0\end{array})}^T.$$

4 Inverse of Non-Singular Perturbed Laplacian Matrices

In our previous paper (Mirzaev and Gunawardena, 2013), we have proven that the perturbed Laplacian matrix of a strongly connected graph is non-singular. In this work, we further claim that the inverse of such a matrix has nonpositive entries. In this section, we prove this and provide a graph theoretic algorithm for the computation of the inverse of perturbed Laplacian matrices. Once again consider a graph G with n nodes. As before Laplacian matrix for this graph is given by matrix (G) ∈ ℝ^n×n and perturbed Laplacian matrix is defined as P = (G) − Δ, where Δ is diagonal matrix with non-negative entries,

$${(\mathit{\Delta })}_{ij}=\{\begin{array}{cc}{\delta }_i& i=j\\ 0& i\ne j\end{array}.$$

Remember from Remark 1 that a perturbed Laplacian matrix of a strongly connected graph is a non-singular matrix. However, a perturbed Laplacian matrix of an arbitrary graph is not necessarily non-singular. Here, we will prove that the inverse of any non-singular perturbed Laplacian matrix is a non-positive matrix. By that we mean all the elements of the inverse matrix, P⁻¹, are non-positive real numbers (henceforth, P represents a non-singular perturbed Laplacian matrix). To accomplish this we first prove the statement for the case when the graph G is strongly connected and then prove it for an arbitrary graph.

4.1 Strongly connected case

When the graph G is strongly connected we will use the explicit formulation of the inverse of a non-singular matrix P, derived from Laplace expansion of the determinant,

$$P^{-1}=\frac{1}{det(P)}\mathit{adj}(P)$$ (32)

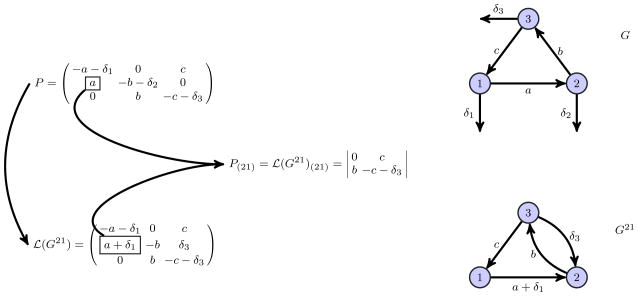
where (adj(P))_ji = (−1)^i+jP_(ij), the ji-th entry of the adjugate being the (ij)-th minor of P (up to the sign). At this point we can reconstruct the i-th row of the matrix P such that the constructed matrix is the Laplacian matrix of a strongly connected graph denoted as G^ij. In particular, the Laplacian of a strongly connected graph G^ij can be obtained by subtracting the row vector 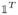· P from the i-th row of perturbed Laplacian matrix P. In fact, this operation erases the degradation edge on vertex i and redirects the rest of the degradation edges to vertex i. As a result we only add new edges (if any) to the core graph G of perturbed Laplacian matrix P. Since the core graph G is strongly connected the resulting graph is also strongly connected, which we denote with G^ij. An illustration of such a reconstruction is given in Figure 4. Then it follows that (G^ij)_(ij) = P_(ij). Thus the ij-th minor of the matrix P can be calculated as the ij-th minor of the matrix (G^ij), which in turn can be calculated using the MTT,

Fig. 4.

2nd row of P is reconstructed to get the Laplacian matrix (G²¹) and the associated strongly connected graph G²¹. At the top (from left to right), perturbed Laplacian matrix P and the associated graph G. In the middle, (21)-th minor of P and (21)-th minor of (G²¹). At the bottom (from left to right), Laplacian matrix (G²¹) and the associated graph G²¹.

$$\begin{array}{l}{(\mathit{adj}(P))}_{ji}={(-1)}^{i+j}{P}_{(ij)}={(-1)}^{i+j}\mathcal{L}{(G^{ij})}_{(ij)}\\ ={(-1)}^{i+j}{(-1)}^{n+i+j-1}{\left({\mathit{\rho }}^{G^{ij}}\right)}_i={(-1)}^{n-1}{\left({\mathit{\rho }}^{G^{ij}}\right)}_i.\end{array}$$ (33)

Since the graph G^ij is strongly connected, from Proposition 1 we find that (ρ^Gij)_i > 0 for each index i. As for the determinant of the matrix P, we can again add one row and one column to the matrix P such that the constructed (n + 1) × (n + 1) matrix is the Laplacian matrix of the strongly connected graph G^{n+1 n+1}. Specifically, we note that the form of this matrix is

$$\mathcal{L}\left(G^{n+1n+1}\right)=\left(\begin{array}{cc}P& \mathbf{a}\\ -{𝟙}^T·P& -{𝟙}^T·\mathbf{a}\end{array}\right),$$

where a stands for n dimensional column vector with positive entries. For the convenience of the notation, hereafter, we refer to the graph G^{n+1 n+1} simply as Gⁿ⁺¹.

Then by the MTT it is implied that

$$det(P)=\mathcal{L}{(G^{n+1})}_{(n+1n+1)}={(-1)}^{3(n+1)-1}{\left({\mathit{\rho }}^{G^{n+1}}\right)}_{n+1}={(-1)}^n{\left({\mathit{\rho }}^{G^{n+1}}\right)}_{n+1}.$$ (34)

Note that the construction of such a row and a column is independent of the existing rows, so we can always reconstruct a strongly connected graph Gⁿ⁺¹. Consequently, from Proposition 1 it follows that (ρ^Gn+1)_n+1 > 0. Therefore, (32), (33) and (34) together imply that

$${(P^{-1})}_{ij}=\frac{1}{\mathit{det}(P)}{(\mathit{adj}(P))}_{ij}=\frac{{(-1)}^{n-1}{\left({\mathit{\rho }}^{G^{ij}}\right)}_i}{{(-1)}^n{\left({\mathit{\rho }}^{G^{n+1}}\right)}_{n+1}}=-\frac{{\left({\mathit{\rho }}^{G^{ij}}\right)}_i}{{\left({\mathit{\rho }}^{G^{n+1}}\right)}_{n+1}}<0,$$

and thus all the entries of the matrix P⁻¹ are strictly less than zero.

4.2 General Case

In the general case, the perturbed Laplacian matrix of an arbitrary graph G may not be a non-singular matrix. In Section 3 we have seen that for a perturbed Laplacian matrix to be non-singular, the diagonal blocks associated to each SCC should be a perturbed Laplacian matrix on their own. Consider an arbitrary graph G with q SCCs, C₁, ···, C_q, we assume that the matrix P can be partitioned analogous to (7),

$$P=\left(\begin{array}{ccc}\begin{array}{|c|}\hline {\mathcal{P}}_1\\ \hline\end{array}& \cdots & \mathbf{0}\\ ⋮& \ddots & ⋮\\ +& +& \begin{array}{|c|}\hline {\mathcal{P}}_q\\ \hline\end{array}\end{array}\right),$$

where each 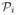= (C_i) − Δ_i, Δ_i ≢ 0 is an a_i × a_i perturbed Laplacian matrix of SCC C_i. Having this decomposition in hand, we are ready to prove that the inverse of the matrix P has all non-positive entries. To do that we will use the results of Section 4.1 and follow the standard path for finding the inverse using the method of Gaussian elimination,

$$\begin{array}{l}(\begin{array}{cc}P& {\mathbb{I}}_n\end{array})=\left(\begin{array}{cccccc}\begin{array}{|c|}\hline {\mathcal{P}}_1\\ \hline\end{array}& \cdots & \mathbf{0}& \begin{array}{|c|}\hline {\mathbb{I}}_{a_1}\\ \hline\end{array}& \cdots & \mathbf{0}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ +& +& \begin{array}{|c|}\hline {\mathcal{P}}_q\\ \hline\end{array}& \mathbf{0}& \mathbf{0}& \begin{array}{|c|}\hline {\mathbb{I}}_{a_q}\\ \hline\end{array}\end{array}\right)\\ \to \left(\begin{array}{cccccc}\begin{array}{|c|}\hline {\mathbb{I}}_{a_1}\\ \hline\end{array}& \cdots & \mathbf{0}& \begin{array}{|c|}\hline {\mathcal{P}}_1^{-1}\\ \hline\end{array}& \cdots & \mathbf{0}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ -& -& \begin{array}{|c|}\hline {\mathbb{I}}_{a_q}\\ \hline\end{array}& \mathbf{0}& \mathbf{0}& \begin{array}{|c|}\hline {\mathcal{P}}_q^{-1}\\ \hline\end{array}\end{array}\right)\end{array}$$

where the minus sign, −, stands for some matrix with non-positive real entries. From Section 4.1 each ${\mathcal{P}}_i^{-1}$ has negative entries. Hence multiplying a block of rows having non-negative real numbers by ${\mathcal{P}}_i^{-1}$ transforms elements of those rows into non-positive real numbers.

Consider the ij-the entry, −a_ij, of the left hand block of the second matrix. Note that jj-th entry of the same blockis equal to 1, e.g. a_jj = 1. Then in order to eliminate this negative element (i.e., −a_ij) we have to multiply the j-th row by a positive real number, a_ij, and add resulting row to the i-th row. Since all the entries of the right hand block are non-positive, this operation places non-positive real numbers on i-th row of the right hand block. Performing operations consecutively, on columns 1, 2, …, n lead to the following matrix

$$\to \left(\begin{array}{cccccc}\begin{array}{|c|}\hline {\mathbb{I}}_{a_1}\\ \hline\end{array}& \cdots & \mathbf{0}& \begin{array}{|c|}\hline {\mathcal{P}}_1^{-1}\\ \hline\end{array}& \cdots & \mathbf{0}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ \mathbf{0}& \mathbf{0}& \begin{array}{|c|}\hline {\mathbb{I}}_{a_q}\\ \hline\end{array}& -& -& \begin{array}{|c|}\hline {\mathcal{P}}_q^{-1}\\ \hline\end{array}\end{array}\right)=(\begin{array}{cc}{\mathbb{I}}_n& P^{-1}\end{array})$$ (35)

As it can be observed from the above equation, (35), all the entries of the matrix P⁻¹ are non-positive real numbers, as desired.

Note that the inverse matrix P⁻¹ preserves lower-block diagonal structure of the perturbed Laplacian matrix P. Moreover, recall that the matrix N defined in (4) is also a non-singular perturbed Laplacian matrix. Hence, all the entries of the inverse matrix N⁻¹ are non-positive real numbers.

4.3 Symbolic computation of P⁻¹ based on the Matrix-Tree Theorem

For a given set of constant edge weights numerical computation of the inverse matrix P⁻¹ is challenging, and even more challenging is a symbolic computation of the inverse. Therefore, here we provide a graph theoretic algorithm for the symbolic computation of P⁻¹. The algorithm is again based on the MTT, and utilizes the theory developed in Section 3.1.

Recall that the perturbed Laplacian P can be written as the Laplacian matrix of a graph G minus the degradation matrix D, i.e. P = (G) − D. For the graph G, we define a complementary graph G^★(s) which is a function of thenonzero, labeled synthesis edges at each vertex, i.e. $\mathbf{s}={(s_1,\dots ,s_n)}^T\in {\mathbb{R}}_{>0}^{n\times 1}$. Since the matrix P is non-singular, each tSCC of G has at least one degradtion edge. Thus the nonzero partial labeled synthesis edges at each vertex makes the complementary graph G^★(s) strongly connected. Now the computation of P⁻¹ can be reformulated as a computation of the steady state of dynamics

$$\frac{d\mathbf{x}}{dt}=P\mathbf{x}+\mathbf{s}=(\mathcal{L}(G)-D)\mathbf{x}+\mathbf{s}.$$ (36)

After applying the framework of the strongly connected case (Section 3.1, (13)) for the synthesis vector, $\mathbf{s}\in {ℝ}_{>0}^{n\times 1}$, we get the graph theoretic representation of the steady state, p(s), i.e.

$${(\mathbf{p}(\mathbf{s}))}_i=\frac{{\left({\mathit{\rho }}^{G★(\mathbf{s})}\right)}_i}{{\left({\mathit{\rho }}^{G★(\mathbf{s})}\right)}_{★}}.$$ (37)

Consider the standard basis of ℝⁿ

$${\left\{{\mathbf{e}}^{(i)}=(0,\dots ,0,1,0,\dots ,0)\right\}}_{i=1}^n.$$

Then, multiplying P⁻¹ by the vector e⁽ⁱ⁾ yields the i-th column of the inverse matrix P⁻¹, allowing us to construct P⁻¹ one column at a time. For that consider the following combinations of specific synthesis edges,

$${\mathbf{a}}^{(0)}={(1,\dots ,1)}^T,{\mathbf{a}}^{(i)}={(1,\dots ,1,2,1,\dots ,1)}^{T}i=1,\dots ,n$$ (38)

where only 2 is the i-th entry of the vector a⁽ⁱ⁾. One can then easily observe that

$$\left\{{\mathbf{a}}^{(i)}-{\mathbf{a}}^{(0)}={\mathbf{e}}^{(i)}={(0,\dots ,0,1,0,\dots ,0)}^{T}i=1,\dots ,n\right\}$$

is standard basis for ℝⁿ. Conversely, G^★(a⁽ⁱ⁾) is strongly connected for each i ∈ {0, 1, …, n}, and so substituting the vectors s =a⁽ⁱ⁾ into (37) gives rise to the steady state solution p(a⁽ⁱ⁾) = p^(i)..8

Then again these steady states can be computed algebraically using (8),

$$-P^{-1}·{\mathbf{a}}^{(i)}={\mathbf{p}}^{(i)}\forall i=0,1,\dots ,n.$$

This in turn can be simplified to

$$P^{-1}·{\mathbf{e}}^{(i)}=P^{-1}·\left({\mathbf{a}}^{(i)}-{\mathbf{a}}^{(0)}\right)={\mathbf{p}}^{(0)}-{\mathbf{p}}^{(i)}\forall i=1,\dots ,n.$$

Since {e⁽¹⁾, …, e⁽ⁿ⁾} is a standard basis for ℝ^n×1, i-th column of the matrix P⁻¹ is given by the vector p⁽⁰⁾ – p⁽ⁱ⁾ or simply as

$$P^{-1}=({\mathbf{p}}^{(0)}\mid {\mathbf{p}}^{(1)}\mid \cdots \mid {\mathbf{p}}^{(n)})·\left(\begin{array}{cccc}1& 1& \cdots & 1\\ -1& 0& \cdots & 0\\ 0& -1& \ddots & ⋮\\ ⋮& 0& \ddots & 0\\ 0& ⋮& \cdots & -1\end{array}\right)$$ (39)

Note that since spanning trees rooted at vertex ★ cannot contain any outgoing edge from vertex ★, the synthesis edges {s₁, …, s_n} will not contribute to (ρ^G★(s))_★. Hence, (ρ^G★(s))_★ remains same for each substitution of a⁽ⁱ⁾. Consequently, we don’t have to calculate (ρ^G★(s))_★ each time and can just factor it out, performing the division at the end.

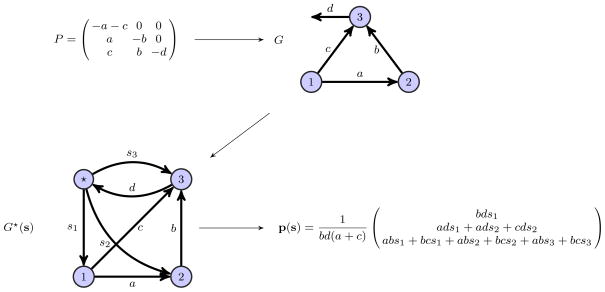
We will illustrate the algorithm presented in this subsection with a simple example. Consider the perturbed Laplacian matrix

$$P=\left(\begin{array}{ccc}-a-c& 0& 0\\ a& -b& 0\\ c& b& -d\end{array}\right).$$

Graph G associated with perturbed Laplacian matrix P and corresponding complementary graph G^★(s) is illustrated in Figure 5. Consequently, by (37) the symbolic steady state is given by

Fig. 5.

Graph theoretic algorithm for computation of P⁻¹. Top left, Perturbed Laplacian matrix P. Top right, graph G associated with perturbed Laplacian matrix P. Bottom left, complementary graph G^★(s) with nonzero labeled synthesis edges added at each vertex of G. Bottom right, the steady state solution of (36).

$$\mathbf{p}(\mathbf{s})=\frac{1}{bd(a+c)}\left(\begin{array}{c}{\mathit{bds}}_1\\ {\mathit{ads}}_1+{\mathit{ads}}_2+{\mathit{cds}}_2\\ {\mathit{abs}}_1+{\mathit{bcs}}_1+{\mathit{abs}}_2+{\mathit{bcs}}_2+{\mathit{abs}}_3+{\mathit{bcs}}_3\end{array}\right)$$ (40)

Then, substituting the synthesis vectors defined in (38) into (40) we find that

$${\mathbf{p}}^{(0)}=\frac{1}{\mathit{\Pi }}\left(\begin{array}{c}bd\\ 2ad+cd\\ 3ab+3bc\end{array}\right),{\mathbf{p}}^{(1)}=\frac{1}{\mathit{\Pi }}\left(\begin{array}{c}2bd\\ 3ad+cd\\ 4ab+4bc\end{array}\right),{\mathbf{p}}^{(2)}=\frac{1}{\mathit{\Pi }}\left(\begin{array}{c}bd\\ 3ad+2cd\\ 4ab+4bc\end{array}\right),{\mathbf{p}}^{(3)}=\frac{1}{\mathit{\Pi }}\left(\begin{array}{c}bd\\ 2ad+cd\\ 4ab+4bc\end{array}\right),$$

where Π = bd(a + c). Thus the inverse matrix P⁻¹ is given by (39),

$$P^{-1}=({\mathbf{p}}^{(0)}\mid {\mathbf{p}}^{(1)}\mid {\mathbf{p}}^{(2)}\mid {\mathbf{p}}^{(3)})·\left(\begin{array}{ccc}1& 1& 1\\ -1& 0& 0\\ 0& -1& 0\\ 0& 0& -1\end{array}\right)=-\frac{1}{bd(a+c)}\left(\begin{array}{ccc}bd& 0& 0\\ ad& ad+cd& 0\\ ab+cb& ab+cb& ab+cb\end{array}\right).$$

5 Biochemical Network Application

In this section we will provide an illustration of how the developed framework is useful for symbolic computation of the steady state solutions of biochemical reaction networks. In particular, we will discuss a popular model for β-cells insulin secretion as well as provide some example insights that are obtained via using the results developed above.

One of the most prevalent diseases, diabetes mellitus (or simply diabetes) is characterized by a high level of blood glucose. Diabetes is the result when either the pancreas does not release enough insulin or when the cells do not respond to insulin produced with increased consumption of sugar (or a combination of both symptoms) (Barg et al., 2002). Insulin is a blood glucose-lowering hormone produced, processed and stored in secretory granules by pancreatic β-cells in Langerhans islets (Olofsson et al., 2002). Consequently, secretory granules are released to extracellular space, which is regulated by Ca²⁺- dependent exocytosis (Wollheim and Sharp, 1981). Since diabetes is related to secretional malfunctions (Rorsman and Renström, 2003), studying the mechanisms of both normal and pathological insulin release in molecular level is crucial for understanding the disease process.

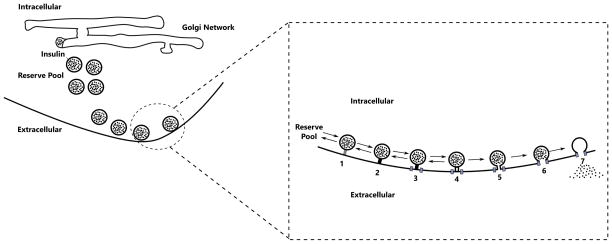
Chen et al. (2008) developed a mathematical model of β-cells to calculate both the rate of granule fusion and the rate of insulin secretion in β-cells stimulated with electrical potential. The authors extended the five-state kinetic model of granule fusion previously proposed by Voets et al. (1999) by adding two-compartments to handle the temporal distribution of Ca²⁺ ion. This seven-state kinetic model is depicted in Figure 6. This model accounts for steps involved in the exocytosis cascade such as re-supply, priming, domain binding, Ca²⁺ triggering, fusion, pore expansion and insulin release. It is assumed that the L-type (not the R-type) voltage-sensitive Ca²⁺-channels are used for secretion of the primed granules through the cell membrane. During this process “microdomains” with high Ca²⁺ concentration are formed at the inner mouth of L-type channels (illustrated as circles in Figure 6). The concentration of Ca²⁺ in the cytosol and the microdomain at time t are denoted by C_i(t) and C_md(t), respectively. These concentrations depend on the electric potential of the cell, and rapidly reach a steady state when the electric potential is kept constant. For instance, (Chen et al., 2008, Figure 2) illustrates that at resting state (electric potential set to V = −70 mV) there is no Ca²⁺ ion in microdomain and only 0.05 μM Ca²⁺ ions in cytosol. Since the number of granules is far less than the number of Ca²⁺ ions, it is also assumed that the dynamics of Ca²⁺ are independent of the exocytosis cascade. For further details we refer the reader to the original paper Chen et al. (2008).

Fig. 6.

Schematic drawing of the exocytosis cascade in β-cells. On the left, the insulin granules produced in Golgi network are transported in membrane-bound vesicles into extracellular space. On the right, the particular steps involved in the exocytosis of the insulin granules. The numbers stand for: 1) Re-supply 2) Priming 3) Domain Binding 4) Ca Triggering 5) Fusion 6) Pore Expansion 7) Insulin Release

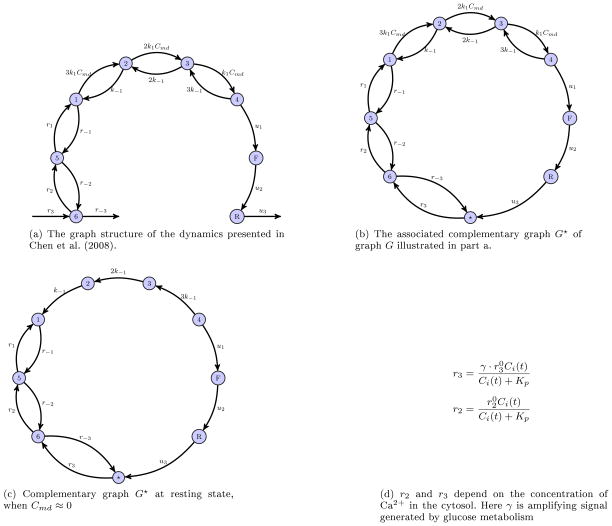
Figure 3B of Chen et al. (2008) illustrates the dynamics associated with the exocytosis cascade as a graph G. For the sake of completeness for this paper we reproduce that graph in Figure 7a. As this model is a system of first-order differential equations, they can be described via

Fig. 7.

Exocytosis cascade of insulin granules in pancreatic β-cells

$$\frac{d\mathbf{n}}{dt}=\mathcal{L}(G)·\mathbf{n}-D·\mathbf{n}+\mathbf{s},\mathbf{n}(0)={\mathbf{n}}_0,$$ (41)

where n = (n₆, n₅, n₁, n₂, n₃, n₄, n_F, n_R) denotes the number of insulin granules at each state, D = diag(r₋₃, 0, 0, 0, 0, 0, 0, u₃) is degradation matrix and s = (r₃, 0, 0, 0, 0, 0, 0, 0)^T is synthesis vector.

Since the complementary graph of G (Figure 7b) is strongly connected, the steady state solutions of the dynamics can be calculated using the algorithm described in Section 3.1. The steady state is given as

$${(n)}_s=\mathit{\Delta }\left(\begin{array}{c}\frac{6r_{-2}{r}_{-1}{k}_{-1}^3}{r_1{r}_2}+\frac{2r_{-2}{r}_{-1}{u}_1{k}_{-1}^2}{r_1{r}_2}+\frac{C_{\text{md}}{k}_1{r}_{-2}{r}_{-1}{u}_1{k}_{-1}}{r_1{r}_2}+\frac{6C_{\text{md}}^3{k}_1^3{u}_1}{r^2}+\frac{6C_{\text{md}}^3{k}_1^3{r}_{-2}{u}_1}{r_1{r}_2}+\frac{2C_{\text{md}}^2{k}_1^2{r}_{-2}{r}_{-1}{u}_1}{r_1{r}_2}\\ \frac{6r_{-1}{k}_{-1}^3}{r_1}+\frac{2r_{-1}{u}_1{k}_{-1}^2}{r_1}+\frac{C_{\text{md}}{k}_1{r}_{-1}{u}_1{k}_{-1}}{r_1}+\frac{6C_{\text{md}}^3{k}_1^3{u}_1}{r_1}+\frac{2C_{\text{md}}^2{k}_1^2{r}_{-1}{u}_1}{r_1}\\ 6k_{-1}^3+2u_1{k}_{-1}^2+C_{\text{md}}{k}_1{u}_1{k}_{-1}+2C_{\text{md}}^2{k}_1^2{u}_1\\ 18C_{\text{md}}{k}_1{k}_{-1}^2+6C_{\text{md}}{k}_1{u}_1{k}_{-1}+3C_{\text{md}}^2{k}_1^2{u}_1\\ 18C_{\text{md}}^2{k}_{-1}{k}_1^2+6C_{\text{md}}^2{u}_1{k}_1^2\\ 6C_{\text{md}}^3{k}_1^3\\ \frac{6C_{\text{md}}^3{k}_1^3{u}_1}{u_2}\\ \frac{6C_{\text{md}}^3{k}_1^3{u}_1}{u_3}\end{array}\right)$$ (42)

where Δ is given as follows

$$\mathit{\Delta }=\frac{r_1{r}_2{r}_3}{r_{-1}{r}_{-2}{r}_{-3}\left(\frac{6k_1^3{r}_1{u}_1{C}_{\text{md}}^3}{r_{-2}{r}_{-1}}+\frac{6k_1^3{r}_1{r}_2{u}_1{C}_{\text{md}}^3}{r_{-3}{r}_{-2}{r}_{-1}}+\frac{6k_1^3{u}_1{C}_{\text{md}}^3}{r_{-1}}+k_1{k}_{-1}{u}_1{C}_{\text{md}}+2k_1^2{u}_1{C}_{\text{md}}^2+2k_{-1}^2{u}_1+6k_{-1}^3\right)}$$

Recall that concentrations C_i(t) (defined implicitly in parameters r₂ and r₃, see Figure 7d) and C_md(t) depend on the electric potential of the β-cell. Hence, in (42) the concentrations C_md(t) and C_i(t) should be interpreted as kinetic parameters, whose value depend on whether the cell is at resting state (V = −70 mV) or depolarized (V = −20 mV). Also, note that the above steady state is a function of only the kinetic parameters, and thus does not depend on the given initial condition. Furthermore, Theorem 4 guarantees stability of this steady state solution. As we can see in (42), the steady state is quite complicated for larger graphs. However, our framework provides steady state value of any given substrate (see (13)), which is not easily found by numerical simulations.

An important discussion in Chen et al. (2008) involves the relationship between various parameters on both the rate of granule fusion J_F and the rate of insulin secretion J_IS. These quantities can be computed from the system variables as J_F(t) = u₁n₄(t) and J_IS(t) = u₃n_R(t), respectively. When the system is assumed to be in a steady state (at some fixed electric potential) our framework can readily provide non-intuitive insights. First, one can observe from (42) that insulin secretion rate, u₃n_R(t), does not depend on u₃ (insulin release rate) and u₂ (pore expansion rate) but rather depends on u₁ (the granule fusion rate). Moreover,

$$\underset{t\to \infty }{lim}\frac{J_F(t)}{J_{IS}(t)}=\frac{u_1{(n_4)}_s}{u_3{(n_R)}_s}=1.$$

In other words, this means that at steady state all the insulin granules fused to the cell membrane are successfully secreted to extracellular space. This is not a conclusion easily accesible using a strictly numerical investigation.

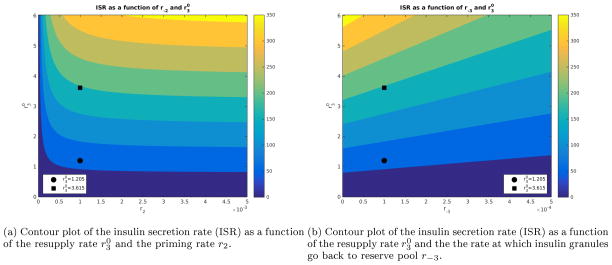
The second conclusion involves computing the steady state insulin secretion rate (ISR). In Figure 8 we have plotted the contours of the ISR as a function of different kinetic parameters. We assume that the electric potential is set to V = −20 mV and the dynamics (41) have reached the steady state. In this case, the time-dependent parameters C_i(t) and C_md(t) rapidly reach a steady state, and their corresponding steady state values, C_i(t) ≅ = 0.3 μM and C_md(t) ≅ = 35 μM, can be computed from Figure 2 of Chen et al. (2008). All the other kinetic parameters of the system is given in Table 2 of Chen et al. (2008). In Chen et al. (2008), Figure 10 depicts the impact of individual parametric perturbations on the ISR; the conclusion is that increases in the resupply rate $r_3^0$ have the largest impact. With the explicit formula in (42), it is straightforward to investigate the impact of simultaneous changes in parameters. Figure 8a depicts contours of the ISR as a function of the $r_3^0$ and the priming rate r₂. Clearly, the relationship between parameters and ISR is more complicated than the one-dimensional investigation suggests, e.g., a slightly lower r₂ value would greatly diminish the impact of higher r₃. This means that once insulin granules are resupplied (no matter how slow is priming rate), the granules are eventually secreted to extracellular space. Figure 8b depicts the ISR as a function of $r_3^0$ and the rate at which insulin granules go back to reserve pool r₋₃. These contours show that higher ISR is achieved for the larger values of the ratio $\frac{r_3^0}{r_{-3}}$. While non-intuitive, this makes sense biologically, because in order to get more insulin granules secreted there is a need to resupply more insulin granules from reserve pool, while keeping insulin granules that go back to reserve pool as low as possible.

Fig. 8.

Contour plots of insulin secretion rate (ISR) as a function of parameters. The ● and ■ markers correspond to steady state value of ISR Chen et al. (2008) at $r_3^0=1205$ and $r_3^0=3.615$, respectively. Note that this threefold increase in $r_3^0$ corresponds with the plots in Chen et al. (2008, Figure 10). Lastly, we note that all other parameters are from Chen et al. (2008, Table 2).

Lastly, as an aside, to see how synthesis and degradation edges affect long term behavior of the dynamics, assume that the synthesis and degradation edges are completely ignored in (41). Consequently, the problem reduces to simple Laplacian dynamics (see equation 2 on page 2). In this case dynamics satisfy a mass conservation law, so all the initial concentration will accumulate at the terminal SCC. This can be also confirmed by calculating steady state solution using the framework described in Mirzaev and Gunawardena (2013),

$${\mathbf{n}}_s={(0,0,0,0,0,0,0,{𝟙}^T·{\mathbf{n}}_0)}^T.$$

6 Conclusions and future work

The “linear framework” developed in Gunawardena (2012); Mirzaev and Gunawardena (2013) unifies many independent time-scale separation methods in molecular biology into a single graph-based mathematical framework. The framework computes steady states of Laplacian dynamics associated with a (biological) network, which has applications in many diverse fields of biology such as enzyme kinetics, pharmacology and receptor theory, protein post-translation modification Xu and Gunawardena (2012); Dasgupta et al. (2014); Thomson and Gunawardena (2009a, b). The main advantage of the framework is that it can be applied to systems in thermodynamic equilibrium as well as the systems remaining far from thermodynamic equilibrium. Ahsendorf et al. (2014) employed this feature of the framework to adapt dissipative mechanisms in gene regulation. We refer reader to Gunawardena (2014) for insightful discussion of scope of applications of the “linear framework”.

Our goal here was to extend the existing framework to the case where zeroth order synthesis and first order degradation are added to Laplacian dynamics. The main motivation came from Gunawardena (2012), where the author discusses the addition of synthesis and degradation to Laplacian dynamics of strongly connected graph. Here we extended the proposed framework for arbitrary graph with synthesis and degradation, and showed that synthesis and degradation dynamics possesses unique stable steady state solution under certain necessary and sufficient conditions. These conditions can be also used to identify whether given synthesis and degradation dynamics reaches a steady state. Moreover, as before, we have developed a mathematical framework to compute that unique steady state. Our algorithm uses the underlying graph structure of the dynamics and the computer implementation of the previous framework (Ahsendorf et al., 2014) can be revised for automatic computations.

To illustrate the power of this approach we have applied the framework to study the exocytosis cascade of insulin granules in pancreatic β-cells. The analysis reveals that the dynamics in this exocytosis cascade reach a steady state for any given initial condition. Moreover, this steady state solution is independent of the given initial condition and only depends on the kinetic parameters of the dynamics. Furthermore, the analysis reveals that at steady state all the insulin granules fused to the cell membrane are successfully secreted to extracellular space. These observations cannot be easily made by numerical methods, and this makes the framework a powerful candidate for qualitative investigation of many biological systems.

Although the framework in this paper is linear in nature, it can be applied to nonlinear systems as well. This can be done by incorporating nonlinearity into the framework through the edge labels. In fact, as we can see in Figure 7d, rates r₂ and r₃ are functions of time dependent variable C_i(t). However, an important restriction must be kept in mind while encoding nonlinearity through edge labels: if a concentration [X] is used in a label, then the substrate X should not be used as a vertex in the graph. This limitation is called uncoupling condition, and we refer reader to Gunawardena (2012) for detailed discussion of nonlinear applications. Hence, the scope of application of our framework to nonlinear systems is limited. Therefore, as our future plan we intend to further extend framework such that it can be applied to broader range of nonlinear dynamics.

Nomenclature

ρ̄^C_i

A column vector, which is the extension of ρ^C_i, see Preliminaries section

ρ^G

Kernel element of strongly connected graph G calculated by MTT

Δ

A diagonal matrix with non-negative entries

$\frac{d\mathbf{x}}{dt}=\mathcal{L}(G)\mathbf{x}$

Laplacian dynamics defined on the graph G

$\frac{d\mathbf{x}}{dt}=\mathcal{L}(G)\mathbf{x}-D\mathbf{x}+\mathbf{s}$

Synthesis and degradation dynamics

${ℝ}_{>0}^{m\times n}$

Set of all m × n matrices with striclty positve entiries

s

Synthesis vector: a column vector with synthesis edges as entries

x_s

Steady state solution

(G)

Laplacian matrix of the graph G

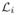
Perturbed matrix corresponding to SCC C_i, 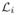= (C_i) − Δ_i, where Δ_i diagonal matrix corresponding to outgoing edges of SCC C_i, if C_i is tSCC then Δ_i ≡ 0

(X)

The set of vertice of graph X

Directed spanning tree

Θ_i(G)

Set of DSTs of graph G rooted at vertex i

a_i

Number of vertices in SCC C_i

A_(ij)

ij -th minor of Laplacian matrix A and is the determinant of (n − 1) × (n − 1) matrix that results from deleting row i and column j

alg_A(0)

Algebraic multiplicity of zero eigenvalue of matrix A

C[i]

SCC containing i

C[i] ⪯ C[j]

SCC containing vertex j can be reached from SCC containing i

C_i ⪯ C_j

SCC C_j can be reached from SCC C_i.

D

Degradation matrix, which is a diagonal matrix with degradation edges as diagonal entries

d_i

Label of degration edge at vertex i

e_ij

an edge from vertex j to vertex i

G

Labeled directed graph

G^★

Complementary graph of G, which is formed by directing all synthesis and degradation edges to new vertex *

geo_A(0)

Geometric multiplicity of zero eigenvalue of matrix A

i ⇔ j

There exists a path from vertex i to vertex j, and a path from vertex j to vertex i

i ⇒ j

There exists a path from vertex i to vertex j

m_i

i^th partial sum of c_i’s, $m_i={\sum }_{k=1}^i{c}_k$

N

Lower-block diagonal submatrix of (G) corresponding to non-terminal SCCs

s_i

Label of synthesis edge at vertex i

T

Block diagonal submatrix of (G) corresponding to tSCCs

DST

Directed spanning tree

MTT

Matrix-Tree Theorem

SCC

Strongly connected component

SD dynamics

Synthesis and degradation dynamics

tSCC

Terminal strongly connected component