Comparisons of characteristic timescales and approximate models for Brownian magnetic nanoparticle rotations

Abstract

Magnetic nanoparticles are promising tools for a host of therapeutic and diagnostic medical applications. The dynamics of rotating magnetic nanoparticles in applied magnetic fields depend strongly on the type and strength of the field applied. There are two possible rotation mechanisms and the decision for the dominant mechanism is often made by comparing the equilibrium relaxation times. This is a problem when particles are driven with high-amplitude fields because they are not necessarily at equilibrium at all. Instead, it is more appropriate to consider the “characteristic timescales” that arise in various applied fields. Approximate forms for the characteristic time of Brownian particle rotations do exist and we show agreement between several analytical and phenomenological-fit models to simulated data from a stochastic Langevin equation approach. We also compare several approximate models with solutions of the Fokker-Planck equation to determine their range of validity for general fields and relaxation times. The effective field model is an excellent approximation, while the linear response solution is only useful for very low fields and frequencies for realistic Brownian particle rotations.

I. DESCRIBING DRIVEN NANOPARTICLE ROTATIONS

In many magnetic nanoparticle (MNP) applications like biosensing,^1–7 hyperthermia,^8,9 and magnetic particle imaging,^10–13 nanoparticles are driven to rotate by oscillating magnetic fields.¹⁴ Understanding the resulting magnetic particle dynamics is important to advance these applications. A typical way to discuss the dynamics is through the timescales of the nanoparticle rotations.^15–17 In particular, we often consider the relaxation time: the timescale for a sample of particles to return to equilibrium after some perturbation (e.g., alignment with a field). Conventional magnetic particles are understood to have two rotational mechanisms. The entire particle can rotate as a rigid body by Brownian rotations,¹⁸ and the particle's magnetic moment can also rotate internally due to restructuring of electronic states in Néel rotation.^19,20 The equilibrium relaxation time is different for each mechanism and depends on many parameters.^21,22 However, because most applications involve magnetically excited particles, it is more important to examine non-equilibrium timescales determining the speed of movements in varying driving fields—these timescales can be very different from the relaxation time. One only needs to imagine that in a stronger field, the particles will align faster to see why this is true. We will hence refer to those non-equilibrium timescales as the “characteristic times” of the rotations.

In reality, the possibility for Néel rotations complicates the matter and it is important to understand which mechanism is dominant for chosen nanoparticles.^23,24 This is an open problem because these processes will in general not be decoupled. If the processes did truly happen independently (in parallel) the more prevalent relaxation mechanism would be that with the shorter relaxation time; but, because the equilibrium relaxation time is not a precise metric, simply comparing these times will not immediately determine the dominant rotation method.^25–27 The notion then of purely Néel or purely Brownian particles is unrealistic, particularly in nanoparticles with a wider size distribution.

It is possible to create a fully general model for the time dynamics of magnetically driven magnetic particles including varying rotation methods as well as the specific conditions the particles experience in various applications.²³ Two main formalisms exist: The Langevin equation formalism describes a single particle's dynamics with a stochastic differential equation that can be solved repeatedly to describe the average properties of an ensemble of particles. The Fokker-Planck formulation instead describes the time evolution of the probability distribution of a sample of magnetizations, so that ensemble averages can be found at any time from the distribution function. In this work, concentrating on Brownian particle rotations that are used in biosensing applications, we solve both types of equations, using them to assess various models for nanoparticle relaxation times and characteristic times as well as approximate models for time dynamics.

II. THE FOKKER-PLANCK EQUATION FOR BROWNIAN NANOPARTICLE ROTATIONS AND ASSOCIATED APPROXIMATE MODELS

The Fokker-Planck equation (FPE) governs the distribution function $W(\theta ,\varphi ,t)$ of an ensemble of particle magnetizations. It can be derived heuristically from a continuity equation with an additional diffusion term.¹⁹ Each nanoparticle's magnetization is imagined to be a vector moving on the unit sphere, and the diffusion is parameterized by D. The general FPE is then written

$$\frac{\partial W}{\partial t}=\nabla ·\left[D\nabla -\frac{d\mathbf{m}}{\mathit{d}\mathit{t}}\right]W,$$ (1)

where the magnetization time dynamics are given by different differential equations for Brownian and Néel rotation. We focus on the Brownian case because fewer assumptions must be made (e.g., constraining the anisotropy axis). The distribution is used to determine magnetization statistics using the definition of the probability moments $\int {\mathbf{m}}^{j}W(\theta ,\varphi ,t)\hspace{0.17em}d\Omega =⟨{\mathbf{m}}^j(t)⟩$. The magnetization dynamics of Brownian particle rotations are dominated by torques caused by an applied field and the viscous drag from the fluid. Several papers go through derivations for the equations of motion.^15,16,22,28 We choose a compact form for the equation

$$\frac{d\mathbf{m}}{\mathit{d}\mathit{t}}=\frac{\left(\mathbf{m}\times \mathit{\xi }\right)\times \mathbf{m}}{2{\tau }_{\mathrm{B}}},$$ (2)

in terms of the equilibrium Brownian relaxation time τ_B

$${\tau }_{\mathrm{B}}=\frac{3\eta V_h}{k_{\mathrm{B}}T},$$ (3)

determined by the suspension viscosity η, the hydrodynamic volume of the particle V_h, and the local temperature T with Boltzmann's constant k_B. The unitless magnetic field $\mathit{\xi }$ is a vector quantity

$$\mathit{\xi }=\frac{\mu \mathbf{H}}{k_{\mathrm{B}}T},$$ (4)

incorporating the nanoparticle's magnetic moment μ and an applied field H. The magnetization m is normalized and therefore unitless. Replacing the velocity of the magnetization in Eq. (1) with that from Eq. (2) and assuming a Maxwell-Boltzmann distribution at equilibrium (when $\frac{\partial W}{\partial t}=0$) we find D = 1/2τ_B and write

$$\frac{\partial W}{\partial t}=\frac{1}{2{\tau }_{\mathrm{B}}}\nabla ·\left[\nabla -\mathit{\xi }+\mathbf{m}\left(\mathbf{m}·\mathit{\xi }\right)\right]W,$$ (5)

for which a general solution is not currently analytically possible. Since many applications use a single oscillating field (see, for example, magnetic particle imaging¹¹ or magnetic nanoparticle spectroscopy^4–6), we choose $\mathit{\xi }\to \xi (t)\hspace{0.17em}\widehat{z}$ and simplify the FPE to only depend on the polar angle and time W(θ, t). Writing out letting $x=\text{cos}\hspace{0.17em}\theta$ the 1-D FPE is written

$$\frac{\partial W}{\partial t}=\frac{1}{2{\tau }_{\mathrm{B}}}\frac{\partial }{\partial x}\left[(1-x^2)\left(\frac{\partial W}{\partial x}-\xi \left(t\right)W\right)\right].$$ (6)

A solution to this equation is possible by expanding with Legendre polynomials.^17,23,29

A. Linear response

Following Debye,³⁰ it is possible to obtain an analytical solution to the FPE assuming a small amplitude oscillating field ξ = ξ₀e^iωt. In the small amplitude case, it is fair to assume the distribution function is linear in x, with the general form W_lin = A + Bx. Inputting W_lin into Eq. (6) leads to the average normalized magnetization in the direction of the oscillating field

$$⟨m⟩=\frac{{\xi }_0}{3}\frac{e^{i\omega t}}{1+i\omega {\tau }_{\mathrm{B}}}.$$ (7)

The susceptibility or slope of this equation is not realistic for larger fields when ξ₀ > 3 because the magnetization is normalized to be on the unit sphere. The results are slightly better (see Fig. 5) if we use

$$⟨m⟩=\mathcal{L}\left({\xi }_0\right)\frac{e^{i\omega t}}{1+i\omega {\tau }_{\mathrm{B}}},$$ (8)

where for small fields, the Taylor expansion of the Langevin function provides the equivalent susceptibility including the factor of 1/3 and for large fields, the magnetization does not grow above unity.

FIG. 5.

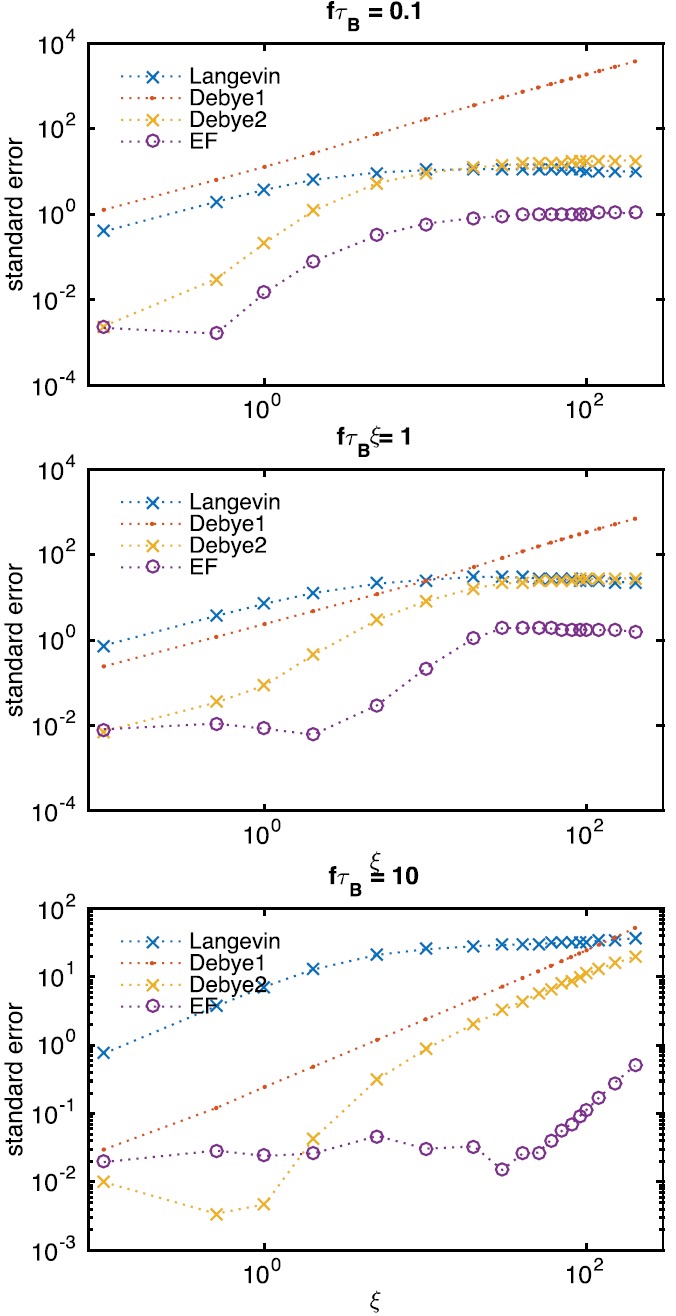
Errors calculated with Eq. (21) for the approximate models with respect to the FPE. Many magnetic field amplitudes are used and the value of fτ_B is varied from 0.1 to 10.

B. Moment equations from the FPE

Moment equations are found from Eq. (6) by multiplication with powers of x and subsequent integration over x. The normalization condition defined by the probability distribution W(x, t) and the definition of the statistical moments are used. For example, after multiplying by x and two steps of integration by parts we find

$$2{\tau }_{\mathrm{B}}\frac{\partial ⟨x⟩}{\partial t}=\xi -2⟨x⟩-\xi ⟨x^2⟩.$$ (9)

The dynamics of the mean thus depend on the second moment and a similar procedure gives the second moment³¹

$${\tau }_{\mathrm{B}}\frac{\partial ⟨x^2⟩}{\partial t}=1+\xi ⟨x⟩-3⟨x^2⟩-\xi ⟨x^3⟩,$$ (10)

and so on. An infinite series of coupled differential equations emerge that can be truncated by a clever closure technique termed the “effective field” method.³²

C. Truncating the moment equation

The moment equation is truncated by assuming a distribution function that is similar to the equilibrium distribution except having an “effective field” ξ_e. The field is free to be slightly different than the applied field.^31,32 The advantages of the effective field model are the simpler more intuitive form and the ease of implementation relative to the stochastic or FPE methods. It is clear that the model describes an exponential decay when the applied field is zero, and when the effective field is equal to the actual field, the mean magnetization does not change. This is equivalent to assuming equilibrium. We note that the calculational simplicity only holds for 1D modeling. Each moment can be computed from the effective normalized distribution function

$$W_e=\frac{{\xi }_e}{2\sinh {\xi }_e}{e}^{x{\xi }_e}.$$ (11)

The mean and the second moments are functions of the Langevin function with respect to the effective field

$${⟨x⟩}_e=\mathcal{L}({\xi }_e)=\coth {\xi }_e-1/{\xi }_e$$ (12)

and

$${⟨x^2⟩}_e=1-\frac{2}{{\xi }_e}\mathcal{L}\left({\xi }_e\right).$$ (13)

Using the first moment equation (Eq. (9)), we now have a differential equation for the mean magnetization purely in terms of the Langevin function and the effective field

$$\frac{d}{\mathit{d}\mathit{t}}{⟨x⟩}_e=-\frac{{⟨x⟩}_e}{{\tau }_{\mathrm{B}}}\left(1-\frac{\xi }{{\xi }_e\left({⟨x⟩}_e\right)}\right),$$ (14)

where the effective field ξ_e is a function of the mean value. To solve this implicit differential equation, the effective field at each time can be found by inverting the Langevin function for a given magnetization using a Padé approximant.³³

D. Analytical characteristic timescales

Martensyuk, Raikher, and Shliomis (MRS) develop an approximation to the characteristic timescale for a general effective field that is a small perturbation on the equilibrium field.³² Here, we show the characteristic time to begin aligned in the perpendicular direction and then evolve to align with the field, so that we may compare with simulated data. The perpendicular characteristic time is

$$\frac{{\tau }_{\text{MRS}}}{{\tau }_{\mathrm{B}}}=\frac{2\mathcal{L}(\xi )}{\xi -\mathcal{L}(\xi )}.$$ (15)

And from this, low- and high-amplitude field approximations to the perpendicular characteristic time can be easily written

$$\frac{{\tau }_{\text{low}}}{{\tau }_{\mathrm{B}}}=1-\frac{1}{10}{\xi }^2,\hspace{0.17em}\hspace{1em}\frac{{\tau }_{\text{high}}}{{\tau }_{\mathrm{B}}}=\frac{2}{\xi }.$$ (16)

In practice, we find that for fields of ξ > 5, the large field approximation suffices. We also summarize the characteristic timescales in Table I.

TABLE I.

Summary of characteristic timescales with descriptions.

Abbreviation	Expression	Description
τB	$\frac{3\eta V_h}{k_{\mathrm{B}}T}$	Equilibrium relaxation time18
τMRS	$\frac{2\mathcal{L}(\xi )}{\xi -\mathcal{L}(\xi )}{\tau }_{\mathrm{B}}$	Timescale to align to a perpendicularly applied static field of amplitude ξ (Ref. 32)
τYE	$\frac{1}{\sqrt{1+0.21{\xi }^2}}{\tau }_{\mathrm{B}}$	Phenomenological fit to FPE simulations of perpendicularly applied static field of amplitude ξ (Ref. 29)

E. Fully general Néel relaxation time

While this paper is designed to focus on Brownian nanoparticle rotations, it is important to consider the fully general expressions for Néel relaxation times, which are not always used in their complete forms. In particular, the Néel event time τ₀ is sometimes determined solely from experiments, but, in principle, can be broken down into several other parameters for more specific measurements as

$${\tau }_0=\frac{\mu }{2k_{\mathrm{B}}T\gamma }\frac{1+{\alpha }^2}{\alpha },$$ (17)

with the Gilbert damping parameter α, the gyromagnetic ratio γ, and the magnetic moment μ.²¹

Depending on the unitless anisotropy constant σ = KV_c/k_BT, where K is the anisotropy constant and V_c is the magnetic core volume, two approximations exist for the equilibrium Néel relaxation time

$${\tau }_N=\{\begin{array}{cc}{\tau }_0\sigma {(1-\frac{2}{5}\sigma +\frac{48}{875}{\sigma }^2)}^{-1}\hfill & \text{if}\hspace{0.17em}\sigma <1\hfill \\ \frac{{\tau }_0}{2}\sqrt{\frac{\pi }{{\sigma }^3}}\hspace{0.17em}\text{exp}(\sigma )\hfill & \text{if}\hspace{0.17em}\sigma \ge 1.\hfill \end{array}$$ (18)

Néel rotations are more likely in smaller single domain nanoparticles where the energy scale to reverse the magnetization is comparable to the thermal energy (i.e., σ ≈ 1 as in superparamagnetic nanoparticles), or in large magnetic fields where ξ > σ Néel rotations are also certainly possible. Especially, in poly-disperse samples, it is less likely that both nanoparticle rotation mechanisms are not simultaneously occurring.³⁴

III. SIMULATION RESULTS

A. Comparison of characteristic timescales

A stochastic Langevin equation can be developed from the magnetization equation (2) in different fashions, though it is important to note that there is no completely general way to add in thermal fluctuations. Typically, a Gaussian fluctuating term is appended to the differential equation defined by

$$⟨\lambda \left(t\right)⟩=0,\hspace{1em}⟨{\lambda }_i\left(t\right){\lambda }_j(t\prime )⟩=\frac{{\delta }_{\mathit{i}\mathit{j}}\delta (t-t\prime )}{{\tau }_{\mathrm{B}}},$$ (19)

with i, j ∈ x, y, z. Simulations of the Brownian Langevin equation (Eq. (2) with additional stochastic torques) can be completed^15,16,28 to examine the characteristic time and compare with the analytical expressions.

Our first result is intuitively obvious. If particles are initiated in a state completely aligned with some axis, and a field is turned on perpendicularly, the magnetizations align with the field. Several example magnetizations simulated with averages over 10⁴ particles using an Euler-Marayuma integration scheme for the stochastic differential equation are shown in Fig. 1. They illustrate the decreasing characteristic time for increasing field strength as ξ = 0 → 30. The large changes in the dynamics indicate that it is incorrect to use the Brownian relaxation time to describe rotations.

FIG. 1.

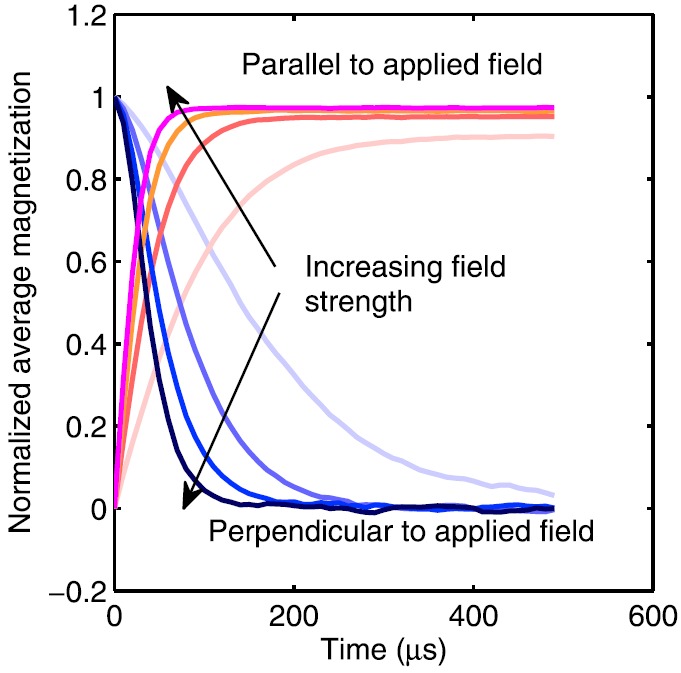
Stochastic Langevin equation simulations of normalized mean magnetizations that begin aligned in the x-direction (perpendicular) and then evolve with static fields applied in the z-direction (parallel) at various amplitudes. As the amplitude increases, the particles align faster to the field in the parallel direction and go to zero faster in the perpendicular direction, so that magnetic saturation occurs in a fraction of the original relaxation time.

The alignment to the field perpendicular to the original state results in magnetization curves that can be fitted with an exponential of the form $⟨m_z⟩\propto 1-e^{-t/{\tau }_c}$. Thus, we can extract the approximate characteristic time for each applied field strength though for strong enough fields the exponential form even breaks down. Yoshida and Enpuku also found the characteristic time using FPE simulations.²⁹ From their simulated data, they developed a phenomenological fit to the relationship between characteristic time and field strength as

$${\tau }_{\text{YE}}=\frac{{\tau }_{\mathrm{B}}}{\sqrt{1+0.21{\xi }^2}}.$$ (20)

The YE form is a good approximation and in the low- and high-amplitude field limits approaches the analytical forms from the effective field characteristic times Eq. (16). The values of the characteristic time (with respect to the applied field) from our simulations agree with both the form of τ_YE and the approximate characteristic time τ_MRS. This is shown in Fig. 2.

FIG. 2.

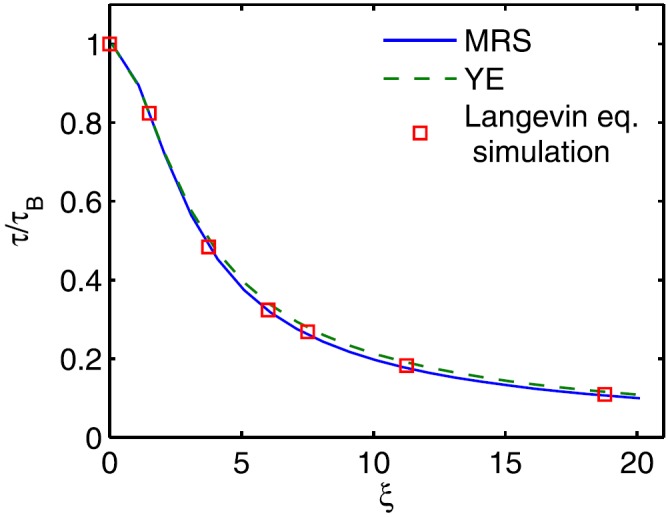
Comparison of the analytical expression (MRS, Eq. (15)) for the characteristic time with the data fit model (YE, Eq. (20)) and stochastic Langevin simulations.

B. Validity regimes between models in oscillating fields

When the applied field is oscillatory $\xi ={\xi }_0\hspace{0.17em}\text{cos}\hspace{0.17em}\omega t$, as in many applications, we can compare the various model approximations at different field strengths ξ₀, frequencies f = ω/2π, and relaxation times τ_B. It has been shown that a complete description of the dynamics using the FPE can be parameterized by the combination variable fτ_B.¹⁷

To connect with biosensing experiments, we use typical values of the relaxation time (500 μs for 100 nm particles at room temperature and water viscosity), fields of 1 kHz then lead to fτ_B ≈ 0.5 and moments of 70 emu/g, and fields of 10 mT/μ₀ lead to ξ₀ ≈ 10. As mentioned previously, when the unitless field is greater than the unitless anisotropy (ξ₀ > σ), however, Néel rotations are expected and the dynamics are more complicated. Typical magnetite nanoparticles may have anisotropies of the order of 1 kJ/m³ and 10 nm core radii leading to σ ≈ 10 as well.^13,35

In principle, the Langevin equation and the FPE approaches should be identical, and averaged solutions of the Langevin equation¹⁵ compared to the FPE truncated after fifty iterations of the series solution moments¹⁷ lead to vanishingly small error. We also note that the advantage of the stochastic model is that it is amenable to different field geometries and additional physics, while even the FPE is only solvable for very specific cases.²³ However, if computation time is a problem, it can certainly be useful to employ the approximate models.

We calculate the error as the squared error E between functions a_t and b_t

$$E={\left[{\int }_T{(a_t-b_t)}^2\hspace{0.17em}dt\right]}^{1/2},$$ (21)

where T is a period of the oscillating field. The error between the Langevin and FPE approaches is constant over fields and can be made as small as desired by more averaging, or shorter time steps, or both. An example is shown in Fig. 3. We see that neither the field nor the frequency relaxation time combination effect the error percentage. This is unlike the other models that have inherent approximations that constrain their range of validity. These simulations use 10⁵ averages of the Langevin equation and thirty components of the series expansion solution to the FPE.

FIG. 3.

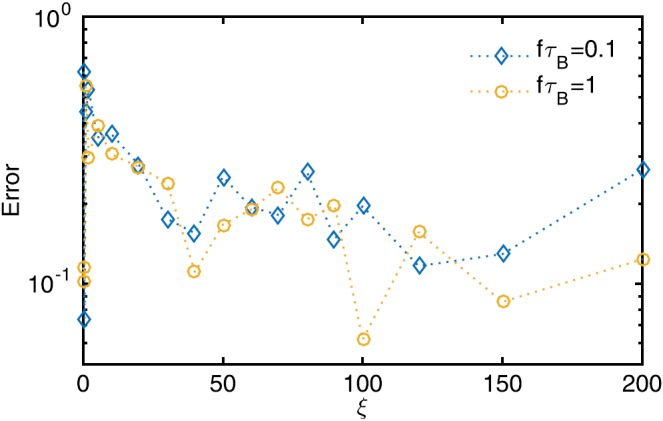
The error of the Langevin equation simulation with respect to the FPE solution at different magnetic fields and for two fτ_B combinations. In principle, this error can be made arbitrarily small by increased averaging.

Fig. 4 qualitatively demonstrates the problems with the models. For small fields, the Debye model is accurate but for larger fields the amplitude is too large. The amplitude error can be slightly corrected by using the Langevin function to choose the susceptibility. The purely equilibrium Langevin function model matches the correct amplitude for larger fields but does not account for phase lags and thus only begins to approach the correct solution at the large fields. For practical purposes, we conclude that this model is useless.

FIG. 4.

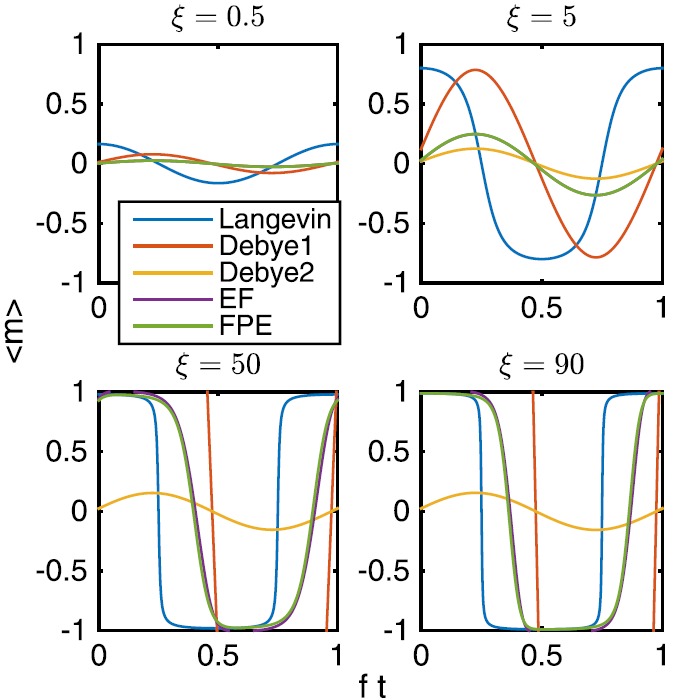
Example magnetizations for the various models (summarized in Table II at different fields and fτ_B = 1 compared to the FPE solution. The amplitude error of the Debye models and the phase error of the Langevin model are clear.

Fig. 5 quantitatively shows the agreement of the various approximate models against the FPE solution. The data include comparisons against the linear response model Eq. (8) with (Debye2) and without (Debye1) the Langevin function susceptibility (see Sec. II A), the equilibrium Langevin function model $⟨m⟩=\mathcal{L}[\xi (t)]$ and the effective field model Eq. (14) over a large range of applied fields and for several field and relaxation time combinations. The error is calculated using Eq. (21).

The results show that the effective field of MRS³² works quite well over a very large range of the variables. The equilibrium Langevin function model begins to be reasonable only at very high fields and never reaches the accuracy of the effective field. The challenge of the Debye model is in determining the susceptibility. If this number is chosen as the value of the Langevin function, the model works very well for low fields. In fact, it even surpasses the accuracy of the effective field model when the amplitude is low, and the frequency relaxation time combination is high. The altered Debye model is thus an accurate predictor of dynamics for a small range of AC susceptibility biosensing.

IV. CONCLUSIONS

We have shown that the useful concept of equilibrium relaxation times for magnetic nanoparticle rotations can be extended to include the amplitude of a field driving the particles. These “characteristic times” are a more general way to describe the timescales of non-equilibrium rotations and are summarized in Table I. Our Langevin equation simulations can be used to calculate the characteristic times, and for dynamics where the distribution function is close to equilibrium (e.g., the driving field is almost adiabatically rotating the nanoparticles) our simulations agree with a numerical approximation (τ_YE) proposed by Yoshida and Enpuku.²⁹ We also demonstrate that our simulations, as well as those of Yoshida and Enpuku can be characterized using the analytical approximation τ_MRS originally derived by Martsenyuk, Raikher, and Shliomis.³² This is no mistake as the high- and low-field approximations to τ_MRS appear numerically similar to the equivalent expressions for τ_YE. These results highlight the importance of considering the characteristic time instead of simply the equilibrium relaxation time in describing particles that are driven to rotate as opposed to those freely relaxing to equilibrium.

Multiple commonly used approximate forms for oscillating dynamics of particles have also been shown, as well as the appropriate ranges of validity for each model. The models are collected in Table II. Each model was compared against the FPE solution simulation. We found that the combination of the Langevin function for the susceptibility and the Debye model to account for relaxation (Debye2 in Table II) is a reasonable approximation (below 1% error) especially at low fields when fτ_B is large and ξ is small. The effective field model (EF in Table II) is consistently accurate to within 1% for lower field amplitudes and is simpler to calculate in a 1D geometry. However, in realistic biosensing applications that require knowledge of Brownian nanoparticle dynamics, and especially if full 3D simulations are required, we conclude that it is likely necessary to use the stochastic Langevin equation model because it is easily amenable to variable field geometries or additional physics.

TABLE II.

Summary of approximate models for the average magnetization parallel to an applied oscillating field $\xi (t)={\xi }_0\hspace{0.17em}\text{cos}\hspace{0.17em}\omega t$.

Abbreviation	$⟨m[\xi (t)]⟩$	Description and validity range
Langevin	$\mathcal{L}[\xi (t)]=\coth \xi (t)-1/\xi (t)$	Equilibrium, frequency is low or field is extremely high
Debye1	$\frac{{\xi }_0}{3}\left(\frac{\hspace{0.17em}\text{cos}\hspace{0.17em}\omega t}{1+{(\omega {\tau }_{\mathrm{B}})}^2}+\frac{\omega {\tau }_{\mathrm{B}}\hspace{0.17em}\text{sin}\hspace{0.17em}\omega t}{1+{(\omega {\tau }_{\mathrm{B}})}^2}\right)$	Linear response, frequency is high or field is extremely low
Debye2	$\mathcal{L}({\xi }_0)\left(\frac{\hspace{0.17em}\text{cos}\hspace{0.17em}\omega t}{1+{(\omega {\tau }_{\mathrm{B}})}^2}+\frac{\omega {\tau }_{\mathrm{B}}\hspace{0.17em}\text{sin}\hspace{0.17em}\omega t}{1+{(\omega {\tau }_{\mathrm{B}})}^2}\right)$	Linear response with Langevin function susceptibility, frequency is high or field is low
EF	$-\int \hspace{0.17em}dt\frac{⟨m(t)⟩}{{\tau }_{\mathrm{B}}}\left(1+\frac{\xi (t)}{{\mathcal{L}}_i(⟨m(t)⟩)}\right)$	Effective field model, quasi equilibrium conditions, requires the inverse Langevin function ${\mathcal{L}}_i$ (see Sec. II C)