Behavioral Dynamics and Neural Grounding of a Dynamic Field Theory of Multi-Object Tracking

Abstract

The ability to dynamically track moving objects in the environment is crucial for efficient interaction with the local surrounds. Here, we examined this ability in the context of the multi-object tracking (MOT) task. Several theories have been proposed to explain how people track moving objects; however, only one of these previous theories is implemented in a real-time process model, and there has been no direct contact between theories of object tracking and the growing neural literature using ERPs and fMRI. Here, we present a neural process model of object tracking that builds from a Dynamic Field Theory of spatial cognition. Simulations reveal that our dynamic field model captures recent behavioral data examining the impact of speed and tracking duration on MOT performance. Moreover, we show that the same model with the same trajectories and parameters can shed light on recent ERP results probing how people distribute attentional resources to targets vs. distractors. We conclude by comparing this new theory of object tracking to other recent accounts, and discuss how the neural grounding of the theory might be effectively explored in future work.

Introduction

We live in a dynamic visual world where objects are routinely moving around us. Given this, the ability to flexibly track and update object representations is crucial. For example, when playing basketball, you must tune out the roaring crowd and other distractions and robustly track where your teammates are on the court. This often requires the very fast tracking of individual players to enable the right pass at the right moment to lead to a score. To examine this ability in the laboratory, researchers often use the multiple-object tracking (MOT) task developed by Pylyshyn and Storm (1988). In this task, participants are shown a collection of dots, a subset is cued, and participants must track the target objects as they move through space. After some period of motion—typically 2 to 10 s—participants are asked to locate the target dots. Participants are typically quite good at tracking up to 4 items. This task has been used to study different aspects of the visual cognitive system, including multifocal attention (Pylyshyn and Storm, 1988), capacity limits (Alvarez and Franconeri, 2007), hemispheric organization (Yantis, 1992; Alvarez and Cavanagh, 2005; Delvenne, 2005), the coordination of fixations and reference frames (Liu et al., 2005; Howe et al., 2010, 2011; Huff et al., 2010), and the impact of object proximity and speed on visual tracking (Shim et al., 2008; Franconeri et al., 2010).

Several theoretical accounts of participants’ performance in the MOT task propose that tracking is carried out by a fixed-capacity, parallel system that dynamically updates the spatial positions of a set of spatial indexes or deictic pointers. These indexes can be updated in a pre-attentive manner (Pylyshyn and Storm, 1988), using attention (Kahneman et al., 1992; Cavanagh and Alvarez, 2005), or using a combination of early visual and attentional processes (Logan, 2002; Bundesen et al., 2005). Recently, however, Oksama and Hyönä (2008) proposed a serial model that accounts for several key findings from the MOT literature. This model proposes that the maintenance of pointers to multiple moving objects requires continuous serial (re)activation and refreshing of identity-location bindings.

Although extant theories of object tracking provide compelling explanations for adults’ performance, there are two key limitations. First, none of these theories are dynamic theories. These theories account for the probability of selecting the correct set of target locations at the end of a trial as a function of speed, target load, and so on. But the theories do not actually track locations dynamically through time—they are not process models of visual cognition. This is related to a second limitation. There is a growing literature on the neural basis of MOT. This literature is based on innovative studies using both ERPs (Drew et al., 2009; Doran and Hoffman, 2011; Sternshein et al., 2011) and fMRI techniques (Culham et al., 1998; Jovicich et al., 2001; Howe et al., 2009). To date, there is only one neurally grounded theory of MOT.

One common form of neural network modeling is connectionism. Although connectionist models have captured a host of findings in visual cognition (see Olshausen et al., 1993; Mozer and Sitton, 1998; Itti and Koch, 2000, 2001), these models are not well-suited for MOT because they often rely on winner-take-all processing and rely on modification of weights for updating. Such models are difficult to use with moving objects because there is no intrinsic visual space to work within. An alternative class of models uses oscillatory neural networks to process visual information (e.g. Raffone and Wolters, 2001). Recently, Kazanovich and Borisyuk (2006) proposed an oscillatory neural model of MOT that maintains target items using separate neural layers, each of which is responsible for tracking a single object. This model effectively captured several behavioral findings from MOT; however, no attempt was made to use this model to interface with neural data directly.

The goal of the present study, therefore, was to examine whether an existing neurally-grounded and dynamic theory of spatial cognition—the Dynamic Field Theory (DFT) (Spencer et al., 2007)—could do something that no other theory of MOT has accomplished: (1) to capture behavioral data from MOT using a dynamic, visual process model, and (2) provide insight into aspects of the emerging neural literature on MOT. One motivation for pursing this goal comes from an interesting thread in the MOT literature which shows that visual working memory capacity (also referred to as visual short-term memory capacity; see Luck and Vogel, 1997) is related to MOT performance (see, e.g., Delvenne, 2005). These results are interesting because the DFT was initially proposed to account for findings from studies of visuo-spatial working memory (Spencer and Hund, 2002; Schutte & Spencer, 2009), and more recent extensions of the theory have captured the details of behavioral studies probing visual working memory (VWM) capacity (Johnson, Spencer, Luck, et al., 2009; Johnson, Spencer, and Schöner, 2009). We were also motivated by a second key observation: to date, we have applied the DFT to somewhat static, information-processing inspired tasks. Although these tasks have a particular time structure, they do not tap the rich, real-time, dynamic processes of the theoretical model. (For one exception, see the time-dependent ‘drift’ in spatial working memory (SWM) studied by Schutte & Spencer, 2009). Thus, we were curious whether a theory benchmarked on more static tasks could be applied to a highly dynamic task like MOT.

In the sections that follow, we first provide a brief overview of our theory of spatial cognition, grounding this overview in one example—data showing delay-dependent ‘drift’ in spatial working memory in simple spatial recall tasks (Schutte and Spencer, 2002; Spencer and Hund, 2002, 2003). Next, we describe the 3-layer variant of the DFT we used in the present study. This same 3-layer architecture has been used to capture findings from studies of spatial recall (Schutte & Spencer, 2009) and visual change detection (Johnson, Spencer, Luck, et al., 2009). We generalize this model to two spatial dimensions and demonstrate how it can track multiple target objects in parallel while staying anchored to the visual structure in the display which includes many distractors (for related ideas, see Zibner et al., 2010).

We then present two sets of simulation results. The first captures findings from a recent study by Franconeri, Jonathan, and Scimeca (2010). This study is useful in the present context because behavioral results show several canonical findings from the MOT literature including effects of delay and speed. Critically, however, these findings were obtained in an experimental context where object spacing was explicitly controlled. Results show that object spacing is a key factor that impacts MOT performance, consistent with results of our model. As we discuss in the conclusion, this creates an interesting point of contrast between the DFT and the neural oscillatory model of Kazanovich and Borisyuk (2006) which keeps targets separated in independent buffers. The second set of simulation results captures ERP data from a recent study examining the distribution of attentional resources to targets and distractors in the MOT task. We show how the DFT captures key aspects of the ERP findings based on how the strength of locally excitatory and laterally inhibitory neural interactions is modulated as a function of the tracking load.

2. The Dynamic Field Theory of Spatial Cognition

In this section, we provide an overview of the Dynamic Field Theory of spatial cognition. This theory specifies how activation in working memory is sustained by a network of neurons during short-term delays, how perceptual and memory processes are linked together from moment-to-moment when individual locations must be held in memory, and how working memory and long-term spatial memory are integrated. For illustration, we focus on one of the central tasks we have examined in past work—spatial recall. This highlights several properties of the model that are central to the present study.

In spatial recall tasks, participants are shown a target item, the target is hidden, there is a short delay (e.g., 5s), and participants must point to the remembered target location. When people are asked to remember targets to the left or right of a reference axis, they reliably exaggerate the distance between the target and the reference axis (Huttenlocher et al., 1991). Such biases increase in magnitude over delays (Spencer and Hund, 2002), providing a window into the moment-to-moment processes that maintain information in SWM. In our view, spatial recall biases reflect three central challenges the neural system must overcome. First, the brain must create an allocentric representation of the target item, a necessity given that the target is perceived in an egocentric frame (retinal space). This is a challenging issue because the egocentric-to-allocentric transformation must be maintained despite, for instance, brief occlusions of the reference frame and movements of the eye (for discussion, see Byrne et al., 2007). The second challenge is that the neural system must actively maintain information about the target location during the delay. We highlight how a basic neural mechanism—recurrent local excitation with lateral inhibition—can create this form of active or ‘working’ memory for delays as long as 10 – 20 s (for related ideas, see Edin Kingberg T., Johansson P., McNab F., Tegner J., Compte A., 2009). Finally, the neural system must integrate solutions to these two challenges, actively maintaining a memory of the target while staying in register with an allocentric reference frame.

Figure 1 shows a simulation of the DFT performing a single spatial recall trial (Spencer et al., 2007). The panels on the left show the cued target at 220° (0° = midline; see Fig 1A) which gives input into the top layer of a 7-layer neural network (Fig 1B–H). Time (in s) is along the x-axis in each layer of the network, while neural activation is along the y-axis (height). The z-axis shows a collection of spatially-tuned neurons that respond maximally when stimuli are presented at each neuron’s ‘preferred’ spatial location. The panels to the right in Figure 1 show 2D views of three particular layers in the model: the egocentric perceptual field (PF_ego; Fig 1I), the allocentric perceptual field (PF_allo; Fig 1J), and two views of the SWM layer (top view: Fig 1K; side view: Fig 1L).

Figure 1.

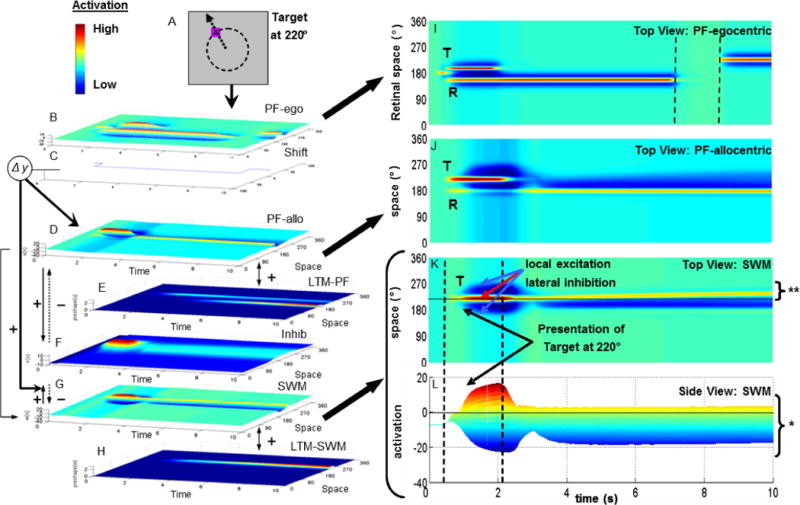
DFT simulation of one spatial recall trial with target at 220° (see dashed circle and arrow in A; 180° = midline of task space). Model architecture (B–H) consists of seven layers of spatially-tuned neurons with time shown on the x-axis, activation on the y-axis (see color inset), and space on the z-axis. Arrows between layers indicate excitatory (solid) and inhibitory (dotted) projections.

Panels in the right column show top view of three fields. The egocentric perceptual field (PF-ego; B) is shown in I with time along the x-axis and space along the y-axis. Input is presented to this field in retinal coordinates. Two activation peaks (red activation) are present at the start of the trial corresponding to the target (T), which disappears, and the reference axis (R), which remains visible. Dashed lines indicate a brief occlusion of the reference (i.e., no input). After the occlusion, the reference shifts from 160° to 230° in the retinal frame.

The allocentric perceptual field (PF-allo; D) is shown in J (axes as in I). Note that the reference peak (R) remains active and centered at 180°, even though it was occluded and shifted in PF-ego. This is because the shift field (C) transforms input from the egocentric to the allocentric frame. The spatial working memory field (SWM; G) is shown in K (axes as in I) and L (activation along the y-axis). The target peak (T) sustains after input is removed (* in L), and drifts away from midline over delay (** in K; see ‘bending’ yellow line).

The first theoretical challenge presented by spatial recall biases is that such biases are allocentric in nature—they are linked to a perceived frame in the world—yet visuo-spatial information is always perceived egocentrically (e.g., in retinal coordinates). The top four layers of the DFT (see Fig 1B–E) do the work of transforming spatial information perceived in egocentric coordinates into an allocentric frame and reliably maintaining this frame from moment-to-moment and from trial-to-trial (for more recent variants of this architecture, see Schneegans and Schöner, n.d.; Schneegans et al., n.d.).

Once target-specific spatial information has been transformed into allocentric coordinates, it must be perceived and then actively maintained in SWM. The 5 layers depicted in Figure 1D–H serve this function. Critically, these ‘dynamic neural fields’ are not simply feed-forward networks that mimic input patterns. Rather, neural interactions within these fields can stabilize ‘peaks’ of activation that represent, for instance, decisions about the spatial information to remember and the information to ignore. In particular, neurons within PF_allo (Fig 1D) and SWM (Fig 1G) have locally excitatory interactions where activated neurons boost the activity of their local neighbors. In addition, neurons in PF_allo and SWM have reciprocal connections to a shared layer of inhibitory interneurons (see Inhib; Fig 1F). When activated, these interneurons project broad inhibition back to PF_allo and SWM. These combined interactions lead to the formation of stabilized activation peaks.

For instance, Figure 1K and 1L show top and side views of the SWM layer. As can be seen in these figures, the presence of the target in the task space builds up strong activation in SWM when the target is visible. Critically, when the target is hidden, the activation peak in SWM sustains itself through the delay period (activation in SWM stays above 0 throughout the trial; see “*” in Fig 1L). Thus, SWM remembers the target location even in the absence of input. We refer to this as a ‘working’ memory state because the activation peak is stable against perturbations (e.g., neural noise). Such stability is a pre-requisite to use the contents of working memory in the service of another task—a central component of Baddeley’s classic definition of the working memory construct (Baddeley, 1986).

The simulation in Figure 1 provides a good illustration of the sense in which the working memory peak is stable. Note that the SWM peak in Figure 1L remains above threshold during the delay even though there is a peak of activation in PF_allo at midline during the delay. The midline input is prevented from entering SWM by the strong lateral inhibition generated by the SWM peak which actively suppresses input from PF_allo. Importantly, this does more than just protect SWM from intrusion—it allows PF_allo to ‘hold on’ to midline and keep the allocentric frame aligned. Although PF_allo and SWM achieve this balancing act, there’s a cost: the SWM peak is repelled from the midline peak in PF_allo, that is, the model shows a delay-dependent bias away from the reference frame. This is evident in Figure 1K (see “**”)—there is a systematic, time-dependent ‘drift’ of the SWM peak away from midline during the delay.

Why does this occur? Recall that PF_allo and SWM share a layer of interneurons. Thus, the midline peak in PF_allo activates inhibitory neurons around 180°, while the target peak in SWM activates inhibitory neurons around 220°. Given that inhibitory interactions are relatively broad (to achieve effective surround inhibition), these two patterns of activation overlap in the inhibitory layer, creating strong inhibition in-between 180° and 220°. As a consequence, the SWM peak is pushed away from midline during the delay because there is stronger inhibition on the midline-side of the SWM peak. Note that the activation peak in PF_allo does not move because it is anchored to perceptual input. This leads to one sense in which this arrangement between PF_allo and SWM can be a very good thing: if the PF_allo and SWM peaks happen to align (e.g., the target is presented at midline) then the model responds very robustly—the SWM peak remains locked-on to midline throughout the delay and the model shows no bias and low variability (for evidence, see Spencer and Hund, 2002).

The DFT provides a framework for thinking about reference-related biases in SWM, and this theory has captured empirical data from spatial recall tasks in quantitative detail (Schutte & Spencer, 2009). More generally, we have extended this theory to capture developmental change in spatial recall performance, including a qualitative shift in recall biases in early development (Schutte & Spencer, 2009; Schutte and Spencer, 2010). We have also generalized the theory to test novel predictions about children’s and adult’s biases in position discrimination tasks (Simmering et al., 2006a; Simmering and Spencer, 2008), and we have examined how SWM and spatial long-term memory interact to form experience-dependent categories that build-up over learning (Lipinski, Simmering, et al., 2010; Lipinski, Spencer, et al., 2010). More recently, we have extended the basic concepts of the DFT to capture how people use spatial prepositions to describe simple object layouts (Lipinski et al., 2011). The goal of the present study is to ask whether our dynamical systems model can effectively capture both behavioral and neural data from a task that taxes the real-time dynamical properties of the model—can the DFT track the motions of objects as they move through time and space?

2.1 Can the DFT track multiple objects?

The first step in our explorations of the MOT task was to simplify the 7-layer model. Many studies of MOT hold fixation constant. This eliminates the need for updating the spatial reference frame; consequently, MOT can be captured within a retinal frame. This was the case in the Franconeri et al. (2010) study we modeled; thus, we dropped the top two layers in our model and presented inputs in a retinal frame of reference directly into the PF and SWM layers.

Next, although some studies suggest that familiarity impacts MOT performance (see, e.g., Oksama and Hyönä, 2008), the majority of studies use novel trajectories and simple dots to eliminate any influence of longer-term spatial memory. Consequently, we eliminated the two long-term memory layers in the model. This simplified the 7-layer model down to three critical layers—PF, Inhib, and SWM. Note that this is the same 3-layer model we have used in previous work to quantitatively model the details of children’s and adults’ spatial recall performance (Schutte & Spencer, 2009), position discrimination (Simmering et al., 2006a; Simmering and Spencer, 2008), and visual change detection (Johnson, Spencer, Luck, et al., 2009; Johnson, Spencer, and Schöner, 2009).

The final step was to generalize the 3-layer model to two spatial dimensions. This is mathematically straightforward. An activation value is assigned to every point in a two-dimensional cortical field, resulting in a two-dimensional activation distribution. An example is shown in Figure 2A. The field equation (see appendix) specifies the rate of change of activation within this two-dimensional field through time. Changes in activation are governed, in part, by an interaction function which specifies how local and far-away neighbors influence one another, but now the interactions are extended to two dimensions. Figure 2B shows the two-dimensional Gaussian shape that specifies the local excitatory interactions within the SWM layer of our model. Figure 2D shows the two-dimensional Gaussian kernel that specifies the laterally inhibitory projection from the layer of inhibitory interneurons shown in Figure 2C to the excitatory SWM layer. To compute the effect of these interactions, the interaction kernel is convolved along both dimensions with the gated output of each layer (see appendix). Note that only neural sites that are sufficiently close to the neural output threshold (an activation value of 0) contribute to excitatory and inhibitory interactions. The convolved output is then added to the resting level, stimulus inputs, and the current pattern of activation to determine the evolution of activation through time.

Figure 2.

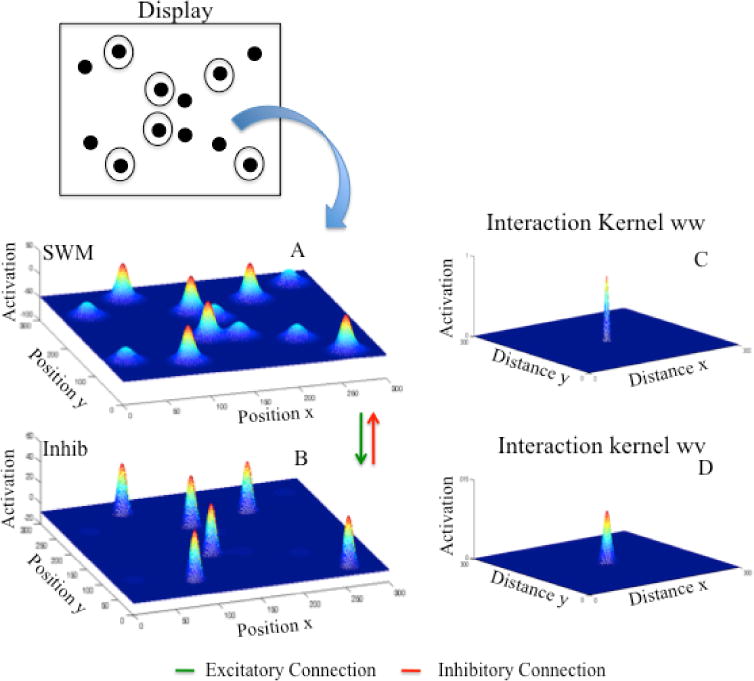
Spatial working memory (SWM; 2A) and inhibitory (Inhib; 2C) layers of the MOT model. At the top is a display with multiple targets distributed in a two-dimensional space. Circled objects show cued targets. 2A shows the activation along horizontal and vertical dimensions in SWM. 2B shows the within-layer local excitatory interactions in SWM. 2D shows the lateral inhibitory projection from the inhibitory layer (2D). Together these interactions create the “Mexican hat” activation profile.

Multi-dimensional cortical fields support the same stable states and instabilities described above. In particular, sufficiently strong input combined with neural interactions can result in the formation of localized peaks of activation in the 2D space (see Fig 2A). Moreover, with sufficiently strong interactions, peaks can become self-sustained, forming a working memory for particular spatial locations. Moreover, strong long-range inhibition can suppress nearby inputs, effectively separating ‘targets’ in SWM from ‘distractors’ in PF. And with localized excitatory and inhibitory interactions such as the kernels shown in Figures 2B and 2D, multiple peaks can form and be self-sustained in the absence of input.

Figure 3 shows how these properties of the neural dynamics in the 2D 3-layer model give rise to real-time, dynamic tracking of object locations in the MOT task. Note that this sample simulation uses one of the actual trajectories used in the study by Franconeri et al. (2010). We discuss these simulations details below in the Method. Note also that we only show PF and SWM in this figure—the inhibitory layer is not shown for simplicity. As a reminder of the full model architecture (see Fig 1 and the appendix), however, we highlight the effective coupling among the fields to the left of Figure 3: (1) the display feeds into both PF and SWM (which is a proxy for input to these layers from early visual cortical areas; see Fig 1), (2) PF has an excitatory influence on SWM, and (3) both fields have a reciprocal inhibitory influence via the shared layer of inhibitory interneurons.

Figure 3.

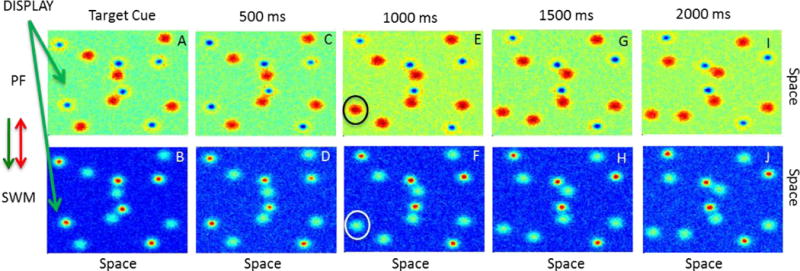
Dynamic tracking of multiple objects in a two-dimensional 3-layer model across 2000 ms. The top row shows the behavior of the perceptual field (PF) and bottom row shows the behavior of the SWM field. 3A shows the cueing of 6 targets which are updated in SWM (see blue inhibitory troughs in PF and red activation peaks in SWM). Across panels C–J, SWM updates the horizontal and vertical position of the cued targets, while PF tracks the positions of the distractors. In panel F, the model loses one of the target peaks in SWM. Consequently, a distractor peak appears in PF (see E).

At the start of the trial, 12 locations were input to PF (Fig 3A) and SWM (Fig 3B). Critically, six of these locations were cued by using stronger inputs. Consequently, these six targets formed peaks in the SWM layer by the end of the 2 s cuing period (Fig 3B). Next, the strengths of the objects were equalized, and all of the items began to move along rotational “orbit” trajectories (see Franconeri et al., 2010). Figure 3 shows a sampling of the object motions across the first 2 s after the cuing event. As can be seen in the lower panels of the figure, the peaks in SWM tracked the motion of the 6 target items for the first 500 ms (see red “hot” spots of activation), but lost one target peak by 1000 ms (see circle in Fig 3F). The five remaining targets are tracked through the remainder of the 2 s interval. Note that there are sub-threshold “bumps” of activation shown in cyan in each SWM panel. These sub-threshold activations reflect the input from the display into the SWM layer. By contrast, the opposite pattern of peaks appears in PF. Here, the model forms peaks for the non-target items in the display (see red “hot” spots) and tracks these items as they move. Left on its own, PF would form peaks for all items in the display. This does not occur for the targets, however, due to the inhibition from SWM to PF.

Why do peaks in PF and SWM track the inputs? This occurs through the same mechanism that underlies peak drift in the model: peaks are attracted toward inputs that fall within the range of locally-excitatory interactions. Consequently, as the inputs move, the peaks follow. Essentially, movement of the inputs recruits new neurons into the locally-excitatory interactions, shifting the peak in the direction of the input. At the same time, neurons on the back edge of a peak fall into the range of surround inhibition. As this process plays out through time, peaks in PF and SWM shift with the inputs.

Critically, this dynamic process of recruiting new neurons into excitatory interactions and inhibiting previously active neurons is sensitive to a host of factors and sometimes SWM peaks are lost. An example is shown in Figure 4 across finer-grained samples through time (50 ms per panel vs. 500 ms per panel in Fig 3). As in the previous example, six target peaks form in SWM by the end of the target cuing event. But as the targets start to move, the circled peak to the lower right begins to lag behind the input (which, in this case, is moving at a fast speed). Consequently, excitation begins to build on the front edge of the inhibitory trough in PF. This excitation builds to sufficiently strong levels in PF such that a peak forms which inhibits the associated sites in SWM. Consequently, the model loses its tracking of the lower right target and begins to treat this item as a distractor, that is, it begins to track the item in PF.

Figure 4.

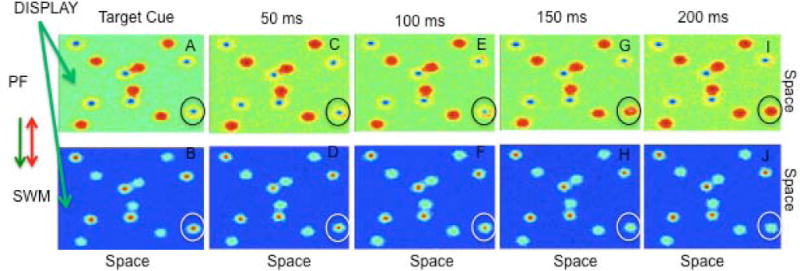
Fine-grained view of the loss of a SWM peak during tracking. 4A shows the cuing of 6 targets which are maintained in SWM (see blue inhibitory troughs in PF and red activation peaks in SWM). Across 4C–F, SWM updates the location of all 6 targets. However, after 100 ms of tracking the circled item in 4F has weakened. By 150 ms, the circled SWM peak spontaneously decays (4H). Consequently, the previously tracked item becomes a distractor, which, in turn, leads to an error at the end of the trial.

Figure 4 shows one example where a SWM peak dies out as it lags behind a moving input. This highlights how speed can impact tracking in the DFT. Below we discuss several other factors that play a role in tracking accuracy in the model.

3. Method and Results: Behavioral Simulations

In our first set of simulations, we quantitatively fit data from Franconeri et al. (2010). As discussed previously, we selected this study because it highlights several canonical factors known to impact MOT such as speed and duration, but this study also controlled for object spacing. In particular, trajectories in this study consisted of orbiting sets of points—multiple sets of points, each of which had two “moons” orbiting around an invisible center point. This controlled for object spacing because each object (i.e., each moon) was always 180° away from the other item in the set, and the center points of the sets were placed relatively far apart. Note each set of objects could rotate clockwise or counterclockwise and they changed direction randomly. The goal of the study was to probe whether spacing could account for many of the errors people make in MOT. The logic was that if object spacing is controlled, errors should be solely dictated by the cumulative distance travelled: the more distance travelled, the more likely participants should be to “lose” a target. Critically, distance travelled can be manipulated by the duration of motion; it can also be manipulated by object speed. Results showed that cumulative distance travelled was the key factor that impacted performance.

To explore whether the DFT could capture data from this innovative study, we selected three conditions from the wider array of conditions explored: a fast speed (1.2 rps) and a long duration (6 s), a fast speed (1.2 rps) and a short duration (2 s), and a slow speed (0.167 revolutions per second) and a long duration (6 s). As can be seen in Figure 5, participants showed graded performance, with poorer performance at the fast speed, and better performance at the slow speed. Interestingly, speed was not the sole factor impacting performance: participants performed better at the fast speed provided the trajectories only moved for 2 s.

Figure 5.

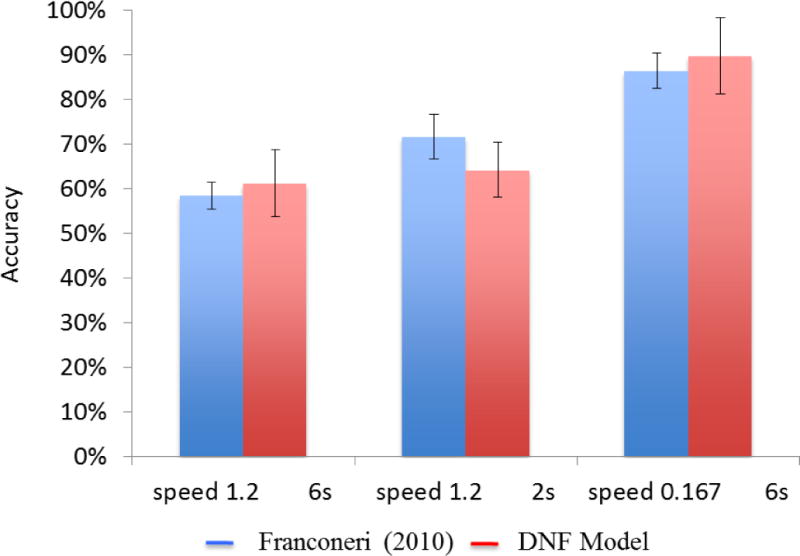
Behavioral results and model simulations showing MOT performance at a fast speed (1.2 rps) and long duration (6 s), a fast speed (1.2 rps) and short duration (2 s), and a slow speed (.167 rps) and long duration (6 s) for participants in Franconeri et al. (2010; blue bars) and the DFT (red bars).

To examine whether the DFT could capture these findings, we obtained the trajectory files used by Franconeri and colleagues and input these trajectories directly into our model. This required scaling the trajectories to our field size. The original trajectories were displayed on a 640 × 480 resolution monitor, and the points were contained within a 410 × 410 pixel region. Preliminary simulations determined that a 301 × 301 field size was sufficient to successfully track peaks. Note that we scaled the trajectories down to 85% of the field size, leaving 15% of the field at the edges without direct input to allow peaks to spread into these non-stimulated regions. Thus, the stimulated field size was 255 × 255, roughly a third smaller than the number of pixels used in the experiment. In addition to this spatial scaling, we also scaled the trajectories temporally. In particular, the trajectories were presented at 120 Hz, while our neural dynamics operate at a faster timescale. Thus, we interpolated between video frames and sampled the neural dynamics such that 1.8 time steps in the model was equal to 1 ms.

We conducted 24 simulations of each condition (which was equal to the number of participants in each condition), using a different trajectory file for each simulation. At the end of each simulation, we recorded the number of peaks in the SWM field and the number that matched the actual locations of the targets. This determined the model’s accuracy on each trial. We then computed the mean accuracy of the model (and SD) across simulations and compared this to the experimental results. As can be seen in Figure 5, the model fit the empirical data relatively well. In particular, the model had a harder time tracking the items at the fast speed than at the slow speed. Moreover, the model showed quantitatively better performance for the fast, short duration condition than for the fast, long duration condition. Inspection of the model’s tracking performance in the short duration condition revealed that it generally tracked 4 of 6 items for at least one second; however, between 1 s and 2 s, the model sometimes lost one of the peaks in SWM.

Why does the model replicate the behavioral findings? The speed result reflects the observations made in Figure 4. At slow speeds, the model is able to keep up with the input, successfully recruiting new neurons into the locally-excitatory interactions as the inputs move. At fast speeds, however, this sometimes breaks down and the SWM peaks “lose” the input. When this occurs, activation grows in PF and the model treats the target as a distractor.

What about the short duration condition? Here, the model does slightly better because the likelihood of losing a fast-moving input is a stochastic process—noise has an influence on the recruitment of new neurons into the locally-excitatory interactions. For instance, consider the case when a fast-moving input moves into a region of the field that currently has a lower level of activation due to a noise fluctuation. In this case, the SWM peak might have a hard time getting new neurons on the front edge of the peak above the 0 threshold. Consequently, the likelihood of losing the peak will be higher. The longer the trajectories move around, the greater the chance that this will happen, and the greater the likelihood that the model will lose a SWM peak. Conversely, short durations favor better performance.

In summary, the DFT does a solid job capturing a sampling of conditions from Franconeri et al. (2010). We will return to these behavioral simulations in the Discussion as we compare the DFT to other theories. But first, we examine the second key question of this study: can the DFT shed light on data from recent studies probing the neural mechanisms that underlie MOT?

4. Method and Results: ERP Simulations

There has been a growing interest in understanding the neural basis of MOT using both electrophysiology and fMRI. Here, we focus on the former approach. Given that we have a real-time neural system, the question is whether neural activation in the model accurately captures findings from studies using ERPs.

We focused on one particular study for illustration. We picked this study because the type of neural interactions reported are complex and not transparently connected to our theory. In particular, Sternshein, Agam and Sekuler (2011) used ERPs to examine how people allocate attentional resources to targets and distractors in MOT. Thus far in this paper, we have focused on SWM within a fixed-capacity neural system. Thus, at face value, it is not clear how our model might relate to findings from a study of attentional resources. To the extent that our theory does capture aspects of the ERP findings, this would suggest that the model provides a useful tool for understanding the neural processes that underlie MOT.

Sternshein and colleagues (2011) asked adults to track 2, 3, or 4 items (among 10 total) in a variant of the MOT task with a fast speed. During the tracking interval, one of the targets or one of the distractors flashed for 100ms. The flashes were task-irrelevant, but they produced an evoked response over occipital and parietal areas. The question was how these evoked responses would differ as a function of whether a target or a distractor was probed and the number of items tracked (2, 3, or 4). Results are shown in Figure 6A. ERP amplitudes (max – min) were higher for targets than for distractors. In addition, ERP amplitudes decreased with increasing tracking load. Sternshein and colleagues concluded that attention plays an important role in distinguishing targets and distractors. Targets are allocated more attentional resources than distractors, but this difference in the allocation of resources diminishes with increasing tracking load, causing the task to become more difficult. These researchers also noted that the response to flashed targets in the highest load condition elicited smaller responses than flashed distractors in the lowest load condition. This suggests that both targets and distractors are processed to some extent; reduced attention to targets alone cannot explain the full pattern of performance.

Figure 6.

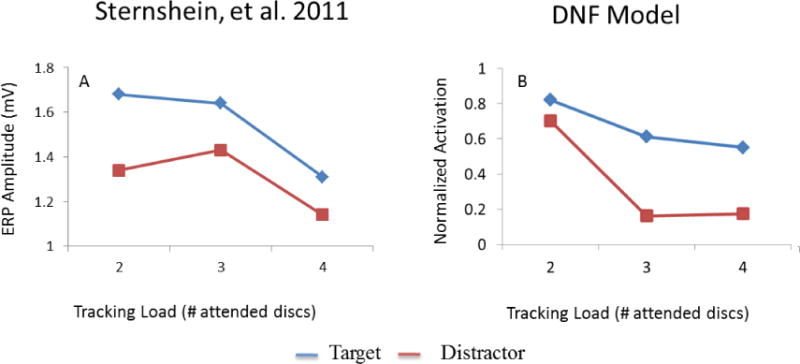
ERP amplitude across tracking load and probe type (target = blue lines vs distractor = red lines) for participants in Sternshein et al. (2011) (6A) and normalized activation amplitude in the dynamic field model (6B).

To examine whether the DFT might shed light on these findings, we used the fast trajectories (i.e., 1.2 rps) from the behavioral simulations above and created a variant of the ERP paradigm. In particular, we cued the targets for 1 s and then asked the model to track 2, 3, or 4 objects across a 2 s interval. One second into the tracking interval, we added a 100 ms boost—the same duration used by Sternshein et al—to either one of the target inputs or one of the distractor inputs. We then recorded all field activities in SWM during the boost that exceeded a conservative threshold (−2 units) and integrated the resultant neural activation across both spatial dimensions. This gave us a measure of the intensity of neural activation in SWM during the “flash” or boosting event. Given the subtlety of this neural activation measure which aggregates over the entire field, we opted to run simulations of the ERP paradigm with a lower noise strength (see Table A1). We conducted 10 simulations of the ERP paradigm for each load and for each type of target flash (i.e., boosting a target vs. boosting a distractor).

We then processed these data in a manner comparable to the ERP analysis used by Sternshein et al. (2011). First, each neural activation time series was set to a baseline level using the value of this measure at the start of each flash period. Next, we normalized all of the time series to the maximum across all observations. Third, we averaged the time series across the runs from each condition, and computed the amplitude of the neural activation signal for each condition by subtracting the maximum activation value from the minimum value.

Results of the simulations are shown in Figure 6B. The model qualitatively captures the pattern reported by Sternshein et al. (2011). Specifically, the neural response to a target flash was generally stronger than the neural response to a distractor flash, and both responses decreased in magnitude as the tracking load increased. Notably, the model shows a stronger neural response to the distractor flash at load 2 than the neural response to the target flash at load 4, consistent with empirical observations. The one deviation of the model relative to the ERP data is that the model shows a steeper decline in the neural response across loads 2 and 3 and a shallower decline between loads 3 and 4. There could be multiple reasons for this difference given that we used trajectories from Franconeri et al. (2010) and tuned the model parameters to that behavioral paradigm. In light of this, we find the results shown in Figure 6 quite compelling.

Given that our model does not have “attentional resources” per se, what drives the neural activation pattern shown in Figure 6B? The stronger neural response to the target flash relative to the distractor flash is readily explained in the model. When a target input is boosted, the boost hits already active neural sites in the field and raises their activity with no resistance. When a distractor is boosted, by contrast, the boost hits a sub-threshold bump of activation and there is only a slight rise in neural activation which is suppressed by the global inhibition in the SWM field. What about the tracking load effect? The critical factor here is that each peak in SWM contributes a small amount of global inhibition to the cortical field. Consequently, as tracking load increases, the overall amount of inhibition in SWM increases. This has the effect of reducing the overall strength of peaks in SWM. Thus, when a target input is boosted, the boost grown from a less excited state and the overall amplitude of the neural response decreases. Similarly, when a distractor is boosted, the boost grows from a more inhibited state and the neural response is weaker. In summary, then, the DFT explains the full pattern of results as a function of whether a peak is boosted vs. a sub-threshold bump, and how the strength of excitation and global inhibition change as tracking load increases.

5. Discussion

The ability to dynamically track moving objects in the environment is crucial to efficient interaction with the local surrounds. Here, we examined this ability in the context of the MOT task. Several recent theories have been proposed to explain how people track moving objects (e.g. Kazanovich and Borisyuk, 2006; Oksama and Hyönä, 2008), but these previous theories have two key limitations. First, most of these theories are not process models. Second, to our knowledge, there has been no direct contact between theories of object tracking and the growing neural literature using ERPs and fMRI.

The goal of the present paper was to examine whether the DFT could overcome these previous limitations. This goal was motivated by previous work using the DFT to examine performance in different SWM tasks (Simmering et al., 2006b; Schutte & Spencer, 2009), and the reported relationship between SWM and MOT performance (Delvenne, 2005). We were also motivated by a simple question: could we take a theory developed in the context of more ‘static’ tasks and have it shed light on a task that probes real-time neural dynamics? Thus, we generalized a 3-layer model used in prior work to two spatial dimensions, and asked whether we could quantitatively capture behavioral data from the MOT task. We also asked whether we could extend the model further and provide—for the first time—a theory that directly interfaces with neural data from the MOT literature.

Simulations of behavioral results from the study by Franconeri and colleagues (2010) provided an interesting first step. The model fit the behavioral data well, reproducing dependencies on speed and duration. These simulations were also innovative in that we used the exact trajectories from the behavioral experiment. This is an exciting step that could open up avenues for more direct theory-experiment relationships. Although our simulation results are promising, it is important to emphasize that this is only a first step—many questions remain. For instance, we used a simple form of response generation, effectively ‘reading out’ the peak locations at the end of each trial and using this to infer the response the model would make. But there are interesting response demands in the MOT literature that have prompted researchers to query responses in different ways. For instance, Franconeri and colleagues (2010) did not ask participants for a full report of all 6 items cued; rather, participants selected the 3 targets in either the upper or lower half of the display (the half selected was randomly determined on each trial). The intuition here is that the generation of a response for all 6 items might de-stabilize SWM peaks. This points toward the need to have a more fully implemented process model of response generation in this task. More generally, we are currently probing whether the DFT can capture findings from a range of MOT studies, including studies that use more standard trajectories. We have already confirmed that the model can track other types of trajectories (such as the trajectories used by Franconeri et al., 2012), but more systematic work on this front is needed.

Next, we asked whether the DFT—with the same parameters and the same trajectories—could shed light on ERP data from a recent study by Sternshein et al. (2011). Note that previous work has used dynamic field models to capture aspects of ERP data in the domain of motor planning (McDowell et al., 2002). The approach we used here was similar to that work, focusing on modulations in the strength of neural activation across different conditions. In the present study, we examined how neural activation in SWM was modulated by the presentation of a target flash vs. a distractor flash as the tracking load was varied from 2 – 4 items. Although our model did not capture the pattern from Sternshein et al. in detail, there were several remarkable correspondences. The model showed a stronger modulation of neural activity with the target flash vs. the distractor flash. Moreover, the model accurately captured a key finding from Sternshein et al—that the amplitude of the distractor response at load 2 was greater than the amplitude of the target response at load 4. Perhaps most importantly, we were able to use the model to help understand why the ERP amplitudes varied systematically across flash type and tracking load. This points toward the utility of this type of model—the model can not only mimic aspects of neural data; it can also help explain why these neural patterns arise. And this can feedback on the concepts used to explain performance. For instance, the DFT has no attentional resources per se, yet it captured findings from a study purported to manipulate attentional resources. This opens important questions regarding what researchers mean by terms like ‘attention’ and ‘working memory’. In our view, formal neural process models can play an important role in clarifying these psychological constructs.

5.1. How does the DFT compare to other theories of MOT?

In the present report, we presented a new theoretical approach to the MOT task using an existing theory of spatial cognition. Thus, it is useful to evaluate how this theory compares to other accounts of MOT. The most expansive model of MOT to date is the serial model by Oksama and Hyönä (2008). This model captures a broad range of findings from MOT, including extensions that address the binding of ‘what’ and ‘where’.

With regard to MOT, Oksama and Hyönä captured a number of key findings from the literature that have not been explained effectively by fixed-capacity, parallel theories. Thus, in the conclusion of their paper, they posed a list of challenges that fixed-capacity, parallel theories must overcome. First, such theories need to explain why MOT performance varies as a function of tracking speed. As we showed here, the DFT captures this finding. Second, fixed-capacity, parallel theories need to explain why performance varies as a function of tracking load, and why speed and tracking load interact. With regard to tracking load, our ERP simulations demonstrate that the DFT captures key modulations of performance across variations in load. With regard to the second issue, there is currently debate in the literature about whether there is, in fact, an interaction between speed and load. Oksama and Hyönä reported evidence consistent with such effects; however, Franconeri and colleagues (Franconeri et al., 2008; Franconeri et al., 2010) have argued that such interactions reflect an uncontrolled source of influence—object spacing. On this front, object spacing plays a key role in the DFT because the basic neural mechanisms that underlie peak maintenance and the updating of peak position as inputs move are all sensitive to the spacing between targets and distractors.

The final challenge put forth by Oksama and Hyönä is that fixed-capacity, parallel models must explain why object familiarity influences tracking. This brings in the more general issue of how ‘what’ and ‘where’ information are bound and how such bindings are updated as objects move. Although it is beyond the scope of the current paper, we note that we have developed a dynamic field theory of ‘what’ and ‘where’ binding (Spencer et al., n.d.). We are currently exploring whether that theory might shed light on the familiarity effects reported by Oksama and Hyönä (2008). Note that integrating the current work on MOT into our binding model is an important next step. This will facilitate deeper comparisons between the DFT and the serial model of Oksama and Hyönä.

It is also useful to ask how the DFT compares to the only other neural model of MOT by Kazanovich and Borisyuk (2006). These researchers used a different neural mechanism—synchronizing and desynchronizing neural oscillations across multiple layers—to capture behavioral findings from the MOT literature. One key difference between the DFT and this model is that the targets are maintained in independent layers. Thus, it is not clear how this model would capture effects of object spacing (see, e.g., Franconeri et al., 2010). By contrast, target peaks can share metric interactions in our SWM field, and target and distractor peaks can share metric interactions across layers. In light of our ERP simulations, a second key challenge for the neural oscillation model moving forward will be to more directly interface with neural data. Such efforts will help clarify the points of contrast with the DFT.

5.2 The neural basis of the DFT and future prospects

Although our ERP simulations are promising, there are many questions about the neural grounding of our theory. Consider, for instance, a recent fMRI study by Howe and colleagues (2009). These researchers identified a network of 5 cortical regions critically involved in MOT: the frontal eye fields (FEF), the anterior intraparietal sulcus (AIPS), the superior parietal lobule (SPL), the posterior intraparietal sulcus (PIPS), and the human motion area (MT+). Do the layers in our model map onto any of these cortical regions?

Based on the analysis of Howe and colleagues, we propose that our SWM field reflects the properties of cortical fields in either AIPS or PIPS. This is consistent with studies of VWM and change detection that have implicated the intraparietal sulcus as a key player in the maintenance of items in SWM (Pessoa and Ungerleider, 2004; Todd and Marois, 2004), and the link between the 3-layer model used here and our work examining the neural and behavioral mechanisms of change detection (Johnson, Spencer, Luck, et al., 2009; Johnson, Spencer, and Schöner, 2009). What about the perceptual field? It is possible that this layer reflects the properties of cortical fields in area MT+, which faithfully respond to object motion, including the motion of distractor items. The question is, however, how we might test these hypotheses. On this front, we are currently developing a linking hypothesis based on the work of Deco and colleagues (Deco et al., 2004) that allows us to directly generate hemodynamics from dynamic field models. Initial work in this direction appears promising. Thus, it might be possible in the near future to directly test hemodynamic predictions of the dynamic field model presented here.

In summary, the current study presented a new theory of how people track multiple moving objects, building on a dynamic field theory of spatial cognition (Spencer et al., 2007). We were able to generalize the model to the MOT task, and capture a set of behavioral data from a recent study of how speed, duration, and object spacing impact performance in this canonical laboratory task. Moreover, we did something no other theory has done to date—we used a neural process model of MOT to help understand recent findings using ERPs. It will be important for future work in this direction to examine the neural grounding of the theory more critically, possibly using other neuroimaging techniques such as fMRI.