Rapid Acquisition of Helium-3 and Proton 3D Image Sets of the Human Lung in a Single Breath-hold using Compressed Sensing

Abstract

Purpose

To develop and validate a method for acquiring helium-3 (³He) and proton (¹H) three-dimensional (3D) image sets of the human lung with isotropic spatial resolution within a 10-s breath-hold by using compressed sensing (CS) acceleration, and to assess the fidelity of undersampled images compared to fully-sampled images.

Methods

The undersampling scheme for CS acceleration was optimized and tested using ³He ventilation data. Rapid 3D acquisition of both ³He and ¹H data during one breath-hold was then implemented, based on a balanced steady-state free-precession pulse sequence, by random undersampling of k space with reconstruction via minimizing the L1 norm and total variance. CS-reconstruction fidelity was evaluated quantitatively by comparing fully-sampled and retrospectively-undersampled image sets.

Results

Helium-3 and ¹H 3D image sets of the lung with isotropic 3.9-mm resolution were acquired during a single breath-hold in 12 s and 8 s using acceleration factors of 2 and 3, respectively. Comparison of fully-sampled and retrospectively-undersampled ³He and ¹H images yielded mean absolute errors <10% and structural similarity indices >0.9.

Conclusion

By randomly undersampling k space and using CS reconstruction, high-quality ³He and ¹H 3D image sets with isotropic 3.9-mm resolution can be acquired within an 8-s breath-hold.

INTRODUCTION

Hyperpolarized noble-gas MRI (1,2) takes advantage of non-equilibrium polarization achieved by optical pumping to provide high-resolution images of lung function (3,4). Wild et alrecently demonstrated that acquisition of hyperpolarized-gas and proton (¹H) images during one breath-hold offers complementary functional and anatomical information (5, 6), and greatly facilitates quantitative analysis of ventilation defects seen in hyperpolarized-gas images (5). Isotropic 3D acquisitions for both hyperpolarized-gas (7) and ¹H would be ideal, but, using currently available methods, a breath-hold of approximately 20 s is required, which can be too long for subjects with compromised respiratory function.

Because MR images often have a sparse representation in the wavelet domain, compressed sensing (CS) enables acceleration of MR acquisitions via random undersampling in k-space followed by nonlinear reconstruction (8). Application of CS in hyperpolarized-gas imaging has potential to reduce acquisition time by requiring fewer RF pulses, while maintaining the basic signal-to-noise ratio by permitting higher flip angles. Ajraoui et al. (9) investigated the sparsity of helium-3 (³He) lung images in the wavelet domain and demonstrated through simulation the feasibility of using CS to accelerate both 2D and 3D acquisitions. Further, prospective undersampling of 2D acquisitions using two-fold acceleration was shown to yield image quality comparable to fully-sampled images (9), and extended to three-fold acceleration using prior knowledge of ¹H lung images acquired in the same subject (10).

The goal of this study was to build upon the previous investigations of Wild et al (5, 6) and Ajraoui et al (9, 10) to develop and validate a method based on CS for acquiring ³He and ¹H 3D image sets of the human lung with isotropic spatial resolution during a single breath-hold of less than 10 s (11). First, properties of the variable-density Poisson-disc k-space undersampling scheme were evaluated and optimized using fully-sampled ³He ventilation data, which were retrospectively undersampled and reconstructed for quantitative comparison to original, fully-sampled images. CS reconstruction used a lifting-scheme wavelet (12, 13), which has the advantages of supporting arbitrary matrix sizes and permitting faster computation. The optimized undersampling scheme was then tested using fully-sampled and prospectively-undersampled ³He acquisitions. Finally, rapid 3D acquisition of both ³He and ¹H data during one breath-hold was implemented by random undersampling of k space with reconstruction via minimizing the L1 norm and total variance. Image sets from this acquisition were compared with those from corresponding fully-sampled acquisitions.

METHODS

Five adult subjects were recruited for imaging, including four healthy volunteers (1 male, 3 female; age 20-24 years) and one subject with cystic fibrosis (male; age 21 years). In addition, data collected previously from three subjects (one healthy, one with asthma and one with cystic fibrosis), who had participated in other research studies, were used to optimize the k-space undersampling scheme for CS acquisitions. Spirometry was performed in each subject immediately before the imaging session using a hand-held device (Koko; PDS Ferraris, Louisville, CO). All studies were performed under a physician’s IND for imaging with hyperpolarized ³He using a protocol approved by our Institutional Review Board. Subjects gave written informed consent prior to participation. Throughout the imaging session the subject’s heart rate and oxygen saturation level were monitored (3150 MRI Patient Monitor; Invivo Research Inc., Orlando, FL). All studies were supervised by a physician.

Helium-3 gas was polarized by optical-pumping and spin-exchange using either a prototype commercial system (Model 9600, Magnetic Imaging Technologies Inc., Durham NC) or a custom-built system (14) to obtain polarization levels of 35-60%. Immediately prior to imaging hyperpolarized ³He gas was dispensed into a Tedlar bag (Jensen Inert Products, Coral Springs, FL) and diluted with medical-grade nitrogen to a volume equaling approximately one-third of the subject’s forced vital capacity as determined from spirometry.

MR imaging was performed using a 1.5T commercial scanner (Avanto, Siemens Medical Solutions, Malvern PA; maximum gradient strength 45 mT/m, maximum slew rate 200 T/m/s). A rigid chest radio-frequency (RF) coil (Rapid Biomedical, Rimpar, Germany) was used for ³He imaging. This RF coil was equipped with proton-blocking circuits to allow ¹H imaging of the chest using the body RF coil of the MR scanner with the ³He RF coil in place. Both ³He and ¹H data were acquired using a 3D balanced steady-state free-precession (bSSFP; TrueFISP on our MR scanner) pulse sequence (7). All ³He and ¹H acquisitions used spatial resolution 3.9 × 3.9 × 3.9 mm³, receiver bandwidth per pixel 1085 Hz, and flip angle 9°. The remaining pulse-sequence parameter values associated with optimization and testing of the undersampling scheme, and with ³He-¹H acquisitions in a single breath-hold, are provided in the respective subsections below.

Reconstruction of the CS acquisitions was performed by seeking minimal solutions of terms combining the L1 norm of the wavelet transform and the total variance (e.g. see Eq. [5] in ref. (9)), and was implemented in MATLAB (MathWorks, Natick, MA) by adapting routines from the SparseMRI toolbox by Lustig (8). Calculation times for reconstruction were approximately 20 minutes for ³He datasets and 30 minutes for ¹H datasets using a desktop PC (Optiplex GX745, Intel Core 2 CPU 6400, 2.13 GHz, 2 GB RAM, Dell Inc, Round Rock, TX). Compressed-sensing reconstructions were compared quantitatively to corresponding fully-sampled images using two metrics: mean absolute error and the structural similarity (SSIM) index (15). The mean absolute error was obtained by calculating the absolute difference between the CS and fully-sampled images on a pixel-by-pixel basis, normalizing by the signal intensities for fully-sampled images, and then taking the mean over the region interest. (For example, the region of interest for ³He images is the lung, as determined by a mask calculated from fully-sampled images.) Compared to conventional image-quality assessment methods, such as mean squared error, the SSIM index considers image degradation as perceived changes in structural information, rather than as differences that do not contribute to perceived image quality, which were proven to not match well with visual quality as perceived by humans (16, 17). The SSIM index ranges from -1 to 1, with the maximal value of 1 obtained only for two identical sets of data (15). For image evaluations performed in this work, an 11×11 square, Gaussian-weighted window function was used. Similarity index maps were calculated from CS and fully-sampled images, and a mean index, representing overall performance, was calculated by averaging the indices over the region of interest (e.g., the ventilated lung). Note that the region of interest in similarity index maps is slightly larger than that in the original images because a sliding window is used to calculate similarity index maps (15).

Optimization and Testing of the Undersampling Scheme

In a preliminary evaluation performed as a precursor to the current study (unpublished results), the sparsity of ³He ventilation images was evaluated by testing several lifted wavelet transforms on data acquired from healthy subjects and subjects with lung disease (asthma or cystic fibrosis). Based on these data we chose the Cohen-Daubechies-Feauveau 9/7 (CDF 9/7) wavelet (18), lifted at a level of 2, as the sparsifying transform. As the second generation of the wavelet transform, a lifted wavelet is faster and can be applied to arbitrary image sizes as compared with the first generation.

Compressed sensing relies on incoherent interference of aliasing in the sparse transform domain. The transform point spread function of the undersampling pattern and the signal behavior of specific datasets together determine the characteristics of aliasing interference. To choose an optimal variable-density sampling scheme for our application, we performed the following calculations using MR data collected previously from healthy, asthma and cystic-fibrosis subjects (as noted above). First, nine Poisson-disc sampling-matrix “pools,” with uniform sampling density from 10% to 90%, with an increment of 10%, were generated. Polynomial weighting (8) and exponential weighting (19) sampling-density schemes were then generated, and for each power-density function sampling points were drawn from the same matrix position out of the sampling-matrix pool with the nearest density to obtain a variable-density Poisson-disc undersampling pattern. For polynomial weighting, powers between 2 and 10 were considered, and for exponential weighting, factors between 1 and 4 were considered. Finally, representative datasets from healthy, asthma and cystic-fibrosis subjects were undersampled by applying these sampling patterns, and the corresponding reconstructed images were compared with the original fully-sampled images by calculating mean absolute error and SSIM metrics. The 3D-bSSFP pulse-sequence parameters for the previously-collected ³He ventilation images included TR/TE 1.78/0.75 ms (healthy, cystic fibrosis) or 1.86/0.79 ms (asthma), and matrix 128 × 80 × 60.

A prospective evaluation of the selected undersampling pattern was then performed by acquiring fully-sampled and accelerated (acceleration factor, R, of 2 or 3) ³He 3D-bSSFP datasets in a healthy volunteer. Compressed-sensing reconstructions from the accelerated acquisitions were qualitatively assessed for obvious image artifacts compared to the fully-sampled images. In addition, the fully-sampled data were retrospectively undersampled at R values of 2 and 3, and the corresponding CS reconstructions were compared with original fully-sampled images by calculating mean absolute error and SSIM metrics. The 3D-bSSFP pulse-sequence parameters included TR/TE 1.86/0.79 ms and matrix 128 × 88 × 52.

³He-¹H Acquisitions in One Breath-hold

Helium-3 and ¹H 3D-bSSFP datasets were acquired within a single breath-hold in four subjects using full sampling and either R = 2 (one healthy) or R = 3 (two healthy and one with cystic fibrosis). Compressed-sensing reconstructions from accelerated ³He and ¹H acquisitions were compared qualitatively to corresponding fully-sampled images. Fully-sampled data for healthy subjects were also retrospectively undersampled (all at R = 3), and corresponding CS reconstructions were compared with original fully-sampled images by calculating mean absolute error and SSIM metrics.

The 3D-bSSFP pulse-sequence parameters included TR/TE 1.86/0.79 ms (³He) or 1.79/0.74 ms (¹H), and matrix 128 × 88 × 52 (³He) or 128 × 110 × 64 (¹H). Elliptical sampling of k space (i.e., not sampling the corners of k space, resulting in a 19% [³He] or 20% [¹H] reduction) was used for fully-sampled acquisitions to keep total acquisition time below 20 s; elliptical sampling was not used for undersampled acquisitions, although could be implemented to further reduce acquisition time. To further decrease imaging time to make the fully-sampled acquisition better tolerated by subjects with lung disease (e.g., when used for the subject with cystic fibrosis), partial Fourier factors of 7/8 in the in-plane phase-encoding direction and 6/8 in the through-plane phase-encoding direction were used. The total acquisition times for the various pulse-sequence configurations were 16.4 s for fully-sampled with full Fourier (6.7 s for ³He, 9.7 s for ¹H), 12.7 s for fully-sampled with partial Fourier (5.2 s for ³He, 7.5 s for ¹H), 10.9 s for undersampled with R = 2 (4.3 s for ³He, 6.6 s for ¹H), and 6.9 s for undersampled with R = 3 (2.8 s for ³He, 4.1 s for ¹H). In addition, a switching delay of approximately 1 s occurred between ³He and ¹H datasets acquired sequentially in a breath-hold; stated breath-hold durations (vs. pulse-sequence acquisition times) include this switching delay.

RESULTS

Optimization and Testing of the Undersampling Scheme

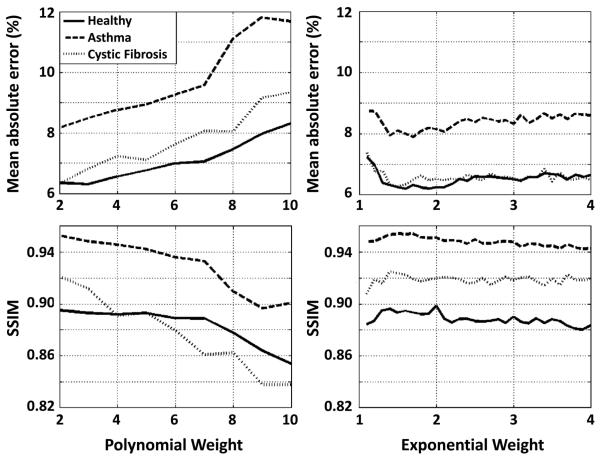
Mean absolute error and SSIM values for datasets from the healthy, asthma and cystic-fibrosis subjects are plotted in Figure 1 for polynomial (Fig. 1, left column) and exponential (Fig. 1, right column) weighting schemes. While both metrics generally became worse (i.e., higher mean absolute error and lower SSIM) with increasing power for polynomial weighting, the metrics were fairly stable with exponential weighting factor for the range of weighting factors considered. Although the specific values of the metrics varied among the three subjects, the general trends were similar for all subjects. The best metric values, occurring at a power of 2 for polynomial weighting and at approximately a factor of 1.5 for exponential weighting, were very similar for the two schemes. Further, the density distributions for the two schemes at these factors were similar. Based on these results we chose polynomial weighting at a power of 2 for the experimental studies in this work.

Figure 1.

Mean absolute error and structural similarity (SSIM) index as a function of the power for a polynomial weighting density function (left column) or an exponential weighing density function (right column) for ³He lung image sets from healthy and diseased subjects reconstructed following retrospective undersampling of fully-sampled data. The general trends for mean absolute error and SSIM index with varying weighting factors were similar for all subjects.

Coronal sections of the lung from a healthy subject are shown in Figure 2 for fully-sampled (Fig. 2 left) 3D ³He acquisitions and accelerated (R = 2, Fig. 2 center; R = 3, Fig. 2 right) acquisitions using the optimized undersampling scheme. No major differences between fully-sampled and CS-reconstructed images sets were observed. For example, a small pulmonary nodule in the left upper lung (an incidental finding in this healthy subject) was clearly seen in all three image sets. Nonetheless, the CS-reconstructed lung images appeared generally smoother, as expected from the nature of CS reconstruction, and also observed in the study by Ajraoui et al (9). The acquisition time for the undersampled datasets was reduced to 4.3 s (R = 2) and 2.8 s (R = 3) from 6.7 s for the fully-sampled (full-Fourier) acquisition. Mean absolute error and mean SSIM values over the lung region, calculated by retrospectively undersampling the fully-sampled data, were 5.1% and 0.94, respectively, for R = 2, and 6.6% and 0.91, respectively, for R = 3. Corresponding difference images and SSIM index maps for a representative coronal section are shown in Figure 3. Although quite minor in both cases, differences for R = 3 were clearly larger than those for R = 2; these differences again indicate that some fine detail was not preserved in the CS reconstruction. The increase seen in the difference image is consistent with lower similarity indices observed in some regions of the lung for the R = 3 case compared to the R = 2 case. Nonetheless, we felt that the performance of the R = 3 case was sufficient to warrant further evaluation of three-fold acceleration.

Figure 2.

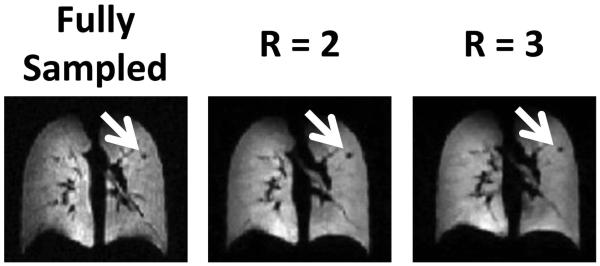
³He ventilation images from a healthy subject acquired with full sampling, or with undersampling using an acceleration factor of 2 or 3. A small pulmonary nodule (white arrows) is clearly seen in all three images.

Figure 3.

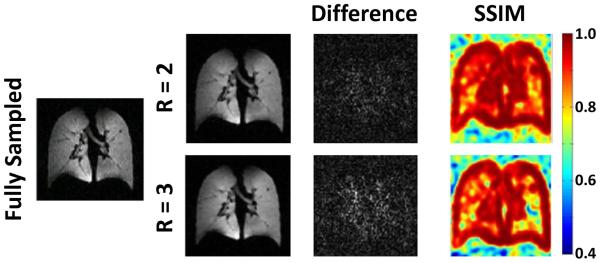
Evaluation of reconstruction fidelity based on undersampling and reconstructing fully-sampled ³He datasets acquired from one of the healthy subjects. Difference images and structural similarity (SSIM) maps for fully-sampled data versus factor 2 or 3 acceleration are shown on the right. Image differences were slightly higher and SSIM index values were slightly lower for R = 3 compared to R = 2 (see text for values).

³He-¹H Acquisitions in One Breath-hold

In each subject, fully-sampled ³He and ¹H data were collected during one breath-hold and corresponding undersampled data were collected during a subsequent breath-hold. The total (³He + ¹H) acquisition time was reduced to 10.9 s and 6.9 s for acceleration factors of 2 and 3, respectively, from 16.4 s for the fully-sampled, full-Fourier acquisition or 12.7 s for the fully-sampled, partial-Fourier acquisition. (Note that breath-hold periods were 1 s longer than acquisition times due to the switching delay.) Figure 4 shows images reconstructed in three planes from one of the healthy subjects. The CS-reconstructed images generally matched the fully-sampled images well. Since the fully-sampled and undersampled images were acquired in different breath-holds, there was generally a slight shift in position between the two acquisitions. Images reconstructed in three planes from the subject with cystic fibrosis are displayed in Figure 5. Similar ventilation defects can be identified in both the fully-sampled and undersampled ³He acquisitions. Nonetheless, because of patient movement and ventilation variation between breath-holds (which, in our experience, is more prominent in diseased subjects), the fully-sampled and undersampled image sets are clearly not identical, and thus direct quantitative comparison on an image-by-image basis is challenging.

Figure 4.

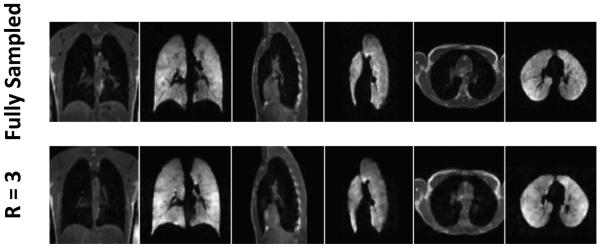
³He-¹H acquisitions in a healthy subject. Images reconstructed in three orthogonal planes are shown from fully-sampled data (upper row, 16.4 s acquisition time; 17-s breath-hold duration) and undersampled data with factor 3 acceleration (lower row, 6.9 s acquisition time; 8-s breath-hold duration).

Figure 5.

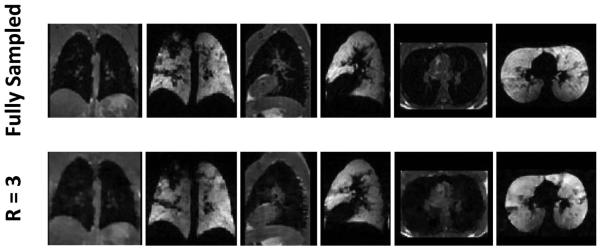
³He-¹H acquisitions in a subject with cystic fibrosis. Images reconstructed in three orthogonal planes are shown from fully-sampled data (upper row, 12.7 s acquisition time; 14-s breath-hold duration) and undersampled data with factor 3 acceleration (lower row, 6.9 s acquisition time; 8-s breath-hold duration).

Mean absolute error and mean SSIM values over the lung region, calculated by retrospectively undersampling the fully-sampled data using an acceleration factor of 3, ranged from 6% to 7%, and from 0.92 to 0.94, respectively, for the ³He images, and from 8% to 9%, and from 0.93 to 0.94, respectively, for the ¹H images. Mean absolute error and mean SSIM values for ³He images from the ³He-¹H acquisition are consistent with those found for the ³He-only acquisition described in the previous subsection.

Discussion

Numerous studies have highlighted the potential clinical utility of quantitative analysis of the ventilation defects seen in hyperpolarized-gas lung images. In severe lung disease, with large ventilation defects bordering the chest wall, accurate quantitative analysis requires knowledge of the thoracic cavity, which is preferably obtained from proton images acquired during the same breath-hold, and with spatial resolution at least similar to the hyperpolarized-gas images (5). Thus, while subjects with severe lung disease are those in which concurrent acquisition of matching proton image sets is of greatest importance for performing accurate ventilation-defect quantification, they are also the subjects most likely to have difficulty complying with the required breath-hold duration. It is in these subjects that the accelerated ³He-¹H acquisitions demonstrated in this work are likely to be useful for obtaining ventilation-quantification results that are more accurate than those based on existing techniques. The 8-s breath-hold period achieved in this study was easily tolerated by all subjects, and should generally be tolerable for subjects with pulmonary disease, thus improving breath-hold compliance compared to longer, unaccelerated acquisitions, except in the most severe cases.

The Poisson-disc sampling pattern used in this study was optimized based on data from a healthy subject and subjects with moderate asthma or cystic fibrosis. Nonetheless, additional evaluation will be required to determine whether the chosen sampling pattern and wavelet transform provide similar image fidelity in more severe disease or in other pulmonary disorders. It may also be possible to improve the quality of our accelerated ³He image sets by taking advantage of prior information from the ¹H images as described recently by Ajraoui et al (10).

Compressed-sensing reconstructed, retrospectively-undersampled images with an acceleration factor of 3 were found to be quantitatively similar to their fully-sampled counterparts (mean absolute error less than 10%, mean SSIM index 0.9 or greater in the lung region). While fully-sampled and prospectively-under-sampled image sets from ³He-¹H acquisitions appeared very similar visually, direct quantitative comparison of the fully-sampled versus prospectively-under-sampled images was not performed because the two acquisitions were acquired in separate breath-hold periods due to the rather long breath-hold duration required to obtain both acquisitions in the same breath-hold.

In conclusion, high-quality, ³He and ¹H 3D image sets with 3.9-mm isotropic resolution can be acquired within an 8-s breath-hold by randomly undersampling k space and using CS reconstruction, without the need for a multi-coil array. The acquisition time is short enough to be well tolerated by subjects with lung disease who may have difficulty with relatively long breath-hold periods. Further studies are needed to verify the performance of this technique for quantification of ventilation defects in pulmonary disease. In this regard, an important next step in the evaluation of these CS-based methods will be assessment of diagnostic content in standard versus accelerated acquisitions by chest radiologists.