Abstract
Objective
Childhood dystonia is a movement disorder that interferes with daily movements and can have a devastating effect on quality of life for children and their families. Although injury to basal ganglia is associated with dystonia, the neurophysiological mechanisms leading to the clinical manifestations of dystonia are not understood. Previous work suggested that long-latency stretch reflex (LLSR) is hyperactive in children with hypertonia due to secondary dystonia. We hypothesize that abnormal activity in motor cortices may cause an increase in the long-latency stretch reflex leading to hypertonia.
Approach
We modelled two possibilities of hyperactive LLSR by either creating a tonic involuntary drive to cortex, or increasing the synaptic gain in cortical neurons. Both models are emulated using programmable Very-Large-Scale-Integrated-circuit (VLSI) hardware to test their sufficiency for producing dystonic symptoms. The emulation includes a joint with two Hill-type muscles, realistic muscle spindles, and 2,304 Izhikevich-type spiking neurons. The muscles are regulated by a monosynaptic spinal pathway with 32ms delay and a long-latency pathway with 64ms loop-delay representing transcortical/supra-spinal connections.
Main results
When the limb is passively stretched, both models produce involuntary resistance with increased antagonist EMG responses similar to human data; also the muscle relaxation is delayed similar to human data. Both models predict reduced range of motion in voluntary movements.
Significance
Although our model is a highly simplified and limited representation of reflex pathways, it shows that increased activity of the long-latency stretch reflex is by itself sufficient to cause many of the features of hypertonic dystonia.
1. Introduction
Dystonia is an involuntary alteration in the pattern of muscle activation during voluntary movement or maintenance of posture (Sanger et al., 2003). In secondary dystonia, symptoms are often caused by injury to cortex, thalamus or basal ganglia (Colton et al., 2002; Sanger et al., 2003; Breakefield et al., 2008), but the link between injury to these areas and the resulting clinical symptoms remains unclear. Previous work suggested that the long-latency stretch reflex (LLSR) is abnormally increased in childhood hypertonia due to secondary dystonia (Kukke and Sanger, 2011). We do not know whether the elevated LLSR is a cause of dystonia or merely an associated phenomenon. To explore this question, we test using simulation whether elevation of LLSR in a highly simplified model is sufficient to cause features of hypertonic dystonia, including resistance to passive stretch, delayed muscle relaxation, and reduced range of motion in voluntary movement.
The eventual manifestation of secondary dystonia may be attributable to increased activity in the motor cortex. Brain imaging provides the direct evidence of increased motor cortical activity in secondary dystonia (Ceballos-Baumann, 1994); other studies using transcranial magnetic stimulation (TMS) over motor cortex also show increased corticospinal excitability (Trompetto et al., 2012; Kojovic et al., 2013). In other forms of dystonia, it was found that patients exhibit reduced intracortical inhibition (Ridding et al., 1995; Edwards et al., 2003; Quartarone et al., 2003; Prescott et al., 2013) and increased cortical plasticity (Quartarone et al., 2003; Edwards et al., 2006; Weise et al., 2006; Prescott et al., 2013). The association between increased motor cortex activity and secondary dystonia could be due to an inhibitory effect of basal ganglia over motor cortex, possibly through thalamocortical pathways (DeLong and Wichmann, 2007; Hallett, 2011). This association is supported by clinical treatments for patients of dystonia, where dystonic symptoms were alleviated after ablative surgeries (Imer et al., 2005; Hashimoto et al., 2010) or deep brain stimulations (McIntyre et al., 2004; Vidailhet et al., 2005; Krauss, 2010; Air et al., 2011) in the globus pallidus internus (GPi). Therefore in this emulation study we focus on how different cortical parameters lead to abnormal reflex behaviors similar to dystonia.
One possible outcome of increased motor cortex excitability is to elevate LLSR due to the role of primary motor cortex in reflex modulation (Evarts and Tanji, 1976; Lee et al., 1983; Morimoto et al., 1984; Capaday et al., 1991; Matthews, 1991; Palmer and Ashby, 1992; Pruszynski et al., 2011). Therefore loss of inhibition in the motor cortex may leak an uncontrolled drive that either lowers the threshold of cortical cells or amplifies their response to afferent input. In both cases the activity of LLSR is expected to increase. In our previous studies, children with secondary dystonia showed increased reflex activity (van Doornik et al., 2009) with long-latency responses (Kukke and Sanger, 2011), which could potentially cause hypertonia in this population. Taken together, existing evidence suggests that the hypertonic manifestation of secondary dystonia may be directly caused by elevated LLSR, which potentially results from many insults including increased motor cortex excitability after injuries in basal ganglia, cerebellum, thalamus, or sensory cortices.
To determine whether this is a plausible mechanism for hypertonic dystonia and not merely an epiphenomenon, we emulate the effect of increased cortical drive or increased afferent input to cortex. The term “emulation” is used to disambiguate from numerical simulations (usually slower than real-time) in software. We do not include a model of the basal ganglia, because we seek to test whether any structure projecting to and causing uncontrolled firing of motor cortical areas could potentially be a cause of dystonia. Other possible areas with oligosynaptic connectivity to motor cortices include prefrontal cortex, primary sensory cortex, thalamus, and cerebellum. We choose the synthetic analysis approach primarily because it allows flexible ways of introducing abnormalities that are physiologically plausible but difficult to obtain from human subjects in laboratory. It also provides information about physiological components at drastically different physical and temporal scales, including millisecond time-scale action potentials in microscopic neurons, and seconds-long contractions in whole muscles. We leverage the recently available technology of programmable Very-Large-Scale-Integrated-circuit (VLSI), which allows us to create emulations of neurons that communicate using spikes, with the ability to increase the number of emulated neurons without sacrificing speed. With VLSI, the neural circuitry and connectivity is also easily modifiable. In this study, we first built a small set of structures to create a non-impaired system with functioning reflexes including a short-latency loop representing the spinal monosynaptic reflex pathway, and a long-latency loop representing the supra-spinal/transcortical pathway. Due to the aforementioned contribution of motor cortex to long-latency response, we selectively increase the activity of the transcortical pathway to emulate a hyperactive LLSR. We hypothesize two possible causes of hyperactive LLSR. First, the cortical neurons may receive a tonic drive that is either sub- or supra-threshold but overall depolarizing. This TONIC model makes the cortical neurons easier to fire or achieve high firing rate, even when receiving the same level of excitatory post-synaptic current (EPSC) from sensory feedback. Second, the synaptic gain of cortical neurons may uniformly increase, which augments the excitability of cortical neurons. This HI-GAIN model amplifies the EPSC provided by ascending sensory feedback, which eventually elevates the overall activity of the transcortical pathway. These two mechanisms are the major categories of abnormality that can lead to increases in LLSR at the cellular level, so we modeled both. We argue it is important to test if different mechanisms are both sufficient to produce dystonia, which may eventually help sub-categorizing secondary dystonia. In both models, the spinal pathway remains intact and therefore only the long-latency component in the reflex pathway is elevated.
We focus on changes in EMG or movement kinematics by comparing both TONIC and HI-GAIN models with the non-impaired condition. There are three experiments in this study:
passive back-and-forth stretch
voluntary relaxation of force
voluntary back-and-forth movement
In the first two experiments, data from human subjects are available and thus compared to verify the sufficiency of our model for producing dystonia; human data are not yet available for the last experiment, therefore the results can be used as testable hypotheses for future experiments.
2. Materials and methods
We focus on using spike-based emulation to determine the functional role of sensorimotor components, especially their sufficiency for causing clinical symptoms in abnormal conditions. The hardware emulation of the spiking neurons and sensorimotor components is constructed using Field Programmable Gate Arrays (FPGA, Xilinx Spartan-6), a programmable version of VLSI electronic chips. We favor FPGAs over pipelined hardware such as GPUs (Graphic Processing Units) or clustered CPUs (Central Processing Units) due to their inherent parallelism that resembles neural circuitry. We also found that when networking multiple units for large-scale disease emulation, FPGAs allow significantly more flexibility than custom-built hardware for communication protocols such as neuromorphic transmission protocols that directly transmit neuron-like spikes.
The activity of the emulated sensorimotor system is recorded using a dedicated data-logging computer. The FPGA communicates with the data-logging computer through a high-speed USB channel and the OpalKelly development kit and interface software (XEM6010, OpalKelly Inc.). The technical details can be located in the previous study (Niu et al., 2014). The biomechanics of the limb is simulated in software. The biomechanical simulation updates its states by first polling muscle force from the FPGAs, followed by sending muscle kinematic variables (length and velocity of lengthening) back to the FPGAs. This hybrid setup containing both hardware and software is slower than pure hardware emulation, but it simplifies the coordination between flexor and extensor FPGA chips.
2.1. Models for the sensorimotor system and increased LLSR
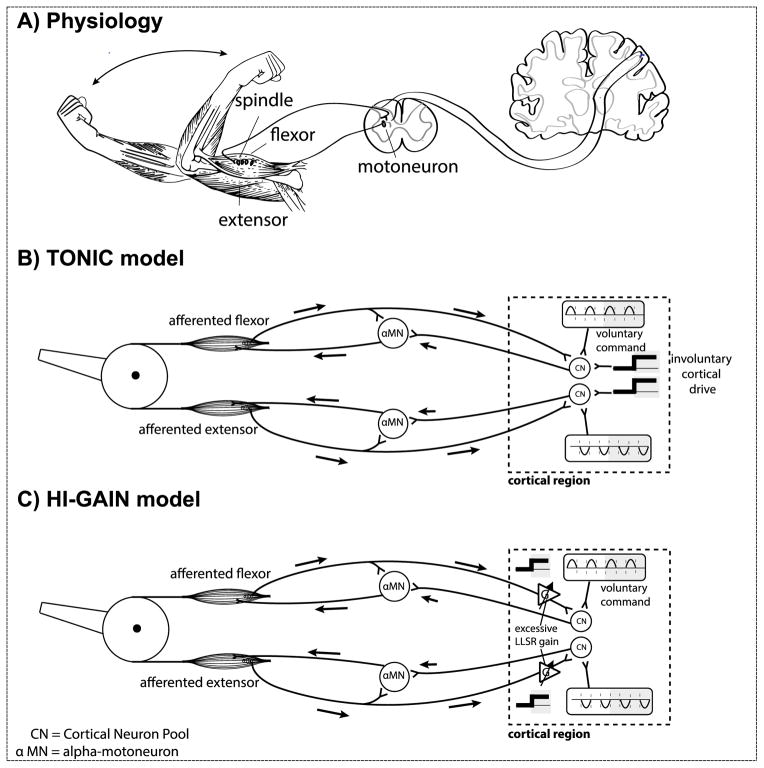
We study a sensorimotor system that includes a limb joint comprising two opposing monoarticular muscles (flexor and extensor), muscle spindles, spindle afferents, alpha-motoneurons and associated supraspinal structures (Fig. 1A). The hardware emulates parallel proprioceptive pathways including monosynaptic connections with 32ms loop-delay representing the spinal proprioceptive pathway, and oligosynaptic pathways with 64ms loop-delay representing the supra-spinal/transcortical components of the stretch reflex loop. The delays were chosen both to approximate known conduction delays and also for efficiency of hardware emulation. Our previous work suggests that in sensorimotor systems, the statistical effect of two fully connected neuron populations is equivalent to ones that are only sparsely connected (Sanger, 2011), therefore we connect the spindle afferents to motoneurons using parallel connections instead of implementing the full connectivity among neurons. In this study we do not introduce inhibitory mechanisms such as Renshaw cells or reciprocal inhibition. Both gamma dynamic and gamma static drive are set to 80Hz, which is a moderate intensity of fusimotor stimulus in the classic experiment chosen for modeling the muscle spindle (Emonet-Denand et al., 1977). No alpha-gamma coactivation is introduced. This provides a baseline system for the non-impaired behavior before introducing the disease model.
Figure 1.
A) Components of human sensorimotor system model. The system includes a limb joint comprising two opposing monoarticular muscles (flexor and extensor), muscle spindles, spindle afferents, alpha-motoneurons, and associated spinal and supraspinal structures. Our model includes a monosynaptic reflex arc with a 32ms loop-delay and a supra-spinal transcortical reflex pathway with a 64ms loop-delay. B) The TONIC model of dystonia. The dashed box shows the procedure of introducing involuntary tonic activity. Before the disease onset (unshaded area), the system executes the voluntary commands received from antagonistic cortical inputs; after the disease onset (shaded area), the voluntary descending commands are superimposed on a tonic input. C) The HI-GAIN model of dystonia. The synaptic gain associated with the afferent cortical projection becomes higher after the disease onset (shaded areas), which directly increases the loop-gain of the transcortical feedback loop.
On top of the non-impaired system, we model two possible mechanisms to increase LLSR: the TONIC model and HI-GAIN model. In the TONIC model (Fig. 1B), we superimpose a tonic input on the voluntary commands via a depolarizing synapse. The tonic input lowers the threshold of the cortical neuron pool and therefore facilitates the transcortical pathway when stimulated by proprioceptive feedback. In the HI-GAIN model (Fig. 1C), the synaptic gain of afferent inputs to the cortical neuron pool is increased by augmenting the excitatory postsynaptic potential (EPSC) in response to afferent input. Therefore the TONIC model is an additive excitatory drive that is present even in the absence of afferent input, while the HI-GAIN model is a multiplicative drive that is present only when afferent input is present. Both TONIC and HI-GAIN models increase the excitability of cortical neuron pools to afferent input, either by lowering threshold or by increasing the effect of the input. We test both models because either or both mechanisms could be active in childhood dystonia.
2.2. Implementation of sensorimotor system on hardware
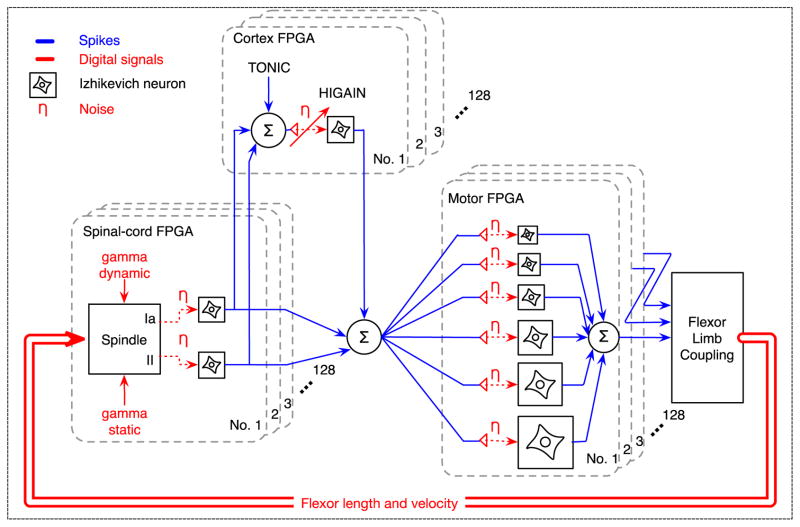
An adult elbow joint is simulated in software as a 34cm beam freely rotating around a single D.O.F. axis, the mass of the beam is 1.52kg as an approximation to a human fore arm (Scheidt and Ghez, 2007); the moment arm of muscle is simplified as constant 30mm, which is in the middle range of moment arm measured from human biceps (Murray et al., 1995). The joint is driven by a pair of antagonistic muscles following Hill-type model (Hill, 1938). The sensorimotor components that interact with the simulated joint are arranged on FPGA hardware as shown in Fig. 2. Each muscle is controlled by 128 spindles as modeled by Mileusnic et al. (2006), simple spiking neurons developed by Izhikevich (Izhikevich, 2003), and a motor-unit action potential (MUAP) model similar as (Fuglevand et al., 1993; Rodriguez et al., 2007; Krutki et al., 2008) producing a surface electromyogram. Izhikevich neurons are used because they permit use of biologically realistic variables including transmembrane currents, yet they can be implemented much more efficiently in hardware than the more complex Hodgkin-Huxley equations that they approximate. A total of 768 alpha-motoneurons were divided into 6 groups representing motor units with various sizes, so that the size principle (Henneman et al., 1965) is present when motor units are recruited. The parameters are tuned such that at maximal spiking rate of the alpha-motoneuron pool, the muscle exerts approximately 5N tangential force at the tip of the joint. In the transcortical loop, the spindle afferent information travels through a population of 128 cortical neurons representing the primary sensory and motor cortices. The main focus of modeling cortex is to enable a longer loop-delay compared to spinal pathways, therefore we accept a pool of 128 neurons as a model of cortex even though it is a clear oversimplification of the real biology. Due to the limited capacity of each FPGA unit, the system must be distributed on multiple FPGAs as indicated by the blocks. The entire system uses 6 interconnected FPGA boards to emulate 2 muscles and 2,304 spiking neurons.
Figure 2.
Detailed configuration of the motor nervous system on neuromorphic hardware. The components are implemented separately for the flexor and extensor, which simultaneously drive the joint modeled as a beam freely rotating around the endpoint (simulated in software outside FPGAs). For each muscle (flexor or extensor), the muscle force is calculated from a Hill-type muscle model activated by 6 motoneuron pools with 6 different motoneuron sizes, each pool comprising of 128 identical motoneurons modeled by Izhikevich (Izhikevich, 2003). The motoneuron pools receive excitatory input from both the spinal loop and transcortical loop. In the spinal loop, the sensory feedback is provided by muscle spindles implemented as Mileusnic and colleagues did (Mileusnic et al., 2006), which include both the Primary (Ia) and Secondary (II) afferents to provide the dynamic and static proprioceptive information about the muscle. A total of 128 spindles are implemented for each muscle, thus providing 256 independently spiking afferents. In the transcortical loop, the spindle afferents synapse on a population of 128 cortical neurons representing the primary sensory and motor cortex. The cortical part is clearly an oversimplification of the cortex but it enables an additional 32ms conduction delay in the proprioceptive feedback loop, which is the main focus of this study rather than modeling a full cortex. In the cortex, spindle afferents may join additional inputs modeling the voluntary motor command. The TONIC model is implemented by adding to the cortical drive a tonic component that is independent from the voluntary drive or the sensory feedback. The HI-GAIN model is implemented by increasing the synaptic gain of the spindle afferents prior to activating the cortical neuron pool. Due to the limited capacity of each FPGA unit, the system must be distributed on multiple FPGAs as indicated by the blocks. The entire system uses 6 FPGA boards enabling 2 muscles with 2,304 neurons. Only half of the system (flexor) is shown.
2.3. Experiments
We have verified the sufficiency of both the TONIC and HI-GAIN models for dystonic symptoms in the following three experiments:
2.3.1. Experiment 1: Passive back-and-forth stretch
We replicate the experiment where a sinusoidal perturbation was applied to a joint of a child with hypertonic arm dystonia (van Doornik et al., 2009). In the original study, the subject was instructed to rest, and the right arm was rotated manually by the experimenter following an approximately sinusoidal time profile with frequency varying from 0.2 Hz up to 2 Hz.
We use the same waveform as in the original study to stretch the emulated system. A pre-recorded waveform of joint displacement is applied to the software-simulated joint. We keep the voluntary command at zero during the passive stretch to capture the fact the subject was at rest. It was found that patients with dystonia failed to relax the muscles and produced cyclic EMG responses to the stretch. The models of dystonia are validated based on their abilities to qualitatively explain human data. To this purpose, we calculate the phase angle between the model-generated EMG and the joint angle using the same approach as in van Doornik et al. (2009). The range of phase angle reflects which kinematic variable could be the main cause of the EMG response. For example, a phase angle of 0° means the EMG response is in line with the joint angle, thus making the EMG position-dependent; while −90° means the EMG response is velocity-dependent; any phase angle between −180° and −90° suggests that the EMG response has acceleration-dependent components; any phase angle between 0° and 180° means that the EMG is active during muscle shortening.
During model validation, we first introduce a small TONIC input (TONIC model) to the cortical neuron pool or a small cortical gain (HI-GAIN model) sufficient to produce dystonic symptoms, i.e. an observable phase angle. Then we progressively increase the intensity of dystonia until the phase angle stopped changing significantly, mainly due to the saturation of neurons. We consider a model sufficient to explain human data if the parameter-scan produces a wide range of phase angle that includes those from human patients.
2.3.2. Experiment 2: Voluntary relaxation of muscle
One of the common manifestations of childhood dystonia is that the voluntary relaxation of muscle contraction is delayed (Sanger et al., 2003). We replicate the experiment that documented this delay by comparing normal subjects to patients with secondary dystonia (Ghez et al., 1988).
Both muscles were first activated at 50% maximum voluntary contraction (MVC), followed by a step decrease in the voluntary command. This experiment simulated when the subject attempts to rapidly relax the co-contracted muscles following a cue signal (Ghez et al., 1988). It was shown that the EMG decreased more slowly in patients with secondary dystonia, and thus the overall duration of muscle relaxation was delayed.
We quantify the rate of muscle relaxation by fitting the filtered EMG to a sigmoid function defined below:
where the free parameter τ denotes the rate at which the EMG decreases during muscle relaxation. The relationship between τ and the severity of dystonia was tested using a similar parameter-scan as in Experiment 1.
2.3.3. Experiment 3: Reduced range of motion in voluntary movements
In clinic, it is commonly observed that patients with dystonia apply great efforts in order to achieve a normal range of movement; otherwise the range of motion in voluntary movements is reduced. These phenomena are, however, not well documented in experimental studies. It is reported that the range of motion is reduced in neck and knee for patients with primary dystonia (Carpaneto et al., 2004; Lebiedowska et al., 2004). We hypothesize that similar reduction in range of motion is likely to occur in secondary dystonia. In addition, we test if the reduced range of motion can be improved by amplifying the voluntary command, which is a straightforward engineering approach to compensate a less responsive system.
The two cortical neuron pools regulating flexor and extensor receive half-wave rectified sinusoidal waveforms (180 degrees out of phase), which produces a back-and-forth joint swinging movement. The peak-to-peak amplitudes of joint angle resulting from these inputs are analyzed. If the amplitude of joint angle is reduced in dystonia models, we linearly increase the sinusoidal voluntary commands to test if the reduction can be compensated.
2.4. Data acquisition and processing
All data are sampled at 1kHz. The EMG signals are first high-pass filtered using 10Hz cut-off frequency (Butterworth, 3rd order), followed by rectification and a low-pass filter at 120Hz cut-off frequency (Butterworth, 3rd order). Phase angle analysis and the nonlinear fitting of the sigmoid function (for quantifying muscle relaxation, explained below) are performed using Matlab (Mathworks, Inc.).
3. Results
3.1. Non-impaired stretch reflex and hypertonia with increased LLSR
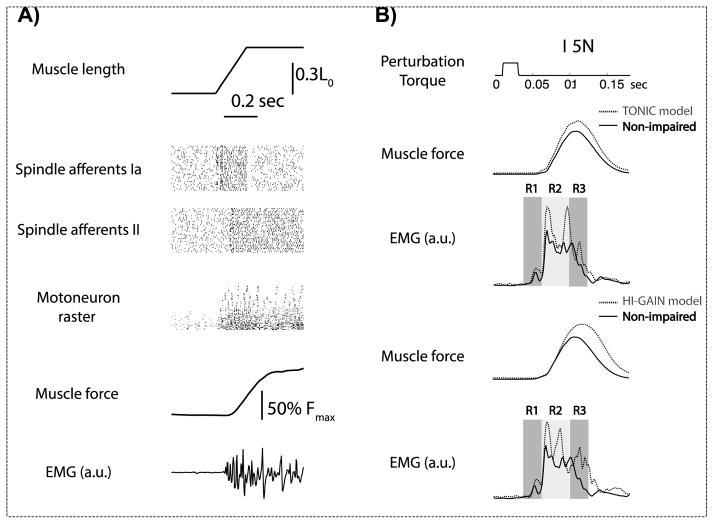
We first verify the quality of emulation by passively stretching the joint and monitoring the reflex behavior elicited by the stretch. The joint was passively extended by 45 degrees within 0.2 seconds from the software interface. The sensorimotor information recorded in response to a virtual stretch in the non-impaired condition is shown in Fig. 3A, including the spindle afferents (group Ia and II), motoneuron rasters, muscle force and EMG. As can be seen, the hardware emulation is capable of producing concurrent multi-scale information during a virtual behavior.
Figure 3.
The emulated stretch reflex in the non-impaired condition and models of increased LLSR. A) EMG responses to a stretch-and-hold perturbation in the non-impaired condition. The joint flexor was stretched by approximately 40% of L0. The emulated EMG showed a burst in response to the stretch. The motoneuron raster showed patterns compatible with both the early burst in EMG response and the subsequent tonic components. B) Emulated hypertonia and increased LLSR. The muscle force increases from baseline in both TONIC and HI-GAIN model, which implemented the increased muscle resistance to passive muscle stretch commonly observed in hypertonic dystonia. EMG responses to a torque pulse perturbation (5N for 20ms) in both the non-impaired condition and the models of dystonia. R1 (30–50ms), R2 (50–80ms), and R3 (80–100ms) regions represent the short-, medium-, and long-latency responses. In both TONIC and HI-GAIN model the R2 response was increased compared with the non-impaired condition.
We further compared the stretch reflex between the non-impaired condition and our two dystonia models. The joint was briefly stretched using a short torque pulse (5N for 20ms, Fig. 3B), which extended the flexor by approximately 40% of L0 (the resting length of muscle). Hypertonia can be seen from the increased flexor force in the dystonia conditions compared to the non-impaired condition (Fig. 3B, Muscle force). The EMG response is divided into R1 (30–50ms), R2 (50–80ms), and R3 (80–100ms) regions representing the short-, long-, and longer-latency responses. By overlapping the non-impaired condition and our models of dystonia (Fig. 3B, EMG), it can be seen that R2 responses are increased by both TONIC and HI-GAIN model, i.e. LLSR is increased in both models.
3.2. Experiment 1: Involuntary responses to passive joint stretch
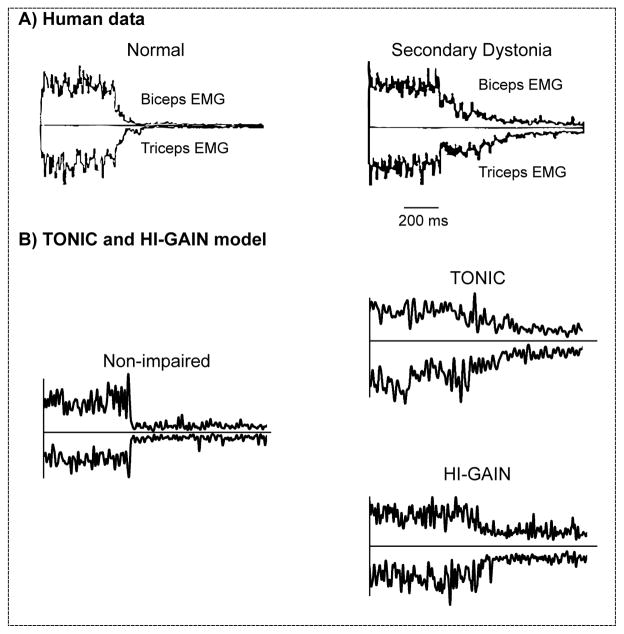
The dystonic subjects showed phasic EMG responses to the manual sinusoidal stretch in their biceps (Fig. 4A). In the emulation, the virtual arm was passively rotated with the identical waveform as shown in Fig. 4A. Our emulated result showed that in both TONIC (Fig. 4B) and HI-GAIN (Fig. 4C) models, the flexor EMG activity modulates with the joint angle similarly to the original human experiment.
Figure 4.
Biceps EMG during arm rotation in a child with hypertonic arm dystonia (A) created based on the data in van Doornik et al. (2009). When the subject was instructed to rest, the right arm was rotated manually by the experimenter following approximately a sinusoidal time profile with frequency varying from 0.2 Hz up to 2 Hz. The biceps showed phasic EMG responses to the manual stretch. In the emulation, the virtual joint was passively rotated with the identical waveform under two models of dystonia. The voluntary command is set to zero to represent the subject being “at rest”. In the TONIC model (B), the EMG is not silent when the joint is passively rotated and shows similar phasic patterns as the human EMG recording. In the HI-GAIN model (C), similar non-silent EMG responses are observed with increased magnitude in phasic response.
The 8 patients with dystonia from human experiments (van Doornik et al., 2009) showed a wide range of phase angle between −101° and 17° (Table 2, van Doornik et al., 2009). There were 2 patients (Subjects 4 and 5) with dyskinetic cerebral palsy (CP) who showed positive phase angles, suggesting EMG responses during muscle shortening (a “shortening reaction” more frequently seen in Parkinsonism). These 2 patients were excluded from the model validation, since their mechanisms were unlikely the same as the other 6 patients who were non-dyskinetic. As can be seen from Fig. 5, 5 out of 6 patients showed phase angles between −90° and 0° (combination of position- and velocity-dependent); 1 out of 6 patients showed a joint angle below −90° (with acceleration-dependent components).
Figure 5.
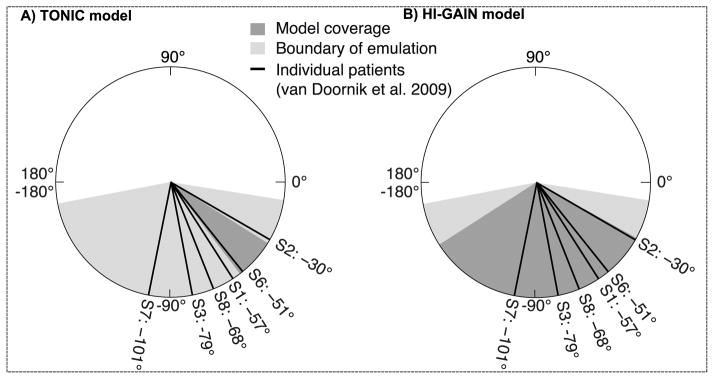
The phase angle calculated from emulation and human data. The thick lines show the phase angles of 6 patients with hypertonic arm dystonia. (A) The TONIC model produces phase angles from −32° to −53° (dark gray area), which includes 1 out of 6 patients. (B) The HI-GAIN model produces phase angles from −29° to −147° (dark gray area), which includes all 6 patients. The boundary of emulation is tested by de-afferenting either the primary (group Ia) or the secondary (group II) spindle fiber, resulting in the minimum phase angle of −169° and the maximum of −9° (light gray area).
We validate our models of dystonia by testing whether the reported phase angles in human can be achieved in emulation. In the TONIC model, we scan the tonic EPSC with fixed increments from 40pA up to 280pA. We stop at 280pA since further increases did not significantly change the phase angle mainly due to the saturation of cortical neurons. The scan of tonic EPSC produces phase angles from −32° to −53°, which explains only 1 out of 6 patients (dark gray area, Fig. 5A). In the HI-GAIN model, we start the scan by selecting a unit gain that amplifies the non-impaired EPSC by 4 times, then we progressively increase the gain to 19 times of a unit. We stop at the gain of 19 for the same reason of saturation. This process produces phase angles from −29° to −147°, which covers the reported phase angles of all 6 subjects (dark gray area, Fig. 5B).
We infer the upper and lower limits of phase angle by setting the emulation to boundary conditions (light gray area in Fig. 5). The upper limit of phase angle is obtained by de-afferenting the secondary fibers (group II) and keeping the loop gain high; and the lower limit is obtained by de-afferenting the primary fibers (group Ia) and keeping the loop gain low. The boundary conditions are constructed based on the factors that may affect the phase shift, e.g. loop delay, loop gain, and the relative contribution between position- and velocity-dependent components, etc. See Discussion for further considerations. The overall range of phase angle (−9° to −169°) is larger than both TONIC and HI-GAIN models.
The sensitivity of phase angle to the intensity of emulated dystonia in each model is shown in Fig. 6. In the TONIC model, the phase angle decreases with increased tonic current input following a significant linear correlation (Fig. 6A, slope = −0.074, p < 0.0001, r2 = 0.59, 4 repetition for each level of TONIC input). In the HI-GAIN model, similar linear correlation is observed (Fig. 6B, slope = −6.50, p < 0.0001, r2 = 0.78, 4 repetitions for each level of HI-GAIN). Overall, the HI-GAIN model can capture more variance in phase angle than could the TONIC model. The results suggest that in terms of phase angle, the HI-GAIN model can explain more data than the TONIC model, although both models produce results qualitatively similar to the human data.
Figure 6.
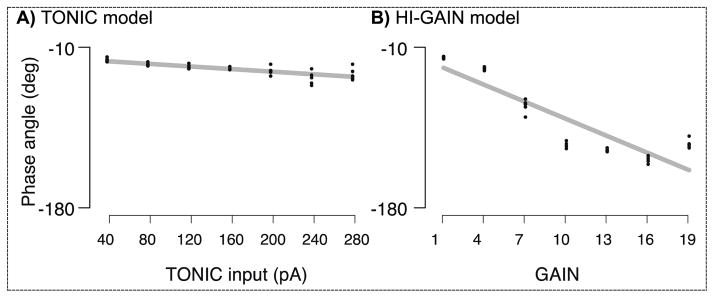
The sensitivity of phase angle to the intensity of emulated dystonia in each model. In the TONIC model, we scan the TONIC input from 40pA to 280pA with fixed increments. The average phase angles produced by these TONIC inputs range from −32° to −53°, where a higher TONIC input significantly reduces the phase angle (slope = −0.074, p < 0.0001, r2 = 0.59, 4 repetition for each level of TONIC input). The linear trend tends to saturate when the TONIC input exceeds 240pA. In the HI-GAIN model, we start the scan of cortical gain by selecting a unit gain that amplifies the non-impaired EPSC by 4 times. The gain is increased to 19 times of a unit with fixed increments. The average phase angles produced by the HI-GAIN model range from −29° to −147°, where a higher cortical gain significantly reduces the phase angle (slope = −6.50, p < 0.0001, r2 = 0.78, 4 repetitions for each level of HI-GAIN). The linear trend tends to saturate when the TONIC input exceeds 16 units. These results suggest that in terms of phase angle, the HI-GAIN model can explain more human data than the TONIC model.
3.3. Experiment 2: Delayed relaxation of muscle force
Fig. 7 shows that both the TONIC and HI-GAIN models suffice to delay muscle relaxation compared with the non-impaired condition. The phenomenon is qualitatively similar to human data.
Figure 7.
Relaxation of muscle activity from a state of co-contraction in biceps and triceps in a normal subject and a patient with secondary dystonia (A), created based on the data in Ghez et al. (1988). Subjects were first required to maximally co-contract the biceps and triceps muscles and upon a visual cue relax the muscle as fast as possible. The duration for muscle relaxation in the patient with secondary dystonia (right) was elongated compared to the normal subject (left). In emulation (B), both TONIC and HI-GAIN models showed delayed EMG relaxation compared with the non-impaired condition, when the voluntary descending command that co-contracts biceps and triceps were abruptly shut off. Single representative trials are shown.
The rate of relaxation (τ) was calculated both from human data and emulated results for model validation. Due to the limited human data, we could only obtain two values of τ based on the original EMG time series in Ghez et al. (1988). The τ calculated from the normal subject almost tripled that from the patient with secondary dystonia (τnormal = 0.044, τdystonia = 0.015), which is compatible with the visual pattern of delayed relaxation (Fig. 7A). These two values of τ are plotted in Fig. 8 (dotted and dashed lines) for comparison with emulated τ.
Figure 8.
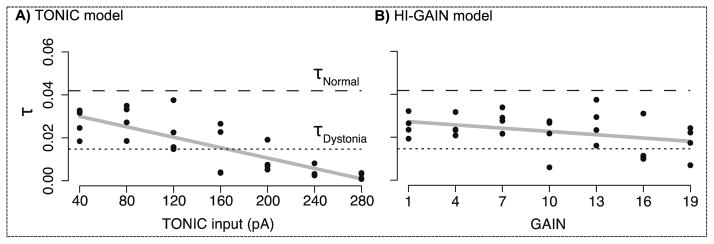
Relationship between the rate of relaxation (τ) and the intensity of either the TONIC or the HI-GAIN model. In both models, the intensity of dystonia is scanned the same as in Experiment 1. Two reference αs calculated from human data are shown, the rate in the normal subject (τnormal= 0.044, dashed line) represents faster relaxation compared to the patient with secondary dystonia (τdystonia = 0.015, dotted line). In the TONIC model (A), the emulated τs are all lower than τnormal, and their range includes τdystonia When the TONIC input increases, the delay of relaxation is significantly longer (slope = −0.00012, p < 0.00001, r2 = 0.65, 4 repetitions for each level of TONIC input). In the HI-GAIN model, the emulated τs are also lower than τnormal (B). But the linear correlation between τ and model intensity is much weaker, represented by modest significance and lower r2 value (slope = −0.00051, p < 0.046, r2 = 0.11, 4 repetitions for each level of HI-GAIN).
In the TONIC model, the level of TONIC input was scanned using the same set-up as in Experiment 1. The emulated τs were all lower than τnormal (Fig. 8A), and τdystonia was included in the emulated range of τ. When the TONIC input increases, the delay of relaxation is significantly longer (slope = −0.00012, p < 0.00001, r2 = 0.65, 4 repetitions for each level of TONIC input). In the HI-GAIN model, the emulated τs were also lower than τnormal (Fig. 8B). But the linear correlation between τ and model intensity is much weaker, represented by modest significance and lower r2 value (Fig. 8B, slope = −0.00051, p < 0.046, r2 = 0.11, 4 repetitions for each level of HI-GAIN). In contrast to Experiment 1, results from Experiment 2 suggest that the TONIC model can explain more data than the HI-GAIN model.
3.4. Experiment 3: Reduced range of motion in voluntary movements
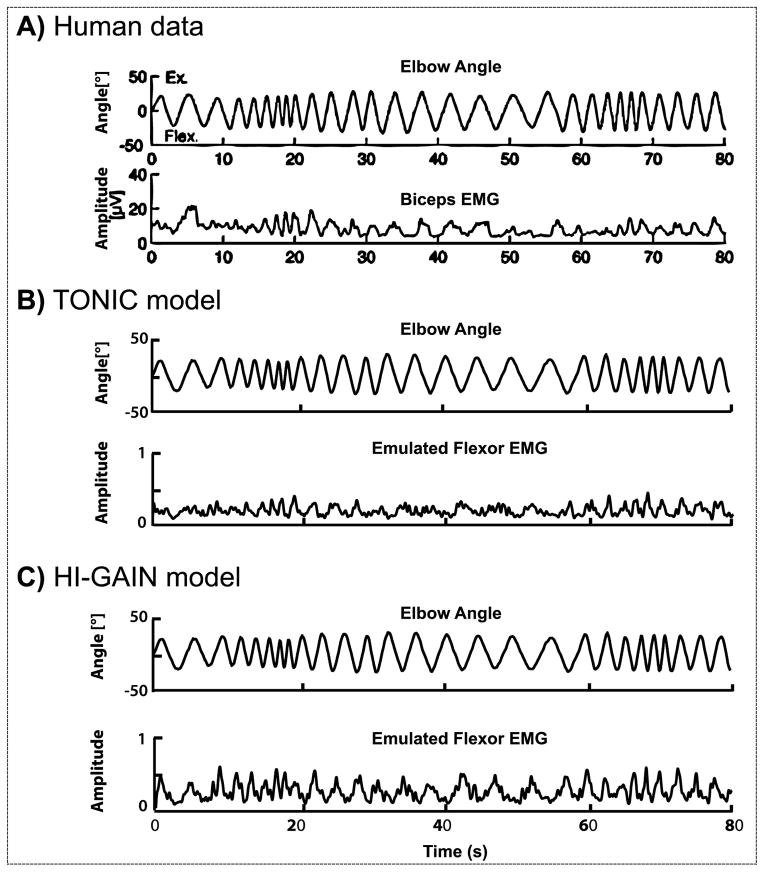
In this experiment, we aimed to predict how dystonia affects movement kinematics. In the TONIC model, just adding a middle level TONIC input is sufficient to reduce the peak-to-peak amplitude of voluntary movement (Fig. 9). The reduced range of motion can almost fully recover if we amplify the voluntary commands, suggesting that patients can compensate the reduced range of motion by increasing voluntary effort. Similar results are produced using the HI-GAIN model. In this experiment, both models predicted similar kinematic consequences using anecdotal parameters. More human data are required to distinguish between these two models.
Figure 9.
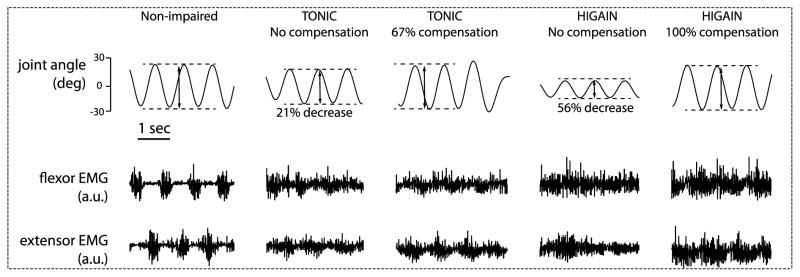
Dystonia models predict that the range of motion in voluntary arm-swing movement should be reduced in dystonia; with certain level of compensation by increasing the voluntary command, the range of movement can be recovered. In the non-impaired condition, the joint was voluntarily swinging at 1Hz with approximately 50° range of movement; the muscles are activated using alternating descending commands at 1Hz as depicted in Fig. 1 and thus generate alternating EMG bursts. In the TONIC model, we maintained the level and frequency of the 1Hz voluntary command, but added a tonic input with 80% of the peak-to-peak magnitude of the voluntary command. This reduces the movement range by 21%, which can be recovered by compensating the voluntary command by 67% of its original magnitude. In the HI-GAIN model, a 4.7 times increase in the synaptic gain of cortical neuron pool decreased the movement range by 56%, which can be recovered by compensating the voluntary command by 100%.
4. Discussion
Using our recently developed technique of neuromorphic emulation in hardware, we tested the hypothesis that increased long-latency stretch reflexes, created by excessive activity in the motor cortex, are sufficient to induce forces and EMGs with similar patterns to those seen in patients with secondary dystonia. In particular, we verified that when the limb is passively stretched as in van Doornik et al. (2009), both an additive tonic input in the cortical neuron pool (TONIC model) and an elevated synaptic gain in the motor cortex (HI-GAIN model) suffice to induce EMG responses in the absence of a voluntary command. The HI-GAIN model explains a wider range of phase angle from human data than does the TONIC model. Furthermore, we verified that both TONIC and HI-GAIN models suffice to delay muscle relaxation similar to the results of Ghez et al. (1988). The rate of relaxation could be better explained by TONIC model than the HI-GAIN model. Our models also predict that the range of movement should be reduced if the magnitude of the voluntary command remains the same in dystonia. Alternatively, we predict that dystonia increases the voluntary effort required to make movements of the same magnitude.
4.1. Relationship between LLSR and secondary dystonia
Our results suggest that increased LLSR may be an intermediate mechanism linking brain injuries and the clinical manifestations of hypertonic dystonia. That is, even though the injuries may occur in various parts of the brain (e.g. thalamus, basal ganglia, cortex, etc.), all these injuries could produce hypertonic dystonia due to excess activity in the motor cortex via elevated LLSR. We show that both TONIC and HI-GAIN models are sufficient for explaining the dystonic symptoms in the demonstrated cases. Nevertheless, the manifestation of these two models could differ when the severity of dystonia increases (Fig. 6); it is also suggested that hypertonia due to tonic input may have a stronger effect than high synaptic gain on the delay in muscle relaxation (Fig. 8). In theory, the TONIC model can be interpreted as a non-intrinsic abnormal drive to the motor cortex, originated from other parts of the brain; while the HI-GAIN model suggests that there is some intrinsic deficit in the motor cortex that amplifies its overall activity. These differences suggest testable hypotheses in future studies to distinguish the heterogeneous causes of dystonia.
Elevated LLSR is not exclusively observed in dystonia but also reported in other disorders such as rigidity. It is possible that dystonia and rigidity may share similarities in mechanism, although due to very different causes. It was not our intent to study rigidity, which is rare in children, but from our prior work (van Doornik et al., 2009) we have noted that even within dystonia there appears to be a continuum between spring-like hypertonia and viscous hypertonia. Rigidity is primarily viscous and it is tempting to conjecture that rigidity may result from increased LLSR involving primarily velocity-dependent (rapidly adapting) afferents, whereas dystonia may result from elevated LLSR involving primarily position-dependent (slowly adapting) afferents.
4.2. Rationale of model validation
When validating our models against human data, we focused on whether varying a single parameter in the model could produce a wide range of outcome measures compatible with the human data. We did not, however, focus on the exact matching between emulated time series and human data. This is because dystonia has been known as a disease with high inter-patient variability, and data from humans are limited. As a result, we argue it is not that useful if the model aims at matching exactly to the physiological signals of human patients. Take Experiment 1 as an example, the power of the HI-GAIN model comes from its ability to explain the phase angle of any of the 6 patients using the same disease structure. Given more data from patients with secondary dystonia, the range of outcome measures also provides an experimentally testable criterion to distinguish different models.
4.3. Thoughts on the two mechanisms of elevated LLSR
Either abnormality modelled by the two models can lead to elevated LLSR. This is important because intuitively it might appear that only the HI-GAIN model would increase the gain of the LLSR. Our results suggest that changes in threshold due to tonic drive can also achieve similar effects. It is possible that there is more than one mechanism of dystonia, and this points out that there may be multiple causes of similar phenomenology. For example, disorders of intrinsic excitability of motor areas (genetic or chemical) can produce dystonia, but so could disorders of other areas that project to primary motor areas. Therefore dystonia could result either from disorders of primary motor areas or from disorders of upstream areas, yet the manifestations will be difficult to distinguish on clinical grounds (although there are some differences).
Another utility of the modeling TONIC and HI-GAIN models is that they potentially represent different etiologies. In particular, a multiplicative increase in the loop gain (HI-GAIN model) cannot be implemented by an additive component added to the system, such as a leak in the trans-membrane current. In consequence, if the experimental data favors one model over the other, it suggests that the clinical diagnosis of dystonia should reflect the characteristics of the favored model, e.g. progressively increased phase angles or delayed relaxation.
4.4. Factors that may affect the phase angle in Experiment 1
Since phase angle is determined by the nonlinearity of a system and also its intrinsic delay, several factors in our neuromorphic emulation could directly affect the phase angle, including 1) the relative contribution between the primary (group Ia, both velocity- and position-dependent) and secondary (group II, mainly position-dependent) afferents of spindle, 2) the relative contribution between short- and long-latency pathway, and 3) the overall loop delay. Within the range from −180° and 0°, higher activity in the primary spindle fiber makes the system more velocity-dependent, resulting in lower phase angles; while higher activity in the secondary spindle fiber increases the phase angle. When scanning the intensity of dystonia we keep the activity similar between primary and secondary spindle afferents. When constructing the boundary condition of emulation, the secondary spindle fibers are removed such that the system is the least position-dependent, which theoretically provides the smallest phase angle, and vise versa for the largest phase angle. The effect of loop delay on the phase angle is much weaker compared to fiber type, therefore loop delay is not considered when building the boundary conditions.
4.5. EMG response during muscle shortening
Two patients (Subject 4 and 5, van Doornik et al., 2009) are excluded from the model since their positive phase angles suggest their muscles were activated by muscle shortening. This “shortening reaction” is mostly seen in Parkinsonism, but it is uncommon in normal afferented muscles since most of the proprioceptive spinal pathways are excitatory. Inhibitory pathways (e.g. Renshaw cells or reciprocal inhibition connections) are capable of reducing the EMG but usually not producing shortening reactions. One possible explanation for these two subjects is that there exists an overflow from the opposing muscle. Our models do not include inhibitory pathways or motor overflow. More experimental and modeling work is required to explain the positive joint angles attested in these two patients.
4.6. Advantage and limitation of neuromorphic hardware emulation
The use of hardware emulation provides a powerful tool for understanding the minimal model complexity for producing normal and pathological behaviors. It is clear that the hardware emulation could not accommodate all the physiological details involved in real behavior. For example, we emulated the closed-loop reflex of a joint with spinal pathways and simplified transcortical pathways. The cortical neuron pool only includes a single layer of 128 neurons that are far from the realistic anatomy in the primary sensory and motor cortices. Nevertheless, this simplified reconstruction of the cortex allows us to adjust only the long-latency component of the proprioceptive feedback independent from the functioning short-latency loop. Compared to studying the real biological system, hardware emulation is advantageous since it allows a precise and physiologically tenable intervention on the non-impaired system.
It is also an important issue whether our simplification of the sensorimotor system would lead to a locally correct conclusion that, however, cannot be generalized. It has been found that reflex of shoulder joint is concurrently modulated by the elbow joint (Pruszynski et al., 2011). This suggests that a standalone reflex loop of a single joint, as modeled in this study, may overlook the contribution from adjacent loops that would increase the LLSR and eventually worsen dystonia. On the contrary, our model did not include inhibitory pathways such as reciprocal inhibition, Renshaw cells, etc., which suggests that a more complex model may decrease LLSR and thus alleviate dystonia. In short, the model is sufficient to create some features of dystonia, but there could certainly be other contributors. It is unlikely that the inclusion of more joints would prevent the occurrence of dystonia, but it is likely to change its nature. It would be important to model dystonia in a multi-joint scenario.
5. Conclusion
In summary, we have shown through neuromorphic emulation that there are at least two possible mechanisms of cortical abnormality that could cause increased long-latency stretch reflexes and result in the clinical phenomenon of dystonia. While an emulation of this type does not prove that this is the mechanism of dystonia, it does provide evidence that a mechanism of this type is sufficient to cause the clinical features of dystonia, and is therefore worthy of further study. We hope that these results provide both insight and guidance for future clinical studies to test whether reducing the long-latency stretch reflex may alleviate symptoms of dystonia.
Acknowledgments
The authors are grateful for support from the National Institute of Neurologic Disorders and Stroke (R01-NS069214), and the James S McDonnell Foundation.
References
- Air EL, Ostrem JL, Sanger TD, Starr PA. Deep brain stimulation in children: experience and technical pearls. Journal of neurosurgery. Pediatrics. 2011;8:566–74. doi: 10.3171/2011.8.PEDS11153. [DOI] [PubMed] [Google Scholar]
- Breakefield XO, Blood AJ, Li Y, Hallett M, Hanson PI, Standaert DG. The pathophysiological basis of dystonias. Nature reviews Neuroscience. 2008;9:222–34. doi: 10.1038/nrn2337. [DOI] [PubMed] [Google Scholar]
- Capaday C, Forget R, Fraser R, Lamarre Y. Evidence for a contribution of the motor cortex to the long-latency stretch reflex of the human thumb. The Journal of physiology. 1991;440:243–55. doi: 10.1113/jphysiol.1991.sp018706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpaneto J, Micera S, Galardi G, Micheli A, Carboncini MC, Rossi B, Dario P. A protocol for the assessment of 3D movements of the head in persons with cervical dystonia. Clinical biomechanics. 2004;19:659–63. doi: 10.1016/j.clinbiomech.2004.04.003. [DOI] [PubMed] [Google Scholar]
- Ceballos-Baumann AO. Overactivity of primary and associated motor areas in secondary hemi-dystonia (SHD) due to thalamic or basal ganglia lesions: a PET study. Movement disorders : official journal of the Movement Disorder Society. 1994;9:238. [Google Scholar]
- Colton CA, Brown CM, Czapiga M, Vitek MP. Apolipoprotein-E allele-specific regulation of nitric oxide production. Annals of the New York Academy of Sciences. 2002;962:212–25. doi: 10.1111/j.1749-6632.2002.tb04070.x. [DOI] [PubMed] [Google Scholar]
- DeLong MR, Wichmann T. Circuits and circuit disorders of the basal ganglia. Archives of neurology. 2007;64:20–4. doi: 10.1001/archneur.64.1.20. [DOI] [PubMed] [Google Scholar]
- Edwards MJ, Huang YZ, Mir P, Rothwell JC, Bhatia KP. Abnormalities in motor cortical plasticity differentiate manifesting and nonmanifesting DYT1 carriers. Movement disorders : official journal of the Movement Disorder Society. 2006;21:2181–6. doi: 10.1002/mds.21160. [DOI] [PubMed] [Google Scholar]
- Edwards MJ, Huang YZ, Wood NW, Rothwell JC, Bhatia KP. Different patterns of electrophysiological deficits in manifesting and non-manifesting carriers of the DYT1 gene mutation. Brain : a journal of neurology. 2003;126:2074–80. doi: 10.1093/brain/awg209. [DOI] [PubMed] [Google Scholar]
- Emonet-Denand F, Laporte Y, Matthews PB, Petit J. On the subdivision of static and dynamic fusimotor actions on the primary ending of the cat muscle spindle. The Journal of physiology. 1977;268:827–61. doi: 10.1113/jphysiol.1977.sp011884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evarts EV, Tanji J. Reflex and intended responses in motor cortex pyramidal tract neurons of monkey. Journal of neurophysiology. 1976;39:1069–80. doi: 10.1152/jn.1976.39.5.1069. [DOI] [PubMed] [Google Scholar]
- Fuglevand AJ, Winter DA, Patla AE. Models of recruitment and rate coding organization in motor-unit pools. Journal of neurophysiology. 1993;70:2470–88. doi: 10.1152/jn.1993.70.6.2470. [DOI] [PubMed] [Google Scholar]
- Ghez C, Gordon J, Hening W. Trajectory control in dystonia. Advances in neurology. 1988;50:141–55. [PubMed] [Google Scholar]
- Hallett M. Neurophysiology of dystonia: The role of inhibition. Neurobiology of disease. 2011;42:177–84. doi: 10.1016/j.nbd.2010.08.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hashimoto T, Naito K, Kitazawa K, Imai S, Goto T. Pallidotomy for severe tardive jaw-opening dystonia. Stereotactic and functional neurosurgery. 2010;88:105–8. doi: 10.1159/000280822. [DOI] [PubMed] [Google Scholar]
- Henneman E, Somjen G, Carpenter DO. Functional Significance of Cell Size in Spinal Motoneurons. Journal of neurophysiology. 1965;28:560–80. doi: 10.1152/jn.1965.28.3.560. [DOI] [PubMed] [Google Scholar]
- Hill AV. The heat of shortening and dynamics constants of muscles. Proc R Soc Lond B. 1938;126:136–95. [Google Scholar]
- Imer M, Ozeren B, Karadereler S, Yapici Z, Omay B, Hanagasi H, Eraksoy M. Destructive stereotactic surgery for treatment of dystonia. Surgical neurology. 2005;64(Suppl 2):S89–94. doi: 10.1016/j.surneu.2005.07.036. discussion S-5. [DOI] [PubMed] [Google Scholar]
- Izhikevich EM. Simple model of spiking neurons. IEEE transactions on neural networks/a publication of the IEEENeural Networks Council. 2003;14:1569–72. doi: 10.1109/TNN.2003.820440. [DOI] [PubMed] [Google Scholar]
- Kojovic M, Parees I, Kassavetis P, Palomar FJ, Mir P, Teo JT, Cordivari C, Rothwell JC, Bhatia KP, Edwards MJ. Secondary and primary dystonia: pathophysiological differences. Brain : a journal of neurology. 2013;136:2038–49. doi: 10.1093/brain/awt150. [DOI] [PubMed] [Google Scholar]
- Krauss JK. Surgical treatment of dystonia. European journal of neurology : the official journal of the European Federation of Neurological Societies. 2010;17(Suppl 1):97–101. doi: 10.1111/j.1468-1331.2010.03059.x. [DOI] [PubMed] [Google Scholar]
- Krutki P, Ciechanowicz I, Celichowski J, Cywinska-Wasilewska G. Comparative analysis of motor unit action potentials of the medial gastrocnemius muscle in cats and rats. Journal of electromyography and kinesiology : official journal of the International Society of Electrophysiological Kinesiology. 2008;18:732–40. doi: 10.1016/j.jelekin.2007.02.013. [DOI] [PubMed] [Google Scholar]
- Kukke SN, Sanger TD. Contributors to excess antagonist activity during movement in children with secondary dystonia due to cerebral palsy. Journal of neurophysiology. 2011;105:2100–7. doi: 10.1152/jn.00998.2009. [DOI] [PubMed] [Google Scholar]
- Lebiedowska MK, Gaebler-Spira D, Burns RS, Fisk JR. Biomechanic characteristics of patients with spastic and dystonic hypertonia in cerebral palsy. Archives of physical medicine and rehabilitation. 2004;85:875–80. doi: 10.1016/j.apmr.2003.06.032. [DOI] [PubMed] [Google Scholar]
- Lee RG, Murphy JT, Tatton WG. Long-latency myotatic reflexes in man: mechanisms, functional significance, and changes in patients with Parkinson’s disease or hemiplegia. Advances in neurology. 1983;39:489–508. [PubMed] [Google Scholar]
- Matthews PB. The human stretch reflex and the motor cortex. Trends in neurosciences. 1991;14:87–91. doi: 10.1016/0166-2236(91)90064-2. [DOI] [PubMed] [Google Scholar]
- McIntyre CC, Savasta M, Kerkerian-Le Goff L, Vitek JL. Uncovering the mechanism(s) of action of deep brain stimulation: activation, inhibition, or both. Clinical neurophysiology : official journal of the International Federation of Clinical Neurophysiology. 2004;115:1239–48. doi: 10.1016/j.clinph.2003.12.024. [DOI] [PubMed] [Google Scholar]
- Mileusnic MP, Brown IE, Lan N, Loeb GE. Mathematical models of proprioceptors. I. Control and transduction in the muscle spindle. Journal of neurophysiology. 2006;96:1772–88. doi: 10.1152/jn.00868.2005. [DOI] [PubMed] [Google Scholar]
- Morimoto C, Distaso JA, Cheney JJ, Reinherz EL, Schlossman SF. Cellular interaction between subsets of T8 population for maximal suppression of antigen-specific antibody response. Cellular immunology. 1984;88:75–84. doi: 10.1016/0008-8749(84)90053-4. [DOI] [PubMed] [Google Scholar]
- Murray WM, Delp SL, Buchanan TS. Variation of muscle moment arms with elbow and forearm position. Journal of biomechanics. 1995;28:513–25. doi: 10.1016/0021-9290(94)00114-j. [DOI] [PubMed] [Google Scholar]
- Niu CM, Nandyala SK, Sanger TD. Emulated muscle spindle and spiking afferents validates VLSI neuromorphic hardware as a testbed for sensorimotor function and disease. Frontiers in computational neuroscience. 2014;8:141. doi: 10.3389/fncom.2014.00141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer E, Ashby P. Evidence that a long latency stretch reflex in humans is transcortical. The Journal of physiology. 1992;449:429–40. doi: 10.1113/jphysiol.1992.sp019094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prescott IA, Dostrovsky JO, Moro E, Hodaie M, Lozano AM, Hutchison WD. Reduced paired pulse depression in the basal ganglia of dystonia patients. Neurobiology of disease. 2013;51:214–21. doi: 10.1016/j.nbd.2012.11.012. [DOI] [PubMed] [Google Scholar]
- Pruszynski JA, Kurtzer I, Nashed JY, Omrani M, Brouwer B, Scott SH. Primary motor cortex underlies multi-joint integration for fast feedback control. Nature. 2011;478:387–90. doi: 10.1038/nature10436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quartarone A, Bagnato S, Rizzo V, Siebner HR, Dattola V, Scalfari A, Morgante F, Battaglia F, Romano M, Girlanda P. Abnormal associative plasticity of the human motor cortex in writer’s cramp. Brain : a journal of neurology. 2003;126:2586–96. doi: 10.1093/brain/awg273. [DOI] [PubMed] [Google Scholar]
- Ridding MC, Sheean G, Rothwell JC, Inzelberg R, Kujirai T. Changes in the balance between motor cortical excitation and inhibition in focal, task specific dystonia. Journal of neurology, neurosurgery, and psychiatry. 1995;59:493–8. doi: 10.1136/jnnp.59.5.493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez I, Gila L, Malanda A, Gurtubay IG, Mallor F, Gomez S, Navallas J, Rodriguez J. Motor unit action potential duration, I: variability of manual and automatic measurements. Journal of clinical neurophysiology : official publication of the American Electroencephalographic Society. 2007;24:52–8. doi: 10.1097/01.wnp.0000236606.53923.0d. [DOI] [PubMed] [Google Scholar]
- Sanger TD. Distributed control of uncertain systems using superpositions of linear operators. Neural computation. 2011;23:1911–34. doi: 10.1162/NECO_a_00151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanger TD, Delgado MR, Gaebler-Spira D, Hallett M, Mink JW Task Force on Childhood Motor D . Classification and definition of disorders causing hypertonia in childhood. Pediatrics. 2003;111:e89–97. doi: 10.1542/peds.111.1.e89. [DOI] [PubMed] [Google Scholar]
- Scheidt RA, Ghez C. Separate adaptive mechanisms for controlling trajectory and final position in reaching. Journal of neurophysiology. 2007;98:3600–13. doi: 10.1152/jn.00121.2007. [DOI] [PubMed] [Google Scholar]
- Trompetto C, Avanzino L, Marinelli L, Mori L, Pelosin E, Roccatagliata L, Abbruzzese G. Corticospinal excitability in patients with secondary dystonia due to focal lesions of the basal ganglia and thalamus. Clinical neurophysiology : official journal of the International Federation of Clinical Neurophysiology. 2012;123:808–14. doi: 10.1016/j.clinph.2011.06.033. [DOI] [PubMed] [Google Scholar]
- van Doornik J, Kukke S, Sanger TD. Hypertonia in childhood secondary dystonia due to cerebral palsy is associated with reflex muscle activation. Movement disorders : official journal of the Movement Disorder Society. 2009;24:965–71. doi: 10.1002/mds.22282. [DOI] [PubMed] [Google Scholar]
- Vidailhet M, Vercueil L, Houeto JL, Krystkowiak P, Benabid AL, Cornu P, Lagrange C, Tezenas du Montcel S, Dormont D, Grand S, Blond S, Detante O, Pillon B, Ardouin C, Agid Y, Destee A, Pollak P French Stimulation du Pallidum Interne dans la Dystonie Study G . Bilateral deep-brain stimulation of the globus pallidus in primary generalized dystonia. The New England journal of medicine. 2005;352:459–67. doi: 10.1056/NEJMoa042187. [DOI] [PubMed] [Google Scholar]
- Weise D, Schramm A, Stefan K, Wolters A, Reiners K, Naumann M, Classen J. The two sides of associative plasticity in writer’s cramp. Brain : a journal of neurology. 2006;129:2709–21. doi: 10.1093/brain/awl221. [DOI] [PubMed] [Google Scholar]