Peripapillary and Posterior Scleral Mechanics, Part I – Development of an Anisotropic Hyperelastic Constitutive Model

Abstract

Background

The sclera is the white outer shell and principal load-bearing tissue of the eye as it sustains the intraocular pressure. We have hypothesized that the mechanical properties of the posterior sclera play a significant role in, and are altered by the development of glaucoma – an ocular disease manifested by structural damage to the optic nerve head.

Method of Approach

An anisotropic hyperelastic constitutive model is presented to simulate the mechanical behavior of the posterior sclera under acute elevations of intraocular pressure. The constitutive model is derived from fiber-reinforced composite theory, and incorporates stretch-induced stiffening of the reinforcing collagen fibers. Collagen fiber alignment was assumed to be multi-directional at local material points, confined within the plane tangent to the scleral surface, and described by the semi-circular von-Mises distribution. The introduction of a model parameter, namely the fiber concentration factor, was used to control collagen fiber alignment along a preferred fiber orientation. To investigate the effects of scleral collagen fiber alignment on the overall behaviors of the posterior sclera and optic nerve head, finite element simulations of an idealized eye were performed. The four output quantities analyzed were the scleral canal expansion, the scleral canal twist, the posterior scleral canal deformation and the posterior laminar deformation.

Results

A circumferential fiber organization in the sclera restrained scleral canal expansion but created posterior laminar deformation, whereas the opposite was observed with a meridional fiber organization. Additionally, the fiber concentration factor acted as an amplifying parameter on the considered outputs.

Conclusions

The present model simulation suggests that the posterior sclera has a large impact on the overall behavior of the optic nerve head. It is therefore primordial to provide accurate mechanical properties for this tissue. In a companion paper [1], we present a method to measure the 3-D deformations of monkey posterior sclera and extract mechanical properties based on the proposed constitutive model with an inverse finite element method.

Introduction

The sclera is the outer shell and principal load-bearing tissue of the eye, which consists primarily of avascular lamellae of collagen fibers [2]. Ninety percent of the collagen fibers in the sclera are Type I, which provide the eye with necessary mechanical strength [3] to sustain the intraocular pressure (IOP). Within the posterior portion of the scleral shell, there is a fenestrated canal, called the optic nerve head (ONH), through which the retinal ganglion cell axons pass transmitting visual signals from the retina to the brain. The meshwork of connective tissue beams which span this opening are collectively called the lamina cribrosa.

Glaucomatous optic neuropathy is the second leading cause of blindness worldwide [4, 5], and is manifested by a structural damage of the ONH under all levels (normal and elevated) of IOP [6]. We hypothesize that the mechanical properties of the posterior sclera are altered during the disease and play a significant role in the development and progression of glaucomatous damage to the lamina cribrosa and ganglion cell axons within the ONH [6, 7]. In order to evaluate the effect of IOP on the connective tissues of the ONH, finite element (FE) models of the eye are being studied by our group [8-10] and others [11, 12]. Our goal is to fully characterize the mechanical behavior of tissue structures around and within the ONH, and to investigate how the mechanical environment in the ONH influences the onset and progression of glaucoma. To build these models, accurate characterization of the mechanical properties of the load-bearing tissues is necessary.

In our previous studies [13-15], experimental and mathematical models were used to determine the uniaxial mechanical properties of the sclera under the assumption of isotropic, linear viscoelasticity. Sigal and coworkers have used a simplified FE model of the posterior sclera with linear elasticity to determine that the elastic modulus of the sclera would be the largest single determinant of strain in the ONH [11, 12]. While this was a good first step, the sclera is a complex structure with varying collagen fiber orientation [16-19], so its mechanical behavior under IOP-induced mechanical stress is likely to be anisotropic and nonlinear. Therefore, new testing and modeling protocols, with anisotropic and nonlinear mechanical characteristics, are necessary to fully describe the 3-D behavior of the sclera in response to IOP elevations.

This report is the first of two that considers the development of an anisotropic hyperelastic constitutive model, with application to an idealized posterior eye geometry. In the second report [1], we present a method to experimentally characterize the 3-D deformation pattern of monkey posterior sclera due to acute elevation of IOP from 5 to 45 mm Hg, and use an inverse FE method to extract mechanical properties for the entire posterior sclera. The methods described in these two reports can be applied to determine the mechanical properties of thin soft tissues that act as pressure vessels and are mechanically loaded in 3-D.

Materials and Methods

Anisotropic Hyperelastic Constitutive Model

For most soft-tissues, collagen is often considered as the primary biomechanical element as it provides tensile strength [3], arising from its long and dense fibrous bundle organization. Accordingly, soft-tissues can be presented as fiber-reinforced composites, and modeled as hyperelastic materials that are characterized by a strain energy function W. An example of such strain energy function has been described by Weiss and coworkers [20] to model ligaments. It is defined as

$$W=W_{\mathit{\text{matrix}}}+W_{\mathit{\text{fiber}}},$$ (1)

where W_matrix is an isotropic contribution from the ground substance matrix which contains the elastin fibers, proteoglycans, fibroblasts, tissue fluid and all other tissue constituents except collagen; W_fiber is an anisotropic contribution from the reinforcing collagen fiber family. In [20], the collagen fibers were aligned along a single direction at local material points to represent transverse isotropy. Moreover, W_fiber was expressed as a nonlinear function of the fourth invariant I₄ [21] defined as

$$I_4={\mathbf{a}}_0·\mathbf{C}·{\mathbf{a}}_0,$$ (2)

where a₀ is a unit vector representing the local fiber direction in the undeformed configuration, and C is the right Cauchy-Green deformation tensor. Here, notice the link between I₄ and the fiber stretch λ. The latter can be expressed as

$$\lambda \mathbf{a}=\mathbf{F}·{\mathbf{a}}_0,$$ (3)

where a is a unit vector representing the local fiber direction in the deformed configuration, and F is the deformation gradient tensor. Since C = F^T · F, the fourth invariant I₄ is equivalent to the squared fiber stretch

$$I_4={\mathbf{a}}_0·\mathbf{C}·{\mathbf{a}}_0={\mathbf{a}}_0·{\mathbf{F}}^{\mathbf{T}}·\mathbf{F}·{\mathbf{a}}_0={\lambda }^2.$$ (4)

For many soft-tissues, however, the collagen fiber alignment is multi-directional at local material points, instead of being uni-directional. In the past, several investigators have successfully implemented new constitutive theories to allow for multi-directionality of the collagen fibers with a statistical distribution so as to model soft-tissues [22] including arterial walls [23], heart valves [24-26], and corneas [27-29]. In this report, we will pursue the same core idea to model the peripapillary and posterior sclera. In the later, the collagen fibers have a large variation in their diameters and are formed into irregularly arranged, multi-layered lamellae, with each lamella having different preferred fiber orientation and thickness [16, 18, 19]. To allow for multi-directionality at local material points, we assumed that the scleral collagen fiber alignment is confined within a plane tangent to the scleral surface, following a 2-D statistical distribution function P defined as

$$P(\theta )=\frac{1}{\pi I_0(k)}exp(kcos(2(\theta -{\theta }_p))).$$ (5)

P is known as the semi-circular von-Mises distribution [30] and I₀ is the modified Bessel function of the first kind (order 0),

$$I_0(k)=\frac{1}{\pi }\underset{0}{\overset{\pi }{\int }}exp(kcos(x))\mathit{\text{dx}}.$$ (6)

θ_p is the preferred fiber orientation relative to a local coordinate system, and k is the fiber concentration factor. Note that P satisfies the normalization condition

$$\underset{{\theta }_P-\pi /2}{\overset{{\theta }_p+\pi /2}{\int }}p(\theta )d\theta =1.$$ (7)

Figure 1 depicts the variations of P for θ_p = 0 with different magnitude of k. k = 0 represents a case of planar isotropy, whereas a larger k represents a fiber distribution relative to θ_p. The statistical distribution P was chosen for its simplicity as it can describe collagen fiber alignment with two parameters.

Figure 1.

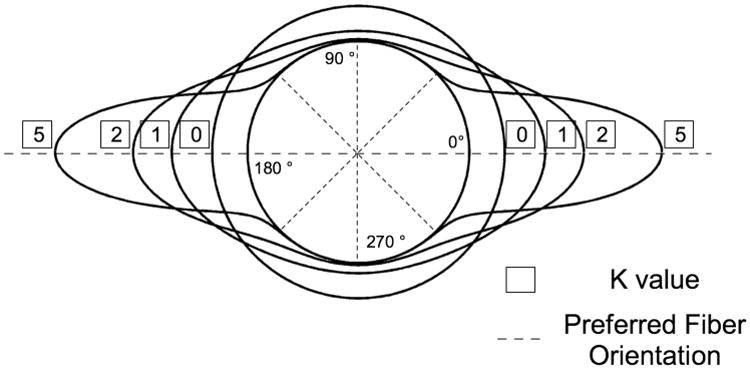
Polar representation of the semi-circular von-Mises distribution describing in-plane collagen fiber alignment. In this case, the preferred fiber orientation θ_p is equal to zero degrees. When the fiber concentration factor k is equal to zero, the collagen fibers have an isotropic distribution in a plane tangent to the scleral wall. As k increases, the collagen fibers align along the preferred fiber orientation θ_p. Note that the distributions were plotted on a circle of unit one to ease visualization.

Using Eq. (1), we propose the scleral strain energy function to be

$$W=W_{\mathit{\text{matrix}}}+\underset{{\theta }_p-\pi /2}{\overset{{\theta }_p+\pi /2}{\int }}P(\theta )W_{\mathit{\text{fiber}}}\circ I_4(\theta )d\theta$$ (8)

where the following notation was used: f ∘ g(x) = f[g(x)]. Here, W_fiber ∘ I₄ is the strain energy associated with the collagen fiber family aligned in the orientation of θ. Thus I₄ becomes a function of θ, such as

$$I_4(\theta )={\mathbf{a}}_0(\theta )·\mathbf{C}·{\mathbf{a}}_0(\theta )={\lambda }^2(\theta ).$$ (9)

To represent tissue nonlinearity, the strain energy associated with the collagen fiber family was defined for each θ orientation such that

$$\lambda (\theta )\frac{\partial W_{\mathit{\text{fiber}}}\circ I_4(\theta )}{\partial \lambda (\theta )}=c_3(exp(c_4(\lambda (\theta )-1))-1),\forall \lambda (\theta )\in \mathbb{R},$$ (10)

where c₃ is the exponential fiber stress coefficient and c₄ is the rate of uncrimping collagen fibers [20]. Finally, the ground substance matrix of the sclera was modeled as a Neo-Hookean material such that

$$W_{\mathit{\text{matrix}}}=c_1(I_1-3),$$ (11)

where I₁ is the first invariant of the right Cauchy-Green deformation tensor (I₁ = tr(C)), and c₁ is the first Mooney-Rivlin coefficient also equivalent to the matrix shear modulus divided by two.

FE Implementation

Note that some of the derivations, if not explained in this section, can be found in the excellent textbook on nonlinear continuum mechanics from Holzapfel [31]. The proposed constitutive model was implemented within the nonlinear FE code Nike3d [32] that was provided by the Lawrence Livermore National Laboratory. Modifications were made to the modules for a transversely isotropic, hyperelastic material with near-incompressibility [33]. A multiplicative decomposition [20, 31, 34, 35] was applied to the deformation gradient tensor F and the right Cauchy-Green deformation tensor C such as

$$\mathbf{F}=J^{1/3}\stackrel{\sim }{\mathbf{F}},\mathbf{C}=J^{2/3}\stackrel{\sim }{\mathbf{C}},$$ (12)

where J = det (F) is the Jacobian of the deformation; $\tilde{\mathbf{F}}\mathrm{and}\tilde{\mathbf{C}}={\tilde{\mathbf{F}}}^{\mathbf{T}}·\tilde{\mathbf{F}}$ are both tensors associated with a volume-preserving (isochoric) deformation since from Eq. (12), $\mathbf{det}(\tilde{\mathbf{F}})=\mathbf{1}$. Accordingly, the strain energy function W was decoupled into two parts: isochoric (W̃) and volumetric (W_vol), such as

$$W(\mathbf{C})=W_{\mathit{\text{vol}}}(J)+\stackrel{\sim }{W}(\stackrel{\sim }{\mathbf{C}}).$$ (13)

The material invariants of $\tilde{\mathbf{C}}$ are defined as

$$\begin{array}{l}{\stackrel{\sim }{I}}_1=\text{tr}(\stackrel{\sim }{\mathbf{C}})=J^{-2/3}\text{tr}(\mathbf{C})\\ {\stackrel{\sim }{I}}_4(\theta )={\mathbf{a}}_0(\theta )·\stackrel{\sim }{\mathbf{C}}·{\mathbf{a}}_0(\theta )=J^{-2/3}{\mathbf{a}}_0(\theta )·\mathbf{C}·{\mathbf{a}}_0(\theta )\end{array}$$ (14)

The second Piola-Kirchhoff stress tensor S is derived from the strain energy function W as

$$\mathbf{S}=2\frac{\partial W(\mathbf{C})}{\partial \mathbf{C}}=2\frac{\partial W_{\mathit{\text{vol}}}(J)}{\partial \mathbf{C}}+2\frac{\partial \stackrel{\sim }{W}(\stackrel{\sim }{\mathbf{C}})}{\partial \mathbf{C}},$$ (15)

where W̃ for the sclera is defined from Eq. (8) as

$$\stackrel{\sim }{W}={\stackrel{\sim }{W}}_{\mathit{\text{matrix}}}+\underset{{\theta }_p-\pi /2}{\overset{{\theta }_p+\pi /2}{\int }}P(\theta ){\stackrel{\sim }{W}}_{\mathit{\text{fiber}}}\circ {\stackrel{\sim }{I}}_4(\theta )d\theta$$ (16)

After complete derivation, the 2^nd Piola Kirchhoff stress tensor S is expressed as

$$\mathbf{S}=pJ{\mathbf{C}}^{-1}+2J^{-2/3}\left[c_1\right(\mathbf{I}-\frac{1}{3}{\stackrel{\sim }{I}}_1{\stackrel{\sim }{\mathbf{C}}}^{-1})+\underset{{\theta }_p-\pi /2}{\overset{{\theta }_p+\pi /2}{\int }}P(\theta ,k){\stackrel{\sim }{W}}_4(\theta )({\mathbf{a}}_0(\theta )\otimes {\mathbf{a}}_0(\theta )-\frac{1}{3}{\stackrel{\sim }{I}}_4(\theta ){\stackrel{\sim }{\mathbf{C}}}^{-1}\left)d\theta \right].$$ (17)

where p is the hydrostatic pressure and

$${\stackrel{\sim }{W}}_4(\theta )=\frac{\partial {\stackrel{\sim }{W}}_{\mathit{\text{fiber}}}\circ {\stackrel{\sim }{I}}_4(\theta )}{\partial {\stackrel{\sim }{I}}_4(\theta )}=\frac{c_3}{2\stackrel{\sim }{\lambda }{(\theta )}^2}\{exp(c_4[\stackrel{\sim }{\lambda }(\theta )-1])-1\}.$$ (18)

From the 2^nd Piola Kirchhoff stress tensor, we obtain the Cauchy stress tensor as follows

$$\sigma =\frac{1}{J}\mathbf{F}·\mathbf{S}·{\mathbf{F}}^{\mathbf{T}}=p\mathbf{I}+\frac{2}{J}\left[c_1\right(\stackrel{\sim }{\mathbf{B}}-\frac{1}{3}{\stackrel{\sim }{I}}_1\mathbf{I})+\underset{{\theta }_p-\pi /2}{\overset{{\theta }_p+\pi /2}{\int }}P(\theta ,k){\stackrel{\sim }{W}}_4(\theta ){\stackrel{\sim }{I}}_4(\theta )(\mathbf{a}(\theta )\otimes \mathbf{a}(\theta )-\frac{1}{3}\mathbf{I}\left)d\theta \right],$$ (19)

where $\tilde{\mathbf{B}}=\tilde{\mathbf{F}}·{\tilde{\mathbf{F}}}^{\mathbf{T}}$ is the Left Cauchy-Green deformation tensor associated with the isochoric deformation.

The material elasticity tensor ℂ is expressed as

$$\mathbb{C}=4\frac{{\partial }^{2}W(\mathbf{C})}{\partial \mathbf{C}\partial \mathbf{C}}=2\frac{\partial \mathbf{S}(\mathbf{C})}{\partial \mathbf{C}},$$ (20)

and the spatial elasticity tensor 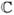is derived from the material elasticity tensor as [36]

$$𝕔=\frac{1}{J}(\mathbf{F}\underset{\_}{\otimes }\mathbf{F}):\mathbb{C}:({\mathbf{F}}^{\mathbf{T}}\underset{\_}{\otimes }{\mathbf{F}}^{\mathbf{T}}),$$ (21)

After a substantive amount of manipulations the spatial elasticity tensor becomes

$$𝕔=p(\mathbf{I}\otimes \mathbf{I}-2\mathbb{S})-\frac{2}{3}[\mathbf{I}\otimes \mathbb{P}:\sigma +\mathbb{P}:\sigma \otimes \mathbf{I}]+\frac{4}{3J}(\frac{\partial \stackrel{\sim }{W}}{\partial \stackrel{\sim }{\mathbf{C}}}:\stackrel{\sim }{\mathbf{C}})(\mathbb{S}-\frac{1}{3}\mathbf{I}\otimes \mathbf{I})+\frac{4}{J}(\stackrel{\sim }{\mathbf{F}}\underset{\_}{\otimes }\stackrel{\sim }{\mathbf{F}}):\frac{{\partial }^2\stackrel{\sim }{W}}{\partial \stackrel{\sim }{\mathbf{C}}\partial \stackrel{\sim }{\mathbf{C}}}:({\stackrel{\sim }{\mathbf{F}}}^{\mathbf{T}}\underset{\_}{\otimes }{\stackrel{\sim }{\mathbf{F}}}^{\mathbf{T}})-\frac{4}{3J}[\stackrel{\sim }{\mathbf{F}}·(\frac{{\partial }^2\stackrel{\sim }{W}}{\partial \stackrel{\sim }{\mathbf{C}}\partial \stackrel{\sim }{\mathbf{C}}}:\stackrel{\sim }{\mathbf{C}})·{\stackrel{\sim }{\mathbf{F}}}^{\mathbf{T}}\otimes \mathbf{I}+\mathbf{I}\otimes \stackrel{\sim }{\mathbf{F}}·(\frac{{\partial }^2\stackrel{\sim }{W}}{\partial \stackrel{\sim }{\mathbf{C}}\partial \stackrel{\sim }{\mathbf{C}}}:\stackrel{\sim }{\mathbf{C}})·{\stackrel{\sim }{\mathbf{F}}}^{\mathbf{T}}]+\frac{4}{9J}(\stackrel{\sim }{\mathbf{C}}:\frac{{\partial }^2\stackrel{\sim }{W}}{\partial \stackrel{\sim }{\mathbf{C}}\partial \stackrel{\sim }{\mathbf{C}}}:\stackrel{\sim }{\mathbf{C}})\mathbf{I}\otimes \mathbf{I},$$ (22)

where 𝕡 is the spatial projection tensor $(𝕡=\mathbb{I}-\frac{1}{3}\mathbf{I}\otimes \mathbf{I})$, which, when applied to a 2^nd order tensor, extracts its deviatoric component [31]. The terms of the spatial elasticity tensor have been derived in Appendix A for the proposed scleral strain energy function.

The 2^nd Piola-Kirchhoff stress tensor from Eq. (17), the Cauchy stress tensor from Eq. (19) and the spatial elasticity tensor from Eq. (22) are the three tensors that were implemented within Nike3d.

Numerical Considerations

Each integral $\underset{{\theta }_p-\pi /2}{\overset{{\theta }_p+\pi /2}{\int }}(•)d\theta$, present in both stress and elasticity tensors (see previously and Appendix A), was calculated numerically with a ten-points Gaussian quadrature rule applied to each of twelve equally-divided intervals between θ_p − π/2 and θ_p + π/2. For a large k value (typically k > 20), the statistical distribution function is highly concentrated in its preferred orientation θ_p. Therefore, the method was applied to the interval $[{\theta }_p-12/\sqrt{4k},{\theta }_p+12/\sqrt{4k}]$ in order to obtain a better accuracy for the numerical integration. Notice that for large k values, the semi-circular version of the von-Mises distribution converges to the Gaussian distribution with standard deviation $\sigma =1/\sqrt{4k}$, i.e.

$$P(\theta )\underset{k\gg 1}{\sim }\frac{1}{\sigma \sqrt{2\pi }}{\mathrm{e}}^{-\frac{{(\theta -{\theta }_p)}^2}{2{\sigma }^2}},\sigma =1/\sqrt{4k}.$$ (23)

Model Verification

In order to verify the numerical accuracy of our constitutive model, a biaxial extension test was simulated on an 8-noded hexahedral element and results were compared to analytical solutions for varying levels of k. The strain energy function was chosen from Eq. (16) and the model parameters were defined as (c₁ = 10 Pa, c₃ = 50 Pa, c₄ = 5, K = 10⁶ Pa), where K is the scleral bulk modulus. Note that for k = ∞, the statistical distribution function of Eq. (5) becomes a Dirac delta function

$$P(\theta )\underset{k=\infty }{\sim }\delta (\theta -{\theta }_p).$$ (24)

Therefore, the isochoric part of the strain energy function is now that of a transversely isotropic material, which can be written as

$$\stackrel{\sim }{W}=c_1({\stackrel{\sim }{I}}_1-3)+{\stackrel{\sim }{W}}_{\mathit{\text{fiber}}}\circ {\stackrel{\sim }{I}}_4({\theta }_p).$$ (25)

Effects of Collagen Fiber Alignment on Scleral and ONH Mechanics

To investigate the effects of collagen fiber alignment on scleral and ONH mechanics, an idealized FE model of the posterior half of the eye was constructed. The posterior sclera was assumed to be a half-sphere with a radius of 10 mm and a constant thickness of 0.5 mm. The scleral canal was circular with a radius of 0.8 mm. The fiber orientation was defined such that θ_p = 0° represents the circumferential orientation (i.e. tangent to the scleral canal boundary) and θ_p = 90° the meridional orientation (i.e. perpendicular to the scleral canal boundary) as shown in Fig. 2. Only the fiber alignment parameters (k and θ_p) were allowed to vary, whereas the other parameters were fixed for all analyses (c₁ = 100 kPa, c₃ = 5 kPa, c₄ = 500, K = 0.1 GPa), which are typical values for monkey posterior sclera [1]. The ONH was modeled as an incompressible, linear isotropic material with an elastic modulus fixed to 0.3 MPa [11]. The nodes at the equator were constrained in all three directions to maintain consistency with the experimental protocol in Part-II [1], and IOP was applied to the inner surface of the shell, then increased from 0 to 45 mm Hg.

Figure 2.

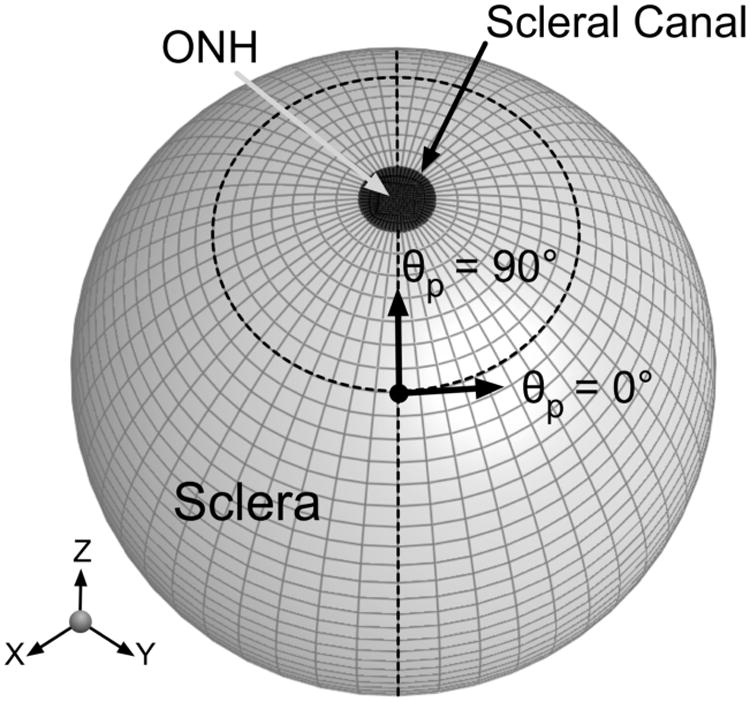
An idealized FE model of the posterior hemisphere of an eye. The fiber orientation was defined such that θ_p = 0° represents the circumferential orientation (i.e. preferred fiber orientation tangent to the scleral canal boundary) and θ_p = 90° the meridional orientation (i.e. preferred fiber orientation perpendicular to the scleral canal boundary). The ONH is considered as the posterior hemisphere's pole, which includes the lamina cribrosa and retinal ganglion cell axons.

We defined four quantities as outputs in order to understand the impact of collagen fiber alignment on scleral and ONH mechanics (Fig. 3). Scleral canal expansion was the percentage change in scleral canal radius. Scleral canal twist was the amount of rotation that the scleral canal undergoes from its undeformed to its deformed configuration. Posterior laminar deformation was the difference in z-displacements between the center of the ONH and the edge of the scleral canal (posterior surface). Finally, the posterior z-displacement of the scleral canal was also examined.

Figure 3.

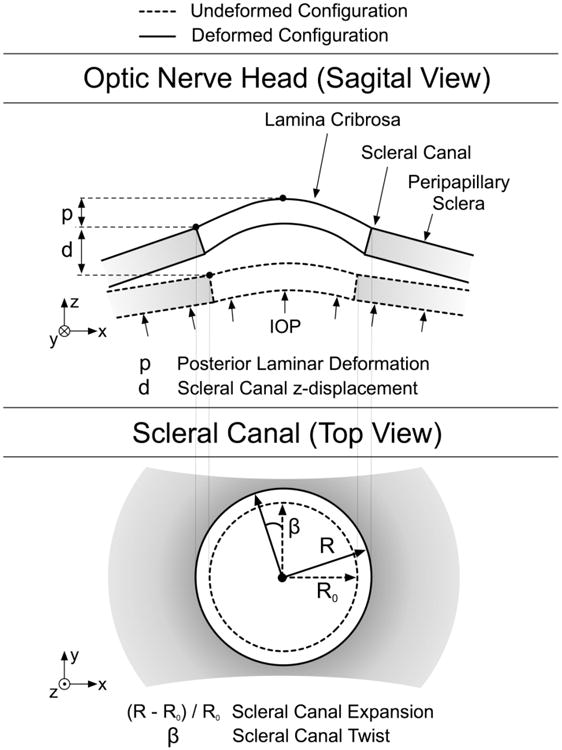
Schematics of the scleral canal and the ONH in the undeformed and deformed configurations to explain how the four output values were calculated. The four output values considered are scleral canal expansion, scleral canal twist, posterior laminar deformation and scleral canal z-displacement.

We chose the following eleven values for the fiber concentration factor k : [0, 0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5], and the following ten values for the preferred fiber orientation θ_p : [0, 10, 20, 30, 40, 50, 60, 70, 80, 90]. Therefore, a total of 110 (= 11 × 10) FE runs was performed to assess the effects of collagen fiber alignment on scleral and ONH mechanics.

Results

Model Verification

A biaxial extension test was simulated on an 8-noded hexahedral element and Fig. 4 demonstrates the excellent agreement between the analytical solutions and the FE simulations. When the fiber concentration factor k is equal to zero, the collagen fibers are unorganized and their orientations are random, which corresponds to isotropy in the xy-plane. Therefore, in Fig. 4, the stresses along the two loading directions (x and y) are identical and nonlinear. As k increases, we observe higher stresses along the y-axis – the axis associated with the preferred fiber orientation. Finally, when k is large, the model exhibits transversely isotropic behavior. In this case the stress reaches its maximum along the preferred fiber orientation (y), whereas the stress is minimum and linear along the second loading direction (x).

Figure 4.

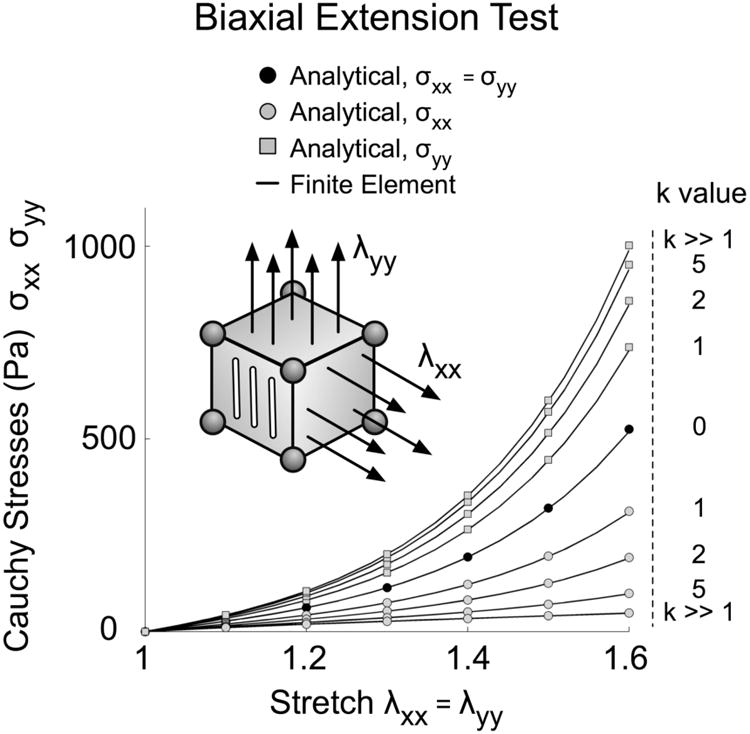
Model verification for a biaxial extension test on an 8-noded hexahedral element where symmetry conditions were applied. Here, the preferred fiber orientation is aligned along the y-axis and collagen fibers are confined within the xy-plane. When the fiber concentration factor k is equal to zero (isotropy in the xy-plane), Cauchy stresses in x- and y-directions are equal, for both the analytical and finite element solutions. When the fiber concentration factor is large (k ≫ 1), the sclera behave like a transversely isotropic material. Notice the good agreement between the analytical and finite element solutions.

Effects of collagen fiber alignment on scleral and ONH mechanics

Figure 5 illustrates the effects of collagen fiber alignment on scleral canal expansion and posterior laminar deformation. Small canal expansion occurs when θ_p = 0°, which is associated with large posterior laminar deformation. Conversely, large canal expansion occurs when θ_p = 90°, which is associated with small posterior laminar deformation. It is also observed from Fig. 5 that the fiber concentration factor k acts as an amplifying parameter on the two considered outputs.

Figure 5.

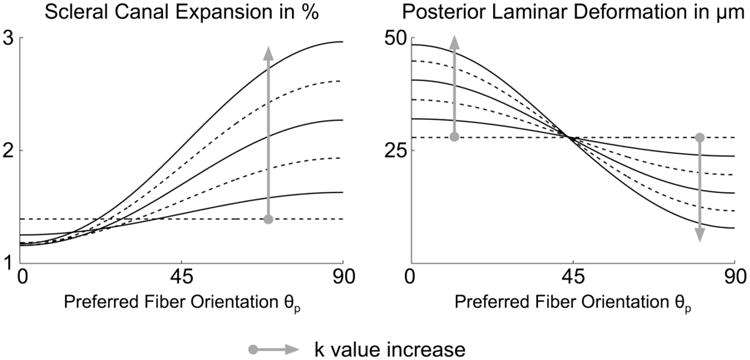
Effects of the preferred fiber orientation θ_p and fiber concentration factor k on scleral canal expansion and posterior laminar deformation at 45 mm Hg. Each curve has a specific k value, where k = 0, 2, or 4 (dashed lines) and k = 1, 3, or 5 (solid lines).

Figure 6 illustrates the effects of collagen fiber alignment on scleral canal twist and posterior z-displacement. The maximum amount of scleral canal twist is observed when θ_p = 45° and increases with the fiber concentration factor k. The maximum posterior z-displacement of the scleral canal occurs when θ_p = 0° and k = 5. In this case, the sclera is reinforced with concentric rings of fibers around the ONH, and the orientation of the maximum principal strains is perpendicular to the scleral canal wall (not shown), which causes the spherically-shaped sclera to deform into an ellipsoid. For θ_p > 45°, the scleral canal starts to move anteriorly (z-direction), which is especially evident when θ_p = 90° and k = 5. In this case, the orientation of the maximum principal strains is tangent to the scleral canal wall (not shown) and the scleral shell bulges in the mid-periphery, which causes anterior movement of the ONH. For both output values shown in Fig. 6, the fiber concentration factor k also acts as an amplifying parameter, and the effects become more significant for larger k values.

Figure 6.

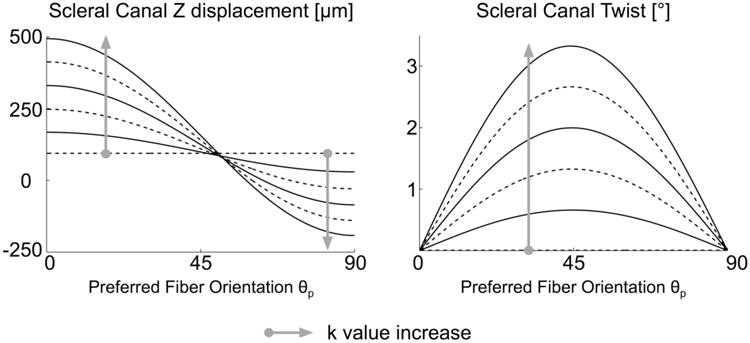
Effects of the preferred fiber orientation θ_p and fiber concentration factor k on scleral canal z-displacement and scleral canal twist at 45 mm Hg. Each curve has a specific k value, where k = 0, 2, or 4 (dashed lines) and k = 1, 3, or 5 (solid lines).

Deformed scleral shapes can be observed in Fig. 7 for the following three idealized cases (θ_p = 0°, θ_p = 45°, θ_p = 90°) where the fiber concentration factor k was equal to five, to accentuate the scleral deformation patterns.

Figure 7.

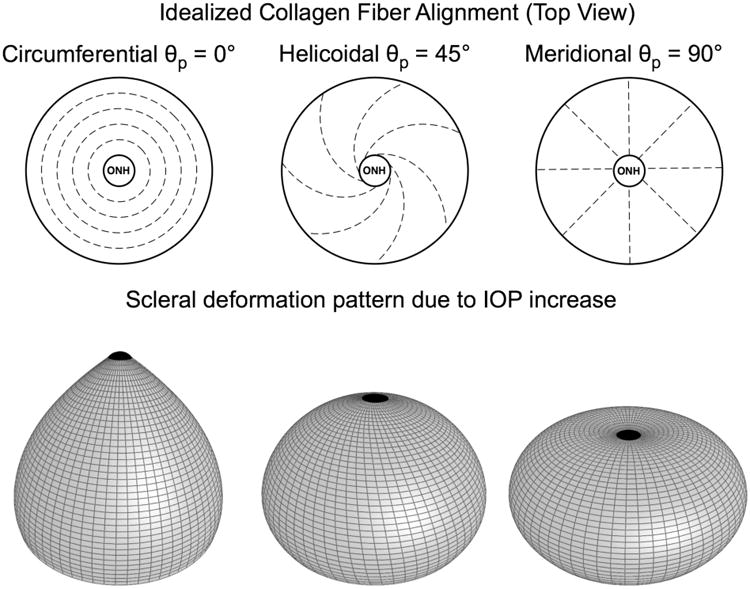
Effects of the preferred fiber orientation θ_p under acute elevation of IOP. Scleral deformations were exaggerated and displayed for three idealized cases with θ_p = 0°, θ_p = 45° and θ_p = 90°, respectively. The fiber concentration factor k was equal to five for all three cases, and deformations were exaggerated ten times to emphasize the scleral deformation patterns observed.

Discussion

In this report, an anisotropic hyperelastic constitutive model is presented that can be applied to ocular soft tissues and is especially suitable for the posterior sclera. A new model parameter, the fiber concentration factor k, along with a statistical fiber distribution function, were implemented. k can be considered as an amplifying parameter for the scleral deformations. To gain a basic knowledge of the constitutive model behavior, effects of the collagen fiber alignment and distribution on scleral deformations due to acute elevations of IOP were analyzed for an idealized posterior scleral shell. Results showed that the observed patterns of the scleral deformation are complex and very different from those of the linear isotropic theory.

Several important points warrant further discussions in terms of the difference between the current model and Weiss’ previous model for ligaments [20]. In the later, the behavior of the collagen fibers was described with a total of four independent model parameters: two for the initial nonlinear toe-region (c₃,c₄), one for the upper stretch limit of the toe-region, and one for the slope of the subsequent linear region. As shown in our previous study [37], porcine posterior sclera exhibits a high degree of nonlinearity for IOPs ranging from 5 to 45 mm Hg, and this behavior has been translated into our constitutive model with a two-parameter fiber strain energy function. Hence, we chose to limit our implementation of fiber nonlinearity to the toe-region to minimize the number of model parameters in our constitutive model, because the sclera is usually subjected to a much lower strain environment than that of tendons and ligaments. The appropriateness of this specification will be confirmed in Part-II, wherein we compare model predictions to experimental measurements of scleral deformations [1].

In this study, we simulated the mechanical behavior of a spherical posterior sclera, with an idealized collagen fiber organization. Although this combination of idealized geometry and fiber alignment is not physiologic, it is clear from these idealized models that the collagen fiber orientation in the sclera has a large impact on the IOP-induced deformations imparted to the contained ONH. We have previously suggested that the circular arrangement of collagen fibers within the peripapillary sclera could provide a protective mechanism of a more delicate lamina cribrosa which spans the scleral canal [37]. The current model simulations demonstrate that a circular arrangement of collagen fibers significantly limits scleral canal expansion, accompanied by a simultaneous increase in posterior laminar deformation. Whether scleral canal expansion or posterior laminar deformation induce ONH damage in glaucoma remains unknown. Future clinical measurements of those quantities in response to acute IOP elevations will provide more insight into the mechanisms of glaucomatous damage.

Scleral canal twist was also estimated from the model simulations, and is created when 0° < θ_p < 90° and k ≠ 0. It reaches its maximum for the very specific case of θ_p = 45°, where collagen fibers are running in a helicoidal manner from the eye equator to the ONH pole as shown in Fig. 7. While the magnitude of scleral canal twist shown here may not be physiological, this twisting feature can add complexity to the mechanical behavior of the scleral shell and could be a factor in ONH damage, but this question remains open.

The final output measure that was considered was the posterior z-displacement of the scleral canal. Our models showed that if the sclera is reinforced with fibers running tangent to the scleral canal the scleral canal deforms posteriorly (Fig. 7), whereas if the fibers are oriented perpendicular to the canal, the canal is anteriorly displaced. This behavior is interesting as it relates to myopia [16], in which the sclera undergoes a large degree of permanent stretching along the anterior/posterior axis.

In this study, one interesting aspect of the model behavior requires special attention. It should be noted that the fiber concentration factor k has very little effect on scleral canal z-displacement and posterior laminar deformation, when the preferred fiber orientation θ_p is close to 45 degrees (Fig. 5 and Fig. 6). Moreover, the fiber concentration factor k has little effect on scleral canal expansion when the preferred fiber orientation θ_p is equal to zero degrees (Fig. 5), and none on scleral canal twist when the preferred fiber orientation θ_p is equal to zero or ninety degrees (Fig. 6). All together, these results raise a potential issue when deriving model parameter estimates based on experimental measurements. It is clear that if only one of the above four output quantities is measured experimentally, it will not provide sufficient information to extract proper model parameter estimates for the peripapillary and posterior sclera as the solution of the inverse problem may not be unique. For example, if we imagine the eye with circumferential fibers in the posterior sclera, measuring scleral canal expansion experimentally does not provide sufficient data to estimate the degree of anisotropy of those fibers. One would also have to measure scleral canal z-displacement experimentally to provide a proper estimate of the fiber concentration factor in the posterior sclera. It is therefore essential to characterize the full 3-D deformations of the posterior scleral shell to obtain proper model parameter estimates as to study the interactions between ONH and scleral mechanics. This work will be undertaken in our second report [1].

Our models depict the scleral canal as the center of the posterior scleral shell although the geometric center of the posterior globe is actually the fovea. The fovea is the target structure of the visual axis, contains the greatest density of light-sensitive cells (photoreceptors), and is responsible for the eye's sharpest vision. In monkey and human eyes, the scleral canal is located 3 to 4 mm away from the fovea along the horizontal midline in the nasal hemisphere of the eye [38]. To the best of our knowledge, no previous work has provided a fiber-based constitutive model for the posterior sclera and studied the effects of scleral anisotropy on the optic nerve head. Because of this, we have chosen to locate the scleral canal in the center of the posterior globe to simplify the problem and to establish an initial understanding of the constitutive model presented herein so as to study the interactions between ONH and scleral mechanics. Moreover, this type of geometry fits well with the work we conducted in Part-II, where the scleral shells were clamped and the ONH was centered with respect to the scleral field of view (at the apex of the pressurized scleral shell). Because the physiologic shape of the posterior globe and the location of the scleral canal relative to its center may importantly contribute to ONH and scleral mechanics, future models will take these features into consideration.

Modeling and mechanical testing of ocular soft tissues will contribute to our understanding of ONH and peripapillary scleral damage in glaucoma, myopia, and a host of other ocular disorders. The knowledge gained in this study using our proposed hyperelastic constitutive model will now be used in a second report [1] to estimate the mechanical properties of monkey posterior sclera.

Nomenclature

Notations

a, A, b, B

0^th order tensors (scalars)

a, b, c

1^st order tensors (vectors)

A, B, C

2^nd order tensors (dyadics)

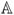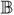, , ℂ

4^th order tensors (tetradics)

Symbols – Scalars

c₁

1^st Mooney-Rivlin coefficient

c₃

fiber stress coefficient

c₄

fiber uncrimping rate coefficient

I₀

modified Bessel function (1^st kind, 0^th order)

I₁, Ĩ₁

1^st invariants of C and C̃

I₄, Ĩ₄

squared fiber stretches (4^th invariants)

J

Jacobian of the deformation

k

fiber concentration factor

K

bulk modulus

p

hydrostatic pressure

P

statistical distribution function

W

strain energy function

W̃

isochoric strain energy function

W_vol

volumetric strain energy function

λ, λ̃

fiber stretches

θ_p

preferred fiber orientation

Symbols – Vectors

a₀

local fiber direction in the undeformed configuration

𝐚

local fiber direction in the deformed configuration

Symbols – 2^nd Order Tensors

B, $\tilde{\mathbf{B}}$

left Cauchy-Green deformation tensors

C, $\tilde{\mathbf{C}}$

right Cauchy-Green deformation tensors

F, $\tilde{\mathbf{F}}$

deformation gradient tensors

I

2^nd order unit tensor, I_ij = δ_ij

S

2^nd Piola-Kirchhoff stress tensor

σ

Cauchy stress tensor

Symbols – 4^th Order Tensors

𝕔

spatial elasticity tensor

ℂ

material elasticity tensor

4^th order unit tensor, _ijkl = δ_ikδ_jl

𝕡

spatial projection tensor

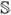
4^th order unit tensor, ${\mathbb{S}}_{ijkl}=\frac{1}{2}({\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk})$

Operators

(A·B)_ij = A_ikB_kj

2^nd order tensor

A : B = A_ijB_ij

scalar

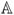( : B)_ij = _ijklB_kl

2^nd order tensor

( : )_ijkl = _ijmn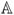mnkl

2^nd order tensor

(A ⊗ B)_ijkl = A_ijB_kl

4^th order tensor

(A⊗B)_ijkl = A_ikB_jl

4^th order tensor

${(\mathbf{A}\odot \mathbf{A})}_{ijkl}=\frac{1}{2}({\mathbf{A}}_{ik}{\mathbf{A}}_{jl}+{\mathbf{A}}_{il}{\mathbf{A}}_{jk})$

4^th order tensor

Appendix A

We will notice that the following operations hold true

$$\frac{\partial }{\partial \stackrel{\sim }{\mathbf{C}}}[\underset{{\theta }_p-\pi /2}{\overset{{\theta }_p+\pi /2}{\int }}(•)d\theta ]=\underset{{\theta }_p-\pi /2}{\overset{{\theta }_p+\pi /2}{\int }}\frac{\partial (•)}{\partial \stackrel{\sim }{\mathbf{C}}}d\theta ,$$ (26)

$$\stackrel{\sim }{\mathbf{C}}:[\underset{{\theta }_p-\pi /2}{\overset{{\theta }_p+\pi /2}{\int }}(•)d\theta ]=\underset{{\theta }_p-\pi /2}{\overset{{\theta }_p+\pi /2}{\int }}\stackrel{\sim }{\mathbf{C}}:(•)d\theta ,$$ (27)

$$\stackrel{\sim }{\mathbf{C}}\otimes [\underset{{\theta }_p-\pi /2}{\overset{{\theta }_p+\pi /2}{\int }}(•)d\theta ]=\underset{{\theta }_p-\pi /2}{\overset{{\theta }_p+\pi /2}{\int }}\stackrel{\sim }{\mathbf{C}}\otimes (•)d\theta ,$$ (28)

$$\stackrel{\sim }{\mathbf{C}}·[\underset{{\theta }_p-\pi /2}{\overset{{\theta }_p+\pi /2}{\int }}(•)d\theta ]=\underset{{\theta }_p-\pi /2}{\overset{{\theta }_p+\pi /2}{\int }}\stackrel{\sim }{\mathbf{C}}·(•)d\theta ,$$ (29)

Below is the evaluation of the terms needed for the spatial elasticity tensor

$$\frac{\partial \stackrel{\sim }{W}}{\partial \stackrel{\sim }{\mathbf{C}}}:\stackrel{\sim }{\mathbf{C}}=\stackrel{\sim }{\mathbf{F}}·\frac{\partial \stackrel{\sim }{W}}{\partial \stackrel{\sim }{\mathbf{C}}}·{\stackrel{\sim }{\mathbf{F}}}^{\mathbf{T}}:\mathbf{I}=c_1{\stackrel{\sim }{I}}_1+\underset{{\theta }_P-\pi /2}{\overset{{\theta }_P+\pi /2}{\int }}P(\theta ,k){\stackrel{\sim }{W}}_4(\theta ){\stackrel{\sim }{I}}_4(\theta )d\theta ,$$ (30)

$$\frac{{\partial }^2\stackrel{\sim }{W}}{\partial \stackrel{\sim }{\mathbf{C}}\partial \stackrel{\sim }{\mathbf{C}}}=\underset{{\theta }_p-\pi /2}{\overset{{\theta }_p+\pi /2}{\int }}P(\theta ,k){\stackrel{\sim }{W}}_{44}(\theta ){\mathbf{a}}_0(\theta )\otimes {\mathbf{a}}_0(\theta )\otimes {\mathbf{a}}_0(\theta )\otimes {\mathbf{a}}_0(\theta )d\theta ,$$ (31)

$$\stackrel{\sim }{\mathbf{F}}·(\frac{{\partial }^2\stackrel{\sim }{W}}{\partial \stackrel{\sim }{\mathbf{C}}\partial \stackrel{\sim }{\mathbf{C}}}:\stackrel{\sim }{\mathbf{C}})·{\stackrel{\sim }{\mathbf{F}}}^{\mathbf{T}}=\underset{{\theta }_p-\pi /2}{\overset{{\theta }_p+\pi /2}{\int }}P(\theta ,k){\stackrel{\sim }{W}}_{44}(\theta ){\stackrel{\sim }{I}}_4^2(\theta )\mathbf{a}(\theta )\otimes \mathbf{a}(\theta )d\theta ,$$ (32)

$$\stackrel{\sim }{\mathbf{C}}:\frac{{\partial }^2\stackrel{\sim }{W}}{\partial \stackrel{\sim }{\mathbf{C}}\partial \stackrel{\sim }{\mathbf{C}}}:\stackrel{\sim }{\mathbf{C}}=\underset{{\theta }_p-\pi /2}{\overset{{\theta }_p+\pi /2}{\int }}P(\theta ,k){\stackrel{\sim }{W}}_{44}(\theta ){\stackrel{\sim }{I}}_4^2(\theta )d\theta ,$$ (33)

$$(\stackrel{\sim }{\mathbf{F}}\underset{-}{\otimes }\stackrel{\sim }{\mathbf{F}}):\frac{{\partial }^2\stackrel{\sim }{W}}{\partial \stackrel{\sim }{\mathbf{C}}\partial \stackrel{\sim }{\mathbf{C}}}:({\stackrel{\sim }{\mathbf{F}}}^{\mathbf{T}}\underset{-}{\otimes }{\stackrel{\sim }{\mathbf{F}}}^{\mathbf{T}})=\underset{{\theta }_p-\pi /2}{\overset{{\theta }_p+\pi /2}{\int }}P(\theta ,k){\stackrel{\sim }{I}}_4^2{\stackrel{\sim }{W}}_{44}(\theta )\mathbf{a}(\theta )\otimes \mathbf{a}(\theta )\otimes \mathbf{a}(\theta )\otimes \mathbf{a}(\theta )d\theta ,$$ (34)

where W̃₄₄ is defined as

$${\stackrel{\sim }{W}}_{44}(\theta )=\frac{{\partial }^2{\stackrel{\sim }{W}}_{\mathit{\text{fiber}}}\circ {\stackrel{\sim }{I}}_4(\theta )}{\partial {\stackrel{\sim }{I}}_4(\theta )\partial {\stackrel{\sim }{I}}_4(\theta )}=\frac{1}{4{\stackrel{\sim }{\lambda }}^3(\theta )}\left[{\mathrm{e}}^{c_4(\stackrel{\sim }{\lambda }(\theta )-1)}\right(c_3{c}_4-\frac{c_3}{\stackrel{\sim }{\lambda }(\theta )}-1)+\frac{c_3}{\stackrel{\sim }{\lambda }(\theta )}+1].$$ (35)