Cortical thickness estimation in longitudinal stroke studies: A comparison of 3 measurement methods

Abstract

There is considerable controversy about the causes of cognitive decline after stroke, with evidence for both the absence and coexistence of Alzheimer pathology. A reduction in cortical thickness has been shown to be an important biomarker for the progression of many neurodegenerative diseases, including Alzheimer's disease (AD). However, brain volume changes following stroke are not well described. Cortical thickness estimation presents an ideal way to detect regional and global post-stroke brain atrophy. In this study, we imaged a group of patients in the first month after stroke and at 3 months. We compared three methods of estimating cortical thickness on unmasked images: one surface-based (FreeSurfer) and two voxel-based methods (a Laplacian method and a registration method, DiRecT). We used three benchmarks for our analyses: accuracy of segmentation (especially peri-lesional performance), reproducibility, and biological validity. We found important differences between these methods in cortical thickness values and performance in high curvature areas and peri-lesional regions, but similar reproducibility metrics. FreeSurfer had less reliance on manual boundary correction than the other two methods, while reproducibility was highest in the Laplacian method. A discussion of the caveats for each method and recommendations for use in a stroke population is included. We conclude that both surface- and voxel-based methods are valid for estimating cortical thickness in stroke populations.

1. Introduction

Cortical thickness is a key biomarker in the diagnosis and prognostication of neurodegenerative disease, used extensively in diseases such as Alzheimer's disease (AD) and the frontotemporal dementias (FTD) (Boccardi et al., 2011; Duering et al., 2012; Hartikainen et al., 2012; Richards et al., 2009). Cortical thinning in critical brain regions has been shown to correlate with disease severity and progression in neurodegenerative disease. For example, reduction in gray matter volume in the hippocampi and orbitofrontal cortices is associated with conversion from mild cognitive impairment to dementia, and correlated with a subsequent diagnosis of AD (Hartikainen et al., 2012; Lerch and Evans, 2005). These methods are now being utilized after stroke, as interest in imaging correlates with post-stroke cognitive decline increases (Brodtmann et al., 2012).

Cognitive impairment is common after stroke, with at least one in three patients developing dementia (Pendlebury and Rothwell, 2009). Pathological studies have revealed that many patients with stroke may have associated AD pathology, including β-amyloid plaques and neurofibrillary tangles (Hesse et al., 2000). Cortical thickness changes have been demonstrated after stroke, both increments and decrements. We have demonstrated significant increases which may represent compensatory mechanisms, mostly in the contralesional hemisphere (Brodtmann et al., 2012). In contrast, decreases in ipsilesional hemisphere have been found with motor recovery, and cortical thinning overlying subcortical strokes has also been demonstrated (Duering et al., 2012).

1.1. The challenge of cortical thickness estimation in stroke

Few researchers have examined changes in cortical thickness over time in stroke populations. Most acute stroke trials do not include a high resolution isotropic T1 scan (An et al., 2011; Lee et al., 2010; Rohrer et al., 2009), often considered the workhorse of brain volume estimation. In addition, cortical thickness estimation in stroke patients brings a unique set of potential difficulties. By definition, all individuals with stroke will have a destructive brain lesion, sometimes large, which can distort surrounding brain structures acutely, secondary to edema, and chronically, from post-lesional involution. In contrast with the brain images of FTD and AD patients, where anatomical distortion is due to the effects of severe atrophy, infarcts in patients with stroke can severely distort the normal anatomy of the brain, causing negative volume effects via involution and atrophy.

1.2. Cortical thickness estimation methods: accuracy and reproducibility

Cortical thickness is normally regarded as a distance metric between two points located in white matter (WM) and gray matter (GM). Its measurement is a challenging task, due to highly folded anatomical layers, with the best method to perform thickness measurement the subject of debate. Moreover, the current definition of cortical thickness is method-dependent (Das et al., 2009; Fischl and Dale, 2000; Jones et al., 2000), itself problematic for researchers seeking a “gold” or criterion standard. The classification of cortical thickness measurement techniques into surface-based methods (SBMs) and voxel-based methods (VBMs) is based on different topological models. These models differ in their methods for defining corresponding points on two surfaces in order to generate the distance metric (Das et al., 2009; Fischl and Dale, 2000; Jones et al., 2000; Yezzi and Prince, 2003). Correspondingly, due to different modeling in these highly curved regions, the cortical thickness values will vary even in the same brain regions dependent on the method used.

Researchers seek methods that are both accurate and precise. Accuracy is defined as the ability of a metric to capture the correct distance between different surfaces. Accuracy of segmentation is critical in order to include in the analysis only those regions of interest to the study (i.e., GM without included WM). This becomes of paramount importance in stroke patients, as the variable contrast in perilesional regions and within the stroke site itself, can produce errors with segmentation, reducing the accuracy of the measures.

Precision is defined as the ability of a metric to provide reproducible results (Lerch and Evans, 2005). In many cortical thickness studies, precision is required in order to reflect true inter-scan change, with minimal bias from such factors as field strength, scanner type and the image atlas used (Clarkson et al., 2011; Han et al., 2006; Schnack et al., 2010). Reproducibility is critical in longitudinal studies, when researchers aim to detect the presence of real change between time points.

1.3. Surface-based methods

Surface-based methods work on the surface model (Fischl et al., 2001). In this model, cortical thickness is calculated as the average of the distance from the WM surface (white-gray interface) to the closest possible point on the pial surface (gray-CSF interface), then from that point back to the closest point on the WM surface again (Fischl and Dale, 2000; Han et al., 2006). This is visualized in Fig. 1. Thus, the precision of cortical thickness is determined by the brain tissue (WM and pial) boundaries, but will be affected by voxel resolution, scanner and workstation type (Gronenschild et al., 2012; Han et al., 2006; Lusebrink et al., 2013). To achieve an accurate approximation of boundaries, many topologic methods such as level sets were utilized to improve the triangulated mesh used to segment WM and GM (Han et al., 2001a; Lohmann et al., 2003). Further improvement in surface topology correction occurred after the WM and GM boundaries were ascertained (Han et al., 2001b), improving the accuracy of segmentation (Dale et al., 1999; Han et al., 2001b). Smoothing and constraints are the normal ways to reduce bias caused by incorrect tissue segmentation and subsequent inaccuracy of topology surface estimation. This topological mesh model makes them very time-consuming to process, and may lack the ability to describe the deep sulci and tightly folded areas (Im et al., 2006; Lohmann et al., 2003; Zeng et al., 1998). Despite these operational disadvantages, surface-based methods, especially FreeSurfer (http://surfer.nmr.mgh.harvard.edu), are popular, and their performance has been demonstrated to be robust in datasets with different field strengths, scanner upgrades and scanner types (Han et al., 2006).

Fig. 1.

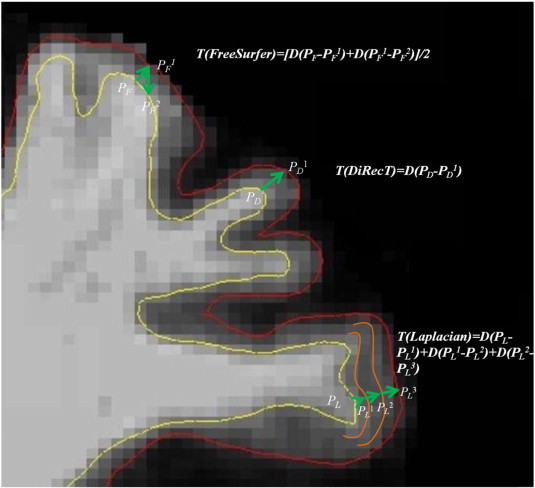
Depiction of gray and white matter boundary estimation: T: cortical thickness; D: distance between two points in following parentheses. In FreeSurfer, P_F¹ and P_F² are the nearest points of PF and P_F¹ in the opposite boundary separately; in DiRecT, P_D and P_D¹ in different boundaries are uniquely corresponded; in Laplacian, P_L¹, P_L² and P_L³, located in streamlines are the nearest points of P_L, P_L¹ and P_L² separately.

1.4. Voxel-based methods

Compared with SBMs, VBMs are more efficient, as they are designed to work directly on the voxel, making a topological mesh model no longer essential (Acosta et al., 2009; Aganj et al., 2009; Das et al., 2009; Hutton et al., 2008; Jones et al., 2000; Yezzi and Prince, 2003). Unlike the cortical thickness definition in SBMs, which may result in finding different corresponding surface points, VBMs require that each voxel in the WM boundary can find unique corresponding points in the opposite boundary (see Fig. 1). Therefore, cortical thickness can be simply and arbitrarily defined as the closest distance from the pial surface to the boundary of WM and GM (Jones et al., 2000). However, VBMs are easily affected by voxel resolution, signal-to-noise ratios and partial volume effects, leading to reduced performance in measuring thickness in highly convoluted areas (Bourgeat et al., 2008; Jones et al., 2000; Yezzi and Prince, 2003). Two VBMs were employed in the current project for comparison: a Laplacian method (Jones et al., 2000) and a registration method, DiRecT (Das et al., 2009). The Laplacian thickness estimation method, one of the classical VBMs, separates areas by a Laplacian scalar field, summing the distance from the neighboring voxel on the same streamlines as cortical thickness, or using a partial differential equation (Acosta et al., 2009; Jones et al., 2000) (see Fig. 1). The DiRecT method was derived from Advanced Normalizing Tools (http://www.picsl.upenn.edu/ANTS/) developed by Das et al. (2009). To minimize errors when measuring the cortical thickness in buried cortex and sulci, a diffeomorphic registration algorithm is used to warp the WM segmentation to match the GM plus WM segmentation in DiRecT methods (Das et al., 2009). The cortical thickness is then calculated as the distance that the WM/GM boundaries moved during the registration.

1.5. Which method should be used in a stroke population?

Infarcts, especially subcortical lesions in stroke patients, represent a challenge to cortical thickness measurement. In FreeSurfer, the accuracy of cortical thickness is based on the performance and consistency of segmentation and deformation, especially in areas of high curvature. While errors in topological correction may lead to inaccurate segmentation and thus to imprecise results, these results are at least consistent (Clarkson et al., 2011). In contrast, any error in tissue classification in the VBM may lead to errors in corresponding points and thus inaccuracies in cortical thickness measures.

Currently there is no perfect method for tissue segmentation and boundary determination in stroke populations (Wardlaw et al., 2013), although recent standards for research in small vessel disease have been proposed. We posit that researchers using automated methods in longitudinal stroke studies would want to know whether and how the stroke lesion was segmented, and how that segmentation affected the perilesional tissue classification; whether the measures were accurate and stable; whether real change could be detected, and whether the cortical thickness measures were biologically plausible. In order to measure cortical thickness in a stroke population, we propose that an estimation method needs to satisfy three important criteria:

• 1Accurate segmentation in the region of infarction, excluding infarcted tissue but including peri-infarct WM and GM for calculation;
• 2Accurate and reproducible estimation of cortical thickness over time in order to assess “real” interval change;
• 3Cortical thickness estimates consistent with those measured in cadaver studies, i.e., biological validity.

For the second criterion, we proposed that a healthy control population would display minimal change over a 3 month period. In people with no history of stroke or dementia, cortical thickness has been reported to be on average 2.5 mm, ranging from 1–5 mm (Fischl and Dale, 2000; Han et al., 2001a). We postulated that cortical thickness values should be close to the average values measured at autopsy (i.e., approximately 2.5 mm) as our measure of biological validity. In healthy populations, the rate of cortical thinning is approximately 2% per decade (Lemaitre et al., 2012). Therefore we would expect very small reductions in cortical thickness over a period of 3 months. On this basis, the minimal change in cortical thickness, as estimated by FreeSurfer, across time, appears more likely to reflect real variance compared to the slight decreases estimated by the two VBM methods.

We are interested in automated cortical thickness estimation techniques that can be applied to large patient groups and their performance of providing reasonable thickness values. In the current study, we sought to compare three methods for the estimation of cortical thickness in a group of stroke patients compared with age-matched controls. Participants were scanned on two occasions, 3 months apart, in order to demonstrate possible inter-scan change (stroke patients) and reproducibility (controls). Based on prior published used and typicality (Acosta et al., 2009; Clarkson et al., 2011; Das et al., 2009; Fischl and Dale, 2000; Hutton et al., 2008; Jones et al., 2000; Lohmann et al., 2003), we selected one SBM (Fischl and Dale, 2000) and two VBMs (Das et al., 2009; Jones et al., 2000), which are commonly available, fully automated and widely used methods for estimating cortical thickness for comparison. The FreeSurfer method is one of the most widely used surface-based techniques for estimating cortical thickness (Sterr et al., 2013). Laplacian and DiRecT methods (Clarkson et al., 2011) were chosen because they are also the most commonly used VBMs, and have been demonstrated to be robust in patient population. Recently, some cortical thickness measurement methods have been developed based on these chosen methods aiming to remove particle volume effects and improve thickness measurement in gyri and sulci (Acosta et al., 2009; Bourgeat et al., 2008). In this study, we performed two analyses, one with standard defaults and one with corrections of the tissue boundary maps. We did not perform masking of the stroke lesion as we were interested in the performance of the automated methods in these regions. We did not perform white matter lesion volume estimation in this study, but it is important to acknowledge that the majority of stroke patients have white matter lesions, and this will be the subject of further analyses in this dataset.

In a frontotemporal dementia patient population, Clarkson et al. compared these methods and found that all three afforded reasonable longitudinal comparisons (Clarkson et al., 2011). They demonstrated that FreeSurfer was the most sensitive method in detecting the hypothesized differences in cortical thickness between the dementia and control groups. We hypothesized that a surface-based method would perform best against our proposed criteria.

2. Materials and methods

2.1. Participants

The study was approved by the local human research ethics committee. Patients presenting with ischemic stroke to the Stroke Unit at Austin Health were offered participation in this study. Participants were included if they had a clinical diagnosis of acute ischemic stroke which was confirmed on subsequent imaging (computed tomography or magnetic resonance imaging). Patients were not included if there was a diagnosis of Transient Ischemic Attack (TIA) or if the diagnosis after clinical work-up was not found to be consistent with ischemic stroke. Healthy control participants were included if they were aged 60–90 years and had no prior neurological disease. Controls were recruited from a variety of sources, including advertisements in the local community, a database of people who had been in research studies previously and family members of participating stroke patients. Participants were scanned within 4 weeks of their stroke (baseline) and scanning was repeated at 3 months post-stroke. The baseline and 3 month scans were compared with a group of control participants. These independently acquired images were also taken 3 months apart on the same MRI scanner. All participants gave written informed consent, and had no evidence of prior neurodegenerative disease or cognitive decline. This was established on interview with the participant, their next of kin and their primary care practitioner, and substantiated with cognitive testing. As all patients suffered an ischemic infarct, we use the terms stroke and infarction interchangeably in this manuscript.

Sixteen stroke patients (13 male), 10 healthy control participants (5 male) were included (see Table 1). The mean age of patients was 68.6 years (SD = 10.0) and the mean age of control participants was 67.8 years (SD = 5.5). Time difference between stroke and baseline scan in patient group was 20.24 (SD = 8) days. There was no significant difference in age between patients and controls. Among the 16 stroke patients, 10 had left hemisphere infarction, 5 of these being posterior cerebral artery strokes affecting occipital cortex including calcarine and pericalcarine regions. Overall, 6 patients had cortical infarcts, 9 had subcortical infarcts, and one had cerebellar infarction.

Table 1.

Demographic and clinical characteristics of the stroke group. Note: M = mean; SD = standard deviation; NIHSS = National Institute of Health Stroke Scale; MRS = Modified Rankin Scale.

Background characteristics
Age in years, M ± SD	66.94 ± 8.55
Gender, male:female	13:3
Education in years, M ± SD	15.47 ± 4.07
Relationship status, married:other	12:4
Previous stroke, yes:no	11:5
Stroke admission information
Days elapsed between admission and baseline scan, M ± SD	20.19 ± 7.99
NIHSS score, M ± SD	2.88 ± 2.6
MRS score, M ± SD	1.25 ± 0.93
Side of stroke, left:right	9:7
Etiology of ischemic stroke, no. (%)
Cardioembolic	4 (25)
Large artery disease	1 (6.3)
Lacunar	2 (12.5)
Other — known	2 (12.5)
Other — unknown	7 (43.8)
Vascular territory involved, no. (%)
Total Anterior Circulation Infarcts (TACI)	0 (0)
Partial Anterior Circulation Infarcts (PACI)	7 (43.75)
Lacunar Infarcts (LACI)	2 (12.5)
Posterior Circulation Infarcts (POCI)	7 (43.75)

2.2. Imaging

Whole brain images were acquired on a 3 T Siemens TIM Trio Scanner at Melbourne Brain Centre, Austin Campus of the Florey Institute of Neuroscience and Mental Health. In both population groups, the MR images were obtained using the same T1-weighted 3D MPRAGE sequence with identical parameters: coronal slices with TR/TE = 1900 ms/2.6 ms, TI = 900 ms, flip angle = 9°, slice thickness = 1.0 mm, matrix size = 256 × 256, number of slices = 160 and voxel size = 1 × 1 × 1 mm³. Isotropic FLAIR and T2 images, as well as DWI images were acquired in the same imaging session, but are not included in the analyses presented in this paper.

2.3. Cortical thickness estimation methods

2.3.1. FreeSurfer

FreeSurfer Version 5.1 was used with standard defaults, including intensity normalization, registration, skull stripping, segmentation of WM, tessellation of the WM boundary, smoothing of the tessellated surface and automatic topology correction in native space (Fischl and Dale, 2000). The deformable surface algorithm was used to find the WM and the pial boundary from the tessellated surface, regarded as the starting points for measurement of thickness (see Fig. 2). The thickness value limit in FreeSurfer is 5 mm. The longitudinal stream provided by FreeSurfer was used to process images at each time points: an unbiased within-subject template space and image are created using robust, inverse consistent registration and processing steps, such as skull stripping, Talairach transforms, atlas registration as well as spherical surface maps and parcellation are then initialized with common information from the within-subject template, significantly increasing reliability and statistical power (Reuter et al., 2012).

Fig. 2.

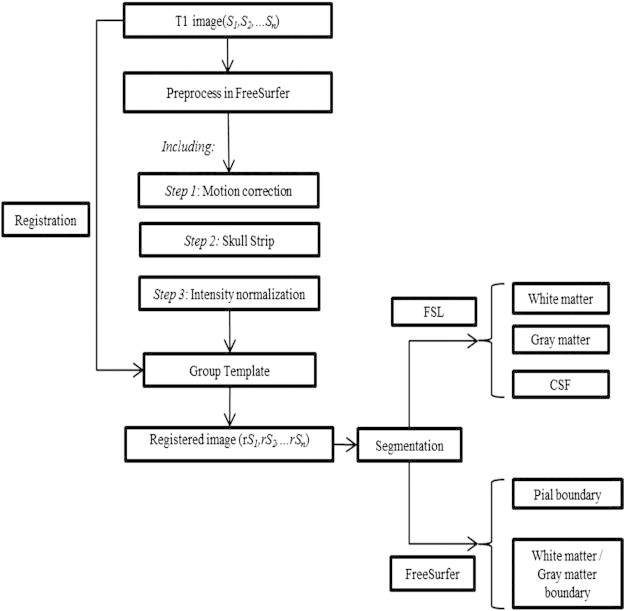
Flow-chart of analysis pipeline.

2.3.2. Laplacian method

We used a Laplacian method as presented by Jones et al. (2000). An initial probabilistic segmentation using FSL software was then generated (Jenkinson et al., 2012) (see Fig. 2). Cortical thickness was measured using commands from Laplacian method (supplied by ANTs) and smoothed using a Gaussian filter (3 mm). The voxel with p (GM) > 0.5 was labeled as the gray matter (p as the value of tissue probability). A prior thickness value of 6 mm was set to limit results to a reasonable range.

2.3.3. DiRecT method

The DiRecT registration based method includes an initial probabilistic segmentation of GM, WM and CSF to generate a probability map for each tissue type. Following this, a diffeomorphic registration algorithm was used to expand the WM segment to match the combined GM/WM segment or until a maximum of 6 mm displacement was reached (see Fig. 2). From the 3 probability maps, a 3-label image was formed by identifying the tissue type with the highest probability at each voxel. Finally, for each boundary voxel on the GM/WM boundary, thickness was calculated as the distance moved under the registration transformation. Then this thickness value was propagated across the GM mask. Parameters of gradient step and smoothing size were set as default at 0.5 and 1 respectively in this study. We generated average subjects as a template for each group of population at time points to reduce morphology bias (Bernal-Rusiel et al., 2012). Image processing and thickness at the group level measurements were performed on this template (Das et al., 2009).

2.4. Comparison

Cortical thickness comparison operated within a coordinate system to avoid morphological error generated by different atlases (Clarkson et al., 2011; Jones et al., 2000). Morphologically, the accuracy of boundary was also considered to influence thickness measurement. Two tests were designed to verify which method is most sensitive to boundary accuracy. In the regional analysis, the cortex was segmented into 34 regions defined by FreeSurfer parcellation labels (see Supplementary Table 3). This was to reduce the possible error introduced by different atlases and anatomical regional definition. The left and right hemispheres were analyzed separately. Hemispheres were not flipped to make them all ipsi- and contralesional, so stroke lesions remained in their native space. In order to identify which method exhibited the best reproducibility, all three methods were performed twice in the control group on the baseline and 3 month scans.

2.4.1. Non-corrected tissue probability maps: Test one

Cortical thickness was measured using Laplacian and DiRecT methods with the tissue probability map from FSL5.0.1 (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki) using default parameters without boundary correction. Segmentation was performed on T1-weighted image using parameters: bias field correction at 0.1 and smoothness using full width half maximum Gaussian filter (8 mm). FreeSurfer was performed to measure cortical thickness with default setting.

2.4.2. Manual boundary correction: Test two

Brain templates were created using FreeSurfer for both the control and patient groups (Bernal-Rusiel et al., 2012). The T1 image is processed by FreeSurfer, and intensity normalization, registration and skull stripping are performed. FreeSurfer's skull stripping method sometimes removes parts of the brain, as well as the skull, or leaves portions of the skull behind. To correct these errors, the input parameters for the skull strip method can be adjusted until a suitable result is obtained. Alternatively, the skull strip can be edited manually. The latter technique was employed in this study. If parts of the brain were missing following FreeSurfer's automatic skull strip, we visually inspected the pre-processed T1 images and added voxels to the processed image where necessary. All images were visually inspected by two observers (Q.L. A.B.) to ensure that obvious errors in skull stripping and tissue segmentation had not occurred. If parts of the skull remained following the automatic skull strip, the corresponding voxels were manually removed following “Fixing a bad skull strip” section provided by FreeSurfer.

In VBM, the segmentation was performed using the same parameters defined in Test one after registration with a brain template. Cortical thickness was measured using the same methods as in Test one.

2.5. Statistical analysis

Descriptive statistics were used to report cortical thickness measurements at each time point. Paired-sample t-tests and paired Pitman–Morgan tests were employed to analyze the difference between means and variability between Test one and Test two. Percentage change values were computed by subtracting the thickness value at baseline from the thickness value at 3 months, divided by the thickness value at baseline and multiplying by 100. Independent t-tests were used to establish whether percentage change values were significantly different between methods. Pearson's correlation coefficients were employed to assess whether the thickness estimates of each of the 3 methods were associated with each other, and also whether the percentage change values recorded by each method were associated with each other. Correlations were compared for each hemisphere and at each time point for patients and controls, and data were averaged across hemispheres for controls. Reproducibility of methods was addressed by intraclass coefficient (ICC) analysis in stroke population.

3. Results

3.1. Test one: non-corrected results in stroke patients and controls

Cortical thickness estimates and percentage change at baseline and 3 months for the 3 methods are shown in Table 2. In both stroke and control groups, the cortical thickness estimates from the Laplacian method (average 4.9 mm) were about twice those of FreeSurfer (2.5 mm), which in turn were about twice those produced by the DiRecT method (1.3 mm in stroke and 1.0 mm in control). One reason for these low values was that the DiRecT method yielded estimates of 0 mm in a substantial number of brain regions in several patients with sub-cortical stroke infarcts, including the cuneus, fusiform, peri-calcarine, corpus callosum, lingual and isthmus-cingulate. FreeSurfer demonstrated less variability (SDs 0.08–0.10 mm) than the Laplacian and DiRecT methods (SDs 0.29–0.38 mm). In terms of percentage change between baseline and 3 months, FreeSurfer and Laplacian produced estimates between 0 and −1% whereas DiRecT produced inconsistent and highly variable change values.

Table 2.

Cortical thickness estimates from the 3 methods in stroke patients (n = 16) and controls (n = 10), using non-corrected tissue probability maps (Test one). Mean and standard deviation (in mm) at baseline and 3 months and percentage change between the two time points.

		Laplacian		DiRecT		FreeSurfer
		LH	RH	LH	RH	LH	RH
Stroke	Baseline	4.87 (0.33)	4.87 (0.31)	1.23 (0.38)	1.28 (0.31)	2.46 (0.09)	2.47 (0.0.7)
	3 months	4.85 (0.34)	4.83 (0.36)	1.31 (0.29)	1.25 (0.33)	2.45 (0.08)	2.46 (0.08)
	% change	−0.49 (2.23)	−0.99 (2.38)	14.94 (38.08)	−1.14 (13.91)	−0.43 (2.01)	−0.50 (2.72)
Control	Baseline	4.91 (0.21)	4.90 (0.20)	1.02 (0.32)	0.89 (0.42)	2.47 (0.10)	2.47 (0.11)
	3 months	4.90 (0.20)	4.89 (0.19)	1.05 (0.29)	0.89 (0.30)	2.49 (0.08)	2.50 (0.08)
	% change	−0.23 (1.26)	0.21 (1.65)	3.71 (13.88)	10.23 (38.86)	0.90 (2.22)	1.35 (2.44)

LH — left hemisphere, RH — right hemisphere; value in brackets: standard deviation.

3.2. Test two—boundary corrected results

3.2.1. Stroke patients

The inclusion of manual boundary correction at the segmentation stage reduced the Laplacian estimates of cortical thickness from mean 4.9–3.5 mm (see Table 3). DiRecT estimates were much higher than in Test one: increasing from mean 1.3–4.6 mm. FreeSurfer estimates were not affected by this correction, remaining at mean 2.5 mm. To analyze changes between Test one and Test two, we did not make all possible comparisons but selected data from the left hemisphere at baseline. Paired-sample t-tests indicated that the differences were significant for Laplacian [t(15) = −31.4, p < 0.001] and DiRecT [t(15) = 27.2, p < 0.001], but not for FreeSurfer [t(15) = −1.6, p = 0.14]. No “0 mm” regions were generated in any patient with this optimization. Paired Pitman–Morgan tests showed that variability was slightly reduced from Test one to Test two for Laplacian [t(14) = −1.23, p = 0.24] and DiRecT [t(14) = −2.04, p = 0.06], but were stable for FreeSurfer [t(14) = 0.01, p = 0.99]. In Test two, the Laplacian and DiRecT methods (SDs 0.19–0.36 mm) remained more variable than FreeSurfer (SDs 0.08–0.11 mm). In terms of percentage change between baseline and 3 months, all the methods produced estimates between 0 and −1.5%. Further analyses are presented using the boundary-corrected data. Significant change was detected in both stroke patients and control (see Supplementary Table 3).

Table 3.

Cortical thickness estimates from the 3 methods in stroke patients (n = 16) and controls (n = 10), using corrected tissue probability maps (Test two). Means and standard deviations (in mm) at baseline and 3 months and percentage change between the two time points.

		Laplacian		DiRecT		FreeSurfer
		LH	RH	LH	RH	LH	RH
Stroke	Baseline	3.56 (0.28)	3.53 (0.28)	4.61 (0.23)	4.59 (0.25)	2.45 (0.09)	2.46 (0.08)
	3 months	3.51 (0.26)	3.49 (0.29)	4.58 (0.23)	4.55 (0.28)	2.44 (0.09)	2.45 (0.09)
	% change	−1.17 (3.08)	−1.23 (2.63)	−0.73 (2.30)	−0.84 (2.69)	−0.49 (2.00)	−0.57 (1.85)
Control	Baseline	3.64 (0.24)	3.60 (0.21)	4.68 (0.24)	4.67 (0.19)	2.47 (0.11)	2.47 (0.11)
	3 months	3.63 (0.22)	3.61 (0.24)	4.64 (0.24)	4.64 (0.22)	2.49 (0.08)	2.50 (0.08)
	% change	−0.27 (0.81)	0.07 (1.74)	−0.79 (1.42)	−0.74 (1.98)	0.95 (2.22)	1.42 (2.44)

LH — left hemisphere, RH — right hemisphere; value in brackets: standard deviation.

Percentage change values were calculated for each region (see Supplementary Table 7). Means and standard deviations (SDs) of cortical thickness for different brain regions generated by the three methods are presented in Supplementary Tables 1, 2, 5 and 6. Changes in thickness estimated by the Laplacian, Direct and FreeSurfer methods were greatest in the right pericalcarine, right pericalcarine and left pericalcarine (percentage values were −6.16%, −7.61% and −7.66% separately). To display method performance in peri-infarct regions, we overlaid the T1 image (one cortical stroke and one sub-cortical stroke) with cortical thickness map from three methods separately in Fig. 3.

Fig. 3.

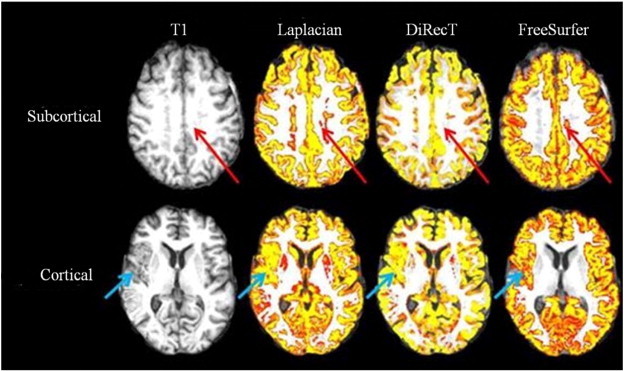
Stroke site and method performance: a simple comparison of cortical thickness (colored yellow) overlaid with T1 image (left) between Laplacian (middle left), DiRecT (middle right) and FreeSurfer (right) demonstrating maps generated from one patient with sub-cortical (top, red arrow) and one patient with a cortical stroke (bottom, green arrow). All 3 methods included the stroke lesion in the gray matter maps, but segmentation was best with FreeSurfer in cortical lesions and with DiRecT in subcortical lesions.

3.2.2. Stroke patients: correlations between methods and tests

Correlations were compared for each hemisphere and at each time point for patients. When mean cortical thickness values from FreeSurfer and DiRecT were compared, no significant correlations were identified (r < 0.31, p > 0.20 in all 4 cases). When FreeSurfer and Laplacian values were compared, again no significant correlations were identified (r < 0.42, p > 0.10 in all 4 cases). For Laplacian and DiRecT, cortical thickness values were strongly correlated at both time points in both hemispheres (r > 0.85, p < 0.001 in all 4 cases). When percentage change values were compared, there was low correlation between FreeSurfer and DiRecT, both in the left (r = 0.27, p = 0.32) and right (r = 0.06, p = 0.83) hemispheres. There was also non-significant correlation between percentage change values for FreeSurfer and Laplacian, both in the left (r = 0.36, p = 0.18) and right (r = −0.09, p = 0.74) hemispheres. There was strong correlation between DiRecT and Laplacian percentage changes (r > 0.70, p = 0.001 in both hemispheres).

3.2.3. Controls

For controls, each of the three methods produced mean cortical thickness estimates that were similar to but slightly higher than corresponding estimates in stroke patients (Laplacian 3.6 mm, DiRecT 4.7 mm, FreeSurfer 2.5 mm; see Table 3). There was less variability in Laplacian and DiRecT estimates for controls (SDs 0.19–0.24 mm) than patients, while variability in FreeSurfer was similar between controls (SDs 0.09–0.11 mm) and patients. At the group level, percentage change estimates for all three methods ranged between +1 and −1%. Laplacian estimates were the closest to 0. DiRecT estimated a slight loss in thickness (−0.8%), and FreeSurfer estimated a slight increase in thickness (+ 0.8%). In terms of reproducibility, variability in individual estimates of percentage change was lowest for Laplacian (SD = 1.0%), higher for DiRecT (SD = 1.6%) and highest for FreeSurfer (SD = 2.3%). Regional change in the DiRecT method was found in five regions in the control group: left transverse temporal, inferior parietal, isthmus cingulate and pars triangularis regions, and right posterior cingulate cortex. In the Laplacian method, changes were found in left entorhinal, insula, superior parietal and right lateral orbifrontal cortices, while regional changes were found in left bankssts and right postcentral in the FreeSurfer method.

3.2.4. Controls: correlations between methods

For these analyses, data for controls were averaged across hemispheres. When mean cortical thickness values were compared at each time point, correlations were identified (see Table 4): the Laplacian method was strongly correlated with DiRecT at both baseline and 3 months; FreeSurfer was highly correlated with both Laplacian and DiRecT at baseline but only moderately correlated at 3 months. In terms of percentage change, there was a moderate positive correlation between Laplacian and DiRecT estimates but no correlation between FreeSurfer and DiRecT or FreeSurfer and Laplacian.

Table 4.

Correlation between the 3 methods in the control group, averaged across hemisphere.

	Laplacian–DiRecT	Laplacian–FreeSurfer	DiRecT–FreeSurfer
Baseline	0.94 (p < 0.001)	0.86 (p = 0.001)	0.77 (p = 0.009)
3 months	0.96 (p < 0.001)	0.58 (p = 0.08)	0.55 (p = 0.10)
% change	0.54 (p = 0.11)	0.24 (p = 0.50)	−0.05 (p = 0.89)

3.2.5. Reproducibility

Test two was performed twice on baseline and 3 months data separately in all three methods. There was no difference between test and retest results in the two voxel based methods with a very high intraclass correlation (ICC = 0.954, p < 0.001) in the stroke group which was found in the FreeSurfer method test and retest.

4. Discussion

We compared the performance of three published, currently used cortical thickness measurement methods at two time-points in a group of stroke patients and healthy control participants. In prior studies, all three methods have been proved to be able to detect brain structure atrophy over time (Clarkson et al., 2011; Das et al., 2009; Fischl and Dale, 2000; Jones et al., 2000). Thickness values were obtained from one SBM (FreeSurfer) and two VBMs (Laplacian and DiRecT). Regional analyses were done at both an individual level and group level. To our knowledge, this is the first paper to compare these three methods in stroke patients compared with healthy controls, as well as to compare thickness changes over time. We discuss the results under each of our predetermined criteria: qualitative peri-infarct segmentation performance, cortical thickness accuracy and reproducibility, and the biological validity of the thickness values.

4.1. Peri-infarct performance: cortical versus subcortical stroke

Infarct delineation and quantification are essential steps in stroke imaging studies, but the presence of a destructive brain lesion is challenging for cortical thickness estimation methods (Wang et al., 2012). This is, in part, caused by the similarity of voxel intensity between the stroke site and the GM. In the past, researchers have relied on manual tracing of the stroke site by a trained professional (Bates et al., 2003). However, the use of automated techniques has been reported to be associated with higher inter-rater and intra-rater reliability, resulting in the development of consensus criteria by research groups for some stroke subtypes (Crinion et al., 2013).

As can be seen in Fig. 3, all three methods did not accurately segment the stroke lesion. The VBMs often included the stroke site in the GM maps. Overall, no method detected cortical thickness change in perilesional regions due to problematic tissue segmentation caused by infarction. FreeSurfer performance was best in cortical strokes, as thickness maps were not generated from the stroke site, with correct inclusion of some peri-lesional GM in appropriate regions. However, in subcortical stroke, DiRecT produced the most accurate segmentation. We concluded that in patients with cortical stroke, cortical thickness studies should be performed at a regional level, with visual inspection and manual correction of peri-infarct tissue segmentation prior to cortical thickness calculation. In patients with subcortical stroke, we found that the adoption of voxel intensity correction in DiRecT resulted in more accurate segmentation. We propose that masking of stroke lesions on an individual level is important to generate accurate measures.

4.2. Cortical thickness: accuracy of segmentation

In Test one, without GM/WM boundary correction, we found that thickness values were displayed as 0 mm in deep sulci and peri-CSF regions in both Laplacian and DiRecT methods. This resulted in the average thickness value produced by the DiRecT method (1.5 mm) to be less than the other two methods. Laplacian and DiRecT methods were found to have a very high correlation in both time points. This is understandable, given they are both VBMs. FreeSurfer correlated highly with the other two methods at baseline, but not at 3 months. There were also differences between the three methods in their performance in highly curved and convoluted regions, such as the insular and entorhinal cortices. Partial volume effects caused by the similar voxel intensity in CSF and GM were inevitable and affected all cortical thickness measurements. In the Laplacian method, the streamlines used to segment fields between GM and WM were crowded together in these regions, which resulted in an overestimation of cortical thickness. Due to the unique correspondence between points in GM and WM, the DiRecT method performed better than the other two methods — see Fig. 3. Both the Laplacian and DiRecT methods included CSF in their cortical thickness maps, while FreeSurfer produced no thickness map in CSF and peri-CSF regions. The significant difference in mean cortical thickness between tests in Laplacian and DiRecT suggests that improved segmentation will provide more accurate cortical thickness results. Moreover, the results emphasize the importance of visual inspection as a means of checking the performance of each method and ensuring that egregious errors in skull stripping and tissue segmentation have not occurred. This is particularly important in the stroke population, because infarcted regions have similar voxel intensities to CSF.

4.3. Cortical thickness: change over time

4.3.1. Controls

We hypothesized that there should be minimal change over the 3 month period in control participants. The presence of six regions with significant percent change in the DiRecT method may be in part due to partial volume effects, as most of the regions are located around CSF and high curvature areas. In the Laplacian method, the significant changes were also found in convoluted regions. The presence of significant regional change over time in highly-convoluted regions using a VBM suggests that such results should be interpreted with caution. In FreeSurfer, the reduction in left bankssts and right postcentral thickness is more than expected, highlighting the problems of using fully automated measures for peri-hippocampal regions. Volume estimates in these regions need to be validated against other “gold standard” measures such as manual tracing, consistent with results published by other researchers (Morey et al., 2009). It has also been demonstrated that FreeSurfer exhibits a systematic overestimate of hippocampal volume (Cherbuin et al., 2009), making its use valid in longitudinal studies if absolute hippocampal volume is not critical.

In controls, all three methods estimated between −1% and 1% change between the two time-points. This is within thinning rates of approximately 2% per decade that have been reported in previous studies (Clarkson et al., 2011; Lemaitre et al., 2012; Salat et al., 2004). Thus, we would expect around 0.05% over the 3 month period between scans. Both the Laplacian and DiRecT methods demonstrated similar longitudinal performance. Indeed, longitudinal performance with high reproducibility is reported to be one of the advantages of Laplacian techniques (Frisoni et al., 2011; Kim et al., 2005). Overall, in this comparison, the Laplacian method demonstrated the lowest variability over time.

4.3.2. Stroke

In the boundary-corrected test in patients, average cortical thickness declined in all three methods, with the most change in the Laplacian method and the least in FreeSurfer. VBMs calculated greater regional change in cortical thickness than FreeSurfer, with greater variability. It has been reported that VBMs are more affected by morphological factors and bias from image processing stages than SBMs (Clarkson et al., 2011). Clarkson et al. found that FreeSurfer had a regional standard deviation of thickness difference significantly lower than either a Laplacian or registration based method, and concluded that FreeSurfer provided the most plausible measure of change over time. In our analyses, correction of tissue probability maps resulted in reductions of the standard deviations in the VBMs. We suggest that the adoption of this method would lead to more accurate longitudinal analyses.

4.3.3. Method correlation

Correlations between these methods differ for a number of reasons, including the current lack of an agreed definition for cortical thickness. Cortical thickness measurement models differ in their methods for defining corresponding points on two surfaces in order to generate the distance metric. Correspondingly, due to different modeling in these highly curved regions, the cortical thickness values will vary even in the same brain regions depending on the methods used.

4.4. Biological validity

In both stroke patients and healthy controls, the overall average cortical thickness measured by Laplacian (stroke: 3.5 mm; control: 3.6 mm) and DiRecT (stroke: 4.6 mm; control: 4.7 mm) was within, or close to, the range (1–4.5 mm) measured by researchers using historical measures (Brodmann and Garey, 1999; Economo, 1929). FreeSurfer cortical thickness estimates were also similar to more recent postmortem studies (stroke 2.5 mm and control 2.5 mm compared with 2.7 mm reported by Pakkenberg and Gundersen, 1997). Given the stable variability of FreeSurfer for both controls and patients, we concluded that the adoption of an SBM may give the most biologically plausible estimate of cortical thickness. The VBMs may produce a consistent overestimate in view of their segmentation process, but given the low variability of the Laplacian method, this represents an arbitrary problem, explicable as systematic error.

4.5. Limitation

There are several limitations to this study. We have a small group size, which may be important given the variety of locations of infarcts included. Laplacian and DiRecT methods were not totally independent of FreeSurfer in pre-processing. FreeSurfer was employed to perform pre-processing and provide brain tissue maps for cortical thickness estimation in Laplacian and DiRecT. However, we believe that this enabled us to detect differences between the methods due to the cortical thickness estimation process, and not to the preprocessing steps. Cortical thickness was measured in native left and right hemispheres, because for this comparison we were averaging results across hemispheres. However, our future practice is to separate hemispheres into contralesional and ipsilesional according to acute stroke infarction for stroke patients, which may be able to address more detailed differences between cortical thickness measurement methods.

5. Conclusion

All three methods performed poorly in peri-infarct regions due to limitations in current tissue segmentation methods, with FreeSurfer providing the best segmentation (and exclusion) of cortical ischemic strokes. The presence of significant regional change over time in a number of regions in control participants using VBMs suggests that such results should be interpreted with caution in highly-convoluted regions. VBMs were improved by manual boundary correction, a step that did not affect the SBM estimates. We conclude that FreeSurfer was a more robust method in the face of poorly segmented brain, but that SBM segmentation accuracy can be improved by voxel intensity correction, especially in the region of subcortical strokes. The two VBMs displayed similar regional thickness estimates between time-points, but FreeSurfer was more stable in both control and stroke populations. The smaller standard deviations in FreeSurfer measures indicated that this method may be more stable than the DiRecT method, although overall the Laplacian method had the least variability over time. We conclude that all 3 methods had acceptable test–retest reproducibility. Cortical thickness measured by FreeSurfer was found to be consistent with the ranges from post-mortem studies (Pakkenberg and Gundersen, 1997; Rabinowicz et al., 1999), with VBMs producing consistently higher results. We conclude that, with caveats and optimization of techniques, both surface- and voxel-based methods are valid for estimating cortical thickness in stroke populations.

Appendix A. Supplementary data

Supplementary material