A tortoise–hare pattern seen in adapting structured and unstructured populations suggests a rugged fitness landscape in bacteria

Significance

The “adaptive landscape” characterizes the relationship between genotype and fitness. As the landscape becomes more rugged, evolution can become more constrained. During the modern evolutionary synthesis, different views about the process of adaptation reflected different assumptions about landscape topography, which motivated the empirical assessment of adaptive landscapes in biological systems. Here, we describe how evolutionary patterns within experimental populations can yield information about landscape topography. Specifically, metapopulations of Escherichia coli are evolved under different patterns of migration. We find bacteria reach higher fitness and accumulate more mutations under restricted migration than unrestricted migration, which is consistent with a rugged topography. In this way, experimental manipulation of population structure can provide insight into fundamental evolutionary constraints.

Abstract

In the context of Wright’s adaptive landscape, genetic epistasis can yield a multipeaked or “rugged” topography. In an unstructured population, a lineage with selective access to multiple peaks is expected to fix rapidly on one, which may not be the highest peak. In a spatially structured population, on the other hand, beneficial mutations take longer to spread. This slowdown allows distant parts of the population to explore the landscape semiindependently. Such a population can simultaneously discover multiple peaks, and the genotype at the highest discovered peak is expected to dominate eventually. Thus, structured populations sacrifice initial speed of adaptation for breadth of search. As in the fable of the tortoise and the hare, the structured population (tortoise) starts relatively slow but eventually surpasses the unstructured population (hare) in average fitness. In contrast, on single-peak landscapes that lack epistasis, all uphill paths converge. Given such “smooth” topography, breadth of search is devalued and a structured population only lags behind an unstructured population in average fitness (ultimately converging). Thus, the tortoise–hare pattern is an indicator of ruggedness. After verifying these predictions in simulated populations where ruggedness is manipulable, we explore average fitness in metapopulations of Escherichia coli. Consistent with a rugged landscape topography, we find a tortoise–hare pattern. Further, we find that structured populations accumulate more mutations, suggesting that distant peaks are higher. This approach can be used to unveil landscape topography in other systems, and we discuss its application for antibiotic resistance, engineering problems, and elements of Wright’s shifting balance process.

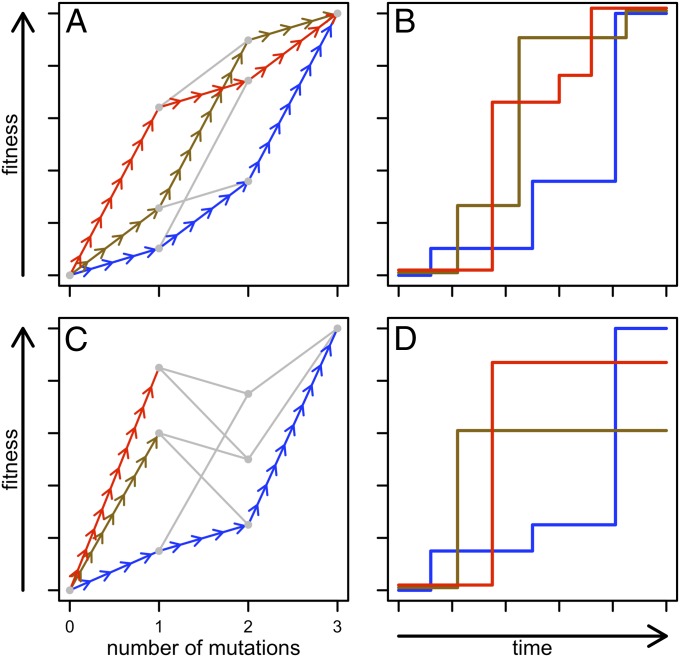
The adaptive landscape was introduced by Sewall Wright (1) to visualize potential constraints faced by evolving systems of genes. Fig. 1 shows a network representation of the landscape (2–5) in which nodes are genotypes and edges connect genotypes differing by a single substitution. This network is embedded in two dimensions, where genotypes are grouped along the abscissa by their mutational distance from a common genotype and along the ordinate by their fitness. Under assumptions of strong selection and weak mutation (2, 3), adaptive evolution of a population involves a series of steps across edges from lower to higher nodes. A genetic network without epistasis (Fig. 1A) is a “smooth landscape,” where the single peak is accessible (i.e., reachable by a series of beneficial mutations) from any other genotype. Despite different initial mutational steps, independent evolutionary trajectories converge at the peak (Fig. 1A) and fitness likewise converges (Fig. 1B). In contrast, Fig. 1C shows a network where the sign of the fitness effect of a mutation depends on the background in which it occurs. Such sign epistasis is a necessary (but not sufficient) condition for the existence of multiple peaks (6). On this “rugged landscape,” the final genotype reached under independent trajectories is contingent upon the initial mutation (Fig. 1C) and fitness can diverge if peaks are heterogeneous in height (Fig. 1D). Thus, a population can become trapped at a suboptimal peak in the presence of epistasis.

Fig. 1.

Adaptive paths in hypothetical landscapes. Here, we consider a simple biallelic three-locus system. (A) Adaptive landscape can be visualized by plotting genotype fitness as a function of the number of mutations on a WT background. Each of the 2³ = 8 genotypes is given by a gray point, and edges (arrows or gray lines) connect genotypes differing by a single mutation. An adaptive peak is a genotype from which all mutations are detrimental. A hypothetical landscape with a single peak (the triple mutant) is shown here. A selectively accessible path exists between two genotypes if a series of beneficial mutations connect the less fit genotype to the more fit genotype. On this “smooth” landscape, all of the 3! = 6 paths between the WT (lacking mutations) and the triple mutant are selectively accessible; three of these paths are shown by the arrows in different colors. (B) Average fitness over time is shown for three possible populations following the paths in A. If we assume that selection is strong and mutation is weak, we can represent the fixation of each beneficial mutation as a step up in the fitness trajectory. All trajectories converge on the same final fitness value. (C) Hypothetical landscape with multiple peaks. Starting with the WT, mutation and selection can take the population to different adaptive peaks on this “rugged” landscape, as illustrated by the different colored trajectories. (D) Average fitness over time is shown again for three possible populations following the paths in C. The final fitness of different evolving populations can vary.

Because Wright thought epistasis was pervasive (7), he was particularly concerned about confinement of populations at suboptimal peaks within rugged landscapes. He proposed the shifting balance process (SBP) to explain how populations move from lower to higher peaks. Integral to the SBP is population structure. Wright (8) envisioned a population that was distributed into semiisolated, sparsely populated demes (subpopulations) in which genetic drift enabled some demes to take downward steps by fixing deleterious mutations. In this way, a subset of the metapopulation is able to move from one peak’s domain of attraction to another, across an “adaptive valley.” The joint action of mutation and selection within this subset drives these demes to the higher peak. Migration among demes then distributes the alleles associated with the higher peak across the metapopulation (9–11). Although there have been various theoretical explorations of the plausibility of the SBP (11–16), Wright’s process has been controversial (14, 17–19), partly due to its reliance on a complex balance of multiple evolutionary processes. The tension inherent in the SBP results from the need for populations to do opposite things in the landscape; for instance, populations must both descend (off lower peaks) and ascend (to higher peaks). In the present study, because we start our population far from a peak, ascent is the sole focus. Adaptation in such a population will be largely influenced by whether this initial genotype has access to one peak (Fig. 1A) or many peaks (Fig. 1C). Therefore, it is Wright’s assumption of ruggedness, and how different kinds of populations respond to it, that is our principal concern. Here, we explore how manipulation of population structure (one major component of the SBP) creates an assay for landscape ruggedness.

Upon first glance, population structure would seem to hinder adaptation. In a population in which migration is not spatially restricted (unstructured population), a beneficial mutant that arises can rapidly fix in what is termed a “selective sweep.” On the other hand, a favored mutant arising in a population with restricted migration (structured population) advances more slowly in what might be termed a “selective creep.” This slow competitive displacement may also allow multiple semiindependent searches of the fitness landscape by geographically distant regions of the population. For a smooth landscape (e.g., Fig. 1A), this enhanced exploration is superfluous because all selectively accessible trajectories lead to the same single peak. However, on a rugged landscape, additional exploration may reveal alternate peaks. For instance, in Fig. 1C, although an unstructured population might exclusively follow one of the colored trajectories, a structured population may be able to explore them all simultaneously. Because discovered peaks may differ in height, a comparison of them enables the population to reach a better end point on average. On a rugged landscape, fitnesses in populations differing in structure emulate the classic fable of the tortoise and the hare. Specifically, the unstructured population initially adapts faster (the hare) but is overtaken by the structured population (the tortoise), which is a poor starter but a strong finisher. Importantly, on a smooth landscape, the tortoise never takes the lead and the crossing of average fitness trajectories is not predicted. Thus, when manipulations to population structure produce a tortoise–hare pattern, we have a signature of ruggedness.

There have been a handful of theoretical and empirical studies tracking adaptation in populations in which structure was manipulated experimentally. For instance, Bergman et al. (15) used an NK computational model (20–22) to track a 1D array of evolving bit strings in which dispersal distance was varied. For rugged landscapes (high K), they found a clear tortoise–hare pattern: Average fitness in populations with low dispersal started out below, but eventually overtook, average fitness in populations with high dispersal. This pattern disappeared in a smooth landscape (low K). On the empirical side, Kryazhimskiy et al. (23) showed that metapopulations of Saccharomyces cerevisiae with higher rates of migration among subpopulations evolved higher fitness over the course of their experiment. This result led the authors to conclude that the adaptive landscape was smooth. Additional studies using different approaches (e.g., tracking diversity across replicates, engineering a small sliver of the landscape) have found support for both rugged (24–27) and smooth (4, 26–30) topographies.

Here, we track average fitness of evolving metapopulations of Escherichia coli, manipulating the pattern of migration among demes. One critical difference between our experiments and some of the previous research is that we start with a poorly adapted strain, ensuring displacement from a peak (a discussion of this point is provided in SI Appendix, section 1). We also build a computational model with the NK system, tailored to our experimental regime. Not only does this model allow us to test our basic theoretical predictions but it also generates predictions about the number of mutations accumulated in evolving populations under different landscape topographies. We then test these additional predictions in our bacterial populations.

Results and Discussion

Computational System.

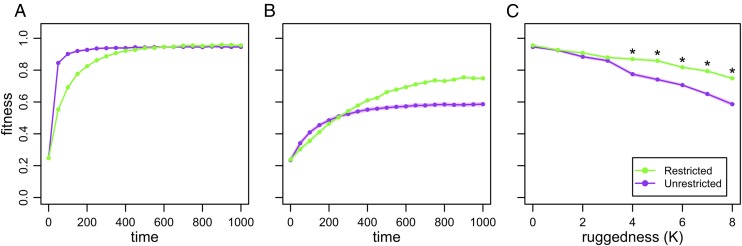
In our NK computational model, simulated organisms are bit strings of length N, and the parameter K is the number of loci affecting the fitness contribution of each locus (Methods). As K increases, the level of epistatic interaction increases, yielding more rugged landscapes (31); hereafter, we refer to K as a “ruggedness” parameter. We explore how ruggedness affects fitness trajectories in evolving metapopulations that differ in population structure. We consider either metapopulations with spatial restrictions to migration (hereafter, the Restricted treatment) or metapopulations where migration can occur between any two demes (hereafter, the Unrestricted treatment). For a smooth landscape topography (K = 0, N = 15), average fitness initially increases more rapidly in the Unrestricted treatment relative to the Restricted treatment; however, both trajectories converge over time (Fig. 2A). For a rugged landscape (K = 8, N = 15), fitness in the Restricted treatment once again lags behind fitness in the Unrestricted treatment at the outset. Instead of converging, however, the fitness trajectories cross, yielding a higher final fitness for the spatially Restricted treatment (Fig. 2B). Indeed, we find significantly higher fitness in the Restricted treatment for K > 3 at the end of our simulation (Fig. 2C; Mann–Whitney tests with Bonferroni corrections, P < 0.001). The pattern in Fig. 2B agrees with the tortoise–hare prediction, whereas the crossing does not occur in Fig. 2A. More generally, with sufficient ruggedness, a structured population can eventually outperform an unstructured population (Fig. 2C).

Fig. 2.

Fitness in the NK model. Metapopulations of bit strings of length N = 15 evolved where migration was restricted to occur between neighboring demes or migration was unrestricted (occurring between any two demes). Average fitness in the metapopulation is shown over time on a smooth landscape (A; K = 0) or a rugged landscapes (B; K = 8). (C) Average fitness at time point 1,000 is shown as a function of the ruggedness parameter, K. Note the values at K = 0 and K = 8 correspond to the values at time point 1,000 in A and B, respectively. In all plots, points represent the mean of 50 replicates, shading gives the SEM, and asterisks indicate significant differences.

There are a few ways to account for the benefit that population structure confers on rugged landscapes (Fig. 2B). First, a population may have access to multiple peaks that differ in height. A structured population can explore multiple domains in parallel, eventually comparing the results. Thus, it will tend to attain a higher end point for the same reasons that the expectation of the maximum of a sample increases with sample size. This effect holds when all peaks are equidistant from the ancestral population (results from a simple model are provided in SI Appendix, section 2). A second possibility (not mutually exclusive with the first) is that peaks differ in both height and distance from the ancestral population. Suppose that the initial mutations on accessible paths to the more distant and higher peaks are less beneficial than mutations leading to the nearby peaks. In this case, intermediate genotypes approaching distant peaks risk being outcompeted in an unstructured population (consider the first mutant on the blue path to the more distant peak in Fig. 1C competing against the other first mutants). This situation occurs because the slower fixation of these intermediates might allow for better competitors (from domains of nearer peaks) to arise. In contrast, these more distant peaks become accessible in a structured population due to reduced competitive displacement (16). If some of these distant peaks are also higher, then structured populations are predicted to achieve better fitness and to accumulate more mutations.

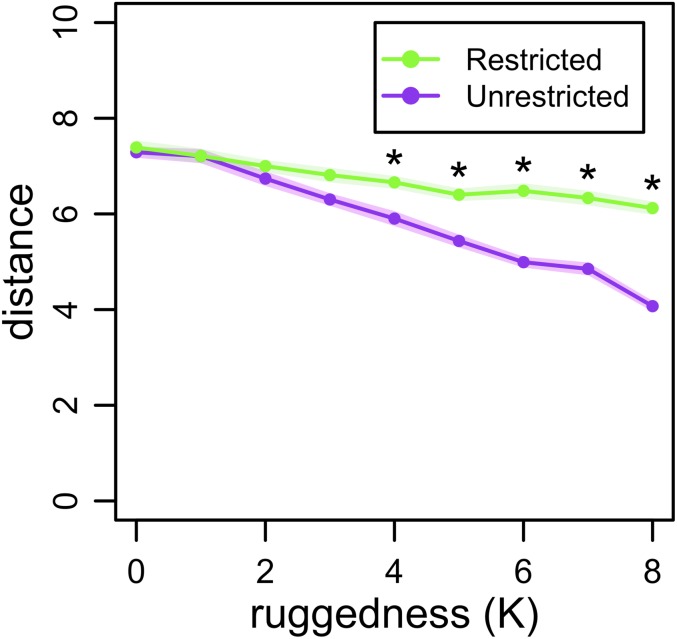
We sought to explore the number of mutations accrued by different evolving populations in the NK computational model. We define evolutionary distance to be the number of mutational differences between an evolved isolate and its ancestor. In the NK model, this evolutionary distance is the Hamming distance (32). As ruggedness increases, the degree of population structure affects final evolutionary distance from the ancestor; for example, we find a significantly higher distance in the Restricted treatment for K > 3 at the end of our simulation (Fig. 3; Mann–Whitney tests with Bonferroni corrections, P < 0.001). Thus, on a rugged landscape, a population with restricted migration moves both higher (Fig. 2C) and further (Fig. 3) than a less structured population.

Fig. 3.

Distance in the NK model. Metapopulations of bit strings of length N = 15 evolved where migration was spatially restricted or unrestricted. Evolutionary distance is the number of bits differing between an evolved isolate and its ancestor (the Hamming distance). Average distance at time point 1,000 is shown as a function of the ruggedness parameter, K. Points represent the mean of 50 replicates, shading gives the SEM, and asterisks denote significant differences.

Bacterial System.

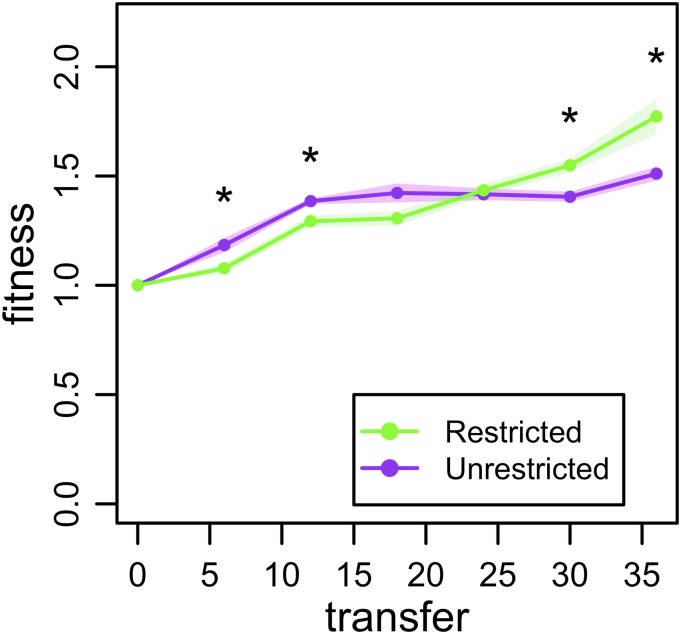
We next turned to examining fitness trajectories in evolving metapopulations of E. coli. Similar to the NK model, we propagated the bacteria under two treatments differing in migration pattern: restricted and unrestricted (Methods). Every six transfers in the evolutionary run, we determined the fitness of five isolates per metapopulation relative to the common ancestor. Early in the experiment (transfers 6 and 12), fitness in the Restricted treatment was significantly lower than in the Unrestricted treatment (Fig. 4; Mann–Whitney test, both P = 0.015). However, at the end of the experiment (transfers 30 and 36), the opposite pattern was found, with fitness in the Restricted treatment surpassing fitness in the Unrestricted treatment (Fig. 4; Mann–Whitney test, both P = 0.015). This pattern is consistent with a rugged landscape topography.

Fig. 4.

Bacterial fitness. Metapopulations of bacteria evolved where migration was spatially restricted or unrestricted. The average relative fitness of five isolates randomly sampled from the metapopulation is shown every six transfers. As in Fig. 2B, the ordering of fitnesses for the two treatments flips over time. Each point represents the mean of five replicate metapopulations, shading gives the SEM, and asterisks denote significant differences.

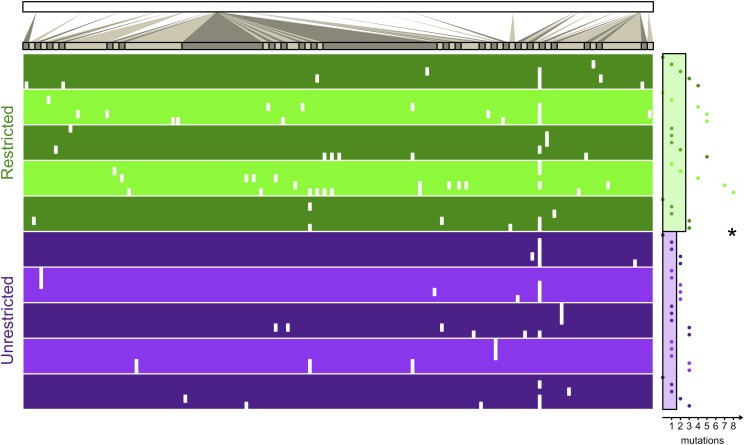
In addition to assessing fitness on the isolates from the end of the experiment (transfer 36), we sequenced their genomes to determine their evolutionary distance from the common ancestor. The locations of all identified mutations in all sequenced isolates are shown in Fig. 5 (a full list is provided in SI Appendix, Table S1). We note that all mutations in coding regions were nonsynonymous; it is thus reasonable that these changes affected phenotype in ways visible to selection. The number of mutations accumulated in each isolate is the evolutionary distance (the points to the right of the table in Fig. 5). We find that isolates have moved a significantly greater distance in the Restricted treatment (Mann–Whitney test, P = 0.045). The increased distance traversed by bacterial populations is again consistent with a rugged landscape, in which more distant peaks are being reached by structured populations.

Fig. 5.

Bacterial distance. Metapopulations of bacteria evolved where migration was spatially restricted or unrestricted. At the end of the experiment, five isolates from each metapopulation were sequenced at the genome level. The top bar represents the genome of E. coli. Genome regions with mutations are magnified for the table. Each isolate is a single row in the table, and the location of each of its mutations is indicated by a white mark (no mutation inside a coding region was synonymous). The five isolates from each of the five replicate metapopulations are grouped by alternating shades of green (for the Restricted treatment) or purple (for the Unrestricted treatment). The horizontal distance of the point to the right of the table denotes the number of mutations in the isolate (its evolutionary distance). The horizontal distance of the green bar and the purple bar to the right of the table gives the average distance (the average of replicate averages) of isolates from the Restricted and Unrestricted treatments, respectively. The asterisk denotes a significant difference between treatments. More information regarding each mutation can be found in SI Appendix.

The ability of the structured populations to move higher (in average fitness) and further (in evolutionary distance) is engendered by the capacity for parallel search. The presence of simultaneous selective creeps should increase the standing diversity within a structured population relative to an unstructured one. In line with this prediction, the metapopulations in the Restricted treatment had significantly higher genotypic diversity than the metapopulations in the Unrestricted treatment (Mann–Whitney test on the nucleotide diversity index π, P = 0.016). We note that greater diversity in structured populations is expected regardless of the topography of the landscape (SI Appendix, section 3); however, such diversity is only advantageous when the landscape is multipeaked.

Wright's SBP.

Our work also sheds light on a central theoretical debate about evolution, originating during the modern evolutionary synthesis. One view considers adaptation as the sequential fixation of beneficial mutations. This perspective (often associated with Fisher) does not highlight epistatic contingency, focusing instead on selection and mutation as the major processes of evolution (33). A second perspective (often linked to Wright) recognizes epistatic interaction as constraining adaptation. Wright developed his SBP as an account of how evolving populations could escape from the domains of suboptimal peaks in a rugged adaptive landscape. Critics of the SBP have noted that it demands a delicate balance of various evolutionary processes, constraining the range of its application (10, 12, 17). For instance, populations need be small enough for effective drift to occur but large enough for effective selection within demes (12), and migration should be sufficiently restricted for drift and selection within demes but sufficiently unrestricted for effective exchange of genotypes among demes (9, 10). However, if we set aside Wright’s goal of explaining how populations cross valleys, many of these tensions vanish (17). The populations in our experiments start in valleys, rather than facing them as obstacles (thus, evolution can be driven primarily by selection). The question that naturally follows is how, in the absence of drift, might a population come to be positioned in a valley in the first place?

Both Fisher and Wright acknowledged that environmental change could alter the landscape, and, in the process, reposition the peaks. Imagine that a population experiences such a change, and subsequently resides somewhere on the new landscape with access to multiple domains. In our experiment, our ancestor contained deleterious mutations and evolved in a stressful environment (Methods), which potentially yielded access to multiple peaks. In this case, demes need not be small for the discovery of multiple peaks (and, indeed, our experimental demes were large). With large subpopulations, selection within demes will proceed efficiently; however, limitations to migration between demes will still allow for a broader search of the landscape. If landscapes are indeed rugged, population structure can retain the critical role Wright foresaw, involving parallel search of different domains, even if all of the details of the SBP are not present.

Applications.

One case where populations are potentially poised in multiple domains on a landscape involves the evolution of microbes exposed to antibiotics. When a bacterial population experiences a sufficiently high concentration of an antibiotic, susceptible genotypes are replaced by resistant mutants. When the drug is removed, these mutants tend to carry fitness costs relative to their susceptible progenitors. The cost can be alleviated by a mutation resulting in reversion to susceptibility or a mutation that compensates for the impairment without loss of resistance (34, 35). There is some evidence that reversion and compensation constitute distinct peaks in a rugged landscape (35). Thus, we see that a changing environment (exposure and removal of a drug) may place a microbial population at a landscape position where multiple peaks are accessible (2). It is at such a position that population structure may influence the evolutionary trajectory. Björkman and Andersson (36) and Nagaev et al. (37) serially passaged Salmonella typhimurium and Staphylococcus aureus resistant to fusidic acid either in well-mixed flasks or within murids (mice or rats). These authors found that the bacteria more often reverted when grown in vivo than in vitro. They explain these results by noting that the flask and murid environments differ markedly, and may consequently place different selective pressures on revertants and compensated strains (indeed, they present data to this effect). In our terminology, the landscape in a flask and a mouse may be different. However, even if the landscape were identical (but rugged) in both, the results might not be unexpected because a murid environment is highly structured and a shaking flask is not. Thus, if the “reversion peak” is higher than most to all of the “compensation peaks” (the authors present data consistent with this ordering), then evolution in a structured environment is predicted to lead to reversion at higher frequency. In this way, the structure that pathogenic bacteria experience (including in the bodies of human hosts) can potentially influence the course of antibiotic resistance evolution (a discussion of additional pilot experiments on antibiotic resistance evolution is provided in SI Appendix, section 4).

Not only can the ideas in this paper apply in a medical context but they may also address practical engineering problems. In the field of evolutionary computation, putative solutions to computational problems constitute a population, new solutions are generated by mutation and recombination, and better solutions can outcompete their contemporaries. One defining feature of a difficult problem is the presence of multiple optima in the map from the specification of a solution (i.e., genotype) to its quality (i.e., fitness). As early as 1967, Bossert (38) suggested that dividing a population of solutions into subpopulations could yield better evolutionary outcomes. Subsequently, the inclusion of population subdivision in evolutionary algorithms has produced better solutions in a variety of applications, including analog circuit design (39), financial trading models (40), and multiobjective scheduling (41). Besides the efficiency in networked computational resources that accompanies population subdivision, a deeper exploration of the landscape of solutions is predicted to occur when multiple domains can be semiindependently searched (42, 43). The success of subdivision strategies speaks to the rugged nature of the solution landscape, because it is precisely such ruggedness that allows slow and steady adaptation to “win the race.”

Methods

Ancestral Bacterial Strain.

The bacterial ancestor was derived from a K-12 strain of E. coli (BZB1011) by selecting for resistance to colicin E2, then colicin D, and then phage T6. Resistance to both colicin E2 and phage T6 is known to be individually costly (44, 45). The initiation of the experiment with an unfit strain was intentional (SI Appendix).

Experimental Treatments.

Each metapopulation comprised 96 subpopulations (the 96 wells of a microtiter plate). The metapopulation was initiated with the ancestral strain in each well. Each subpopulation grew for 12 h in 200 μL of lysogeny broth (LB–Miller) supplemented with a subinhibitory concentration of tetracycline (0.25 μg/mL). After growth, each well in the metapopulation was diluted 40-fold into fresh growth medium using a 96–slot-pin multiblot replicator (5 μL into 200 μL). Immediately following dilution, migrations among wells occurred. Every well had a 1/3 probability of experiencing an immigration event from one random well in its neighborhood. In the Restricted treatment, this neighborhood included the wells directly north, east, south, or west of the focal well (using periodic boundary conditions to eliminate edge effects). In the Unrestricted treatment, the neighborhood included all wells minus the focal well. All migration events were executed by a BioRobot 8000 liquid-handling robot (Qiagen), which transferred 5 μL from the source well within the plate from the previous transfer into the destination well within the plate from the current transfer. Between transfers, plates were incubated (37 °C) and shaken (350 rpm at 1/16 inch circular orbit using a Bellco digital mini-orbital shaker). Each metapopulation was propagated for a total of 36 transfers, and each treatment contained five replicates.

Competition Assay.

We chose five random isolates every six transfers from each metapopulation (here, each evolved strain is labeled E). We marked our ancestor with resistance to phage T5 (the marked ancestor is labeled A). Before the competition, E and A were grown separately in 200 μL of growth medium for two 12-h cycles (with 40-fold dilution at transfer). After this acclimation phase, we added 5 μL of E and 5 μL of A to a well containing 200 μL of fresh growth medium. The titer of each strain was assessed, through selective plating with and without phage T5, immediately after the competition was initiated and again after 12 h. If X(t) is the titer of strain X at time t, then the fitness of the evolved strain relative to its ancestor is

$$w\left(E,A\right)=\frac{\text{log}\left(\frac{E\left(12\right)}{E\left(0\right)}\right)}{\text{log}\left(\frac{A\left(12\right)}{A\left(0\right)}\right)}.$$

In SI Appendix, section 5, we explore how well fitness relative to the ancestor predicts fitness relative to other (evolved) strains.

Whole-Genome Resequencing.

Using the same isolates from the last transfer, we performed chromosomal DNA extractions using Qiagen Mini DNA Kits. Each sample was barcoded and multiplexed to 24 samples per lane with Illumina TruSeq. Whole-genome resequencing (University of Washington High Throughput Genomics Unit) was performed with single-end, 36-bp unpaired reads on Illumina HiSeq to an average of 30-fold coverage. Illumina reads were aligned for mutational discovery by breseq 0.19 (46) against E. coli W311 (GenBank accession no. AP009048). Alignments were considered only if they covered 95% of a read. For every isolate, Sanger sequencing of several loci (fimE, marR, ompF, and stfR) was used to confirm putative mutations.

NK Model.

For the simulations, individuals were embedded within 96 demes in an 8 × 12 array. Each deme contained 1,000 organisms. Each organism’s genotype was a bit string (a vector of 0’s and 1’s) of length N = 15. The fitness of an organism was the sum of the fitness contributions of each of the 15 loci divided by the number of loci. The contribution of locus i was determined by its allelic state and the allelic states of loci {(i + 1) modulo N} through {(i + K) modulo N}. For each locus, 2^K+1 random numbers (uniformly distributed between 0 and 1) described all possible fitness contributions of that locus (given any possible combination of alleles at relevant loci). Thus, a mutation at a single locus affected the fitness contribution of the mutated locus and K other loci. Selection within a deme involved the removal of a random organism, regardless of fitness, and its replacement by the birth of an organism from the same deme chosen by a fitness-weighted lottery. Upon birth, the offspring bit string differed from its parent at a random locus with probability of 0.001 (the mutation rate). This death/birth process was iterated 1,000 times for each deme, followed by migration between demes. During each migration event, 25 individuals were chosen at random and removed from one deme (the destination), and then replaced by copies of 25 individuals chosen at random from the other deme (the source). Each deme experienced an immigration event with a 1/3 probability. Migration was either restricted or unrestricted in the same manner as in the bacterial experiment above. Each replicate run of the Unrestricted treatment was paired with a replicate of the Restricted treatment, using the same NK landscape and the same ancestor (a random bit string used to populate the entire metapopulation). In the figures, one selection-migration episode is termed an “update.”