An estimate of the number of tropical tree species

Significance

People are fascinated by the amazing diversity of tropical forests and will be surprised to learn that robust estimates of the number of tropical tree species are lacking. We show that there are at least 40,000, but possibly more than 53,000, tree species in the tropics, in contrast to only 124 across temperate Europe. Almost all tropical tree species are restricted to their respective continents, and the Indo-Pacific region appears to be as species-rich as tropical America, with each of these two regions being almost five times as rich in tree species as African tropical forests. Our study shows that most tree species are extremely rare, meaning that they may be under serious risk of extinction at current deforestation rates.

Abstract

The high species richness of tropical forests has long been recognized, yet there remains substantial uncertainty regarding the actual number of tropical tree species. Using a pantropical tree inventory database from closed canopy forests, consisting of 657,630 trees belonging to 11,371 species, we use a fitted value of Fisher’s alpha and an approximate pantropical stem total to estimate the minimum number of tropical forest tree species to fall between ∼40,000 and ∼53,000, i.e., at the high end of previous estimates. Contrary to common assumption, the Indo-Pacific region was found to be as species-rich as the Neotropics, with both regions having a minimum of ∼19,000–25,000 tree species. Continental Africa is relatively depauperate with a minimum of ∼4,500–6,000 tree species. Very few species are shared among the African, American, and the Indo-Pacific regions. We provide a methodological framework for estimating species richness in trees that may help refine species richness estimates of tree-dependent taxa.

Despite decades of biological inventories worldwide, we still do not know how many species exist and how they are distributed (1). Although global patterns of estimated vascular plant species richness and distribution have become more clear (2–5), no previous study has focused on trees as a distinct growth form. As a consequence, our estimation of the number of tree species in tropical forests still depends on untested expert opinions (6–8) rather than on an appropriate methodological framework and data set.

Given the importance of trees as key structural components of forest ecosystems, sources of timber and nontimber products, and providers of vital ecosystem services (9, 10), the lack of reliable estimates of the total number of tropical tree species represents a critical knowledge gap that has direct consequences for estimating the diversity of other tree-dependent taxa (11). A classic example is Erwin’s (6) estimate of the existence of 30 million arthropod species, which was based on observed host specificities of arthropods with individual tropical tree species combined with an estimate of the total number of tropical tree species. Global arthropod richness has subsequently been revised downward (7, 11), but current estimates still suffer from the lack of information on the number of tropical tree species.

In recent decades, the number of tree inventory plots across the tropics has grown to such an extent that species richness estimation at the continental and pantropical scale can now be addressed using standardized species lists with abundance data. Prior estimates of plant richness at such broad scales have mostly been based on analyses of incidence data obtained from herbarium collections and flora treatments (2–5). However, these methods are highly sensitive to collecting biases and ignore valuable information on species’ abundances (12). Abundance data enable extrapolation of richness from local to global scales using diversity estimators that fit the observed species rank abundance data (13–15).

Results and Discussion

We estimate the number of tropical tree species from a standardized dataset of old-growth tropical forest tree inventories, including gymno- and angiosperms with diameters at breast height (dbh) ≥10 cm. This dataset contains tree species abundance data for 207 1° grid cells (locations) originally dominated by closed-canopy forests across the tropics (Fig. 1). By calculating Fisher’s alpha (16) at the pantropical scale and combining this value with the estimated potential number of stems present within 500 km of each location, we arrive at a minimum number of tropical tree species of at least ∼40,000 and possibly more than ∼53,000 (Table 1), i.e., at the high end of current total estimates of 37,000 (7), 43,000 (8) and 50,000 (6), which are based on expert opinion.

Fig. 1.

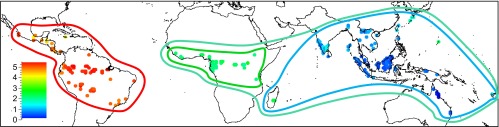
Overview of sample locations and their floristic affinities (point colors correspond to scores on the first DCA axis with similar colors indicating similar generic composition, and the lines indicate the floristic affinities as determined by cluster analysis).

Table 1.

Species richness estimates for the tropics and the three main tropical subregions

Region	Species observed	Stems observed	Unidentified stems, %	Fisher’s alpha minimum	Fisher’s alpha maximum	Stems estimated	Species minimum	Species maximum
Africa	1,376	117,902	8.4	218.7	286.6	3.4 × 1011	4,626	5,984
America	4,375	116,754	13.5	897.2	1,203.4	8.9 × 1011	18,589	24,580
Indo-Pacific	5,672	422,974	9.6	925.8	1,225.2	7.7 × 1011	19,014	24,819
Pantropical	11,371	657,630	10.1	1953.0	2,607.7	2.0 × 1012	40,517	53,345

Observed values represent the numbers in the original dataset. Unidentified stems were excluded from estimation of minimum Fisher’s alpha, but used to calculate maximum Fisher’s alpha. Estimated stems represent the number of stems predicted to occur within 500 km of each of the 207 sample locations.

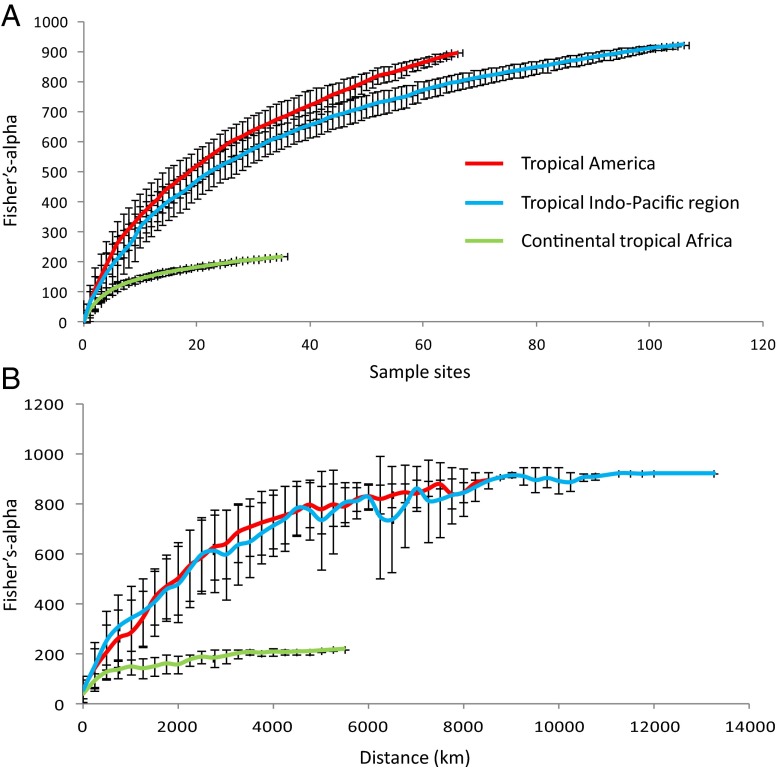
When the analysis was restricted to each of the three main tropical regions, we found that the Indo-Pacific had comparable tree species richness to that found in tropical America (Table 1). Moreover, these two regions show similar rates of species turnover for a given increase in geographical distance between locations (Fig. 2). This result contradicts the widely held view that the Neotropics are the most diverse and species-rich region for tropical trees (8, 15, 17, 18). This underestimation of Indo-Pacific tree species richness, and our inclusion of dry as well as moist and wet forests, may explain why some of the previous estimates (7, 8) are lower than ours. Nevertheless, the high species richness in the Indo-Pacific is understandable given the highly variable topography, complex geological history, steep environmental gradients, past and ongoing merging of several contrasting floras from Madagascar, India, Southeast Asia, and New Guinea–Australia (19, 20), as well as the large current and time-integrated forest area (8).

Fig. 2.

Increase in Fisher’s alpha with (A) increasing numbers of locations (average of 50 replicates per region with random input order of locations), i.e., regional diversity, and (B) increasing distance around locations (based on 50 replicates per region each with a randomly selected starting location), i.e., species turnover. Error bars indicate SD among location reorderings. Fisher’s alpha can decline if the number of stems added to the sample increases disproportionally to the number of new species detected.

Tropical continental Africa has a relatively depauperate tree flora, a finding consistent with earlier studies (21, 22). This region shows comparatively low species turnover; in other words, as sample area increases, the number of tree species increases at a much slower rate than in either the Indo-Pacific or the Neotropics (Fig. 2). The differences in species richness and spatial turnover, when comparing continental Africa with the other tropical regions, cannot be explained solely by Africa’s smaller forest area or lower environmental variability (Table 1 and Figs. S1 and S2). Rather, these disparities further support the hypothesis that African forests have experienced severe extinction events due to repeated shrinkage of forest area during the Pleistocene (19, 23). When these forests expanded to their present size, they could only be repopulated by a severely depleted species pool derived from a limited number of refugia. In contrast, tropical America retained considerable forest cover and equatorial forests of the Indo-Pacific may even have expanded during the same period (19, 20, 23, 24).

We provide, to our knowledge, the first survey-based minimum estimate of tropical tree species richness and its distribution. We acknowledge, however, that the current estimate is just a first step in an ongoing effort. Estimates of species richness will become more refined and increasingly accurate as forest surveys continue to expand. This study highlights the usefulness and critical importance of forest surveys, and we emphasize once more the existence of large numbers of tree species with exceptionally small population sizes, which may necessitate novel conservation approaches for effective preservation of current tree diversity (25, 26).

Materials and Methods

Data Set.

Tree inventory data (gymnosperms and angiosperms only; trunk dbh ≥10 cm) from old-growth forest plots without signs of recent human disturbance were compiled from across the tropics and subtropics (i.e., within 30° north and south of the equator). Individual trees from the inventories were pooled within their respective 1° grid cells (henceforth called locations). Species names were standardized using The Plant List (www.theplantlist.org), Taxonomic Name Resolution Service (tnrs.iplantcollaborative.org/TNRSapp.html), and The Asian Plant Synonym Lookup (phylodiversity.net/fslik/synonym_lookup.htm). Unknown taxa were not used in diversity and composition analyses. We removed all locations with fewer than 250 identified individuals to minimize effects of sample size, resulting in 207 retained locations (Dataset S1), each showing a reasonably high sample coverage (0.96 ± 0.3, mean ± SE) that did not differ among geographic areas (Table S1), thus suggesting that our estimations of species richness were not biased by differences in sample coverage among regions.

Phylogeographic Analyses.

To identify the main tropical regions for species richness comparison, we performed minimum variance clustering with squared Euclidean distances on square root-transformed relative abundance data at the genus level (Fig. S1). These analyses were conducted at the genus level because virtually no overlap existed between continents at the species level. We subsequently ran a detrended component analysis to visualize these floristic patterns across the tropics (Fig. 1). To assess if difference in species richness and turnover among regions are related to differences in environmental variability among regions, we performed a principal component analysis of locations vs. environmental variables [climatic data (27) and edaphic data (28)] (Fig. S2).

Sample Coverage and Nonparametric Estimators of Species Richness.

Because estimates of species richness can be strongly dependent on differences in inventory completeness (29, 30), we estimated the inventory completeness for the complete database and for each region separately using the sample coverage estimator recommended by Chao and Shen (31), which is a reduced-bias estimator of sample completeness:

$${\widehat{C}}_n=1-\frac{f_1}{n}\left[\frac{\left(n-1\right)f_1}{\left(n-1\right)f_1+2f_2}\right],$$

where f₁ and f₂ are the number of species represented by one (singletons) and two (doubletons) individuals in the sample, respectively, n is the total number of individuals in the sample, and ${\widehat{C}}_n$ is the proportion of the total number of individuals in an assemblage (observed and not observed) that belong to the species represented in the sample. Sample coverage was almost identical in all regions (Table S1), suggesting that our regional comparisons of species richness were not biased by differences in sample coverage among regions, and our pantropical estimate were not disproportionately influenced by any one region (30).

Estimates of sample coverage indicated that more than 90% of all of the trees present in the tropics belonged to species included in our recorded samples (Table S1). We also computed estimates of species richness based on several nonparametric estimators (Table S2). In particular, we considered nine of the estimators available in the software Species Prediction and Diversity Estimation (SPADE) (31), and they estimated that, on average, we have recorded between 79% and 91% of the species present in all regions (Table S2). However, consistent with ter Steege et al. (15), we found that these methods underestimated the species richness, because estimates for each tropical region (1,539–1,680 species in Africa; 4,959–5,540 in America; and 6,232–6,784 species in Asia) were between one-half and one-third of previous estimates based on expert opinion and available floras (6–8). In fact, recent estimates suggest that there are ∼16,000 tree species in the Amazon (15), so having fewer than 5,540 tree species in the whole Neotropics is highly unlikely (Table S2). As ter Steege et al. (15) argued, the failure of these nonparametric methods to yield plausible estimates arises from fact that these estimators are designed to estimate the expected number of species at a local scale, based on samples that are fully representative of the area sampled (15, 32). However, like ter Steege et al. (15), we are attempting to estimate the number of species for the whole tropics, including areas that have been poorly sampled.

Selection of Species Abundance Distribution Model to Predict Species Richness.

Several models have been proposed to describe observed species abundance distributions (SADs) within a community (33). SAD models allow for an understanding of the abundance structure of biological communities, and can be useful for predicting unsampled portions of communities. The fit of SAD models to the data depends, among other factors, on community evenness and sampling intensity (33, 34). For instance, extremely uneven SADs are predicted by the geometric series (35), whereas unusually even SADs are predicted by the broken stick model (36). The log series (16) and log normal (37) models are intermediate, differing in the assumed proportions of rare species: Fisher’s log series assumes very high proportions of rare species, whereas the log-normal model assumes very low proportions of rare species (33). Regarding sampling intensity, complete surveys usually follow log-normal types of SADs, whereas incomplete sampled communities usually deviate from log normality (34).

Here we used Fisher’s log series to estimate the expected number of species within each region. The log series distribution is one of the most frequently used and thoroughly investigated models of the relationship between species richness and the relative abundance of species (33), and it has been successfully used to estimate the number of species at different spatial scales (14, 15, 25), although not previously at an intercontinental scale. To fit and compare the log series model with other commonly used SAD models [i.e., log normal, broken stick, and Pareto (power law) distributions], we used maximum-likelihood tools with the sads package for R 3.0.3 (38). We ranked the models from the best to the worst based on Akaike’s information criterion (AIC). The set of models with a difference in AIC (Δ) <2 can be considered to have equivalently strong empirical support and similar plausibility (39).

Graphical comparison of the models showed that the log series provided the best fit to our data (Fig. S3); this result was confirmed by the AIC analyses, in which the log series model had the strongest support (Table S3). The visual analysis of the frequency of species in octaves of abundance (so-called “Preston plots”) predicted by each SAD model also supported the idea that log series fit the data well and was the best model to predict the proportion of rare species (Figs. S4–S7). Therefore, we can conclude that the log series is an appropriate SAD model to fit our data.

Application of Fisher’s Log Series.

Fisher’s alpha values can be used to extrapolate species richness of a defined region if the number of individuals is known. Extrapolations with Fisher’s alpha, however, rely on two assumptions: (i) species abundances are distributed in a log-series manner, and (ii) the plant community is homogeneous at the scale of the sampling. The first assumption held true in our case and is generally valid even for small sample sizes in tropical forests (13). The second assumption may be an adequate approximation at small spatial scales for most lowland tropical forests (15, 40) but is unquestionably violated at larger spatial scales due to increasingly biogeographically, environmentally, and spatially structured plant communities. In such cases, a large number of randomly placed sample sites are needed to capture this heterogeneity, which might adequately approximate the homogeneity assumption at a large spatial scale. Despite the large number of plots used in this study, the second assumption was not completely met at the continental scale, as shown by the incomplete leveling off of the Fisher’s alpha curves (Fig. 2A); this means that our regional Fisher’s alpha values, and thus our species richness estimates, remain minimum estimates of the true values.

Lower-Bound Estimation of Species Richness.

For each 1° grid cell located within 500 km of our 207 locations (excluding major water bodies), we calculated the total number of stems as the inverse distance-weighted average of the stem density observed in the five nearest locations, multiplied by the size of each grid cell (Fig. S8). Latitudinal change in grid cell size was taken into account. Because our analysis was focused on original (potential) tree species richness, we ignored recent deforestation. Uncertainty in this spatial extrapolation was assessed with a jackknife approach using 100 runs. Jackknifing removes each data point in turn and recomputes the spatial surface based on the remaining points. The differences between the original data values and the cross-validated values indicate the prediction accuracy of the surface model (Fig. S8).

The lower bound of species richness at the pantropical and continental scales was then calculated using Fisher’s log series, with Fisher’s alpha and total number of stems as input variables at each spatial scale. Because the total number of stems was upscaled by several orders of magnitudes, one might expect that this extreme extrapolation could potentially cause a large error in our species richness estimates. However, a simple sensitivity test, in which we varied stem numbers between 0.1 and 1.9 times the estimated values for each spatial scale (a range much larger than the observed error in our stem number predictions), showed that this extreme perturbation in stem number resulted in only a 3–11% difference in number of species predicted (Table S4).

Upper-Bound Estimation of Species Richness.

Our species richness estimates are near the true value if the unidentified species (individual recorded, but not identified) in the tree inventories, which we excluded from the analyses, follow the same rank abundance pattern as the identified species. However, if rare species are disproportionately represented in the unidentified category, our analyses may have underestimated the true Fisher’s alpha and thus the species richness estimates. Because we did not know the relative abundance of rare species in the category of unidentified individuals, we selected a dataset of multiple tree inventories with a total of 10,647 individual trees from eastern Borneo for which this information was available. All individuals in this dataset were either identified to species or only to morphospecies (unidentified). A Mann–Whitney U test showed that, not surprisingly, rare species were disproportionately represented in the unidentified category (df = 1, n = 1,103, W = 194,798, P < 0.0001).

Using logistic regression of species square root-transformed abundance vs. identification status (identified vs. unidentified), we predicted the probability that a tree species would be classified as identified. This classification probability was then assigned to each individual tree belonging to that species. After adding a random number between 0 and 1 to the classification probability of each individual tree, to account for the fact that even individuals belonging to common species may remain unidentified, we sorted the whole list of individuals from high to low. We produced 10 such sorted lists, each time varying the random number added to the classification probability of an individual tree. For each list we could then count the number of species present within any level of identified individuals and calculate a minimum Fisher’s alpha. The average of these 10 minimum Fisher’s alpha values could then be compared with the actual Fisher’s alpha observed for the whole list. Dividing the actual Fisher’s alpha by the minimum Fisher’s alpha gives an inflation factor with which observed Fisher’s alpha values can be multiplied to estimate the upper boundary of Fisher’s alpha for any percentage of identified species. The inflation factor (Y) showed a power–function relationship with ratio of identified individuals (X) given by Y = 1.2237 × X^−0.767. Using the appropriate inflation factor, we calculated the maximum expected species richness at all spatial scales (Table 1).