Estimating the global number of tropical tree species, and Fisher’s paradox

How many tropical tree species are there in the world? Slik et al. (1) address this question in an elegant way, but this question is far harder than one might initially suppose. Significant uncertainties still remain, which I attribute in large part to an unsolved conundrum that I call “Fisher’s paradox.” Except for a few charismatic groups of organisms such as birds and butterflies, ecologists still do not know the numbers of species in most taxonomically or functionally defined groups, including tropical trees. Surveying herbaria and published species descriptions cannot tell us how many tropical tree species remain undiscovered and undescribed. Experienced tropical botanists and plant biogeographers may provide expert opinions on how many tropical tree species there are, but Slik et al. note that it is difficult to assess the accuracy of such opinions. Is there some way to come up with a more reliable estimate?

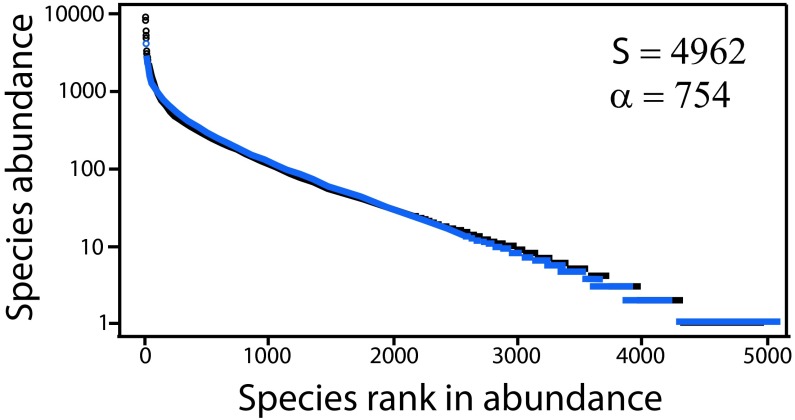
Slik et al. think so and use a method first applied to estimating tree species richness in Amazonia (2, 3). The method involves extrapolating estimates of species richness to an entire biogeographic region from tree species inventories in many sample plots scattered across the region. The accuracy of this extrapolation relies on a curious stability property of Fisher’s logseries (4), a statistical distribution widely used to describe patterns of relative species abundance in ecological communities, including tropical tree communities. The stability property has to do with the relative stability of Fisher’s $\mathit{\alpha }$, the diversity parameter of the logseries, in the face of changes in sample size. The fit of the logseries to relative tree species abundance data over large numbers of plots is often remarkably precise. Consider Fig. 1, which is a fit of the logseries to rank species abundance data for 4,962 tree species in 1,170 plots scattered across Amazonia (figure S6 in 3). On the y axis is the logarithm of species abundance, plotted against the rank in species abundance on the x axis, from the most to least abundant species, left to right.

Fig. 1.

Rank abundance curve for data on relative tree species abundance for trees >10-cm DBH in 1,170 inventory plots across Amazonia. Black: empirical data. Blue: fitted logseries distribution. Reproduced with permission from AAAS, ref. 3.

Slik et al. estimated species richness for trees having a trunk diameter of 10 cm or larger at breast height (DBH) in the three main tropical forest-containing biogeographic regions of the world: Central and South America, the tropical Indo-Pacific, and continental tropical Africa. Slik et al. computed their species richness estimates in three steps. First, they estimated the asymptotic value of Fisher’s $\mathit{\alpha }$ in each biogeographic region. Second, they estimated N, the total number of individual trees >10-cm DBH in each region. Finally, they calculated the number of species S in the region or world from the equation $S=\mathit{\alpha }\ln \left(1\mathrm{+}\mathit{N}/\mathit{\alpha }\right)$, the formula for the logseries that relates S to total number of individuals N and Fisher’s $\mathit{\alpha }$ (4). Slik et al. obtain minimum and maximum estimates for total tropical tree species richness in the world of 40,517 and 53,345, respectively, depending on uncertainties in estimating Fisher’s $\mathit{\alpha }$ and other estimation problems, such as unidentified species.

However, there are other issues with the estimation, associated with Fisher’s paradox. To explain this paradox, it is useful to unpack the steps in the estimation procedure by explaining Fisher’s logseries in a bit more detail. Ecologists commonly write the logseries as $\mathit{\varphi }\left(n\right)=\mathit{\alpha }\left(x^n/n\right)$, where $\mathit{\varphi }\left(n\right)$ is the number of species having n individuals in a sample, $\mathit{\alpha }$ is Fisher’s alpha, the diversity parameter, and x is a parameter very close to, but slightly less than, unity. Because $x\mathrm{\approx }1$, the logseries is almost a perfect hyperbolic function of n, $\mathit{\varphi }\left(n\right)\mathrm{\approx }\mathit{\alpha }/n$. From this, we draw two conclusions. First, when n = 1, we see that $\mathit{\varphi }\left(1\right)\mathrm{\approx }\mathit{\alpha }$, so Fisher’s $\mathit{\alpha }$ is the number of singleton species having a single individual in the sample. Second, we see that the singleton category is always the category with the most species, no matter how large a sample one takes because all abundance categories for n > 1 have fewer than $\mathit{\alpha }$ species by a factor 1/n.

In big samples when n can be large, the frequency of species at any given abundance n is typically small because S << N, so instead of plotting $\mathit{\varphi }\left(n\right)$ versus n, ecologists plot the logarithm of the abundance of individual species on the y axis against species rank in abundance on the x axis. Fig. 1 is an example of such a rank abundance curve. At higher ranks after the most abundant species have been plotted, log species abundance becomes very nearly linearly and negatively related to species rank in species-rich samples. As sample sizes increase, the logseries retains the same linearity and it also retains very nearly the same position on the y axis, provided that the y axis is plotted as log of fractional or percentage relative abundance instead of the log of absolute abundance. As sample sizes increase, more and more rare species are added to the sample, and the rank abundance curve extends further down and to the right to ever rarer species. It is this invariance of the slope and y-axis position of the logseries rank abundance curve as one collects larger and larger samples, that allows ecologists to extrapolate from inventory plot data to estimate how many species to expect in larger areas or entire biogeographic regions.

Now I unpack the three steps in the procedure that Slik et al. used to make their estimates. First, they needed Fisher’s $\mathit{\alpha }$ for each of the three biogeographic regions. They computed Fisher’s $\mathit{\alpha }$ from the number of individual trees and the number of identified tree species cumulated over successively pooled datasets from inventory plots in each biogeographic region. The curves in their figure 2, showing asymptotic behavior in the value of Fisher’s $\mathit{\alpha }$ with increasing number of inventory plots, inspire confidence that their estimate of Fisher’s $\mathit{\alpha }$ is converging on its limiting value for each region. Second, Slik et al. needed to know how many individual trees >10-cm DBH are in each biogeographic region. They already had tree densities in their inventory plots. On large landscape scales, tree densities are not too variable, particularly for large trees, so Slik et al. could estimate tree numbers in large biogeographic regions. The regional numbers of trees N are very large, on the order of 10¹¹ for trees >10-cm DBH, and on the order of $2\mathrm{\cdot }{10}^{12}$—two million million trees—for the world’s tropical forests combined. The third and final step, discussed above, is to plug N and $\mathit{\alpha }$ into the equation $S=\mathit{\alpha }\ln \left(1\mathrm{+}N/\mathit{\alpha }\right)$ and calculate the number of species in each biogeographic region and in the world.

However, now comes Fisher’s paradox. The logseries is an infinite series that mathematically goes on forever. But the world’s forests are finite in size. So what happens to estimates of species abundance when the entire world is your sample? Recall that Fisher’s $\mathit{\alpha }$ is the number of singleton species in a sample. Fisher’s logseries, applied to the totality of tropical forests worldwide by Slik et al., says that between $\mathit{\alpha }$= 1,953 and $\mathit{\alpha }$ = 2,608 species should be so rare that they only have a single individual in the entire world. Are these species real? These predicted singleton species are not a trivial fraction of the total number of species that Slik et al. estimate for tropical tree species richness (4.8% and 4.9%, respectively, of the minimum and maximum global number of tropical tree species). The paradox would seem to run even deeper, because Fisher’s logseries predicts that many more of the world’s tropical tree species are hyperrare. For example, using the maximum estimate for species richness from Slik et al., more than a third of the world’s tree species (19,520 species; 36.8%) should have total population sizes of less than 1,000 individuals.

In defense of Slik et al., they did nothing wrong. Our intuition that so many tropical tree species cannot be so rare may be incorrect, in which case there is no paradox to explain because this hyperrarity is real. We simply cannot answer this question at present. Existing data from inventory plots, including those analyzed by Slik et al., are fully consistent with the reality of hyperrarity. Consider, for example, tree species in the tropical forest plots of the Center for Tropical Forest Science (CTFS). Of the 8,500 species recorded in these plots, the rarest half (4,250) of all species make up just 2% of all individuals. Over 600 species (about 7%) are so rare that they occur just once as a single individual among over 6 million identified trees in the CTFS network (5). Among the 1,170 inventory plots in Amazonia analyzed by ter Steege et al. (3), there were 647 singleton species out of 639,631 trees, or 13.0% of all 4,962 species present.

The truth is, we still have inadequate data to definitively answer the “how many tropical tree species?” question. Ecologists at present are forced to make huge extrapolations from existing inventory plot data to the entire world. Even though Slik et al. observed 657,630 trees in their global sample, this is just 0.0000329% of all tropical trees in the world. This enormous data gap leaves a lot of wiggle room for unexpected things to happen beyond the geographical reach of existing inventory plots.

Because the logseries provides the engine for all of these species richness estimates, a few words explaining the theory underlying the logseries are perhaps in order. When Ronald Fisher et al. first published the logseries in 1943 (4), it was simply a generic statistical distribution that seemed to fit data on relative species abundance in large collections of butterflies and moths. Not until nearly 60 y later, with the introduction of neutral theory in ecology, did a mechanistic biological explanation for the parameters of the logseries arise (6, 7). Fisher’s $\mathit{\alpha }$, beyond the statistical phenomenology of being the number of singleton species in a sample, in neutral theory turns out to be a fundamental biodiversity number equal to the per-capita speciation rate $\mathit{\nu }$ in a self-contained biogeographic region (the “metacommunity”) times J_m, the sum of the abundances of all species in the same metacommunity. Fisher’s $\mathit{\alpha }$ is thus the product of a very small number $\mathit{\nu }$ and a very large number J_m, which helps explain the stability of the logseries in the face of sample size variation. Parameter x of the logseries turns out to be the ratio of the average per-capita birth rate b to the average per-capita death rate d in the metacommunity. Parameter x is slightly less than unity because the birth rate is slightly less than the death rate, which in turn is because all species under neutrality eventually go extinct and are replaced by newly originating species. In the theory, if we add the per-capita speciation rate $\mathit{\nu }$ to the per-capita birth rate b, and divide by d, then x would equal unity, bringing the birth–death–speciation process into mass balance. The per-capita speciation rate is a very small number, which explains why x is very close to, but less than, unity. In the logseries, x does not include $\mathit{\nu }$ because if x = 1, the logseries does not converge, and we can no longer calculate the number of species having a particular abundance. For the entire planet, the estimated per-capita speciation rate of tropical trees calculated from data in table 1 of Slik et al. is $\nu =1.3\cdot {10}^{-9}$.

So Fisher’s paradox is this: how can a model that fits data so well on tropical tree species abundances in sample plots scattered all over large biogeographic regions of tropical forest be reconciled with its predictions of hyperrarity at the global scale? Resolving Fisher’s paradox is of paramount importance to conservation and management of tropical forests (5). I personally speculate that hyperrare species do exist, but that there is a mismatch between when we recognize distinct species taxonomically and what is going on during speciation. If it were possible to trace speciation-initiating events back to individual variants, then perhaps what Fisher’s logseries is really describing is the fractal geometry of evolution, right down to the individual level. Speciation is a protracted process in which species only become detectable to taxonomists after sufficient time has passed (8). Whatever the case, the most important practical message is that we need far better data on the geographic ranges and abundances of tropical tree species to finally put the “how many species?” question to rest (9). It seems to me that our priorities are misplaced. We spend many billions of dollars to look for extraterrestrial life but far less to understand life and its distribution on our own planet.