Defining and identifying Sleeping Beauties in science

Significance

Scientific papers typically have a finite lifetime: their rate to attract citations achieves its maximum a few years after publication, and then steadily declines. Previous studies pointed out the existence of a few blatant exceptions: papers whose relevance has not been recognized for decades, but then suddenly become highly influential and cited. The Einstein, Podolsky, and Rosen “paradox” paper is an exemplar Sleeping Beauty. We study how common Sleeping Beauties are in science. We introduce a quantity that captures both the recognition intensity and the duration of the “sleeping” period, and show that Sleeping Beauties are far from exceptional. The distribution of such quantity is continuous and has power-law behavior, suggesting a common mechanism behind delayed but intense recognition at all scales.

Abstract

A Sleeping Beauty (SB) in science refers to a paper whose importance is not recognized for several years after publication. Its citation history exhibits a long hibernation period followed by a sudden spike of popularity. Previous studies suggest a relative scarcity of SBs. The reliability of this conclusion is, however, heavily dependent on identification methods based on arbitrary threshold parameters for sleeping time and number of citations, applied to small or monodisciplinary bibliographic datasets. Here we present a systematic, large-scale, and multidisciplinary analysis of the SB phenomenon in science. We introduce a parameter-free measure that quantifies the extent to which a specific paper can be considered an SB. We apply our method to 22 million scientific papers published in all disciplines of natural and social sciences over a time span longer than a century. Our results reveal that the SB phenomenon is not exceptional. There is a continuous spectrum of delayed recognition where both the hibernation period and the awakening intensity are taken into account. Although many cases of SBs can be identified by looking at monodisciplinary bibliographic data, the SB phenomenon becomes much more apparent with the analysis of multidisciplinary datasets, where we can observe many examples of papers achieving delayed yet exceptional importance in disciplines different from those where they were originally published. Our analysis emphasizes a complex feature of citation dynamics that so far has received little attention, and also provides empirical evidence against the use of short-term citation metrics in the quantification of scientific impact.

There is an increasing interest in understanding the dynamics underlying scientific production and the evolution of science (1). Seminal studies focused on scientific collaboration networks (2), evolution of disciplines (3), team science (4–7), and citation-based scientific impact (8–10). An important issue at the core of many research efforts in science of science is characterizing how papers attract citations during their lifetime. Citations can be regarded as the credit units that the scientific community attributes to its research products. As such, they are at the basis of several quantitative measures aimed at evaluating career trajectories of scholars (11) and research performance of institutions (12, 13). They are also increasingly used as evaluation criteria in very important contexts, such as hiring, promotion, and tenure, funding decisions, or department and university rankings (14, 15). Several factors can potentially affect the amount of citations accumulated by a paper over time, including its quality, timeliness, and potential to trigger further inquiries (9), the reputation of its authors (16, 17), as well as its topic and age (8).

Studies about fundamental mechanisms that drive citation dynamics started already in the 1960s, when de Solla Price introduced the cumulative advantage (CA) model to explain the emergence of power-law citation distributions (18). CA essentially provisions that the probability of a publication to attract a new citation is proportional to the number of citations it already has. The criterion, now widely referred to as preferential attachment, was recently popularized by Barabási and Albert (19), who proposed it as a general mechanism that yields heterogeneous connectivity patterns in networks describing systems in various domains (20, 21). Other processes that effectively incorporate the CA mechanism have been proposed to explain power-law citation distributions. Krapivsky and Redner, for example, considered a redirection mechanism, where new papers copy with a certain probability the citations of other papers (22).

An important effect not included in the CA mechanism is the fact that the probability of receiving citations is time dependent. In the CA model, papers continue to acquire citations independently of their age so that, on average, older papers accumulate higher number of citations (19, 22, 23). However, it has been empirically observed that the rate at which a paper accumulates citations decreases after an initial growth period (24–27). Recent studies about growing network models include the aging of nodes as a key feature (24, 27–30). More recently, Wang et al. developed a model that includes, in addition to the CA and aging, an intuitive yet fundamental ingredient: a fitness or quality parameter that accounts for the perceived novelty and importance of individual papers (9).

In this work, we focus on the citation history of papers receiving an intense but late recognition. Note that delayed recognition cannot be predicted by current models for citation dynamics. All models, regardless of the number of ingredients used, naturally lead to the so-called first-mover advantage, according to which either papers start to accumulate citations in the early stages of their lifetime or they will never be able to accumulate a significant number of citations (23). Back in the 1980s, Garfield provided examples of articles with delayed recognition and suggested to use citation data to identify them (31–34). Through a broad literature search, Glänzel et al. gave an estimate for the occurrence of delayed recognition, and highlighted a few shared features among lately recognized papers (35). The coinage of the term “Sleeping Beauty” (SB) in reference to papers with delayed recognition is due to van Raan (36). He proposed three dimensions along which delayed recognition can be measured: (i) length of sleep, i.e., the duration of the “sleeping period;” (ii) depth of sleep, i.e., the average number of citations during the sleeping period; and (iii) awake intensity, i.e., the number of citations accumulated during 4 y after the sleeping period. By combining these measures, he identified a few SB examples that occurred between 1980 and 2000. These seminal studies suffer from two main limitations: (i) the analyzed datasets are very small, especially if compared with the size of the bibliographic databases currently available; and (ii) the definition and the consequent identification of SBs are to the same extent arbitrary, and strongly depend on the rules adopted. More recently, Redner analyzed a very large dataset covering 110 y of publications in physics (37). Redner proposed a definition of revived classic (or SB) for articles satisfying the three following criteria: (i) publication date antecedent 1961; (ii) number of citations larger than 250; and (iii) ratio of the average citation age to publication age greater than 0.7. Whereas Redner was able to overcome the first limitation mentioned above, his study is still affected by an arbitrary selection choice of top SBs, justified by the principle that SBs represent exceptional events in science. In addition, Redner’s analysis has the limitation to be field specific, covering only publications and citations within the realm of physics.

Here we perform an analysis on the SB phenomenon in science. We propose a parameter-free approach to quantify how much a given paper can be considered as an SB. We call this index “beauty coefficient,” denoted as B. By measuring B for tens of millions of publications in multiple scientific disciplines over an observation window longer than a century, we show that B is characterized by a heterogeneous but continuous distribution, with no natural separation between papers with low, high, or even extreme values of B. Also, we demonstrate that the empirical distributions of B cannot be easily reconciled with obvious baseline models for citation accumulation that are based solely on CA or the reshuffling of citations. We introduce a simple method to identify the awakening time of SBs, i.e., the year when their citations burst. The results indicate that many SBs become highly influential more than 50 y after their publication, far longer than typical time windows for measuring citation impact, corroborating recent studies on understanding the use of short time windows to approximate long-term citations (38–40). We further show that the majority of papers exhibit a sudden decay of popularity after reaching the maximum number of yearly citations, independently of their B values. Our study points out that the SB phenomenon has two important multidisciplinary components. First, particular disciplines, such as physics, chemistry, and mathematics, are able to produce top SBs at higher rates than other scientific fields. Second, top SBs achieve delayed exceptional importance in disciplines different from those where they were originally published. Based on these results, we believe that our study may pave the way to the identification of the complex dynamics that trigger the awakening mechanisms, shedding light on highly cited papers that follow nontraditional popularity trajectories.

Materials and Methods

Beauty Coefficient.

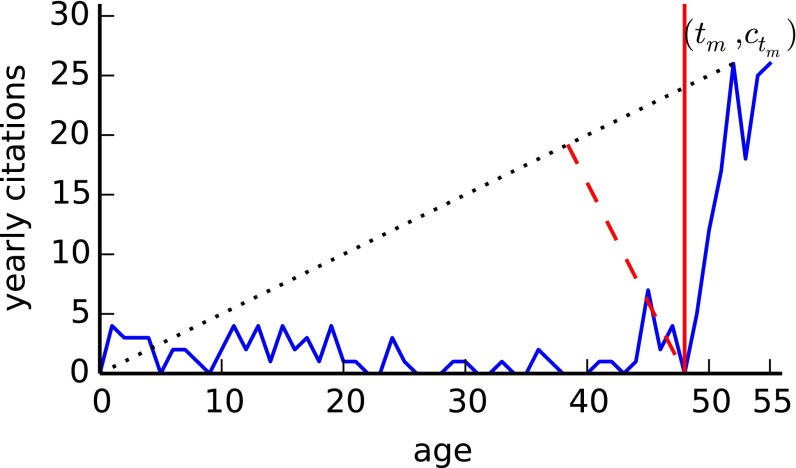
The beauty coefficient value B for a given paper is based on the comparison between its citation history and a reference line that is determined only by its publication year, the maximum number of citations received in a year (within a multiyear observation period), and the year when such maximum is achieved. Given a paper, let us define $c_t$ as the number of citations received in the tth year after its publication; t indicates the age of the paper. Let us also assume that our index B is measured at time $t=T$, and that the paper receives its maximum number $c_{t_m}$ of yearly citations at time $t_m\in \left[0,T\right]$.

Consider the straight line ${\ell }_t$ that connects the points $\left(0,c_0\right)$ and $\left(t_m,c_{t_m}\right)$ in the time–citation plane (Fig. 1). This line is described by the equation

$${\ell }_t=\frac{c_{t_m}-c_0}{t_m}\cdot t+c_0,$$ [1]

where $\left(c_{t_m}-c_0\right)/t_m$ is the slope of the line, and $c_0$ the number of citations received by the paper in the year of its publication. For each $t\le t_m$, we then compute the ratio between ${\ell }_t-c_t$ and $\text{max}\left\{1,c_t\right\}$. Summing up the ratios from $t=0$ to $t=t_m$, the beauty coefficient B is defined as

$$B={\displaystyle \sum _{t=0}^{t_m}\frac{\frac{c_{t_m}-c_0}{t_m}\cdot t+c_0-c_t}{\text{max}\left\{1,c_t\right\}}}.$$ [2]

By definition, $B=0$ for papers with $t_m=0$. Papers with citations growing linearly with time $\left(c_t={\ell }_t\right)$ have $B=0$. B is nonpositive for papers whose citation trajectory $c_t$ is a concave function of time. Our index B has a number of desirable properties: (i) B can be computed for any paper and does not rely on arbitrary thresholds on the sleeping period or the awakening intensity, paving the way to treat the SB phenomenon not as just an exception; (ii) B increases with both the length of the sleeping period and the awakening intensity; (iii) B takes into account the entire citation history in the time window $0\le t\le t_m$; and (iv) The denominator of Eq. 2 penalizes early citations so that, at parity of total citations received, the later those citations are accumulated the higher is the value of B.

Fig. 1.

Illustration of the definition of the beauty coefficient B (Eq. 2) and the awakening time $t_a$ (Eq. 3) of a paper. The blue curve represents the number of citations $c_t$ received by the paper at age t (i.e., t represents the number of years since its publication). The black dotted line connecting the points $\left(0,c_0\right)$ and $\left(t_m,c_{t_m}\right)$ is the reference line ${\ell }_t$ (Eq. 1) against which the citation history of the paper is compared. The awakening time $t_a\le t_m$ is defined as the age that maximizes the distance from $\left(t,c_t\right)$ to the line ${\ell }_t$ (Eq. 3), indicated by the red dashed line. The red vertical line marks the awakening time $t_a$ calculated according to Eq. 3. The figure refers to ref. 49.

Awakening Time.

We now give a plausible definition of awakening time—the year when the abrupt change in the accumulation of citations of SBs occurs. Being able to pinpoint the awakening time may help identify possible general trigger mechanisms behind said change. For example, in SI Appendix we show that around the awakening time, the SBs cocitation dynamics exhibit clear topical patterns (SI Appendix, Fig. S11) (37). We define the awakening time $t_a$ as the time t at which the distance $d_t$ between the point $\left(t,c_t\right)$ and the reference line ${\ell }_t$ reaches its maximum:

$$t_a=\arg \left\{\underset{t\le t_m}{\max }{d}_t\right\},$$ [3]

where $d_t$ is given by

$$d_t=\frac{\left|\left(c_{t_m}-c_0\right)t-t_m{c}_t+t_m{c}_0\right|}{\sqrt{{\left(c_{t_m}-c_0\right)}^2+t_m^2}}.$$

As we shall show, the above definition works well for limit cases where there are no citations until the spike, and seems to well capture the qualitative notion of awakening time when a strong SB-like behavior is present.

Datasets.

We use two datasets in the following empirical analysis, the American Physical Society (APS) and the Web of Science (WoS) dataset (SI Appendix, section S1). The APS journals are the major publication outlets in physics. WoS includes papers in both sciences and social sciences. We focus on the 384,649 papers in the APS and 22,379,244 papers in the WoS that received at least one citation. Those papers span more than a century, and thus allow us to investigate the SB phenomenon for a long observation period. Whereas the APS dataset can be viewed as a perfect proxy to characterize citation dynamics within the monodisciplinary research field of physics and is used to compare our analysis with a previous study (37), the WoS dataset allows us to underpin multidisciplinary features of the SB phenomenon.

Results

SBs in Physics.

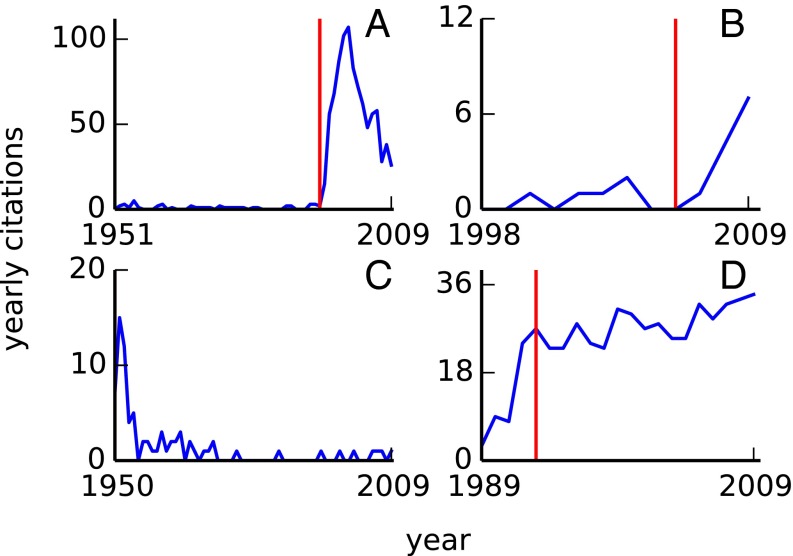
First, we qualitatively demonstrate the resolution power of B for four papers with radically different citation trajectories. Fig. 2A shows a paper with a very high B value. Published in 1951, this paper collected a small number of yearly citations until 1994, when it suddenly started to receive many citations until reaching its maximum in 2000. Fig. 2B exhibits a qualitatively similar citation trajectory for a recently published paper with a very low $c_{t_m}$ and consequently a much smaller B. The paper in Fig. 2C achieved its maximum yearly citations at $t=1$. The citation history $c_t$ therefore coincides with the reference line ${\ell }_t$ in $0\le t\le t_m$, yielding $B=0$. Note that our measure B only examines how the citation curve reaches its peak, but does not consider how it decreases after that. The paper in Fig. 2D is characterized by a negative B value, as $c_t$ is above the reference line.

Fig. 2.

Dependence of the beauty coefficient on citation history. Blue curves show yearly citations of four papers with different B values in the APS dataset: (A) ref. 50, $B=\mathrm{1,722}$; (B) ref. 51, $B=22$; (C) ref. 52, $B=0$; (D) ref. 53, $B=-5$. Red lines indicate their awakening time. The awakening year in C is 1950, i.e., $t_a=0$.

Second, we test the effectiveness of B to identify top SBs in the APS by using the 12 revived classics, previously identified by Redner, as a benchmark set (37). Our results are in excellent agreement with Redner’s analysis (37): 6 out 12 of the revived classics detected by Redner are in our top 10 list; the other 6 have also very high B values, although they occupy less important positions in the ranking according to B (SI Appendix, Table S1). Differences are due to the principles underlying the two approaches, with ours not relying on threshold parameters for the sleeping time and the number of citations. To better clarify the diversity of the two approaches, SI Appendix, Figs. S2 and S3 report the citation history of the 24 papers with highest B values in the APS dataset. We see that our measure identifies papers with a long hibernation period followed by a sudden burst in yearly citations, without the need to reach extremely high values of citations. As already pointed out by Redner (37), the list of top SBs in the APS reveals a natural grouping into a relatively small number of coarse topics, with papers belonging to the same topic exhibiting remarkably similar citation histories (SI Appendix, Fig. S11). This suggests that a “premature” topic may fail to attract community attention even when it is introduced by authors who have already established a strong scientific reputation. A corroborating evidence is provided by the famous EPR paradox paper by Einstein, Podolsky, and Rosen that is among the top SBs we found in this dataset (SI Appendix, Fig. S2B).

How Rare Are SBs?

In contrast with previous SB definitions (35–37), ours does not rely on the arbitrary choice of age or citation thresholds. This fact puts us in the unique position of investigating the SB phenomenon at the systemic level and asking fundamental questions from the macroscopic point of view: Are papers with extreme values of B exceptional occurrences? Do the majority of papers behave in a qualitatively different way from the extreme cases discussed above, when their sleeping period and bursty awakening are considered?

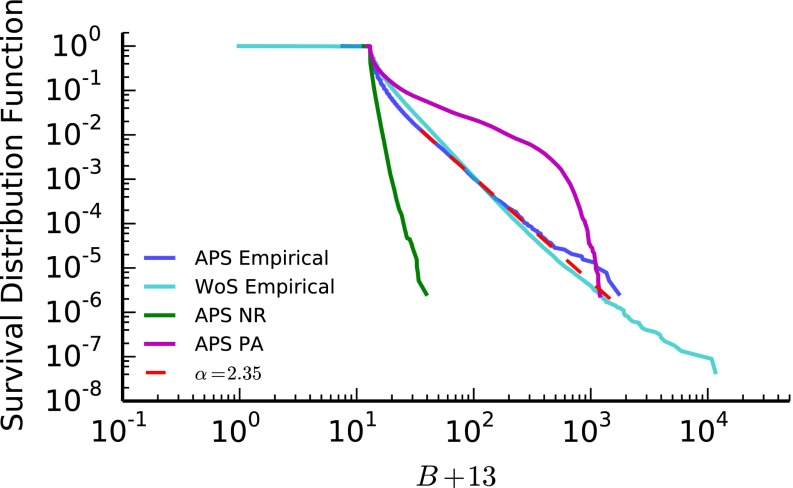
To this end, we provide a statistical description of the distribution of beauty coefficients across all papers in each of the two datasets. Fig. 3 shows the survival distribution functions of B for all papers in the APS and WoS datasets. We observe a heterogeneous but continuous distribution of B, spanning several orders of magnitude. Except for the cutoff—which is much larger for the WoS dataset—APS and WoS exhibit remarkably similar distributions. Although the vast majority of papers exhibit low values of B, there is a consistent number of papers with high B. The distributions also show no typical value or mode; there are no clear demarcation values that allow us to separate SBs from “normal” papers: delayed recognition occurs on a wide and continuous range, in sharp contrast with previous results claiming that SBs are extraordinary cases (35, 37, 41).

Fig. 3.

Survival distribution functions of beauty coefficients. On the horizontal axis, we shift the values by 13 (i.e., the minimal value of B is $-12.02$) to make all points visible in the logarithmic scale. The blue and cyan curves represent the empirical results obtained on the APS and WoS datasets, respectively. Results obtained with the NR and PA model are plotted as green and magenta lines, respectively. The red dashed line stands for the best estimate of a power-law fit of the APS curve: exponent $\alpha =2.35$ and the minimum value of the range of the fit $B_m=22.27$ are estimated using the statistical methods developed by Clauset et al. (54). In the APS and WoS, $4.68\text{\%}$ and $6.56\text{\%}$ of papers, respectively, have negative B values.

It may appear as not entirely fair to compare beauty coefficients for papers of different ages (42): Later papers have by definition less chance to develop a long sleeping period and to exhibit a sudden awakening. This may, to some extent, dictate the shapes of observed distributions. On the other hand, the vast majority of papers tend to have a single and well-defined peak in their yearly citations early during their lifetime, implying that their B values do not change with moving the observation time T far into the future. In particular, our estimations indicate that nearly $90\text{\%}$ of the papers have already experienced a drastic decrement after their maximum number of yearly citations, irrespective of their B value (SI Appendix, section S3). The shapes of the empirical distributions remain essentially unchanged if we consider only the papers that have experienced the typical sharp decline of the postmaximum yearly citation rate.

Is the SB Phenomenon Statistically Significant?

The result of the previous section implicitly suggests that the SB phenomenon could be in principle described via a simple mechanism that works essentially at all scales. This leads naturally to the question whether the observed distributions of B can be accounted for by idealized network evolution models. To address this question, we first consider a citation network randomization (NR) process where citations are randomly reshuffled, preserving time order (SI Appendix, section S4). SI Appendix, Fig. S2 compares the citation history of the top nine SBs in the APS dataset and the corresponding ones obtained through the NR process. They typically show opposite trends, with NR histories exhibiting a rapid decline. This is not surprising: As later papers are considered, the probability for an existing paper to receive a citation from one of such late papers decreases simply because there is a larger number of papers that could potentially receive the citation. This leads to typically smaller beauty coefficients, as evident in the sharp decrease of the NR distribution in Fig. 3, and the associated small maximum value $B=30$.

Next, we consider the preferential attachment (PA) mechanism as another baseline model, as it is one of the most fundamental ingredients used in most modeling efforts aimed at describing citation histories of papers. In the PA baseline, references of progressively added citing papers are reassigned according to the PA mechanism (SI Appendix, section S4). SI Appendix, Fig. S2 also shows slowly increasing yearly citations by the PA model, explained by the positive feedback effect generated via the PA mechanism. The overall number of citations according to PA baseline for the nine papers in SI Appendix, Fig. S2 remains small. Those are relatively young papers in the dataset and their probability to receive citations, according to PA, is reduced by that of older papers. The resulting distribution of B in Fig. 3 shows a much smaller range and a well-defined cutoff. It remains to be seen to what extent a recently proposed model for citation histories (9) is compatible with the SB phenomenon.

SBs in Science.

The occurrence of extreme cases of SBs is not limited to physics. Table 1 lists basic information about the 15 papers with the highest B values in the WoS dataset (see SI Appendix, Fig. S4 for their citation histories). This list contains four SBs that were published in the 1900s. Consistent with previous studies, we find that many SBs are in the field of physics and chemistry (35). Two papers are, however, in the field of statistics, which failed to be noted before as a top discipline producing SBs. One of them slept for more than one century: the paper by the influential statistician Karl Pearson, published in 1901 in the journal Philosophical Magazine, shows the relation between principal component analysis and the minimization chi distance. The other one, published in 1927 (therefore sleeping for more than 70 y), introduces the Wilson score interval, one type of confidence interval for estimating a proportion that improves over the commonly used normal approximation interval. The 3rd ($B=\mathrm{5,923}$), 12th ($B=\mathrm{2,584}$), and 15th ($B=\mathrm{2,184}$) top-ranked papers in the WoS dataset were published in Physical Review, but were not ranked as top papers in the APS dataset, suggesting that the bulk of their citations are mainly from journals not contained in the APS dataset. The EPR paradox paper (the 14th), however, is ranked at the top in both datasets.

Table 1.

Top 15 SBs in science

B	Author(s)	Title	Publication, awakening year	Journal	Field
11,600	Freundlich, H	Concerning adsorption in solutions	1906, 2002	Z Phys Chem	Chemistry
10,769	Hummers, WS	Preparation of graphitic oxide	1958, 2007	J Am Chem Soc	Chemistry
	Offeman, RE
5,923	Patterson, AL	The Scherrer formula for X-ray particle size determination	1939, 2004	Phys Rev	Physics
5,168	Cassie, ABD	Wettability of porous surfaces	1944, 2002	Trans Faraday Soc	Chemistry
	Baxter, S
4,273	Turkevich, J	A study of the nucleation and growth processes in the synthesis of colloidal gold	1951, 1997	Discuss Faraday Soc	Chemistry
	Stevenson, PC
	Hillier, J
3,978	Pearson, K	On lines and planes of closest fit to systems of points in space	1901, 2002	Philos Mag	Statistics
3,892	Stoney, GG	The tension of metallic films deposited by electrolysis	1909, 1989	Proc R Soc Lond A	Physics
3,560	Pickering, SU	CXCVI.–Emulsions	1907, 1998	J Chem Soc, Trans	Chemistry
2,962	Wenzel, RN	Resistance of solid surfaces to wetting by water	1936, 2003	Ind Eng Chem	Chemistry
2,736	Wilson, EB	Probable inference, the law of succession, and statistical inference	1927, 1999	J Am Statist Assoc	Statistics
2,671	Langmuir, I	The constitution and fundamental properties of solids and liquids. Part I. Solids	1916, 2003	J Am Chem Soc	Chemistry
2,584	Moller, C;	Note on an approximation treatment for many-electron systems	1934, 1982	Phys Rev	Physics
	Plesset, MS
2,573	Pugh, SF	Relations between the elastic moduli and the plastic properties of polycrystalline pure metals	1954, 2005	Philos Mag	Metallurgy
2,258	Einstein, A	Can quantum-mechanical description of physical reality be considered complete?	1935, 1994	Phys Rev	Physics
	Podolsky, B
	Rosen, N
2,184	Washburn, EW	The dynamics of capillary flow	1921, 1995	Phys Rev	Physics

From left to right, we report for each paper its beauty coefficient B, author(s) and title, publication and awakening year, publication journal, and scientific domain. See SI Appendix, Fig. S4 for detailed citation histories of these papers.

SI Appendix, Tables S2 and S3 list basic information about the top 10 SB papers in statistics and mathematics, respectively. Publications introducing many important techniques, like Fisher’s exact test, Metropolis–Hastings algorithm, and Kendall rank correlation coefficient, have high beauty coefficients. We also find numerous examples of SBs in the social sciences (SI Appendix, Table S4), in contrast with previous results about their alleged absence (35).

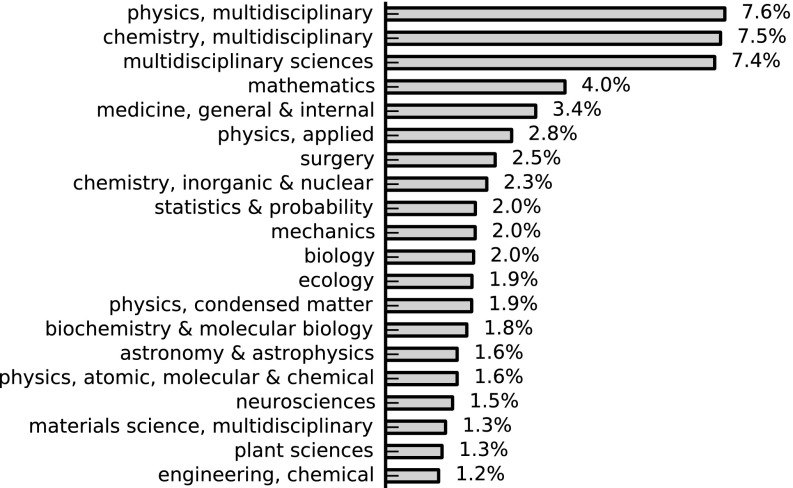
How are SBs distributed among different (sub)disciplines? To further investigate the multidisciplinary character of the SB phenomenon, we took advantage of journal classifications provided by Journal Citation Reports (JCR) (thomsonreuters.com/en/products-services/scholarly-scientific-research/research-management-and-evaluation/journal-citation-reports.html), which classify scientific journals into one or more subject categories (e.g., physics, multidisciplinary; mathematics; medicine, general and internal). We first consider only papers published in journals belonging to at least one JCR subject category, and focus on the top $0.1\text{\%}$ of papers with highest B values. Then, we compute the fraction of those papers that belong to a given subject category. Fig. 4 shows the top 20 categories producing SBs. Subfields of physics, chemistry, and mathematics are noticeably the top disciplines, consistent with previous studies (35). Some disciplines not previously noted include medicine (internal and surgery), statistics, and probability. Particularly interesting is the category multidisciplinary sciences, ranked third, that includes top journals like Nature, Science, and PNAS, because (i) delayed recognition signals that such contributions may be perceived by the academic community as too premature or futuristic, although it is common ground among academics to speculate that such venues only publish trending topics, and (ii) journals in the multidisciplinary sciences subject category are really more fit to attract publications that become field-defining even decades after their appearance.

Fig. 4.

Top 20 disciplines producing SBs in science. We consider papers with beauty coefficient in the top $0.1\text{\%}$ of the entire WoS database, and compute the fraction of those papers that fall in a given subject category.

What Triggers the Awakening of an SB?

A full answer to this question would require a case-by-case examination, but it can be addressed in a systematic way by studying the papers that cite the SB before and after its awakening. To illustrate this strategy, we examine two paradigmatic examples of top SBs.

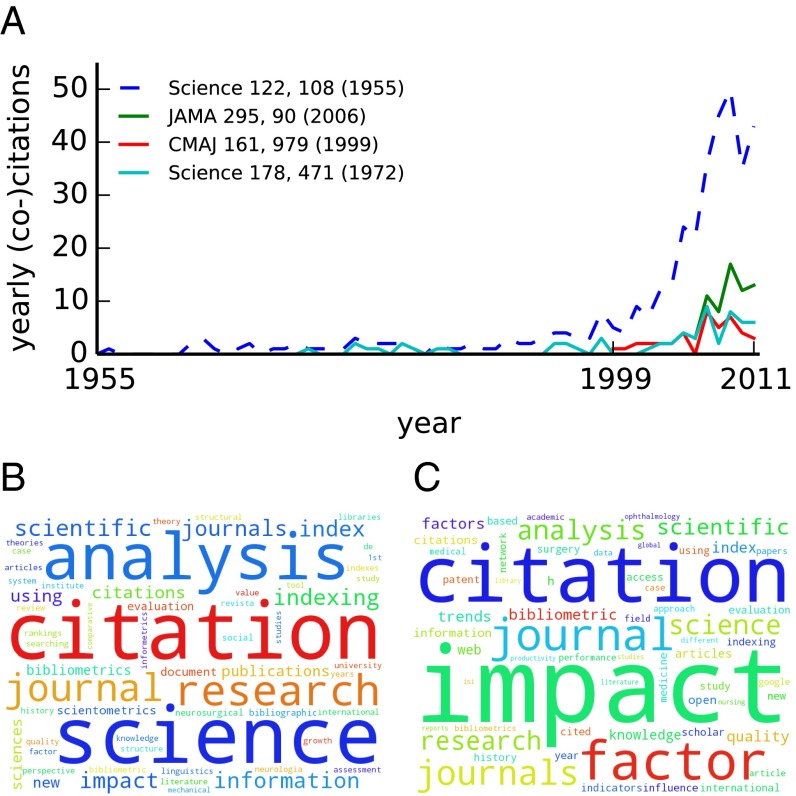
The first is the 1955 Garfield paper introducing the ancestor of the WoS database (43). This paper slept for almost 50 y, becoming suddenly popular around 2000. A simple investigation based on cocitations, similar to the one performed in ref. 44, reveals that the delayed recognition of the 1955 paper by Garfield was triggered by later articles by the same author (Fig. 5A). Such papers, in turn, were cited by very influential works in two different contexts: (i) the 1999 article by Kleinberg about the hyperlink-induced topic search (HITS) algorithm, which can be considered one pioneering work in network science (45); and (ii) the 1998 paper by Seglen on the limitations of the journal impact factor, which historically represents the beginning of the ongoing debate about the (mis)use of citation indicators in research evaluation (46). The change in contextual importance of the 1955 paper by Garfield is further revealed by the frequency of keywords appearing in the titles of its citing papers before and after year 2000 (Fig. 5 B and C), with the notion of “impact factor” becoming the main recognizable difference. With a similar motivation, the 1977 paper by Zachary also tops the ranking of SBs coming from the social sciences (47). This paper was essentially unnoticed for about 30 y, but then became suddenly important in network science research after the publication of the seminal paper by Girvan and Newman, which adopts the social network described in the Zachary paper as a paradigmatic benchmark to validate community detection methods on graphs (48) (SI Appendix, Fig. S12).

Fig. 5.

Paradigmatic example of the awakening of an SB. (A, blue) Citation history of ref. 43. The three most cocited papers are green, ref. 55; cyan, ref. 56; and red, ref. 57. (B and C) Clouds of the most frequent keywords appearing in the title of papers citing ref. 43, published, respectively, before (B) and after (C) year 2000.

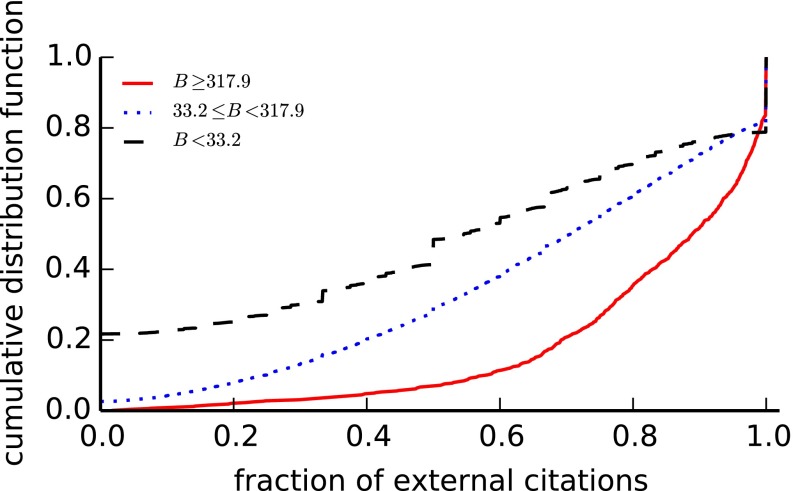
The examples above suggest that a partial explanation behind the sudden awakening of top SBs may lie in the fact that the paper in question is suddenly “discovered” as relevant by an entire community in another discipline. To support this hypothesis, in Fig. 6 we divide the papers in the WoS dataset into three disjoint subsets with high, medium, and low values of B. For each subset we compute the cumulative distribution for the fraction of citations received by a paper from publications in a discipline (as inferred by the journal of publication) different from that of the cited paper. Top SBs are clearly different from the other two categories and are characterized by a typically very high fraction of citations from other disciplines: for about 80% of the top SBs, as much as 75% or more of citations are of interdisciplinary nature.

Fig. 6.

Interdisciplinary nature of top SBs. Cumulative distribution functions of fraction of external citations for the group of (red) top 1,000 SBs ($B\ge 317.93$); (blue) from the 1,001st to the top 1% ($33.21\le B<317.93$); and (black) the rest ($B<33.21$). The horizontal axis measures for each paper the fraction of its citations that originate from other subject categories.

Discussion

The main purpose of this work was to introduce a parameter-free method to quantify to what extent a paper is an SB. Through a systematic analysis carried out on large-scale bibliographic databases and over observation windows longer than a century, we have shown that our method correctly identifies cases that meet the intuitive notion of SBs. We noticed that our measure is not entirely free of biases: Comparing the degree of beauty between papers in different disciplines or ages may be problematic due to differences in the overall citation patterns. Despite this limitation, we found that papers whose citation histories are characterized by long dormant periods followed by fast growths are not exceptional outliers, but simply the extreme cases in very heterogeneous but otherwise continuous distributions. Simple models based on cumulative advantage, although consistent with overall citation distributions, are not easily reconciled with the observed distributions of beauty coefficients. Further work is needed to uncover the general mechanisms that may be held responsible for the awakening of SBs.