A Novel Method for Quantifying Smooth Regional Variations in Myocardial Contractility Within an Infarcted Human Left Ventricle Based on Delay-Enhanced Magnetic Resonance Imaging

Short abstract

Heart failure is increasing at an alarming rate, making it a worldwide epidemic. As the population ages and life expectancy increases, this trend is not likely to change. Myocardial infarction (MI)-induced adverse left ventricular (LV) remodeling is responsible for nearly 70% of heart failure cases. The adverse remodeling process involves an extension of the border zone (BZ) adjacent to an MI, which is normally perfused but shows myofiber contractile dysfunction. To improve patient-specific modeling of cardiac mechanics, we sought to create a finite element model of the human LV with BZ and MI morphologies integrated directly from delayed-enhancement magnetic resonance (DE-MR) images. Instead of separating the LV into discrete regions (e.g., the MI, BZ, and remote regions) with each having a homogeneous myocardial material property, we assumed a functional relation between the DE-MR image pixel intensity and myocardial stiffness and contractility—we considered a linear variation of material properties as a function of DE-MR image pixel intensity, which is known to improve the accuracy of the model's response. The finite element model was then calibrated using measurements obtained from the same patient—namely, 3D strain measurements—using complementary spatial modulation of magnetization magnetic resonance (CSPAMM-MR) images. This led to an average circumferential strain error of 8.9% across all American Heart Association (AHA) segments. We demonstrate the utility of our method for quantifying smooth regional variations in myocardial contractility using cardiac DE-MR and CSPAMM-MR images acquired from a 78-yr-old woman who experienced an MI approximately 1 yr prior. We found a remote myocardial diastolic stiffness of $\overline{C_0}=0.102\mathrm{\hspace{1em}}\mathrm{kPa}$, and a remote myocardial contractility of $\overline{T_{\max }}=146.9\mathrm{\hspace{1em}}\mathrm{kPa}$, which are both in the range of previously published normal human values. Moreover, we found a normalized pixel intensity range of 30% for the BZ, which is consistent with the literature. Based on these regional myocardial material properties, we used our finite element model to compute patient-specific diastolic and systolic LV myofiber stress distributions, which cannot be measured directly. One of the main driving forces for adverse LV remodeling is assumed to be an abnormally high level of ventricular wall stress, and many existing and new treatments for heart failure fundamentally attempt to normalize LV wall stress. Thus, our noninvasive method for estimating smooth regional variations in myocardial contractility should be valuable for optimizing new surgical or medical strategies to limit the chronic evolution from infarction to heart failure.

Introduction

Heart failure is a worldwide epidemic that is likely to continue as the population ages and life expectancy increases. Nearly 70% of heart failure cases are caused by MI-induced adverse left ventricular (LV) remodeling. Previous studies in clinically relevant large animal experiments have demonstrated that one of the key features by which an acute MI leads to chronic heart failure resides in the formation of a BZ outside the infarcted area, which is normally perfused but shows reduced contractility, and hence abnormally high stretching [1,2]. A clinical method for quantifying in-vivo regional myocardial contractility would be invaluable for the design of novel approaches to treat or prevent MI-induced heart failure. Recently, we assessed regional (i.e., in the BZ and remote region to the infarct) contractile function in the remodeled human heart by coupling cardiac catheterization, magnetic resonance imaging (MRI), and computational cardiac modeling [3]. We found, for an MI human patient, that the BZ contractility was greatly reduced relative to the remote contractility.

In most of our previous LV finite-element modeling studies, we assumed that contractility is homogeneous within the predefined BZ, remote, and infarct regions. Consequently, contractility changes abruptly at the infarction-BZ and the BZ-remote boundaries. In Ref. [4], however, we hypothesized that the BZ defines a smooth transition in contractility between the remote region and the infarct. To test this hypothesis, we developed a finite-element model of an infarcted sheep LV that has a contractility that varies linearly within the BZ and examined if such a model can better predict the measured strain obtained from tagged MRI. We demonstrated that a linear variation in contractility within the BZ, when compared to a homogeneous BZ contractility, reduces the mean square errors between the measured and the predicted strain fields. This result was later confirmed by direct force measurements in skinned fiber preparations from infarcted sheep LVs [5,6]. This improved description of regional ventricular mechanics is critical for using patient-specific models to predict the efficacy of existing or novel surgical procedures or devices for treating ischemic cardiomyopathy [7,8].

The goal of this paper is twofold: first to describe a method for constructing a patient-specific finite-element model of an infarcted LV and second to demonstrate the utility of such a model in quantifying smooth regional variations in myocardial contractility. Here, we describe how we constructed this model using geometry derived from cine MR images and included infarct morphologies obtained directly from DE-MR images. These images are known to be a good indicator of tissue viability [9,10] and to correlate well with scar measurements obtained by electroanatomical mapping [11]. Instead of separating the LV into discrete regions (e.g., the infarct, BZ, and remote regions) with each having a homogeneous myocardial material property, we assumed a functional relation between the normalized pixel intensity of DE-MR images (i.e., the viability maps) and myocardial stiffness and contractility. This process allows us to replace the highly subjective manual delineation of scar tissue by the objective use of DE-MRI data. We then calibrated this model using measurements obtained from the same patient—specifically, strain measurements—using CSPAMM-MR images.

Methods

Finite Element Left Ventricular Modeling.

We start by briefly describing our LV finite-element modeling framework, emphasizing the improvement with regard to the previous work from our group [4,12–14].

Basic Hypotheses.

We established a few hypotheses to make our models well posed and computationally tractable. First, we neglected inertial and gravitational forces, so that the problem is quasi-static and the balance principle simply requires the stress field to be divergence free. We also assumed that the early diastolic configuration can be considered stress free, thus neglecting the effect of residual stress and remaining contractile forces. Finally, we followed the time-varying elastance principle [15] to model active contraction, so that there is no need to simulate complex electromechanical interactions. This framework allows computation of end of diastole (ED) and end-systolic (ES) pressure–volume relationships, which are the key characteristics of the ventricular pump function.

For boundary conditions, we fixed the basal edge of the left ventricular models to account for the large stiffness of the annulus compared to the myocardium. The loading was applied as a uniform pressure on the endocardial surface. We neglected the effect of the right ventricle and external body parts, so the epicardial surface remains unloaded.

For the mechanical behavior, we decomposed the stress into passive and active parts. The passive part simply derives from the strain energy potential, while the active part is given by a simple time-varying function built from cellular level considerations. The following sections (passive mechanical behavior and active contraction) describe each of these stress components.

Passive Mechanical Behavior.

We first decomposed the strain energy potential into volumetric and deviatoric parts and associated the volumetric part with a large bulk modulus to impose quasi-incompressibility [16]. For the deviatoric part, we used a transversely isotropic Fung law [17–19]

$$\overline{\psi }\left(\underset{¯}{\underset{¯}{\overline{E}}}\right)=\frac{C_0}{2}(e^{Q\left(\underset{¯}{\underset{¯}{\overline{E}}}\right)}-1)$$

where $\underset{¯}{\underset{¯}{\overline{E}}}$ is the isochoric Green–Lagrange strain tensor and $Q$ is defined by

$$\begin{array}{c}\multicolumn{1}{c}{Q\left(\underset{¯}{\underset{¯}{\overline{E}}}\right)=b_f{\overline{E}}_{\mathit{ff}}^2+b_t({\overline{E}}_{\mathit{ss}}^2+{\overline{E}}_{\mathit{nn}}^2+\frac{{\overline{E}}_{\mathit{sn}}^2+{\overline{E}}_{\mathit{ns}}^2+{\overline{E}}_{\mathit{sn}}{\overline{E}}_{\mathit{ns}}+{\overline{E}}_{\mathit{ns}}{\overline{E}}_{\mathit{sn}}}{2})+b_{\mathit{ft}}(\frac{{\overline{E}}_{\mathit{fs}}^2+{\overline{E}}_{\mathit{sf}}^2+{\overline{E}}_{\mathit{fs}}{\overline{E}}_{\mathit{sf}}+{\overline{E}}_{\mathit{sf}}{\overline{E}}_{\mathit{fs}}}{2}+\frac{{\overline{E}}_{\mathit{fn}}^2+{\overline{E}}_{\mathit{nf}}^2+{\overline{E}}_{\mathit{fn}}{\overline{E}}_{\mathit{nf}}+{\overline{E}}_{\mathit{nf}}{\overline{E}}_{\mathit{fn}}}{2})}\end{array}$$

$b_f$, $b_t$, and $b_{\mathit{ft}}$ are three material parameters defining the relative contributions of longitudinal, transverse, and shear strain components into the strain energy function, hence the material anisotropy. We consider here the values defined in Ref. [14] for normal humans, shown in Table 1. The law has another parameter, $C_0$, which scales the stiffness of the material, and usually needs to be personalized for each patient. More details on the formulation can be found in Refs. [4,12–14].

Table 1.

Fixed material parameters. $b_f$, $b_t$, and $b_{\mathit{ft}}$ define the material anisotropy, values established in Ref. [14] for normal humans are considered here.

$b_f$ ()	$b_t$ ()	$b_{\mathit{ft}}$()
14.40	5.76	10.08

The main difference with the previous studies is that here, the local material behavior was assumed to be a function of local tissue viability as assessed through DE-MR. For low pixel intensities, i.e., healthy tissues, the local stiffness $C_0$ corresponds to the “normal” value $\overline{C_0}$, which then represents the scaling parameter for the material behavior away from the infarct. Conversely, for high pixel intensities, i.e., infarcted tissues, the local stiffness $C_0$ corresponds to a much higher stiffness of $10\hspace{1em}\overline{C_0}$, following the infarct to remote stiffness ratio of Ref. [13]. As represented in Fig. 1, we assumed a linear variation of stiffness between two pixel intensity thresholds, ${\alpha }_1$ and ${\alpha }_2$, which are additional parameters of the model, and thus define the infarct and BZ areas as a function of pixel intensity of the viability maps.

Fig. 1.

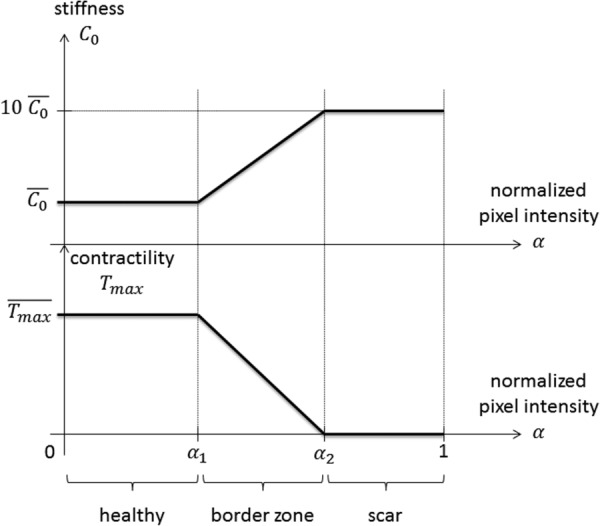
Relationship between local tissue viability (i.e., pixel intensity measured by DE-MR imaging, normalized by the maximal pixel intensity) and local passive stiffness, as well as local active contractility. For low pixel intensities, i.e., healthy myocardium, the local stiffness, and contractility are equal to their normal values. Conversely, for high pixel intensities, i.e., damaged myocardium, the local stiffness is much higher than normal, and the local contractility is null. We assumed linearly varying material properties across the BZ. The parameters ${\alpha }_1$ and ${\alpha }_2$ must be personalized for each patient.

Active Contraction.

For the active stress, we use a time-varying function of the sarcomere length-dependent contractile force generated by the myocytes, originally proposed in Refs. [20,21]

$$T(t,E_{\mathit{ff}})=T_{\max }\frac{{\mathit{Ca}}_0^2}{{\mathit{Ca}}_0^2+{\mathit{ECa}}_{50}^2\left(E_{\mathit{ff}}\right)}\frac{1-\cos \left(\omega (t,E_{\mathit{ff}})\right)}{2}$$

where ${\mathit{Ca}}_0$ is the peak intracellular calcium concentration and ${\mathit{ECa}}_{50}$ is the length-dependent calcium sensitivity. More details on the formulation and the definition and values of the parameters, can be found in Refs. [4,12–14]. The parameter $T_{\max }$ scales the tissue contractility and, similar to $C_0$ for the passive law, needs to be personalized for each patient.

Once again, the main difference with the previous studies is that here the local contractility was assumed to be a function of local tissue viability: for low pixel intensities, i.e., healthy tissues, the local contractility $T_{\max }$ corresponds to the normal value $\overline{T_{\max }}$, whereas for high pixel intensities, i.e., infarcted tissues, the local contractility $T_{\max }$ reduces to zero. We assumed a linearly varying function, following Ref. [4]. The corresponding function is also represented in Fig. 1.

Spatial and Temporal Discretization.

The models were solved using the finite element method, with the commercially available software ls-dyna (LSTC, Livermore, CA)2. The LV geometries were discretized using linear hexahedrons. We used reduced spatial integration for computational efficiency as well as to prevent locking, and the standard hourglass control procedure offered in ls-dyna. We used an explicit time-integration scheme with the standard, automatic, and time-stepping procedure offered in ls-dyna. The blood chamber was meshed using an “airbag,” i.e., a closed membrane whose volume and pressure can be controlled throughout the computation.

MRI-Based Model Personalization.

To demonstrate the applicability of our method, we studied a 78-yr-old female patient who was treated at the UCSF cardiac catheterization lab after a heart attack and suffered from MI (max CK level = 2691, max CK-MB level > 300). We performed all experiments in accordance with national and local ethical guidelines. Approximately 1 yr after the heart attack, the patient was scanned on a 1.5 T MRI scanner (Philips Achieva, Cleveland, OH). Blood pressure was also monitored during the scan.

Ventricular Anatomy, Volumes, and Microstructure.

Cine MR images, in both short-axis and radial long-axis directions, were acquired to cover the entire LV. We manually segmented the endocardium and epicardium on the frame corresponding to early diastole using mevislab (MeVis Medical Solutions AG and Fraunhofer MEVIS, Bremen, Germany)3. The surfaces were exported, and the LV geometry was meshed using truegrid 4. We also segmented the endocardium on the frame corresponding to ED and used the extracted endocardial surfaces at both time points to compute beginning of diastolic volume and end-diastolic volume.

We defined a rule-based fiber orientation map on the LV mesh, using the following algorithm:

• (1)Define a ventricular axis that is orthogonal to the short-axis imaging plane and goes through the ventricular apex, which was manually located.
• (2)Define a normalized pseudoprolate spheroidal coordinates system in the ventricle, by assigning to each element a transmural, circumferential, and longitudinal normalized position according to its centroid. The transmural position is defined as the relative distance to the endocardial and epicardial surfaces, which equals 0 at the endocardium and 1 at the epicardium. The circumferential position simply corresponds to the angle around the ventricular axis. The longitudinal position is the relative distance to the apex and base, which equals 0 at the apex and 1 at the base.
• (3)Define the associated basis vectors. The local transmural direction is the distance-weighted average of the outward-pointing normal of the endocardial and epicardial surfaces at the location of their closest point to the element centroid, which corresponds to the endocardial outward-pointing normal at endocardium, and to the epicardial outward-pointing normal at epicardium. The local circumferential direction simply corresponds to the circumferential direction around the ventricular axis. The local longitudinal direction is the cross product of the local transmural and circumferential directions, and thus follows the myocardial wall.
• (4)Rotate the local basis around the radial basis vector, by a linearly varying helix angle, from +60 deg at the endocardium to −60 deg at the epicardium.

This algorithm was implemented using custom vtkpython5 scripts.

Tissue Strain.

To measure strain, CSPAMM-MR images were acquired using the GyroTools6 “3D Tagging” patch. The images were postprocessed using our own implementation of the HARmonic Phase (HARP) method [22,23] in mevislab. The experimental strain data were projected onto the finite element mesh for optimization purposes using custom vtkpython scripts. To this end, every element was assigned an experimental strain tensor corresponding to the average of the strain tensor of all data points contained in that element.

Tissue Viability.

Delayed-enhancement images of the myocardium were obtained approximately 10 min after gadolinium injection (Gadovist, Bayer Healthcare, Leverkusen, Germany). DE-MR imaging was performed with breath holding and cardiac gating and utilized an inversion pulse to generate contrast. Data acquisition was tuned to occur a short period of time after the inversion (typically 200–250 ms) at which time the signal from normal myocardium is nulled and diseased myocardium produces a strong signal. Since the delayed-enhancement images are not acquired during early diastole, the cardiac phase upon which the mesh was built, we used implemented nonrigid registration method in the fenics in Ref. [24]7 framework to morph the delayed-enhancement image to the early diastolic configuration. We then projected the pixel intensities onto the mesh using custom vtkpython scripts, using the same method as for the strain data, i.e., every element was assigned a delay-enhanced intensity corresponding to the average of the values of all pixels contained in that element. We normalized the pixel intensities by dividing the maximum intensity of the projected pixels, following Ref. [25].

Regional Mechanical Properties.

Personalized myocardial parameters $(\overline{C_0},\overline{T_{\max }},{\alpha }_1,{\alpha }_2)$ were then determined, as the values minimizing the distance between measured and computed end-diastolic volume, end-systolic volume, and the circumferential strain field. The associated objective function is

$$\mathrm{OBJ}={\left(\frac{V_{\mathrm{ED}}-\overline{V_{\mathrm{ED}}}}{\overline{V_{\mathrm{ED}}}}\right)}^2\hspace{1em}+\hspace{1em}{\left(\frac{V_{\mathrm{ES}}-\overline{V_{\mathrm{ES}}}}{\overline{V_{\mathrm{ES}}}}\right)}^2\hspace{1em}+\hspace{1em}\sum _i{(E_{\mathrm{cc}}^i-\overline{E_{\mathrm{cc}}^i})}^2$$

where $V_{\mathrm{ED}}$, $V_{\mathrm{ES}}$, and $E_{\mathrm{cc}}^i$ are the end diastolic and end-systolic volumes, and circumferential strains at every strain measurement point, predicted by the model, and the overlined terms are the target values measured from MRI. To systematically perform the optimization, we used LS-Opt8, with a hybrid adaptive simulated annealing (to find an approximated global optimum)/leapfrog optimizer (to refine the optimum) algorithm, coupled to a sequential response surface method. The algorithm accounts for both patient-specific (i.e., geometry, volumes, strain, viability, and end-systolic pressure) and generic (i.e., myofiber orientation and end-diastolic pressure) data.

Results

The cine, tagged, and delayed-enhancement images were successfully acquired, as illustrated in Fig. 2. Cuff pressure was 133/63 mm Hg before the scan and 143/76 mm Hg after it. The cine images were then segmented and Fig. 3 shows the finite-element mesh of the patient-specific left ventricular geometry in early diastole and the generic fiber map. End-diastolic and end-systolic endocardial surfaces were extracted as well and used to compute an end-diastolic volume of 75.02 ml and an end-systolic volume of 39.68 ml.

Fig. 2.

Magnetic resonance images used for model personalization. (a) 3D cine images are used for ventricular geometry, (b) 3D CSPAMM-MR images for tissue strain, and (c) 2D DE-MR images for tissue viability.

Fig. 3.

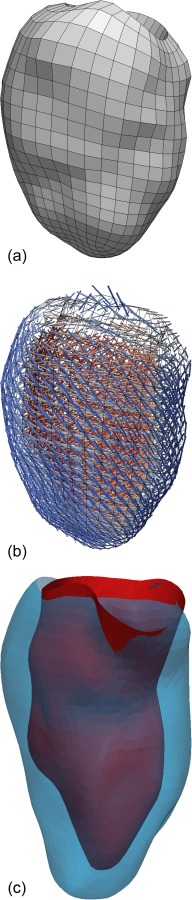
(a) Finite-element mesh of the left ventricular geometry in early-diastole. The contours were created by manual segmentation of cine MR images in mevislab. The fully hexahedral mesh was generated with truegrid. (b) Generic fiber field prescribed to the mesh using custom vtkpython scripts. Helix angle varies transmurally from +60 deg at the endocardium to −60 deg at the epicardium. Transverse and sheet angles are null. (c) Endocardial surface at end-diastole (blue) and end-systole (red), extracted by manual segmentation of cine MR images in mevislab.

The tagged images were successfully postprocessed and the obtained strain field projected onto the finite-element mesh. Similarly, the viability images were registered to the cine images, and the corresponding viability map projected onto the finite-element mesh, as illustrated in Fig. 4. The obtained scar map is consistent with the patient medical record, which references an occlusion of the left circumflex coronary artery.

Fig. 4.

Nonrigid registration of the viability data with the anatomical data, based on method in Ref. [24]. One short-axis slice of the anatomical mask is shown in blue (outside the ventricular wall) and red (inside), and the gray-scale viability map is superimposed. (a)–(c) Different iterations of the registration process showing initial mismatch and final match between the viability map and the anatomy.

Material parameters, including healthy stiffness $\overline{C_o}$ and contractility $\overline{T_{\max }}$, were successfully optimized, and the obtained numerical values are presented in Table 2. The personalized viability and contractility maps are shown in Fig. 5. The remote zone corresponds to low pixel intensity and high contractility. Conversely, the infarct area corresponds to high pixel intensity and low contractility. The BZ defines the smooth transition between the remote and infarct areas. Figure 5 also includes a contour plot of the normalized pixel intensity at 95%, which, according to the material optimization, represents the area with less than 10% contractility compared to the remote region and matches closely with a manual segmentation of the infarct.

Table 2.

Optimal material parameters determined by numerically minimizing the prediction error for end-diastolic volume, end-systolic volumes, and circumferential strain field, compared to MRI-extracted data. $\overline{C_0}$ and $\overline{T_{\max }}$ represent the reference stiffness and contractility of the healthy myocardium, while ${\alpha }_1$ and ${\alpha }_2$ define the change in mechanical behavior (reduced compliance and contractility) induced by MI.

$\overline{C_0}$ (kPa)	$\overline{T_{\max }}$ (kPa)	${\alpha }_1$ (%)	${\alpha }_2$ (%)
0.102	146.9	70.5	99.4

Fig. 5.

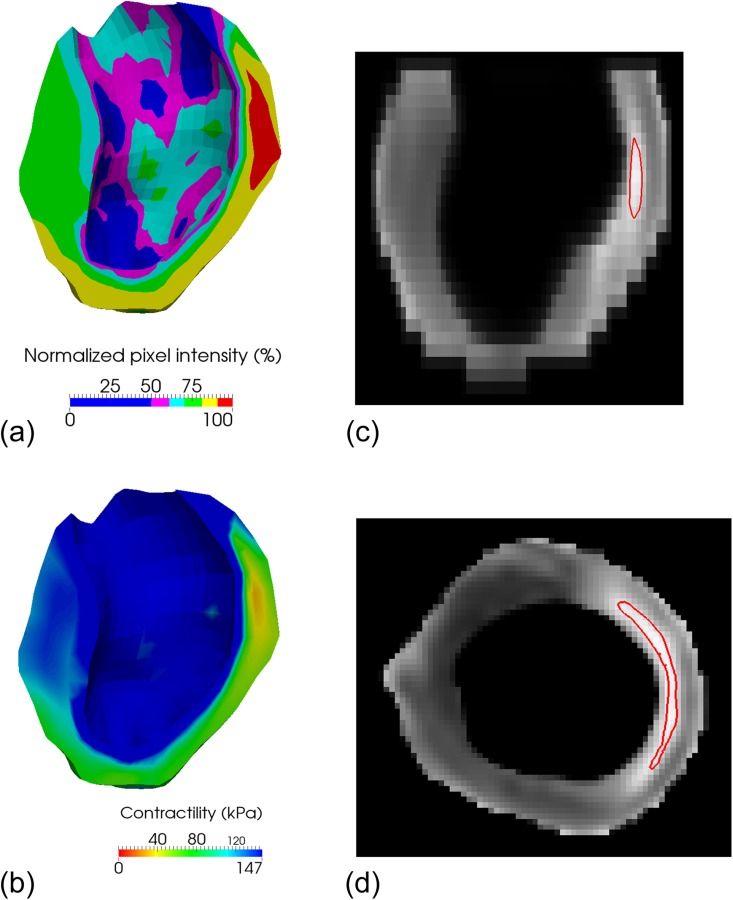
(a) Viability map in early diastole. Healthy regions (low pixel intensity) appear in blue, while the infarcted region (high pixel intensity) appears in red. (b) Personalized contractility map determined through numerical optimization. The colors are inverted compared to those in the viability map, so that the regions are consistent: healthy regions (high contractility) appear in blue, while the infarcted region (low contractility) appears in red. Note that because the core infarct area is rather small, the region with zero contractility (red) is small as well. (c) Contour plot, in a long-axis plane, of the 95% normalized pixel intensity, which corresponds, according to the material optimization, to the area with less than 10% contractility compared to the remote region. (d) Same contour plot, as in (c), in a midventricular short-axis plane.

After optimization, the average circumferential strain error (i.e., strain predicted by the model versus measured by CSPAMM-MRI) over the 17 AHA segments was 0.089. Figure 6 shows the good agreement between the overall deformation predicted by the personalized ventricular model and the actual deformation as measured by the cine MRI at the two cardiac phases simulated by the model, i.e., end-diastole and end-systole. The myofiber stress fields computed with the personalized ventricular model at the end of diastole and end of systole are shown in Fig. 7. The scar is especially visible in the end-of-systole myofiber stress map, where the reduced contractility induces a significant drop in total stress (which combines both passive and active stresses) as compared to the scar neighborhood.

Fig. 6.

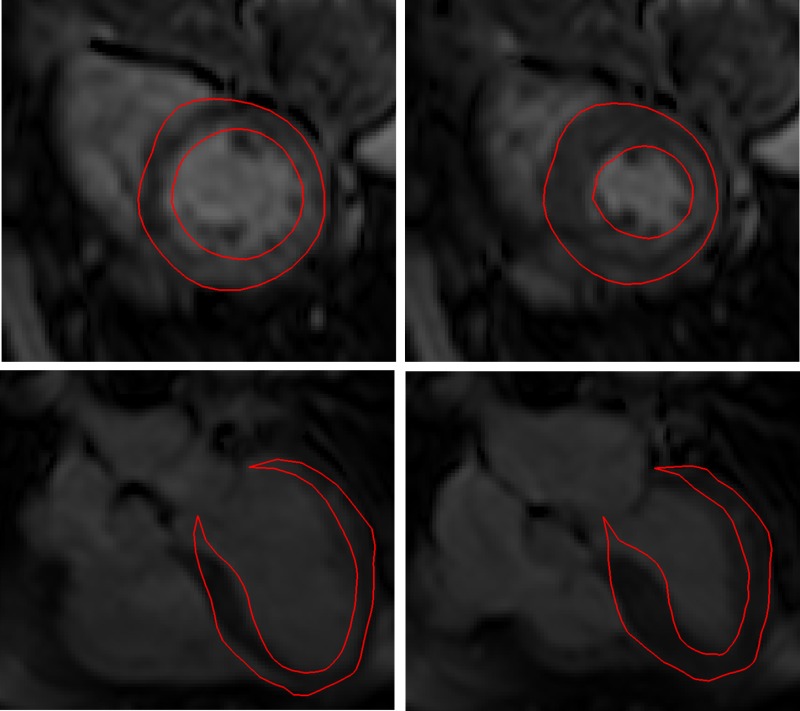
Comparison of the ventricular deformation at ED (left) and end-systole (right), predicted by the personalized finite-element model (red line) and measured by cine MRI, in short-axis (top) and long-axis (bottom) views. The overall deformation pattern is well reproduced by the model.

Fig. 7.

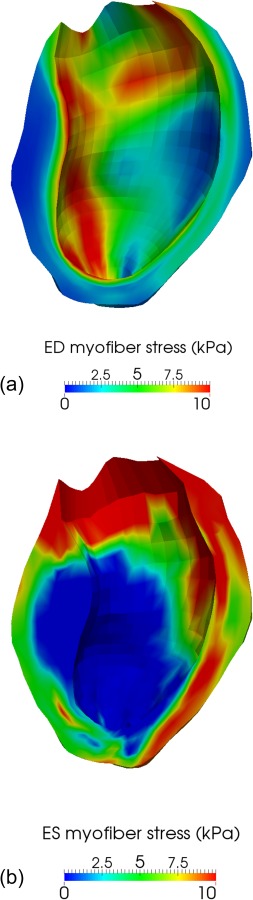
(a) Myofiber stress at ED, in kPa. Because of increased stiffness, the infarcted region seems slightly less stressed than the remote region. (b) Myofiber stress at end-systole, in kPa. Because of reduced contractility, the total stress, which combines both passive and active stresses, is significantly lower in the BZ than in the region remote to the infarct.

Discussion

Our study details significant advancements in the quantification of regional variations in myocardial contractility within an infarcted human LV. We used a patient-specific LV geometry derived from MR images and included infarct morphologies integrated directly from DE-MR images. Instead of separating the LV into discrete regions, we assumed a functional relation between the DE-MR images pixel intensity and T _max. To our knowledge, this is the first biomechanical model of the infarcted human LV that includes DE-MR data directly to describe the spatial extent of the MI, thus avoiding the very subjective step of the manual segmentation of the DE-MR images. This allows us to quantify a smooth regional variation in $T_{\max }$, which is known to improve the fidelity of ventricular models [4]. Consistent with all of our previous studies of regional T _max in numerous infarcted LVs, T _max in the BZ was depressed relative to that in the remote region.

Historical Context.

Myofilament dysfunction appears to contribute to impaired myocardial contractility in the infarct BZ, at least in sheep [5]. More precisely, Shimkunas et al. found that two weeks after induced anteroapical infarction, contractility in the BZ was reduced by 31±2% compared to regions remote from the infarct. In our first step toward developing clinical tools for noninvasively estimating regional myocardial contractility in vivo [12], we studied a sheep heart 14 weeks after anteroapical infarction, which is well past the 8–12 weeks required for an aneurysm to fully develop. In that case, there is not enough MRI signal in the 1–3 mm thick LV aneurysm to measure myocardial strain, so we quantified aneurysmal material properties by using ex vivo biaxial mechanical testing. After incorporating those properties in a finite-element model, we performed a formal optimization of regional contractility using tagged MRI and cardiac catheterization pressures. The optimized remote and BZ contractility for that sheep were 190.1 kPa and 60.3 kPa, respectively, with 90% confidence intervals at 14.9% and 16.9%, respectively. The significant depression in optimized BZ contractility relative to remote was confirmed by direct ex vivo force measurements from skinned fiber preparations. The optimized contractilities were not overly sensitive to the passive material parameters specified.

With confidence in our method, we applied it to the longitudinal study of the effect of LV aneurysm repair using an undersized patch (Dor procedure) on regional contractilities [26]. We found that the Dor procedure decreases end-diastolic and end-systolic stress but fails to improve BZ contractility. Interestingly, the NIH-sponsored surgical treatment for ischemic heart failure (STICH) trial found no difference in composite outcome between coronary artery bypass grafting (CABG) and CABG plus the Dor procedure [27]. Perhaps the inability of the Dor procedure to improve BZ contractility is the primary reason for the neutral STICH trial outcome. In fact, Sun et al. [26] concluded that the future work should focus on measures that will enhance BZ function alone or in combination with surgical remodeling. When Shimkunas et al. [5] studied the effect of doxycycline, an inhibitor of matrix metalloproteinases, rigor stiffness, and essential light-chain phosphorylation was not reduced in BZ myocardium, suggesting that doxycycline had a protective effect on BZ contractility.

Fortunately, ex vivo biaxial tissue testing is not required to quantify in vivo regional contractilities for the case of a posterobasal or posterolateral MI because the thickness of the infarcted wall segment is at least 50% of normal [3,6,13]. In the previous studies [3,6,13], we could measure 3D myocardial strain in the MI. In all three of those studies, however, it was not necessary to use a nonzero $T_{\max }$ value in the MI for the LV finite-element models to predict strain fields as measured with tagged MRI. Also, in those studies, BZ contractility was depressed relative to remote contractility. In Ref. [6], BZ $T_{\max }$ was significantly reduced for all samples (18.9%, p = 0.0067); moreover, myocyte cross-sectional area increased by 61% (p = 0.021) in the BZ, but there was no increase in fibrosis.

A linear variation in contractility within the BZ, when compared to homogeneous BZ contractility, reduces the mean square errors between the measured and the predicted strain fields [4]. Figure 1 of Ref. [5] shows how $T_{\max }$ also increases linearly with distance from the infarct. In the present study, we established a novel methodology to systematically localize the scar and BZ areas in personalized computational models of a patient who suffered an LV MI. In addition to existing MRI-based personalization procedures focused on anatomy and strain [28], here we also introduce personalized scar maps, which are extracted from delayed-enhancement MRI. The procedure consists of (i) a nonrigid registration of the viability and anatomy data and (ii) a projection onto the finite-element mesh. We were then able to identify the patient-specific relationship between viability and myocardial stiffness and contractility.

Comparison to Normal and Infarcted LV Myocardial Material Properties.

The material parameters found here through numerical optimization are consistent with already published values. For example, the myocardial stiffness of $\overline{C_0}=0.102\mathrm{\hspace{1em}}\mathrm{kPa}$ found using our method is very close to the range of normal human stiffness characterized in Ref. [14], i.e., $0.105-0.123\mathrm{\hspace{1em}}\mathrm{kPa}$ (mean ± standard deviation: $0.115\pm 0.00817\mathrm{\hspace{1em}}\text{kPa}$). Similarly, the calculated remote myocardial contractility of $\overline{T_{\max }}=146.9\mathrm{\hspace{1em}}\mathrm{kPa}$ is inside the range of normal human contractility characterized in Ref. [14], i.e., $130-155\mathrm{\hspace{1em}}\mathrm{kPa}$ (mean ± standard deviation: $143\pm 11.1\mathrm{\hspace{1em}}\mathrm{kPa}$).

There appears to be a slight discrepancy in the position of the BZ (in pixel intensity space) found in our study compared to published studies [25,29,30]. This is probably because the previous studies such as Refs. [25,30] used large animal models that suffered extremely severe MI; in contrast, the patient we studied had only a mild infarction, and was revascularized very quickly after her heart attack. Consequently, it is expected that there was a good functional recovery of the contractile function [9,31], leading to a rather small, dense scar area. However, the extent of the BZ itself is consistent with published values. In a prior study [25], the total scar area was defined as the region where the normalized pixel intensity was above 50%, and the dense scar area was above 80%, so that the BZ represents a 30% range in normalized pixel intensity, which is consistent with the value of 29.9% (99.4–70.5%) found here.

Limitations.

We wish to note some limitations, which should be overcome by future developments. First, we only considered the effect of an MI on tissue stiffness and contractility and neglected potential myofiber remodeling. Since the assessment of myofiber architecture is usually only possible ex vivo, it remains a long-standing limitation of patient-specific computational cardiac modeling, and our hypothesis is the only one that can be truly investigated at the moment. Recent developments in MRI technology have brought us closer to in vivo assessment of myofiber architecture [32,33], which has the potential to significantly improve the reliability of personalized computational cardiac models.

Another limitation is that we estimated end-systolic pressure from cuff pressure measurement, while using normal end-diastolic pressure. Since it is neither desirable nor we are allowed to perform cardiac catheterization on human patients for research purposes, this will remain a general limitation of patient-specific computational cardiac modeling until it is directly used within the clinic, or when tools to assess ventricular pressure in vivo and noninvasively become available. In either case, we feel the cuff pressure provides a reasonable enough estimate.

Future Directions.

Thanks to the automatic use of DE-MR data to characterize local tissue viability, the method established here reduces the amount of manual work needed to develop patient-specific ventricular models. However, to systematically characterize infarcted LV mechanics in humans based on MRI, our method will have to be applied to a larger number of patients. It will thus open the door to personalized and quantitative diagnosis, prognosis, and treatment planning and optimization.

Glossary

Nomenclature

BZ =

border zone

CSPAMM-MRI =

complementary SPAtial modulation of magnetization MRI

DE-MRI =

delayed-enhancement MRI

ED =

end of diastole

ES =

end of systole

LV =

left ventricle

MI =

myocardial infarction

MRI =

magnetic resonance imaging