Time-Frequency Analysis of Peptide Microarray Data: Application to Brain Cancer Immunosignatures

Abstract

One of the gravest dangers facing cancer patients is an extended symptom-free lull between tumor initiation and the first diagnosis. Detection of tumors is critical for effective intervention. Using the body’s immune system to detect and amplify tumor-specific signals may enable detection of cancer using an inexpensive immunoassay. Immunosignatures are one such assay: they provide a map of antibody interactions with random-sequence peptides. They enable detection of disease-specific patterns using classic train/test methods. However, to date, very little effort has gone into extracting information from the sequence of peptides that interact with disease-specific antibodies. Because it is difficult to represent all possible antigen peptides in a microarray format, we chose to synthesize only 330,000 peptides on a single immunosignature microarray. The 330,000 random-sequence peptides on the microarray represent 83% of all tetramers and 27% of all pentamers, creating an unbiased but substantial gap in the coverage of total sequence space. We therefore chose to examine many relatively short motifs from these random-sequence peptides. Time-variant analysis of recurrent subsequences provided a means to dissect amino acid sequences from the peptides while simultaneously retaining the antibody–peptide binding intensities. We first used a simple experiment in which monoclonal antibodies with known linear epitopes were exposed to these random-sequence peptides, and their binding intensities were used to create our algorithm. We then demonstrated the performance of the proposed algorithm by examining immunosignatures from patients with Glioblastoma multiformae (GBM), an aggressive form of brain cancer. Eight different frameshift targets were identified from the random-sequence peptides using this technique. If immune-reactive antigens can be identified using a relatively simple immune assay, it might enable a diagnostic test with sufficient sensitivity to detect tumors in a clinically useful way.

Introduction

Cancer is a dangerous disease that presents numerous challenges for diagnosis and treatment. Because cancer cells are technically foreign, the host immune system is often slow to respond to tumor antigens,^1,2 or the immune system can be evaded or suppressed in numerous ways.³ In addition, the patient may not experience symptoms for months or years after tumor initiation.⁴ The quiescent time between tumorigenesis and diagnosis is a window of opportunity for intervention. Unfortunately, until tumors are large enough to be detected by standard clinical methods, subclinical or presymptomatic detection is challenging. Biomarker molecules that are specific to the tumor are still very rare and become diluted in the bloodstream.⁵ Clearly, then, some form of amplification must be done to increase the tumor signal over biological noise.

DNA or RNA may present a biological molecule that can be amplified outside the host. By isolating a sufficient quantity of blood, one might capture enough tumor-specific nucleic acid molecules to amplify a signal. However, one must know target sequences, and nucleic acids are notoriously unstable, especially in historical samples. In contrast, antibodies are amplified by the body itself, are stable in blood, and are self-renewing. If a B-cell is stimulated, it will continue to produce its antibody in amounts up to 1% of the total circulating immunoglobulins. Therefore, it is quite possible that antibodies may provide a solution to the biomarker dilution problem.^6–8 However, as with nucleic acids, the question remains: what antibody is the most predictive, sensitive, and accurate for a given disease?

There are 10⁹ different antibodies circulating at any given time. Which antibody or group of antibodies is informative? There must be a way to interrogate antibodies in an unbiased way. Previously, immunosignatures have been shown to provide a “snapshot” of the humoral immune system.^9–12 Although these examples demonstrate the diagnostic potential of the “signature,” there is no biological understanding conveyed, at least not directly. These demonstrations of immunosignatures as diagnostic agents ignored the wellspring of information contained in the sequences of the signature peptides. Although not required for diagnosis, the sequences must convey some information about the antibodies that make up the signature. Previous experiments with a relatively low-density peptide microarray of 10,000 (10K) different 20-mer peptides showed that epitope identification from these few random-sequence peptides was extremely difficult.¹³ Recently, we developed a 330,000(330K)-peptide microarray that greatly enhances identification of informative sequences.¹²

Immunosignature technology

Immunosignatures may provide a link between the genetic alterations that occur within tumor cells and the way in which the immune system responds to aberrant cells.¹⁴ Immunosignatures represent the pattern of binding between serum antibodies and random-sequence peptides attached to a microarray surface. Technically, this interaction would be considered “off-target” or “nonspecific” because no actual epitopes or protein sequences were intentionally included as part of the peptide library. Statistically, in 330K short random-sequence peptides, there would be little homology to existing proteins. Perfect matches to full epitopes are thus extremely rare. One might therefore expect little-to-no binding between these peptides and a monoclonal antibody. However, binding between antibody and peptide is enhanced when peptides are packed at a particular density, enabling local avidity to increase the apparent affinity by lowering the off rate.¹¹ Low-affinity interactions that would normally be dissociated during a wash step are instead retained, generating reproducible patterns of binding between peptides and antibodies. Three general classes of signatures are typically seen when serum is processed on these immunosignature peptide microarrays: 1) signals that are person specific, with little-to- no population-specific disease information; 2) signals that are invariant regardless of person or disease state; 3) signals that change according to disease and are common within a disease cohort. This third class represents antibodies that are raised against a pathogen or against an aberrant cell, such as a tumor, commonly across persons with the same disease. The peptides that bind these antibodies become the “immunosignature” for that disease.^10–12,15 This implies that a disease, whether chronic,^9,16,17 autoimmune,^18,19 or infectious,^12,15,20 has some immunological stimulus that can be diagnostic or even prognostic.

Immunosignatures are composed of “features,” or peptides, which define the diagnostic pattern. To date, very little has been done with the sequence information, mostly because early immunosignature arrays had only 10K peptides.¹³ Computer lithography techniques have enabled logarithmic increases in peptide density; now, hundreds of thousands of peptides can be synthesized in smaller spaces.¹² With this increase in peptide number comes an increase in the ability to recognize epitope motifs within the feature peptides.²¹

A challenge faced when analyzing random-sequence peptide microarrays is how to integrate peptide sequences and mean fluorescence intensity (MFI) measurements to identify epitope sequences. Although mimotopes can be abundant, they do not help in tracking of an eliciting antigen. NNAlign is an algorithm that attempts to solve this problem by generating neural network models from subsets of the peptide array data and then combining those multiple models into a single motif.²² This algorithm provides a representation of amino acid probabilities at each position in the estimated motif. Another method for motif/epitope estimation uses regular expressions to estimate epitopes and includes a dependence on the position of the subsequence within the peptide sequence.²¹

Random-sequence peptide microarrays differ from panning methods (phage display, mRNA display) and focused arrays containing only the proteome of interest^23,24 in fundamental ways. Respectively, these methods require either biochemical selection with potential bias, possibly leading to loss of ancillary information, or assumptions about specificity within and between pathogen proteomes, which may prove too optimistic.

In this manuscript, we propose and explore a signal-processing-based method to estimate epitope and mimotope sequences using random-sequence peptide microarrays. We then explore an example of finding epitopes of predicted frameshift antigens in serum samples from patients with brain cancer.

Methods

Immunosignature random-sequence peptide microarrays

The proposed algorithm is first validated using immunosignatures obtained from eight different monoclonal antibody samples. The immunosignature assay is performed by incubating antibodies on a microarray of random-sequence peptides. The peptides are synthesized on silicon dioxide wafers and diced into standard 25 mm by 75 mm slides. The 330K random-sequence peptide microarrays have 330,034 probes. The sequences are sufficiently long such that binding occurs between an antibody and a subsequence of the peptide, but probably not to the entire peptide sequence. The average length of the peptide sequences on the 330K microarray is 11.2 amino acids, with a standard deviation of 1.3; 95% of the peptides are between 5 and 14 residues long, the maximum length being 22. From among the 20 different natural amino acids, cysteine, isoleucine, methionine, and threonine are excluded. These lengths do not include the constant C-terminal sequence glycine–serine–glycine, which links the peptide to the array substrate.

Processing of the microarrays was done as published by Stafford et al.¹¹, with the exception that the arrays were first washed in dimethylformamide for 1 hour. The solvent phase was transitioned to an aqueous phase over a 6-hour period using a phosphate-buffered saline incubation buffer before incubating in the presence of antibodies or serum. To enable binding of the antibodies to the arrays, the arrays were washed in distilled water and then loaded into a multiwell 24-up gasket. Each well received an incubation buffer and diluted antibody, typically at a final concentration of 500 pM. A secondary fluorescent detection antibody was applied to the array at 500 pM and allowed to bind to the primary antibody. After incubation for 1 hour, the arrays were washed using an enzyme-linked immunoassay plate washer. When using patient serum, a primary dilution of 1: 1500 was done, but all other steps remained the same. The arrays were dried, scanned at 1 µm resolution, and the resulting images were processed to provide raw microarray image data using GenePix Pro (Molecular Devices, Santa Clara, CA, USA). The antibody binding strength was measured by the fluorescence; stronger binding results when more antibodies bind to the peptide and thus more secondary antibodies bind to the primary antibodies. A calibrated picture was taken of the fluorescing array, wherein pixels in the image had been associated with specific peptides.

The problem of identifying motifs from relatively short, random-sequence peptides is substantial. In a study conducted by our group²¹, we demonstrated several successes, but we were unable to correlate failures to any known mathematical or biochemical source. We also did not examine samples where the target epitope is not a naturally occurring protein. We therefore wished to approach the problem using time–frequency (TF) mapping rather than multiple alignment methods, and we examined cancer rather than infectious disease. The approach that follows describes one possible path for using TF transformations, which might enhance the precision of motif identification, and we apply this method to an analysis of brain cancer. The description of the algorithm is provided in the context of the immunosignature data of monoclonal antibodies against known, linear, contiguous peptide targets. We first describe how the peptides are dissected into subsequences and then explain how those subsequences are fed into a time-variant transformation.

Forming peptide subsequences

Our objective is to detect and identify subsequences from the peptides obtained from the 330K random-sequence microarray. The peptides we examine are identified (down selected) by a feature-selection method described in the study by Stafford et al.¹⁰ Subsequences are partial sequences within the peptides selected. Note that the selected peptides from a given monoclonal antibody could correspond to the actual linear epitope or the peptides could be mimotopes, sequences with no homology to the cognate antigen. We consider an immunosignature microarray consisting of M peptide sequences; we denote the mth peptide sequence of length L_m as V_m, where m = 1, …, M. As the maximum number of amino acids in a peptide sequence is 22 using the 330K microarray, the maximum value of L_m = 22. By shifting one amino acid at a time in the mth peptide sequence, we obtain at most N_m ≤ (L − Λ + 1) unique, length Λ, subsequences of V_m. In particular, the γth shifting operation, γ= 1, …, N, generates the γth subsequence, whose first and last amino acids correspond to the γth and (γ + Λ)th amino acids of the peptide, respectively. We denote the aforementioned shifting function by h_γ(V_m; Λ), γ = 1, …, N_m, m = 1, …, M. This function generates the length-Λγth subsequence of the mth peptide V_m in the array by shifting the starting position of the subsequence from the first amino acid position of the peptide to the γth amino acid position of the peptide. Using this function, we represent the γth unique subsequence of V_m as follows:

$$\chi \left(\gamma ,d_m,\mathrm{\Lambda }\right)=h_{\gamma }\left(V_m;\mathrm{\Lambda }\right)$$

Here, d_m is the MFI of the mth peptide sequence V_m; it is the same value for all subsequences of peptide V_m. For example, considering the L_m = 10 amino acid peptide V_m = ARVY-HKKHE, we can generate at most (L_m − Λ + 1) = 8 unique subsequences of length Λ = 3. The subsequences are χ (1, d_m, 3) = ARV, χ(2, d_m, 3) = RVY, χ(3, d_m, 3) = VYH, χ(4, d_m, 3) = YHK, χ(5, d_m, 3) = HKH, χ(6, d_m, 3) = KHK, χ(7,d_m, 3) = HKH, χ(8, d_m, 3) = KHE. Because two of the subsequences are identical, χ(5, d_m, 3) = χ(7, d_m, 3) = HKH, the number of unique sequences is N_m = 7.

To achieve our objective, we find the number of times each unique subsequence of length Λ is repeated on the microarray. We form all possible unique subsequences as the union of all subsequences from the M microarray peptides. Specifically, there are at most $J\le {\displaystyle {\sum }_{m=1}^M{N}_m}$ unique subsequences, χ_j, where j = 1, …, J, in the set

$$S_{\mathrm{\Lambda }}={\displaystyle \underset{m=1}{\overset{M}{\cup }}{\displaystyle \underset{\gamma =1}{\overset{N_m}{\cup }}\chi \left(\gamma ;d_m,\mathrm{\Lambda }\right)}}$$

In practice, it is uncommon for a single peptide to contain repeated subsequences. Even when this occurs, it is only for the smaller length subsequences of Λ = 4 or Λ = 5 amino acids at most. It is much more common that different peptides share the same subsequences.

TF mapping of peptide subsequences

The proposed peptide subsequence estimation algorithm is based on first mapping the peptide amino acids to unique signals and then using TF signal-processing techniques to detect recurring patterns. The mapping uses the basic Gaussian signal, g_b(t) = π^−0.25 exp(−0.5t²),t ∈ (−T_g,T_g), as it is the most localized signal in the TF plane. The effective duration 2T_g is normally chosen to ensure minimum computational processing complexity. The basic Gaussian signal has unit energy and is centered at the TF origin. We design the amino acid-to-signal mapping as follows. Considering Nm subsequences of length L formed from the mth peptide V_m of length L_m, we map each amino acid to the time-shifted and frequency-shifted Gaussian signal.

$$g\left(t;l,k\right)=g_b\left(t-lT\right)\exp \left(j2\pi kFt\right),t\in \left(lT-T_g,lT+T_g\right)$$ (1)

The time-shift parameter lT is used to represent the lth amino acid in the peptide subsequence l = 1, …, Λ. The frequency shift parameter, kF, k = 1, …, 20, is used to map the 20 existing amino acids, as shown in Figure 1A. Using this mapping, the Λ-amino acid-long γth subsequence χ (γ,d_m, Λ), γ = 1, …, N_m, in Equation (1) can be represented by the linear combinaation of Λ TF-shifted Gaussian signals as follows:

$$\begin{array}{l}{x}_{\gamma ,m}(t)={\displaystyle \sum _{l=1}^{\mathrm{\Lambda }}g\left(t;l,u\left[\left\{{\alpha }_l\right\}\right]\right)}\\ ={\displaystyle \sum _{l=1}^{\mathrm{\Lambda }}g\left(t-lT\right)\exp \left(j2\pi u\left[\left\{{\alpha }_l\right\}\right]Ft\right),t\in \left(\gamma T-T_g,\left(\gamma +\mathrm{\Lambda }\right)T+T_g\right)}\end{array}$$ (2)

Figure 1.

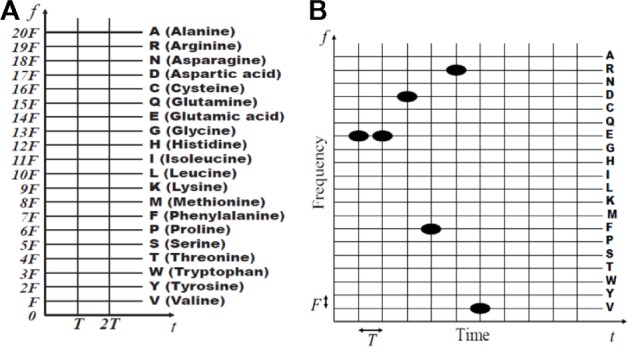
TF representations: (A) mapping amino acid type to frequency shifts; (B) the mapped amino acid subsequence EEDFRV.

Note that we denote x_γ,_m(t) to be dependent on m to clarify that the mapped signal originated from the mth peptide. This dependence is required for the estimation algorithm because we need to track the MFI of the subsequence. Both the peptide and any of its generated subsequences have the same MFI. The term k in Equation (1) is replaced by the function u[{l}], where u[{l}] is the integer-valued frequency shift that is used to map the type of the lth amino acid. Figure 1B provides an example of the mapping of the subsequence EEDFRV of length Λ = 6 amino acids. Note, for example, that time shifts l = 1, 2, etc share the same frequency shift u[{α₁}] = 14, because the type of amino acid (glutamate) is the same for both positions in the subsequence. Using the mapping, the weighted Gaussian signal representation for the mth peptide Vm is given by the following equation:

$$\begin{array}{l}{v}_m(t)={\displaystyle \sum _{i=1}^{L_m}\left(g(t;i,u)\left[\left\{{\alpha }_i\right\}\right]\right)}\\ ={\displaystyle \sum _{i=1}^{L_m}{g}_b(t-iT)\exp \left(j2\pi u\left[\left\{{\alpha }_{li}\right\}\right]Ft\right),t\in \left(T-T_g,L_{m}T+T_g\right)}\end{array}$$ (3)

where L_m is the length of the peptide sequence, m = 1, …, M.

Peptide subsequence estimation algorithm

Once the set S_Λ of all unique subsequences of length Λ on a microarray consisting of M peptides are formed as in Equation (2), we need to find the occurrence count (OCRC) of each subsequence. As we discuss in the section on “Peptide sequence down selection and bias normalization”, with details of feature selection, we perform a peptide down-selection process to reduce the computational cost, as not all peptides contribute to antibody binding.^11,25 As a result, the OCRC of each subsequence is obtained by considering the M ≤ M down-selected peptides on a microarray. In particular, we want to detect the signal x_γ,m(t) that represents the γth subsequence χ(γ, d_m, Λ) of length Λ, γ = 1, …, N_m, of the mth peptide within all possible signals v_m(t), m = 1, …, M that represent the M down-selected peptides. This process is analogous to searching for similarity between a given subsequence and all the peptide sequences on the microarray. Essentially, we use this approach to estimate epitopes and identify candidate mimotopes. We perform the subsequence estimation and identification method in TF using the matching pursuit decomposition (MPD) algorithm. The MPD is an iterative signal expansion technique that can be used to represent a signal with time-varying spectral characteristics as a linear combination of basis functions. Normally, the basis functions are selected from a dictionary that consists of a basic Gaussian signal that is centered at the TF origin as well as timeshifted, frequency-shifted, and scaled transformed versions of this basic signal. Transformed Gaussian signals form the dictionary as they are highly localized in the TF plane; however, based on the application, the MPD can give a sparse representation if the dictionary is formed using real signals. If the signal under processing is well matched in TF to the Gaussian basis functions, then the algorithm converges after only a few iterations; otherwise, the MPD can be computationally intensive. For our application, the processed signals are perfectly matched to the Gaussian basis functions as we map the amino acids in the peptide sequences directly to Gaussian signals. Thus, the MPD will converge quickly when used to identify subsequences, provided that the time-shift and frequency-shift transformations of the MPD dictionary are selected to be integer multiples of the time- and frequency-shift parameters T and F in Equation (3), respectively. Equation (1) provides the steps of our proposed approach to determine the OCRC of each unique subsequence χ_j = 1, …, J, of length Λ, in a microarray. To compute both the OCRC of each subsequence as well as keep track of the MFIs of the peptides that contributed to the count, we compute the OCRC of the length-Λ γth unique subsequence χ(γ d_m, Λ) of the mth peptide, m = 1, …, M. The subsequence is represented by the signal x_γ,m (t) with duration (ΛT + 2T_g) and MFI d_m. To reduce computational cost, we need to ensure that we do not unnecessarily process two or more subsequences when their corresponding mapped signals x_γ,m(t) and xy′m′(t), m ≠ m′ and any γ or γ′, are identical; each subsequence to be processed is generated only once because of how the subsequences are defined in Equation (2). The algorithm computes inner products between the linear combination of Gaussian signals in x _γ,_m(t) that represent the γth subsequence and the linear combination of Gaussian signals v_m(t) that represent the γth peptide. A perfect match is determined only when the sum of the inner product outputs is exactly equal to Λ. The OCRC of the γth subsequence is the total number of perfect matches after processing all down-selected microarray peptides.

Estimation of subsequences with single amino acid substitutions

Subsequences formed by replacing a single amino acid with another amino acid are called point mutations or single amino acid substitutions. Although substituting one amino acid can significantly change the peptide structure and binding characteristics, sometimes the effect is unimportant to structure or binding. Silent mutations occur when the substitution is by an amino acid with similar properties as the original amino acid, resulting in no significant change in functionality. As a result, single substitutions of amino acids with similar properties are important to consider for estimating specific types of subsequences such as epitopes and mimotopes.

Equation (1) can be modified to estimate subsequences with single amino acid substitutions at a time. In particular, the design of the proposed algorithm is inherently matched to handle substitutions with computational ease. This is because the algorithm only needs to find subsequence matches with identical mapped time shifts, as they represent the position of an amino acid in the sequence; all frequency shifts are allowable as they represent the amino acid type. Note, however, that we need to keep track of the exact amino acid substitution to determine the OCRC of a silent mutation. The resulting approach for estimating silent mutations is described in Equation (2).

Peptide sequence down selection and bias normalization

Although the 330K peptide microarray has a large number of unique peptides, not all peptides are applicable for detecting antibody subsequences that bind to specific antigens. To avoid unnecessary processing, we down select the peptides using two different schemes. The first scheme down selects peptides with high MFIs; this is because only a small fraction of the peptides binds strongly and specifically to the monoclonal antibody samples. The remaining peptides bind weakly and nonspecifically, and thus do not provide sufficient information on the sample antibodies. Antibody peptides that bind specifically, but only somewhat strongly, to antigens are not down selected. These peptides can be down selected by the second scheme that is based on the Pearson’s correlation coefficient (PCC). The PCC down selects peptides that bind strongly to only one of the monoclonal antibody samples. It is calculated between a vector of MFIs and a reference vector, and it measures the similarity between the two vectors. PCC values of −1, 0, and 1 imply negative correlation, no correlation, and positive correlation, respectively. For each of the M, peptides in the ρth microarray sample, ρ = 1, …, P the PCC is calculated as follows:

$$r_{\rho ,m}={\left(S_m-{\overline{S}}_m{1}_P\right)}^T\left(b_{\rho }-\frac{1}{P}{1}_P\right)$$

for m = 1, …, M. Here, S_m = [S_1,m … S_P,m]^T, s_ρ,m is the mean MFI of the mth peptide in the ρth sample, ${\overline{S}}_m=\left(1/P\right){\displaystyle {\sum }_{\rho =1}^P{s}_{\rho }}$, m is the MFI of all the mth peptides in the P microarray samples, 1_P is a (Px1) column vector of ones, b_ρ is a (Px1) reference vector that is defined as the ρth column of a (PxP) identity matrix, and T denotes vector transpose. The reference vector indicates the correlation pattern needed to match the ρth array. Down selecting based on the PCC provides an effective ranking metric for various cases, as illustrated in the following three examples. The first example assumes that all P = 8 samples have approximately the same MFI. Such a situation can occur when all samples are either binding nonspecifically to something in the antibody or not binding to anything. Using the reference vector b₁ = [10₇] for the sample ρ = 1, the PCC is computed as r_1,m = 0.01 in equation directly above, and 0_ρ is a (ρx1) vector of zeros. The second example assumes a specific binding at the microarray for which the PCC is computed. Specifically, as shown in Figure 2A, the MFI of the specific binding in the ρ = 1 sample is higher than the values of the nonspecific binding in the ρ = 2, …, 8 samples. Using reference vector b₁, the PCC is r_1,m = 0.98 for the ρ = 1 sample. In the last example, the specific binding is for the ρ = 2 sample, as shown in Figure 2B; using b₁, the PCC for the ρ = 1 sample is r_1,m = 0.22. Thus, the correlation for the MFI in Figure 2A is very large as the binary vector matches the MFI pattern, whereas the correlation for the MFI in Figure 2B is negative as the binary vector does not match the pattern. The PCC provides a better metric than MFI for ranking peptides with antigen-binding subsequences. The nonspecific binding strength of some monoclonal antibody samples can be approximately the same as the specific binding. If that occurs, peptides with larger MFIs on the sample of interest, relative to the same peptide on other samples, will be retained due to that binding. This is demonstrated for the monoclonal antibody Ab8 in Figure 2C. Using the PCC instead of MFI to rank peptides resulted in a larger fraction of peptides with epitopes. This behavior was typical for most of the monoclonal antibody samples. In the few cases where MFI ranking resulted in a higher percentage of the selected peptides containing epitopes, the PCC also performed well in estimating the epitope. Note that when we used the MFI as the ranking metric for monoclonal antibody Ab8, the epitope was not correctly estimated. In some cases, it was found that the subsequence estimation performance increased when the MFIs of the down-selected peptides were normalized. The normalization tends to remove biases in the data resulting from interexperimental variation (wafer-to-wafer synthesis variation, temperature, duration, and mechanical forces) or intraexperimental variation (subwafer variation, peptide location effects). The normalization approaches used include logarithmic (log₁₀) normalization (resulting in Gaussian-like characteristics), median normalization, and linear model normalization. The effect of normalization is demonstrated in Figure 2C for monoclonal antibody Ab8. For example, logarithmic normalization of the MFIs before computing the PCC resulted in more peptides with subsequences than combined logarithmic and median normalizations. Note, however, that the best estimation results were obtained when the MFIs were not normalized, indicating that the data are of consistent quality.

Figure 2.

The MFIs in (A) and (B) are due to specific binding for the first and second monoclonal antibody samples, respectively, and nonspecific binding for all other samples; (C) fraction of peptides with epitopes for different numbers of down-selected peptides for monoclonal antibody Ab8.

Results

The data analyzed consisted of 330K peptide microarrays for eight monoclonal antibody samples. Algorithm 1 provides the steps for estimating epitopes and identifying mimotopes based on finding unique subsequences and their OCRC. The most frequently occurring subsequences in the down-selected peptides are selected as the estimated epitopes. The algorithms also provide a list of additional subsequences that do not occur as frequently as the epitope estimates but still occur a sufficiently large number of times to warrant further investigation. These subsequences are proposed as potential antigen mimotopes as they appear to have readily permissible substitutions of the true epitopes.

Using the proposed algorithms, we estimated epitopes for the eight monoclonal antibody samples listed in Table 1A, together with their corresponding OCRC, OCRC (before down selection), and mean MFI. The estimate for each sample corresponds to the subsequence that occurred most frequently on the sample microarray after peptide down selection. As shown, the algorithms estimated exact subsequences for the full epitopes for five monoclonal antibodies, 2C11, A10, Ab1, Ab8, and DM1A; close matches were obtained for 4C1, FLAG, and HA. The expanded results for monoclonal antibodies 2C11, A10, and HA are provided in Tables 2, 3, and 4, respectively, listed in descending order by OCRC. The tables provide details, further considered in the Discussion section, on how Algorithm 1 was applied to provide the final estimated epitopes in Table 1A. These results demonstrate both the diversity of the peptides on the microarray, spanning enough of the possible sequence space to bind all eight monoclonal antibodies, as well as the high performance of the epitope estimation algorithm in finding relevant epitopes. We also used the algorithms to identify potential mimotopes for the monoclonal antibody samples, as listed in Table 1B. Although these mimotopes do not match the amino acid subsequences of the full epitopes, they can potentially act as subsequences that uniquely bind to the monoclonal antibodies, without matching the amino acid composition of the epitope. We deduced the following considerations for potential mimotopes when analyzing random-sequence peptide microarrays: mimotopes are (i) distinctively different from the epitope of a specific monoclonal antibody sample; (ii) distinct across all eight monoclonal antibody samples; (iii) notably different from other peptide subsequences when comparing binding strength and/or OCRC. From these considerations, we developed the following four criteria to identify potential mimotopes. A mimotope subsequence of a monoclonal antibody sample

• C1: is not an exact or a single substitution match to a full or an estimated monoclonal antibody epitope.

• C2: is not sufficiently similar to high–occurring peptide subsequences of other monoclonal antibody samples

• C3: has a sufficiently large MFI

• C4: has a large OCRC, obtained using the down-selected monoclonal antibody peptides.

Table 1.

(A) Epitope estimates with OCRC, OCRC before down selection (no DS), and mean MFI; and (B) potential mimotopes for the monoclonal antibody (mAb) samples.

(A) Sample mAb	Full Epitope	Estimated Epitope	OCRC	OCRC no DS	Mean MFI	(B) Sample mAb	Full Epitope	Potential Mimotope
2C11	NAHYYVFFEEQE	VFFEEQE	7	22	805	2C11	NAHHYYVFFEEQE	DARWFN
A10	EEDFRV	EDFRV	20	34	65,535	4C1	LQAFDSHYDY	ADSWP
Ab1	NTFFRHSVVV	RHSVV	186	209	65,535	A10	EEDFRV	EWDVA
Ab8	TFSDLWKLLPE	DLWKL	6	63	1,174	Ab1	NTFFRHSVVV	–
DM1A	AALEKDYEEVGV	AALEKD	5	2,053	2,368	Ab8	TFSDLWKLLPE	–
Flag	DYKDDDDK	AALEKD	1,323	2,001	44,567	DM1A	AALEKDYEEVGV	–
4C1	LQAFDSHYDY	GYDSR	13	21	8,731	Flag	DYKDDDDK	ALEKDGD
HA	YPYDVPDYA	YDAPE	14	16	61,414	HA	YPYDVPDYA	EDLPD

Table 2.

Algorithm 1 results for 2C11 sorted in descending order according to OCRC; also listed are the estimated sequences (of varying lengths ℒ), OCRC before down selection (no DS), and mean and maximum MFIs (the shaded rows correspond to estimated epitopes).

(A) 2C11 SUBSEQUENCES OF LENGTH ℒ = 5					(B) 2C11 SUBSEQUENCES OF LENGTH ℒ = 5					(C) 2C11 SUBSEQUENCES OF LENGTH ℒ = 7
Sub-seq.	OCRC	OCRC no DS	Mean MFI	Max MFI	Sub-seq.	OCRC	OCRC no DS	Mean MFI	Max MFI	Sub-seq.	OCRC	OCRC no DS	Mean MFI	Max MFI
FEEQE	7	168	586	5,826	FFEEQE	7	116	636	5,826	VFFEEQE	7	85	694	5,826
FFEEQ	7	117	636	5,826	VFFEEQ	7	86	685	5,826	YVFFEEQ	3	22	805	2,089
VFFEE	7	87	676	5,826	DARWFN	4	10	1,197	65,535	AALEKDG	2	2,000	630	16,310
ARWFN	6	54	931	65,535	AWRGFN	3	7	997	1,692	ALEKDGY	2	111	701	16,310
AVNWF	6	64	760	187	FARLRE	3	9	1,183	3,327	AVARPFQ	2	2	1,849	2,182
PWFNK	6	139	848	2,144	FKYARL	3	24	1,208	2, 414	AVGWQAR	2	3	1,922	16,130
WFNRL	6	3	1,010	1,704	HFFKAL	3	6	954	1,693	AWRGFNY	2	3	997	1,616
ARLRP	5	120	1,098	4,613	KARLRP	3	6	1,652	4,613	FARLREY	2	2	1,415	1,647
ARRVR	5	30	1,980	4,142	WFARLL	3	6	1,050	1,769	FEEQERY	2	13	656	1,559
DARWF	5	37	834	65,535	WFNGYA	3	12	938	1,470	FFEEQER	2	23	759	1,559

Table 3.

Algorithm 1 results for A10 sorted in descending order according to OCRC; also listed are the estimated subsequences (of varying lengths ℒ). OCRC before down selection (no DS), and mean and maximum MFIs.

(A) A10 SUBSEQUENCES OF LENGTH ℒ = 4					(B) A10 SUBSEQUENCES OF LENGTH ℒ = 5					(C) A10 SUBSEQUENCES OF LENGTH ℒ = 6
Sub-seq.	OCRC	OCRC no DS	Mean MFI	Max MFI	Sub-seq.	OCRC	OCRC no DS	Mean MFI	Max MFI	Sub-seq.	OCRC	OCRC no DS	Mean MFI	Max MFI
WDVA	52	272	17,534	65,535	EDFRV	20	34	65,535	65,535	DFRVDW	8	22	35,188	65,535
DVAW	52	473	8,790	65,535	EWDVA	15	41	65,535	65,535	FRVDWK	8	40	5,252	65,535
DSAW	46	442	8,763	65,535	EDVAW	14	35	65,535	65,535	EDFRVD	5	6	65,535	65,535
WQEA	46	135	65,535	65,535	WFEGA	14	53	65,535	65,535	EDVRPF	5	10	39,784	65,535
DAAW	40	385	11,101	65,535	WDVAP	13	33	65,535	65,535	PWQEAS	5	7	65,535	65,535
DVSW	36	239	19,765	65,535	DAAWP	11	52	16,042	65535	AVWFEG	4	11	7,222	65,535
QEYA	35	323	37,316	65,535	DVAWG	11	57	10,288	65,535	DVAWPF	4	12	22,508	65,535
EDVA	34	242	20,428	65,535	EWDAA	11	44	31,044	65,535	EDARSG	4	6	34,672	65,535
WFEA	34	267	8,875	65,535	PWFEA	11	69	10,370	65,535	EDVAPN	4	9	6 0,074	65,535
EWDA	32	346	10,617	65,535	WDVAW	11	42	19,322	65,535	EDVAWP	4	6	65,535	65,535

Table 4.

Algorithm 1 results for HA sorted in descending order according to OCRC; also listed are the estimated subsequences (of varying lengths ℒ), OCRC before down selection (no DS), and mean and maximum MFIs.

(A) HA SUBSEQUENCES OF LENGTH ℒ = 4					(B) HA SUBSEQUENCES OF LENGTH ℒ = 5					(C) HA SUBSEQUENCES OF LENGTH ℒ = 6
Sub-seq	OCRC	OCRC no DS	Mean MFI	Max MFI	SUB-SEQ.	OCRC	OCRC no DS	Mean MFI	Max MFI	Sub-seq.	OCRC	OCRC no DS	Mean MFI	Max MFI
YDAP	44	91	6,400	65,535	YDAPE	14	16	61,414	65,535	FNYDP	4	6	2,146	65,535
DAPE	31	114	1,537	65,535	PYDAP	10	11	44,289	65,535	GYDAPE	4	4	59,422	65,535
ADAP	27	285	864	65,535	YDSPE	9	13	12,542	65,535	NQYDAP	4	4	47,437	65,535
DVPE	25	93	1,008	65,535	FDAPV	8	12	9,961	56,901	NYDSPE	4	4	11,997	65,535
DAPG	24	168	1,122	65,535	PFDAP	8	8	47,053	65,535	AALEKD	3	2,053	694	11,285
DVPD	24	33	31,506	65,535	QYDAP	8	10	31,196	65,535	ALEKDG	3	2,002	697	11,285
DAPV	23	112	1,027	65,535	YDVPE	8	9	51,759	65,535	APYDAP	3	3	44,289	65,535
YDVP	23	47	4,846	65,535	ADAPE	7	18	10,457	65,535	EDHPDG	3	3	4,984	40,563
LDVP	20	153	823	65,535	EDLPD	7	15	1,706	11,385	EDLPDS	3	4	6,698	11,385
FDAP	18	47	2,071	65,535	FYDAP	7	11	5,583	65,535	FFYDAP	3	3	6,135	65,535

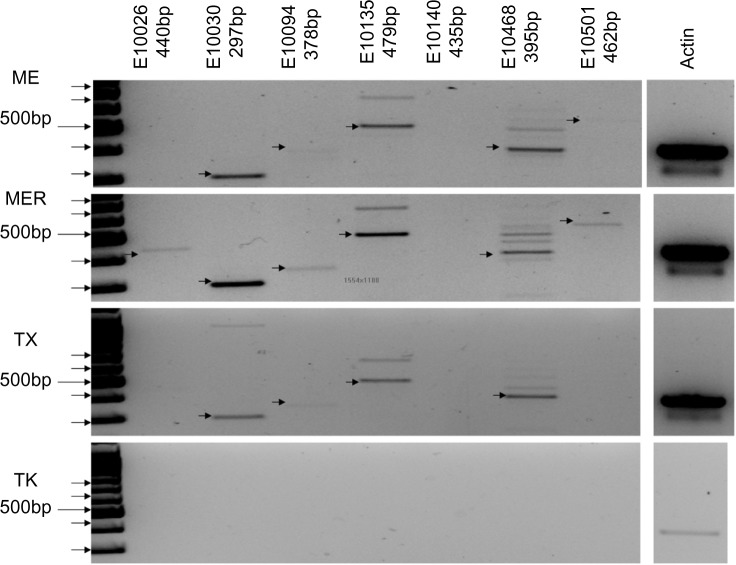
By following these criteria, we were led to potential mimotopes for the monoclonal antibody samples 2C11, 4C1, A10, FLAG, and HA shown in Table 1B. Subsequences of the remaining monoclonal antibody samples did not meet all of the aforementioned criteria, and thus they were not identified as potential mimotopes. The expanded results that demonstrate the choice of identified mimotope for samples 2C11, A10, and HA are also provided in Tables 2, 3, and 4, respectively. Given these results, we examined data generated using the same 330K peptide microarrays. Glioblastoma multiformae (GBM) is a dangerous and difficult-to-diagnose stage IV astrocytoma, a very aggressive brain cancer.^26,27 Twenty patients with clinically diagnosed GBM donated blood before surgery and chemotherapy (ASU IRB# 0905004024, samples kindly donated by Dr Adrienne Scheck, Barrow Neurological Institute, Phoenix, AZ, USA). Twenty GBM patients were compared to 20 healthy nondisease controls and 20 patients each with esophageal, breast and ovarian cancer. The immunosignature platform possesses high specificity relative to diagnosis of cancer. The low-density 10K-peptide microarray can distinguish a blinded cohort of patients with five different cancers¹⁰ simultaneously; the higher-density 330K peptide microarray can distinguish seven cancers and seven infectious diseases simultaneously.¹² The peptides selected for GBM were filtered for cross-reactivity against the other cancers from Figure 5 and should be considered highly specific for GBM. Previously, we demonstrated that the low-density 10K-peptide microarray was able to discriminate GBM patients with and without methylation of O(6)-methylguanine-DNA methyltransferase,¹⁴ suggesting that immunosignatures were composed of reactivity to both known molecular biomarkers as well as other antigens. In Figure 5, we show the peptides selected for GBM. At first glance, one can see short, common motifs. By using more rigorous alignments, we find motifs common to translated mRNA libraries from GBM patients. The top right panel of Figure 5 lists a subset of the random-sequence peptides that specifically react with antibodies from patients with GBM but not with samples from patients with breast, esophageal, or ovarian cancer. The red letters highlight the conservation of a given motif and are aligned to the translated GBM mRNA library. The boxes are alignments with a different library of peptides, those from the low-density 10K-peptide microarrays run in a previous experiment. In some cases, the 10K library peptides align with peptides from the 330K library. Figure 6 shows the polymerase chain reaction results using primers flanking the region containing the frameshifts. The target RNA was obtained from GBM tumor tissue lysate (obtained from Dr Adrienne Scheck, Barrow Neurological Institute, Phoenix, AZ, USA). Nearly all of the mRNA amplified is the frameshifted sequence, with little wild-type sequence. Peptides from samples of breast, ovarian, and esophageal cancers were also compared to the GBM sequences, and no significant alignments were identified.

Figure 5.

Specificity of immunosignatures (left) and mapping of Glioblastoma multiformae-specific peptide motifs to translations of RNA libraries from tumor libraries: Upper left: heatmap demonstrates the differences in immunosignatures among four different cancers, stage III breast cancer, esophageal adenocarcinoma, Glioblastoma multiformae (GBM, a stage IV astrocytoma), and stage IV (a and B) ovarian cancer. Peptide intensities are shown on the Y-axis, and patients on the X-axis. Peptides and patients are grouped by hierarchical clustering based on the data, indicating which patient samples show reactivity with which peptides. the principal components analysis map (PCA) immediately below the heatmap shows further grouping by inter- and intragroup variances. Top right: panel lists peptides reactive in GBM patients. Below right: panel shows the alignment of sequences from a translated RNA tumor library obtained from GBM patients, with the alignment of GBM-specific immunosignature peptides and the particular gene or gene constituents (if a translocation) preceding each line. The red letters indicate the motifs found in the GBM-specific peptides found using the 330,000-peptide (high-density) library, with the height indicating the amount of conservation in that position. The larger the letter, the more often that amino acid was found at that specific position in the translated library. Squares indicate that a motif was also found using a 10,000-peptide (low-density) printed peptide microarray.

Figure 6.

Molecular evidence of frameshift RNA sequences in brain cancer tumor samples: samples are listed on the left (ME, MER, TX, and TK). Only seven of the frameshifts from Figure 5 are tested. each frameshift is listed along the top and uses the same designation as in Figure 5. Actin is provided as a control (far right). Arrows indicate the correct size of the predicted frameshift product.

Discussion

Herein, we examine a method by which antigen motifs may be estimated from very short random-sequence peptides. The peptides were obtained from a process known as “immunosignaturing,” a process by which sera or monoclonal/polyclonal antibodies are exposed to random-sequence peptides in a microarray format. Disease diagnosis can be made without the need to determine epitope information^{9–12,14,15,17–22} from the peptides. Early low-density 10K-peptide microarrays provided almost no legible motifs, even when examining peptides from monoclonal antibodies against known linear targets.¹³ However, the 330K-peptide high-density arrays¹² have provided far more precision in motif identification.²¹ We therefore attempted a signal-processing method to extract epitope information from hundreds or thousands of short, random-sequence peptides. We tested the concept using monoclonal antibodies and then present a use case where sera from patients with GBM were used to generate an immunosignature, from which peptide sequences are compared to a translated mRNA library from GBM tumor lysate. We show that motif finding in short random-sequence peptides is possible and, in some cases, can offer details about eliciting epitopes.

Epitope estimation performance analysis

The epitope estimation performance is analyzed in Tables 2–4 for monoclonal antibody samples 2C11, A10, and HA. We first obtain estimates using Algorithm 1 as the subsequences that occur most frequently within the down-selected peptides for varying subsequence lengths L = 5, L = 6, L = 7. Then, we declare the estimated epitope to be the longest, consistent top subsequence. Considering monoclonal antibody sample 2C11, the shaded length L = 5 subsequences FEEQE, FFEEQ, and VFFEE in Table 2A all have maximum OCRC = 7; in Table 2B, the two shaded subsequences, FFEEQE and VFFEEQ, of length L = 5 have maximum OCRC = 7. The resulting top subsequences from these two tables infer that there must be a longer-length epitope subsequence. This is shown in Table 2C, in which the shaded subsequence VFFEEQE of L = 7 is the only one with the highest OCRC. Similarly for HA, the top shaded subsequences in Table 4A are YDAP and DAPE; in Table 4B, the highest OCRC subsequence is YDAPE. While this sort of trend is seen in many of the monoclonal antibody samples, occasionally, the binding strength appears to be dependent on a more complete epitope. An example of this is seen for A10 in Table 3B, where the top L = 5 subsequence EDFRV is the epitope estimate. Subsequences EDFR and DFRV of L = 4 are not seen in Table 3A; however, DFRV and FRV are present in the top three L = 6 subsequences in Table 3C. We followed these two trends to determine which length subsequence to choose as the epitope estimate for each of the monoclonal antibody samples.

Factors affecting algorithm performance

As the microarray peptides are typically much longer than the estimated epitopes, the monoclonal antibodies must bind to only a fractional portion of a peptide. It is therefore possible to infer that a particular subsequence contributed to the binding if that subsequence is present on multiple peptides with large mean MFIs. The success of the estimation algorithm also depends on the diversity of the microarray peptides; this is achieved using the sufficiently large 330K random-sequence peptide microarray – the earlier 10K printed microarray had longer 20-mer peptides but did not perform well enough to estimate epitopes.¹³ In particular, many of the shorter-length subsequences were found to repeat numerous times throughout the 330K library. As a result, this increased the robustness of the estimation algorithm and also allowed for an analysis of single amino acid substitutions based on binding strength. To determine how well subsequences of different lengths are represented, we list the number of potential subsequences on the microarray in Table 5. On the 330 K-peptide microarray, approximately 90% of Length = 4 and 50% of Length = 5 subsequences occur on the array. Moreover, many of these subsequences are repeated multiple times, as shown in Table 6. As observed, most of the L = 4 and L = 5 subsequences of the monoclonal antibody epitopes are present on the array and repeated multiple times. This occurs for the epitopes of monoclonal antibody samples 2C11, A10, Ab1, Ab8, and DM1A, for which we obtained exact epitope estimates. The results for the remaining three monoclonal antibody samples, 4C1, FLAG, and HA did not provide exact matches to the actual epitopes but did to similar epitopes. This is likely due to the low OCRCs on the microarray of the real epitopes. By nature, the arrays are limited in the number of sequential repetitive residues, due to the method by which the peptides are synthesized.¹² The subsequences of partial matches would have only moderately strong binding, which is what was seen. It is important to emphasize that the performance of the proposed estimation algorithm depends on the design of the random peptides on the microarray. More specifically, the performance depends on how frequently subsequences of the full epitope occur, whether the actual perfect subsequences are present, how strongly the antibodies bind to the peptides with these subsequences, and how promiscuous single antibodies are.

Table 5.

Number of possible and unique subsequences of varying lengths on the microarray.

SUBSEQUENCE LENGTH	# OF UNIQUE SUBSEQUENCES	# OF POSSIBLE SUBSEQUENCES	% OF UNIQUE SUBSEQUENCES
4	58,700	65,500	89.5%
5	550,000	1,050,000	48.1%
6	1,490,000	1,680,000	9%
7	1,880,000	2,680,000	0.7%

Table 6.

Percentage of subsequences of varying lengths that are repeated on the microarray at least G times.

SUBSEQUENCE LENGTH	% OF SUBSEQUENCES REPEATED AT LEAST G TIMES
	G = 5	G = 10	G = 50	G = 100	G = 500	G = 1,000
4	99.8%	99.5%	95.2%	90%	69.1%	46.1%
5	94.2%	89.2%	61.5%	38.6%	1.2%	0.3%
6	57.8%	37%	2.6%	0.4%	0.2%	0.2%
7	5.9%	1.2%	0.2%	0.2%	0.1%	0.1%

The performance of the epitope estimation algorithm is tightly coupled to the frequency and diversity of the subsequences in a microarray. By “frequency,” we mean how often a specific subsequence (of fixed length) occurs in the whole microarray. This is important because it affects the total number of peptides to which the antibodies bind. As a result, the number of down-selected peptides containing an epitope subsequence increases. Those subsequences are at the top of the OCRC. “Diversity” implies the variety of peptide subsequences that are included in the entire 330K library. As it is not possible to provide the details of every selected epitope, to demonstrate the effect of these factors and the data trends on algorithm performance, we next discuss specific subsequences for monoclonal antibody samples Ab1, 4C1, FLAG, and HA.

Our analysis demonstrated that it is possible that the full epitope does not correspond to the subsequence with the highest binding strength. This is demonstrated for the monoclonal antibody sample Ab1, with full epitope NTFFRHSVVV. Table 7A lists the matched subsequences, their OCRCs, and the corresponding mean MFIs for Ab1. Although the residue T occurs in the full epitope, we do not consider this residue in our estimation as it was not used to generate the peptides.³³ Furthermore, when computing the OCRC of a short subsequence whose identical amino acid pattern appears in a longer subsequence, we do not include the OCRC of the longer subsequences. For example, when computing the OCRC of HSVV, we did not include the peptides that contain RHSVV, RHSVVV, or any other higher-length subsequences of NTFFRHSVVV. This is because we wanted to ensure that the OCRC metric for HSVV is not influenced by the binding strength of longer subsequences. From Table 7A, we can conclude that although RHSVV has the highest binding strength, the smaller HSVV also has a high binding strength when compared to other subsequences. No conclusions can be made from the single occurrence of RHSVVV because some variability exists in the MFI measurements and because multiple subsequence occurrences are required to disambiguate which subsequence on a peptide caused the antibody binding. Moreover, longer subsequences such as FFRHS, FRHSV, and HSVVV have very low binding strength. Thus, the results for Ab1 are apparently typical for other samples in that not all sub-subsequences of the epitope bind strongly to the antibody. Typically, the longest subsequence was estimated and is listed in Table 1A. This often corresponded to the most dominant subsequence – the subsequence with the highest binding strength. For Ab1, the dominant subsequence was RHSVV (shaded in Table 7A). Note that not only RHSVV but also HSVV occurred more frequently than the other L = 4 and L = 5 epitopes. However, RHSVV has comparatively larger binding strength.

Table 7.

Subsequences of varying lengths Λ for (A) Ab1 and (B) HA₁, and (C) HA₂ subsequences that do not occur as often or that have lower binding strength.

(A) Ab1 sample	OCRC	Mean MFI	(B) HA1 sample	OCRC	Mean MFI	(C) HA2 sample	OCRC	Mean MFI
ℒ = 4			ℒ = 4			ℒ = 4
FFRH	44	1,394	YDAP	75	5,028	YPYD	22	813
FRHS	28	2,711	DAPE	98	884	PYDV	18	688
RHSV	87	3,119	ℒ = 5			YDVP	42	3,377
HSVV	402	11,455	YDAPE	16	61,414	DVPD	28	21,429
SVVV	5	1,087				VPDY	19	746
ℒ = 5						PDYA	462	757
FFRHS	4	2,250				ℒ = 5
FRHSV	2	1,308				YPYDV	0	–
RHSVV	208	65,535				PYDVP	1	31,435
HSVVV	7	2,062				YDVPD	3	65,535
ℒ = 6						DVPDY	1	65,535
RHSVVV	1	10,502				VPDYA	0	–
						ℒ = 6
						YPYDVP	0	–
						PYDVPD	1	65,535
						YDVPDY	0	–
						DVPDYA	0	–

The exact epitope was not estimated for the monoclonal antibody HA. The full epitope of this monoclonal antibody is YPYDVPDYA. The estimated epitope YDAPE appears to be a substitution (at positions 3 and 5) of the exact epitope YDVPD. We thus selected this nonexact epitope as our estimate because the exact subsequence occurred very infrequently on the array. Tables 7B and 7C show the occurrences of different epitope subsequences and the mean MFIs for the antibody epitope subsequence YDVPD and the estimated epitope sequence YDAPE, respectively. Although the antibody epitope sequence YDVPD occurred on the array with a high binding strength, the estimated epitope subsequence YDAPE occurred more frequently and with almost as high binding strength. The exact epitope was also not estimated for the monoclonal antibody FLAG. The nonexact estimate for FLAG was ALEKDGD. The similarity of this estimated epitope for FLAG, and the true epitope of DM1A, may be due to the similarities between their true epitopes and the scarcity of sufficiently long true epitope subsequences of FLAG. The important overlap between these two epitopes is the KD amino acid pair and the permissive binding of FLAG antibodies, which may reflect its unusual highly charged epitope.

The sparse distribution of true epitope subsequences of FLAG on the array is seen in Table 8A. The only true epitope subsequence with high binding strength was DYKDD; however, this subsequence only occurred twice on the array, which is not very frequent for a length L = 5. Therefore, it is difficult to identify it as an important subsequence. The overlap between the epitopes of the monoclonal antibodies FLAG and DM1A is the amino acid pair KD. The MFI effects of this overlap can be seen by comparing the MFIs of peptides that contain subsequences similar to the epitopes. Figure 3A and B provides MFI scatter plots for all the peptides on the array that contain L = 4 or longer subsequences of peptide ALEKDGD. In Figure 3A, the MFIs of HA are plotted with respect to the MFIs of FLAG. As expected, the MFIs for HA are low as this sample has the unrelated true epitope YPYDVPDYA. This is in contrast to the scatter plot in Figure 3B, which shows the MFIs of DM1 A with respect to the MFIs of FLAG, which have similar epitopes. Therefore, we surmise that the peptides containing these subsequences are bound most strongly.

Table 8.

(A) Subsequences of varying length Λ for FLAG and (B) identified mimotopes for five monoclonal antibody samples with corresponding OCRC, OCRC without down selection (no DS), mean MFI, and maximum MFI.

(A) Flag Sample	OCRC	Mean MFI	(B) Sample mAb	Full Epitope	Potential Mimotope	OCRC	OCRC no DS	Mean MFI	Max MFI
ℒ = 4			2C11	NAHYYVFFEEQE	DARWFN	4	10	1,197	65,535
DYKD	16	947	4C1	LQAFDSHYDY	ADSWP	10	20	12,769	65,535
YKDD	9	799	a10	EEDFRV	EWDVA	15	41	65,535	65,535
KDDD	2	523	flag	DYKDDDDK	ALEKDGD	250	267	65,535	65,535
DDDK	90	391	Ha	YPYDVPDYA	EDLPO	7	15	1,706	11,385
ℒ = 5
DYKDD	2	23,744
DDDDK	22	376

Figure 3.

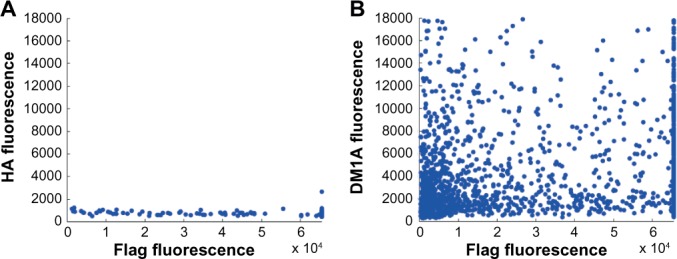
Scatter plots of the MFIs of FLAG compared to the MFIs of (A) HA and (B) DM1A.

Substitution analysis

The epitope estimates are derived from the array peptides that contain that specific epitope subsequence. In addition to that specific subsequence, there are other peptides on the array that contain that same subsequence, but with a single amino acid substitution. Our proposed algorithm for detecting subsequences using single amino acid substitutions is provided in Algorithm 2. Using this algorithm, we can analyze how these single residue substitutions affect the binding strength. In so doing, we see that antibody: peptide binding is not exact, but that some of the amino acids in the epitopes can be substituted without much of a loss in binding strength. In some cases, these substitutions increase the binding strength. We have previously reported on this phenomenon.^11,28 However, specific residues in the epitope subsequence are also absolutely required for the binding. Substituting them with different amino acids can dramatically decrease the binding strength. One example of this is seen in Tables 9 and 10, which show amino acid substitutions at positions that are tolerant of substitutions and intolerant of substitutions, respectively. Figure 4A and B contains plots of the MFIs listed in the tables; the plots clearly show how much more tolerant of substitutions 4C1 is for epitopes in the first amino acid of the subsequence YDS than it is for substitutions in the third amino acid of the subsequence GYS. The tolerance for amino acid substitutions is particularly helpful when trying to estimate an epitope whose exact subsequences do not appear frequently on the array. This is true for FLAG, where the third residue of the exact subsequence KDDD is substituted to form subsequence KDGD. This subsequence appears more frequently on the microarray.

Table 9.

Amino acid substitutions for GY_S with OCRC and mean MFI.

AA	A	R	N	D	Q	E	G	H	L	K	F	P	S	W	Y	V
OCRC	267	195	26	158	13	21	6	20	165	42	13	47	21	16	9	37
mean MFI	803	1, 0 11	947	3,667	873	805	867	784	784	859	775	837	813	856	780	751

Table 10.

Amino acid substitutions for_YDS with OCRC and mean MFI.

AA	A	R	N	D	Q	E	G	H	L	K	F	P	S	W	Y	V
OCRC	11	19	100	6	85	129	158	201	5	67	107	55	9	50	6	16
mean MFI	1,457	982	977	3,792	1,776	4,337	3,667	1,337	693	1,119	883	2,503	1,624	1,194	844	855

Figure 4.

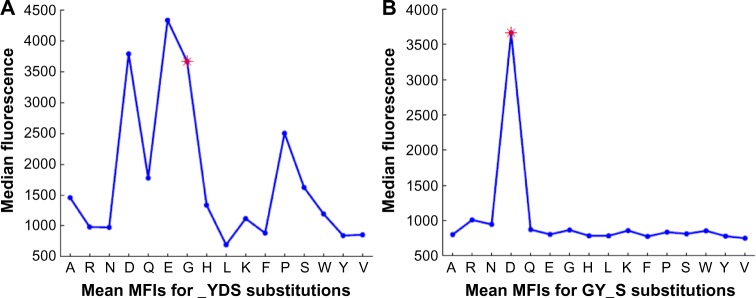
The mean MFIs for two different substitutions of GYDS: (A) substitution_YDS is tolerant of substitutions; and (B) substitution GY_S is not tolerant of substitutions.

Mimotope identification performance analysis

The proposed approach identified some potential mimotopes in Table 1B, for five of the monoclonal antibody samples we analyzed. As discussed in the Results section, we provide selected criteria that we developed using mimotopes to monoclonal antibodies. Although our mimotope analysis is only theoretical, we found that our criteria seem to match mimotope identification approaches in recent publications.^20,29,30 More specifically, in the study by Roche et al.⁸, mimotopes were identified from peptide sequences by T cells with common receptors as they resulted in increased antigen-specific immunity. As the authors discuss, optimizing the identification of mimotopes can lead to improvements in antigen-specific vaccines. Mimotopes were identified for a monoclonal cancer antibody using phage display screening of random peptide libraries.⁶ Similar to our findings, the mimotopes were selected based on their strong binding to the original peptides. It was also noted that stronger binding was obtained with single residue substitutions. In the study by Reineke, et al.³⁰, mimotopes for monoclonal antibodies were investigated for biomarker assay development. It was found that the diversity of mimotopes is inversely correlated with binding strength.³¹

Tables 2–4 contain information about the potential mimotopes for monoclonal antibody samples 2C11, A10, and HA. For example, the potential mimotope for 2C11 is the lightly shaded subsequence DARWFN in Table 2B. This subsequence meets the four criteria C1–C4 listed for mimotopes in the Results section. Furthermore, some of its subsequences, ARWFN, ARWF, and WFN, are seen in the L = 5 lightly shaded subsequence in Table 2A. Similarly, the potential mimotopes for A10 and HA meet the necessary criteria, and subsequences of these mimotopes are seen in the top OCRC lists of smaller lengths. Table 8B provides additional information on how we identified the mimotopes for the five monoclonal antibodies in Table 1B. For each monoclonal antibody, the four criteria in the Results section are met. In particular, all these mimotope subsequences have very large median or maximum fluorescence intensities.

Applications

As seen in Figure 5, the 330K-peptide microarray is capable of identifying peptides for disease-specific antibodies even through the milieu of nondisease antibodies that compose the humoral immune repertoire. For each disease in Figure 5, there are hundreds of peptides that specifically bind to patient sera for a given cancer type, but not to sera from patients with other types of cancer. The peptides selected in this way probably have reasonably high selectivity for the disease of interest, in this case GBM, a grade IV astrocytomal brain cancer. Peptides are shown on the top right of Figure 5, and simple alphabetical sorting illustrates a strong tendency to common motifs that extend to the N-terminus of these peptides. Deeper searches reveal common motifs buried within the peptides, and some found near the C-terminal linker. A simple alignment against a three-frame translated mRNA tumor library reveals numerous “hits” when the brain cancer peptides are aligned to the brain cancer mRNA library but not when aligned to esophageal, breast, or ovarian cancer mRNA libraries. In fact, when these GBM samples were processed on the 10K-peptide low-density arrays, some overlap was seen between the 10K library and the 330K library, although there was no intentional overlap in these libraries. To ensure that the RNAs thus identified were actually generated in diverse tumor samples and were not an artifact of the RNA library construction, a tumor lysate from multiple GBM patients was used as the source for extracting RNA. These RNA molecules were amplified using flanking primers to the predicted frameshift mutations. In every case, the predicted frameshift was amplified. Although there are probably many nonlinear or nonprotein, or even wild-type, autoantigens generated by tumors, this experiment demonstrates that the principles espoused in this manuscript may enable deciphering of the eliciting antigens produced by tumor cells in the same way that the monoclonal antibodies were deciphered.

Conclusion

We propose an advanced signal-processing technique for detecting unique subsequences from microarray peptide sequences. The technique combines a unique mapping of the peptide amino acids to highly localized Gaussian signals and a time–frequency processing method that iteratively extracts Gaussian signals undergoing the same time and frequency shifts. We use the technique with the immunosignature of random peptide sequences to effectively estimate epitope antigen subsequences. We demonstrated this result by analyzing eight monoclonal antibody samples, for which we estimated the exact (or close-to-the-exact) epitope subsequence matches. As our approach inherently allows mapping and processing of amino acid substitutions in peptide sequences, we were also able to analyze the effect of substitutions on the binding strength of the estimated subsequences. In particular, we showed that shorter subsequences, with lengths of four or five amino acids, resulted in many single amino acid substitution subsequences on the peptide array. We also applied the technique to identify plausible mimotope antigen subsequences, and we found a number of potential mimotopes for the monoclonal antibody samples. Using actual human serum samples from patients with advanced brain cancer, we demonstrated that subsequence epitope identification can work even within the complex mix of nondisease immunoglobulins. Immunodiagnostics and immunotherapeutics are possible results from this research. Although mimotopes as vaccines and therapeutics may not have been the panacea once envisioned, this method enables a rapid screen on inexpensive microarrays with fair-to-high resolution of both natural and mimotope targets.