Abstract
The correlation between sub-band gap absorption and the chemical states and electronic and atomic structures of S-hyperdoped Si have been extensively studied, using synchrotron-based x-ray photoelectron spectroscopy (XPS), x-ray absorption near-edge spectroscopy (XANES), extended x-ray absorption fine structure (EXAFS), valence-band photoemission spectroscopy (VB-PES) and first-principles calculation. S 2p XPS spectra reveal that the S-hyperdoped Si with the greatest (~87%) sub-band gap absorption contains the highest concentration of S2− (monosulfide) species. Annealing S-hyperdoped Si reduces the sub-band gap absorptance and the concentration of S2− species, but significantly increases the concentration of larger S clusters [polysulfides (Sn2−, n > 2)]. The Si K-edge XANES spectra show that S hyperdoping in Si increases (decreased) the occupied (unoccupied) electronic density of states at/above the conduction-band-minimum. VB-PES spectra evidently reveal that the S-dopants not only form an impurity band deep within the band gap, giving rise to the sub-band gap absorption, but also cause the insulator-to-metal transition in S-hyperdoped Si samples. Based on the experimental results and the calculations by density functional theory, the chemical state of the S species and the formation of the S-dopant states in the band gap of Si are critical in determining the sub-band gap absorptance of hyperdoped Si samples.
Silicon (band gap Eg = 1.12 eV) that is hyperdoped with chalcogens (S, Se or Te) beyond the equilibrium solubility limit exhibits sub-band gap light absorption, making it a suitable material for Si-based infrared (IR) and photovoltaic applications1,2,3,4,5. In earlier studies it was claimed that above a critical concentration of dopants in Si, an insulator-to-metal transition (IMT) is caused by the formation of an intermediate band of the dopant states within the band gap of Si. Optically sensitive dopant states relatively deep in the band gap of the Si are generally believed to be responsible for the significant increase in the IR absorption. Such dopant states have been accepted as the origin of non-radiative recombination, facilitating the absorption of photons with energy that is less than the band gap of the Si. Previous investigations reported that sub-band gap absorption can be deactivated and reactivated through thermal treatment with laser irradiation3,4. The dopant diffusion causes the deactivation of sub-band gap absorption after thermal annealing and stabilization of high concentration of point defects/dopant states at high temperatures responsible for the reactivation. This phenomenon can be explained briefly in terms of diffusion theory6,7. The dopants contribute to IR absorption because they are present within crystalline grains and are coordinated with the Si lattices, consequently precipitating as a non-optically sensitive species6,7. Recently, Newman et al.8 performed Se K-edge extended x-ray absorption fine structure (EXAFS) studies of Se-hyperdoped Si samples and found that during annealing, the Se precipitated at grain boundaries and formed non-IR absorbing silicon diselenide (SiSe2) precipitates, reducing the sub-band gap absorption. The results of an EXAFS study revealed that thermal treatment facilitated the return of Se-hyperdoped Si samples to equilibrium atomic structural order with a reduction of the sub-band gap optical absorption. An Si L3,2 x-ray emission spectroscopic (XES) study of S-doped Si samples [up to 0.7 atomic percentage (at.%)]9 exhibited induced emission feature intensity above the Si valence-band-maximum (EVBM), which scaled linearly with S concentration associated with the S-dopant, and the line-shape of the S-dopant feature changed across the IMT. The annealing of the S-doped Si samples reduced the induced emission intensity, which was associated with the quenching of sub-band gap absorption9. Theoretical calculations suggested that the geometries and coordinations of the S impurities in clusters change upon annealing, altering the electronic and atomic structures and quenching sub-band gap absorption10. Density Function Theory (DFT) suggested that the chalcogen-induced IMT arises from the merging of dopant states and conduction bands in chalcogens hyperdoped Si4,5,11.
To understand better the optical properties that are relevant to IR or photovoltaic applications and to elucidate the physics of the IMT in Si-based hyperdoped with chalcogens, the relationship between the sub-band gap absorption and electronic and atomic structures need to be studied. Although many of investigations have focused on the optical properties of hyperdoped Si, the electronic and atomic structures of chalcogen dopants and the Si host, respectively, and their optical activity in relation to sub-band gap absorption in hyperdoped Si remain unclear.
This study investigates S-hyperdoped Si samples using synchrotron-based techniques such as x-ray photoelectron spectroscopy (XPS), x-ray absorption near-edge spectroscopy (XANES), EXAFS, valence-band photoemission spectroscopy (VB-PES) and first-principles DFT calculations. The XPS reveals that a high concentration of S, particularly as S2− (monosulfide) species, in an absorbing sample with a high (~87%) sub-band gap and thermal annealing, increases the formation of non-IR absorbing larger S clusters [polysulfides (Sn2−, n > 2)]. The results of XANES and VB-PES reveal that doping with S modifies the electronic structures of the hyperdoped Si samples. A Si K-edge EXAFS study further shows that S-hyperdoping induces high structural disorder around Si atoms. However, the nearest-neighbor (NN) bond length of Si-Si remains constant as the doping concentration of S is varied. There is no clear evidence that thermal annealing at 500 °C and 700 °C yields Si-S precipitates, presumably owing to the decrease in the sub-band gap absorption in chalcogen hyperdoped Si samples. Based on our experimental measurements, the chemical state of the S species and the S-dopant states in the band gap of Si are critical in determining the sub-band gap absorption of hyperdoped Si samples. A first-principles calculations using DFT method supports experimental results as well as the occurrence of the IMT at/above a critical concentration of S dopants in the hyperdoped Si samples. Our study provides clear evidence of the active chemical state of S species on the surface of Si and S-dopant states deep in the band gap of Si, are responsible for the sub-band gap absorption in the hyperdoped Si samples.
Results and Discussion
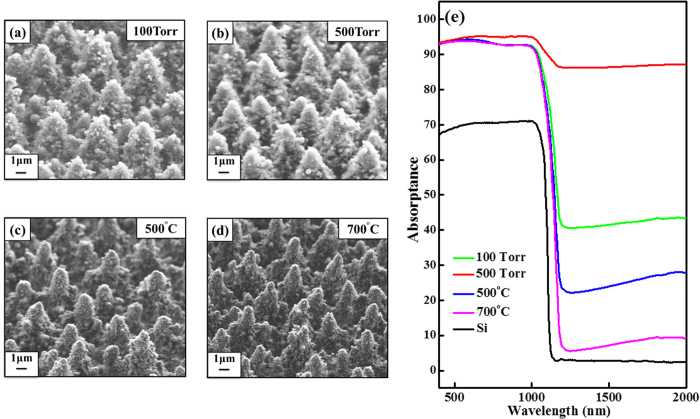
Figure 1(a)–(d) present scanning electron microscope (SEM) images of the surfaces of the S-hyperdoped Si samples that were formed by femtosecond (fs) laser irradiation and annealing. The surface morphology of the S-hyperdoped Si samples varied from smooth to needle-like structure as the pressure of the SF6 gas increased. The needle-like microstructure of the samples prepared with a gas pressure of 500 Torr became increasingly porous as the annealing temperature increased from 500 °C to 700 °C. Figure 1(e) displays the IR absorption of S-hyperdoped Si samples and undoped Si(100) for reference. All S-hyperdoped Si samples exhibit broad and featureless absorption which is consistent with the results reported in the literature6,7,9,12,13. Clearly, the 100 Torr sample shows an average IR absorptance of ~42%, while that of the 500 Torr sample was much greater, ~87%. However, annealing the 500 Torr sample at 500 °C reduces the IR absorptance to ~23%, and annealing at 700 °C reduces it further to ~7%. Interestingly, the average IR absorptance of the sample that was annealed at 700 °C was closer to that of reference Si(100) than those of other hyperdoped Si samples. These results reflect the fact that the sub-band gap absorption of the hyperdoped Si samples was strongly related to concentration of S dopant and also affected by thermal annealing. Detailed investigations of the morphology and optical properties of hyperdoped Si samples, as effect of SF6 gas pressure and annealing temperature, can be found elsewhere12,13,14,15,16.
Figure 1.
(a–d) SEM images of S-hyperdoped Si samples 100 Torr, 500 Torr, and the latter annealed 500 °C and 700 °C, respectively. (e) IR absorptance of S-hyperdoped Si samples.
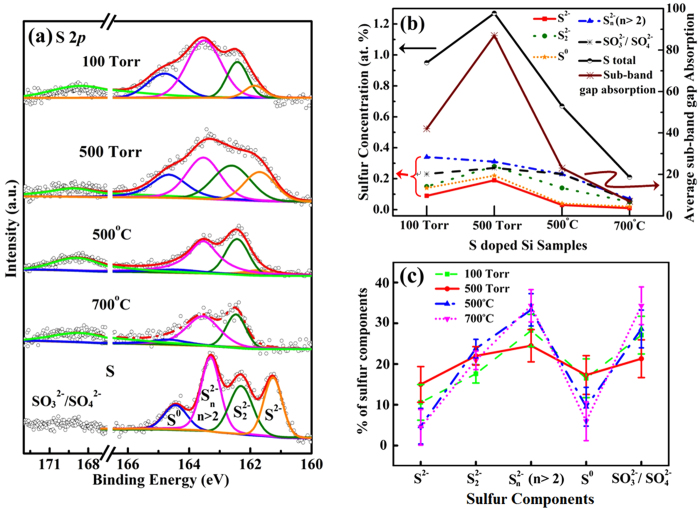
Figure 2(a) presents the S 2p core-level XPS spectra of S-hyperdoped Si samples prepared at 100 Torr and 500 Torr, and the 500 Torr sample that was further annealed at 500 °C and 700 °C, respectively. The S 2p core-level XPS spectrum of powder S is included for comparison. The XPS spectra of all the samples were deconvoluted into several features and Table SI of the Supplementary Information present detailed parameters such as energy position, full width at half maximum (FWHM) of the features and the percentage of each corresponding component. The at.% of each S species on the sample surface is obtained by dividing the integrated area under a characteristic feature by the total area under their corresponding core-level XPS spectra. The binding energies (BE) of S2− (monosulfide), S22− (disulfide), Sn2− (n > 2, polysulfides) and S0 (elemental S) are located at ~161.2 eV, 162.3 eV, 163.3 eV and 164.4 eV, respectively17,18,19,20,21. In the spectra of the hyperdoped Si samples, one extra broad and weak feature at ~169–170 eV was observed and attributed to SO32− (sulfite) and/or SO42− (sulfate)20. Overall, as presented in Fig. 2(a), the general line-shape of S 2p spectrum of the S-hyperdoped Si samples is shifted to a higher BE (0.3–0.5 eV) than that of pure S and their characteristic features are broader, owing to a change in the chemical environment of the S-dopant in the Si matrix. Also, S species in the sample have more chemically inequivalent atoms than the reference S22. Clearly, as shown in Tab. SI, the 500 Torr sample yield a stronger S2− (monosulfide) feature as compared to the 100 Torr sample. On the other hand, the annealed 500 Torr samples (annealed at 500 °C or 700 °C) have barely visible S2− (monosulfide) feature [Fig. 2(a) & Tab. SI]. Annealing reduces the overall XPS intensity of the S 2p core-level features, revealing a lower concentration of S species on the surfaces of the annealed samples than those of the 100 Torr and 500 Torr samples. To calculate total at.% of S on the surface of each sample, XPS survey scans (in Fig. S1 of Supplementary Information) were performed and presented in the Tab. SI of the Supplementary Information. Although the sample surface was cleaned using HF to remove the surface oxides or carbon-related compounds before the synchrotron measurements were made, a considerable amount of O/C and small amount of N were observed in survey scan (Fig. S1 and Tab. SII of the Supplementary Information). The total at.% of the S 2p feature on the surface of the 100 Torr, 500 Torr and annealed samples (annealed at temperatures of 500 °C and 700 °C) were ~0.95%, 1.27%, 0.67% and 0.20% (Tab. SI), respectively. The surface XPS analysis revealed that the 500 Torr sample had a higher concentration of S than the other three S-hyperdoped Si samples. The observed diminution in the S concentration upon annealing of the 500 Torr sample (at 500 °C and 700 °C) is attributed to the diffusion of S atoms deep into the Si matrix as a result of thermal annealing6,15.
Figure 2.
(a) Core-level XPS spectra of S 2p of hyperdoped Si samples, and for comparison, a standard sample of pure S. (b) Plot of S at.% and average sub-band gap absorptance in hyperdoped Si samples. (c) Plot of percentage of each S component in individual hyperdoped Si samples.
To obtain a correlation between the optical properties and the concentration of the S-dopant in the S-hyperdoped Si samples we have plotted the average sub-band gap absorption and the S at.% of the S-hyperdoped Si samples, shown in Fig. 2(b). The 500 Torr sample, which had the highest total S at.% (1.27%), exhibited the highest sub-band gap absorptance ~87%. The average sub-band gap absorptance reached ~42% in the 100 Torr sample, which contained 0.95% S in total. Annealing the 500 Torr sample at 500 °C and 700 °C drastically deactivate their absorptances to ~23% and 7%, corresponding S total at.% value 0.67% and 0.20%, respectively. As mentioned above, previous studies have attributed the deactivation of sub-band gap absorptance upon thermal annealing to the diffusion of dopants6,15. Those studies found that the sub-band gap absorptance of the samples decreases as the diffusion length of the dopant in the Si matrix increases. The diffusion lengths of S in Si samples which annealed at 500 °C and 700 oC were ~30 nm and 250 nm, respectively. [The diffusion length of S dopant was calculated using diffusion length d = √Dt, where t is the annealing time; D is the bulk diffusivity of S dopant in the Si matrix, given by D = D0exp(−Ea/kT); k is Boltzmann’s constant; T is the annealing temperature; and Ea and D0 are temperature-independent constants that were obtained from the literature on the bulk diffusivity of dopants]6. According to the analysis of S 2p core-level XPS results [Fig. 2(b)], the 500 Torr sample contains more S at.% than other S-hyperdoped Si samples. To understand further how the percentages of S in various chemical states varies among the samples and the effect of the S species in the sub-band gap absorptance, Fig. 2(c) presents the percentage of each S species in S-hyperdoped Si samples by normalization of total S concentration 100 on a scale in each corresponding samples. In the 100 Torr sample, the concentrations of the S2− and S22− species are 9.1% and 15.4%, respectively and that of the Sn2− species is 36.0%. Notably, that S0 and SO32−/SO42− species generally do not absorb energy in the IR range23,24. The 500 Torr sample contains 15.1% S2−, 21.8% S22− and 24.6% Sn2− species. Annealing of the 500 Torr sample at 500 °C (700 °C) reduced the concentrations of the S2− and S22− species to 4.6% (2.3%) and 20.8% (22.7%), respectively, but increased the concentration of Sn2− to 34.5% (36.6%). Interestingly, the difference between the percentages of S2− and Sn2− species is ~10% in 500 Torr, 17% in 100 Torr and much larger ~30% in the annealed samples. The percentage of S2− species is higher in the 500 Torr sample than in the other S-hyperdoped Si samples. However, annealing the 500 Torr sample at 500 °C or 700 °C considerably increases the number of larger S clusters (Sn2−) in relative to that of 500 Torr sample. However, annealing does not affect much the S22− species concentration. Mo et al.10 theoretically proposed that the formation of large clusters of dopant makes Si optically transparent, but S dimer species remain optically absorbing; they also claimed that in Si matrix S dopants are preferentially present at substitution sites and so S-dopant may introduce electronic states deep inside the band gap of Si, making the sample light-absorbing. Annealing of the samples increase the clusters of S species as Sn2− (n > 2), changing the optical properties as the geometry and coordination of S atoms get modified in the clusters. The results of the S 2p core-level XPS spectra provide clear evidence that the 500 Torr sample with the largest (~87%) sub-band gap absorption contains the highest concentration of S-dopant, especially S2− species, and that thermal annealing increases the percentage of larger clusters Sn2− relative to that of S22− (Tab. SI), reducing the sub-band gap absorptance to 23% and 7% for the 500 °C and 700 °C samples, respectively. Therefore, a clear relationship is obtained between the chemical states of the S species and the sub-band gap absorptance of the S-hyperdoped Si. The classification of the IR-absorbing S species reveals that S2− are the optically active species and thermal annealing increases the number of non-IR absorbing larger S clusters (Sn2−, n > 2) in S-hyperdoped Si samples. The S22− species remain optically absorbing and concentration of these species does not change much after thermal annealing10.
Figure S2 in Supplementary Information presents the Si 2p core-level XPS spectra of S-hyperdoped Si samples. The Si 2p core-level XPS spectra of all the samples are deconvoluted, and the related parameters are presented in detail in Tab. SIII of the Supplementary Information25,26,27,28,29. Features that are associated with various O-containing Si species, Si2O (Si1+), Si2O3 (Si3+) and SiO2 (Si4+), were observed as presented in Fig. S2 and Tab. SIII. The Si 2p3/2 features of the 100 Torr and 500 Torr samples were shifted to a lower BE (at 99.3–99.4 eV) than that of the reference Si(100) (at 99.6 eV) and the shift was reversed by annealing. The observed feature shift (0.2–0.3 eV) is attributed to the structural disordering by presence of amorphous Si at the surface29,30. Micro-Raman spectroscopy verified the pressure-induced formation of Si polymorphs, as presented in Fig. S3 of the Supplementary Information. This result is consistent with previously made micro-Raman measurements on fs-laser-irradiated Si as the effect of pressure, indicating the formation of pressure-induced amorphous Si and/or Si polymorphs on the sample surface31 and they are recovered close to that of reference Si(100) upon annealing at high temperature.
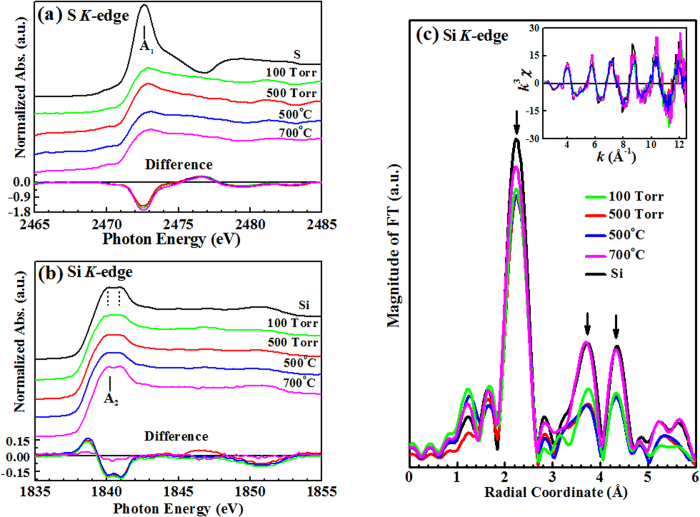
Figure 3(a) displays the S K-edge XANES of the S-hyperdoped Si samples and pure S as a reference. According to the dipole-selection transition rule, the S K-edge XANES spectrum arise from the transitions of S 1s core electrons to unoccupied density of states (DOSs) with 3p character above the Fermi level. The line-shape of the S K-edge XANES spectra in the region 2472–2480 eV (denoted as A1) is broadened and the feature of the S-hyperdoped Si samples reduce gradually with incident photon energy, varying quite differently from that of pure S, which was sharp and intense. The lower panel in Fig. 3(a) shows the difference between the S K near-edge absorption spectra of S-hyperdoped Si samples and reference pure S. The intensity of feature A1 of the 100 Torr, 500 Torr and annealed samples (that are at 500 °C or 700 °C) is lower than that of reference pure S. The chemical states of the S species in S-hyperdoped Si samples are responsible for the broad and declining feature, which is unlike that of pure S. Figure 3(b) displays the Si K-edge XANES spectra of S-hyperdoped Si samples and the reference undoped Si(100) sample. The spectra are normalized to have the same area in the energy region between 1855 and 1865 eV [not fully shown in the Fig. 3(b)]. The threshold energy and general line-shape of the Si K-edge XANES spectra of the S-hyperdoped Si samples are similar to that of the reference Si(100). The characteristic double-peak feature (indicated by two dashed lines, denoted as feature A2) of S-hyperdoped Si samples and reference Si(100) above the threshold and its approximate 1.1 eV energy separation are consistent with earlier studies32,33,34,35. Hitchcock et al.32 interpreted the splitting-feature (A2) at ~1840 eV at the Si K-edge as associated with the excitation from Si 1s to the unoccupied Si 3p above the conduction-band-minimum (ECBM), based on crystal symmetry. Clearly, the doublet Si K-edge near-edge feature of reference Si(100) arises from long-range ordering. In S-hyperdoped Si samples, a very slight blurring of the doublet as the SF6 gas pressure increases was observed, implying the degradation of the long-range order of sample surface and possible formation of amorphous Si34,36. Si K-edge XANES further supports the Si 2p XPS and micro-Raman measurements revealing the pressure-induced formation of amorphous Si and/or Si polymorphs on the surface of the S-hyperdoped Si samples. Annealing the 500 Torr sample at 700 °C causes the relatively clear splitting of the feature again, suggesting that the S-hyperdoped Si sample that was annealed at a high temperature exhibited a structurally ordered surface that reverted closely to that of the reference Si(100). The lower panel in Fig. 3(b) shows the difference between the Si K near-edge absorption spectra of S-hyperdoped Si samples and reference Si(100). Notably, the overall net intensity of various spectra (obtained by integrating the feature area in the energy range of 1837–1842 eV) is negative, and the intensity of feature A2 of the 100 Torr, 500 Torr and annealed samples (that are at 500 °C or 700 °C) is lower than that of reference Si(100), indicating an increase (or decrease) in the number of the occupied (unoccupied) DOSs of Si 3p in the conduction band of the S-hyperdoped Si samples relative to that of Si(100). This phenomenon can be associated with the partially S-dopant states within the band gap of Si, located close to ECBM; these merge with the conduction bands of Si and act as electron donors, as proposed by several studies4,5,10,11. Annealing the 500 Torr sample at 700 °C caused the difference in the feature A2 almost to disappear, suggesting that annealing the sample to 700 °C made the DOSs of Si 3p in the hyperdoped Si very close to that of pure Si(100). Evidently, the fact that Si K-edge XANES exhibit variations in the DOSs of Si 3p at/above ECBM demonstrate that S hyperdoping modifies the electronic structure of Si and create structural disordering in the samples. However, annealing the 500 Torr sample to 700 °C caused the DOSs of the Si 3p orbital to revert to one similar to that of reference Si(100). It also indicates that a high temperature annealing reduces structural disorder in S-hyperdoped Si and exhibited a structurally ordered surface that reverted closely to that of the reference undoped Si(100).
Figure 3.
(a) S K-edge XANES of hyperdoped Si samples and pure S as a reference. Bottom panel shows the difference spectra of hyperdoped Si samples and reference pure S. (b) Si K-edge XANES of hyperdoped Si samples and reference undoped Si(100). Bottom panel shows the difference spectra of hyperdoped Si samples and reference Si(100). (c) FT of Si K-edge EXAFS spectra of hyperdoped Si samples for k between 2.3 and 12.5 Å−1. Inset plots EXAFS k3χ data.
Figure 3(c) plots the Fourier transform (FT) of the Si K-edge EXAFS spectra, and corresponding k3χ data (inset) for the S-hyperdoped Si samples and the reference Si(100), further confirming the structural ordering of Si atoms in the S-hyperdoped Si samples. The first main feature in the FT spectra of the S-hyperdoped Si samples (indicated by the first vertical arrow) is at ~2.3 Å and corresponds to the NN Si-Si bond length (without phase correction); this position is almost the same as that of the feature of reference undoped Si(100)25,37. The second and third main FT feature (also indicated by vertical arrows) at ~3.6 Å and 4.3 Å reveal the high-shell Si-Si bond distances. The general line-shape and radial distribution of the FT spectra of the 100 Torr, 500 Torr and annealed samples (annealed at 500 °C and 700 °C) are close to those of reference Si(100), indicating that the local atomic structures of Si atoms in the S-hyperdoped Si samples are similar to that of reference Si(100). However, the S-hyperdoped Si samples exhibit large structural disorder (or high Debye-Waller factors) around Si atoms, as evidenced by the lower main feature intensities in the FT spectra than those of the reference Si(100). The structural disordering of Si may have been caused by the S-dopant diffusion which increases structural disorder and affects the intensity of the FT-feature of the S-hyperdoped Si samples to be lower than that of reference Si(100). Especially, the intensity of the main FT-features of the sample that was annealed at 700 °C is higher than those of the other S-hyperdoped Si samples. The moderately high intensity of the feature in the FT spectrum of 700 °C sample in Fig. 3(c) suggests that the structural ordering of Si in the annealed sample, resembles closely that of reference Si(100). This result reveals that annealing at 700 °C restores structural ordering close to that of reference Si(100), which finding is consistent with the finding Si K-edge XANES spectra that are shown in Fig. 3(b). On the other hand, as discussed by Newman et al.8, the Se K-edge EXAFS revealed that the NN Se-Si bond distance increased with the sub-band gap absorptance. Newman et al. also observed that annealing the samples reduces the Se-Si bond length and the sub-band gap absorptance, owing to the formation of the SiSe2 precipitate. In Si K-edge EXAFS spectra that are shown in Fig. 3(c), no clear change in the Si-Si bond length is observed and the formation of Si-S precipitates in S-hyperdoped Si samples is unlikely. If Si-S precipitates were formed in the S-hyperdoped Si samples, then the extra feature of NN Si-S would have appeared at a bond length of ~2.1 Å in the FT spectrum10,38. The FT spectra in Fig. 3(c) show no clear changes in the general line-shape, and the splitting of the first main feature (near 2.3 Å) in the FT spectra rules out the possibility that the change of the sub-band gap absorption is directly related to the formation of Si-S precipitates in the S-hyperdoped Si samples. Importantly, the 500 Torr sample has an average IR absorptance of ~87%, but annealing at 500 °C reduces the average IR absorptance to ~23% and annealing at 700 °C reduce it further to ~7%. Both the Si K-edge XANES and EXAFS results showed that the sample annealed at the high temperature of 700 °C and the undoped Si(100) reference have similar near-edge absorption feature and structural ordering, illustrating that the sub-band gap absorption of the S-hyperdoped Si samples is clearly related to their electronic states and atomic structural ordering, which are also influenced by the concentration of S-dopant and thermal annealing.
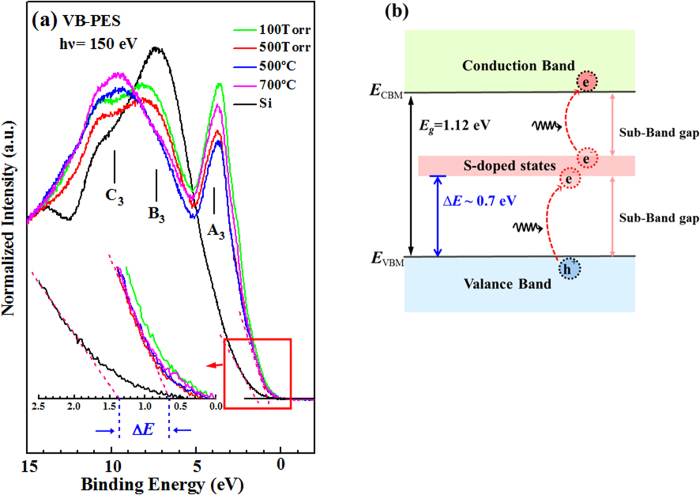
Figure 4(a) displays the VB-PES spectra of S-hyperdoped Si and reference undoped Si(100) samples that were obtained using a photon energy of 150 eV; the spectra include three major features, A3-C3. The VB-PES spectra of the S-hyperdoped Si samples and reference Si(100) differ strikingly. Strong S-dopant states, feature A3 (at ~3.5 eV), were clearly observed in the S-hyperdoped Si samples and the 100 Torr sample had the most intense feature A3. Notably, the SEM images of S-hyperdoped Si samples [Fig. 1(a)–(d)] reveal that the surfaces of the S-hyperdoped Si samples are quite rough and S cannot be distributed uniformly over the sample. In the SPEM measurement39, the randomly selected region of the surface of the highly S-hyperdoped sample may have contained less S, explaining the non-linear increase of the intensity A3 with the concentration of S. Although the 500 Torr sample has the highest concentration of S, it does not have the most intense feature A3 in Fig. 4(a). Since the photoionization cross-section of S 3p is nearly four times that of Si 3p at an excitation photon energy of hν = 150 eV40, feature A3 of S-hyperdoped Si samples can be assigned mainly to the S-dopant states at/near EVBM or below zero energy (corresponding to 0 eV)41,42,43. The reference Si(100) exhibits broad features that are centered at ~7.5 eV and 10 eV below the zero energy denoted as B3 and C3, respectively, attributed to the Si 3s-3p and 3s-like bands25,43,44,45,46. Apparently, the EVBM of the S-hyperdoped Si samples was closer to zero energy than that of the reference Si(100). Typically, the EVBM of the samples is precisely determined by extrapolating the leading edge of the spectrum to the baseline at its largest slope47,48,49,50. The magnified region in the lower panel of Fig. 4(a) reveals an EVBM of the S-hyperdoped Si samples is at ~0.7 eV, which is 0.7 eV shifted above in relative to that of the reference Si(100) which has EVBM at ~1.4 eV. The shift in the EVBM of the S-hyperdoped Si samples from that of reference Si(100) reveals that S dopants induced formation of electron states or an impurity band at ~0.7 eV above the EVBM of pure Si as shown in Fig. 4(b)42,51,52, which is schematically depicted as an energy level between the S-dopant states and EVBM/ECBM of Si. Earlier studies have suggested that chalcogen dopants, which can introduce various electron states deep in the band gap of Si, act as electron donors and may form an impurity band2,53,54. Such localized impurities have been accepted as being responsible for non-radiative recombination, in which process a free electron and a free hole recombine in the material. When the impurity band is formed in an adequately high concentration of dopant, and two photons have less energy than the band gap (sub-band gap), a free electron-hole pair is formed via an impurity energy level somewhere in the band gap, as schematically presented in Fig. 4(b), significantly increasing the absorption of IR energy from the solar spectrum2,55,56. Recently, Fabbri et al.57 found that S-induced luminescence around 0.85 eV which is at an energy that is deep inside the band gap of a substitutional S atom or a charged S dimer in Si; they also observed that the quenching of luminescence correlated closely with predicted overlap between the impurity band and the conduction band of Si. The VB-PES spectra of S-hyperdoped Si samples herein reveal that the S dopants introduced electron states ~0.7 eV above the EVBM of pure Si, not only forming an impurity band deep inside the band gap of Si that gives rise to strong sub-band gap absorption, but also causing an IMT when the S dopant is at/above a critical concentration4,5,11. The concentrations of S dopant should be similar to or greater than the Mott transition critical concentration in order to observe metallic-like conduction owing to overlap of the wave-functions of two impurity sites48. The critical concentration for a Mott transition to metallic-like conduction for hyperdoped Si samples has been estimated to be near 1019 cm−32,3. Accordingly, in this study, in which the S doping in the Si was estimated to be greater than approximately 1020 cm−3, the S donors were at/above the critical density for a Mott transition; the induced deep S-dopant states presumably behaved in a manner that was similar to metallic-like conduction owing to a delocalized electron wave-function inside the band gap of Si, and the S-dopant states, assumed to be delocalized states, formed an impurity band, which was responsible for the metallic-like conduction inside the band gap of the hyperdoped Si samples42,51,52.
Figure 4.
(a)VB-PES spectra of hyperdoped Si samples and reference undoped Si(100). (b) S dopants introduce electron states or impurity band 0.7 eV above EVBM of reference Si. S-dopant states or impurity band located in band gap of Si facilitates generation of charge carriers that participate in absorption of two or more lower-energy photons.
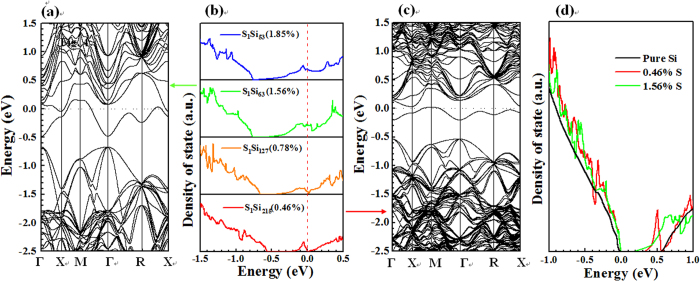
The S dopants introduced electron states, forming an impurity band within the band gap of the hyperdoped Si, and an IMT was observed at a critical concentration of S dopant. Related theoretical calculations were performed by means of the first-principles full-potential projector augmented wave (PAW) method58, implemented in the Vienna ab initio simulation package (VASP) package59. These calculations were based on the DFT method in the generalized gradient approximation with the Perdew–Burke–Ernzerh of (PBE) functional60. The plane-wave energy cutoff has been set to 500 eV. The Brillouin zone has been sampled in a 8×8×8 k-grid to carry out the total energy calculation and defect-induced structural optimization. The atomic positions have been relaxed until all of the residual forces were converged to better than 0.001 eV/Å−1. To simulate various concentrations of S doping in Si, the electronic DOSs for supercells of size n×n×n for a two-atom primitive cell (n = 2, 3, 4 and 5) and an eight-atom cubic cell (n = 2 and 3) were calculated. This sampling corresponds to systems of S1: SiN−1, for N = 16, 54, 64, 128, 216 and 250 in which the defect spacing increases uniformly from one supercell to the next. The calculated total DOSs in Fig. 5(b) and the corresponding band structures in Fig. 5(a) with specific S-dopant concentrations of 1.56% and 0.46%, respectively, show that the S-dopant states gradually merge into the conduction bands as the concentration of S dopant increases. In particular, the significant decrease in the bandwidth of the doping state from ~0.6 eV to 0.2 eV with the reduction of the S-dopant concentration from 1.56% to 0.46% reveals that the localization of S-dopant states is enhanced substantially as the doping concentrations decreases. Indeed, the calculations further predicted the IMT of S-doped Si at a dopant concentration of about 0.46% (~2.3 × 1020 cm−3). This result is consistent with previous measurements of the IMT in S-doped Si (1.8 × 1020 < n < 4.3 × 1020 cm−3)4 although the underestimate of the band gap in the DFT calculation could be improved by performing large-supercell calculations with the advanced hybrid functional [Fig. S4(a) of the Supplementary Information]61, G0W0 approximation62 or more sophisticate quantum Monte Carlo (QMC) method63, if the highly computational demand can be met. However, a recent investigation on a similar chalcogen-hyperdope Se:Si system4 also illustrated such dopant-induced IMT could be a strong Mott-type transition in which DFT calculation provides a reasonable prediction of IMT transition point even though the semi-local functional of PBE may delocalize the defect states. Meanwhile, to compare the VB-PES data with the theoretical data, Fig. 5(d) presents the DOSs that was aligned with EVBM. The calculated total DOSs are similar to the observed VB-PES data, showing the yield of the S-dopant states near EVBM. According to a partial DOSs analysis [Fig. S4(b) and S4(c) of the Supplementary Information], the host Si p orbital clearly dominates the DOSs near EVBM. However, a non-negligible contribution by the p-orbital of the S dopant is also evident in the region of EVBM. Like that of Se-hyperdoped Si5, the calculated DOSs of S-hyperdoped Si, shown in Fig. 5(a)–(d), clearly indicate that the enhancement of the DOSs at/above (at/below) the ECBM (EVBM) is associated with the S-dopant states that are created by the S hyperdoping of the Si samples. The calculations also reveal the onset of the IMT in S-doped Si samples at a dopant concentration of lower than 0.5%. The XANES spectra, VB-PES data and theoretical calculations demonstrate that the S hyperdoping changes the electronic structure of Si by forming S-dopant states in the band gap of Si, which is closely associated with the sub-band gap absorptance.
Figure 5. Doping induced IMT in S-hyperdoped Si.
(b) Normalized total DOSs (referenced to Fermi energy indicated as dashed line) versus S doping concentration (also denoted as S1:SiN−1). (a) and (c) Corresponding band structures of S1:Si63 and Si1Si215, respectively. (d) Calculated normalized DOSs of pure Si (black), 1.56% (green), and 0.46% (red) S doping concentrations (aligned with the EVBM).
Janzén et al.53 investigated the S-dopant states in Si using high-resolution IR absorption; they identified that the neutral S (S0) form states ~0.75 eV above the valence band edge. The shallow S level resides 0.45 eV above the valence band. The other S states have an energy that is close to the conduction band of Si. However, our S-hyperdoped Si absorptance spectra do not show any feature corresponding to sulfur related energy states in the band gap. In the future, we will plan to probe sulfur related deep states in the band gap at low temperature and at far-IR wavelength in an attempt to reduce thermal broadening as well as deep-level transient spectroscopy measurements could be useful to learn more about the specific transition energy for infrared absorption3,12.
Based on experimental and theoretical studies above, we have proposed explanation for the sub-band gap absorptance in the S-hyperdoped Si samples. In the present study, the observed changes in the sub-band gap absorptance of the S-hyperdoped Si samples were clearly related to the chemical state of the S species and the S-dopant states in the band gap of Si. The XPS study indicated that the maximum (~87%) sub-band gap absorbing sample (500 Torr sample) contains a high concentration of S, and especially S2− species. Annealing the 500 Torr sample at 700 °C forms large clusters of Sn2− (n > 2) and reduces the sub-band gap absorpatnce to ~7%. According to the VB-PES spectra and theoretical calculations, the S-dopant forms an impurity band at ~0.7 eV above the EVBM of pure Si(100), giving rise to the sub-band gap absorptance that was measured herein. Despite the fact that the larger S clusters (Sn2−, n > 2) may also form deep levels above the valence band, the high concentration of larger S clusters (Sn2−, n > 2) in the annealed samples may have been responsible for the drop in the sub-band absorptance5. Again, the overall integrated intensity of feature A2 is negative [as presented in the lower panel of Fig. 3(b)], indicating that the increase (decrease) in the DOSs of occupied (unoccupied) Si 3p orbitals is related to the S-dopant states, because these merge with the conduction band and act as electron donors in the S-hyperdoped Si samples.
In summary, the formation of S-dopant states in the band gap of Si that contains at/above critical concentration of S leads to high sub-band gap absorption in S-hyperdoped Si samples. The annealing of S-hyperdoped Si sample at 700 °C returns back to the electronic and atomic structures as that of reference Si(100), and cause S species to form larger clusters (Sn2−, n > 2), reducing the sub-band gap absorption. Our theoretical calculations based on the DFT method are consistent with experimental results and the IMT of S-doped Si is predicted to occur at an S concentration at a critical value of 0.46% (~2.3 × 1020 cm−3).
Methods
Preparation of S hyperdoped Si
Si can typically be hyperdoped with S by either ion implantation plus pulse laser annealing or fs-laser doping2,14. One advantage of fs-laser doping is that the process can roughen the material surface, increasing its absorption of light. S-hyperdoped Si is fabricated by irradiation of Ti: sapphire laser pulses (70 fs) in the presence of SF6, which is a precursor of the S as dopant. The p-type Si(100) wafer has high resistivity (3–10 kΩ · cm) to minimize other effects of dopants. Before irradiation, the wafer was cleaned by the RCA (Radio Corporation of America) method to remove possible contamination from the surface. The laser pulses were focused to 150 μm and the surface was raster-scanned at 8 kJ/m2 and 50 shots/area. Each sample had a size of 1 cm2. The SF6 pressure was varied to fabricate hyperdoped Si samples with a range of concentrations of S13,15. The concentration of S-hyperdoped in the Si samples was estimated to be approximately 1020 cm−3.2,3 Two pressures (100 Torr and 500 Torr) were used to achieve a difference in S doping level of about one order of magnitude (The concentration of S in Si samples was verified by Rutherford backscattering spectroscopy and secondary ion mass spectroscopy)2. The 500 Torr sample was respectively annealed at 500 °C and 700 °C for 30 min. to elucidate the effect of annealing on the chemical states and electronic and atomic structures of both the S dopant and the Si host, and to investigate further their correlations with the sub-band gap absorption in the hyperdoped Si samples.
Synchrotron-related measurements and characterizations
S K-edge XANES, Si K-edge XANES, EXAFS and VB-PES experiments were performed at the 16A- and 09A-beamline, at the National Synchrotron Radiation Research Center (NSRRC) in Hsinchu, Taiwan. The XANES and EXAFS measurements at the S and Si K-edge were performed in total electron yield modes. The VB-PES spectra were obtained by SPEM. The SPEM measurements were made using a flexure scanning stage and a hemispherical electron-analyzer system. A hemispherical analyzer with a 16-channel multichannel detector was used to collect photoelectrons. The VB-PES spectra were calibrated with reference to the zero energy of clean gold metal, and the energy of the incident X-ray was fixed at 150 eV with the energy resolution set to better than 0.1 eV. The zero energy is the threshold of the emission spectrum. The S and Si core-level XPS spectra of hyperdoped Si samples were also obtained at the 09A-beamline at NSRRC. Before the synchrotron-related measurements were conducted, hydrofluoric (HF) acid solution (1%) was utilized to eliminate the possibility of the presence of native oxides on the sample surface, and the samples were immediately transferred to a vacuum chamber. The core-level XPS spectra were feature-fitted using XPSPEAK41 software after a Shirley-type background had been subtracted from them. The IR absorption of hyperdoped Si samples was measured using an ultraviolet-visible-near IR spectrophotometer that was equipped with an integrating sphere to calculate the absorptance, A = 1-R-T (R = reflectance and T = transmittance). The surface morphology of the hyperdoped Si samples was also characterized using a field-emission SEM.
Additional Information
How to cite this article: Limaye, M. V. et al. Understanding of sub-band gap absorption of femtosecond-laser sulfur hyperdoped silicon using synchrotron-based techniques. Sci. Rep. 5, 11466; doi: 10.1038/srep11466 (2015).
Supplementary Material
Acknowledgments
The authors (H.C.H. and W.F.P.) are grateful to the Ministry of Science and Technology of Taiwan for financial support in this research under Grant No. NSC 101-2112-M-032-001-MY3. HCH also thanks NCTS of Taiwan for support. MVL and SBS would like to thank Department of Science and Technology (DST), India for financial support under DST-INSPIRE Faculty scheme. Authors would like to thank Dr. Y.-T. Lin and Prof. E. Mazur (School of Engineering and Applied Sciences, Harvard University, Cambridge, Massachusetts 02138, USA) for providing the S-doped Si samples, the SEM images and the absorption spectrum. Also, we sincerely thank them for the discussions regarding XPS and x-ray absorption spectroscopy.
Footnotes
Author Contributions M.V.L., S.C.C. and W.F.P. designed the experiments. All experimental measurements are performed by S.C.C., C.Y.L., S.B.S., Y.C.S., Y.F.W., S.H.H., H.T.W., J.W.C., C.H.C., L.Y.J., C.L.C. and Y.F.H. The theoretical calculations are done by L.Y.C. and H.C.H. The data were analyzed and manuscript prepared by M.V.L., S.C.C., H.C.H., S.B.S. and W.F.P. All authors discussed the results and contributed to finalization of the manuscript.
References
- Carey J. E., Crouch C. H., Shen M. & Mazur E. Visible and near-infrared responsivity of femtosecond-laser microstructured silicon photodiodes. Opt. Lett. 30, 1773–1775 (2005). [DOI] [PubMed] [Google Scholar]
- Kim T. G., Warrender J. M. & Aziz M. J. Strong sub-band-gap infrared absorption in silicon supersaturated with sulfur. Appl. Phys. Lett. 88, 241902 (2006). [Google Scholar]
- Winkler M. T. Non-equilbrium chalcogen concentrations in silicon: Physical structure, electronic transport, and photovoltaic potential. PhD thesis, Harvard University, Cambridge (2009). [Google Scholar]
- Winkler M. T. et al. Insulator-to-metal transition in sulfur-doped silicon. Phys. Rev. Lett. 106, 178701 (2011). [DOI] [PubMed] [Google Scholar]
- Ertekin E. et al. Insulator-to-metal transition in selenium-hyperdoped silicon: Observation and origin. Phys. Rev. Lett. 108, 026401 (2012). [DOI] [PubMed] [Google Scholar]
- Tull B. R., Winkler M. T. & Mazur E. The role of diffusion in broadband infrared absorption in chalcogen-doped silicon. Appl. Phys. A 96, 327–334 (2009). [Google Scholar]
- Newman B. K., Sher M.-J., Mazur E. & Buonassisi T. Reactivation of sub-bandgap absorption in chalcogen-hyperdoped silicon. Appl. Phys. Lett. 98, 251905 (2011). [Google Scholar]
- Newman B. K. et al. Extended X-ray absorption fine structure spectroscopy of selenium-hyperdoped silicon. J. Appl. Phys. 114, 133507 (2013). [Google Scholar]
- Sullivan J. T. et al. Soft x-ray emission spectroscopy studies of the electronic structure of silicon supersaturated with sulfur. Appl. Phys. Lett. 99, 142102 (2011). [Google Scholar]
- Mo Y., Bazant M. & Kaxiras E. Sulfur point defects in crystalline and amorphous silicon. Phys. Rev. B 70, 205210 (2004). [Google Scholar]
- Shao H. et al. Hybrid functional studies on impurity-concentration-controlled band engineering of chalcogen-hyperdoped silicon. Appl. Phys. Exp. 6, 085801 (2013). [Google Scholar]
- Sher M.-J. et al. Mid-infrared absorptance of silicon hyperdoped with chalcogen via fs-laser irradiation. J. Appl. Phys. 113, 063520 (2013). [Google Scholar]
- Sheehy M. A., Winston L., Carey J. E., Friend C. M. & Mazur E. Role of the background gas in the morphology and optical properties of laser-microstructured silicon. Chem. Mater. 17, 3582–3586 (2005). [Google Scholar]
- Tull B., Carey J. & Mazur E. Silicon surface morphologies after femtosecond laser irradiation. MRS Bull. 31, 626–633 (2006). [Google Scholar]
- Crouch C. H., Carey J. E., Shen M., Mazur E. & Génin F. Y. Infrared absorption by sulfur-doped silicon formed by femtosecond laser irradiation. Appl. Phys. A 79, 1635–1641 (2004). [Google Scholar]
- Her T.-H., Finlay R. J., Wu C., Deliwala S. & Mazur E. Microstructuring of silicon with femtosecond laser pulses. Appl. Phys. Lett. 73, 1673 (1998). [Google Scholar]
- Chandra A. P. & Gerson A. R. The mechanisms of pyrite oxidation and leaching: A fundamental perspective. Surf. Sci. Rep. 65, 293–315 (2010). [Google Scholar]
- Murphy R. & Strongin D. Surface reactivity of pyrite and related sulfides. Surf. Sci. Rep. 64, 1–45 (2009). [Google Scholar]
- Esbitt H. W. N., Ancroft G. M. B. & Ratt A. R. P. Sulfur and iron surface states on fractured pyrite surfaces. Am. Mineral. 83, 1067–1076 (1998). [Google Scholar]
- Ko T. H. & Chu H. Spectroscopic study on sorption of hydrogen sulfide by means of red soil. Spectrochim. Acta. A. Mol. Biomol. Spectrosc. 61, 2253–2259 (2005). [DOI] [PubMed] [Google Scholar]
- Smart R. S. C., Skinner W. M. & Gerson A. R. XPS of sulphide mineral surfaces: Metal-deficient , polysulphides , defects and elemental sulphur. Surf. Interface Anal. 28, 101–105 (1999). [Google Scholar]
- Ferretti N., Balkaya B., Vollmer A., Neeb M. & Eberhardt W. Inner-shell photoelectron spectroscopy of size-selected Cu-clusters on Si. J. Electron Spectros. Relat. Phenomena 156-158, 124–127 (2007). [Google Scholar]
- Meyer B. Elemental sulfur. Chem. Rev. 76, 367–388 (1976). [Google Scholar]
- Khan S. A. UV-ATR spectroscopy study of the speciation in aqueous polysulfide electrolyte solutions. Int. J. Electrochem. Sci. 7, 561–568 (2012). [Google Scholar]
- Zhang Y. F., Liao L. S., Chan W. H., Lee S. T. & Sham T. K. Electronic structure of silicon nanowires: A photoemission and x-ray absorption study. Phys. Rev. B 61, 8298–8305 (2000). [Google Scholar]
- Park C.-M. et al. Characterizations and electrochemical behaviors of disproportionated SiO and its composite for rechargeable Li-ion batteries. J. Mater. Chem. 20, 4854 (2010). [Google Scholar]
- López J. A. L. et al. Morphological, compositional, structural, and optical properties of Si-nc embedded in SiOx films. Nanoscale Res. Lett. 7, 604 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu Z. H., Graham M. J., Jiang D. T. & Tan K. H. SiO2/Si(100) interface studied by Al Kα x-ray and synchrotron radiation photoelectron spectroscopy. Appl. Phys. Lett. 63, 2941 (1993). [Google Scholar]
- Thøgersen A. et al. An experimental study of charge distribution in crystalline and amorphous Si nanoclusters in thin silica films. J. Appl. Phys. 103, 024308 (2008). [Google Scholar]
- Vilkov O. et al. Controlled assembly of graphene-capped nickel, cobalt and iron silicides. Sci. Rep. 3, 2168 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith M. J. et al. The origins of pressure-induced phase transformations during the surface texturing of silicon using femtosecond laser irradiation. J. Appl. Phys. 112, 083518 (2012). [Google Scholar]
- Hitchcock A. P. et al. Polarization dependence of the Si K-edge X-ray absorption spectra of Si-Ge atomic layer superlattices. Surf. Sci. 301, 260 (1994). [Google Scholar]
- Pong W. F. et al. X-ray absorption spectroscopy of CoSi2. Phys. Rev. B 53, 16510 (1996). [DOI] [PubMed] [Google Scholar]
- Chemical Applications of Synchrotron Radiation: Part II, X-ray Applications, Advances Series, in Physical Chemistry, Sham T.-S., Ed. (World Scientific, Singapore, 2002). [Google Scholar]
- Sham T. et al. Electronic structure and optical properties of silicon nanowires: A study using x-ray excited optical luminescence and x-ray emission spectroscopy. Phys. Rev. B 70, 045313 (2004). [Google Scholar]
- Sammynaiken R. et al. Structure and electronic properties of SiO2/Si multilayer superlattices: Si K edge and L3,2 edge x-ray absorption fine structure study. J. Appl. Phys. 92, 3000 (2002). [Google Scholar]
- Crescenzi M. De, Lozzi L. & Picozzi P. Structural determination of crystalline silicon by extended energy-loss fine-structure spectroscopy. Phys. Rev. B 39, 8409–8422 (1989). [DOI] [PubMed] [Google Scholar]
- Peters J. & Krebs B. Silicon disulphide and silicon diselenide: A reinvestigation. Acta Crystallogr. B 38, 1270–1272 (1982). [Google Scholar]
- Ray S. C., Chiou J. W., Pong W. F., Tsai M. H. The electronic properties of nanomaterials elucidated by synchrotron radiation–based spectroscopy. Crit. Rev. Sol. Stat. Mater. Sci. 31, 91–110 (2006). [Google Scholar]
- Yeh J. Atomic calculation of photoionization cross-sections and asymmetry parameters (Gordon & Breach Science, Langhorne, PA, 1993).
- Hrbek J., Rodriguez A., Huang H. & Xu Q. Synthesis of sulfur films from S2 gas: spectroscopic evidence for the formation of Sn species. Chem. Phys. Lett. 267, 65–71 (1997). [Google Scholar]
- Umebayashi T. et al. Sulfur-doping of rutile-titanium dioxide by ion implantation: Photocurrent spectroscopy and first-principles band calculation studies. J. Appl. Phys. 93, 5156–5160 (2003). [Google Scholar]
- Kobayashi K., Daimon H. & Murata Y. Resonant photoemission from Si. Phys. Rev. Lett. 50, 1701–1704 (1983). [Google Scholar]
- Ley L., Kowalczyk S., Pollak R. & Shirley D. X-ray photoemission spectra of crystalline and amorphous Si and Ge valence bands. Phys. Rev. Lett. 29, 1088–1092 (1972). [Google Scholar]
- Buuren T. Van, Tiedje T. & Way B. M. Photoelectron spectroscopy measurements of the band gap in porous silicon. Appl. Phys. Lett. 63, 2911–2913 (2001). [Google Scholar]
- Alay J. L. The valence band alignment at ultrathin SiO2/Si interfaces. J. Appl. Phys. 81, 1606–1608 (1997). [Google Scholar]
- Yao Z. Q. et al. Fabrication and surface characterization of pulsed reactive closed-field unbalanced magnetron sputtered amorphous silicon nitride films. Surf. Coatings Technol. 200, 4144–4151 (2006). [Google Scholar]
- Pao C.-W. et al. Photoconduction and the electronic structure of silica nanowires embedded with gold nanoparticles. Phys. Rev. B 84, 165412 (2011). [Google Scholar]
- Chang C. K. et al. Band gap engineering of chemical vapor deposited graphene by in situ BN doping. ACS Nano 7, 1333–1341 (2013). [DOI] [PubMed] [Google Scholar]
- Chuang C. H. et al. The effect of thermal deduction on the photoluminescence and electronic structures of graphene oxides. Sci. Rep. 4, 4525 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X. et al. X-ray spectroscopic study of the electronic structure of visible-light responsive N-, C- and S-doped TiO2. J. Electron Spectros. Relat. Phenomena 162, 67–73 (2008). [Google Scholar]
- Glenis S., Nelson A. J. & Labes M. M. Sulfur doped graphite prepared via arc discharge of carbon rods in the presence of thiophenes. J. Appl. Phys. 86, 4464–4466 (1999). [Google Scholar]
- Janzén E., Stedman R., Grossmann G. & Grimmeiss H. High-resolution studies of sulfur-and selenium-related donor centers in silicon. Phys. Rev. B 29, 1907–1918 (1984). [Google Scholar]
- Grimmeiss H. G., Janzen E. & Skarstam B. Deep sulfur‐related centers in silicon. J. Appl. Phys. 51, 4212–4217 (1980). [Google Scholar]
- Luque A. & Marti A. Increasing the efficiency of ideal solar cells by photon induced transitions at intermediate levels. Phys. Rev. Lett 78, 5014–5017 (1997). [Google Scholar]
- Luque A., Marti A., Antolin E. & Tablero C. Intermediate bands versus levels in non-radiative recombination. Phys. B: Condens. Matt. 382, 320–327 (2006). [Google Scholar]
- Fabbri F. et al. Depth-resolved cathodoluminescence spectroscopy of silicon supersaturated with sulfur. Appl. Phys. Lett. 102, 031909 (2013). [Google Scholar]
- Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994). [DOI] [PubMed] [Google Scholar]
- Kresse G. & Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mat. Sci. 6, 15–50 (1996) and references therein. [DOI] [PubMed] [Google Scholar]
- Perdew J. P., Burke K. & Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996). [DOI] [PubMed] [Google Scholar]
- Heyd J. Scuseria G. E. & Ernzerhof M. Erratum: “Hybrid functionals based on a screened Coulomb potential” [J. Chem. Phys. 118, 8207 (2003)]. J. Chem. Phys.124, 219906 (2006).
- Hybertsen M. S. & Louie S. G. Electron correlation in semiconductors and insulators: Band gaps and quasiparticle energies. Phys. Rev. B 34, 5390 (1986). [DOI] [PubMed] [Google Scholar]
- Foulkes W. M. C., Mitas L., Needs R. J. & Rajagopal G. Quantum Monte Carlo simulations of solids. Rev. Mod. Phys. 73, 33 (2001). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.