Abstract
Computational fluid dynamics (CFD) modeling is well suited for addressing species-specific anatomy and physiology in calculating respiratory tissue exposures to inhaled materials. In this study, we overcame prior CFD model limitations to demonstrate the importance of realistic, transient breathing patterns for predicting site-specific tissue dose. Specifically, extended airway CFD models of the rat and human were coupled with airway region-specific physiologically based pharmacokinetic (PBPK) tissue models to describe the kinetics of 3 reactive constituents of cigarette smoke: acrolein, acetaldehyde and formaldehyde. Simulations of aldehyde no-observed-adverse-effect levels for nasal toxicity in the rat were conducted until breath-by-breath tissue concentration profiles reached steady state. Human oral breathing simulations were conducted using representative aldehyde yields from cigarette smoke, measured puff ventilation profiles and numbers of cigarettes smoked per day. As with prior steady-state CFD/PBPK simulations, the anterior respiratory nasal epithelial tissues received the greatest initial uptake rates for each aldehyde in the rat. However, integrated time- and tissue depth-dependent area under the curve (AUC) concentrations were typically greater in the anterior dorsal olfactory epithelium using the more realistic transient breathing profiles. For human simulations, oral and laryngeal tissues received the highest local tissue dose with greater penetration to pulmonary tissues than predicted in the rat. Based upon lifetime average daily dose comparisons of tissue hot-spot AUCs (top 2.5% of surface area-normalized AUCs in each region) and numbers of cigarettes smoked/day, the order of concern for human exposures was acrolein > formaldehyde > acetaldehyde even though acetaldehyde yields were 10-fold greater than formaldehyde and acrolein.
Keywords: CFD, PBPK, acetaldehyde, acrolein, formaldehyde, cigarette smoke, respiratory tract, risk assessment
For all but the most corrosive materials, toxicity to inhaled gases, vapors, and aerosols is mediated by a combination of relative sensitivities and clearance capabilities of individual cell types and their proximities to inhaled airflows that deliver local exposures at a rate sufficient to produce adverse response. Accurately predicting toxicologically relevant internal doses across species and exposure conditions has therefore been an ongoing need in inhalation toxicology and human risk assessment.
In a preceding companion paper, we briefly discussed modeling approaches that have been used to predict target tissue dosimetry in the respiratory systems of animals and humans focusing upon recent advances in imaging-based, 3-dimensional (3D), computational fluid dynamics (CFD) airflow and material transport modeling (Corley et al., 2012). Such models specifically account for critical species-specific differences in anatomy and physiology that are not possible with simplified empirical or compartmental representations of the respiratory system. With these advances, it is now feasible to develop CFD-based exposure models that incorporate highly detailed airway geometry from the external nares (or mouth) to the bronchiolar region of the lung. By developing models for both laboratory animals and humans, comparisons of local inhaled dose provides a quantitative basis for relating animal and human exposures within a integrated framework. This more rigorous accounting of known biological differences between species and material properties affecting fate and transport effectively reduces uncertainty in predicted target tissue dose, and more clearly illuminates critical factors that drive dose–response relationships.
To demonstrate the utility of extended airway CFD models, we previously applied Schroeter et al.’s (2008) CFD/physiologically based pharmacokinetic (PBPK) approach to describe the uptake and clearance of acrolein in our rat, monkey, and human models (Corley et al., 2012). Acrolein is a reactive, water-soluble aldehyde that primarily produces pathologies in nasal tissues of rats as well as lesions in conducting airways beyond the nose at higher concentrations (Cassee et al., 1996, 2008, Lam et al., 1985; Leach et al., 1987). Since humans breathe through the mouth as well as the nose, the extended airway models allowed for direct comparisons between breathing modalities across species to evaluate the extent of acrolein penetration and tissue uptake in conducting airways. Our combined CFD/PBPK approach was calibrated against prior nasal extraction studies conducted in the rat (Morris, 1996; Struve et al., 2008), and all simulations employed steady-state inhalation conditions as previously utilized by Schroeter et al. (2008). The results confirmed that regional acrolein uptake is sensitive to airway geometry, airflow rates, atmospheric concentrations, regional tissue thickness, air:tissue partition coefficients, and metabolic capacity. For human models of either nasal or oral breathing, greater penetration and uptake of acrolein by lower tracheobronchial tissues was predicted than in either the rat or monkey.
Until now, the vast majority of all respiratory CFD models have focused on steady-state solutions that are not encumbered by the technical difficulties and computational costs associated with more realistic, transient airflow simulations. Nevertheless, in a series of recentarticles, Tian and Longest (2010a, b, c) demonstrated the importance of transient CFD simulations in simplified compartmental and partial airway models These studies progressed from idealized geometries to image-based descriptions for portions of the conducting airway tree in humans and the application of steady state to fully transient airflow and uptake solutions. However, these prior models only focused on a single, or at most, a few breaths, and they did not account for tissue reactivity, regional blood flows, or tissue metabolism. Still, these important findings clearly showed that steady-state CFD simulations do not always properly reflect the local uptake patterns that actually occur under more realistic, yet computationally intensive, transient/time-dependent exposures.
In this study, we overcame many prior computational challenges to perform transient CFD simulations with fully coupled (2-way), time-dependent PBPK boundary conditions in extended airway models for the rat and human. We also expanded the PBPK boundary conditions to include tissue reactions, first-order and saturable metabolism, metabolic interactions, distribution of metabolic enzymes, and local blood perfusion rates to simulate multiple breaths until breath-by-breath, steady-state kinetics was achieved in all tissues lining the airways. Since reactive vapors generally exert their effects directly in respiratory tissues, we demonstrated the importance of transient breathing by simulating exposures to a series of aldehydes (acrolein, formaldehyde, and acetaldehyde) with previous steady-state PBPK or CFD models (Kimbell and Subramaniam, 2001; Kimbell et al., 2001a, b; Schroeter et al., 2008; Teeguarden et al., 2008).
Like acrolein, formaldehyde and acetaldehyde are highly water-soluble with varying degrees of reactivity, metabolic clearance, and tissue toxicity. Acetaldehyde and formaldehyde also produce toxicity and tumors within the respiratory tissues of chronically exposed laboratory animals (Appelman et al., 1982; Dorman et al., 2008a, b Kamata et al., 1997; Morgan and Monticello, 1990; Morgan et al., 1986; Woutersen and Feron, 1987; Woutersen et al., 1984, 1986). Human exposure to all 3 aldehydes is normally associated with cigarette smoking since all are reactive byproducts of burning tobacco (Counts et al., 2005). Nevertheless, relative hazards remain largely unknown. Particularly, prior attempts to rank the relative hazards for different smoke constituents were all based upon traditional toxicity studies of individual chemicals using diverse designs, endpoints, exposures, and species, and did not include critical pharmacokinetic differences between species or realistic exposure patterns that could significantly affect exposure–dose–response relationships that would normally drive comparative risk evaluations (Burns et al., 2008; Fowles and Dybing, 2003; Pankow et al., 2007; WHO, 2008).
The issue of relative risks for different smoke constituents was recently highlighted by the 2009 Family Smoking Prevention and Tobacco Control Act that gives the U.S. FDA regulatory authority over tobacco products. This historic legislation requires companies to reveal all of the ingredients in tobacco products. Provisions in the act also allow the FDA to either regulate constituents individually, or respond to manufacturer claims of so-called ‘reduced harm’ products. FDA initiated this process by establishing a list of over 90 constituents in tobacco products and smoke that are candidates for regulation (DHHS, 2012). Still, no generally accepted risk assessment framework has yet been established to facilitate such decisions.
For decades, pharmacokinetic models have been successfully applied to address issues of extrapolation between species, dose, dose–rate, or types of exposure to drugs or chemicals. PBPK models in particular have become a staple for chemical risk assessments by the EPA and WHO’s International Program on Chemical Safety (IPCS); primarily, because they account for species differences in physiology and processes associated with absorption, distribution in the body, metabolism, and elimination (EPA, 2002, 2009; WHO, 2010). In its latest assessment of formaldehyde, the EPA employed CFD models because of their ability to address important species differences in anatomy as well as providing a detailed accounting of both toxicity and carcinogenic response at site- and cell-specific levels (US EPA, 2010). Here, we extended our previous CFD/PBPK approach for acrolein to improve comparative risk evaluations of cigarette smoke constituents by focusing upon common target tissue dose metrics across species that are achieved under realistic exposure conditions. Under the brief, but repeated exposures typical for cigarette smoke, we demonstrate that transient CFD simulations with time-dependent PBPK boundary conditions will provide the most informative approach for predicting site-specific tissue aldehyde doses across different species and exposures. By exploiting the PBPK boundary condition to determine site-specific respiratory tissue concentrations for each aldehyde, and not just airway wall flux rates, our results also provide unique opportunities to improve dose–response assessments relative to steady-state simulations that have been previously used in CFD models.
MATERIALS AND METHODS
Construction of CFD Models for the Rat and Human
Model structures
The rat extended airway geometry is the same as that reported in Corley et al. (2012). This geometry was based upon CT imaging of the upper airways of a 315 g male Sprague Dawley rat and an in situ lung cast from the same animal (see Jacob et al., 2013). The computational mesh used for CFD simulations consists of 1.86 million elements having 10.5 million nodes and 0.63 million surface facets that were organized (blocked) according to cell type (nose) or anatomic region (remaining airways) for interfacing with tissue-specific PBPK models. The rat model encompassed the external nares through 17 ± 7 airway generations (see Supplementary Fig. S1a).
The human nasal model used to compare steady-state with transient CFD/PBPK simulations was also the same as that reported in Corley et al. (2012). This model was based upon CT imaging of an 84-year-old female encompassing 9 ± 2 pulmonary airway generations as well as all the upper conducting airways needed to simulate nasal and oral breathing. The resulting model contains 1.1 million elements, 6.1 million nodes, and 0.24 million surface facets (nasal breathing model) that are also blocked according to cell type (nose) and anatomic region (remaining airways) (see Supplementary Fig. 1b) for interfacing with PBPK models.
Simulations of oral breathing by humans used measured post-puff breathing profiles for a typical smoker and an additional human model of a male volunteer (18 years of age, weighing 72 kg) using the identical approach described for the female in Corley et al. (2012). The development of polyhedral computational meshes and the definition of airway surfaces by cell type or anatomic region was also the same. The new male human oral breathing model extended from the external face to 8 ± 4 airway generations (117 total outlets) and contained 782 000 elements, 442 000 nodes, and 181 000 surface facets, each with their anatomically defined PBPK model boundary condition.
Approvals
The Institutional Review Boards of the University of Washington and PNNL approved all human volunteer work conducted under this study.
PBPK boundary conditions for aldehyde uptake
Tissue compartment surface areas and thicknesses for the rat and female human have been reported previously (Corley et al., 2012); related data for the new male human model are summarized in Table 1. Boundary conditions for each aldehyde constituent and their simultaneous numerical solutions for 2-way coupled CFD/PBPK models were modified to account for transient airflow and time-dependent material transport and tissue clearance processes. Details of the time-stepping and numerical coupling approaches that enabled these simulations are provided in the Appendix.
Table 1.
Anatomic parameters used in the male human CFD/PBPK model
| Dimension | Compartment 1 | Compartment 2 |
|---|---|---|
| Tissue/region | (Mucus + Epithelium)a | (Subepithelium)b |
| Compartment surface area (cm2)c | ||
| Oral | 103.1 | 103.1 |
| Pharyx/Larynx | 100.0 | 100.0 |
| Trachea | 59.7 | 59.7 |
| Main Bronchi | 39.8 | 39.8 |
| 2 Bronchi + bronchioles | 163.6 | 163.6 |
| Compartment thickness (L, cm)d | ||
| Oral | 0.0065 | 0.0015 |
| Pharyx/Larynx | 0.0065 | 0.0015 |
| Trachea | 0.0066 | 0.0015 |
| Main Bronchi | 0.0066 | 0.0015 |
| 2 Bronchi + bronchioles | 0.0066 | 0.0015 |
aCompartment 1 consists of both mucus and epithelium. The thickness of the mucus layer was 0.0015 cm in the oral, pharynx and larynx; and 0.0011 cm in all other compartments.
bThe subepithelium compartment consists of connective tissue, capillaries, glands, macrophages, lymph vessels, etc. just below the epithelium as defined by ICRP (1994). This compartment receives the cardiac output in the model from Table 2.
cComputed from CFD model surface.
Acrolein
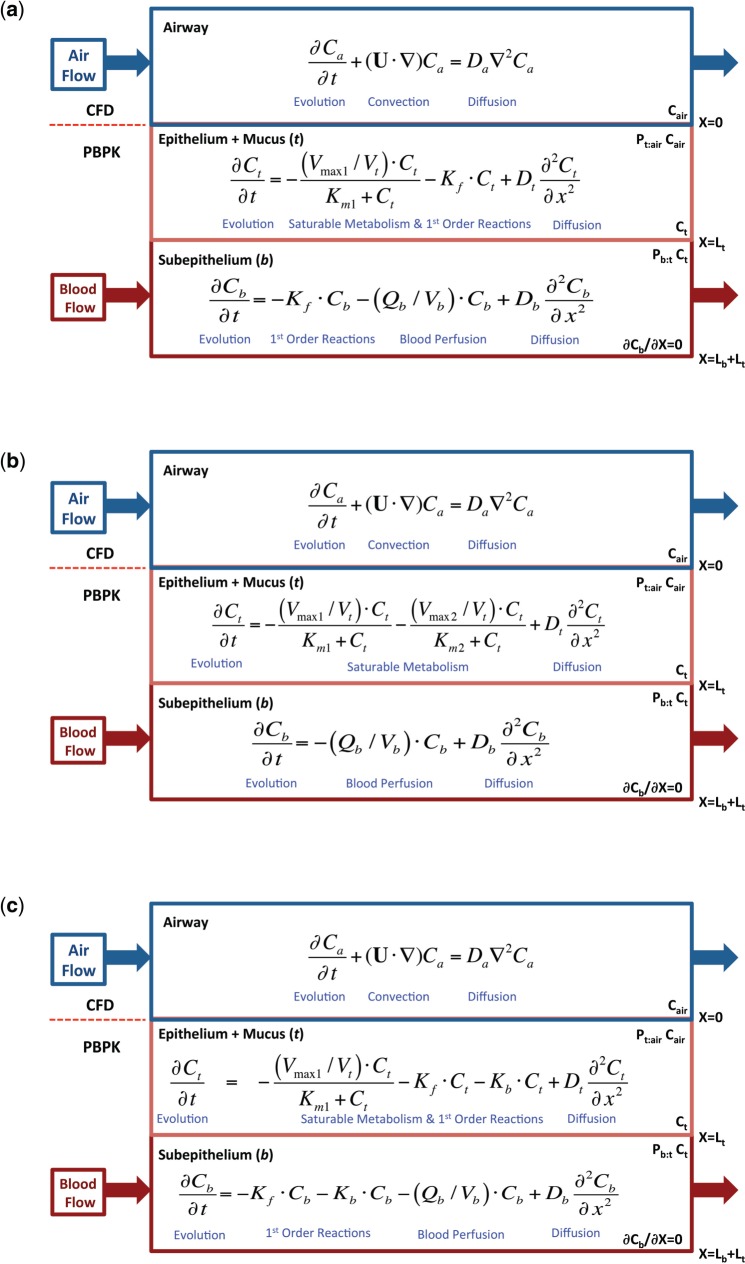
With the exception of the evolution terms for transient simulations (see Appendix), the structure of the 2-compartment acrolein PBPK model (Fig. 1a) and associated biological- and chemical-specific parameters (Tables 1–3) were the same as those used previously (Corley et al., 2012). The uptake of acrolein in non-mucus-coated squamous epithelium (nasal vestibule and ventral floor of anterior nose) was driven by a mass transfer coefficient (Ks, cm/s) as described by Schroeter et al. (2008). For the remaining mucus-coated tissues and airways, uptake was driven by the air and tissue phase diffusion coefficients (D, cm2/s), tissue:air and tissue:blood partition coefficients (Pta, Pbt), first-order non-specific reactions with tissue macromolecules (Kf, s−1), saturable metabolic clearance by aldehyde dehydrogenase enzymes (Km1, µg/l; Vmax1C, µg/l/s), regional blood perfusion rates (fraction of cardiac output [CO], ml/min), regional tissue thicknesses (L, cm), and a zero-flux (zero-Neumann) boundary condition of the subepithelial compartment. The distribution of metabolic enzymes between epithelial and subepithelial layers by cell type in the nose and regions of the remaining conducting airways are also the same as in Corley et al. (2012).
FIG. 1.
Conceptual diagram of the 1D (a) acrolein, (b) acetaladehyde, and (c) formaldehyde PBPK models used as airway surface boundary conditions for all tissue compartments except olfactory epithelium where saturable metabolism associated with aldehyde dehydrogenases are located only in the subepithelium compartments of the CFD/PBPK models of the rat and human. The basis for these 2-compartment tissue models were described by Schroeter et al. (2008) as modified by Corley et al. (2012). A detailed description of the equations used to compute the coupled 3D CFD/1D PBPK models is provided in the Appendix.
Table 2.
Chemical-Specific Parameters used in the Rat and Human CFD/PBPK Model
| Parameter | Acrolein | Source | Acetaldehyde | Source | Formaldehyde | Source |
|---|---|---|---|---|---|---|
| Diffusivity (D—cm2/s) | ||||||
| Air (Dair) | 0.105 | a | 0.124 | b | 0.150 | c |
| Tissue (Dt) | 1.22 x 10−5 | a | 3.33 x 10−6 | d | 8.08 x 10−6 | e |
| Blood (Db) | 1.22 x 10−5 | a | 3.33 x 10−6 | d | 1.62 x 10−5 | e |
| Partition coefficients (P) | ||||||
| Tissue:air (Pta) | 88.0 | a | 224.0 (rat), | d | 101.5 | f |
| 190.0 (human) | d | |||||
| Tissue:blood (Pbt) | 1.0 | a | 1.0 | a | 1.0 | a |
| Metabolism—Rat | ||||||
| Km1 (µg/l) | 0.5 | a, g | 2.39 x 106 | d, h, i | 2.13 x 103 | j |
| Vmax1C (µg/l/s) | 572.9 | a, g | 3910 | d, h, i | 1.0 x 105 | h, f, j |
| (3050, Olfactory Subepithelium) | ||||||
| Km2 (µg/l) | - | - | 441 | d, h, i | - | - |
| Vmax2C (µg/l/s) | - | - | 881 | d, h, i | - | - |
| Kf (s−1) | 5.0 x 10−2 | a | - | - | 1.8 x 10−2 | j |
| Metabolism—Human | ||||||
| Km1 (µg/l) | 0.5 | a, g | 3.3 x 106 | d | 201 | h, j |
| Vmax1C (µg/l/s) | 112 | a, g | 766 | d, h | 1.96 x 104 | h |
| Km2 (µg/l) | - | - | 441 | d, h | - | - |
| Vmax2C (µg/l/s) | - | - | 173 | d, h | - | - |
| Kf (s−1) | 2.0 x 10−2 | a, g | - | 1.8 x 10−2 | j | |
| VmaxC region-specific adjustment factor | ||||||
| Nose | 1.0 | g | 1.0 | g | 1.0 | g |
| Mouth, Pharyx, Larynx, Trachea, | ||||||
| Bronchi | 0.25 | g | 0.25 | g | 0.25 | g |
| Bronchioles | 0.5 | g | 0.5 | g | 0.5 | g |
| Non-specific binding | ||||||
| Kb (s−1) | – | – | – | – | 1.07 × 10−7 (rat and human) | j |
| Mass-transfer coefficients for non-mucus-coated squamous epithelium (e.g. vestibule) | ||||||
| Ks (cm/s) | 7.1 × 10−4 | a | 1.6 × 10−3 | d | 0.41 | f |
cEPA (1998)
f Calculated from Kimbell et al. (2001) as described in Methods.
gFranks (2005) as described in Corley et al. (2012).
hRecalibrated and rescaled by body weight and respective tissue volumes as described in Methods.
jConolly et al. (2008).
Table 3.
Exposure conditions for comparing target tissue doses in rats at NOAEL levels in subchronic inhalation bioassays and humans exposed via mainstream cigarette smoke
| Acrolein | Source | Acetaldehyde | Source | Formaldehyde | Source | |
|---|---|---|---|---|---|---|
| Rat | ||||||
| Subchronic NOAEL ppm | 0.2 | a | 50 | b | 1 | c |
| BW (kg) | 0.3 | d | 0.3 | d | 0.3 | d |
| Breathing rate (minute volume; MV) (ml/min) | 217 | e | 217 | e | 217 | e |
| Breathing frequency (Breaths/min) | 100 | f | 100 | f | 100 | f |
| Human (male) | ||||||
| Body weight (kg) | 72 | d | 72 | d | 72 | d |
| Cardiac output (Q) | ||||||
| Total (Q, ml/min) | 5920.6 | g | 5920.6 | g | 5920.6 | g |
| Cigarette Yield (µg/cig) | 100 | h | 857 | h | 61.2 | h |
| Puffs/cig | 11 | i | 11 | i | 11 | i |
| Amount/puff (µg) | 9.09 | j | 77.91 | j | 5.56 | j |
| Volume oral cavity (ml) | 42.07 | k | 42.07 | k | 42.07 | k |
| Initial concentration oral cavity (ppm) | 94 | l | 1,028 | l | 108 | l |
dBody weight of rat or human used to develop model.
fAssumed 100 bpm for these simulations. Typical range is 70–115 bpm (Harkness et al., 2010).
gCalculated as Q (ml/min) = 15 l/h/kg * (BW, kg)0.74 * 1000 ml/l * 1 h/60 min. Distribution (fraction of cardiac output, Qb) to each airway subepithelium as described by Corley et al. (2012) with the exception of acetaldehyde where nasal blood flows were based upon Teeguarden et al. (2008) and vasodilation occurs at concentrations >25 ppm (see Methods).
hOverall average of yield in use data for RJR low and high tar brands (Kathman, S.J. personal communication). Estimated yields are within published ranges for Phillip Morris products and reference cigarettes (Counts et al., 2005).
iDHHS (1988).
jCalculated.
kActual geometry from human oral model described in text.
lCalculated from yield data and actual geometry: Conc. (ppm) = .
Acetaldehyde
The structure of the 2-compartment acetaldehyde PBPK model (Fig. 1b) and sources for chemical-specific parameters (Tables 2 and 3) were based upon the CFD-informed PBPK model of Teeguarden et al. (2008). The uptake of acetaldehyde in non-mucus-coated squamous epithelium was also driven by a mass transfer coefficient (Ks), derived using the approach followed by Schroeter et al. (2008) for acrolein. Air and tissue diffusivities (D), tissue:air and tissue:blood partition coefficients (Pta, Pbt) were obtained from Teeguarden et al. (2008). Unlike PBPK models for the other aldehydes (Franks, 2005; Schroeter et al., 2008), Teeguarden et al. assumed that 0.1, not 1%, of cardiac output perfused rat nasal subepithelial tissues. This value was used as-is in the current CFD/PBPK for exposure concentrations below 25 ppm. However, at 25 ppm and higher concentration, nasal tissue perfusion had to be increased to 0.5% of cardiac output to adequately describe prior nasal extraction data (Morris and Blanchard, 1992), consistent with prior observations of vasodilation at these concentrations (Stanek et al., 2001).
Teeguarden et al. described acetaldehyde metabolism using 2 saturable aldehyde dehydrogenase enzymes; 1 was a high capacity, low affinity pathway (ALDH1), while the other was a low capacity, high affinity enzyme (ALDH2) that varies in the human population. To account for differences in model structures between the current CFD/PBPK model and the Teeguarden et al. PBPK model, metabolism rate constants (ALDH1: Km1, Vmax1C; ALDH2: Km2, and Vmax2C) were re-calibrated from published nasal extraction data for the rat (Morris and Blanchard, 1992) due to differences in respective tissue compartment volumes in the anatomically correct CFD/PBPK model versus the original PBPK model of Teeguarden et al. (2008). The distribution of metabolism in epithelial and subepithelial compartments in each airway region, and scaling of metabolism to the human and across tissue compartments, was the same as described for acrolein in Corley et al. (2012).
Formaldehyde
The 2-compartment PBPK model for formaldehyde (Fig. 1c) and sources for chemical-specific parameters (Tables 2 and 3) were based upon prior CFD-informed compartmental models (Conolly et al., 2000; Franks, 2005; Georgieva et al., 2003). The model consisted of clearance by a saturable pathway (formaldehyde dehydrogenase; Km1, Vmax1C), a first-order pathway assumed to represent intrinsic reactivity of formaldehyde with tissue constituents (Kf), and a first-order binding of formaldehyde to DNA responsible for DNA-protein crosslinks (DPX) formation (Kb). As with the other aldehydes, results describe how the metabolism rates in respiratory tissues were re-calibrated from published nasal extraction data in rats to conform with our model-specific airway and tissue geometries (Kimbell et al., 2001b).
Since our PBPK model structure combines mucus with the epithelium, we used Kimbell et al.’s (2001a, b) skin:air partition coefficient for formaldehyde rather than the water:air partition coefficient used in prior mechanistic models that separated the mucus and epithelium compartments (Asgharian et al., 2012; Franks, 2005; Georgieva et al., 2003). Unlike acrolein and acetaldehyde, the water:air partition coefficient for formaldehyde is orders of magnitude greater than its skin:air because it undergoes reversible hydration interactions in water forming methylene glycol. We confirmed that the flux of formaldehyde into the tissues is dominated by the tissue:air partition coefficient using an alternative version of the PBPK model that explicitly separated the mucus from the epithelium. In this model, the mucus layer acts as a capacitor that rapidly charges with formaldehyde due to the very high water:air partition coefficient, but the flux into the tissues is restricted by the lower tissue:mucus partition coefficient (calculated as tissue:air/mucus:air).
Airflow and aldehyde transport simulations
The coupled airflow and aldehyde transport simulations were performed using OpenFOAM, a free, open-source CFD software package distributed by the OpenFOAM Foundation (http://www.openfoam.com). Our computational investigations have shown that upper-airway turbulence in the human geometries has little influence on predicted uptake. Thus, the airflow predictions were based on laminar, 3D, incompressible Navier–Stokes equations for fluid mass and momentum:
| (1) |
| (2) |
where is the density, is the kinematic viscosity, u is the fluid velocity vector, and p is the pressure. Aldehyde transport was then described using the time-dependent convection-diffusion scalar transport equation:
| (3) |
where Cair and Dair are the concentration and diffusivity of each aldehyde in the airway lumen, and u is the fluid velocity vector from equations 1 and 2.
Coupled PBPK boundary models differ according to inhaled species and airway region. Using acrolein as an example (Fig. 1a), boundary conditions are given by the following 1-dimensional equations for the combined mucus + epithelium layer (designated by the subscript t for tissue), and the corresponding subepithelial layer (designated by the subscript b for blood-perfusion layer) at every triangular facet on the airway walls:
| (4) |
| (5) |
where Dt and Db are the respective diffusion coefficients, Ct and Cb are the respective soluble vapor concentrations, x is the distance from lumen (i.e. radial distance), kf is the non-specific first-order metabolism rate constant, Vmax1C is a coefficient that represents saturable metabolism per unit volume of tissue (scaled from the rat by the ratio of human:rat body weights raised to the −0.3 power as described in Corley et al. 2012), Km1 is the Michaelis constant, Qb is blood flow in the subepithelial layer (fraction of cardiac output), and Vb is total volume of the subepithelial layer. As discussed in Corley et al. (2012), saturable metabolism occurs only in the epithelial tissues and not in the subepithelium in all regions of the respiratory tract except the olfactory tissues, where aldehyde dehydrogenases are located only in the subepithelium. Thus, equations 4 and 5 are adjusted accordingly by cell type and region. The depth of each tissue compartment is Lt, while the depth of each subepithelial compartment is Lb (Table 1). At x = 0 (air-tissue interface), equation 4 is coupled to the lumen convection diffusion equation by matching of diffusive flux by:
| (6) |
where n is the surface normal direction in the 3D domain.
The tissue concentration, Ct, is related to the air concentration via the air–tissue partition coefficient (i.e. Ct = Pta · Cair). At x = Lt (epithelial–subepithelial interface), subepithelial concentration is related to epithelial concentration via the tissue–blood partition coefficient (i.e. Cb = Pbt · Ct), assuming that Pbt = 1. At (the deepest portion of subepithelial compartment), we assumed a zero-flux boundary condition (i.e. ) as used previously (Corley et al., 2012; Georgieva et al., 2003).
At every 3D convection–diffusion equation time step, we computed a single time-step of the 1D equations 4 and 5 to find the diffusive flux, , at x = 0 that is consistent with equations 4 and 5, the Ct value at x = 0, and the zero Neumann condition at x = Lt + Lb at the current time. This flux then determines the normal gradient of the concentration field in the CFD domain , which is required by the convection–diffusion equation in the 3D domain. Details of the computation of the 1D partial differential equation (PDE) time-step are given in the Appendix.
For all CFD/PBPK simulations, air at room temperature was considered to be the working fluid, with a density of 1.0 kg/m3 and a kinematic viscosity of 1.502 × 10−5 m2/s. The properties of inhaled air were assumed constant for the entire duration of the simulation and did not account for changes in temperature and humidity in the respiratory tract. The inlet (at mouth or nose) was prescribed a ‘time-dependent flow rate’ boundary condition in which the CFD code adjusts the magnitude of the inlet velocity to match the user specified volumetric flow rate at each time-step; the pressure variable was set to have zero gradient. The outlets (terminal openings in the distal lung part of the model) were assigned a zero velocity gradient and a zero pressure. In the rat model where periodic breathing was modeled, upon exhale the distal lung pressure boundary condition was changed to zero total pressure. A no-slip condition was applied to the remaining airway wall boundaries, which were assumed to be rigid and impermeable to air. For the convection-diffusion equation (3) upon inhale, the inlet of the rat nose (Supplementary Fig. S1) was assigned a specified chemical concentration. For the human model, the oral cavity was initialized with the appropriate concentration to represent the correct mass of chemical in the bolus puff being inhaled. Upon exhalation in both species, a zero concentration boundary condition was applied at all distal lung airway outlets (i.e. any aldehyde mass exiting the distal airway outlets during inhalation is assumed to be absorbed in deep lung tissues and not available for return to the CFD model airways during exhalation).
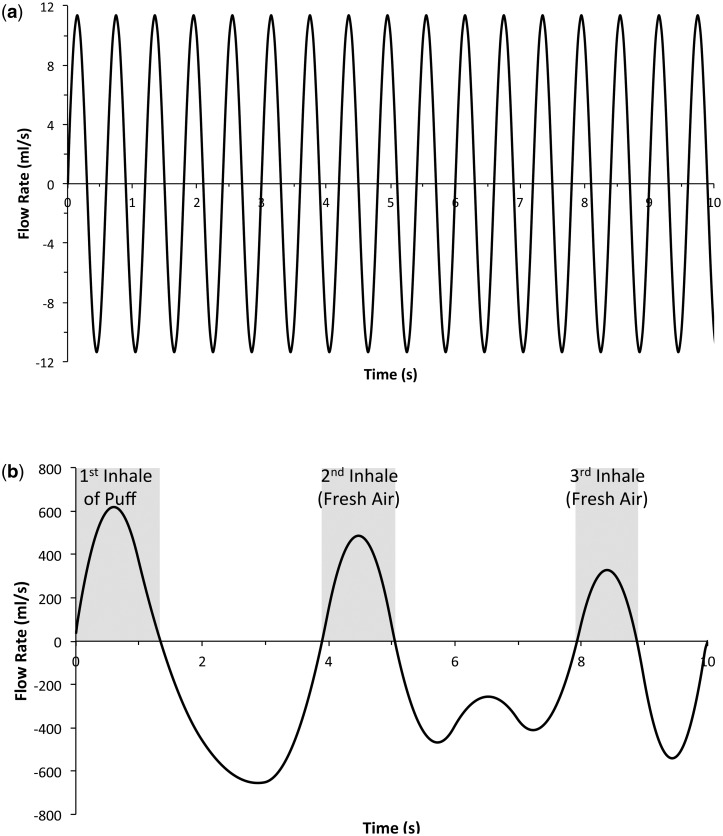
Time-varying flow rates for the rat was assumed to be represented by a sine wave mimicking inhalation and exhalation, and was computed using a breathing frequency of 100 breaths per minute and a minute volume of 0.217 l/min (Fig. 2a; Table 3). To facilitate comparison of acrolein uptake under steady state and transient flow conditions in the 84-year-old female human nasal model, the time-varying flow rate sine wave was computed assuming a minute volume of 6.9 l/min and a breathing frequency of 20 breaths per minute. For the human oral model, an average time-varying flow rate representing a measured human post-cigarette puff breathing profile was used (Fig. 2b) (St Charles et al., 2009). The simulations were verified to be independent of mesh density using acetaldehyde as the test case since exposure scenarios were considerably higher and, as a result, distributed to more tissue compartments, than either acrolein or formaldehyde.
FIG. 2.
Transient CFD airflow simulation profiles for (a) rat sinusoidal respiratory cycle (MV = 217 ml/min; 100 breaths/min) and (b) human cigarette smoking profile for the first 3 full breaths following the initial puff (inhale shown in gray) as measured by St. Charles et al. (2009).
RESULTS
Calibration of Aldehyde Metabolism
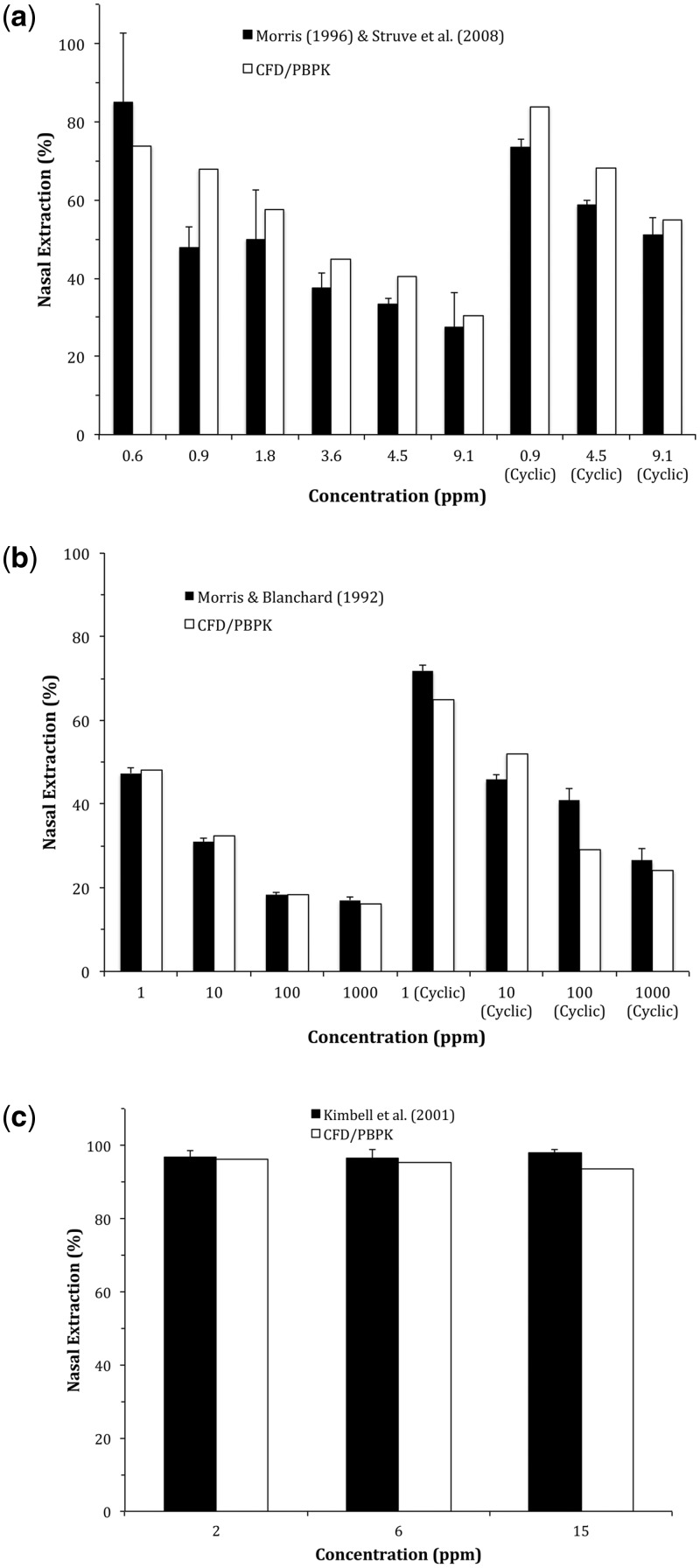
As with our prior studies with acrolein (reproduced in Fig. 3a), rate constants associated with acetaldehyde and formaldehyde metabolism were recalibrated to fit within our 3D respiratory tissue model based upon published nasal extraction experiments with results summarized in Table 2. For acetaldehyde, nasal extraction experiments originally used by Teeguarden et al. (2008) to describe 2 saturable aldehyde dehydrogenase pathways: 1 low affinity/high capacity (ALDH1) enzyme and 1 high affinity/low capacity (ALDH2) enzyme were used to recalibrate metabolism (Morris and Blanchard, 1992). The resulting CFD/PBPK simulations (Fig. 3b) were only sensitive to parameter estimates for the ALDH2 pathway at the lowest concentrations (primarily 1 ppm and to a lesser extent, 10 ppm) while ALDH1 accounted for most of the nasal uptake at higher concentrations. As described previously, the blood flow to nasal tissues had to be increased from 0.1 to 0.5% of the cardiac output at concentrations >25 ppm to account for acetaldehyde-induced vasodilation at higher concentrations.
FIG. 3.
Comparisons of CFD/PBPK model-predicted nasal extraction efficiencies with experimental data from rats reported by Morris and Blanchard (1992), Morris (1996), Kimbell et al. (2001), and Struve et al. (2008) for (a) acrolein, (b) acetaldehyde, and (c) formaldehyde. Steady-state inhalation data at inspiratory flow rates of 300 ml/min (acrolein and acetaldehyde) or 135 ml/min (formaldehyde) were used to re-calibrate metabolic parameters (Table 2) for each aldehyde using the specific male Sprague Dawley rat nasal airway geometry and tissue boundary conditions as described in Corley et al. (2012). Simulations and data for cyclic breathing are shown for (a) acrolein (207 ml/min) and (b) acetaldehyde (100 ml/min).
Previously published formaldehyde nasal extraction data were limited to 2 concentrations (2, 6, and 15 ppm) at a unidirectional flow rate of 135 ml/min (Kimbell et al., 2001b). At these concentrations and flow rate, very little adjustments were made to prior respiratory tissue metabolism rates as nasal extraction efficiencies were ∼97% with no exposure–response differences observed at these concentrations (Fig. 3c).
The re-calibrated acrolein and acetaldehyde CFD/PBPK models compared favorably with nasal extraction data under cyclic airflow conditions (Morris, 1996; Morris and Blanchard, 1992). No comparable data are available for evaluating the formaldehyde model under transient, full breathing cycle conditions.
Comparisons Between Steady-State and Transient Simulations
In our previous paper (Corley et al., 2012), we conducted steady-state inhalation simulations of exposures to acrolein at 0.6 ppm using twice the average minute volumes representing peak inhalation to compare site-specific flux rates for acrolein uptake in the extended airway models of the rat, monkey, and human as was done in prior nose-only CFD models (Schroeter et al., 2008). Now that it is possible to efficiently conduct transient CFD airflow and vapor transport simulations that are fully coupled (2-way) with time-dependent PBPK models, we evaluated the impact of this added realism and computational complexity on internal dose metrics that are relevant for toxicity and mode of action assessments.
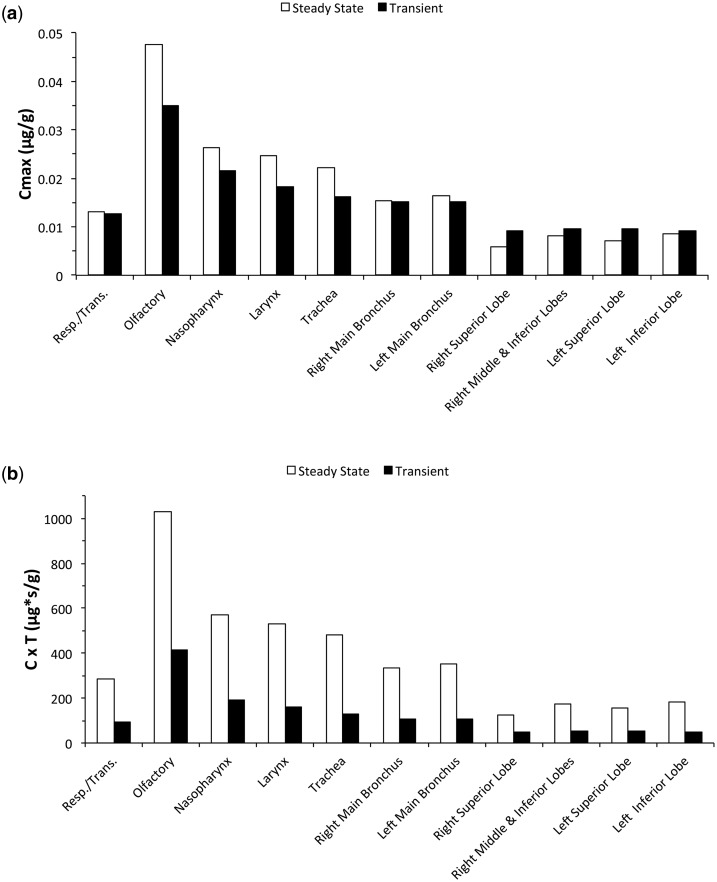
Since acrolein is directly toxic to airway epithelial cells, we compared both compartment-averaged peak concentrations (Cmax) and concentration × time profiles in each airway tissue of our female human CFD/PBPK model computed during nasal breathing at normal minute volumes (6.9 l/min). Peak compartment-averaged tissue concentrations showed only modest differences between steady-state and transient simulations at the same exposure concentration (0.6 ppm) and volumetric flow rate. In this case, airways proximal to the nares reached Cmax’s that were slightly greater under steady-state conditions but trended toward slightly lower peak concentrations than transient simulations in the bronchiolar region due primarily to a rolling wash-in/wash-out effect that occurred in the transient simulations (Fig. 4a). Thus, if peak or Cmax concentrations in each airway region (normalized for volume of tissue in each defined region) are the most appropriate internal dose surrogate for comparisons, the less computationally intensive steady-state simulations can be effective for a reactive, rapidly metabolized chemical like acrolein.
FIG. 4.
Comparisons between steady-state and transient breathing cycles on acrolein epithelial tissue concentrations (compartment averaged) in the female human CFD/PBPK model of Corley et al. (2012). Simulations were conducted at a normal minute volume (6.9 l/min) and a 0.6 ppm inhalation exposure using nasal cyclic breathing at 22 bpm versus steady-state inhalation. Comparisons are shown for (a) peak tissue concentrations (Cmax) and (b) concentration × time (C × T) profiles for a 6-h total exposure. For steady-state simulations, C × T (µg*s/g) = Cmax (µg/g) * 60 s/min * 360 min where Cmax represents the steady-state tissue concentration. For transient simulations, C × T (µg*s/g) = AUC for final breath once periodicity was reached (µg*s/g/breath) * bpm * 360 min.
If, however, residence time is an important factor in toxicity, then transient CFD/time-dependent PBPK would be the method of choice. To demonstrate, the tissue concentrations following steady-state inhalation airflow simulations were used to compute concentration-times-time (C × T) profiles over a 6-h inhalation exposure to 0.6 ppm acrolein. For transient simulations, C × T profiles were derived from areas under the tissue concentration time profiles (AUC) for a representative full breath (inhalation + exhalation) once breath-by-breath periodicity was reached in all airway tissues. AUC’s/breath were then summed over all breaths (22 bpm) in a 6-h exposure. As expected from the transient nature of the local airway exposures and wash-in/wash-out of acrolein from tissues as airway lumen concentrations change over the course of a full breathing cycle, regional C × T profiles were significantly lower than those that occur under steady-state conditions (Fig. 4b). These differences between steady-state and transient approaches can be especially important when comparing internal doses across species given the significant differences in airway geometries, airflows, tissue properties, and breathing patterns. Further differences between steady-state and transient simulations occur as time-dependent tissue doses are compared in ‘hot spots’ located in discrete airway locations as described below.
Rat No-Observed-Adverse-Effect Levels (NOAELs) Inhalation Exposures
Simulations were conducted at the NOAELs for nasal toxicity in rats following subchronic, 6 h/day, 5 days/week inhalation exposures for each aldehyde (0.2, 50, and 1 ppm for acrolein, acetaldehyde, and formaldehyde, respectively; Table 3) (Dorman et al., 2008a, b; Kerns et al., 1983; Monticello et al., 1996; Morgan, 1997; NAS, 2011). For acrolein and formaldehyde, steady-state, breath-by-breath tissue concentrations were reached in all respiratory compartments, except olfactory epithelium within the first 2–3 breaths. Since metabolism in the olfactory region was confined to the submucosal layer rather than the epithelial layer (Bogdanffy et al., 1986; Corley et al., 2012; Keller et al., 1990), more breaths were required to reach steady-state conditions in the olfactory epithelial compartment (10–15 breaths). For acetaldehyde, the NOAEL for nasal toxicity was considerably higher than the other, more reactive aldehydes (50 ppm), thus, at least 22 breaths were required for all tissue compartments to reach steady-state conditions, except olfactory epithelium, which required at least 35 breaths.
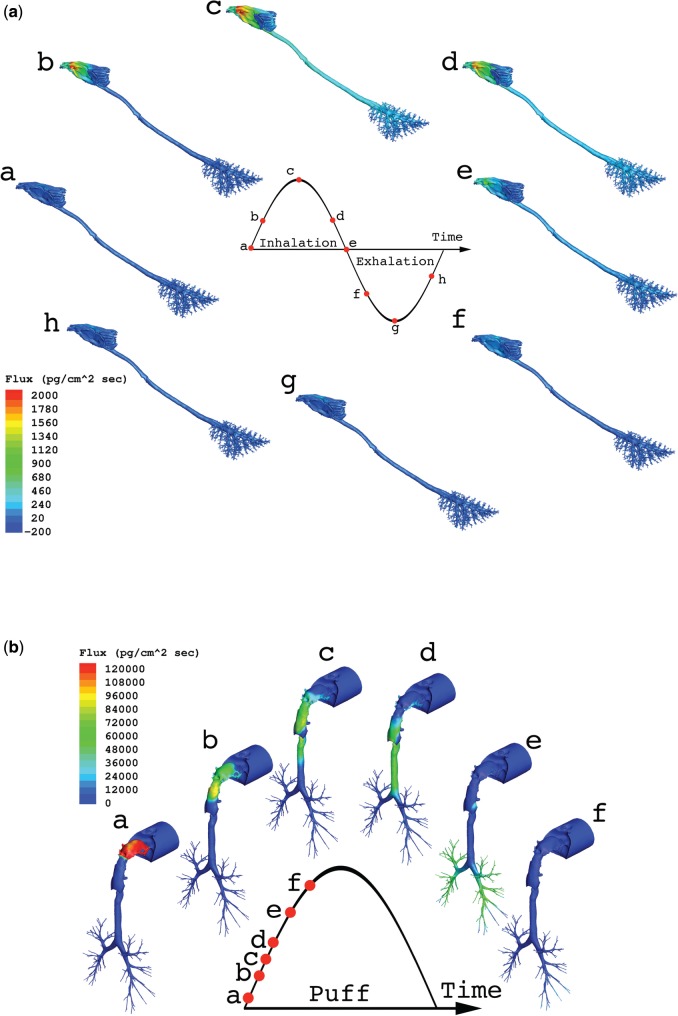
Site-specific airway wall flux rate patterns were remarkably similar across the 3 aldehydes although their magnitudes differed according to airway concentrations and driving forces for tissue uptake (diffusivity, partition coefficients, metabolism, reactivity, blood perfusion). Flux rates are shown for formaldehyde in the rat and human models at multiple times over a single full breathing cycle once steady-state conditions were reached in all tissues (Fig. 5). Additional results for acrolein and acetaldehyde are included in the Supplementary Figures S2 and S3.
FIG. 5.
Airway surface fluxes of formaldehyde as a representative example of aldehyde uptake in the (a) rat and (b) human CFD/PBPK model using the ventilation profiles shown in Figure 4. Rat simulations were performed at the NOAEL for nasal toxicity in subchronic inhalation studies (1 ppm) over the final full breathing cycle while the human simulation depicts airway fluxes during the initial puff inhalation at a representative cigarette smoke yield as described in Table 3.
Both peak (Cmax) and AUC for compartment-averaged tissue concentrations of each aldehyde in the rat were determined for a single representative breath at steady state (Supplementary Fig. S4). Similar results for the human simulations following aldehyde exposures at concentrations found in cigarette smoke are also included in Supplementary Figure S5.
Hot-Spot Target Tissue Doses Following Rat NOAEL Inhalation Exposures
While compartment-averaged internal dose metrics are commonly used in lower dimensional models, the site-specific differences in surface fluxes that were observed over each cell type or tissue compartment (Fig. 5) suggest that this approach is overly simplistic and could be potentially misleading when comparing results across species and exposure scenarios. In previous studies with formaldehyde, Kimbell et al. (2001b, c) used a flux-binning approach to derive relationships between tissue uptake and site-specific lesions that could be used to predict internal doses across species. In this study, we extended their concept by calculating ‘hot spots’ for tissue doses that reflected the residence times, penetration distances, and volumes of each tissue type that reached the highest concentrations of each aldehyde once breath-by-breath steady state tissue concentrations were reached (rat) or under realistic cigarette smoke exposure conditions (human).
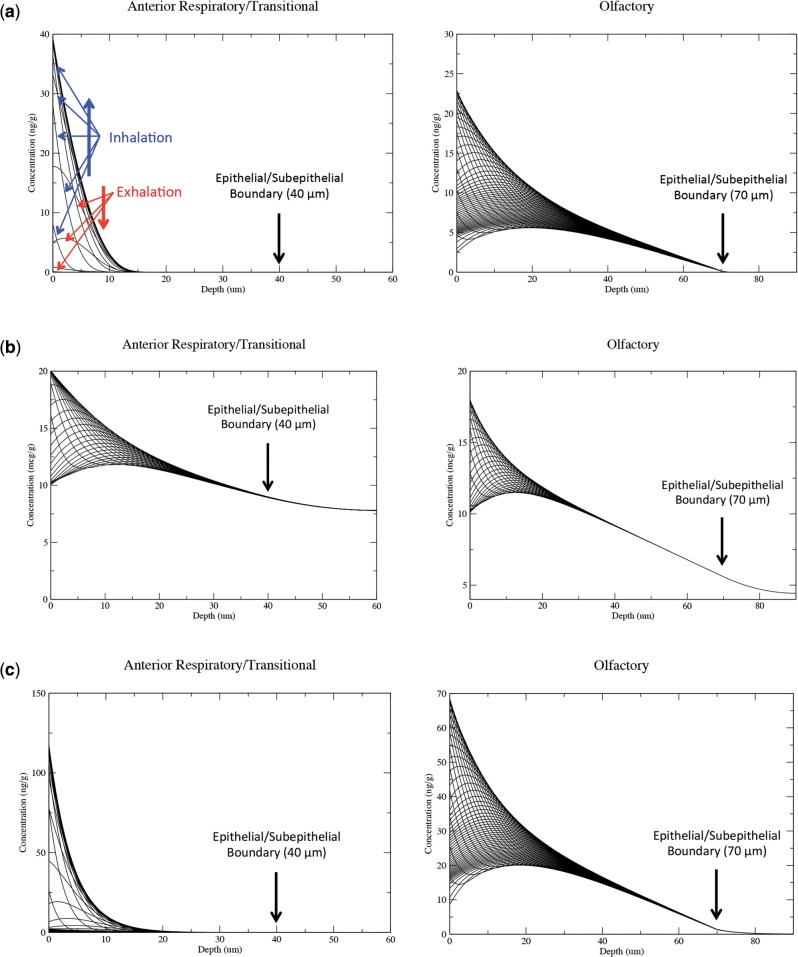
The time- and penetration depth-dependent tissue concentration profiles determined by the PBPK models at each airway surface facet were thus used as the basis for determining hot spot target tissue dose profiles that could be compared across exposure, tissue, and species. Examples of the highest predicted aldehyde tissue concentrations obtained in a single facet within target tissues over the course of the full respiratory cycle are shown in Figure 6 for rats exposed to each aldehyde at the NOAEL for nasal toxicity. For acrolein and formaldehyde, the most reactive of the 3 aldehydes, essentially no material penetrated to the subepithelium in every tissue compartment except olfactory epithelium as each chemical was extensively metabolized or bound to macromolecules as it diffused through the tissues or was washed out during exhalation. Since metabolism by aldehyde dehydrogenases occurs in the olfactory subepithelium and not the epithelial layer, there was a greater degree of penetration by acrolein and formaldehyde although very little material reached the subepithelium, even for the worst-case single airway surface facets with the highest AUCs shown in Figure 6.
FIG. 6.
Tissue concentration profiles for the surface facet with the highest concentrations of (a) acrolein, (b) acetaldehyde, and (c) formaldehyde in rat target tissues (anterior respiratory/transitional region and olfactory region) as a function of penetration depth and time. Representative 0.01–0.03 s time series of each aldehyde concentration × depth profile is shown over the course of a full inhalation/exhalation cycle (see orientation arrows in the acrolein olfactory simulations). Exposure concentrations represented NOAEL’s for nasal lesions from subchronic inhalation studies (0.2, 50, and 1.0 ppm for acrolein, acetaldehyde, and formaldehyde, respectively). The breathing profile used in each CFD simulation is shown in Figure 2a and simulations were conducted until breath-by-breath steady-state concentrations were attained in all tissue compartments.
For acetaldehyde, exposures were considerably higher and the clearance rates were lower than the other 2 aldehydes. Thus, there was significantly greater penetration and residence time in nasal respiratory/transitional and olfactory epithelium once tissues reached steady state. In fact, concentrations of acetaldehyde were strikingly consistent over the full inhalation/exhalation cycle in tissues deeper than 30 µm from the airway lumen (Fig. 6b).
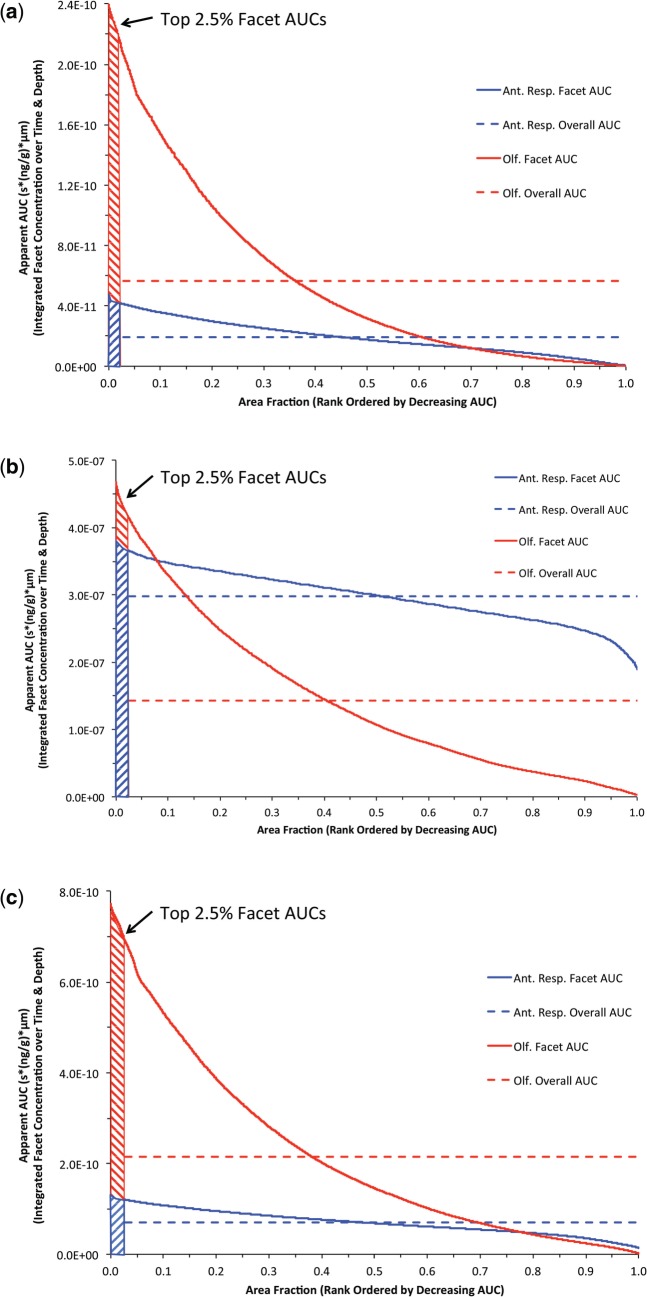
To calculate a time- and penetration depth-dependent internal dose that could be compared across species and exposure, we computed a surface area normalized AUC for the concentrations of each aldehyde in the 1D/PBPK tissue models at each surface facet of the 3D/CFD model (i.e. for each surface facet, we derived an AUC by integrating the concentration profile in the spatial dimension normal to the facet as well as over total time of exposure). Then for each compartment consisting of a particular cell type (nose) and particular airway region (remaining airways; see Supplementary Figure S6 for surface maps), we ranked the facet AUCs in decreasing order and plotted them against their corresponding relative compartment surface area fraction. We then arbitrarily defined our ‘hot spot’ tissue dose as the average AUC that covered the highest 2.5% of the relative surface area fractions within each surface compartment. For rats, results are shown for the 2 target tissues in the nose: the anterior respiratory and transitional epithelium and the olfactory epithelium (Fig. 7).
FIG. 7.
Rank ordered (descending) plot of aldehyde surface area normalized AUC tissue concentrations for each airway surface facet integrated over time and tissue depth in nasal airway target tissues of the rat (blue: anterior respiratory and transitional epithelium; red: olfactory epithelium) following NOAEL inhalation exposures to (a) 0.2 ppm acrolein, (b) 50 ppm acetaldehyde, and (c) 1 ppm formaldehyde using breathing patterns shown in Figure 2. The ‘hot-spots’ (shaded regions) were defined as the top 2.5% of AUCs for each airway compartment as described in the text. The overall compartment averaged AUC’s (dashed line) are shown for comparison.
For all 3 aldehydes, the ‘hot-spot’ analysis identifies those cells at greatest risk (e.g. have the highest time-dependent aldehyde concentrations). Results yielded significantly different predictions and rank ordering of target tissue dose than would be obtained by using compartment-averaged AUC evaluations, which are also shown for each target tissue in Figure 7 and Supplementary Figure S4. For acrolein and formaldehyde, the top 2.5% of surface area normalized AUC’s were obtained in the anterior region of the olfactory epithelium (Figs. 7a and 7c and Supplementary Fig. S6), which overall, had significantly higher time- and penetrated depth-predicted tissue concentrations than the anterior respiratory/transitional epithelium. For acetaldehyde the top 2.5% of surface area normalized AUC’s were also obtained in the anterior region of the olfactory epithelium (Fig. 7b and Supplementary Fig. S6) although the AUC’s predicted for the anterior respiratory/transitional epithelium overall were greater (higher overall percentage of the compartment surface areas had greater time- and tissue depth-dependent concentrations). These ‘hot-spot’ predictions are in contrast to the compartment-averaged approach (summarized in Supplementary Fig. S4), where cells with little or no aldehyde contribute to the overall compartment concentrations thus differentially ‘diluting’ the relative internal doses (see also dashed lines in Figs. 7a–c).
Hot-Spot Target Tissue Doses Following Human Cigarette Smoking Exposures
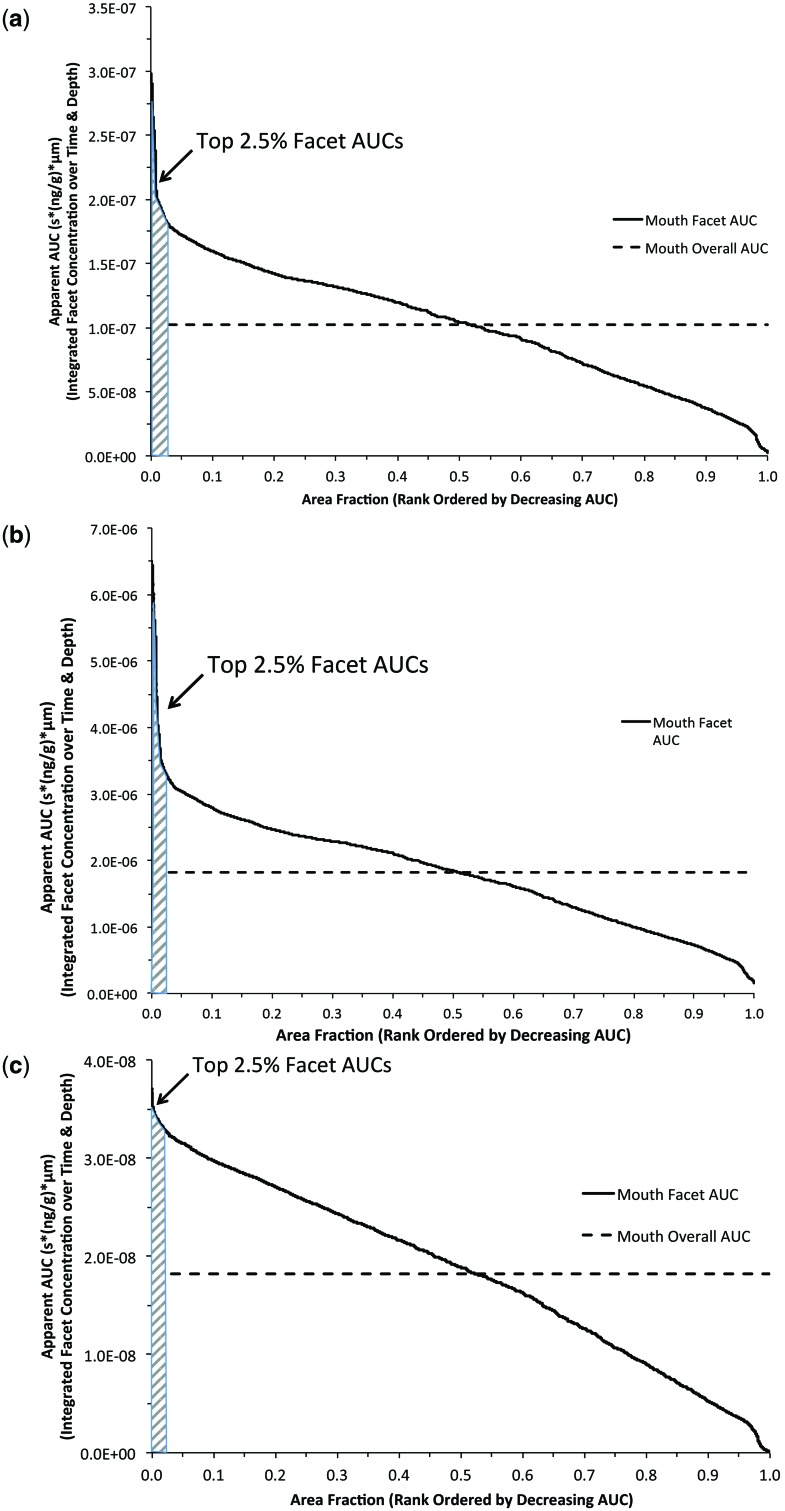
Human simulations were conducted using a representative measured puff breathing profile (Fig. 2b) and cigarette aldehyde yields (Counts et al., 2005; St Charles et al., 2009). Each simulation was initiated by assigning all volumetric cells of the oral cavity with a starting aldehyde concentration based upon cigarette yield, average puffs/cigarette, and the volume of the oral cavity at a full puff (Table 3). Even ignoring the residence time of the initial puff before initiating the first post-puff inhalation, the oral cavity achieved the highest tissue doses for all 3 aldehydes followed by the oropharynx, larynx, and conducting airways of the lung as the initial inhalation of the puff moved distally.
Similar to the profiles generated for the rat nasal tissues, the rank ordered surface area normalized AUCs for each airway surface facet and hot spots (top 2.5%) are shown in Figure 8 for human mouth tissues following each aldehyde exposure. The highest hot-spot AUCs were predicted for acetaldehyde due to its high initial puff exposure concentration (1028 ppm) followed by acrolein then formaldehyde. Although acrolein and formaldehyde had similar initial puff exposure concentrations (94 vs. 108 ppm, respectively), the higher rate of metabolic clearance of formaldehyde significantly reduced the time-dependent tissue concentration and penetration depth and thus, the hot spot AUCs.
FIG. 8.
Rank ordered (descending) plot of surface area normalized AUC in each airway surface facet integrated over time and tissue depth in human mouth following single puff of cigarette smoke containing (a) 94 ppm acrolein, (b) 1028 ppm acetaldehyde, and (c) 108 ppm formaldehyde using breathing patterns shown in Figure 2. The ‘hot–spots’ (shaded regions) were defined as the top 2.5% of AUCs for each airway compartment as described in the text. The overall compartment averaged AUC’s (dashed line) are shown for comparison.
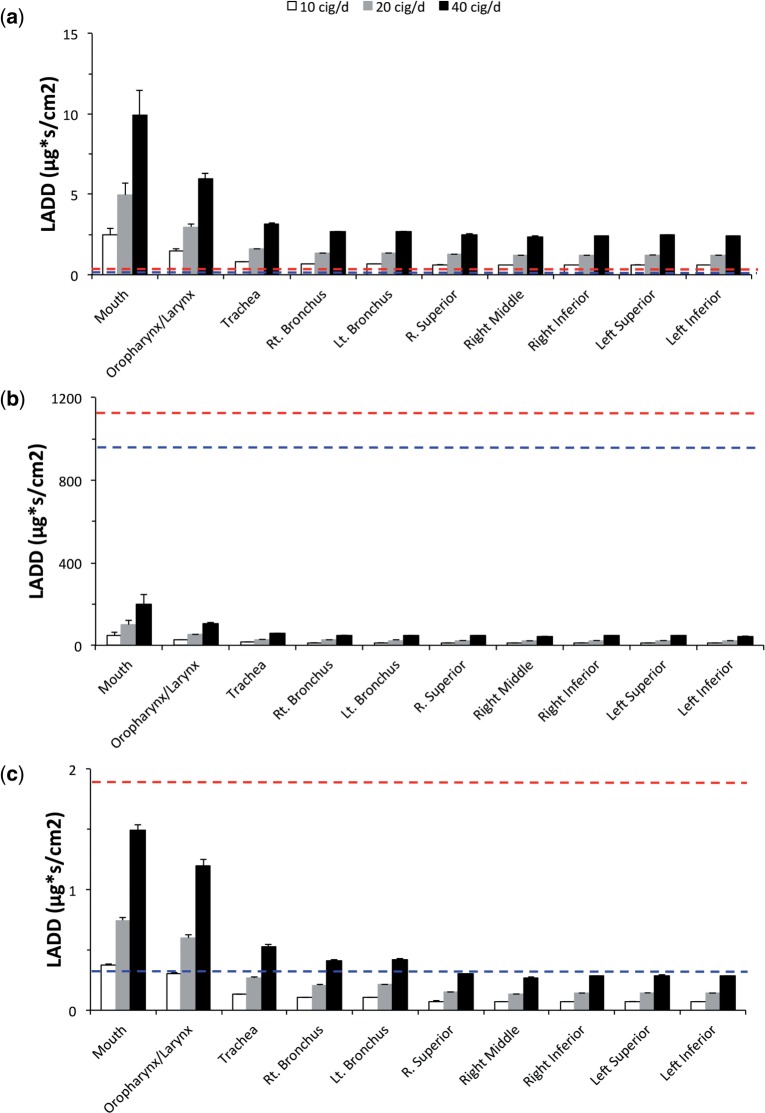
Comparing Lifetime Average Daily Doses
Lifetime average daily doses (LADDs) were calculated for target tissues in the rat nose (anterior respiratory/transitional epithelium and olfactory epithelium) following subchronic NOAEL inhalation concentrations (Table 3) for comparison with LADDs determined for each airway region in the human following aldehyde exposures after smoking 10, 20, or 40 cigarettes/day. For purposes of this comparison, LADDs were calculated from the highest 2.5% hot-spot AUCs (AUC2.5) of each airway compartment surface facet during the final simulated breath (rat) and human cigarette smoking exposures as follows:
| (7) |
| (8) |
Assuming no site concordance (e.g. rat nasal tissues are a sentinel for all human airways), the resulting rat LADDs for target tissues in the nose were compared against all conducting airways in the human (Fig. 9).
FIG. 9.
Comparisons between LADDs determined in the rat at NOAEL for nasal toxicity (top dashed red line—olfactory epithelium; bottom dashed blue line—anterior respiratory epithelium) in subchronic inhalation bioassays and LADD’s determined in the human for each epithelial tissue compartment of the conducting airways after smoking 10, 20, or 40 cigarettes/day (bars) for (a) acrolein, (b) acetaldehyde, and (c) formaldehyde in humans at representative cigarette yields (Table 3). LADD’s were calculated from the highest 2.5% of each airway compartment surface facet AUC (concentrations integrated over time, depth and normalized by facet surface area) during the final breath (rat) or puff inhalation (human) as shown in Figures 7 and 8 and described in the text.
For acrolein, all human airways achieved LADDs that were higher than those calculated for the rat target tissues even at exposures to 10 cigarettes/day. At the other extreme, no human airway tissue LADD approached those determined for acetaldehyde in target tissues of the rat even after 40 cigarettes/day. Formaldehyde results were intermediate with several human tissues exceeding LADD’s in rat target tissues depending upon the number of cigarettes/day and whether the anterior respiratory/transitional or olfactory epithelium LADDs in the rat are used to drive the comparisons.
Sensitivity Analyses
The computational intensity of fully transient, 2-way coupled CFD/PBPK models precluded the implementation of a formal sensitivity analysis that is commonly employed for simple PBPK models. However, selective analyses were conducted during the course of recalibrating metabolism rates from published experimental data and hot-spot determinations to assess their impact on reported results. Thus, in addition to parameters previously demonstrated to affect acrolein uptake under steady-state inhalation conditions (Corley et al., 2012) that also affected formaldehyde simulations, additional parameters were identified specifically for acetaldehyde due to its higher exposure concentration and lower metabolic rates. As discussed previously, acetaldehyde can penetrate significantly deeper than either acrolein or formaldehyde and reach the subepithelial compartment where blood flows can become a factor in acetaldehyde clearance. This observation was important for adequately simulating exposure concentrations >25 ppm in the rat. In addition, metabolic rate constants for ALDH2 significantly affected nasal uptake at low concentrations (up to 10 ppm) in the rat while rate constants associated with ALDH1 metabolism were more important for uptake at concentrations >10 ppm acetaldehyde. Other physiological parameters used in the acetaldehyde model, specifically the values for epithelial and subepithelial thickness (assumed to be constant over each cell-type or tissue compartment) also affected uptake, clearance and thus, estimations of tissue dose due to the compartmentalization of metabolism and blood flows. In addition, enzyme localization, especially for the olfactory epithelium where aldehyde dehydrogenases are present in the subepithelium rather than the epithelium, strongly affected tissue concentrations in the nose, especially in the rat. Furthermore, the arbitrary reductions in aldehyde dehydrogenase activity along conducting airways of the lower respiratory tract discussed by Corley et al. (2012) significantly affected tissue uptake and concentration profiles in these regions, especially in humans following oral breathing. Lastly, the use of a zero-flux subepithelial layer boundary condition for acetaldehyde was important to determinations of tissue uptake and penetration but had no impact on formaldehyde and acrolein simulations.
DISCUSSION
With the improvements in imaging, computer hardware, and software over the past decade, the barriers to developing and applying realistic CFD models of the entire respiratory system have significantly diminished. In our previous article, we applied these advancements to develop the first suite of CFD respiratory airway models that extended from the external nares to the respiratory bronchiole region of the rat, monkey, and human (Corley et al., 2012). To evaluate the performance of these complex airway models, we also exploited phase-contrast 3He gas MRI for the first validation of CFD airflow predictions in live rats (Minard et al., 2012).
In our previous study (Corley et al., 2012), we applied a PBPK model developed by Schroeter et al. (2008) to describe the uptake of acrolein in all conducting airways of each species. Under steady-state inhalation, site-specific uptake of acrolein was strongly influenced by species-specific airway anatomy and physiology. The highest regional extraction efficiencies were predicted for the rat nose, followed by the monkey, then human noses. Greater penetration of acrolein into the bronchiolar region of the lung was predicted in the human following nasal and oral breathing than predicted for either the rat or monkey. While regional, volume-averaged tissue concentrations of acrolein in human pulmonary tissues were similar to those produced by computationally less-intensive mechanistic models, such as that of Asgharian et al. (2012), the site-specificity afforded by the CFD/PBPK simulations provided greater correlations with local responses observed in rat toxicity studies that could be compared with human simulations (Schroeter et al., 2008). At that time, CFD simulations of airflows were conducted under steady-state inhalation conditions because of their reduced complexity and computational demands. Thus, the impact of realistic, species-specific breathing patterns on site-specific tissues doses in extended airway models had never been evaluated.
Here, we reported the first high-resolution CFD/PBPK comparisons of respiratory tissue dosimetry under typical breathing conditions in rats and humans. This was accomplished using fully transient, 2-way coupled CFD/PBPK airflow and material fate and transport models and improved airway meshing procedures that enabled convergence of transient airflow simulations. Our initial comparisons focused upon acrolein (used in our previous companion study) plus 2 additional reactive, water-soluble aldehydes (acetaldehyde and formaldehyde) that are known to produce toxicity and tumors in rat nasal tissues, and have also been associated with potential adverse outcomes in cigarette smokers.
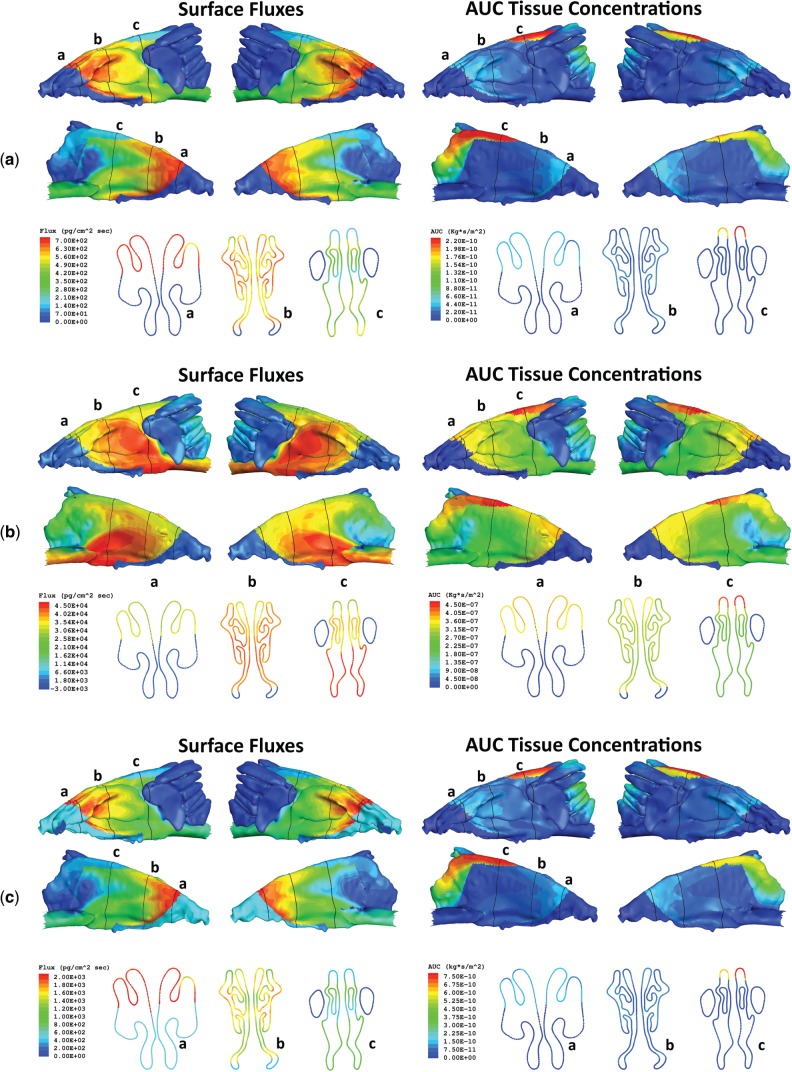
In the past, vapor fluxes across airway walls have been used in CFD and CFD/PBPK models as internal dose metrics for highly reactive vapors such as formaldehyde, hydrogen sulfide, and ozone, as they correlated well with sites of injury in respiratory airways (Kimbell et al., 1997, 2001a; Overton et al., 1987; Schroeter et al., 2006a, b, 2008). The inherent assumption in these prior models was that surface flux rates were predictive of local tissue concentrations that are necessary for toxicity. Asgharian et al. (2012) confirmed this relationship for formaldehyde, but for less reactive vapors, such acetaldehyde, site-specific flux rates did not necessarily correlate with tissue concentrations using their mechanistic model of the human lung. In this study, surface fluxes predicted for even highly reactive chemicals like formaldehyde and acrolein were not well correlated with local time-dependent tissue concentration AUC’s estimated for nasal tissues of the rat (Fig. 10). This is especially true for the anterior olfactory epithelium where the location of aldehyde dehydrogenase metabolism was restricted to the subepithelium rather than the epithelium compartments of the PBPK model resulting in significantly higher AUCs for each aldehyde than predicted by surface fluxes alone as compared with other regions of the nose. Thus, the importance of the histochemical localization of aldehyde dehydrogenase enzymes by Bogdanffy et al. (1986) and Keller et al. (1990) to these results cannot be understated.
FIG. 10.
Surface maps of airway surface flux rates (left) and AUCs for time and penetration-depth integrated tissue concentrations (right) for (a) acrolein, (b) acetaldehyde, and (c) formaldehyde in the rat nose at NOAEL exposures. Surface maps are shown for left and right lateral (top) and septal views (middle) with cross-sections taken at 3 locations (labeled a–c) for each surface view (bottom).
Although we continue to report results for site-specific fluxes across airway walls (e.g. flux rates at peak inhalation that balance wash-in vs. wash-out processes of chemical transport), the PBPK airway boundary condition allowed us to focus our vapor exposure and species comparisons upon commonly used pharmacokinetic metrics such as Cmax or AUC for parent aldehyde over the course of the full breathing cycle once breath-by-breath steady-state conditions were reached in all tissues.
We initially determined cell type (nose) or anatomic region (remaining airways) specific compartment-averaged Cmax’s and AUC’s for parent aldehyde concentrations and clearly demonstrated that steady-state inhalation conditions, while attractive to use because of the reduced computational demands can provide inadequate or even erroneous predictions of local tissue concentrations, even using these anatomically correct respiratory airway models (Fig. 4). Thus, fully transient airflow and material transport simulations with 2-way coupled airway tissue boundary conditions for tissue uptake, metabolism, distribution, and elimination (in this case with PBPK models) may be warranted, especially for highly cleared vapors, unless proven otherwise.
By incorporating tissue-specific PBPK model to each facet of airway surfaces, we predicted the local time- and penetration depth-dependent tissue concentrations that most closely approximate exposure conditions experienced by small, subgroups of cells in airway epithelium or subepithelium. This then enabled quantitative comparisons as a function of species, aldehyde exposure, and breathing pattern (Fig. 6), as well as their precise locations (Fig. 10). Of the 3 aldehydes, the 2 with higher metabolic clearance and tissue reactivity (acrolein and formaldehyde) are unlikely to penetrate deep into epithelial or subepithelial tissues, even in the olfactory region where metabolism occurs only in the subepithelium. Thus, even for the worst-case scenario (individual surface facets with highest aldehyde concentration in rat target tissues), it is unlikely that either of these aldehydes would penetrate directly into the systemic blood circulation at exposure concentrations up to their respective NOAELs for subchronic toxicity. In contrast, both epithelial and subepitheilial acetaldehyde nasal tissues can reach breath-to-breath equilibrium concentrations that are affected and cleared by local blood perfusion, especially at concentrations >25 ppm where vasodilation can occur in the rat nose (Stanek et al., 2001).
By addressing realistic breathing and exposure patterns, the resulting CFD/PBPK models described here offer unprecedented insights into airway and species differences that mediate tissue dose. Importantly, comparable insight is not achievable using simpler, compartmental modeling, or tissue-averaging approaches. For our study, we estimated the AUCs for each surface facet aldehyde concentration as a function of time and penetration depth. To compare site-specific airway tissue internal doses between rats and humans under realistic breathing and estimated cigarette yields, ‘hot-spots’ for each aldehyde in each cell type (nose) or region (other airways) were determined along with overall regional AUCs (Figs. 7 and 8). These simulations clearly demonstrated that there is a great deal of variability in tissue dose within each compartment that is missed using simpler compartmental models. By focusing on those cells within each tissue compartment that have significantly greater internal dose, future research could to test the potential sensitivity differences between cell or tissue types.
This study focused on producing more informed human risk assessments through more realistic coupling of external exposures to site-specific tissue doses and LADDs. In this example, LADDs based upon the highest 2.5% of each airway compartment’s ‘hot-spot’ analysis were calculated for each aldehyde at a representative cigarette yield in each region of the human conducting airways following exposures to 10, 20, or 40 cigarettes/day. Each airway region was then compared with LADDs determined in target tissues of the nose of rats (anterior respiratory/transitional and olfactory epithelium) following NOAEL exposures assuming equivalent tissue sensitivity and mode of action between species (Fig. 9). These high-resolution comparisons of tissue doses produced a rank ordering of acrolein > formaldehyde > acetaldehyde for potential concerns associated with aldehyde toxicity based upon common internal dose metrics.
Clearly, other potential interactions between these aldehydes and the myriad of volatile, semi-volatile and particulate constituents of cigarette smoke along with the changes in air temperature and humidity during breathing and smoking are ignored in this comparison. These assumptions should be confirmed in future studies such as breath analysis of human volunteers during smoking. However, such interactions have also been ignored in prior attempts to rank the relative risks of chemical constituents in cigarette smoke according to existing individual chemical risk assessments such as cancer potency factors, reference concentrations (RfCs), or reference exposure levels (RELs) (Fowles and Dybing, 2003; Pankow et al., 2007). While this alternative approach is convenient and easy to implement, it results in a different rank ordering of risk for the 3 aldehydes with acrolein > acetaldehyde > formaldehyde since appropriate routes of exposure, target tissues, or species differences in dosimetry are not considered.
While the primary goal of this study was to overcome prior computational challenges for conducting realistic, transient airflow, and tissue dosimetry simulations in extended airway models, there remains a number of limitations and thus, opportunities for improving CFD/PBPK models for the chemicals used in this case study as well as other airborne materials in general. For example, imaging technologies have improved the anatomic foundations for the CFD/PBPK models used in this study. In fact, it is now possible to develop multiple models for each species to assess variability in dosimetry based upon differences in anatomy and physiology. However, the numbers of pulmonary airways that are currently captured using clinical imaging systems for humans have been limited to the upper tracheo-bronchial region (typically 5–9 generations on average). For the aldehyde simulations and comparative LADD calculations for cigarette smoke exposures, this limitation did not affect the purpose or conclusions of this study as the highest tissue concentrations were obtained in the upper conducting airways that were captured in the 3D models. However, for other materials that target the deep lung or penetrate past the 3D CFD airways during inhalation by humans (as we observed with acetaldehyde), a more explicit description of airways beyond the current resolution of imaging systems will need to be included to fully capture material transport, tissue interactions, and potentially, exhalation. Several approaches have been proposed to accomplish this goal including expanding the 3D airway geometries with recursive or guided space-filling algorithms or by coupling of the 3D models with 1D models representing the deep lung at each 3D airway outlet (Kuprat et al., 2013; Tawhai and Burrowes, 2003).
For many inhaled materials, the combined mucus/epithelium compartment in the PBPK model airway boundary condition used in the current case study could be an important over-simplification. While explicitly including a mucus layer is more realistic, such an expansion in the CFD/PBPK model places greater demands upon the resolution needed in experiments for model development and performance evaluation to support the added complexity. In fact, the differences between model and experimental resolution are clearly important for nearly every aspect of the CFD/PBPK model development and evaluation. For example, aldehyde dosimetry in all airway tissues was highly sensitive to the location of aldehyde dehydrogenase enzymes. Other than histochemical studies conducted in the rat nose by Bogdanffy et al. (1986) and Keller et al. (1990), little else is known about the locations of key enzymes involved in aldehyde clearance, or how their catalytic activities vary along the conducting airways of the rat and, more importantly, the human as we described in our previous paper (Corley et al., 2012).
In addition, tissue thicknesses and blood perfusion rates within a region (or compartment) are poorly documented across species. For example, the thicknesses of each epithelial and subepithelial tissue compartment in the rat and human airway models were based upon limited histological measurements from selected slices through each airway region. A more complete morphometric analysis could improve the airway boundary conditions and transitions within and between adjacent compartments. Similarly, blood perfusion to and within nasal, oral, pharyngeal, laryngeal, and tracheal tissues are based upon a handful of studies conducted at the gross tissue level and assumptions on distribution within each region. This has led to variability in blood perfusion rates used in prior PBPK models for aldehydes described in this manuscript (e.g. nasal blood perfusion).
With regard to model evaluations, the only pharmacokinetic data currently available to compare against predicted airway tissue uptake and local concentrations of each aldehyde are the nasal airway extraction studies conducted by Morris, Kimbell et al. in rats (Fig. 3). To our knowledge, no data are available that currently matches the resolution of CFD/PBPK predicted site-specific airway tissue dose within the rat nose, much less other airways or the human. To address this issue, prior models have relied upon correlations between predicted site-specific doses and mapping of the locations of airway-specific lesions (Kimbell and Subramaniam, 2001; Kimbell et al., 1997, 2001a, b; Postlethwait et al., 2000; Schroeter et al., 2008). However, such correlations provide only indirect confirmation of predicted site-specific dosimetry. Thus, newer approaches that explicitly determine site-specific dosimetry within tissues are needed. In animal studies, micro-dissection and analysis of airway tissues or newer imaging techniques, such as mass spectrometry imaging (Lanekoff and Laskin, 2015; Lanekoff et al., 2012, 2013, 2015; Laskin et al., 2012) may prove useful for some materials. For humans, less invasive approaches such as region-specific breath analysis (Hinderliter et al., 2005) or breath analysis using controlled breathing maneuvers that target different regions of the respiratory system as has been done with particles and cigarette smoke (Darquenne and Prisk, 2004; Darquenne et al., 2000; McGrath et al., 2009; Mills et al., 2002; Peterson et al., 2008) could be used to improve confidence in model predictions.
In conclusion, this study successfully extended our prior CFD/PBPK models that focused upon steady-state inhalation to simulate site-specific airway tissue doses to common aldehyde vapors inhaled under realistic exposures. For these reactive constituents of cigarette smoke, 2-way coupling of CFD airflow and material transport models with PBPK airway tissue models enabled transient simulations that provided a significant improvement over steady-state predictions. With the new CFD/PBPK models reported in this study, LADDs were compared for each aldehyde under realistic cigarette smoking in humans with those produced in target tissues of rats following subchronic inhalation exposures. The resulting comparison of LADDs therefore provides important additional insights for determining relative constituent risks for smokers that otherwise lack species- and exposure-specific tissue dosimetry information. These models are likewise useful for updating and refining individual chemical risk assessments for workplace and environmental exposures; thus, each model is available upon request.
SUPPLEMENTARY DATA
Supplementary data are available online at http://toxsci.oxfordjournals.org/.
FUNDING
National Heart, Lung, and Blood Institute of the National Institutes of Health (R01 HL073598). R.J. Reynolds Tobacco Co. under a separate contract with Battelle (Project 56296 to R.A.C., S.K., A.P.K., D.R.E., and C.T.) and published previously (Corley et al., 2012).
APPENDIX
Computation of 1D PDE Time-Step
To compute a single time-step of the 1D PDEs in equations 4 and 5 to find the boundary flux at every 3D convection–diffusion equation time step, we discretize equation 4 in space with mt uniform intervals (each of length dxt = Lt/mt) and similarly we discretize equation 5 in space with mb uniform intervals (each of length dxb = Lb/mb). Over each CFD time step from t − Δt to t, we perform a first-order backwards difference time step of our 1D PDEs from t − Δt to t. At time t, at grid point i in the 1D domain of the PDEs we make the following approximations:
| (A1) |
where is the tissue concentration at grid point i at time t and is the tissue concentration at grid point i at the previous time t − Δt, and similarly for and . We can drop the superscripts t and b by noting that for , the concentration is a tissue concentration and for , the concentration is a subepithelial concentration. This uses that fact that = , since the partition coefficient Pbt is assumed to be unity.
The diffusion term is discretized in the standard fashion:
| (A2) |
where D = Dt or Db depending on whether grid point i is in the epithelial or subepithelial domain. To keep our equations linear we discretize the saturable metabolism term by
| (A3) |
In other words, the denominator uses the lagged concentration , justified by the assumption that Ci does not vary much during a small time step Δt. Finally, the discretization of the first-order kinetics term and the blood loss term is seen to be trivial.
With these discretization assumptions, we see that our PDEs are equivalent to the following tri-diagonal system:
| (A4) |
where we define the coefficients ai, bi, and ci of the matrix as follows:
| (A5) |
| (A6) |
| (A7) |
This system is solved in time using the relatively trivial and well-known tri-diagonal solution algorithm (Press et al., 1992). This yields the concentrations C1, C2,… at time t from which we can compute the flux into the tissue domain from which we can derive the normal gradient of the concentration for the CFD code using equation 6. The zero Neumann condition at x = Lt + Lb is seen to be enforced by the value of . Note that there is no ‘2' in front of Db for this coefficient. The awkward diffusion coefficient contributions for a, b, and c at grid point mt reflect the transitional case where Δxb is not necessarily Δxt and Db is not necessarily Dt. The value of C0 in the first entry on the right-hand side drives the diffusion into the epithelial compartment. C0 is the value of the concentration at the air-tissue interface and is .
However, care must be taken when using the relation
| (A8) |
Here is the unknown value of concentration on the air side of the air-tissue interface at time t. If instead we set , where is the known value of concentration on the air side of the air-tissue interface at time t − Δt, we find that using this lagged value leads to overly large fluxes out of the CFD domain, which in turn leads to negative concentrations in the CFD domain which invalidate the solution. This is especially true if dxt, the tissue mesh spacing, is sufficiently fine. Instead, we derive the correct value of to use as follows. At the air-tissue interface we have the 2 equations
| (A9) |
where λf is the rate of the ‘forwards' reaction where a free molecule of substance in the air becomes bound in the tissue at the interface and λb is the rate of the ‘backwards' reaction where a tissue bound molecule of substance gets unbound and become a free molecule in the air. If we divide through the first of these equations by λb, we obtain
| (A10) |
Assuming λb and λf are very large so that we have equilibrium at each time step, we obtain equation A8 with Notice also that summing the 2 equations in equation A9 yields
| (A11) |
implying the sum C0 + Cair is constant. This is only true on the fast time scale of concentration equilibration at the air–tissue interface. Over longer timescales (i.e. several tens or hundreds of Δt timesteps which are typically small of order 10−5 s) we have that the sum C0 + Cair slowly changes as substance diffuses out of (or into) the lumen and into (or out of) the tissue, but over a single tiny Δt timestep, it is a good approximation that
| (A12) |
Solving equations A8 and A12 for C0 and Cair, we obtain
| (A13) |
It can be seen that in the case which occurs as an initial condition when the simulation code is started that we obtain , which is a much smaller value than using and so it is clear that equation A13 leads to a much gentler ‘startup’ when the lumen region has non-zero initial values and the tissue region has initial null values. Yet, over a medium time-scale (of several tens or hundreds of Δt time intervals), we will obtain that equation A13 relaxes and .
In summary, our more stable way of setting a value to use in the system above is to set
| (A14) |
where C0 is tissue concentration at the air–tissue interface at time t, is the previous, known tissue concentration at the air–tissue interface at time t − Δt, and is previous known air concentration at the air–tissue interface at time t − Δt.
Supplementary Material
ACKNOWLEDGMENTS
A portion of the research was performed using the PNNL Institutional Computing (PIC) Facilities at the Pacific Northwest National Laboratory. The measured human post-puff breathing profile for a smoker was kindly provided by Dr F.K. St. Charles, Consultant. The authors are grateful to Dr. Jeff Schroeter, ARA, RTP, NC, for his assistance with the initial CFD/PBPK acrolein model and refinements to mapping locations of each cell type in the rat nasal airways.
REFERENCES
- Appelman L. M., Woutersen R. A., Feron V. J. (1982). Inhalation toxicity of acetaldehyde in rats. I. Acute and subacute studies. Toxicology , 23, 293–307. [DOI] [PubMed] [Google Scholar]
- Asgharian B., Price O. T., Schroeter J. D., Kimbell J. S., Singal M. (2012). A lung dosimetry model of vapor uptake and tissue disposition. Inhal. Toxicol. , 24, 182–193. [DOI] [PubMed] [Google Scholar]
- Bogdanffy M. S., Randall H. W., Morgan K. T. (1986). Histochemical localization of aldehyde dehydrogenase in the respiratory tract of the Fischer-344 rat. Toxicol. Appl. Pharmacol. , 82, 560–567. [DOI] [PubMed] [Google Scholar]
- Burns D. M., Dybing E., Gray N., Hecht S., Anderson C., Sanner T., O'Connor R., Djordjevic M., Dresler C., Hainaut P., et al. (2008). Mandated lowering of toxicants in cigarette smoke: a description of the World Health Organization TobReg proposal. Tob. Control , 17, 132–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cassee F. R., de Burbure C. Y., Rambali B., Vleeming W., van de Kuil A., van Steeg H., Fokkens P. H., van Amsterdam J. G., Dormans J. A., Opperhuizen A. (2008). Subchronic inhalation of mixtures of cigarette smoke constituents in Xpa-/-p53+/- knock-out mice: a comparison of intermittent with semi-continuous exposure to acetaldehyde, formaldehyde, and acrolein. Food Chem. Toxicol. , 46, 527–536. [DOI] [PubMed] [Google Scholar]
- Cassee F. R., Stenhuis W. H., Groten J. P., Feron V. J. (1996). Toxicity of formaldehyde and acrolein mixtures: in vitro studies using nasal epithelial cells. Exp. Toxicol. Pathol. , 48, 481–483. [DOI] [PubMed] [Google Scholar]
- Conolly R. B., Lilly P. D., Kimbell J. S. (2000). Simulation modeling of the tissue disposition of formaldehyde to predict nasal DNA–protein cross-links in Fischer 344 rats, rhesus monkeys, and humans. Environ. Health Perspect ., 108(Suppl 5), 919–924. [DOI] [PubMed] [Google Scholar]
- Corley R. A., Kabilan S., Kuprat A. P., Carson J. P., Minard K. R., Jacob R. E., Timchalk C., Glenny R., Pipavath S., Cox T., et al. (2012). Comparative computational modeling of airflows and vapor dosimetry in the respiratory tracts of rat, monkey, and human. Toxicol. Sci. , 128, 500–516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Counts M. E., Morton M. J., Laffoon S. W., Cox R. H., Lipowicz P. J. (2005). Smoke composition and predicting relationships for international commercial cigarettes smoked with three machine-smoking conditions. Regul. Toxicol. Pharmacol. , 41, 185–227. [DOI] [PubMed] [Google Scholar]
- Darquenne C., Paiva M., Prisk G. K. (2000). Effect of gravity on aerosol dispersion and deposition in the human lung after periods of breath holding. J. Appl. Physiol. , 89, 1787–1792. [DOI] [PubMed] [Google Scholar]
- Darquenne C., Prisk G. K. (2004). Aerosol deposition in the human respiratory tract breathing air and 80:20 heliox. J. Aerosol Med. , 17, 278–285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DHHS (2012). Harmful and potentially harmful constituents in tobacco products and tobacco smoke; established list. Federal Register 77, 20034–20037. [Google Scholar]
- Dorman D. C., Struve M. F., Wong B. A., Gross E. A., Parkinson C., Willson G. A., Tan Y. M., Campbell J. L., Teeguarden J. G., Clewell H. J., 3rd, et al. (2008a). Derivation of an inhalation reference concentration based upon olfactory neuronal loss in male rats following subchronic acetaldehyde inhalation. Inhal. Toxicol. , 20, 245–256. [DOI] [PubMed] [Google Scholar]
- Dorman D. C., Struve M. F., Wong B. A., Marshall M. W., Gross E. A., Willson G. A. (2008b). Respiratory tract responses in male rats following subchronic acrolein inhalation. Inhal. Toxicol. , 20, 205–216. [DOI] [PubMed] [Google Scholar]
- EPA (2002). A review of the reference dose and reference concentration processes. Final Report. December, 2002. EPA/630/P-02/002F. http://www.epa.gov/iris. [Google Scholar]
- EPA (2009). Risk assessment guidance for superfund. Vol. I: Human health evaluation manual (Part F, Supplemental guidance for inhalation risk assessment). Office of Superfund Remediation and Technology Innovation (OSWER). OSWER 9285.7-82. Final Report. January, 2002. EPA-540-R-070-002. [Google Scholar]
- Fowles J., Dybing E. (2003). Application of toxicological risk assessment principles to the chemical constituents of cigarette smoke. Tob. Control , 12, 424–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franks S. J. (2005). A mathematical model for the absorption and metabolism of formaldehyde vapour by humans. Toxicol. Appl. Pharmacol. , 206, 309–320. [DOI] [PubMed] [Google Scholar]
- Georgieva A. V., Kimbell J. S., Schlosser P. M. (2003). A distributed-parameter model for formaldehyde uptake and disposition in the rat nasal lining. Inhal Toxicol. , 15, 1435–1463. [DOI] [PubMed] [Google Scholar]
- Harkness J. E., Turner P. V., VandeWoude S., Wheler C. L. (2010). Harkness and Wagner's Biology and Medicine of Rabbits and Rodents. Wiley-Blackwell, Singapore. [Google Scholar]
- Hinderliter P. M., Thrall K. D., Corley R. A., Bloemen L. J., Bogdanffy M. S. (2005). Validation of human physiologically based pharmacokinetic model for vinyl acetate against human nasal dosimetry data. Toxicol. Sci. , 85, 460–467. [DOI] [PubMed] [Google Scholar]
- ICRP (1994). Human respiratory tract model for radiological protection. A report of a Task Group of the International Commission on Radiological Protection. Annals of the ICRP , 24, 1–482. [PubMed] [Google Scholar]
- Jacob R. E., Colby S. M., Kabilan S., Einstein D. R., Carson J. P. (2013). In situ casting and imaging of the rat airway tree for accurate 3D reconstruction. Exp. Lung Res. , 39, 249–257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamata E., Nakadate M., Uchida O., Ogawa Y., Suzuki S., Kaneko T., Saito M., Kurokawa Y. (1997). Results of a 28-month chronic inhalation toxicity study of formaldehyde in male Fisher-344 rats. J. Toxicol. Sci. , 22, 239–254. [DOI] [PubMed] [Google Scholar]
- Keller D. A., Heck H. D., Randall H. W., Morgan K. T. (1990). Histochemical localization of formaldehyde dehydrogenase in the rat. Toxicol. Appl. Pharmacol. , 106, 311–326. [DOI] [PubMed] [Google Scholar]
- Kerns W. D., Pavkov K. L., Donofrio D. J., Gralla E. J., Swenberg J. A. (1983). Carcinogenicity of formaldehyde in rats and mice after long-term inhalation exposure. Cancer Res. , 43, 4382–4392. [PubMed] [Google Scholar]
- Kimbell J. S., Gross E. A., Richardson R. B., Conolly R. B., Morgan K. T. (1997). Correlation of regional formaldehyde flux predictions with the distribution of formaldehyde-induced squamous metaplasia in F344 rat nasal passages. Mutat. Res. , 380, 143–154. [DOI] [PubMed] [Google Scholar]
- Kimbell J. S., Overton J. H., Subramaniam R. P., Schlosser P. M., Morgan K. T., Conolly R. B., Miller F. J. (2001a). Dosimetry modeling of inhaled formaldehyde: binning nasal flux predictions for quantitative risk assessment. Toxicol. Sci. , 64, 111–121. [DOI] [PubMed] [Google Scholar]
- Kimbell J. S., Subramaniam R. P. (2001). Use of computational fluid dynamics models for dosimetry of inhaled gases in the nasal passages. Inhal. Toxicol. , 13, 325–334. [DOI] [PubMed] [Google Scholar]
- Kimbell J. S., Subramaniam R. P., Gross E. A., Schlosser P. M., Morgan K. T. (2001b). Dosimetry modeling of inhaled formaldehyde: comparisons of local flux predictions in the rat, monkey, and human nasal passages. Toxicol. Sci. , 64, 100–110. [DOI] [PubMed] [Google Scholar]
- Kuprat A. P., Kabilan S., Carson J. P., Corley R. A., Einstein D. R. (2013). A bidirectional coupling procedure for multiscale respiratory modeling. J. Comput. Phys , 244, 148–167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lam C. W., Casanova M., Heck H. D. (1985). Depletion of nasal mucosal glutathione by acrolein and enhancement of formaldehyde-induced DNA–protein cross-linking by simultaneous exposure to acrolein. Arch. Toxicol. , 58, 67–71. [DOI] [PubMed] [Google Scholar]
- Lanekoff I., Burnum-Johnson K., Thomas M., Cha J., Dey S. K., Yang P., Prieto Conaway M. C., Laskin J. (2015). Three-dimensional imaging of lipids and metabolites in tissues by nanospray desorption electrospray ionization mass spectrometry. Anal. Bioanal. Chem. , 407, 2063–2071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lanekoff I., Heath B. S., Liyu A., Thomas M., Carson J. P., Laskin J. (2012). Automated platform for high-resolution tissue imaging using nanospray desorption electrospray ionization mass spectrometry. Anal. Chem. , 84, 8351–8356. [DOI] [PubMed] [Google Scholar]
- Lanekoff I., Laskin J. (2015). Imaging of lipids and metabolites using nanospray desorption electrospray ionization mass spectrometry. Methods Mol. Biol. , 1203, 99–106. [DOI] [PubMed] [Google Scholar]
- Lanekoff I., Thomas M., Carson J. P., Smith J. N., Timchalk C., Laskin J. (2013). Imaging nicotine in rat brain tissue by use of nanospray desorption electrospray ionization mass spectrometry. Anal. Chem. , 85, 882–889. [DOI] [PubMed] [Google Scholar]
- Laskin J., Heath B. S., Roach P. J., Cazares L., Semmes O. J. (2012). Tissue imaging using nanospray desorption electrospray ionization mass spectrometry. Anal. Chem. , 84, 141–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leach C. L., Hatoum N. S., Ratajczak H. V., Gerhart J. M. (1987). The pathologic and immunologic effects of inhaled acrolein in rats. Toxicol. Lett. , 39, 189–198. [DOI] [PubMed] [Google Scholar]
- McGrath C., Warren N., Biggs P., Mcaughey J. (2009). Real-time measurement of inhaled and exhaled cigarette smoke: implications for dose. J. Phys.: Conf. Ser . 151, 012018. [Google Scholar]
- Mills C. N., Darquenne C., Prisk G. K. (2002). Mode shift of an inhaled aerosol bolus is correlated with flow sequencing in the human lung. J. Appl. Physiol. , 92, 1232–1238. [DOI] [PubMed] [Google Scholar]
- Minard K. R., Kuprat A. P., Kabilan S., Jacob R. E., Einstein D. R., Carson J. P., Corley R. A. (2012). Phase-contrast MRI and CFD modeling of apparent (3)He gas flow in rat pulmonary airways. J. Magn. Reson. , 221, 129–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monticello T. M., Swenberg J. A., Gross E. A., Leininger J. R., Kimbell J. S., Seilkop S., Starr T. B., Gibson J. E., Morgan K. T. (1996). Correlation of regional and nonlinear formaldehyde-induced nasal cancer with proliferating populations of cells. Cancer Res. , 56, 1012–1022. [PubMed] [Google Scholar]
- Morgan K. T. (1997). A brief review of formaldehyde carcinogenesis in relation to rat nasal pathology and human health risk assessment. Toxicol. Pathol. , 25, 291–307. [DOI] [PubMed] [Google Scholar]
- Morgan K. T., Jiang X. Z., Starr T. B., Kerns W. D. (1986). More precise localization of nasal tumors associated with chronic exposure of F-344 rats to formaldehyde gas. Toxicol. Appl. Pharmacol. , 82, 264–271. [DOI] [PubMed] [Google Scholar]
- Morgan K. T., Monticello T. M. (1990). Airflow, gas deposition, and lesion distribution in the nasal passages. Environ. Health Perspect. , 85, 209–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris J. B. (1996). Uptake of acrolein in the upper respiratory tract of the F344 rat. Inhal. Toxicol. , 8, 387–403. [Google Scholar]
- Morris J. B., Blanchard K. T. (1992). Upper respiratory tract deposition of inspired acetaldehyde. Toxicol. Appl. Pharmacol. , 114, 140–146. [DOI] [PubMed] [Google Scholar]
- National Research Council of The National Academies (NAS) (2011). Review of the environmental protection agency's draft IRIS assessment of formaldehyde. National Academies Press, Washington, DC: ISBN: 978-0-309-21193-2. [Google Scholar]
- Overton J. H., Graham R. C., Miller F. J. (1987). A model of the regional uptake of gaseous pollutants in the lung. II. The sensitivity of ozone uptake in laboratory animal lungs to anatomical and ventilatory parameters. Toxicol. Appl. Pharmacol. , 88, 418–432. [DOI] [PubMed] [Google Scholar]
- Pankow J. F., Watanabe K. H., Toccalino P. L., Luo W., Austin D. F. (2007). Calculated cancer risks for conventional and ‘potentially reduced exposure product' cigarettes. Cancer Epidemiol. Biomarkers Prev. , 16, 584–592. [DOI] [PubMed] [Google Scholar]
- Peterson J. B., Prisk G. K., Darquenne C. (2008). Aerosol deposition in the human lung periphery is increased by reduced-density gas breathing. J. Aerosol. Med. Pulm. Drug Deliv. , 21, 159–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Postlethwait E. M., Joad J. P., Hyde D. M., Schelegle E. S., Bric J. M., Weir A. J., Putney L. F., Wong V. J., Velsor L. W., Plopper C. G. (2000). Three-dimensional mapping of ozone-induced acute cytotoxicity in tracheobronchial airways of isolated perfused rat lung. Am. J. Respir. Cell Mol. Biol. , 22, 191–199. [DOI] [PubMed] [Google Scholar]
- Press W. H., Teukolsky S. A., Vetterling W. T., Flannery B. P. (1992). Numerical Recipes in C (2nd ed.): The Art of Scientific Computing. Cambridge University Press, New York. [Google Scholar]
- Schroeter J. D., Kimbell J. S., Andersen M. E., Dorman D. C. (2006a). Use of a pharmacokinetic-driven computational fluid dynamics model to predict nasal extraction of hydrogen sulfide in rats and humans. Toxicol. Sci. , 94, 359–367. [DOI] [PubMed] [Google Scholar]
- Schroeter J. D., Kimbell J. S., Bonner A. M., Roberts K. C., Andersen M. E., Dorman D. C. (2006b). Incorporation of tissue reaction kinetics in a computational fluid dynamics model for nasal extraction of inhaled hydrogen sulfide in rats. Toxicol. Sci. , 90, 198–207. [DOI] [PubMed] [Google Scholar]
- Schroeter J. D., Kimbell J. S., Gross E. A., Willson G. A., Dorman D. C., Tan Y. M., Clewell H. J., 3rd (2008). Application of physiological computational fluid dynamics models to predict interspecies nasal dosimetry of inhaled acrolein. Inhal. Toxicol. , 20, 227–243. [DOI] [PubMed] [Google Scholar]
- St Charles F. K., Krautter G. R., Mariner D. C. (2009). Post-puff respiration measures on smokers of different tar yield cigarettes. Inhal. Toxicol. , 21, 712–718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanek J., Symanowicz P. T., Olsen J. E., Gianutsos G., Morris J. B. (2001). Sensory-nerve-mediated nasal vasodilatory response to inspired acetaldehyde and acetic acid vapors. Inhal. Toxicol. , 13, 807–822. [DOI] [PubMed] [Google Scholar]
- Struve M. F., Wong V. A., Marshall M. W., Kimbell J. S., Schroeter J. D., Dorman D. C. (2008). Nasal uptake of inhaled acrolein in rats. Inhal. Toxicol. , 20, 217–225. [DOI] [PubMed] [Google Scholar]
- Tawhai M. H., Burrowes K. S. (2003). Developing integrative computational models of pulmonary structure. Anat. Rec. B , 275, 207–218. [DOI] [PubMed] [Google Scholar]
- Teeguarden J. G., Bogdanffy M. S., Covington T. R., Tan C., Jarabek A. M. (2008). A PBPK model for evaluating the impact of aldehyde dehydrogenase polymorphisms on comparative rat and human nasal tissue acetaldehyde dosimetry. Inhal. Toxicol. , 20, 375–390. [DOI] [PubMed] [Google Scholar]
- Tian G., Longest P. W. (2010a). Application of a new dosimetry program TAOCS to assess transient vapour absorption in the upper airways. Inhal. Toxicol. , 22, 1047–1063. [DOI] [PubMed] [Google Scholar]
- Tian G., Longest P. W. (2010b). Development of a CFD boundary condition to model transient vapor absorption in the respiratory airways. J. Biomech. Eng. , 132, 051003. [DOI] [PubMed] [Google Scholar]
- Tian G., Longest P. W. (2010c). Transient absorption of inhaled vapors into a multilayer mucus-tissue-blood system. Ann. Biomed. Eng. , 38, 517–536. [DOI] [PubMed] [Google Scholar]
- US EPA (2010). Draft IRIS Assessment of Formaldehyde . [Google Scholar]
- WHO (2008). The scientific basis of tobacco product regulation: Second report of a World Health Organization (WHO) study group. In (Vol. WHO Technical Report Series No. 951. [PubMed] [Google Scholar]
- WHO (2010). International Programme on Chemical Safety (IPCS) Harmonization Project. Characterization and Application of Physiologically Based Pharmacokinetic Models in Risk Assessment. Final Report. Harmonization Project Document 9. WHO. ISBN 978 92 4 150090 6. [Google Scholar]
- Woutersen R. A., Appelman L. M., Feron V. J., Van der Heijden C. A. (1984). Inhalation toxicity of acetaldehyde in rats. II. Carcinogenicity study: interim results after 15 months. Toxicology , 31, 123–133. [DOI] [PubMed] [Google Scholar]
- Woutersen R. A., Appelman L. M., Van Garderen-Hoetmer A., Feron V. J. (1986). Inhalation toxicity of acetaldehyde in rats. III. Carcinogenicity study. Toxicology , 41, 213–231. [DOI] [PubMed] [Google Scholar]
- Woutersen R. A., Feron V. J. (1987). Inhalation toxicity of acetaldehyde in rats. IV. Progression and regression of nasal lesions after discontinuation of exposure. Toxicology , 47, 295–305. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.