Patient-specific finite element modeling for femoral bone augmentation

Abstract

The aim of this study was to provide a fast and accurate finite element (FE) modeling scheme for predicting bone stiffness and strength suitable for use within the framework of a computer-assisted osteoporotic femoral bone augmentation surgery system. The key parts of the system, i.e. preoperative planning and intraoperative assessment of the augmentation, demand the finite element model to be solved and analyzed rapidly. Available CT scans and mechanical testing results from nine pairs of osteoporotic femur bones, with one specimen from each pair augmented by polymethylmethacrylate (PMMA) bone cement, were used to create FE models and compare the results with experiments. Correlation values of R² = 0.72–0.95 were observed between the experiments and FEA results which, combined with the fast model convergence (~3 min for ~250,000 degrees of freedom), makes the presented modeling approach a promising candidate for the intended application of preoperative planning and intraoperative assessment of bone augmentation surgery.

1. Introduction

The rate of mortality one year after hip fracture in elderly patients with osteoporosis is catastrophic and is reported to be as high as 23%; it accounts for $10–15 billion of annual treatment costs in the United States [1,2]. Current approaches for fracture prevention include muscle strengthening, use of hip protectors and a variety of drugs for bone loss reduction [3], most of which have a limited impact due to high costs and/or lengthy treatment requirements associated with their effectiveness.

Bone augmentation using polymethylmethacrylate (PMMA) bone cement is proposed as an alternative near-term solution, especially for patients at high risk of fracture [2–4]; however, this is not currently part of clinical practice, and improper introduction of augmentation material can produce unfavorable results. Specifically, poor cement placement or excessive injection volumes can reduce or eliminate blood supply to healthy bone tissue potentially resulting in osteonecrosis [3,5]. Although there is a wealth of research on the effects of augmentation on the vertebral bodies, namely vertebroplasty, there is very limited literature regarding optimal femoral augmentation. In the study of Sutter et al. [2], some subtrochanteric fractures were observed in augmented femora as a result of load shift from the neck of the femur to the distal parts. In another study [6] they concluded that 15 ml volume of cement does not provide enough mechanical augmentation. In contrast, Beckmann et al. [5] achieved significant increase in fracture load and energy using only 12 ml of cement on average, except in the case of double drilling augmentation where fracture load was decreased which, presumably, was due to the additional cortical weakening of the augmentation technique.

Because of the possible complications associated with the surgery, we propose a precise planning and execution routine which is still in pre-clinical stages. We are developing a system for patient-specific planning, optimization and execution of the bone augmentation surgery. Modeling of the mechanical behavior of the femur bone under various loading conditions and different augmentation scenarios is of crucial importance to the success of this procedure. Initially, the model will be used for preoperative optimization of the bone cement injection specifically aimed at minimizing the required injection volume while reducing or eliminating the likelihood of fracture under standard loading conditions. The optimization requires several iterations of the Finite Element Analysis (FEA), often within a loop, in order to achieve the optimum plan. During the procedure, it is also desirable that the model be used for intraoperative assessment and to update the augmentation plan. For this to be viable, the finite element model must be solved and analyzed in relatively short amounts of time.

The objective of our study was to describe a process for developing patient-specific finite element models of the proximal femur, investigate the sensitivity of the model to mesh resolution, and to validate its capability of predicting stiffness and yield load using results of previously performed mechanical tests on human cadaveric femora.

2. Methods

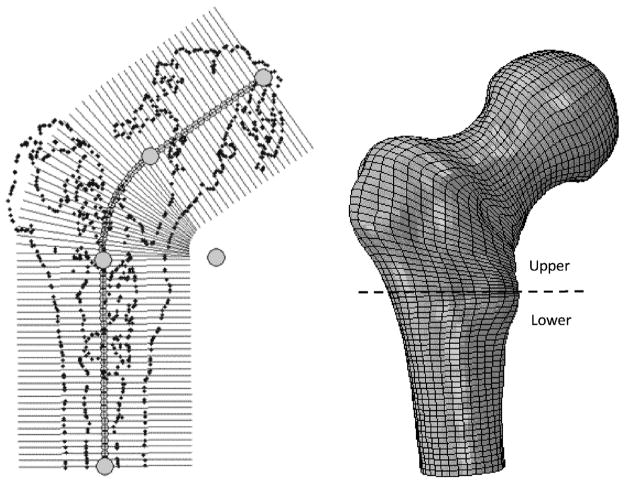
A customized user interface allowed the user to manipulate the CT scan data of the study of Sutter et al. [6], obtained from nine pairs of osteoporotic femurs prior to mechanical fracture tests, before and after one femur of each pair was augmented by PMMA bone cement, and to perform pre-processing steps for the finite element solver. These steps included creating a patient-specific finite element mesh, assigning material properties and defining loading and boundary conditions. First, the isosurface of the image volume was used to estimate (with manual refinement) the main geometrical features of the bone including the long bone axis and head center to establish a local coordinate frame. Using the graphical interface, slices of the 3D model were created orthogonal to the defined path along the femoral long axis and up through the head of the femur as shown in Fig. 1. An arc was used to smoothly connect the femoral long axis with the axis traveling through the neck and head of the femur. The user was free to change the control points to refine slicing including the diameter of the connecting arc and/or the number/spacing of slices along the path to ensure that critical features of the femur are captured. For each slice, an estimated section of the femur was created from the CT by interpolating intersecting voxel data. This interpolated section was then automatically processed using intensity based segmentation, followed by manual refinement, to estimate the outer geometry of the bone. A radial grid was then defined about the center axis of the path orthogonal to the slice, with concentric grid lines laid out to increase mesh density in the cortical bone. The number of discrete circumferential points aligned in each section was constant, therefore the grids could be easily combined to form a finite element mesh of quadratic 15-node wedge and 20-node brick elements [7]. Smoothing splines were finally applied to the resulting model to create a smooth outer surface.

Fig. 1.

Oblique user-defined slices (left) and the corresponding finite element mesh (right). The gray circles represent the control points that determine the properties of the curve of the slices.

In order to estimate the structural response of the osteoporotic femurs, inhomogeneous material properties were assigned to each element based on the bone density observed from CT scan performed with a density phantom. First, we calculated the average radiodensity in Hounsfield Unit (HU) intensity values for each element. This was done using 3 sampling points along each of the edges of the element, which resulted in 21 and 27 points for the wedge and brick elements, respectively. The HU value was sampled at these points and, to only take into account the bone tissue, the average of the non-negative values was considered as the element intensity number. The next step involved converting the intensity values to elastic modulus constants. For this purpose, we divided the bone into two main regions (Fig. 1): the 90 mm upper part of the proximal femur (the “upper” region) and the rest of the bone (the “lower” region). We considered the upper region as mostly trabecular bone and the lower region to be mostly cortical bone. To account for the bone marrow, elements of HU_mean < 100 were added to the marrow material group. Individual HU_mean values of bone elements were converted to ash densities using linear interpolation of the known data for plastic phantoms. The ash densities were finally converted to apparent densities using Eq. (1) [8]:

$${\rho }_{\text{app}}=1.79{\rho }_{\text{ash}}+0.0119$$ (1)

where ρ_app and ρ_ash denote the apparent and ash densities in gr/cm³, respectively. The last step was to convert the density values to isotropic elastic modulus. Eq. (2) was used for this purpose [9,10]:

$$\begin{array}{l}E=10500{\rho }_{\text{ash}}^{2.29}\text{Cortical}\text{Bone}\\ E=6850{\rho }_{\text{app}}^{1.49}\text{Trabecualr}\text{Bone}\end{array}$$ (2)

where E is the elastic modulus in MPa and a Poisson’s ratio of 0.4 was assumed for the bone elements [11,12]. Bone elements elastic moduli ranged from 187 MPa to 28.4 GPa. For bone marrow elements, the elastic modulus was set to 20 MPa with a Poisson’s ratio of 0.499 [13]. To account for the high radiodensity of bone cement injected in the femoral neck and prevent an artificial increase in the intensities of the bone tissues surrounding the cement, we co-registered and re-sampled the augmented femurs before and after injection of cement. The co-registration was performed using an affine transformation based on mutual image intensity information (Analyze, Mayo Clinic, Rochester, MN). We then calculated the mean HU intensity for each element based on both image volumes, namely HU_nonaug, HU_aug and if the difference was larger than a threshold for any of the elements, we added the element to the bone cement material group. We then assigned to this material group an isotropic elastic modulus of 1.2 GPa [14] and a Poisson’s ratio of 0.4.

Boundary conditions replicating the mechanical tests were applied to the finite element models. The bone model was first reoriented according to the rotations applied for the mechanical test [6]. The distal vertices were then fixed in all three directions and the surface vertices on the 10 mm left most side of the greater trochanter were restricted to move only in the y-z plane (perpendicular to the plane of Fig. 1). Finally, load was applied on the surface vertices of the femoral head to the right side of the head center (Fig. 1). Loaded vertices were allowed to move in all three directions. Load magnitude was set to an arbitrary value of 500 N and it was evenly distributed among the loaded nodes.

A static FE analysis was performed on the model using ABAQUS (ABAQUS/Standard V6.8, SIMULIA, Providence, RI). Output parameters from the FE solver included the displacement component of the loaded nodes in the direction of the load and maximum and minimum principal strain values, reported at the centroid of each element. Bone stiffness was calculated as the ratio of the load to the average displacement of the loaded nodes in the direction of loading. Maximum (ε_max) and minimum (ε_min) principal strain values of the elements were used to determine element yield. Using the FEA results at the load of 500 N and assuming linearity, ε_max and ε_min could be scaled for any desired load. For each element the greater value of |ε_max| and |ε_min| was chosen as the element strain and it was compared with the appropriate (compressive ε_yC or tensile ε_yT = 0.7ε_yC [15]) yield strain. If the element strain exceeded its yield value, its volume was added to the volume of the failed elements. We increased the load until the total volume of the failed elements reached 1% of the total volume of the specimen [16]. The load at that point was the assumed yield load of the femur. We varied the yield strains, using the data and models for the two pairs of specimens with the lowest and highest yield loads (the “training” set), to determine the values of ε_yC and ε_yT that resulted in the best agreement between the FEA and experimental yield loads. For the rest of the models, we used those values for estimation of the yield load. For PMMA cement elements, yield strain was set to a symmetric value of 2% [17]. We performed correlation and error analyses on the experimental and FE simulation results for stiffness and yield load. We also performed paired sample t-tests on stiffness and yield load values obtained from non-augmented and augmented specimens, both for experiments and FE simulation results.

To verify model convergence, we varied the mesh element density for one randomly chosen femur bone and applied the same boundary conditions on them as mentioned before. The FE results were then recorded for the models, with one additional output of the sum of the stored strain energy values in all the elements. Assuming the densest model as the reference, the model with minimum number of elements and stiffness and energy within less than 2% of the reference values was considered the optimum model. We then created the rest of the models with the same number of elements found for the optimum model. This was done to avoid unnecessary calculation overhead resulting from overly fine meshes. Simulations were performed on a machine with 3.2 GHz Core2^™ Duo processor and 8GB of physical memory under 64-bit Windows^™ 7 operating system.

3. Results

Results of the sensitivity of the finite element analysis to the density of the mesh are depicted in Fig. 2. Each of the two plots shows a plateau when the number of degrees of freedom (DOF) in the model increases beyond ~250,000 and the last three dense models produce closely similar results. Assuming that the densest model analyzed (with 528,081 DOFs) has the most accurate results, we see that the model with 244,671 DOFs produces a stiffness and absorbed energy within 1.23% and 1.15% of the dense model, respectively. The time associated with solving these models was 950 s for the dense and only 180 s for the less dense model. Based on the nominal anticipated increase in accuracy associated with increasing the DOFs beyond 250,000 and because of the excessive increase in computation time, we selected 250,000 (20,000 elements) as the target DOF for creating the models. Similar convergence trends can be found in the literature [18].

Fig. 2.

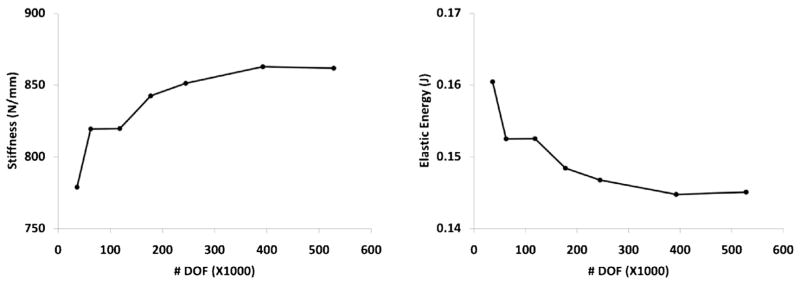
Stiffness (left) and absorbed energy (right) as a function of mesh density.

The value of ε_yC that produced the closest agreement between the FEA and experimental data of the yield loads for the “training” specimens was found to be 0.0427 (with the corresponding value of ε_yT of 0.0299). Fig. 3 compares the results of FE simulations with the data gathered from the experiments. Table 1 also shows a comparison between the experimental and simulation results. The average errors in predicting the stiffness were 17.2% and 17.7% for control and augmented specimens, respectively. The corresponding errors for yield load were 9.8% and 15.6%. For seven out of the nine pair comparisons, FEA predicted correctly, according to the experimental data, whether the augmentation increased or decreased the yield load.

Fig. 3.

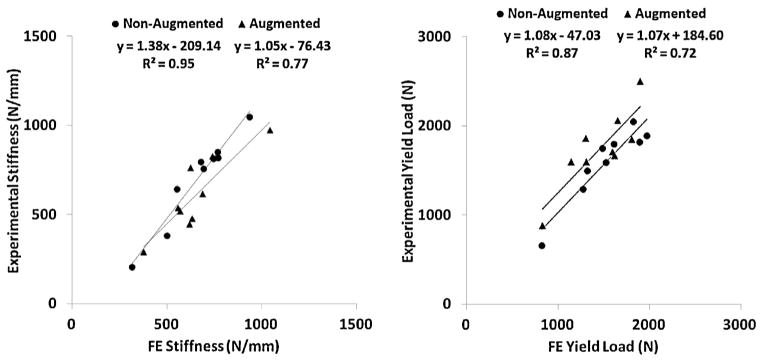
Comparison of stiffness (left) and yield load (right) values between experiments and FEA analyses.

Table 1.

Summary of experimental and FEA results.

Specimen	Stiffness (N/mm)				Yield load (N)
	Measured control	Predicted control	Measured augmented	Predicted augmented	Measured control	Predicted control	Measured augmented	Predicted augmented
1	851	767	616	688	1820	1890	1600	1305
2	815	746	446	618	1800	1610	1710	1590
3	797	678	828	740	1750	1480	1860	1300
4	206	314	290	377	660	820	880	825
5	644	551	539	557	1500	1315	1600	1140
6	818	770	480	633	2050	1820	2500	1895
7	1047	936	763	625	1890	1970	1670	1615
8	756	693	520	568	1590	1520	1850	1805
9	383	500	976	1042	1290	1270	2060	1650
Mean (±SD)	702 (±257)	662 (±182)	607 (±213)	650 (±179)	1594 (±416)	1522 (±359)	1748 (±432)	1458 (±343)

Similar to the experiments [6], FEA showed no significant difference (P > 0.05) in stiffness or yield load between augmented and control specimens. An evaluation of the distribution of the failed elements before and at the onset of yielding showed that, for all the non-augmented specimens, FEA predicts the yielding to start at the superior aspect of the femoral neck. For the augmented specimens, the yielding region was slightly shifted, either toward the proximal part of the neck or the trochanteric area, and there was always a region of concentrated failed elements at the cement-bone boundary. None of the augmented models had yielded cement elements up to the onset of predicted yielding.

4. Discussion

Results of our study support the original hypothesis that patient-specific FEA can accurately predict femoral stiffness and yield load for both augmented and non-augmented specimens. The models showed slightly lower accuracy in predicting the properties of augmented specimens compared to the intact bone models. This could be due to the added assumptions regarding the mechanical behavior of the bone cement, including its stiffness and its bond with the bone tissue, which was assumed perfectly rigid in the current study. Also the neglected effects of volume fraction information obtained from CT data could have affected the element properties at the boundary between the bone and the cement.

In order for the model to predict the yield loads accurately, tuning of the failure strain of the elements was inevitable. There is a wide range of reported values for experimental yield and ultimate compressive and tensile strains for human cancellous bone, e.g. 0.003–0.03 [19], with some studies reporting values as large as 11.6% [20]. Furthermore, individual elements of the model generally contain several trabeculae as well as soft tissue and marrow, and we hypothesize that the combination of the yielding of those will result in the total element failure. Therefore total element failure is likely to happen at a larger apparent strain [18,21]. In addition, it is likely that the trabecular structure acts differently within the bone structure compared to when tested as excised specimens in mechanical tests. It is also well documented that bone fails at lower strains in tension than in compression [15], hence our assumption of ε_yT = 0.7ε_yC.

The simulated load was increased until only 1% of the volume of the elements within the model failed. This value is grounded in experimental testing of distal radius failure [16]. Due to the substantial structural and geometrical differences in the femur and the radius bone, the 1% failure criteria may not be most suitable for the femur. It is not precisely known what percentage of the elements fail at the onset of yielding and the 1% yield criterion is somewhat arbitrary [16]. However, with 1% criterion, failed elements populated a relatively small area inside the bone which helped identify the region of initial failure. Because of our strain-based yield criteria, errors can also propagate when converting loads to stress and subsequently to strain values.

For two pairs of specimens (#3 and #5), FEA predicted a decrease (−12% and −13%) in the yield load of augmented vs. control specimen, while in practice an increase (+6% and +7%) was measured. The measured changes were within error margins of the simulation which could partially explain the deviation of FEA from experiment. On average, as shown in both experiments and simulations, augmentation did not improve the mechanical properties of the femurs. This was mainly due to the relatively small injection volume of cement (15 ml) as opposed to the conventional gross filling patterns [2–4]. The injection volume was kept small to reduce thermal damage to the bone tissue. However, for most of the specimens, a major portion of the cement volume was populated in the trochanteric area, while the target augmentation region was the femoral neck. Therefore femoral neck, and especially the superior aspect of the neck where there is a stress concentration, was not properly supported by the cement. We are planning to use the proposed modeling scheme, potentially combined with heat generation and transfer models, to optimize the injection so that small amounts of bone cement result in successful augmentations.

The time to solve the static finite element model and estimate the stiffness and yield load was about 3 min total. This is orders of magnitude less than the times reported in similar studies, especially ones for which dynamic or quasi-dynamic analyses are employed [16,21,22], due to the quasi-static nature of our FEA and use of limited number of necessary elements. For our application, as also noted by Yosibash et al. [15], static yield prediction is sufficient to predict the onset of bone tissue failure in a near-real time environment. Therefore more time-consuming dynamic FEA are prohibitive and seem to be unnecessary for this effort. The proposed model can be conveniently incorporated in an optimization framework for finding optimum cement placement with the best outcome.

Since the original experiments did not include high speed video data, in this study we were not able to directly compare the simulations and experiments for the location of first yielding. Similar experimental studies by Dragomir-Daescu et al. [21] and de Bakker et al. [23] have shown that, under similar loading conditions, there is often a local compressive yielding at the superior aspect of the femoral neck prior to final fracture. This is the same pattern that was observed in the current study for non-augmented models. During a fall to the side, compressive stress acts on the superior neck, while tensile stress is applied on the inferior side [23]. Although bone is stronger in compression than in tension, it is suggested that the reduced thickness of the cortical bone in the superior aspect compared to the inferior aspect is responsible for this yielding [23].

5. Conclusions

The current study assesses the feasibility of creating a patient-specific finite element model of the proximal femur for predicting the onset of bone failure and assessing the effect of mitigating interventions (bone augmentation with bone cement). This analysis approach has the potential to be used in a system for pre-operative planning and intra-operative assessment of bone augmentation surgery. A crucial step in the planning process is to determine the optimum volume and filling pattern of the cement so that the best outcome is achieved. For this purpose, numerous augmentation scenarios and cement placements, within an optimization loop, must be simulated, and this can only be practical if the finite element analysis can be performed in a relatively short amount of time. In this paper, we presented a framework for patient-specific femur finite element model generation and analysis. Our FE simulations showed acceptable errors and correlated well with the experimental data of previously tested femurs, while being solved in relatively short times. Work is underway to employ structural optimization techniques in combination with the proposed finite element modeling framework to optimize the augmentation procedure so that a minimal amount of cement injection results in the best augmentation outcome.