Monte Carlo simulation of inverse geometry x-ray fluoroscopy using a modified MC-GPU framework

Abstract

Scanning-Beam Digital X-ray (SBDX) is a technology for low-dose fluoroscopy that employs inverse geometry x-ray beam scanning. To assist with rapid modeling of inverse geometry x-ray systems, we have developed a Monte Carlo (MC) simulation tool based on the MC-GPU framework. MC-GPU version 1.3 was modified to implement a 2D array of focal spot positions on a plane, with individually adjustable x-ray outputs, each producing a narrow x-ray beam directed toward a stationary photon-counting detector array. Geometric accuracy and blurring behavior in tomosynthesis reconstructions were evaluated from simulated images of a 3D arrangement of spheres. The artifact spread function from simulation agreed with experiment to within 1.6% (rRMSD). Detected x-ray scatter fraction was simulated for two SBDX detector geometries and compared to experiments. For the current SBDX prototype (10.6 cm wide by 5.3 cm tall detector), x-ray scatter fraction measured 2.8–6.4% (18.6–31.5 cm acrylic, 100 kV), versus 2.1–4.5% in MC simulation. Experimental trends in scatter versus detector size and phantom thickness were observed in simulation. For dose evaluation, an anthropomorphic phantom was imaged using regular and regional adaptive exposure (RAE) scanning. The reduction in kerma-area-product resulting from RAE scanning was 45% in radiochromic film measurements, versus 46% in simulation. The integral kerma calculated from TLD measurement points within the phantom was 57% lower when using RAE, versus 61% lower in simulation. This MC tool may be used to estimate tomographic blur, detected scatter, and dose distributions when developing inverse geometry x-ray systems.

1. INTRODUCTION

Scanning-Beam Digital X-ray (SBDX) is an inverse geometry x-ray fluoroscopy technology for cardiac procedures that uses a unique narrow-beam scanning technique (Fig. 1) to minimize detected scatter, reduce skin dose, and perform real-time tomosynthesis.¹ Although efforts are underway to optimize SBDX for various applications,² convenient Monte Carlo (MC) tools for simulating scatter and dose properties in this unique geometry are not widely available. Recently, the MC-GPU Monte Carlo code package was developed for CT and radiographic simulations on GPU-accelerated platforms.³ The purpose of this study was to develop a flexible MC tool based on a modified MC-GPU framework which would allow for rapid investigation of x-ray fluence distribution, detected scatter, and imaging properties, and aid the development of inverse geometry x-ray systems. Details of the modified code are presented, and predictions from the MC code are compared to experimental measurements made on two SBDX prototypes.

Figure 1.

Inverse geometry x-ray system. An electron beam is raster scanned over a large area target, dwelling at fixed positions behind a multi-hole collimator. The collimator defines a sequence of narrow overlapping x-ray beams (A) directed at a small photon-counting detector. Tomosynthesis images are reconstructed at multiple planes (B) for each scan frame. Part (C) shows the geometry and input variables used in the modified MC-GPU code.

1.1 Scanning Beam Digital X-ray (SBDX)

The inverse scanning geometry of SBDX is shown schematically in Figure 1A. The x-ray tube contains an electron beam that is raster scanned over a large-area transmission target. A multi-hole collimator between the target and patient defines a series of narrow overlapping x-ray beams, each of which is directed at a distant, small area detector array. As the electron beam is electromagnetically deflected from one collimator hole to the next, the narrow x-ray beam sweeps over the patient volume. Simultaneously captured detector images are reconstructed into full field-of-view images in real time using digital tomosynthesis.

Details of a recently constructed SBDX prototype are reported in Ref 4. This system has 100 × 100 focal spots on a 0.23 cm pitch, a 150 cm target plane-to-detector distance, and a 10.6 cm wide by 5.3 cm photon-counting detector array. The x-ray source is typically operated in a mode that scans 71 × 71 focal spot positions at a rate of 15 scan frames per second. In this configuration, each focal spot position is illuminated 8 times per 1/15 s frame. A detector image is captured every 1.28 μsec using a 2-mm thick CdTe detector array. The native array is 320 × 160, with 0.33 wide elements. At the front end of the image reconstructor, 2×2 binning is applied to produce a 160 × 80 array with 0.66 mm effective element size. Shift-and-add tomosynthesis is performed in real time to produce a stack of 32 planes (Figure 1B) with 0.5 cm plane-to-plane spacing. In these reconstructed images, in-plane objects appear in focus and out of plane objects are increasingly blurred as their distance from the plane of reconstruction increases. For live 2D display, a composite image is formed.¹

Narrow-beam scanning in an inverse geometry system enables dose reduction through several mechanisms.⁵ Narrow beam scanning with a large air gap results in a low detected scatter fraction (~5–10%), which in turn allows a given signal-to-noise ratio to be achieved with fewer primary x-rays. The inverse geometry distributes primary x-rays over a larger area at the patient entrance compared to a conventional cone beam geometry, reducing dose to points on the skin. Dose may be further reduced in high-transmission regions of the patient (e.g. lungs) using a technique termed “regional adaptive exposure” (RAE).⁶ In RAE, the accumulated detector counts are monitored for each collimator hole position as the electron beam makes multiple passes over the holes (8 passes per hole per scan frame). The x-ray beam is turned off for a given collimator hole position when a defined threshold is exceeded. Figures 2A and 2B demonstrate the number of illuminations per hole for regular versus RAE scanning of an anthropomorphic chest phantom. In the adaptive mode the number of illuminations varies from 8 in the central spine region down to 1 in the lateral lung regions. A tomosynthesis image reconstructed from an RAE scan is shown in Figure 2C.

Figure 2.

Scan maps for regular and regional-adaptive-exposure (RAE) scanning (A and B), and an example tomosynthesis reconstruction from an RAE scan (C). Each pixel in a scan map represents the relative output from a collimator hole in a 71 × 71 scan. The scale ranges from 0 to 8 to indicate the number of hole illuminations per scan frame. In MC-GPU simulation, relative x-ray outputs are specified in the range [0 1]. An RAE scan reduces the number of illuminations in higher transmission regions, e.g. the lung fields lateral to the spine in (C).

1.2 MC-GPU

This work was based on MC-GPU v1.3 (Badal et al.³), a public domain GPU-accelerated Monte Carlo x-ray transport package for simulating projection radiographs and CT scans. MC-GPU uses the PENELOPE 2006 subroutine package for material cross sections and modeling photon interactions and transport.⁷ Simulation acceleration is achieved through GPU computing and implementation of the Woodcock tracking algorithm.³ CT simulation setup consists of a user-defined x-ray energy spectrum, voxelized phantom definition and material files, parameters defining a circular x-ray source trajectory with co-rotating flat detector, detector size, and number of detector elements.⁸ Outputs consist of a voxelized kerma distribution and simulated detector images which tally the accumulated energy of photons passing through the defined detector elements. Five separate images are available for each view angle, corresponding to primary (noninteracting) x-rays, single Compton scatter, single Rayleigh scatter, multi-scatter, and all x-rays striking the detector elements. Radiographic simulations are similar to CT simulations, except that only one source point is defined.

2. METHODS

The MC-GPU code was modified to simulate any arbitrary inverse geometry x-ray fluoroscopic system. After the code was adapted, simulations were compared to experimental measurements for two SBDX imaging geometries. These experiments involved quantification of tomographic blur, measurements of x-ray scatter fraction (SF), and evaluation of dose distribution for both regular and RAE scanning.

2.1 Adaptation of MC-GPU code for inverse geometry

The MC-GPU code base is well-suited to adaptation for inverse geometry due to the similarities between CT scanning with a flat detector and an inverse geometry system. Both systems incorporate multiple source spots with x-ray beams collimated to a flat detector array. The following modifications were made to MC-GPU v1.3 to achieve inverse geometry simulation:

1. X-ray source: Code which defines source points on a circle for the purpose of CT simulation was replaced with code that defines a 2D array of source points on a plane (set_CT_trajectory replaced with set_SBDX_trajectory in ‘MC-GPU_v1.3.cu’). For each source point, direction cosines are automatically calculated so that the x-ray beam is always directed at the center of the detector. Polar and azimuthal angles define the angular extent of each beam.

2. Detector: The rotating detector motion used in CT simulations was replaced with a stationary detector parallel to the source plane (read_input in ‘MC-GPU_v1.3.cu’). The detector position and orientation are fixed throughout the simulation.

3. Tallies: To simulate the photon-counting detector of SBDX, the detector image tallies were modified to record the number of photons passing through each detector element, rather than the integrated energy. This change was implemented in the tally_image function within the kernel code ‘GPU_kernel_v1.3.cu’.

4. Geometry specification: The input file format allows user specification of the source array size, source pitches, detector width and height, detector element pitch, the first projection to be simulated, and the number of following projections to be simulated. The 3D centers of the source array and detector array are independently specified. The source-detector distance is calculated from the Y-distance between the two centers. Optionally, a flag may be set to simulate regional adaptive exposure (RAE) scanning. If the flag is set, the name of an external text file with relative x-ray outputs is specified. The read_input function was modified to accept the modified input file format.

5. X-ray output modulation: The ability to independently modulate x-ray output from each source point was added for RAE simulations (set_relative_output). The relative output is defined in an external file which contains a value between 0 and 1 for each source point. These values are used as a multiplier to scale the number of histories to be simulated for each focal spot.

For ease of implementation, we retained the 3D coordinate system used for MC-GPU radiographic simulations. As shown in Figure 1C, the source plane and detector reside in Y-planes. The ‘row’ direction of the source (or detector) corresponds to +Z, and the ‘column’ direction corresponds to +X. The origin of the 3D coordinate system is defined by a corner of the voxelized world geometry. Note that under this convention, the user must shift the (X, Y, Z)-centers of the source and detector to ensure that the voxel geometry is properly centered.

The source array is defined in terms of the array size (Nsx by Nsz) and the pitches (Lx, Lz). A 3D coordinate (Xs, Ys, Zs) is used to specify the position of the central source point in the source array. For odd-sized array dimensions, the sources are symmetrically distributed about the center point. For even-sized arrays, the ‘extra’ source appears on the negative side. Sources are indexed starting from 1, and the code works through source points in row-major order. That is, for a 71 by 71 scan size, the first row will be indexed 1 to 71, the next row will be 72 to 142, etc. The detector center is defined by the 3D coordinate (Xd, Yd, Zd) and the detector area (Dx by Dz) is centered on this point.

2.2 Simulated geometry

Two different SBDX systems were simulated (Table 1). These geometries are modeled after the current system⁴ and a previously reported prototype.¹ The key difference is that the current system has a wider (10.6 cm) rectangular detector, which results in higher image fluence for a given x-ray technique and a wider tomographic angle. For the current SBDX system, 2×2 detector binning was simulated (160 × 80 array). For both setups, ideal beam collimation to the detector was simulated.

Table 1.

SBDX geometries simulated.

Geometry	Current Prototype	Previous Prototype
Source-detector-distance [cm]	150	150
Source array pitch [cm]	0.23×0.23	0.23×0.23
Scan size [# focal spot positions]	71×71	71×71
Detector array width by height [cm]	10.6×5.3	5.5×5.5
Number of detector elements [width by height]	320×160 (160×80 binned)	48×48
Source - isocenter distance [cm]	45	45

A 3D arrangement of spherical objects was defined to test the accuracy of the simulated imaging geometry. The sphere phantom contained 2.5-mm diameter titanium spheres, arranged in a 4 × 7 pattern in the field-of-view. Sphere position along the source-detector axis ranged from 380 mm to 520 mm from the source plane, in 5 mm increments. A 100 kV x-ray energy spectrum previously calculated using EGSnrcMP was used to define the source x-ray energies.⁹ The density of the titanium spheres was adjusted to achieve the same areal density as steel spheres at the mean energy of the spectrum. Shift-and-add tomosynthesis reconstruction was applied to the MC-simulated detector images, using a Matlab-based implementation of the SBDX reconstruction algorithm. The image planes were reconstructed at distances 325 mm to 574 mm in 1 mm increments. Following reconstruction, the sphere positions were determined using a 3D localization method for SBDX tomosynthesis.¹⁰ Simulations used the source output map shown in Figure 2A, where output is constant across focal spot position except in the corners.

For experimental validation, tomographic blurring vs out-of-plane distance was quantified from the simulations and compared to measurements made with the current SBDX prototype. For the experiment, 2.38 mm diameter steel ball bearings were placed in an 18 cm thick stack of acrylic and imaged at 100 kV. Simulations recreated the experimental setup using 0.15625 mm voxels. Images were reconstructed with 1 mm plane-to-plane spacing. The artifact spread function (ASF) for a small, high contrast object¹¹ was then measured from the images to characterize the reduction in contrast caused by out-of-plane blurring. First a profile was generated for each image plane by integrating along the vertical direction in the image. Next the background value was subtracted from each profile, and the maximum signal difference in the resulting profile was located. This value was normalized by the maximum signal difference measured at the plane of the object.

2.3 Kerma distribution

Entrance and integral kerma distributions were evaluated for an anthropomorphic adult chest phantom (CIRS Adult Male Atom Dosimetry Verification Phantom model 701, CIRS Inc., Norfolk, VA, USA). The phantom was positioned supine with the heart plane placed at system isocenter and the C-arm in the anterior-posterior direction such that the beam entered from the phantom posterior. Two types of scanning were performed experimentally with the current SBDX geometry and then reproduced in simulation: 1) a scan with all focal spots at equal intensity, and 2) an RAE scan, as described in Ref. 6, in which the total beam-on time at each focal spot position is modulated downward in 8 increments (1x, 7/8x,…,1/8x, 0) to reduce dose in high transmission regions and equalize the number of x-rays detected from each focal spot.

The kerma distribution at the phantom entrance was experimentally measured using Gafchromic XR-RV3 film (ISP Corp., Wayne, NJ, USA). The film was positioned at the phantom entrance and separate film measurements were made for regular and RAE scanning techniques. The film was calibrated and scanned using previously described methods.¹² Dose to points inside the phantom was measured using thermoluminescent dosimeters (TLDs). The phantom used was designed to allow for the placement of TLDs at predetermined internal locations for dosimetric purposes. For TLD measurements, an exposure was performed with an air kerma level of 200 cGy at the phantom entrance which generated a minimum signal-to-noise ratio of 50 for the TLDs experiencing the lowest exposure.¹³

For simulations, a voxelized virtual phantom was created by segmenting a CT scan of the chest phantom into its three component materials: lung, bone, and soft tissue. This virtual phantom was positioned to mimic the experimental positioning. For the RAE simulation, the experimental x-ray source fluence map was re-used. Kerma was extracted from points inside the voxelized phantom at the positions corresponding to the TLDs. The simulated kerma distribution at the phantom entrance was calculated by extracting kerma from a plane just posterior to the phantom entrance. The relative reduction in entrance kerma-area-product (KAP) and integral kerma from regular versus RAE scans was evaluated in both simulation and experiment.

2.4 Detected scatter

Scatter fraction (SF) is defined as the ratio of detected scattered photons relative to all detected photons. The scatter prediction of the MC code was compared to experiment by two methods. In the first method, SF was evaluated for isocentered acrylic phantoms of a varying thickness. The second method utilized a single thickness acrylic phantom with varied position to give SF measurements at multiple air gaps. Thicknesses of isocentered acrylic ranged from 18.6 cm to 31.5 cm along the source-detector direction. The lateral dimensions of the phantom were 20.3 cm by 20.3 cm. For the varying air gap method, 23.3 cm of acrylic was placed such that the air gap from the phantom exit to the detector surface ranged from 14.5 cm to 88.4 cm.

SF was measured experimentally using a standard beam stop method.^14,15 The measurement was performed using an array of uniformly spaced 2.2 mm diameter, 3 mm thick lead beam stops on a 1 cm pitch.⁵ The array was placed on the entrance side of the acrylic phantom. Images were acquired with and without the beam stop array. Images were then reconstructed at the plane of the beam stops. A ratio image was formed from the images acquired with and without beam stops, and SF was then calculated as the ratio of the signal in the umbra of the beam stop divided by the signal in an annular region just around the beam stop. Note that in a real inverse geometry system, the signal behind the beam stop may also be due to deterministic offsets in the detector, or off-focus primary radiation arising from collimator holes lateral to the active hole. Since these effects are not present in the Monte Carlo simulations, the SF values were corrected.⁵ Detector dark signal was evaluated from images acquired with the x-rays turned off. Off-focus radiation fraction was determined using a low-scatter copper phantom positioned at the source. The corrected experimental SF value is referred to as the “x-ray SF”.

In MC simulations, the SF was computed as the ratio of the integrated scatter value from detector images, for all types of scatter, divided by the integrated photon counts for both primary and scatter. Detector images from a central 11 × 11 patch of source points were used in the integrations. The detected scatter was further analyzed by separating the scatter into single Compton, single Rayleigh, and multi-scattered events. For a comparison, a conventional cone beam system was simulated with 100 cm source-to-detector distance, 5 cm air gap, and an x-ray beam collimated to a 13.7 cm by 13.7 cm detector (no anti-scatter grid).

2.5 Computational setup

Simulations were carried out on a desktop workstation with an Intel Xeon X5690 12-core, 3.47GHz CPU and Ubuntu 12.04 operating system. The workstation was equipped with an Nvidia Tesla K20 GPU (2496 cores, 5 GB memory, compute capability 3.5). The MC-GPU code was compiled with CUDA version 5.0. Simulations not involving RAE scanning used 10⁷ photons per active focal spot position, as defined by the map in Fig 2A. There were 4473 active positions in this map, giving 4.473 × 10¹⁰ total histories per simulation. In an RAE simulation the number of histories was reduced at certain positions according to the map shown in Figure 2B (2.425 × 10¹⁰ total histories). All simulations were executed sequentially. Recorded execution time includes the time to initialize the simulation.

3. RESULTS

3.1 System geometry

Figure 3 shows isocenter-plane tomosynthesis reconstructions. Figure 3A was generated experimentally with the current SBDX geometry, and Figures 3B and 3C were reconstructed from MC-simulated detector images for the current and previous SBDX geometries, respectively. The sphere in the plane of reconstruction is indicated with a box. In the experimental image, the central sphere resides in the plane of reconstruction, and sphere position along the source-detector axis increases in 27 mm increments as sphere position changes along the diagonal, from top left to bottom right. In MC-simulated images, the sphere position increases in increments of 5 mm, in row-major order, from top left to bottom right. The images demonstrated the expected blurring behavior for SBDX tomosynthesis, where in-plane objects appear in focus, and objects above and below are symmetrically blurred increasing with the distance from the image plane. In MC-simulated images the localized X, Y, and Z coordinates of the spheres differed from the known coordinates by −0.061 ± 0.022 mm, −1.26 ± 0.37 mm, and 0.066 ± 0.023 mm respectively.

Figure 3.

Tomosynthesis reconstructions produced by experiment with the current SBDX prototype (A) and from SBDX simulations using the current rectangular detector (B) and previous square detector (C). In the simulations, the sphere position increases in 0.5 cm increments toward the detector, in row major order (top left to bottom right). The in-plane sphere is indicated with a yellow box.

The tomographic angles along the horizontal image direction are 6 and 3 degrees, respectively, for the current and previous SBDX system. Both have a 3 degree tomographic angle in the vertical direction. As expected, the system with the wider tomographic angle demonstrated stronger blurring in the horizontal direction for a given out-of-plane displacement (compare Figures 3B and 3C). The image with the current prototype has higher fluence and a brighter appearance because, with the wider detector, there is an increase in the number of backprojected detector images overlapping each point in the image plane.⁴ Also evident is the inverted magnification behavior of SBDX reconstructions, wherein objects closer to the detector appear larger and spaced farther apart compared to those closer to the source. This behavior is a consequence of the SBDX implementation of tomosynthesis. The pixel grid is defined on a cone that diverges from the center of the detector.¹⁰

Figure 4A shows simulated and experimental artifact spread functions for an isocentered sphere in the current SBDX geometry. The relative RMS deviation between the ASFs was 1.56%. The horizontal profiles that were used to generate the ASFs are arranged as 2D images and displayed in Figures 4B and 4C. Each row corresponds to a different plane position.

Figure 4.

Comparison of artifact spread functions along the horizontal image direction (A), for the current SBDX prototype. The ASF was measured from a 2.38 mm diameter ball bearing. Parts (B) and (C) show the profile data that was used to calculate the ASFs.

3.2 Kerma distribution

Figure 5A shows simulated kerma distributions at the chest phantom entrance plane for the regular and RAE scanning methods, in comparison to film measurements. Figure 5B shows simulated kerma distributions in an axial plane for the regular and adaptive scan, and tomosynthesis images generated from each scan simulation. Kerma and image brightness in the more transmissive lung regions were reduced when using the RAE scan, whereas image brightness in the more attenuating spine region was unchanged relative to the regular scan. Experimentally, the entrance KAP was reduced by 45% when using RAE scanning versus the regular scanning mode. Simulations were in good agreement, demonstrating a 46% reduction in KAP.

Figure 5.

(A) Measured and simulated kerma at the phantom entrance plane, for regular and regional adaptive (RAE) scanning. Imaging was performed for an anthropomorphic chest phantom. (B, top row) shows SBDX images reconstructed from simulated detector images, for each scanning mode. (B, bottom row) shows the change in axial kerma distribution resulting from the regional adaptive exposure method.

When integral dose was estimated by summing kerma over the TLD measurement points in the phantom, it was found that the simulated RAE scan provided a 61% integral dose reduction. In comparison, experimental TLD measurements demonstrated a 57% reduction. Although these two results were in reasonable agreement, a discrepancy between integral dose reduction and KAP reduction was not anticipated. With the MC-simulations it was possible to obtain a more accurate estimate of integral dose using the sum of kerma over all voxels in the phantom. With this method the integral dose reduction from RAE scanning was 48%, in close agreement with the KAP reduction results. This finding suggests that integral dose values measured by the TLD sampling method may be biased by the relatively sparse sampling positions.

3.3 Detected scatter

Figure 6 shows simulations and measurements of x-ray scatter SF for four thicknesses of isocentered acrylic (18.6, 23.3, 28, and 31.5 cm) and 100 kV tube voltage. Experimental x-ray SF increased with phantom thickness, measuring 1.8% to 3.9% on the previous SBDX prototype and 2.8% to 6.4% on the current prototype. Simulated x-ray SF followed the same trends, ranging from 1.3% to 2.6% for the previous prototype and 2.1% to 4.5% for the current prototype. Simulations displayed the experimentally observed effect that an increase in x-ray beam and detector area is accompanied by a similar increase in x-ray SF.

Figure 6.

Simulated and experimental x-ray scatter fraction for current (A) and previous (B) SBDX systems imaging isocentered acrylic phantoms (100 kV). Data for the previous SBDX system was taken from studies reported in Ref.5.

Figure 7 shows the experimental and simulated SF values for a 23.3 cm acrylic phantom as the air gap varied from 14.5 cm to 88.4 cm. (An isocentered phantom has a 93.4 cm air gap.) SF values ranged from 26.9% to 5.2% for experimental measurements versus 26.4% to 3.1% in simulation. For the scatter studies shown in Figs 6 & 7, the signed difference between simulated and experimental SF values ranged from −0.5% to −2.0% and averaged −1.1%.

Figure 7.

Simulated and experimental x-ray scatter fraction as a function of air gap, for the current SBDX prototype imaging a 23.3 cm acrylic phantom (100 kV).

The relative composition of scatter reaching the detector is shown in Figure 8A, for a 23.3 cm acrylic phantom centered at isocenter (single Compton scatter, single Rayleigh scatter, and multi-scatter). For comparison with the SBDX system, simulation results are also shown for a conventional cone beam imaging scenario. The overall SF was 2.9% for the current SBDX prototype simulation and 53% for the conventional simulation.

Figure 8.

(A) Composition of detected scatter for previous and current SBDX prototypes, for an isocentered 23.3 cm acrylic phantoms The scatter composition for an example conventional cone-beam geometry (5 cm air gap, no grid) is shown for comparison. (B) Composition of scatter versus acrylic phantom thickness, for previous and current generations of SBDX.

Simulation shows the SBDX geometry leads to a reduction in total scatter reaching the detector, as well as a change in relative scatter composition. For SBDX, detected scatter was approximately half single-Rayleigh-scatter and half multi-scatter (which may arise from a mixture of Rayleigh and Compton interactions). In the conventional geometry with a small air gap and no grid, multi-scatter and Compton scatter accounted for 93% of total scatter, and Rayleigh was a minority component. This difference may be understood by observing that Rayleigh scatter is primarily forward directed and not easily removed by air gaps.¹⁶ The composition of scatter in the SBDX system is explored further in Figure 8B, which demonstrates that the fraction of detected photons undergoing multiple scattering increases with increasing phantom thickness.

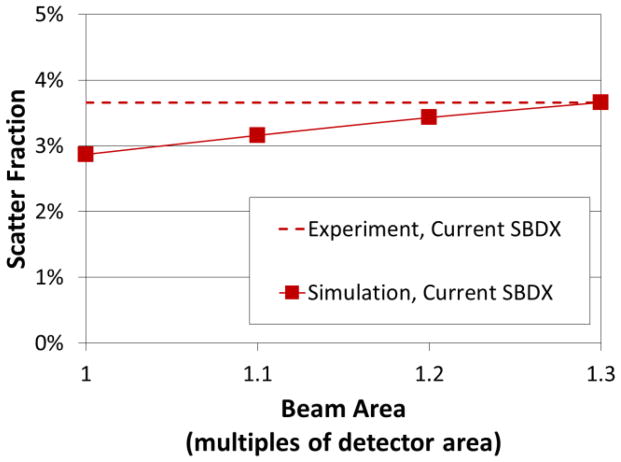
In Figures 6 and 7, the trends in scatter fraction agree between simulation and experiment. However the simulated values tended to systematically underestimate the measured values by a small amount (~ 1–2% difference in scatter fraction). The underestimation may be due in part to details of beam collimation which were not simulated. In MC simulations, each focal spot is an ideal point and each x-ray beam is perfectly collimated to the detector area. This is in contrast to the actual SBDX system, which can have imperfect collimation and x-ray beam penumbra. An increase in the phantom volume irradiated due to imperfect collimation can increase detected scatter. To investigate this possibility, simulations were performed where the angular width of the beam was symmetrically increased in polar and azimuthal directions such that the beam area at the detector ranged from 1.0x to 1.3x the size of the SBDX detector area (current system). A value of 1.14x is expected for the current system, based on detailed simulation of the collimator and focal spot geometry.⁴ Simulation results for a 23.3 cm thick isocentered phantom are shown in Figure 9. The simulations indicated that a 1.14x increase in beam area would increase the scatter fraction by 0.4% and reduce the difference between simulated and measured SF values to −0.4%.

Figure 9.

Simulated x-ray scatter fraction as a function of beam area, expressed as a multiple of the detector area, for the current SBDX geometry and a 23.3 cm thick acrylic phantom (100 kV). The horizontal line represents the experimental value under the same conditions.

3.4 Timing

Simulations of acrylic phantoms with 4.473 × 10¹⁰ histories per phantom averaged 1.09 hours each. The average number of acrylic voxels was 1.23 × 10⁷ and the average simulation rate was 7.31 × 10⁸ histories/min. In comparison, the anthropomorphic phantom (1.21 × 10⁸ voxels) simulation proceeded at 1.10 × 10⁸ histories/min, and the high resolution simulation of a single metal sphere proceeded at 4.50 × 10⁷ histories/min.

4. DISCUSSION

This paper reports a modified version of the MC-GPU program designed for Monte Carlo x-ray transport in an inverse geometry fluoroscopic system. The original CT imaging geometry was altered by fixing the detector position in space and replacing the circular CT source trajectory with a 2D planar array of source points. Features specific to inverse geometry imaging were also added. Specifically, the ability to independently modulate the number of x-rays from each source position was included, and photon-counting detector tallies were implemented. The input file format was modified to allow a user to easily specify any arbitrary inverse geometry x-ray system.

Previous authors have reported on modeling of the SBDX source¹⁷, GEANT4 Monte Carlo simulation to evaluate scatter in an inverse-geometry dedicated breast computed tomography system¹⁸, and optimization of inverse geometry tomosynthesis for the detection of lung tumors.² The present work represents an additional modeling tool which may be easily implemented on a desktop computer equipped with a GPU.

Predictions made with the MC code were in good agreement with experimentally measured trends in tomographic blur, dose distribution, and detected x-ray scatter levels. For isocentered acrylic phantoms, x-ray scatter fraction measured 2.8–6.4% on the current SBDX prototype, versus 2.1–4.5% in MC simulation. When imaging an anthropomorphic chest phantom, the reduction in kerma-area-product resulting from RAE scanning was 45% in film measurements, versus 46% in simulation. The integral kerma calculated from TLD measurement points within the phantom was 57% lower when using RAE, versus 61% lower in simulation. Interestingly, when all phantom voxels were included in the simulated integral kerma, integral kerma reduction (48%) was much closer to the kerma-area-product reduction. This result suggests that TLD based measurements may be biased by sampling point sparsity.

Discrepancies between simulation and experiment may be partly due to differences between the simulated and true imaging geometry. The current code models point-like focal spots with ideal beam collimation to the detector. Although reasonable agreement with experiment was obtained with this approach, it was found that imperfect beam collimation can influence detected scatter estimates. Improved accuracy may be obtained by including a finite-sized focal spot and details of the multi-hole collimator geometry. The code also uses a simplified detector model that assumes 100% efficient photon counting. Inclusion of detector energy response would improve estimates of dose efficiency. Last, the inclusion of user-specified C-arm orientations in the input file would enable simulation of inverse geometry CT.

It was found that single Rayleigh scatter forms a large component of total detected scatter in the SBDX system. This finding calls attention to the importance of accurate modeling of Rayleigh scattering physics for inverse geometry simulations. The version of MC-GPU used for this adaptation employs the independent atomic approximation (IAA) model for Rayleigh scattering cross sections. Recently, the Rayleigh scattering physics in MC-GPU was refined through the inclusion of a molecular interference factor.¹⁹ The effects of this refinement on inverse geometry simulations should be investigated.

5. CONCLUSIONS

This work presents a new Monte Carlo simulation program based on MC-GPU that is designed to aid in the development and evaluation of inverse geometry x-ray systems. Agreement between simulation and experimental results indicates that this simulator may be used to estimate x-ray scatter levels, determine relative kerma distributions, and evaluate tomographic blurring behavior for different inverse geometry systems. More detailed modeling of the focal spot and collimator details may provide further improvements in accuracy.