Nonperfect Synchronization of Reaction Center Rehybridization in the Transition State of the Hydride Transfer Catalyzed by Dihydrofolate Reductase

Abstract

It has been suggested that the magnitudes of secondary kinetic isotope effects (2° KIEs) of enzyme-catalyzed reactions are an indicator of the extent of reaction-center rehybridization at the transition state. A 2° KIE value close to the corresponding secondary equilibrium isotope effects (2° EIE) is conventionally interpreted as indicating a late transition state that resembles the final product. The reliability of using this criterion to infer the structure of the transition state is examined by carrying out a theoretical investigation of the hybridization states of the hydride donor and acceptor in the Escherichia coli dihydrofolate reductase (ecDHFR)-catalyzed reaction for which a 2° KIE close to the 2° EIE was reported. Our results show that the donor carbon at the hydride transfer transition state resembles the reactant state more than the product state, whereas the acceptor carbon is more productlike, which is a symptom of transition state imbalance. The conclusion that the isotopically substituted carbon is reactant-like disagrees with the conclusion that would have been derived from the criterion of 2° KIEs and 2° EIEs, but the breakdown of the correlation with the equilibrium isotope effect can be explained by considering the effect of tunneling.

1. Introduction

Kinetic isotope effects (KIEs) have been widely used to analyze complicated reaction mechanisms, especially in organic chemistry¹ and enzyme-catalyzed reactions.² Their interpretation also provides information about nuclear quantum effects, which are reflected in the quantized vibrations of the reactants and transition state and in quantum mechanical tunneling along the reaction coordinate or multidimensional tunneling path.^3-7

Although primary kinetic isotope effects (1° KIEs), which involve isotopic substitutions of atoms whose chemical bonding changes in the course of the reaction, are typically larger in magnitude^1,3,8,9 than secondary kinetic isotope effects (2° KIEs), defined as the effects of isotopic substitutions of atoms not directly involved in the bond breaking and forming process, 2° KIEs are also of great interest.^1,3,9,10 For example, unusually large 2° KIEs have been suggested as signifying tunneling and coupled motions involving primary and secondary atoms.¹¹

A particularly interesting quantity is the magnitude of a 2° KIE relative to the corresponding equilibrium isotope effect (2° EIE), which is the ratio of the isotopically unsubstituted equilibrium constant to the isotopically substituted one.^12-16 For an atom transfer reaction, where the 2° isotopic atom is bonded to the donor (or the acceptor atom), the 2° KIEs are often considered to be mainly a consequence of the change in the hybridization state of donor or acceptor in proceeding from the reactant to the transition state.^1,9 Such hybridization changes have important effects on bending and stretching frequencies between the reactant and the transition state.^12,17-21 On the basis of this relationship between hybridization and KIEs, an empirical criterion has been widely used to infer the location of the transition state by comparing the 2° KIE for deuterium substitution to the 2° EIE. Thus a 2° KIE that is close to the 2° EIE is taken as an indication that the rehybridization of the reaction center bonded to the deuterium has already been accomplished at the transition state, yielding a late transition state that resembles the product.^{1,9,13-16,22-29} The same criterion was also used to suggest that a small 2° KIE (close to unity) results from an early transition state (i.e., one resembling the reactant), and the fractional position of a 2° KIE between unity and the relevant 2° EIE ([2° KIE – 1]/[2° EIE – 1]) represents the fractional location of the transition state between reactant and product.^9,16,22-30 However, this criterion seems to be oversimplified by neglecting factors other than the structural change from the reactant to the transition state that can significantly contribute to 2° KIEs.^18,19,31 Simply comparing the magnitude of the 2° KIE to that of the 2° EIE without considering such factors may lead to an incorrect characterization of the transition state structure.

In this article, we present a theoretical study designed to examine the reliability of inferring the transition state structure for an enzyme-catalyzed hydride transfer reaction on the basis of this empirical criterion. In particular, we present calculations of the hybridization states of the hydride donor and hydride acceptor carbon atoms along the reaction coordinate of a hydride transfer reaction catalyzed by dihydrofolate reductase of Escherichia coli (ecDHFR). The analysis is based on an ensemble average of configurations that have been sampled in a molecular dynamics simulation reported previously.³² DHFR is a critical enzyme in maintaining the intracellular concentration of tetrahydrofolate, which is an important reductive cofactor in the biosynthesis of DNA building blocks and several amino acids, and it is a target for anti-cancer and anti-bacteria drugs.³³ A thorough investigation of the properties of the transition state in this enzyme can provide valuable information to understand the activities and function of DHFR and to aid the rational design of drugs that are transition state analogues. In addition, the present results have fundamental significance as the first study of this kind for any enzyme-catalyzed reaction, and ecDHFR is ideally suited for this investigation because it is a small, monomeric enzyme that has been successfully modeled in past work.^32,34,35

Section 2 describes the theoretical model and computational details of the calculation of the hybridization states of the reaction centers of interest. Note that the present calculations do not change our previously published variational transition state theory calculations of the KIE, but rather they involve a further, more detailed analysis of the configurations underlying the previous calculations. Results and Discussion are presented in sections 3 and 4. Concluding remarks and a summary of findings are given in section 5.

2. Computational Details

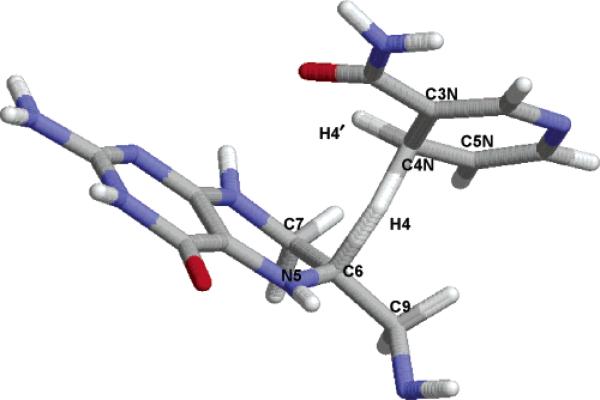
Figure 1 shows a schematic representation of the transition state configuration of the hydride transfer reaction catalyzed by dihydrofolate reductase. In this reaction, a hydride ion (H4) is transferred from the C4N position of the cofactor nicotinamide adenine dinucleotide phosphate (NADPH) to the C6 position of the substrate 7,8-dihydrofolate (DHF) as the key step in reducing the substrate to 5,6,7,8-tetrahydrofolate (THF). In the 2° isotopic substitution, a deuterium atom replaces the nontransferring hydrogen atom at the spectator H4′ (the pro-S) position.

Figure 1.

Labeling of the atoms near the hydride transfer center in the ecDHFR-catalyzed reaction, which transfers H4 from C4N to C6.

We calculate the hybridization states of C4N (the hydride donor carbon) and C6 (the hydride acceptor carbon) with an algorithm based on the local geometry of these carbon atoms and their directly bonded neighboring atoms. The equations (based on the ideas of Pauling³⁶) are identical to those used in the generalized hybrid orbital (GHO) method³⁷ and other applications,³⁸ and the hybridization state (that is, the character of the instantaneous atomic orbital constituents of the hybrid orbitals) on the center of interest is inferred from the instantaneous geometrical coordinate³⁷ during molecular dynamics simulations. To derive the hybridization state of a given atomic center, a local coordinate system is first defined as depicted in Figure 2. The atom of interest is placed at the origin of the local coordinate system; the origin is labeled O in Figure 2. In the present study, the atoms of interest are the hydride donor and acceptor carbons. The central atom at the origin is connected to three neighboring atoms, denoted A, B, and D, through three σ-bonds each formed by overlapping a valence orbital of A, B, or D (which are not being transferred) with an sp^x hybrid orbital of O. Since A, B, and D are not being transferred, the three orbitals associated with their bonds are called auxiliary hybrid orbitals (ϕ_aux). The hybridization state variable x defines the extent of the p contributions to each of these three hybrid orbitals. Figure 2 shows unit vectors a, b, and d, pointing from O toward A, B, and D, respectively. Then one can construct an active hybrid orbital ϕ_act (which is involved in the bond with the atom being transferred) orthogonal to the plane ζ determined by the end points of vectors a, b, and d. The coefficients of the s and p components in the active hybrid orbital are:

$$c_{\mathrm{s}}^{\mathrm{act}}=\sqrt{\frac{L}{1+L}}\text{and}{c}_{\mathrm{p}}^{\mathrm{act}}=\sqrt{\frac{1}{1+L}}$$ (1)

where L measures the distance from atom O to the plane ζ. If we choose the average of the remaining s and p components distributed equally over the three auxiliary hybrid orbitals, we obtain the composition of the auxiliary hybrid orbitals as:

$$c_{\mathrm{s}}^{\mathrm{aux}}=\sqrt{\frac{1}{3}[1-{\left(c_{\mathrm{s}}^{\mathrm{act}}\right)}^2]}$$ (2)

$$c_{\mathrm{p}}^{\mathrm{aux}}=\sqrt{\frac{1}{3}[3-{\left(c_{\mathrm{p}}^{\mathrm{act}}\right)}^2]}$$ (3)

where c_s^aux and c_p^aux represent the coefficients of the s and p components of each of the auxiliary orbitals. We find that the composition of these auxiliary hybrid orbitals can be used satisfactorily to monitor the change of the hybridization state of the central carbon atoms during the hydride transferring process. The hybridization state variable x is obtained by normalizing the p orbital contribution with respect to the s orbital contribution in these auxiliary orbitals:

$$x={(c_{\mathrm{p}}^{\mathrm{aux}}∕c_{\mathrm{s}}^{\mathrm{aux}})}^2$$ (4a)

Note that eqs 1–4a yield

$$x=2+3L$$ (4b)

Because a, b, and d are unit vectors, L depends on the bond angles, but not on the bond distances at the atom whose hybridization is being considered. Three angles of 120° will result in an L value of 0 and an x value of 2. In contrast, a symmetrical sp³ molecule such as methane has L = 1/3 and x = 3. Specifically, for the hydride transferring between C4N and C6 in the ecDHFR-catalyzed reaction, the hydride donor carbon (C4N) changes from sp³ hybridization to sp² hybridization (x: 3 → 2), while the hydride acceptor carbon (C6) changes from sp² to sp³ hybridization (x: 2 → 3) by accepting a hydride ion.

Figure 2.

(a) The molecular environment at the carbon atom C changing its hybridization; A, B, and D are spectator atoms (hydrogen or carbon), H is the transferred hydride, ϕ_act is the active hybrid orbital, and the auxiliary hybrid orbitals are labeled ϕ_aux. (b) The local coordinate system defined around the central atom to determine the hybridization state of the central atom in GHO. The origin O is at atom C, and a, b, and d are unit vectors pointing to atoms A, B, and D.

The hybridization states of the donor and acceptor carbon atoms are monitored as functions of a predefined reaction coordinate z, where z measures the difference between the donor-to-H distance and the H-to-acceptor distance. Constant-temperature (at 298 K) molecular dynamics simulations were carried out based on a well-calibrated^32,34 combined quantum mechanical and molecular mechanical (QM/MM) potential by employing umbrella sampling³⁹ to generate the reaction ensemble along the hydride transfer reaction coordinate z. A detailed description of simulation protocols can be found elsewhere.³² The data were collected over 19 molecular dynamics simulation windows from z = −1.4 to 1.4 Å, where 200–300 configurations were used within a range of ±0.1 Å about the z value of the center of each window. The results were further sorted into bins with a bin size of 0.01 Å and averaged over each bin.

3. Results

Table 1 gives the geometric parameters averaged for the reactant state, for the variational transition state (TS) determined as the maximum of the quantized potential of mean force (PMF) for the perprotio (i.e., isotopically unsubstituted) case,^40,41 and for the product state. The changes of these parameters in proceeding from the reactant to the transition state and from the reactant to the product are listed in Table 2. The ensemble-averaged hybridization states of the hydride-donating carbon and hydride acceptor carbon atom for reactant, the transition state, and the product are given in Table 3. Tables 2 and 3 also give a unitless progress variable λ defined so that it gives the inferred position of the transition state as a fraction of the difference from reactant to product. Thus, for any variable y that varies approximately linearly along the reaction path from reactant (R) to transition state (TS) to product (P), we have:

$$\lambda =\frac{\mid y\left(\mathrm{R}\right)-y\left(\mathrm{TS}\right)\mid }{\mid y\left(\mathrm{P}\right)-y\left(\mathrm{R}\right)\mid }$$ (5a)

$$=\frac{\mid y\left(\mathrm{R}\right)-y\left(\mathrm{TS}\right)\mid }{\mid y\left(\mathrm{P}\right)-y\left(\mathrm{TS}\right)\mid +\mid y\left(\mathrm{R}\right)-y\left(\mathrm{TS}\right)\mid }$$ (5b)

Table 1.

Ensemble-Averaged Bond Distances and Bond Angles for Transferring H4 between the Hydride Donor (C4N) and the Hydride Acceptor (C6)^a

label	bond or angle	reactant	transition state	product
r 1	C4N–H4	1.127	1.302	(1.881)b
r 2	H4′–C4N	1.125	1.120	1.110
r 3	C3N–C4N	1.488	1.455	1.412
r 4	C5N–C4N	1.480	1.448	1.397
θ 1	H4′–C4N–H4	106.2	96.1	(76.3)
θ 2	C3N–C4N–H4	107.8	106.7	(98.4)
θ 3	C5N–C4N–H4	109.7	106.4	(102.9)
θ 4	H4′–C4N–C3N	109.5	114.6	119.5
θ 5	C3N–C4N–C5N	112.9	114.7	118.8
θ 6	C5N–C4N–H4′	110.4	115.7	121.2
r 7	C6–H4	(2.299)	1.448	1.154
r 8	N5–C6	1.315	1.365	1.449
r 9	C7–C6	1.519	1.542	1.555
r 10	C9–C6	1.520	1.548	1.562
θ 7	N5–C6–H4	(95.7)	108.0	112.4
θ 8	C7–C6–H4	(76.6)	97.8	105.7
θ 9	C9–C6–H4	(99.0)	99.4	106.2
θ 10	N5–C6–C7	120.9	116.3	111.1
θ 11	C7–C6–C9	114.8	111.1	107.1
θ 12	C9–C6–N5	124.3	120.0	113.8
θ 13	C4N–H–C6	(156.5)	160.2	(151.7)
z	r1 – r7	–1.172	–0.146	0.726

^aCalculated from 13 structures for reactants, products, and transition states. Transition state structures were optimized to the nearest saddle point starting from the selected in the PMF bin with z = –0.145 ± 0.05 Å. The reactants and products were optimized to the nearest energy minimum starting from the same structures, but optimized as energy minima. In each case (reactants, products, and transition state), 13 members of the ensemble were selected essentially at random for the present analysis, and the results were fully averaged over these configurations. Bond distances are in Å, and bond angles are in degrees.

^bParenthesis denotes that the bond or angle is actually “nonbonded” in the specific state. For example, the breaking bond C4N–H4 is not present in the product.

Table 2.

Unsigned Differences of the Internal Coordinates of Transition State (TS) Structure Compared with Those of the Reactant (R) and Product (P) Structures^a

label	bond or angle	TS vs R	TS vs P	λ
r 1	C4N–H4	0.175	(0.579)
r 2	H4′–C4N	0.004	0.010	0.29
r 3	C3N–C4N	0.033	0.043	0.43
r 4	C5N–C4N	0.032	0.051	0.39
θ 1	H4′–C4N–H4	10.1	(19.8)
θ 2	C3N–C4N–H4	1.1	(8.3)
θ 3	C5N–C4N–H4	3.3	(3.5)
θ 4	H4′–C4N–C3N	5.1	4.9	0.51
θ 5	C3N–C4N–C5N	1.8	4.1	0.31
θ 6	C5N–C4N–H4′	5.3	5.5	0.49
r 5	C6–H4	(0.851)	0.294
r 6	N5–C6	0.049	0.085	0.37
r 7	C7–C6	0.024	0.013	0.65
r 8	C9–C6	0.027	0.014	0.66
θ 7	N5–C6–H4	(12.3)	4.3
θ 8	C7–C6–H4	(21.2)	7.9
θ 9	C9–C6–H4	(0.4)	6.8
θ 10	N5–C6–C7	4.6	5.2	0.47
θ 11	C7–C6–C9	3.7	3.9	0.49
θ 12	C9–C6–N5	4.3	6.2	0.41
θ 13	C4N–H–C6	(3.7)	(8.5)
average bond length differenceb		0.049c	0.073d	0.40
average bond angle differenceb		4.2e	5.8f	0.42
C4N (bond length)g		0.023	0.035	0.40
C4N (bond angle)g		4.1	4.8	0.46
C6 (bond length)h		0.034	0.037	0.48
C6 (bond angle)h		4.2	5.1	0.45

^aBond distances are in Å, and bond angles are in degrees.

^bNumbers in parentheses are not included in these averages for a given column, as explained further in footnotes c–f.

^cAverage over r_i (i = 1–4, 6–8).

^dAverage over r_i (i = 2–4, 5–8).

^eAverage over θ_i (i = 1–6, 10–12).

^fAverage over θ_i (i = 4–6, 7–12).

^gSame as footnote c, d, e,or f, except it only counts bond lengths and angles involving C4N in both R and P. For example, the r₁ bond is broken in P, and thus r₁ is not included in the C4N bond length row.

^hSame as footnote c, d, e, or f, except it only counts bond lengths and angles involving C6 in both R and P.

Table 3.

Hybridization States of C4N and C6 in Reactant (R), Transition State (TS), and Product (P) Ensembles^a

atom	R	TS	P	λ
donor, C4N	2.92 ± 0.01b	2.68 ± 0.02	2.13 ± 0.02	0.30
acceptor, C6	2.04 ± 0.02	2.62 ± 0.04	2.94 ± 0.01	0.64

^aThe quantity tabulated is ($c_{\mathrm{p}}^{\mathrm{aux}}∕c_{\mathrm{s}}^{\mathrm{aux}}$)², averaged over 13 structures, each obtained by optimizing the primary subsystem of a randomly selected member of the R, TS, or P ensembles to the nearest stationary point, as explained further in ref 32.

^bThe quantity after ± is the standard deviation for the 13 structures.

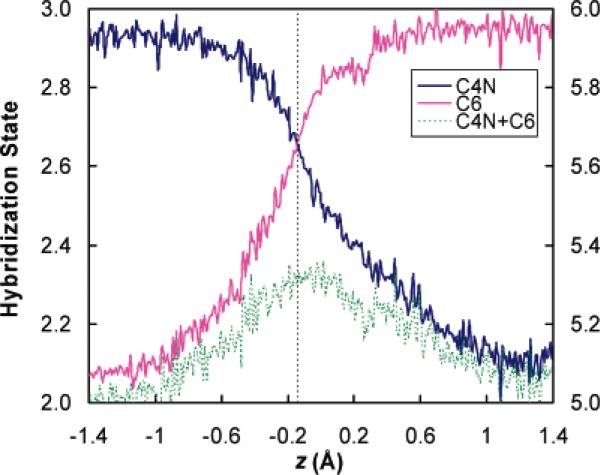
The ensemble-averaged hybridization state variable x (computed from eq 4a) of the hydride-donating carbon (C4N) and the hydride acceptor carbon (C6) as well as the sum of them are plotted as a function of the hydride transfer reaction coordinate z in Figure 3, which shows several interesting features. First, we notice that for both reaction-center carbon atoms, the hybridization state does not progress linearly with respect to the hydride transfer reaction coordinate. The rehybridization process is slow near the stable species and experiences the fastest change around the transition state region, which can be easily identified from the slopes of the hybridization curves in Figure 3. This kind of nonlinear behavior has been observed in other reactions, such as the pyramidalization process of the methyl radical in the CH₄ → CH₃ + H reaction⁴² (an example of an sp³ → sp² hybridization change with a minimum of additional complications). In fact, the plot of the pyramidalization force constant versus C–H distance (Figure 2 of ref 42) looks very much like the C4N plot in Figure 3. The nonlinearity of the curves in Figure 3 raises doubt about using the closeness of the 2° KIE and 2° EIE as a criterion to infer the location of the transition state, since a linear relationship between the rehybridization and the reaction coordinate is assumed in a relationship such as that in eq 5a or 5b. Second and rather amazingly, at the transition state (i.e., the free energy bottleneck located as the maximum of the quantized potential of mean force along the hydride transfer reaction coordinate at z = −0.145 Å)³² both C4N and C6 adopt the same hybridization of sp^2.64; that is, the C4N and C6 curves in Figure 3 cross at the transition state. Since the 2° isotopic substitution is made on the hydrogen (H4′ in Figure 1) that is covalently bonded to the C4N atom, the secondary kinetic isotope effect is primarily associated with the change of the hybridization state of the hydride-donating carbon C4N. A hybridization state variable of 2.64 at the transition state indicates an early transition state. In particular, since the reactant has a hybridization value of 2.92 for C4N and the product has a value of 2.13, eq 5 with 2.64 at the transition state (as determined from Figure 3) yields λ = 0.35, and eq 5 with 2.68 at the transition states (as determined by the slightly different methodology used in Table 3) yields λ = 0.30.

Figure 3.

Hybridization states of the hydride donor carbon (C4N) and hydride acceptor carbon (C6) along the hydride transfer reaction coordinate z, where z = r_C4N–H – r_C6–H. The data are collected over 19 molecular dynamics simulation windows from z = −1.4 to 1.4 Å where 200–300 configurations are selected within ±0.1 Å of the z value of the center of each window. The results are further sorted and averaged with a bin size of 0.01 Å. The vertical dashed line corresponds to the transition state at z = −0.145 Å. (The values of the transition state show a small difference from the TS values in Table 3 because those in Table 3 are based on 13 randomly selected TS structures, each optimized to the nearest saddle point, whereas this figure uses a collection of configurations from the PMF calculations, sorted into narrow bins. The key point is not the subtle differences, but rather the robustness of the key features, which are qualitatively the same by both methods of analysis.)

It is also very interesting to note that the rehybridizations of the donating and accepting carbon centers do not occur synchronously, in that the hydride acceptor C6 has almost accomplished its change of the hybridization at the transition state. Thus, the transition state is early from the point of view of C4N but late from the point of view of C6. This is therefore a very clear example of nonperfect synchronization and transition state imbalance, which have been widely studied in organic chemistry.^43,44 We will return to this point later in the article.

Third, we note that the total hybridization state for the two reaction center atoms is not conserved during the hydride transfer process. In Figure 3, the sum of the hybridization exponents of C4N and C6 (we will call the sum “hybridization looseness perpendicular to the reaction coordinate”; see below), defined as:

$$x_{\mathrm{tot}}=x_{\mathrm{C}4\mathrm{N}}+x_{\mathrm{C}6}$$ (6)

is plotted (the green curve) with its numerical values indicated on the right ordinate. We find a maximum of 5.3 for the hybridization looseness perpendicular to the reaction coordinate z in the range −0.2 to 0.0 Å; this range contains the position (z = −0.145 Å) where we locate the transition state.

4. Discussion

The 2° H/D KIE for the ecDHFR–catalyzed hydride transfer step has been measured experimentally by Kohen and coworkers,⁴⁵ who found a value of 1.13, in good agreement with the value that was predicted³² (prior to the experiment) from a combined QM/MM simulation employing ensemble-averaged variational transition state theory with multidimensional tunneling^41,46 (VTST/MT). Often, experimental 2° KIEs are analyzed by comparison to their corresponding 2° EIEs.^9,16,30 Since the EIE expresses the complete change in rehybridization from reactant to product (sp³ to sp² in the case of the donor atom in the present DHFR reaction), it is usually assumed that the value of the 2° KIE ranges from unity (no isotope effect) to that of the EIE. If the 2° KIE is close to unity, it is interpreted as indicating a TS close to the reactant state, and if the 2° KIE is close to the EIE, it is interpreted as indicating a TS resembling the product state. Between these extremes a linear relationship is typically used to determine the position of the TS. The intrinsic 2° H/D EIE for DHFR in equilibrium with reactants and products has not been investigated, and it would be very difficult to measure because the reaction is practically irreversible. Nevertheless, since no significant rehybridization change is expected on the binding step of the reactant or the release step of the product, the overall 2° EIE for NADPH expresses the full extent of rehybridization change from reactant to product, and the overall reaction's EIE should not depend on which catalyst is used to reach equilibrium. The 2° EIE for NADPH was measured under the same conditions as the kinetic experiments, and a value of 1.129 ± 0.006 was obtained.⁴⁷ Not surprisingly, this value is very close to the 2° EIE measured before for NADH oxidation.¹⁴ Since the 2° KIE for the DHFR-catalyzed reaction (1.13 ± 0.02)⁴⁵ is equal (within experimental error) to the 2° EIE, the common interpretation using the simple empirical criterion^9,16,30 stated earlier would suggest a transition state structure that resembles the product.

In contrast to the expectation just expressed, the ensemble-averaged hybridization state calculations reveal an early transition state in terms of the rehybridization of the isotopically relevant carbon atom. In particular, most of the λ values in Table 2 are less than 0.5. The most statistically significant values in Table 2 are the highly averaged ones in the last six rows. All six of these values are in the range 0.40–0.48, with the largest λ estimated based on the C6 bond length being 0.48. However, in Table 3, one λ is 0.30, and the other is 0.64. Thus, different measures of progress along the reaction coordinate are out of balance. Such imbalance has also been observed in gas-phase proton-transfer reactions between carbon centers.⁴⁸ In general, it has been postulated that reactions with strongly unbalanced transition states, such as when hybridization changes lag behind or precede bond length changes, have a higher intrinsic barrier.⁴³ If this is the case, evolutionary pressure might be expected to decrease transition state imbalance, but the only requirement for optimizing a catalytic process is to speed up the catalytic step enough to make its rate compatible with the preceding and following processes in the enzyme mechanism and the enzymatic cycle, not necessarily to optimize every factor that might contribute to speedup.

A reaction coordinate based on bond distances, such as the reaction coordinate z employed in our previous studies,^32,34 has been widely used to monitor the free energy change for enzyme-catalyzed reactions. But other reaction coordinates have been used as well. For example, solvation energy gap coordinate^49,50 or bond order⁵¹ can be used with great generality. Gronert and Keeffe studied bond distances and charge development as progress measures in hydride transfer reactions,⁵² but did not study hybridization state. In contrast, Haddon and Chow⁵³ advocated hybridization as the best general metric for reaction progress in various reactions. The nonlinear relationship between bond distance and hybridization reaction coordinates in Figure 3 suggests that there are advantages in using the hybridization state as a complementary reaction coordinate since it reflects a different measure of reaction progress than bond distance reaction coordinate. Furthermore, the crossing over of the hybridization curves for the hydride donor and acceptor at the transition state suggests a correlation between the isohybridization point and the position of the transition states, which has never been noted before. This correlation is probably limited to nearly thermal neutral reactions. It is possible that one could understand this kind of observation by expressing the energies of valence bond states in terms of deformation energies⁵⁴ and using the model of avoided crossing states,⁵⁵ but we leave such elaboration as a subject for future investigation.

The hybridization looseness x_tot, defined by eq 6, may be thought of as the variable perpendicular to the reaction coordinate in a More O'Ferrall–Jencks diagram^56–59 or as an alternative way to express the information contained in the tightness parameter of Albery and Kreevoy.⁶⁰ This can be illustrated by a two-dimensional map based on the hybridization coordinates as shown in Figure 4. In Figure 4, the progress of the hybridization states for each of the two carbon centers is represented by the abscissa and ordinate, respectively. The reactant is located at the upper left corner of the map, where C4N (hydride donor) adopts an sp³ hybridization and C6 (hydride acceptor) adopts an sp² hybridization. Correspondingly, the product is located at the lower right corner of the map, where the C4N and C6 exchange their hybridization states after the hydride transfer. Making use of an analogy to the diagram used by one of the authors and Kreevoy⁵⁸ to characterize the location of the transition state, we can introduce two orthogonal parameters in the rehybridization map, where the first parameter (η) monitors the hybridization changes along the hydride transfer, and the second parameter (x_tot) measures the looseness of the transition state.

Figure 4.

Two-dimensional map for characterizing the transition state by using the reaction center rehybridizations as a reaction progress indicator. The perfectly synchronous rehybridization pathway is represented by the upper-left-to-lower-right diagonal. The total hybridization parameter x_tot roughly measures the tightness of the transition state. The red curve represents a reaction path of the ecDHFR-catalyzed hydride transfer between carbon centers C4N and C6, where a tight transition state (shown by a red dot labeled with ‡) is found at $x_{\mathrm{tot}}^{‡}\simeq 5.31$, slightly prior to the maximum value of x_tot, which is ~5.34. The deviation of the reaction path from the upper-left-to-lower-right diagonal indicates a nonperfect synchronization of the carbon center rehybridizations.

In a More O'Ferrall–Jencks diagram, each point represents the transition state for a possible reaction. As one considers systems with transition states arrayed along the axis associated with the perpendicular hybridization looseness parameter, the total hybridization state variable x_tot changes from 4 to 6, where the upper right corner represents a hypothetical loose (“exploded”) transition state (or intermediate), C4N···H···C6, with both carbon centers adopting sp² hybridizations, and the lower left corner represents the hypothetical tight (“compressed”) transition state, C4N–H–C6, in which both carbons take sp³ hybridizations. If the two hydride transfers occur in a completely sequential fashion, with the C4N–H bond breaking first, x_tot would change from 5 to 4 and back to 5. On the other hand, if the hydride transfer step were to occur by going through an associative intermediate, with the H–C6 bond forming first, x_tot would change from 5 to 6 to 5. One might expect that if the reaction is perfectly synchronous and perfectly balanced, x_tot would remain constant at 5, corresponding to the upper-left-to-lower-right diagonal sequence of transition states on the hybridization map. A similar principle of conserving the bond orders has been postulated in previous work.^3,51,61 However, as shown in Figure 3, the perpendicular hybridization looseness parameter x_tot is not conserved along the reaction coordinate of hydride transfer, suggesting a significant deviation from the perfectly synchronized rehybridization pathway.

Figure 4 also shows a schematic representation (the red curve) of a sequence of transition states with such imbalanced rehybridization paths, where x_tot takes a maximum value of 5.3 around the transition state region. Along such an unbalanced reaction path, the rehybridization of the hydride acceptor carbon (C6) is significantly advanced compared to that of the hydride donor carbon (C4N), resulting in a compressed transition state, represented by a “‡” sign in Figure 4. In particular, for the present reaction, x_tot^‡ is ~5.31 at the variational transition state (and ~5.34 at its maximum, which occurs a little later than the variational transition state). According to the “principle of nonperfect synchronization” (PNS) proposed by Bernasconi,⁴⁴ which states that “a product stabilization factor that lags behind bond changes at the transition state increases the intrinsic barrier, while a product stabilizing factor that develops ahead of bond changes lowers the intrinsic barrier”, the greater progress of rehybridization of the hydride acceptor (C6) as compared to other progress variables (bond distances and rehybridization at the donor) may provide a mechanism to stabilize the product and hence change the shape of the reaction's free energy profile. From the point of view of stabilization of the transition state, charge delocalization can be better achieved in a tight transition state than in a relatively loose one, and this requires an unbalanced development of hybridization at the two carbon centers so that the hydride acceptor can rapidly adopt a more p–like hybridization at the transition state.

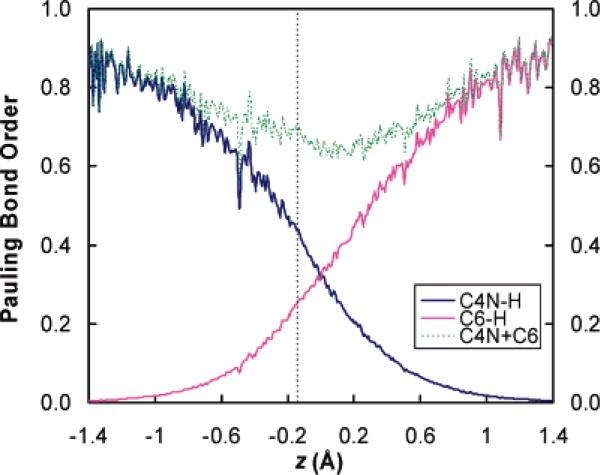
It is interesting to compare the transition state characterized from reaction center rehybridizations with the results obtained from the traditional bond order analysis,⁵¹ since bond orders have been widely used by physical organic chemists to discuss the lateness of the transition state. In Figure 5, we plot the Pauling bond orders⁶² of both the bond being made (C6–H) and the bond being broken (C4N–H) as functions of the hydride transfer reaction coordinate z. Figure 5 shows that the bonds involving the hydride donor and acceptor also change in an imbalanced fashion along the reaction coordinate, providing complementary evidence of the nonperfect synchronization that we have observed based on the reaction center hybridization analysis in the DHFR-catalyzed hydride transfer reaction. In particular, the breaking bond C4N–H adopts a bond order of 0.44 in the transition state, whereas the C6–H bond is less than half formed (a bond order of 0.25 is found for the forming bond at the transition state). Monitoring the change of bond orders along the reaction coordinate of hydride transfer suggests that the C4N–H bond in the transition state resembles that in the product state but the C6–H bond in the transition state resembles that in the reactant state. Figure 5 also provides the total bond order (sum of the bond orders of the breaking and forming bonds) along the reaction coordinate of hydride transfer, which yields a minimal value of 0.7 at the transition state region. Interstingly, total bond orders at the transition states have been dervied from measurement of the Brønsted α parameters for a series hydride transfer reactions between hetrocyclic nitrogen-containing cations in the solution phase,^63,64 which may be treated as analogues of the DHFR-catalyzed enzyme reaction that involves the NADPH cofactor. We find that the total bond order of 0.7 obtained from the present study for the enzyme-catalyzed reaction is in a good agreement with the solution phase results, which yield total bond orders of 0.77⁶³ and 0.64–0.68,⁶⁴ respectively. The total bond order has been demonstrated to be a useful parameter to characterize the transition state.^63,64 In particular, a total bond order smaller than unity suggests an inflated transition state that corresponds to the region above the strictly synchronized diagonal on a More O'Ferrall–Jencks diagram. In contrast to the hybridziation state analysis we presented here, the bond order calculations seem to suggest a much looser transition state. One possible reason the bond order analysis tends to give a loose transition state is that the bond order is calculated as an exponentially decreasing function of the equilibrium bond distance, and there is some arbitrariness in the rate of decay of bond order for a bond that is still significantly partially formed in a transition state. Since there is no unanimous agreement about which variable is more appropriate to be used to describe the tightness/looseness of the transition state, it seems that the combined analysis of both the hybridization state and the bond order provides complementary pictures of the transition state character.

Figure 5.

Pauling bond orders of the breaking bond (C4N–H) and the forming bond (C6–H) along the hydride transfer reaction coordinate z, where z = r_C4N–H – r_C6–H. The data are collected following the same procedure as described in Figure 3. The vertical dashed line corresponds to the transition state at z = −0.145 Å.

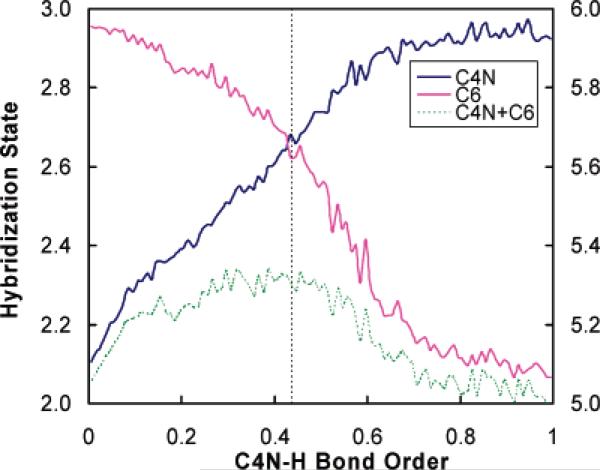
To examine whether the hybridization imbalance depends on the choice of a specific form of the reaction coordinate (we use a geometric coordinate in our analysis in Figure 3), we also test the correlation of hybridization states with the reaction progress by using a bond order variable as the reaction coordinate. Figure 6 plots the hybridization states of the hydride donor carbon (C4N) and the hydride acceptor carbon (C6) as well as their total hybridization states against the Pauling bond order of the bond being broken (C4N–H) during the hydride transfer. The hybridization curves in Figure 6 are very similar to those given in Figure 3, where a different type of reaction coordinate is adopted, and our conclusion of the imbalance of the reaction center rehybridization is not altered.

Figure 6.

Hybridization states x of the hydride donor carbon (C4N) and hydride acceptor carbon (C6) plotted against the Pauling bond order of the bond being broken (C4N–H); these values are associated with the scale on the left side of the figure. The green curve is the hybridization state looseness variable x_tot, which is associated with the right side of the figure. The results are sorted and averaged with a bin width of 0.01 bond order unit. The vertical dashed line corresponds to the transition state at z = −0.145 Å.

A key issue not reflected in the above discussion is that a perpendicular looseness parameter inferred from kinetics or kinetic isotope effects must refer to the quantum mechanical critical configuration (defined as the most probable structure for crossing the transition-state dividing surface that separates reactants from products) rather than to the classical molecular dynamics one when these differ, as they often do, because of corner-cutting tunneling (a nonclassical internal centrifugal effect).⁶⁵ Furthermore, factors that affect the KIE but do not affect the EIE should not be included in the KIE:EIE comparison. These considerations provide a possible explanation for why the empirical criterion of using secondary isotope effects may fail to give a correct prediction of the transition state location. In particular, this may occur because there are more factors contributing to 2° KIEs than contribute to 2° EIEs.^18,65,66 For KIEs, quantum mechanical tunneling must be taken into account, especially when the reaction involves light-atom transfer. Since tunneling is multidimensional, the secondary isotopic substitution can couple to the motion of the atom being transferred. Thus, multidimensional tunneling can contribute significantly to 2° KIEs. Because 2° EIEs measure the change of equilibrium constants upon isotope replacement, tunneling does not contribute to 2° EIEs. It is of interest to test the usefulness of the correlation between 2° isotope effects and reaction center rehybridization in the transition state when the tunneling contribution is removed from 2° KIEs. A best estimate of such a quantity is provided by calculations reported previously,³² where 2° H/D KIEs of 1.13 and 1.03 are obtained with and without the multidimensional tunneling contributions, respectively. The tunneling-excluded 2° H/D KIE (1.03) should be more informative for reflecting structural changes such as rehybridization at the transition state. This adjusted 2° H/D KIE suggests an early transition state [λ = (1.03–1)/(1.129–1) = 0.23] that closely resembles the reactant, which is consistent with the hybridization state calculations [λ = 0.30, Table 3] in the present work.

The factorization of the KIE into a tunneling part and the rest, where the latter correlates more strongly with the structural properties, is a consequence of the general separation^67,68 of rate constants into a transmission coefficient and a quasithermodynamic (or “substantial”) part, where the latter is associated with transition state structure by the usual relations of molecular statistical mechanics, but the former is not.

5. Concluding Remarks

In the present article, we have examined the validity of the empirical correlation of secondary isotope effects (2° KIE versus 2° EIE) with the location of the transition state in terms of reaction center rehybridization. In particular, we studied this issue for the hydride transfer reaction catalyzed by the enzyme ecDHFR by analyzing the change of hybridization state along the reaction coordinate; the analysis is based on ensemble-averaged structural information extracted from molecular dynamics simulations carried out with a combined QM/MM potential. The geometry dependence of hybrid orbitals directed along bonds is used to map the sequence of structural changes along the hydride transfer reaction coordinate to a sequence of donor/acceptor hybridization states. For the donor carbon that was isotopically substituted in the experiments, an early transition state that resembles the hybridization state in the reactant is found, contradicting the conclusion that would be inferred from the closeness of the 2° KIE to its corresponding 2° EIE. We propose that a more realistic correlation of these secondary isotope effects can be found if the quantum tunneling contribution of the 2° KIE is removed from the overall 2° KIE; the remaining part of the 2° KIE (the “substantial” contribution) reflects the structural properties of the transition state more faithfully.

The present calculations show how computer simulations can shed new light on interpretive tools used by experimentalists. In particular, our results provide the first molecular-level evidence (to the best of our knowledge) that a transition state of an enzyme-catalyzed reaction resembles the reactant in terms of the hydrogen donor hybridization state although the closeness of the 2° KIE to its 2° EIE suggests a productlike transition state.